As long as there has been communication, there has been an interest in keeping some of this information confidential. As written messages became more widespread, especially over distances, people learned how susceptible this particular medium is to being somehow compromised: The messages can be easily intercepted, read, destroyed, or modified. Some protective methods were employed, such as sealing a message with a wax seal, which serves to show the communicating parties that the message is genuine and had not been intercepted. This, however, did nothing to actually conceal the contents.
This chapter explores some of the simplest methods for obfuscating the contents of communications. Any piece of written communication has some set of symbols that constitute allowed constructs, typically, words, syllables, or other meaningful ideas. Some of the simple methods first used involved simply manipulating this symbol set, which the cryptologic community often calls an alphabet regardless of the origin of the language. Other older tricks involved jumbling up the ordering of the presentation of these symbols. Many of these techniques were in regular use up until a little more than a century ago; it is interesting to note that even though these techniques aren't sophisticated, newspapers often publish puzzles called cryptograms or cryptoquips employing these cryptographic techniques for readers to solve.
Many books have been published that cover the use, history, and cryptanalysis of simple substitution and transposition ciphers, which we discuss in this chapter. (For example, some of the resources for this chapter are References [2] and [4].) This chapter is not meant to replace a rigorous study of these techniques, such as is contained in many of these books, but merely to expose the reader to the contrast between older methods of cryptanalysis and newer methods.
It's certain that, as long as people have been writing, people have been using codes to communicate — some form of writing known only to the communicating parties. For example, the two people writing each other secret letters might agree to write the first letter of each word last, or to exchange some letters for alternate symbols. Even many children experiment with systems and games of writing based on similar ideas.
The most basic kind of cipher is one in which a piece of text is replaced with another — these are called substitution ciphers. These can be single-letter substitutions, in which each letter in each word is exchanged one at a time, or whole-block substitutions, in which whole blocks of text or data are exchanged for other whole blocks (block ciphers, which are discussed in detail in Chapter 4).
One family of simple substitution ciphers related to the above is the family of monoalphabetic ciphers — ciphers that take the original message and encrypt it, one letter (or symbol) at a time, using only a single new alphabet to replace the old. This means that each character is encrypted independently of the previous letter, following the same rule. Since these rules must always translate a character in the same way every time, a rule can be represented as a new alphabet, so that a message can be encrypted via a conversion table between the two alphabets.
The simplest example of a monoalphabetic cipher is to perform a single shift on the alphabets. In other words, replace all a's with b's, b's with c's, and so forth, and wrap around the end so that z's are replaced with a's. This means that the word cat would be encrypted as DBU, and the word EPH would be decrypted as dog.
One of the first, and certainly the most widely known, monoalphabetic ciphers was one used by ancient Romans. It is affectionately called the Caesar cipher after the most famous of Romans [4]. This system was reportedly used to encrypt battle orders at a time when having the orders written at all was almost good enough to hide them from the average soldier, and it is extraordinarily simple. To obtain the ciphertext for a plaintext using the Caesar cipher, it is necessary simply to exchange each character in the plaintext with the corresponding character that occurs three characters later in the common order of the alphabet (so that a encrypts to D, b encrypts to E, etc., and wrapping around, so that x encrypts to A).
Naturally, getting the plaintext back from the ciphertext is simply a matter of taking each character and replacing it with the character that appears three characters before it in the common order of the alphabet (see Table 1-1).
For example, the text retreat would be encoded as UHWUHDW.
To decrypt a message, simply reverse the table so that d →a, e →b, and so on.
Table 1-1. Caesar Cipher Lookup Table
PLAINTEXT ↔ CIPHERTEXT | |||
|---|---|---|---|
a ↔ d | h ↔ k | o ↔ r | v ↔ y |
b ↔ e | i ↔ l | p ↔ s | w ↔ z |
c ↔ f | j ↔ m | q ↔ t | x ↔ a |
d ↔ g | k ↔ n | r ↔ u | y ↔ b |
e ↔ h | l ↔ o | s ↔ v | z ↔ c |
f ↔ i | m ↔ p | t ↔ w | |
g ↔ j | n ↔ q | u ↔ x | |
As a quick example, the text
the quick brown roman fox jumped over the lazy ostrogoth dog
can be easily encrypted by shifting each character three to the right to obtain
WKH TXLFN EURZQ URPDQ IRA MXPSHG RYHU WKH ODCB RVWURJRWK GRJ
However, as any person experienced in newspaper crypto-puzzles can tell you, one of the key features to breaking these codes is found in the placement of the spaces: If we know how many letters are in each word, it will help us significantly in guessing and figuring out what the original message is. This is one simple cryptanalytic piece of knowledge we can use right away — we are not encrypting the spaces! There are two solutions: We can either encrypt the spaces as an additional "27-th" letter, which isn't a terrible idea, or remove spaces altogether. It turns out that it makes slightly more sense, cryptanalytically speaking, to remove the spaces altogether. This does make it hard to read and write these codes by hand; thus, we often just remove the spaces but add in new ones at regular intervals (say, every four or five characters), giving us ciphertext such as
WKHTX LFNEU RZQUR PDQIR AMXPS HGRYH UWKHO DCBRV WURJR WKGRJ
When encrypted, the lack of the correct spaces in the ciphertext means nothing to either party. After decryption, though, when the party has plaintext with few spaces in the correct place, the inconvenience is usually minor, as most people can read the message anyway. The added security of removing all spaces from the plaintext before encryption is worth the small added difficulty in reading the message. The spaces added at regular intervals add no new information to the data stream and are therefore safe to keep.
With these examples, it is easier to see exactly what is meant by the term monoalphabetic. Essentially, to use a monoalphabetic cipher, we only need to consult a single lookup table. This will contrast shortly with other techniques, which consult multiple tables.
The Caesar cipher has a prominent flaw: Anyone who knows the cipher can immediately decrypt the message. This was not a concern to Caesar 2,000 years ago, as having the message in writing often provided sufficient subterfuge, considering the high illiteracy of the general population. However, the simplicity of the cipher allowed field commanders to be able to send and receive encrypted messages with relative ease, knowing that even if a message was intercepted and the enemy was literate, the opposition would have little hope of discovering the content.
As time progressed, more people became aware of the algorithm, and its security was therefore lessened. However, a natural evolution of the Caesar cipher is to change the way the letters are transformed into other letters, by using a different ordering of the alphabet.
But easily communicating an alphabet between two parties is not necessarily so easy. There are 26! = 403,291,461,126,605,635,584,000,000 different possible arrangements of a standard 26-letter alphabet, meaning that both sides would need to know the encrypting alphabet that the other was using in order to decrypt the message. If the two parties first agree on an alphabet as a key, then, since they both know the algorithm, either can send messages that the other can receive. However, if they number the alphabets individually, they would have an 89-bit key (since 26! ≈ 289), which is difficult to work with. Instead, most cryptographers would typically use a few simple transformations to the alphabet, and have a much smaller key.
For example, the most common method is simply to shift the letters of the output alphabet to the right or left by a certain number of positions. In this way, the Caesar cipher can be viewed as having a shift of +3. There are then 26 different keys possible, and it should be fairly easy for two parties to exchange such keys. Moreover, such a short key would also be easy to remember.
Other common transformations are typically a combination of the shifting operation above and another simple operation, such as reversing the order of the output alphabet [4].
To increase the number of alphabets available for easy use, a popular keying method is to use a keyword, such as swordfish, to generate an alphabet.
An alphabet can be derived, for example, by removing the letters in the keyword from the alphabet, and appending this modified alphabet to the end of the keyword. Thus, the alphabet generated by swordfish would be
swordfihabcegjklmnpqtuvxyz
Note that the second s was removed from the keyword in the alphabet and that the alphabet is still 26 characters in length.
There are a few disadvantages to using such a technique. For example, encrypting a message that contains the keyword itself will encrypt the keyword as a string of letters starting something along the lines of ABCDEFGH. Another, probably more severe disadvantage is that letters near the end of the alphabet will not be shifted at all unless the keyword has one or more characters appearing at the end of the alphabet, and even so, would then likely be shifted very little. This provides patterns for the experienced code breaker.
A modern example of a monoalphabetic cipher is ROT13, which is still used on the Internet, although not as much as it has been historically. Essentially, this is a simple cipher in the style of the Caesar cipher with a shift of +13.
The beauty of this cipher is in its simplicity: The encryption and decryption operations are identical. This fact is simply because there are 26 letters in the Latin alphabet (at least, the way we use it in English); thus, shifting twice by 13 yields one shift of 26, which puts things back the way they were. Also note that it doesn't matter in which "direction" we shift, since shifting left by 13 and shifting right by 13 always yield the same results.
But why use such an easy-to-break cipher? It's, in fact, trivial to break since everyone knows the cipher alphabet! Despite the fact that this style of cipher has been obsolete for centuries, ROT13 is useful to protect slightly sensitive discussions. For example, readers of a message board might discuss the endings of books using ROT13 to prevent spoiling the conclusion for others.
Looking through articles or posts on the Internet where sensitive topics might be displayed, and suddenly having the conversation turn into strange-looking garbage text in the middle (often with other parties replying in the exact same code) often means that the posters are writing in ROT13. Plus, ROT13 often has a very distinctive look that one can recognize after a while. For example, our standard text from above,
the quick brown roman fox jumped over the lazy ostrogoth dog
would display as
GUR DHVPX OEBJA EBZNA SBK WHZCRQ BIRE GUR YNML BFGEBTBGU QBT
when encrypted with ROT13.
I would like to delve into a language other than English for a moment, to show that these cryptographic (and later, cryptanalytic) techniques are not reliant on English, but can have similar properties in other languages as well, including even constructed languages. An example language that might be easy to follow is the Klingon language.
Klingon [1] (more properly, "tlhIngan Hol"), as seen in the Star Trek films and television shows, is an artificial language invented mostly by Marc Okrand using only common Latin characters and punctuation. This allows the use of encryption techniques similar to the ones we have used in English so far, showing some different properties of the language.
Table 1-2 shows all of the characters of tlhIngan Hol as they are commonly spelled in the Latin alphabet. From this table, we can then determine that the 25 characters, abcDeghHIjlmnopqQrStuvwy', are the only ones we should be seeing and therefore need to encrypt (note that English has 52 characters, if you include capital letters).
Using the character ordering of the previous paragraph, we can perform a ROT13 of the Klingon text:
Heghlu'meH QaQ jajvam
(In English, this translates as "Today is a good day to die.") After the ROT13, we obtain the enciphered text:
trStyIn'rt DoD wowjo'
We can naturally think of several ways to make the monoalphabetic cipher a more powerful encryption scheme without increasing its complexity too much. For example, why not use two different ciphers, and switch off every other letter? Or use three? Or more?
This would be an example of a polyalphabetic cipher. These began to be widely adopted over the past 500 years or so owing to the increasing awareness of how weak monoalphabetic ciphers truly are. There are a few difficulties in managing the alphabets. A key must be used to select different alphabets to encrypt the plaintext.
However, this necessitates an increase in key complexity. If a key represents some set of k alphabets, then there are (26!)k different sets of alphabets that could be chosen. (This is 26 factorial to the k -th power. In other words, take the number 26 and multiply it by 25, 24, and so on down to 2, and take that number, and multiply it by itself k times. With k = 1, this is about four hundred million billion billion, or a 4 followed by 23 zeros. The number of zeros roughly doubles with each increment of k.) To reduce this number, cryptographers often use a small number of alphabets based on easily remembered constructions (such as shifts and reversals of the normal alphabetic ordering), and use parts of the key to select alphabets used for substitution.
The most common table used to select alphabets is the famous Vigenère Tableau, as shown in Table 1-3. The Vigenère Tableau is a pre-selected set of alphabets, along with some guides to help encrypt and decrypt text characters if you know the key. When using the Vigenère Tableau to select alphabets for a polyalphabetic cipher, we obtain the Vigenère cipher. For this polyalphabetic cipher, the key is a word in the alphabet itself.
Encrypting a message using the Vigenère Tableau is fairly easy. We need to choose a keyword, preferably of short length to make it easy to remember which alphabet we are using at every point in the message. We then take our message and encrypt it character by character using the table and the current character of the keyword (start with the first of each). We merely look up the current character of the keyword in the left column of the Tableau.
To show an example, we can use our favorite phrase:
the quick brown roman fox jumped over the lazy ostrogoth dog
We then encrypt it with the key caesar to obtain the ciphertext:
VHI IUZEK FJONP RSEAE HOB BUDREH GVVT TLW LRBY SKTIQGSLH UQG
Table 1-3. The Vigenère Tableau
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z |
| b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z | a |
| c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z | a | b |
| d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z | a | b | c |
| e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z | a | b | c | d |
| f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z | a | b | c | d | e |
| g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z | a | b | c | d | e | f |
| h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z | a | b | c | d | e | f | g |
| i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z | a | b | c | d | e | f | g | h |
| j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z | a | b | c | d | e | f | g | h | i |
| k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z | a | b | c | d | e | f | g | h | i | j |
| l | m | n | o | p | q | r | s | t | u | v | w | x | y | z | a | b | c | d | e | f | g | h | i | j | k |
| m | n | o | p | q | r | s | t | u | v | w | x | y | z | a | b | c | d | e | f | g | h | i | j | k | l |
| n | o | p | q | r | s | t | u | v | w | x | y | z | a | b | c | d | e | f | g | h | i | j | k | l | m |
| o | p | q | r | s | t | u | v | w | x | y | z | a | b | c | d | e | f | g | h | i | j | k | l | m | n |
| p | q | r | s | t | u | v | w | x | y | z | a | b | c | d | e | f | g | h | i | j | k | l | m | n | o |
| q | r | s | t | u | v | w | x | y | z | a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p |
| r | s | t | u | v | w | x | y | z | a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q |
| s | t | u | v | w | x | y | z | a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r |
| t | u | v | w | x | y | z | a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s |
| u | v | w | x | y | z | a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t |
| v | w | x | y | z | a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u |
| w | x | y | z | a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v |
| x | y | z | a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w |
| y | z | a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x |
| z | a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y |
The preceding encryption mechanisms are all substitution ciphers, in which the primary operation is to replace each input character, in place, with some other character in a reversible way. Another general class of ciphers mentioned briefly above is transposition ciphers (or permutation ciphers), in which instead of characters being substituted for different ones, they are shuffled around without changing the actual characters themselves. This preserves the actual contents of the characters but changes the order in which they appear. For example, one of the simplest transposition ciphers is simply to reverse the characters in the string — cryptology becomes YGOLOTPYRC.
In order for a transposition cipher to be secure, its encryption mechanism can't be so obvious and simple as merely reversing the string, since even an amateur eye can easily see what is happening. In the following sections, we explore some of the more popular and effective methods of implementing transposition ciphers.
Probably the most common, simple transposition cryptographic method is the columnar transposition cipher. A columnar transposition works in the following way: We write the characters of the plaintext in the normal way to fill up a line of a rectangle, where the row length is referred to as k; after each line is filled up, we write the following line directly underneath it with the characters lining up perfectly; to obtain the ciphertext, we should read the text from top to bottom, left to right. (Often, spaces can be removed from the plaintext before processing.)
For example, to compute the ciphertext of the plaintext all work and no play makes johnny a dull boy with k = 6, write the message in a grid with six columns:
a l l w o r k a n d n o p l a y m a k e s j o h n n y a d u l l b o y
Now, reading from the first column, top to bottom, then the second column, and so forth, yields the following message. Spaces are added for clarity.
AKPKNL LALENL LNASYB WDYJAO ONMODY ROAHU
To decrypt such a message, one needs to know the number of characters in a column. Decryption is then just writing the characters in the same order that we read them to obtain the ciphertext, followed by reading the text left to right, top to bottom.
The key can then be viewed as the integer k, the number of columns. From this, we can calculate the number of rows (r) by dividing the message length by k and rounding up.
It does not take an advanced cryptanalyst to see an immediate problem with the above columnar transposition cipher — we can easily guess the number of columns (since it is probably a low number for human-transformable messages), or just enumerate all possibilities for k and then check to see if any words are formed by taking characters that are k.
To protect messages more without increasing the complexity of the algorithm too much, it is possible to use two columnar transpositions, one right after the other. We simply take the resulting ciphertext from the single columnar transposition above and run it through the columnar transposition again with a different value of k. We refer to these values now as k1 and k2.
For example, if we take the encrypted string, shown earlier, from all work and no play makes johnny a dull boy, encrypt it with k = 6 (as above, obtaining the ciphertext from the previous section), and encrypt it again with k2 = 8, we get:
ALYOA KEBNH PNWMU KLDON LYDLN JYLAA RASOO
To show how jumbled things get quite easily, we will take the plaintext P to be the alphabet:
abcde fghij klmno pqrst uvwxy z
Encrypting with k1 = 5, we get the ciphertext C1:
AFKPU ZBGLQ VCHMR WDINS XEJOT Y
And we encrypt the ciphertext C1 with k2 = 9 to obtain the next and final ciphertext C2:
AQNFV SKCXP HEUMJ ZROBW TGDYL I
In the previous sections, we explored the evolution of several simple cryptographic systems, many of which were used up until the previous century (and some still find limited use, such as ROT13). Now we will discuss the weaknesses in the above methods and how to defeat these codes.
The first topic we covered was monoalphabetic ciphers. These simple ciphers have several weaknesses, a few of which were alluded to previously. There are a few important tools and techniques that are commonly used in the evaluation and breaking of monoalphabetic ciphers, which we explore in the following sections.
The most obvious method is called frequency analysis — counting how often individual letters appear in the text.
Frequency analysis is based on patterns that have evolved within the language over time. Most speakers of English know that certain letters occur more often than others. For example, any vowel occurs more often than X or Z in normal writing. Every language has similar character properties like this, which we can use to our advantage when analyzing texts.
How? We simply run a counter over every character in the text and compare it to known samples of the language. For the case of frequency analysis, monoalphabetic ciphers should preserve the distribution of the frequencies, but will not preserve the matching of those relative frequencies to the appropriate letters. This is how these ciphers are often broken: trying to match the appropriate characters of a certain frequency in the underlying language to a similarly acting character in the ciphertext. However, not all ciphers preserve these kinds of characteristics of the origin language in the ciphertext.
A distribution of English is shown in Figure 1-1, which is derived from The Complete Works of William Shakespeare. The graph shows the frequency of each character in the Latin alphabet (ignoring case) in The Complete Works of William Shakespeare [3].
Each language has a unique footprint, as certain letters are used more than others. Again, in Figure 1-1, we can see a large peak corresponding to the letter E (as most people know, E is the most common letter in English). Similarly, there are large peaks in the graph around the letters R, S, and T.
For monoalphabetic substitution ciphers, the graph will be mixed around, but the frequencies will still be there: We would still expect to see a large peak, which will probably be the ciphertext letter corresponding to E. The next highest occurring letters will probably correspond to other high-frequency letters in English.
![Frequency distribution table for Shakespeare's complete works [3]. The letters are shown left to right, A through Z, with the y-value being the frequency of that character occurring in The Complete Works of William Shakespeare [3].](http://imgdetail.ebookreading.net/career_development/career_development_detail1_2/9780470135938/9780470135938__modern-cryptanalysis-techniques__9780470135938__figs__0101.png)
Figure 1-1. Frequency distribution table for Shakespeare's complete works [3]. The letters are shown left to right, A through Z, with the y-value being the frequency of that character occurring in The Complete Works of William Shakespeare [3].
Frequency distributions increase in utility the more ciphertext we get. Trying to analyze a five-letter word will have practically no information for us to derive any information about frequencies, whereas several paragraphs or more will give us more information to derive a frequency distribution.
Note, however, that just as frequency distributions are unique to languages, they can also be unique to particular samples of languages. Figure 1-2 shows a frequency analysis of the Linux kernel source code that has a different look to it, although it shares some similar characteristics.
One of the first questions we might ask is if a particular message is encrypted at all. And, if it is encrypted, how is it encrypted? Based on our discussion above about the different kinds of cryptography, we would want to know whether the message was encrypted with a mono- or polyalphabetic cipher so that we can begin to find out the key.
We can begin with the index of coincidence (the IC), a very useful tool that gives us some information about the suspect ciphertext. It measures how often characters could theoretically appear next to each other, based on the frequency analysis of the text. You can think about it as a measure of how evenly distributed the character frequencies are within the frequency distribution table — the lower the number, the more evenly distributed. For example, in unencrypted English, we know that letters such as E and S appear more often than X and Z. If a monoalphabetic cipher is used to encrypt the plaintext, then the individual letter frequencies will be preserved, although mapped to a different letter. Luckily, the I C is calculated so that the actual character does not matter, and instead is based on the ratio of the number of times the character appears to the total number of characters.

Figure 1-2. Frequency distribution table for "vanilla" Linux 2.6.15.1 source code (including only alphabetic characters). The total size is approximately 205 megabytes.
The index of coincidence is calculated by the following:
This means that we take each character in the alphabet, take the number of them that appear in the text, multiply by that same number minus one, and divide by the ciphertext length times the ciphertext length minus one. When we add all of these values together, we will have calculated the probability that two characters in the ciphertext could, theoretically, be repeated in succession.
How do polyalphabetic ciphers factor into this? In this case, the same letter will not be encrypted with the same alphabet, meaning that many of the letter appearances will be distributed to other letters in a rather random fashion, which starts to flatten out the frequency distribution. As the frequency distribution becomes flatter, the IC becomes smaller, since the amount of information about the frequencies is decreasing.
An adequate representation of the English language is The Complete Works of William Shakespeare [3]. We can easily calculate the index of coincidence, ignoring punctuation and spaces, by counting the occurrences of each character and applying the above formula. In this case, we calculate it to be approximately 0.0639.
While Shakespeare provides an interesting reference point and is fairly representative of English, it is necessary to consider the source of the message you are analyzing. For example, if your source text likely is C code, a better reference might be a large collection of C code, such as the Linux kernel. The Linux 2.6.15.1 kernel has an IC ≈ 0.0585. Or, if the text is in Klingon, we can take a sample size of Klingon with a few English loan words (taken from about 156 kilobytes of the Qo'noS Qonos), and find the IC ≈ 0.0496.
The theoretically perfect IC is if all characters occurred the exact same number of times so that none was more likely than any other to be repeated. This can be easily calculated. For English, since we have 26 characters in our Latin-based alphabet, the perfect value would be that each character occurs exactly 1/26-th of the time. This means that, in the above equation, we can assume that length = 26 × count(c) for all c.
This gives us the following formula to calculate the perfect theoretical maximum. We can assume that the count is n, to make the formula easier to read. To see what happens as we get more and more ciphertext, the counts will be more precise; therefore, we will assume that the amount of ciphertext is approaching an infinite amount.
We can simplify this a little (since we know that each part of the sum is always the same):
And we can even simplify a little further:
Most calculus courses teach L'Hôpital's Rule, which tells us that the above limit can be simplified again, giving our theoretical best:
IC = 1 / 26 ≈ 0.03846
This can be seen intuitively by the fact that, as n gets very large, the subtraction of the constant 1 means very little to the value of the fraction, which is dominated by the n/26 n part. This is simplified to 1/26.
Note that this technique does not allow us to actually break a cipher. This is simply a tool to provide us more information about the text with which we are dealing.
There are some proposed methods of strengthening basic ciphers (monoalphabetic, polyalphabetic, transposition, or others). See Reference [5] for some of these examples.
One very simple method is to throw meaningless characters called nulls into the ciphertext. For example, the character X does not appear very often in texts. Therefore, we could just throw the letter X randomly into the plaintext before encrypting. This technique isn't terribly difficult to spot: Frequency analysis will show a fairly normal distribution of characters, except for an extra, large spike in the distribution. Once any suspected nulls are removed, the analysis should be easier. Another common null is to remove spaces from the plaintext and add them to the ciphertext in a random, English-like manner.
Another popular mechanism is to use monophones — where one plaintext letter can be represented by more than one ciphertext letter. They can be chosen randomly or with some certain pattern. This is slightly more difficult to detect, since it will have the property of flattening the distribution a bit more. Since using monophones quickly depletes the normal alphabet, extra symbols can often be introduced.
The opposite of a monophone is a polyphone — where multiple plaintext characters are encoded to the same ciphertext character. This requires the receiver to know this is happening and be a bit clever about decrypting the message, since there may be multiple interpretations of the characters.
There are no good ways of automatically detecting and removing these security measures — a lot of them will involve a human using the preceding and following tools, along with practice, and simply trying out different ideas.
The key to breaking a polyalphabetic cipher of a keyed type (such as Vigenère) is to look for certain patterns in the ciphertext, which might let us guess at the key length. Once we have a good guess for the key length, it is possible to break the polyalphabetic ciphertext into a smaller set of monoalphabetic ciphertexts (as many ciphertexts as the number of characters in the key), each a subset of the original ciphertext. Then, the above methods, such as frequency analysis, can be used to derive the key for each alphabet.
The questionis, how do we guess at the key length?There are two primary methods: The first is a tool we described above — the index of coincidence.
As stated above, the index of coincidence is the probability of having repeated characters and is a property of the underlying language. After a text has been run through a monoalphabetic cipher, this number is unchanged. Polyalphabetic ciphers break this pattern by never encrypting repeated plaintext characters to be the same character in the ciphertext. But the index of coincidence can still be used here — it turns out that although the ciphers eliminate the appearance of repeated characters in the plaintext being translated directly into the ciphertext, there will still be double characters occurring at certain points. Ideally (at least from the point of view of the person whose messages are being cracked), the index of coincidence will be no better than random (0.03846). But, luckily (from the viewpoint of the cryptanalyst), the underlying language's non-randomness comes to the rescue, which will force it into having a non-perfect distribution of the repeated characters.
Just as longer keys for polyalphabetic ciphers tend to flatten out the frequency distributions, they also flatten out the non-random measurements, such as the index of coincidence. Hence, a smaller key will result in a higher index of coincidence, while a longer key gives us an index of coincidence closer to 0.03846. Table 1-4 shows us the relationship between the number of characters in the key and the index of coincidence.
As can be seen, the measurement starts to get pretty fuzzy with key lengths of around six or so characters. Without a great deal of ciphertext, it becomes very difficult to tell the difference between a polyalphabetic key length of six and seven, even.
We clearly cannot rely completely on the IC for determining the key length, especially for smaller amounts of ciphertext (since it is only effective with large amounts of text, and not very precise for larger keys). Luckily, we have another method for guessing at the likely key length.
Friedrich Kasiski discovered that there is another pattern that can be seen, similar to the index of coincidence [4]. In English, for example, the is a very common word. We would, therefore, assume that it will be encrypted multiple times in a given ciphertext. Given that we have a key length of n, wecanhope that we will have the word the encrypted at least n times in a given ciphertext. Given that it is encrypted at least that many times, we will be guaranteed to have it be encrypted to the exact same ciphertext at least twice, since there are only n different positions that the can be aligned to with regard to the key.
We know that we can expect there to be repetitions of certain strings of characters of any common patterns (any common trigraphs, e.g.). But what does this reveal about the key? This will actually give us several clues about the length of the key.
Table 1-4. Relationship between Key Length of a Polyalphabetic Cipher and the Resulting Index of Coincidence of the Ciphertext in The Complete Works of William Shakespeare [3]
KEY LENGTH | APPROXIMATE IC |
|---|---|
1 | 0.0639 |
2 | 0.0511 |
3 | 0.0468 |
4 | 0.0446 |
5 | 0.0438 |
6 | 0.0426 |
7 | 0.0423 |
8 | 0.0417 |
9 | 0.0412 |
10 | 0.0410 |
... | ... |
∞ | 0.0384 |
If we are very certain that two repetitions of ciphertext represent the exact same plaintext being encrypted with the same pieces of the key, and we know that the key is repeated (such as in Vigenère) over and over again, this means that it must be repeated over and over again in between those two pieces of ciphertext. Furthermore, it means that they were repeated an integral number of times (so that it was repeated 15 or 16 times, but not 14.5). Therefore, we calculate the difference in the positions of the two pieces of ciphertext, and we know that this must be a multiple of the length of the ciphertext. Given several of these repetitions, and several known multiples of the length of the cipher key, we can start to hone in on the exact length of the key.
A good example may help clear up what is going on. The following plaintext is from the prologue to Romeo and Juliet [3]:
twoho useho ldsbo thali keind ignit yinfa irver onawh erewe layou rscen efrom ancie ntgru dgebr eakto newmu tinyw herec ivilb loodm akesc ivilh andsu nclea nfrom forth thefa tallo insof these twofo esapa irofs tarcr ossdl overs taket heirl
We can encrypt this using the key romeo (the key in this case has length 5), to obtain the following ciphertext:
KKALC LGQLC CREFC KVMPW BSURR ZUZMH PWZJO ZEHIF FBMAV VFQAS COKSI IGOIB VTDSA RBOMS EHSVI UUQFF VOWXC ESIQI KWZCK YSDIQ ZJUPP CCAHA RYQWQ ZJUPV RBPWI EQXIO ETDSA WCDXV KVQJO KOXPC ZBEST KVQWS KKAJC VGMTO ZFAJG KODGF FGEHZ FJQVG KOWIH YSUVZ
These repetitions occur at the paired positions:
(0, 160), (34, 169), (61, 131), (99, 114), (140, 155), (174, 189)
This corresponds to differences of 160, 135, 70, 15, 15, and 15. We can factor these, giving us 160 = 2 × 2 × 2 × 2 × 2 × 5, 135 = 3 × 3 × 3 × 5, 70 = 2 × 5 × 7, and 15 = 3 × 5.
The only common factor of all of them is 5. Furthermore, the sequence with difference 15 occurs many times (once with five-character repetition), and 70 occurs with a four-character repetition, giving us strong evidence that the key length is a common factor of these two numbers.
Now that we know how many different alphabets are used, we can split the ciphertext into many ciphertexts (one for each character in the key), and then perform frequency analysis and other techniques to break these ciphers. Note that each of these ciphertexts now represents a monoalphabetic substitution cipher.
Breaking the simple transposition ciphers is not incredibly difficult, as the key space is typically more limited than in polyalphabetic ciphers (the key space being the total possible number of distinct keys that can be chosen). For example, the key space here is limited by the size of the grid that the human operator can draw and fill in reliably.
The preferred method is performing digraph and trigraph analysis, particularly by hand.[9] A digraph is a pair of letters written together. Similarly, a trigraph is a set of three letters written together. All languages have certain letter pairs and triplets that appear more often than others. For example, in English, we know that characters such as R, S, T, L, N, and E appear often — especially since they appear on Wheel of Fortune 's final puzzle — thus it should come as no shock that letter pairs such as ER and ES appear often as well, whereas letter pairs such as ZX appear very infrequently. We can exploit this property of the underlying language to help us decrypt a message. Tables 1-5 and 1-6 show some of the most common digraphs and trigraphs for English (again, from Shakespeare) and Klingon, respectively.
Table 1-5. Most Common Digraphs and Trigraphs in The Complete Works of William Shakespeare
DIGRAPH | PROBABILITY | TRIGRAPH | PROBABILITY |
|---|---|---|---|
| 3.16% |
| 1.45% |
| 2.28% |
| 0.87% |
| 1.63% |
| 0.58% |
| 1.62% |
| 0.53% |
| 1.47% |
| 0.50% |
| 1.45% |
| 0.48% |
| 1.27% |
| 0.48% |
| 1.27% |
| 0.41% |
| 1.24% |
| 0.40% |
| 1.24% |
| 0.38% |
| 1.24% |
| 0.37% |
| 1.19% |
| 0.35% |
| 1.14% |
| 0.34% |
| 1.07% |
| 0.33% |
| 1.02% |
| 0.32% |
| 1.01% |
| 0.31% |
How exactly do we exploit these language characteristics? This isn't terribly difficult, even without a computer. The trick is to write out two or more copies of the ciphertext vertically, so that each ciphertext strip looks like
We take out the two or more copies of this sheet we have made, and line them up side by side. We then use the sliding window technique — essentially moving the sheets of paper up and down with respect to each other. Then we measure how common the digraphs (and trigraphs with three letters, or 4-graphs with four letters, etc.) found in the resulting readout are. Next, we measure how far apart they are (in characters), and this length will be the number of rows (represented as r) in the matrix used to write the ciphertext. We then calculate the number of columns (based on dividing the ciphertext
Table 1-6. Most Common Digraphs and Trigraphs in Klingon, Taken from Qo'noS QonoS Sample
DIGRAPH | PROBABILITY | TRIGRAPH | PROBABILITY |
|---|---|---|---|
| 2.53% |
| 1.44% |
| 2.27% |
| 0.71% |
| 1.71% |
| 0.58% |
| 1.57% |
| 0.57% |
| 1.49% |
| 0.53% |
| 1.44% |
| 0.50% |
| 1.21% |
| 0.50% |
| 1.15% |
| 0.49% |
| 1.14% |
| 0.45% |
| 1.13% |
| 0.41% |
| 1.13% |
| 0.41% |
| 1.02% |
| 0.38% |
| 0.99% |
| 0.37% |
| 0.91% |
| 0.36% |
| 0.91% |
| 0.35% |
| 0.87% |
| 0.34% |
size by the number of rows and rounding up), so that we have the original key (k, the number of columns).
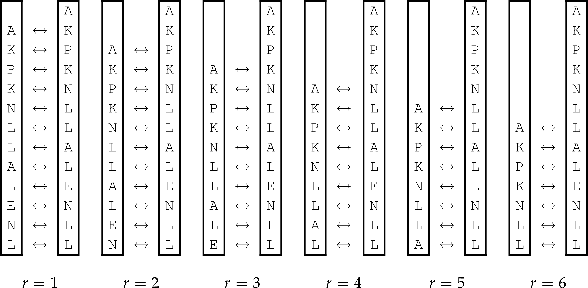
To show this method, let's take the first transposition-cipher example ciphertext (from Section 1.4.1) and show how to break it using the sliding window technique. The ciphertext obtained from encrypting "all work and no play ..." was
AKPKNL LALENL LNASYB WDYJAO ONMODY ROAHU
The sliding windows for this ciphertext are shown in Figure 1-3.
Examining the example in Figure 1-3 can reveal a great deal about the best choices. Looking at r = 1, we have letter pairs in the very beginning such as KP and PK. We can consult a table of digraphs and trigraphs to check to see how common certain pairs are, and note that these two letter pairs are veryinfrequent. For r = 2, letter pairs such as KK and PN are also fairly uncommon. It would not be too difficult to create a simple measurement of, say, adding up the digraph probabilities with all of the pairs in these examples, and comparing them.
However, a word of caution is necessary — since we removed all of the spaces, there is no difference between letter pairs inside a word and letter pairs between words. Hence, the probabilities will not be perfect representations, and we cannot simply always go for the window with the highest probability sum.
It is also useful to note that digraphs and trigraphs can also be easily used for helping to break substitution ciphers. If we calculate the most common digraphs and trigraphs appearing in a ciphertext, then we can see if those correspond to common digraphs and trigraphs in the assumed source text.
Breaking double columnar transposition ciphers is still possible by hand, but a little more complex to work out visually, as we did with the sliding window technique for single columnar ciphers. The operations required are much more suited to computers, because of the large amount of bookkeeping of variables and probabilities.
The primary technique for breaking the double transposition ciphers is the same, in theory, as the sliding window technique: We want to simulate different numbers of columns and calculate the digraph, trigraph, and so on probabilities from these simulations. For double (or even higher-order) transposition ciphers, we simply have to keep track of which character winds up where.
It is best to examine these ciphers slightly more mathematically to understand what is going on. Let's assume that we have ciphertext length n, with k1 being the number of columns in the first transposition and r1 being the number of rows in the first transposition (and similarly, k2 and r2 for the second transposition).
In all cases, to our luck, the character in position 0 (computer scientists all start to count from 0) always stays in position 0. But after the first transposition, the character in position 1 ends up in position r1. The character in position 2 ends up in position 2 r1. Going further, the character in position k1 − 1 ends up in position (k1 − 1) r1. The next position, k1, falls under the next row, and therefore will end up in position 1. Then k1 + 1 ends up in position r1 + 1. In general, we might say that a ciphertext bit, say, P [i], ends up in position C1 [i/k1] + (i mod k1) r1]. Here, "mod" is simply the common modulus operator used in computer programming, that is, "a mod b" means to take the remainder when dividing a by b. The x operation (the floor function) means to round down to the smallest integer less than x (throwing away any fractional part), for example, [1.5] = 1, [−2.1] = −3, and [4] = 4.
Things start to get jumbled up a bit more for the next transposition. Just as before, the character in position 1 ends up in position r2, but the character that starts up in position 1 is C1[1], which corresponds to P [k1].
We can draw this out further, but it's needlessly complex. Then we can simply write out the two formulas for the transformation, from above:
P[i] = C1 [i/k1] + (i mod k1)r1]
C1[i] = C2 [i/k2] + (i mod k2)r2]
Now we have equations mapping the original plaintext character to the final ciphertext character, dependent on the two key values k1 and k2 (since we can derive the r-values from the k-values). In order to measure the digraph (and other n-graph) probabilities, we have to check, for each k1 and k2 guess, the digraph possibility for P [i] and P [i + 1] for as many values of i as we deem necessary.
For example, to check values i = 0 and i = 1 for, say, k1 = 5 and k2 = 9, we then run through the numbers on the previous double columnar transposition cipher used (the alphabet, thus n = 26). We know that P [0] = C1[0 + 0] = C1[0] = C2[0 + 0] = C2[0] = A, just as it should be. We can then calculate P[1] = C1[0 + 1 ×r1] = C1[r1] = C2[r1/9] + (r1 mod 9) ×r2]. Knowing that r1 = [26/k1] = [26/5] = 6 and r2 = [26/k2] = [26/9] = 3, we have P[1] = C2[0 + 6 · 3] = C2 [18] = B. Although performing digraph analysis would be useless on this ciphertext (since the plaintext is not from common words, but simply the alphabet), we could easily then calculate the digraph probability for this pair. Also, this pair ensures that the calculations came out correctly, since the alphabet was encrypted with those two keys in that order, and we know that the first two characters in the plaintext were ab.
In this chapter, we discussed many techniques used regularly throughout civilization until the start of the twentieth century. As can be seen from the demonstrated analysis, the encryption techniques are very weak from a modern standpoint, although easy to implement. However, the ideas behind these ciphers, including substitutions and transpositions, represent the core of modern ciphers, and we can learn a lot by studying the analyses of these now mostly defunct ciphers.
Furthermore, we looked at many of the simple cryptanalytic methods used to break apart these cryptographic schemes. Although modern ciphers are not this easy to break, analyzing these ciphers illustrates ideas that resonate throughout the rest of the book. Particularly, it is important to know that ciphers are not broken by accident — it takes a lot of work, patience, cleverness, and sometimes a bit of luck.
Exercise 1. The following message is encrypted with a monoalphabetic cipher. Ignoring spaces and punctuation, decrypt the message.
WKH FDW LQ WKH KDW VWULNHV EDFN
Exercise 2. Write a program to find the most common digraphs in a Latin-based alphabet, ignoring everything except alphabetic characters.
Exercise 3. Write a program to find the most common trigraphs in a non-Latin-based language (say, using Unicode).
Exercise 4. Write a program to use a dictionary file (a listing of valid words in the appropriate language) to break single transposition ciphers. Your program should work by choosing the decryption with the highest number of dictionary words formed. Such dictionary files can either be compiled (by finding a large enough source of similar text to the kind being analyzed, and making a list of the words found in it), or by using a pre-constructed dictionary file.
Exercise 5. Implement Kasiski's method for breaking polyalphabetic ciphers. The first step should be producing a candidate list of numbers that could be the key length. Then, assuming that the underlying cipher is a Vigenère polyalphabetic cipher, attempt to break the ciphertext into multiple ciphertexts and perform a frequency analysis on each. The program should produce a reasonable guess to a certain selection of keys, as well as accompanying plaintexts. Use of a dictionary file is encouraged to increase the precision.
References
[9] A computer program could easily try every value of the key and analyze each decrypted text to see if it makes sense in the language, for example, by dictionary lookups. This method would also work on any other small key space, such as monoalphabetic shift ciphers.
[10] [1] Marc Okrand.The Klingon Dictionary. (Pocket Books, New York, 1992).
[11] [2] Charles P. Pfleeger.Security in Computing, 2nd ed. (Prentice-Hall, Upper Saddle River, NJ, 2000).
[12] [3] William Shakespeare.The Complete Works of William Shakespeare. (Project Gutenberg, 1994); http://www.gutenberg.org.
[13] [4] Simon Singh.The Code Book. (Anchor, New York, 2000).
[14] [5] Jeff Thompson. Monoalphabetic cryptanalysis. Phrack Magazine, 51 (September 1997); www.phrack.org/issues.html?issue=51.