The previous chapter used a hefty dose of mathematics to develop some nice cryptographic algorithms, which are still used today. Now, we are going to look at methods used to break these algorithms.
To quickly review from the end of the last chapter, factoring and discrete logarithms represent two classes of problems of growing importance in cryptanalysis. A growing number of ciphers rely on the difficulty of these two problems as a foundation of their security, including number theoretic ciphers such as RSA and algebraic ciphers such as the Diffie-Hellman key exchange algorithm. The methods themselves aren't secure; they rely on the fact that both factoring and the discrete logarithm are difficult to do for very large numbers. To date, no methods are known to solve them very quickly for the key sizes typically used.
The algorithms here may not be suitable for breaking many in-use implementations of algorithms like RSA and Diffie-Hellman, but it is still important to understand how they work. Any future developments in the fields will likely build on this material.
Factorization refers to the ability to take a number, n, and determine a list of all of the prime factors of the number. For small numbers, we can just start going through the list of integers and seeing if they divide into n. However, this method doesn't scale well, since the numbers we are often concerned with are hundreds of digits long — of course, these numbers are hundreds of digits long merely because that is the time-security tradeoff point, since the algorithms presented here start to drag their feet, so to speak, around that point.
In the previous chapter we learned about RSA, which uses exponentiation of numbers by public and private exponents. If we recall, the first step in the RSA algorithm to create these exponents is to construct a number n = pq, where p and q are both large prime numbers. Since we know p and q, we can calculate the totient of n, ø(n)= (p − 1), which we then use to find two numbers,e and d, such that ed ≡ 1 (mod (p − 1)(q − 1)). The numbers e and n will be made public and can be used to communicate securely with anyone who knows d and n. However, if anyone were to be able to factor n into its two prime factors, then they could easily calculate d using the extended Euclidean algorithm (as that is exactly how d was originally derived), allowing them to read any messages encrypted with e and n.
RSA is therefore very reliant on factoring large values of n to be a difficult problem, or its security will be compromised. The following sections discuss the fundamental algorithms for factoring numbers.
Note that there are, theoretically, other ways to break RSA. For instance, since an attacker has access to the public key, (e, n), then he could take a message (perhaps a very cleverly constructed message) and encrypt it, knowing that when this encrypted message is encrypted again with the private key, and therefore exponentiated by d modulo n, there may be some clever way to derive d. However, at this time, no such method is known.
Just as this is not a book on mathematics, it is also not a book on the algorithm theory. Hence, we will not require the reader to have a great deal of understanding of the methods used to determine the exact running time and storage requirements of any of the algorithms we will be discussing. However, it is important to have a decent understanding of how the various algorithms compare to each other.
Algorithmic running time and storage space are often written in terms of order, also known as "Big-Oh" notation, like O (1) and O (n2), where n is usually our input size. For an algorithm to have a worst-case running time of, say, O (n), means that, roughly speaking, the algorithm will terminate within some fixed multiple of n steps (i.e., proportional to the size of the input). Naturally, if an algorithm has, say, O (n2) storage requirements in the worst-case scenario, it will require, at most, some fixed multiple of n2 (i.e., proportional to the square of the size of the input).
For example, suppose we devised a method for testing to see if a number is even by dividing it by 2, using the long-division method everyone learned in elementary school. For the sake of this, and other algorithms in this chapter, we let n be the size of the number in terms of digits. For example, 12345 has length 5 in decimal, or length 14 in binary; the two numbers will always differ by about 1/log 2 ≈ 3.322, because of using logarithms[33] to convert bases; thus, it doesn't affect our running time to use one or the other, since an order expressed in one will always be a constant multiple of the other, and hence have the same order in Big-Oh notation. In this book, we typically use key size in terms of the number of bits.
The previous simple division algorithm has a running time of O (n) and storage requirements of O (1). Why? Because the standard division algorithm we learn early on is to take each digit, left to right, and divide by 2, and then take the remainder, multiply by 10, and add it to the next digit, divide again, and so on. Each step takes about three operations, and there will about the same number of steps as there are digits, giving us about 3 n operations or thereabouts — this is a simple multiple of n; thus, our running time is O (n). Since we didn't have to keep track of more than one or two variables other than the input, we have a constant amount of storage. Algorithms with O (n) running time are typically called linear algorithms.
This is a suboptimal algorithm, though. We might also recall from elementary school that the last digit can tell us if a number is even or odd. If the last digit is even, the entire number is even; otherwise, both are odd. This means that we could devise an O (1) even-checking algorithm by just checking the last digit. This always takes exactly two operations: one to divide, and one to check if the remainder is zero (the number is even) or one (the number is odd). Algorithms that run in less than O (n) time are called sublinear.
Who needs all that input anyway, right? It's just taking up space. If an algorithm runs in O (np) time, where p is some fixed number, then it is said to be a polynomial-time algorithm. This is an important class, often denoted simply as P. The reason this class is important is because it is merely a polynomial-time algorithm — other worse-performing classes of algorithms exist, known as superpolynomial-time algorithms. For example, the class of algorithms that can be bounded in O (an) time (for some number a) is called an exponential-time algorithm. In general, superpolynomial- and exponential-time algorithms take significantly longer to run than polynomial-time algorithms. Algorithms that take less than an exponential of n to finish are called subexponential. Figure 3-1 shows the running time of the various classes of algorithms.
There is also another way to analyze an algorithm: by its storage complexity. Storage complexity is, for most of the algorithms we are considering, not too much of a concern. However, requiring large amounts of storage can quickly become a problem. For example, we could just pre-compute the factors for all numbers up to some extremely large value and store this, and then we would have a very small running time (only as long as it takes to search the list) for finding the factors of a number. However, the pre-computation and storage requirements make this technique silly.
We will see this kind of concept used in a more clever way in Chapter 5.

Figure 3-1. The running time of algorithms for order O (n) (linear and polynomial), O (4eln n ln ln n) (subexponential), and O (2n) (exponential) for various values of n.
There is another important notion in understanding algorithms: writing them out clearly, and unambiguously. For doing so, authors typically take one of three approaches: picking a programming language du jour to write all examples in, inventing a programming language, or writing everything in various forms of pseudocode (writing out the instructions in some mesh of natural language and a more formal programming language).
The first approach, picking a popular or well-known language, has an obvious disadvantage in that it dates a book immediately: a book written 40 years ago might have used FORTRAN or ALGOL to implement its algorithms, which would be difficult for many readers to understand. The second approach can be all right, but it requires that the reader learn some language that the author thinks is best. This approach can have mixed results, with some readers distracted so much by learning the language that they do not comprehend the text.
The final approach is often used, especially in abstract books. While usually very clear, it can sometimes be a challenge for a programmer to implement, especially if important details are glossed over.
The approach we use in this book is to have a combination of pseudocode and writing out in an actual programming language. The pseudocode in this and the following chapters is very simple: I merely state how a program would operate, but in mostly plain English, instead of some abstract notation. The intent of this book is not to alienate readers, but to enlighten.
For some examples, I will like a reader to be able to easily see an algorithm in action and to have some kind of source code to analyze and run. When these situations arise, I implement in a language that, in my opinion, has a complete, free version available over the Internet; is easy to read even if the reader is not fluent in the language; and in which the reader won't get bogged down in housekeeping details (like #include <stdio.h>-like statements in C, import java.util.*; statements in Java, etc.). A few languages fulfill these requirements, and one that I like in particular is Python.
If you are not familiar with Python, or Python is long forgotten in the tomes of computing history when this book is read, the implementations in Python should be simple enough to easily reproduce in whatever language you are interested in.
We shall start with a very, very short course in Python syntax and a few tricks. This is by no means representative of all of Python, nor even using all of the features of any given function, but merely enables us to examine some simple programs that will work and are easy to read.
A typical Python program looks like that shown in Listing 3-1.
Example 3-1. A simple program in Python. The brackets inside quotes indicate a space character
x = 5 y = 0foriinrange(0, 4): y = y + x
The output of the program in Listing 3-1 will be
x = 5 y = 0 x = 5 y = 5 i = 0 x = 5 y = 10 i = 1 x = 5 y = 15 i = 2 x = 5 y = 20 i = 3 x = 5 y = 20
We don't want to get bogged down in too many details, but a few things are worth noting. Assignments are done with the simple = command, with the variable on the left and the value to put in on the right.
Program structure is determined by white space. Therefore the for loop's encapsulated code is all the code following it with the same indentation as the line immediately following it — no semicolons or braces to muck up.
The for loop is the most complicated thing here. It calls on the range function to do some of its work. For our uses, range takes two arguments: the starting point (inclusive) and the ending point (not inclusive), so that in Listing 3-1, range(0, 4) will expand to [0, 1, 2, 3] (the Python code for an array).
The for loop uses the in word to mean "operate the following code one time for each element in the array, assigning the current element of the array to the for-loop variable." In Listing 3-1, the for-loop variable is i. The colon is used to indicate that the for line is complete and to expect its body immediately after.
The only other thing to mention here is the print statement. In the case I provided above, we can print a literal string, such as "x = ", or a value (which will be converted to a string). We can print multiple things (with spaces separating them) by using a comma, as is shown above.
Let's go through one more quick example to illustrate a few more concepts.
Example 3-2. A factorial function written in Python.
deffactorial(n):ifn == 0orn== 1:return1else:returnn * factorial(n - 1) x = 0 f = 0whilef < 100: f = factorial(x)
The program shown in Listing 3-2 will have the following output:
1 1 2 6 24 120
This program gives a taste of a few more tools: functions, conditionals, and the while loop.
Functions are defined using the def statement, as in the above example (its parameters specified in parentheses after the function name). Values of functions are returned using the return statement.
Conditionals are most commonly performed using if statements. The if statement takes an argument that is Boolean (expressions that return true or false), such as a comparison like == (equals) and < (less than), and combinations of Booleans, combined using and and or. There can be an optional else statement for when the if's condition evaluates to false (and there can be, before the else, one or more elif, which allow additional conditionals to be acted on).
Finally, we have another loop, the while loop. Simply put, it evaluates the condition at the beginning of the loop each time. If the condition is true, it executes the loop; if false, it breaks out and continues to the next statement outside the loop.
Python automatically converts fairly well between floating point numbers, arbitrarily large numbers, strings, and so on. For example, if we used the above code to calculate factorial(20), we would simply obtain
2432902008176640000L
The L on the end indicates that the result is a large integer (beyond machine precision). No modification of the code was necessary — Python automatically converted the variables to these large-precision numbers.
I'll spread a little Python here and there throughout this and later chapters to have some concrete examples and results. The rest of this chapter is devoted to algorithms for factoring integers and solving discrete logarithm problems, of different complexities and speeds.
When we refer to the speeds of the factoring methods, we are usually concerned not so much with the number itself, but with its size, typically in binary. For example, the number 700 (in decimal) would be written in binary as
10 1011 1100
Thus, 700 takes 10 bits to represent in binary. In general, we can use the logarithm function to calculate this. The base 2 logarithm calculates what power of 2 is required to get the desired number. With the above example, we can calculate
log2 700 ≈ 9.4512
We round this up to determine the number of bits needed to represent the number, which is 10 bits.[34]
Since, by nature, we do not know the actual number to be factored, but we can generally tell the size of the number, this is how we categorize factorization algorithms. Categorizing them by this method also lets us see how well the algorithms do when the numbers start to get very large (hundreds or thousands of digits).
This chapter is concerned with exponential-time algorithms. As we defined earlier, this means that the algorithm running time will be O (an), where n is the size of the number (in bits) and a is some number greater than 1.
Exponential factoring methods are often the easiest to understand. Unfortunately, while they are simple and often elegant, they are also incredibly slow. Nevertheless, some have advantages over even the fastest algorithms in some circumstances.
Brute-force algorithms are usually the simplest method to solve most problems with a known set of solutions: just try every possible solution. Brute-force's motto is, if we don't know where to start, just start trying. Throw all of your computing power at the problem, and hope to come out on top!
The natural way to brute-force factors? Just try them all. Well, maybe not every number. If you have divided a number by 2 and found it is not divisible, it's fairly pointless to divide it by 4, 6, 8, and all the rest of the multiples of 2. It is similarly pointless to divide by 3 and then by 6, 9, 12, and the rest of the multiples of 3, and if we follow suit, then with the multiples of the rest of the numbers we try.
Therefore, we will limit ourselves to merely trying all of the prime numbers and dividing our target number by each prime. If the division succeeds (i.e., no remainder), then we have a factor — save the factor, take the result of the division (the quotient), and continue the algorithm with the quotient. We would start with that same factor again, since it could be repeated (as in 175 = 5 × 5 × 7).
This technique provides an upper-bound on the amount of work we are willing to do: If any technique takes more work than brute forcing, then the algorithm doesn't work well.
An immediate assumption that many make when naively implementing this algorithm is to try all prime numbers between 1 and n − 1. However, in general, n − 1 will never divide n (once n > 2). As the numbers get larger, then n − 2 will never divide n, and so forth. In general, the largest factor that we need to try is
The only other small trick is the ability to find all of the prime numbers in order to divide by them. Figure 3-2 shows an example of brute-force factorization using such a list. Although for smaller numbers (only a few digits), the list of primes needed would be small, it would be prohibitive to have a list of all the prime numbers required for large factorization lying around. Furthermore, even checking to see if a large number is prime can be costly (since it would involve a very similar algorithm to that above).
The answer is that we would just hop through the list of all integers, skipping ones that are obviously not primes, like even numbers, those divisible by three, and so forth. For more details on implementations and behavior of this algorithm, see Reference [6].
We leave it as an exercise to the reader to implement the brute-force algorithm.
In order to see how much time this takes to run, we need to know how many prime numbers there are. We could simply count them, which would be the only exact method. But there is a well-known rough approximation, saying that if we have a number a, then there are approximately
prime numbers less than or equal to a. In reality, there are a bit more than this, but this provides a good lower bound. In terms of the length of a (in binary digits), we have n = log2a digits.
The running time will then be one division operation per prime number less than the square root of the number a, which has n/ 2 digits. Therefore, dividing by every prime number of less than
The storage requirements for this are simply storing the factors as we calculate them, and keeping track of where we are. This won't take up too much space; thus, we need not be worried at this point.
As terrible as this may seem when compared to other algorithms in terms of time complexity, it has the advantage that it always works. There is no randomness in its operation, and it has a fixed, known upper-bound. Few other algorithms discussed here have these properties. Also, other algorithms are not guaranteed to find complete prime factorizations (whereas this one does) and often rely on trial division to completely factor numbers less than some certain bound.
A method attributed to Fermat in 1643 [6] uses little more than normal integer arithmetic to siphon large factors from numbers. In fact, it doesn't even use division.[35]
The algorithm works from a fact often learned in basic algebra:
(x + y) (x − y) = x2 − y2
for any integers x and y. Fermat theorized using this to factor a number: If we can discover two squares such that our target number (a) is equal to the difference of the two squares (x2 −y2), we then have two factors of the n, namely, (x + y) and(x − y).
Fermat's method just tries, essentially, to brute-force the answer by going through the possible squares and testing them. The algorithm is written out concisely in Reference [15], although I have changed some of the variable names for the following:
Fermat's Difference of Squares. Take an integer, a, to factor. The goal is to calculate x2 and y2 so that (x + y)(x −y) = x2 −y2 = a. In the following, d = x2 − a (which should, eventually, be equal to y2).
Set x to be
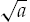
Set t = 2x + 1.
Set d = x2 − a.
In the algorithm, d will represent x2 − a, the difference between our current estimate of x2 and a, and thus will represent y2 when we have found the correct difference of the squares. This means that d is positive (if a is not a perfect square in the first step) or zero (if a is a perfect square).
Make t the difference between x2 and the next square: (x + 1)2 = x2 + 2 x + 1, and hence the difference is 2x + 1 to start with. The next square will be (x + 2)2 = x2 + 4x + 4, which is 2x + 3 more than the last. Following this trend (which can be verified using calculus), the difference between the squares increases by 2 each time.
If d is a square (

Set d to d + t. We are adding in the distance to the next x2 attempt to the difference of x2 − a.
This works because we already have (x + c)2 − a (for some c, the current step), and we wish to calculate [(x + c) + 1]2 − a = (x + c)2 + 2(x + c) + 1 − a = (x + c)2 − a + 2x + (2c + 1) = d + 2x + 2c + 1, the next value of d. We use the value oft to stand in for 2x + 2c + 1, which increases by 2 every time, since c increases by 1 with each step.
Set t to t + 2. The distance between the next pair of squares is increased by 2 each time.
Go to Step 4a.
Set x to
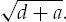
Set y to be

Return two factors, x + y and x − y.
For a simple example, Figure 3-3 shows this algorithm being run on the number 88.
Pollard has come up with several very clever mechanisms for factoring integers, as well as other ones we shall study below in this chapter.
Pollard's rho (ρ) method works by finding cycles in number patterns. For example, using the modular arithmetic from the previous chapter, we may want to successively square the number, say, 2, repeatedly modulo 14. This would result in a sequence
2, 4, 8, 2, 4, 8,...
This sequence repeats itself forever. Pollard figured out a way to have these sequences give us clues about the factors of numbers.
We'll show the algorithm, and then explain the nifty trick behind it.
Pollard's ρ. Factors an integer, a.
Set b to be a random integer between 1 anda − 3, inclusive.
Set s to be a random integer between 0 anda − 1, inclusive.
Set A = s.
Set B = s.
Define the function f (x) = (x2 + b) mod a.
Let g = 1.
If g ≠ 1, then go to Step 8.
Set A = f (A).
Set B = f (f (B)).
Set g = gcd(A −B, a).
Repeat (go to Step 7).
If g is less than a, then return g. Otherwise, the algorithm failed to find a factor.
Why does this work? Well, the first leap of faith is that the function f (x) will randomly jaunt through the values in the field. Although it is fairly simple (just a square with a constant addition), it will work, in general.
The second notion here is what is going on with the function calls. The value B is "moving" through the values of the field (values modulo a) twice as "fast" (by calling the function f twice). This will give two pseudorandom sequences through the elements of the field.
Listing 3-3 shows a simple implementation of this program in Python, and Figure 3-4 shows an example run of the program.
The reason this algorithm is called the ρ algorithm is because, if drawn out on paper, the paths of the two values, A and B, chase each other around in a way that resembles the Greek letter ρ (see Figure 3-5).
The Pollard ρ algorithm has time complexity of approximately O (n1/4) for finding a factor and no significant amount of storage [15]. Completely factoring a number will take slightly more time, but finding the first factor will usually take the longest.

Figure 3-5. Figure showing the path of a run of the Pollard ρ algorithm. The path will eventually loop back upon itself, hence the name " ρ." The algorithm will detect this loop and use it to find a factor.
Example 3-3. Python code for Pollards ρ algorithm for factoring integers.
#Euclidean algorithm for GCDdefgcd(x, y):ify==0:returnxelse:returngcd(y, x % y) #Stepping functiondeff(x, n):return(x*x+3)%n #Implements Pollard rho with simple starting conditionsdefpollardrho(a): x = 2 y = 2 d = 1whiled == 1: x = f(x, a) y = f(f(y, a), a) d = gcd(abs(x - y), a)ifd>1anda > d:returnd if d == a:return−1
John M. Pollard also has another method attributed to him for factoring primes [12]. Pollard's p − 1 method requires that we have a list of primes up to some bound B. We can label the primes to be, say, p1 = 2, followed by p2 = 3, and p3 = 5, and so on, all the way up to the bound B. There are already plenty of lists of primes to be found on the Internet, or they could be generated with a simple brute-force algorithm as described above, since we don't need very many of them (only a few thousand in many cases).
The algorithm works by Fermat's little theorem, that is, given a prime p and any integer b, then
We want to find p such that p is a prime factor of a, the number we are trying to factor. If L is some multiple of (p − 1), then p | gcd(bL − 1, a). The best way to try to get L to be a multiple of (p − 1) is to have L be a multiple of several prime factors. We can't compute bL mod p, but we can compute bL mod a. The algorithm works by computing
Pollard's p − 1 . Factors an integer, a, given a set of primes, p1, . . ., pk.
Set b = 2.
For each i in the range {1, 2, . . ., k} (inclusive), perform the following steps:
Set e to be ei = [(logB)/(logpi)] (the logarithm, base 10, of B divided by the logarithm of the i-th prime), rounded down.
Set f to be pei(the i-th prime raised to the power of the above number).
Set b = bf mod a.
Set g to be the GCD of a − 1 and b.
If g is greater than 1 and less than b, then g is a factor of b. Otherwise, the algorithm fails.
I won't show an implementation of this algorithm, since it requires such a large list of primes.
Pollard's p − 1 algorithm runs in time relative to the size of the upper-bound B. For each prime number less than B (≈ B/ln B of them), we calculate e (assume this is negligible), then f (this takes log2 e operations), and then b (this takes log2f operations). This gives us a total of a bit more than B ln B operations to complete. This, therefore, grows very large very fast, in terms of the largest prime number we are concerned with.
One optimization to this can be to pre-compute the values of e and f, since they will not change between runs, saving us a little bit of time.
A method of factoring based on square forms, to be discussed in this section, was devised by Shanks in References [9] and [14].
Before we dive in to the Square Forms Factorization method (SQUFOF), I'll first set up a little of the mathematics.
Let the ordered triple of integers (a, b, c) correspond to all values of
ax2 + bxy + cy2
for all integers x and y. We say that (a, b, c) represents some value m if, and only if, we can find two values x and y such that ax2 + bxy + cy2 = m.
We say that two forms of (a, b, c) are equivalent if the two forms represent the same set of numbers. One way in which this can be done is by a linear change of variables of x and y, where x' = Ax + By, y' = Cx + Dy, and AD − BC = 1 or −1. For example, if A = 1, B = 3, C = 1, and D = 4, then we would have x' = x + 3y, y' = x + 4y, and
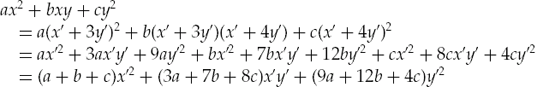
For example, (1, 1, 2) and (4, 26, 29) are equivalent.
This has two implications: The two forms represent the same set of numbers, and their discriminants of the form
D = b2 − 4ac
will be the same.
A square form is a form of (a, b, c), where a = r2 for some integer r — that is, a is a perfect square.
We will want to find a reduced square form, similar to finding the smallest CSR earlier. This is not hard ifD < 0, but if D> 0, then we define a form as reduced if
The SQUFOF algorithm works by finding equivalent reduced forms related to the integer we want to factor.
For more information on implementing the square form factorization, see, for example, Stephen McMath's SQUFOF analysis paper [9].
The elliptic curve factorization method (ECM) works similarly to Pollard's p − 1 algorithm, only instead of using the field of integers modulo p, weusean elliptic curve group based on a randomly chosen elliptic curve. Since many of the same principles work with elliptic curve groups, the idea behind Pollard's p − 1 also works here. The advantage is that the operations tend to take less time. (It's easier to multiply and add smaller numbers required for elliptic curves than the larger numbers for exponential-based group multiplication.) ECM was originally developed by Lenstra Jr. [7].
As before, we assume that we have a list of all of the primes {2, 3, 5,... } stored as {p1,p2,p3,...} less than some bound B.
Elliptic Curve Factorization Method. The elliptic curve will be generated and used to try to find a factor of the integer a. The elliptic curve operations and coordinates will be taken modulo a.
Generate A and B as random numbers greater than (or equal to) zero and less than a. Thus, we have an elliptic curve defined by y2 = x3 + Ax + B (modulo a).
Choose a random point on the elliptic curve, P, that is not the point at infinity. For example, choosing a random positive integer x less than a, plugging it into x3 + Ax + B, and solving for the square root will yield a y-value. (I show how to solve for the square root in Chapter 2.)
Calculate g, the GCD of the discriminant, (4a3 + 27b2), and a. If by some odd chance g = n, then generate a new A, B, and P, and try again. If g ≠ 1, then it divides a, so it is a factor of a, so the algorithm can terminate and return a.
Do the following operations for each prime p less than B (each of the p i values from earlier):
Let e = [(log B)/(log) p]. Here, we are taking the prime number and forming an exponent out of it by the logarithm of the bound B and dividing by the logarithm of p. The [] operators are called the ceiling function, so that you take the integer closest to what is in between them, rounding "up" (taking the opposite action as the floor function).
Set P = (pe)P — that is, add P to itself pe times.
Here, we might find a factor, g, of a. How? Recall calculating the inverse of a number (say, x) modulo a. We find a number, x−1, such that x−1x + kn = 1. But, this operation only succeeds if the numbers are relatively prime. If we perform the calculation (using one of the Euclidean algorithms), we will have also calculated the GCD of x and a. If the GCD is not 1, then we have a factor of a. In that case, we terminate the algorithm and return g, the GCD.
If we have failed to find a factor, g (via the GCD above), then we can either fail or try again with a new curve or point, or both.
Furthermore, g is not guaranteed to be prime, but merely a factor.
If p is the least prime dividing the integer a to be factored, then the expected time to find the factor is approximately
The first term in this will typically dominate, giving a number a bit less than ep.
In the worst-case scenario, when a is the product of two large and similar magnitude primes, then the running time is approximately
This is going to be a bit less than en, but not so much. In both cases, the average and worst case, these are still exponential running times.
The previous factoring methods were all exponential in running time. There are known methods that operate much faster (in subexponential time). However, these algorithms are more complicated, since they all use really nifty, math-heavy tricks to start to chip away at the running time and find factors fast.
Most subexponential factoring algorithms are based on Fermat's difference of squares method, explained above. A few other important principles are also used.
If x, y are integers and a is the composite number we wish to factor, and x2 ≡ y 2 (mod a) but x ≡ ±y (mod a), then gcd(x − y, a) and gcd(x + y, a) are factors of a.
The continued fraction factorization method is introduced in Reference [10]. The following explanation draws on this paper, as well as the material in References [9] and [15].
First, let's learn some new notation. If we wish to convey "x rounded down to the nearest integer," we can succinctly denote this using the floor function [x]. This means that [5.5] = 5, [−1.1] = −2 and [3] = 3, for example. I have avoided using this notation before, but it will be necessary in the following sections.
One more quick definition. A continued fraction is a fraction that has an infinite representation. For example:
Furthermore, a continued fraction for any number (say, c) can be constructed noting that c = [c] + c − [c], or
Furthermore, with a continued fraction form like the above (written compactly as [c0, c1, ..., ck]), we can find Ak//Bk, the rational number it represents, by the following method:
Let A−1 = 0, B−1 = 1,A0 = c0, B0 = 1.
For each i, compute Ai = ciAi−1 + Ai−2 and Bi = ciBi−1 + Bi −2.
The above algorithm will eventually terminate if the number being represented is irrational. Otherwise, it continues forever.
Using this method, we can now compute quadratic residues, Qi — remainders when subtracting a squared number. The quadratic residues we are interested in are from
We will use the quadratic residues to derive a continued fraction sequence for
We need an upper-bound on factors we will consider, B. The algorithm for exploiting this works by factoring each Qi as we calculate it, and if it is B-smooth (contains no prime factors less than B), we record it with the corresponding Ai. After we have collected a large number of these pairs, we look at the exponents of the factors of each Qi (modulo 2) and find equivalences between them. These will represent a system of equations of the form:
x2 ≡ y2 (mod n)
When x is not equal to y, we use the same principle of Fermat's difference of squares to factor n.
The reason this works is that a square is going to have even numbers as exponents of prime factors. If we have two numbers that when multiplied together (adding their exponents) have even numbers in the exponent, we have a perfect square.
Two final methods that we shall not delve too deeply into are the quadratic sieve (QS) and the general number field sieve (GNFS). Both rely on the principle of Fermat's difference of squares and produce factors using this idea.
For QS, the idea is very similar to the continued fraction method in the previous section, using sieve instead of trial division for factorizations. The running time of QS tends to be on the order of about
A lot of focus has been on the GNFS, since it is the fastest known method for factoring large integers, or in testing the primality of extremely large integers.
The GNFS works in three basic parts. First, the algorithm finds an irreducible polynomial that has a zero modulo n [where n is the modulo base we are working with, so that gcd(x − y, n)> 1, to find a factor]. Next, we find squares of a certain form that will likely yield factors. Then we find the square roots.
The "sieve" in the GNFS comes from the finding of squares in the second step. The special form that the squares come into involves calculating products of the sums of relatively prime integers. These relatively prime integers are calculated using sieving techniques.
For more information on the GNFS, see, for example, References [2] and [8].
Many algorithms use large group operations, such as exponentiation and large integer multiplication, to hide data.
For example, we can choose a finite field such as (Z23, +, ×) and a generator 2. We can easily calculate 29 = 6 in Z23. But, if someone saw a message passed as the integer 6, even with the knowledge that the generator is 2 and the field is over Z23, it is still, in general, a difficult problem to discover the exponent applied to the generator that yielded the given integer.
Solving an equation
ax = b
for x in a finite field while knowing a and b is called solving for the discrete logarithm. (The standard logarithm is solving for the exponent in ax = b with real numbers.)
For groups defined by addition of points on elliptic curves, the operation becomes taking a fixed point and adding it to itself some large number of times, or, for P, computing aP in the elliptic curve group over (Zp, +, ×) for some prime p.
Examples of such algorithms are the Diffie-Hellman key exchange protocol [4], ElGamal public key encryption [5], and various elliptic curve cryptography methods. To provide a concrete example, the Diffie-Hellman key exchange protocol on a finite field Zp works as follows:
Two parties, A and B, agree on a finite field Zp and a fixed generator g.
A generates a secret integer a, and B generates a secret integer b.
A → B: ga ∈ Zp
B can then compute (ga)b = gab in Zp.
B → A: gb ∈ Zp
A can then compute (gb) a = gab in Zp.
Both parties now share a secret element, gab. An interceptor listening to their communications will know Zp, g, ga, and gb and will strive to find gab from this information. The easiest way of accomplishing this is to solve for a = logg (ga) or b = logg (gb), which is computing the discrete logarithm. However, this problem, it turns out, is incredibly difficult.
For the following problems, we will consider the case that we are in a finite field Zp, where p is a prime number. To make notation consistent, we will consider finding x such that ax = b in our finite field, where a is a generator and b is the desired result.
Note, however, that the following algorithms are equally applicable on other algebraic structures, such as elliptic curve groups.
There are, in general, two brute-force methods for computing a discrete logarithm.
If the number of elements in the field is small enough (less than a few billion or so, at least with today's computers), we can pre-compute and store all possible values of the generator raised to an exponent. This will give us a lookup table, so that any particular problem will take only as much time as it takes to look up the answer.
Obviously, there are some strong limitations here. With large fields, we can have extremely large tables. At some point, we aren't going to have enough storage space to store these tables.
At the other end of the spectrum is the second method for computing a discrete logarithm. Here, each time we want to solve a discrete logarithm problem, we try each and every exponent of our generator. This method takes the most amount of time during actual computation but has the advantage of no pre-computation.
It's easy to see that there should be a trade-off somewhere, between pre-computing everything or doing all the work every time. However, we need to be a little clever in choosing that trade-off point. Some people have put a lot of cleverness into these trade-off points, discussed below (and similar concepts are discussed in later chapters).
The baby-step giant-step algorithm is one of the simplest trade-offs on time versus space, in that we are using some pre-computed values to help us compute the answers we need below.
Baby-Step Giant-Step. For the following algorithm, assume we are working in finite field over Zp, solving ax = b in Zp for x.
Compute L =

Pre-compute the first L powers of a, {a1,a2,..., aL}, and store them in a lookup table, indexed by the exponents {1, 2, 3,..., L}.
Let h = (a−1)L, our multiplier.
Let t = b, our starting point.
For each value of j in {0, 1,..., L − 1}, do the following:
If t is in the lookup table (some index i exists such that a i = t in the field), then return i + j × L.
Set t = t ×h.
Basically, we are computing b × hj in the loop and terminating when it equals some ai, where 0 ≤ i < L, giving us
b × hj = ai
b × ((a−1)L)j = ai
b × a− Lj = ai
b = ai. a Lj
b = aLj+i
Therefore, the discrete logarithm of b is Lj + i.
The baby-step giant-step algorithm represents a hybrid of the first two brute-force methods. It has on the order of
Like the previous brute-force methods, this method will find us an answer eventually, and there is no randomness involved. However, the space requirements are fairly large. For example, when p has hundreds or thousands of digits, then
Pollard's ρ method for discrete logarithms [11] relies on a similar principle as Pollard's ρ method for factoring — that is, we are looking for a cycle when stepping through exponents of random elements.
Here, assume that the group we are working with (the field) is the set of integers between 0 and p − 1 (written as Zp) along with normal addition and multiplication.
To perform Pollard's ρ algorithm for discrete logarithms, we partition the set of all integers between 0 and p − 1 into three partitions of roughly equal size: P0, P1, and P2. These three sets can be simple, such as either the integers below p divided into three contiguous sets (the first third of numbers less than p, the second third, the third third), or split by the remainder of the number when divided by 3 (so that 2 belongs in P2, 10 belongs in P1, and 15 belongs in P0).
The algorithm expects to solve the problem ax = b in the group G, thus it takes a and b as arguments.
It relies on three functions to operate: the function f, which takes one argument — an integer modulo p — and returns an integer modulo p; the function g, which takes an integer modulo p and a normal integer and returns an integer modulo p − 1; and a function h that takes an integer modulo p and an integer and returns an integer module p − 1.
The functions are defined based on the partition they are in. Thus:
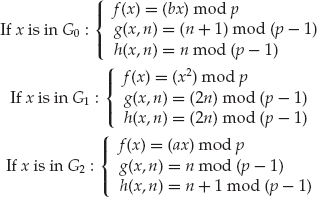
Pollard's ρ for Discrete Logarithms.
Set a0 = 0 and b0 = 0, two of our starting helper values.
Set x0 = 1, our starting point in G.
Let i = 0.
Repeat the following steps until, at the end, xi = x2i, and thus, we have found that our paths have merged.
Let i = i + 1.
Now, we calculate the next value for the function traveling slowly:
Calculate the next x: xi = f (xi−1).
Calculate the next a: ai = g (xi−1, ai−1).
Calculate the next b: bi = h (xi−1, bi−1).
Now, we calculate the next value for the function traveling quickly:
Calculate the next x: x2i = f (f (x2i−2)).
Calculate the next a: a2i = g (f (x2i−2),g (x2i−2,a 2i−2)).
Calculate the next b: b2i = h (f (x2i−2),h (x2i−2,b 2i−2)).
If our b's match, that is, bi = b2i, then the algorithm failed.
Set m = ai − a2i mod (p − 1).
Set n = b2i − bi mod (p − 1).
Solve, for x, the equation mx ≡ n (mod (p − 1)). More than likely, this will result in a few possible values of x (usually a fairly small amount). Unfortunately, the only thing to do is to check each one and see if it is the correct answer.
Pollard also proposed a generalization of the ρ algorithm for discrete logarithms, called the λ method (λ is the Greek letter lambda). Pollard's λ method of finding a discrete logarithm is a neat algorithm — interesting name, an amusing description, and very clever. Here, we want to compute the discrete logarithm for gx = h in a group G where we have some bound on x, such that a ≤ x < b.
The following description is derived from References [11] and [15]. This method is sometimes called the method of two kangaroos (or hares, or rabbits, depending on the author). The concept is that two kangaroos (representing iterative functions) are going to go for some "hops" around the number field defined by the integer we wish to factor. These two kangaroos (or 'roos, as we like to say) consist of a tame one, controlled by us and represented by T, and a wild one that we are trying to catch, W.
The tame 'roo, T, starts at a random point,t0 = gb, while W starts at w0 = h = gx. Define d0(T) = b, the initial "distance" from the "origin" that the tame 'roo is hopping, and let d0(W) = 0, the initial distance of our wild 'roo from h.
Let S = {gs1, ..., gsk} be a set of jumps, and let G be partitioned into k pieces G1, G2, ..., Gk, with 1 ≤ f (g) ≤ k being a function telling to which partition g belongs. These exponents of g in S should be positive and small compared to (b −a). Most often, we will pick these numbers to be powers of 2 (2i). These are the hops of both kangaroos.
Now, the two kangaroos are going to hop.T goes from ti to
The tame 'roo will have distance
Similarly, W goes from w i to
giving the wild 'roo distance
di+1 (W) = di (W) + sf (wi)
Eventually, T will come to rest at some position tm, setting a trap to catch W. If ever dn (W) > dm (T), then the wild kangaroo has hopped too far, and we reset W to start at w0 = hgz, for some small integer z > 0.
The index calculus method provides a method analagous to quadratic and number field sieves of factoring, shown above. This method is particularly well suited to solving the discrete logarithm on multiplicative groups modulo prime numbers. It was first described as the first subexponential discrete logarithm function by Adleman and Demarrais [1].
In general, this can be a very fast method over multiplicative groups, with on the order of e
For more information on the index calculus method, please refer to Reference [1].
Public key cryptographic systems and key exchange systems often rely on algebraic and number theoretic properties for their security. Two cornerstones of their security are the difficulty of finding factors of large numbers and solving discrete logarithms.
In this chapter, I discussed techniques for attempting to crack these two problems. While factoring and discrete logarithms for large problems are not easy, they represent the best way to perform cryptanalysis on most number theoretic and algebraic cryptosystems.
For any of the programming exercises in this chapter, I recommend using a language that supports large number arithmetic. Languages that support such features are C/C++(through gmp), Java, and Python, although most languages will have at least some support for large number arithmetic.
Other languages and environments would also be useful for many of these problems, such as Mathematica and MATLAB. However, I find it difficult to recommend these packages for every reader, since they can be very expensive. If you have the ability to experiment with these and other advanced mathematical tools, feel free to use them.
Exercise 1. To get your fingers warmed up, take the Python Challenge, which is available online at www.pythonchallenge.com. This is a set of puzzles, some quite difficult, that require writing programs of various kinds to complete.
Although it is called the "Python" Challenge, there is no reason that any other language could not be used. It just happens that they guarantee that there are usually the appropriate packages available for Python (such as the Python Imaging Library for some of the image manipulation puzzles), along with Python's built-in support for string manipulation, large integer mathematics, and so forth.
Again, I am not trying to condemn or recommend any particular language for any particular purposes. This just happens to be, in my opinion, a good set of programming exercises.
Exercise 2. Implement the standard brute-force factoring algorithm as efficiently as possible in a programming language of your choice. Try only odd numbers (and 2) up to
Exercise 3. Make improvements to your brute-force algorithm. For example, skipping multiples of 3, 5, 7,.... Discuss the speed improvements in doing so.
Exercise 4. Implement Fermat's difference of squares method in the programming language of your choice. Discuss its performance (running times) with inputs of integers varying in size from small numbers (< 100) up through numbers in the billions and further.
Exercise 5. Implement Pollard'sp − 1 factorization algorithm.
Exercise 6. Building on the elliptic curve point addition used in the previous chapter, implement elliptic curve factorization (ECF).
Next, provide a chart to compare the performance of Pollard'sp − 1 and ECF for the same inputs (with the same, or similar, parameters).
Exercise 7. Implement Pollard's ρ algorithm for both factoring and discrete logarithms.
References
[33] As my friend Raquel Phillips pointed out, "logarithm" and "algorithm" are anagrams!
[34] Sometimes, you may only have the natural logarithm (ln) or the base 10 logarithm (plain log). In these cases, you can convert to the base 2 logarithm by using the equation log2(x) = log(x)/log(2) = ln(x)/ ln(2).
[35] Division by 2 in computers is different from normal division. With numbers written in binary, simply removing the least significant bit is equivalent to dividing by 2. For example, 24 is 11000 in binary. If we remove the last bit, we get 1100, which is 12 — the same result as dividing by 2.
[36] [1] Leonard M. Adleman and Jonathan Demarrais. A subexponential algorithm for discrete logarithms over all finite fields. Mathematics of Computation 61 (203): 1–15 (1993).
[37] [2] J. A. Buchmann, J. Loho, and J. Zayer. An implementation of the general number field sieve. In Advances in Cryptology – Crypto '93, (ed. Douglas R. Stinson), pp. 159–165. Lecture Notes in Computer Science, Vol. 773. (Springer-Verlag, Berlin, 1993).
[38] [3] J. A. Davis and D. B. Holdridge. Factorization using the quadratic sieve algorithm. In Advances in Cryptology: Proceedings of Crypto '83, (ed. David Chaum), pp. 103–116 (Plenum, New York, 1984).
[39] [4] Whitfield Diffie and Martin E. Hellman. New directions in cryptography. IEEE Transactions on Information Theory IT-22 (6): 644–654 (1976); http://citeseer.ist.psu.edu/diffie76new.html.
[40] [5] T. ElGamal. A public key cryptosystem and a signature scheme based on discrete logarithms. In Advances in Cryptology: Proceedings of Crypto '84, (eds. G. R. Blakley and David Chaum), pp. 10–18. Lecture Notes in Computer Science, Vol. 196. (Springer-Verlag, Berlin, 1985).
[41] [6] Donald E. Knuth. The Art of Computer Programming: Seminumerical Algorithms, Vol. 2, 3rd ed. (Addison Wesley, Boston, 1998).
[42] [7] H. W. Lenstra, Jr. Factoring integers with elliptic curves. The Annals of Mathematics, 2nd Ser. 126(3): 649–673 (1987).
[43] [8] Arien K. Lenstra and Henrik W. Lenstra, Jr., eds. The Development of the Number Field Sieve, Vol. 554 of Lecture Notes in Mathematics. (Springer-Verlag, Berlin, 1993).
[44] [9] Stephen McMath. Daniel Shanks' Square Forms Factorization. (2004); http://web.usna.navy.mil/~wdj/mcmath/SQUFOF.pdf.
[45] [10] Michael A. Morrison and John Brillhart. A method of factoring and the factorization of f7. Mathematics of Computation 29(129): 183–205 (1975).
[46] [11] John M. Pollard. Monte carlo methods for index computation. Mathematics of Computation 32(143): 918–924 (1978).
[47] [12] John M. Pollard. Theorems of factorization and primality testing. Mathematical Proceedings of the Cambridge Philosophical Society 76: 521–528 (1974).
[48] [13] C. Pomerance. The quadratic sieve factoring algorithm. In Advances in Cryptology: Proceedings of EuroCrypt '84, (eds. Thomas Beth, Norbert Cot, and Ingemar Ingemarsson), pp. 169–182. Lecture Notes in Computer Science, Volume 209. (Springer-Verlag, Berlin, 1984).
[49] [14] Daniel Shanks. Five number-theoretic algorithms. Congressus Numerantium 7 (Utilitas Mathematica, 1973).
[50] [15] Samuel S. Wagstaff. Cryptanalysis for Number Theoretic Ciphers. (Chapman & Hall/CRC, Boca Raton, FL, 2003).



