Really Long Falls

6.1 Falling into the Sun

What if, instead of a long fall through Earth’s atmosphere, we had the atmosphere itself, the oceans, the continents—everything, the entire Earth—fall into the Sun? How long would that take? If we allow our imaginations even more freedom, how long would it take to fall from Heaven to Hell? Outrageous as that question no doubt seems, it is raised and answered in both ancient Greek theology and in more recent English poetry. So, as an inverted form of the Earth-into-the-sun question, we might ask how far it is from Earth to Heaven. Mathematical physics can answer both these questions if we assume Newton’s inverse square law of gravity holds in Heaven and Hell, as well as on Earth and in the rest of the universe.

Let’s do the more realistic Earth-into-the-Sun analysis first. I’ll take Earth as a point object, which is probably not a bad assumption, considering the relative sizes of Earth and the Sun. To set the problem up analytically, I’ll make the following definitions:

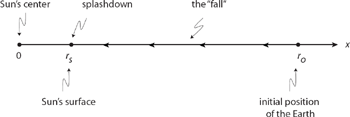
Figure 6.1. Falling into the Sun.

What I’ll now calculate is the time T for the Earth to travel, from an initial position of rest with respect to the Sun (the Earth is somehow brought to a dead stop in its orbit—now there’s a great scenario for a Hollywood disaster movie!), all the way to the Sun’s surface. T, then, is the time interval from the start of the fall to the instant the Earth just starts to splash into the Sun. I will be assuming that the Earth hasn’t been vaporized¹ before splashdown. That is, I’ll assume that the mass of Earth is unchanged over the entire duration of the fall. Figure 6.1 shows the geometry of the fall.

Conservation of energy says that the sum of the kinetic and the gravitational potential energies of Earth, at any distance x from the Sun’s center (r _s ≤ x ≤ r _o), will equal the initial (x = r _o) gravitational potential energy. There is, of course, zero initial kinetic energy, because the fall starts from rest. To find the gravitational potential energy of Earth at distance x from the Sun’s center requires that we calculate the energy needed to move Earth in from infinity to a position of rest at distance x, which will of course be a negative quantity, because the Sun’s attractive gravity is doing the work as Earth moves closer to the Sun. That energy is, with m _e as the mass of Earth,

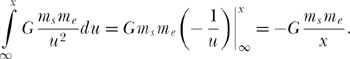
So, from conservation of energy (the right-hand side of (6.1) is the initial gravitational potential energy, that is, the energy at x = r _o), we have

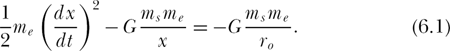
Notice that m _e is in every term, and so cancels away. (Remember, we are assuming m_e ≠ m_e(t).) Thus,

Since we know Earth is falling toward the Sun, we know that x is decreasing, and so we use the negative square root to write

Notice that = 0 when x = r _o, just as it should for a fall starting from rest. If you plug numbers into this result you can verify that, at splashdown (x = r _s), Earth is moving at a speed of 383 miles per second (in its orbit around the Sun, the average speed of Earth is about 18 miles per second).

Our result for says that

or, integrating t from 0 to T as x varies from r _o to r _s,

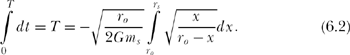
To do the integral, change the variable to

and so

or

Thus,

So,

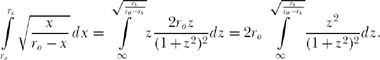
Now we have an integral easy to find in standard math tables. In particular,

and so, with a = 1,

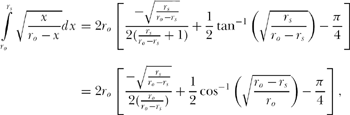
where you can see how we got from the tan⁻¹ to the cos⁻¹ simply by sketching a triangle and then using the Pythagorean theorem; continuing,

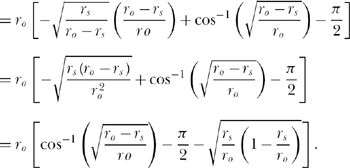
Thus, putting this result for the integral in (6.2) back into (6.2), we have

Now,

—again, sketch a triangle and use the Pythagorean theorem to see this—and so, at last,

Remember, since m_e cancelled out in (6.1), T is the time for any (non-vaporizing) mass to fall into the Sun, starting from rest at a distance of Earth’s orbital radius. (This is the basis for one imaginative proposal for disposing of radioactive waste: somehow reduce the orbital speed of the waste to zero and then let it fall into the Sun.) Inserting numbers, (6.3) tells us that it would take just slightly more than 64.6 days for Earth to fall into the Sun. More than enough time, I think, for a movie screen science-hero type guy or gal to save the planet!

6.2 Falling from Heaven to Hell

Let’s now take a look at the Heaven-to-Hell travel question. Centuries before Christ, in his Theogony, the Greek poet Hesiod (who lived about the time of Homer, 700 BC), wrote “a brazen anvil falling down from Heaven nine nights and days would reach the Earth on the tenth: and again, a brazen anvil falling from Earth nine nights and days would reach Tartarus upon the tenth.”² Tartarus was a terrible place, believed to be below even Hell, but let’s suppose it was Hell that Hesiod had in mind for the anvil’s final destination (we are, after all, mathematical physicists, not poets or theologians, and so we won’t worry over such piffles). And further, let’s go along with the common idea that Hell is at the center of the Earth.³ From this information we can now solve for the distance that separates Earth from Heaven, and this is the inverse of the Earth-falling-into-the-Sun question, where we knew the distance to fall and wanted to learn the duration of the fall. For the anvil-in-Heaven-falling-to-Earth question we know the duration and want to calculate the distance.

The very same issue is raised in Milton’s epic 1667 poem Paradise Lost, where we read of Satan being driven by the command of God (along with his crew of fallen angels) out of Heaven into Hell: “Into the wastful Deep; the monstrous sight Strook them with horror backward, but far worse Urg’d them behind; headlong themselves they threw Down from the verge of Heav’n, Eternal wrauth Burnt after them to the bottomless pit…. Nine days they fell….” Milton was quite clearly influenced by Hesiod,⁴ although he did change Hesiod’s anvil into the Devil and made the duration of the fall from Heaven to Hell a total of just nine days.

Some readers may wonder at the usefulness of calculating anything having to do with what is simply a fanciful tale (and I think that to be a fair description of a literal interpretation of the endless burning of screaming sinners in boiling lakes of molten sulfur), but the extreme thermal nature of Hell has provided physicists with lots of amusing jokes. My favorite is the “proof” that whatever the temperature of Hell may be, the place is certainly at a perfectly uniform temperature. After all, if that isn’t the case, then some bad-boy physicist who ended up there (surely, over all of historical time, there is at least one rotten, dead physicist who headed in Hell’s direction!) could use his knowledge of thermodynamics to harness the resulting thermal gradient to make a refrigerator—which would go a long way to defeating the entire purpose of being there!⁵

To set the analysis up for Hesiod’s description, I’ll make the following definitions:

Hesiod is not entirely clear on the point, but let’s assume that each of the two parts of the fall, Heaven to Earth and Earth to Hell, starts from rest. Let’s do the Earth-to-Hell analysis first. We have the anvil starting from rest at distance x = r_e from Earth’s center (which is at x = 0). When the anvil is at some intermediate point along its fall into Hell, the gravitational force on it is due only to the mass of the Earth that remains “below” it, that is, the mass of a sphere of density ? and radius x. (We’ll prove this, a result due to Isaac Newton, in Discussion 10.) Thus, the gravitational force on the anvil is given by

where the minus sign indicates the force is in the direction opposite that of increasing x. Now, from Newton’s second law of motion, we have

and so the mass of the anvil cancels away, and we have

(I am obviously ignoring air drag in this analysis.)

It is well-known that the solution for x(t) is what is called “simple harmonic motion,” and I suppose I could just plop the answer down on the page and move on. But it is such a pretty mathematical problem, and one very quick to do, that I’ll show it to you here. The trick is to assume the solution is given by

where A and s are both constants. Then, under that assumption, we’ll see that we can actually find a solution that satisfies both the differential equation and the initial conditions of (6.4), and so (mathematicians tell us) we must have the solution. From (6.5) we have

and so, from (6.4),

which says

That is, there are two possible constant values for s, which are given by

where

The most general solution to (6.4) is the sum of these two specific solutions, because (6.4) is what mathematicians call a linear differential equation, and so I’ll write

where, to be most general, I have not assumed that the same constant A goes with each of the two different values of s. To find the values of A ₁ and A ₂ we can use the two initial conditions in (6.4). Since x (0) = r _e, we have

and since

then the second initial condition says (as iα ≠ 0),

These two results say that , and so

or, using Euler’s fabulous formula e^iθ = cos(θ) + i sin(θ), we have the amazingly simple result of

The anvil reaches Hell when x = 0, and that occurs when . Since t = T at that fearsomely hot moment, we have

or

Before continuing with the central goal of this calculation, that of determining the distance between Earth and Heaven, we can use (6.8) to show that while Hesiod was an interesting writer, he certainly wasn’t much of a physicist. We can rewrite (6.8) to solve for ρ;

which, if we use T = 9 days=777,600 seconds, gives ρ = 1.46 · 10⁻⁵g/cm³, which is far, far too low, many times less than even the density of air, and certainly much less than that of the Earth!⁶

Now let’s do the Heaven-to-Earth part of the anvil’s fall. Looking back at (6.3) for inspiration, we see that we can write

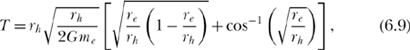
where I’ve written r _h for r _o, m _e for m _s, and r _e for r _s. Since Hesiod tells us that the Heaven-to-Earth journey takes the same time as the Earth-to-Hell journey, then we can equate (6.8) and (6.9) to write

Writing , this becomes (with the obvious cancellation of G and ρ on both sides),

or, writing u = r _e /r _h, and doing a little algebra, we get the transcendental equation

This equation can be numerically solved using the Newton-Raphson method (see note 5 in Discussion 4 for details), with the result being

Thus,

which means Heaven is (as the opening quotation says) just 1.57 Earth radii from Earth’s center, that is, from Hell. In other words, Heaven is just 0.57 Earth radii above the surface of the Earth, or 2,257 miles. Astronauts on their way to the moon must have passed right through Heaven!

You should, of course, take all this talk of Heaven and Hell with a grain of salt, since you’ll recall that Hesiod’s poem didn’t even come close to getting the correct value for Earth’s density. If Hesiod was equally wrong in locating Heaven, then Heaven is more likely much farther out in space, perhaps a million (billion, trillion?) miles or more beyond the moon. Oh, well, what does it matter where heaven is? How many of us are going there, any way?⁷

CP. P6.1:

Notes and References

1. Because of the inverse square law, the rate at which the sun’s energy falls on Earth quadruples every time their separation is halved. When still nearly three million miles from the sun’s center, the center of the falling Earth will have halved its distance from the sun’s center five times, meaning the sun’s radiation intensity on Earth will have increased by a factor of 4⁵ > 1,000 times! The atmosphere, the oceans, and the polar ice caps would be long gone, and probably a good chunk of Earth proper would at that point have been vaporized and blown away into space, as well.

2. See Hesiod, the Homeric Hymns, and Homerica, edited and translated by H. G. Evelyn-White (Cambridge, Mass.: Harvard University Press, 1964).

3. In Western culture it is the Bible that we might turn to as an “authoritative” source on how people, or at least how Christians, have viewed the location of Hell. In Acts 2:31 we are told that when Jesus died, His soul descended into Hell, while in Matthew 12:40 we learn that “the Son of man [Jesus] be three days and three nights in the heart of the Earth.” The Bible greatly influenced all of Western literature that came after; for example, in Dante Alighieri’s The Divine Comedy (ca. 1320), Hell is in the downward direction. Of course, the casting of Satan out of Heaven is supposed to have occurred when all in the universe was still in chaos, long before the Earth (and its center) was made, and so one could reasonably argue that Hell must be “somewhere else.” We’ll probably never really know, of course, at least not while we are still here on Earth.

4. Lawrence Babb, The Moral Cosmos of “Paradise Lost” (Lansing: Michigan State University Press, 1970, p. 113).

5. All engineering students at Stanford, at least when I was there, are required to take a course in thermodynamics. Usually this is a class offered by the Mechanical Engineering Department, but after looking at the assigned text—stuffed with engineering steam tables!—I decided I would rather have the flu all term than suffer through such stuff. I therefore petitioned the Engineering School to let me take thermo in the Physics Department, and so autumn quarter of 1961 I was lucky enough to be in Physics 173 with the famous Felix Bloch (Nobel Prize in Physics, 1952). That was a memorable class. It was in Professor Bloch’s class that I first heard the temperature-of-Hell joke, and it was at the beginning of one lecture that Bloch burst into the room and announced, “No class today. Instead, everybody over to the Physics Department office for cookies and milk—Professor [Robert] Hofstader [also a professor of physics at Stanford] has just won the Nobel Prize!” Cookies and milk? How times have changed!

6. The paper that served as the primary inspiration for this part of the discussion is B. G. Dick’s “Hesiod’s Universe” (American Journal of Physics, July 1983, pp. 666–667). Nobody, as far as I know, ever commented on the curious value of the starting page number of Dick’s paper.

7. Additional interesting calculations of the same nature as the one done in this discussion can be found in Andrew J. Simosen, Hesiod’s Anvil: Falling and Spinning through Heaven and Earth (Washington, D.C.: The Mathematical Association of America, 2007).