8
Meta-Regression for Relative Treatment Effects
8.1 Introduction
Heterogeneity in relative treatment effects is an indication of the presence of effect-modifying covariates, in other words of interactions between the treatment effect and trial-level or patient-level variables whose distribution might vary across included trials. A distinction is usually made between (i) true clinical variability in treatment effects due to variation between patient populations, protocols or settings across trials and (ii) biases related to methodological flaws in the way in which trials were conducted.
Clinical variability in relative treatment effects is said to represent a threat to the external validity of trials (Rothman et al., 2012) and limits the extent to which one can generalise trial results from one situation to another. The trial may deliver an unbiased estimate of the treatment effect in a certain setting, but it may be ‘biased’ with respect to the target population in a specific decision problem (Chapter 1). Careful consideration of inclusion and exclusion criteria can help to minimise this type of bias, but often at the expense of having little or no evidence to base decisions on. That is, if inclusion criteria are too strict, the majority, or even all, of the evidence may be discarded as ‘not relevant’, leaving no synthesis option. On the other hand, inclusion criteria that are too broad risk pooling populations with very different relative treatment effects, thus inducing a large heterogeneity and making interpretation of results very difficult. Biases or interaction effects due to imperfections in trial conduct represent threats to the internal validity of the results from RCTs. Although some of the methods presented in this chapter can be used to adjust for bias due to lack of internal validity, more powerful methods are described in detail in Chapter 9.
In this chapter we focus on methods for meta-regression that can address the presence of heterogeneity caused by known, and observed, effect modifiers. Although regression is usually seen as a form of adjustment for differences in covariates, here we consider it as a method for ‘bias adjustment’ since these covariates affect the ‘external validity’ of trials (Turner et al., 2009) that may lead to biased results for the target population. The aim is therefore to remove unwanted variability in relative treatment effects that can be explained by known, and measured, effect modifiers, which vary between studies. We focus particularly on the technical specification of models that can adjust for potential causes of heterogeneity and on the interpretation of such models in a decision context. In a network meta-analysis context, effect modifiers causing variability in relative treatment effects across studies can also induce inconsistency across pairwise comparisons, so these methods are also appropriate for dealing with inconsistency (see Chapter 7). Unless otherwise stated, when we refer to heterogeneity, this can be interpreted as heterogeneity and/or inconsistency.
The term ‘meta-regression’ can cause confusion in network meta-analysis. Our basic network meta-analysis models are already ‘regression’ models in a technical sense, but the regression coefficients, which are the treatment effect parameters, have special properties conferred on them by randomisation. Most of this chapter is devoted to models in which additional interaction terms are introduced for covariates to which patients have not been randomised to (e.g. age or disease severity). However, we also discuss models where the covariate is part of the treatment definition (Section 8.6). These include dose–response models for treatment effects, which at first sight one might wish to include as a type of covariate adjustment. We see these models in a rather different way, partly because patients are randomised to different doses and partly because rather than adding interaction terms, these models reconstruct the treatment effects as functional parameters, derived from a different set of basic parameters (Section 2.2.2).
The chapter begins by setting out the fundamental concepts (Section 8.2): types of covariate (trial or patient level, within- and between-trial comparisons, continuous or categorical covariates, aggregate data vs. individual patient data), how heterogeneity can be measured and implications of heterogeneity for decision making, in particular the predictive distribution. In Section 8.3 a pairwise meta-analysis is used to illustrate the impact of large heterogeneity in decision making, how covariate adjustment can be used to reduce heterogeneity, how results should be interpreted and how it can impact decisions.
Section 8.4 sets out the algebra and WinBUGS code for a series of meta-regression models for network meta-analysis. Worked examples are presented throughout to illustrate the main points. In Section 8.5 we discuss meta-regression with IPD. In Section 8.6 we introduce treatment effects models for dose–response, combination of treatment components and class effects. Section 8.7 reviews the chapter from a decision-making perspective, where we draw attention to some pragmatic considerations in model choice.
In Chapters 2–4, the general network meta-analysis model and methods for model comparison and criticism were described. In all that follows, it is implicit that those ideas can be applied throughout this chapter.
8.2 Basic Concepts
Meta-regression is used to relate the size of a treatment effect obtained from a meta-analysis to certain numerical characteristics of the included trials, with the aim of explaining some, or all, of the observed between-trial heterogeneity in relative treatment effects. These characteristics can be due to specific features of the individual participants in the trial or can be directly due to the trial setting or conduct. Meta-regression can be based on aggregate (trial-level) outcomes and covariates, or IPD may be available. However, even if we restrict attention to RCT data, the study of effect modifiers, with the exception of those relating to intervention definition (Section 8.6), is inherently observational (Higgins and Green, 2008; Borenstein et al., 2009). This is because it is not possible to randomise patients to one covariate value or another. As a consequence, the meta-regression techniques described in Section 8.4 inherit all the difficulties of interpretation and inference that attach to non-randomised studies: confounding, correlation between covariates and, most importantly, the inability to infer causality from association. However, there are major differences in the quality of evidence from a meta-regression that depend on the nature of the outcome, the covariate in question and the available data.
8.2.1 Types of Covariate
We will define trial-level covariates as those that relate to trial or participant characteristics that have been aggregated at the trial level and for which IPD, or a suitable breakdown of results by characteristic, are not available. Patient-level covariates are defined as covariates that relate to patient attributes and can be attributed to specific patients in each trial, either because IPD are available or because a sufficient breakdown of results has been provided.
For categorical covariates, we can distinguish between the following scenarios:
- A1. Trial-level covariates that relate to trial characteristics: This type of covariate relates to a between-trial treatment–covariate interaction and is often termed subgroup analyses. All patients in all arms of a trial share the same characteristic, and these only differ between trials, for example, trials that have been conducted in primary or secondary care settings. This is equivalent to A2(a) (see Section 8.4.4). Risk of bias indicators also fall under this category and are discussed in Chapter 9.
- A2. Trial-level covariates that relate to patient characteristics: In this case, the covariate relates to a patient characteristic, but it is aggregated at the trial level. Examples of such covariates include sex (male/female) or treatment status, that is, patients who are treatment naïve (first-line therapy) versus those that have previously failed on another therapy (second-line therapy). Data may be reported in different formats:
- Trials that have been conducted on patients with homogeneous characteristics only, for example, trials including only treatment-naïve patients and trials including only second-line therapy patients. In this case we can think of treatment status as a between-trial covariate, even though strictly it refers to a patient characteristic. This is equivalent to A1. An example is given in Section 8.4.4.
- Trials that include patients with mixed characteristics and report only the proportions of patients with each characteristic in the trial. For example, trials may include both naïve and second-line therapy patients and report the proportion of each type of patient included. This proportion is sometimes taken as a between-trial continuous covariate, which is then equivalent to B2. See Section 8.4.3.1.
- Trials that include patients with mixed characteristics but do not report proportions or a breakdown of outcomes by characteristic. No meta-regression can be carried out unless further assumptions are made.
- A3. Patient-level covariates: In this case the covariate relates to a patient characteristic, and we can identify the outcome for each patient and covariate value. Data may be reported in different formats:
- Trials that have IPD available for the outcome and covariate of interest or where sufficient statistics are reported, for example, cross-tabulations for categorical outcomes and covariates or full covariance matrices for continuous outcomes. In this case the covariate can be used to explore within-trial covariate effects, which can then be explored further in the meta-regression. Methods for this type of meta-regression are discussed in Section 8.5.
- Trials that include patients with mixed characteristics but report the treatment effect with a measure of precision separately for each covariate values or sufficient data (e.g. in contingency tables) that would allow these to be derived. This is a within-trial effect and, for the purpose of meta-regression, is equivalent to having IPD on that characteristic, if only this covariate is being modelled. This is true whether binary or continuous outcomes are reported, but only applies to categorical covariates. This type of meta-regression is discussed in Section 8.5.
A similar set of distinctions can be drawn for continuous covariates:
- B1. Trial-level covariates that relate to trial characteristics: For example, duration of the treatment, timing of intervention (e.g. how many hours after surgery) or trial setting (e.g. community/hospital care). An example is given in Section 8.4.3.1.
- B2. Trial-level covariates that relate to patient characteristics: For example, the mean age or mean disease duration of patients recruited to the trial. Baseline risk of patients in a trial, defined as the log odds of an event of patients on the reference treatment or similar, can also be thought of as a trial-level covariate that relates to unmeasured patient characteristics (see Section 8.4.1). This is equivalent to B1 and examples are given in Sections 8.4.3.2 and 8.4.3.3.
- B3. Patient-level covariates: With binary outcomes (e.g. death), if the mean for that characteristic and its variance are reported separately (or can be derived) for events and non-events, then, for the purpose of meta-regression, this is as good as having IPD with each patient’s exact characteristic (e.g. age or disease duration) recorded. If the mean covariate values are not reported separately, then IPD would be needed to perform meta-regression. For continuous outcomes with continuous covariates, IPD are always required for meta-regression. This is discussed in Section 8.5.
When investigating an interaction between treatment and covariate, one is comparing the treatment efficacy at different covariate values for categorical covariates and the linear change in efficacy per unit change in continuous covariates. There are two key differences between within- and between-trial comparisons. With between-trial comparisons, a given covariate effect (i.e. interaction) will be harder to detect as it has to be distinguishable from the ‘random noise’ created by the between-trial variation. However, for within-trial comparisons, the between-trial variation is controlled for, and the interaction effect needs only to be distinguishable from sampling error. With between-trial comparisons, because the number of observations (trials) may be very low while the precision of each trial may be relatively high, it is quite possible to observe a highly statistically significant relation between the treatment effect and the covariate that is entirely spurious (Higgins and Thompson, 2004).
A second difference is that between-trial comparisons are vulnerable to ecological bias or ecological fallacy (Rothman et al., 2012). This is a phenomenon in which, for example, a linear regression coefficient of treatment effect against the covariate in the between-trial case can be entirely different to the coefficient for the within-trial data. It is perfectly possible, of course, to have both within-trial and between-trial information in the same evidence synthesis. Depending on the availability of IPD, it may be possible to fit a model that estimates both a between-trial coefficient based on the mean covariate value and a within-trial coefficient based on the individual variation of the covariate around the mean. With continuous covariates and IPD, not only does the within-trial comparison avoid ecological bias, but it also has far greater statistical power to detect a true covariate effect. This is because the variation in patient covariate values will be many times greater than the variation between the trial means and the precision in any estimated regression coefficient depends directly on the variance in covariate values. See Section 8.5 for further details.
Finally, in cases where the covariate does not interact with the treatment effect, but modifies the probability of an event or the mean on the reference treatment (baseline risk), the effect of pooling data over the covariate is to bias the estimated treatment effect towards the null effect. This is a form of ecological bias known as aggregation bias (Rothman et al., 2012), which does not affect strictly linear models. Usually it is significant only when both the covariate effect on baseline risk and the treatment effect are quite strong. It is a particular danger in survival analysis because the effect of covariates such as age on cancer risk can be particularly marked and because the log-linear models routinely used are highly non-linear. When covariates that affect risk are present, even if they do not modify the treatment effect, the analysis must be based on pooled estimates of treatment effects from a stratified analysis for categorical covariates and regression for continuous covariates and not on treatment effects estimated from pooled data (Govan et al., 2010). See Chapter 5 for further details.
8.3 Heterogeneity, Meta-Regression and Predictive Distributions
A number of standard methods for measuring between-trial heterogeneity have been proposed (Sidik and Jonkman, 2007; Higgins and Green, 2008; Borenstein et al., 2009). In this book, and in keeping with the Bayesian framework, we compare the residual deviance and DIC statistics from fixed and random effects models to choose the preferred model (Chapter 3). If a random effects model is chosen, we examine the estimated heterogeneity in the context of the estimated treatment effects. An advantage of the Bayesian approach is that it provides a posterior distribution of the between-trial variance and – perhaps easier to interpret – the between-trial standard deviation, which gives investigators some insight into the range of values that are compatible with the data (Spiegelhalter et al., 2004, table 5.2). It is also possible to obtain a measure of uncertainty for the between-trial variance using classical approaches (Higgins and Thompson, 2002), but this is not often done. However, as stated in Chapter 2, the posterior distribution for the between-trial standard deviation is likely to be extremely sensitive to the prior distribution, and in particular using vague prior distributions is likely to result in posterior distributions that allow for unrealistically high levels of heterogeneity whenever the number of trials on each comparison is small or when the majority of trials are small. Informative prior distributions based on expert opinion or on meta-epidemiological data are possible solutions. See Chapters 2 and 4 for further comments on choice of prior distribution for between-study heterogeneity parameters.
In the presence of large between-trial variability in treatment effects (heterogeneity), interpretation of results requires care, since the uncertainty around the posterior mean of the treatment effects will not reflect the true uncertainty around the likely values of a future roll-out of the intervention or a future trial. The predictive distribution (Chapter 3) provides some insight into the wider uncertainty due to both the finite sample size and the variability across effects from different studies. It is also informative to compare the size of the heterogeneity to the largest estimated relative treatment effect. If the heterogeneity indicates that the between-trial variability is of the same order of magnitude as the observed effects, this will cast doubts on the suitability of the results for decision making. Again, the predictive distribution will be a better guide to the true uncertainty around the relative treatment effects.
In this section we illustrate the implications of substantial heterogeneity on the interpretation of results and decision making using a worked example. We return to this example in Section 8.4.3.2 where the model, its fit and interpretation of results are described in detail.
8.3.1 Worked Example: BCG Vaccine
A meta-analysis of trials evaluating the efficacy of a BCG vaccine for preventing tuberculosis (TB) showed large between-study heterogeneity (Berkey et al., 1995; Welton et al., 2012). Data were available on the number of vaccinated and unvaccinated patients and the number of patients diagnosed with TB during the study follow-up period for each group as well as the absolute latitude at which the trial was conducted (Table 8.1).
Table 8.1 BCG vaccine example: number of patients diagnosed with TB, r, out of the total number of patients, n, in the vaccinated and unvaccinated groups and the absolute latitude at which the trial was conducted, x.
Adapted from Berkey et al. 1995.
| Trial number | Not vaccinated | Vaccinated | Absolute degrees latitude | ||
| Number diagnosed with TB | Total number of patients | Number diagnosed with TB | Total number of patients | ||
| ri1 | ni1 | ri2 | ni2 | xi | |
| 1 | 11 | 139 | 4 | 123 | 44 |
| 2 | 29 | 303 | 6 | 306 | 55 |
| 3 | 11 | 220 | 3 | 231 | 42 |
| 4 | 248 | 12,867 | 62 | 13,598 | 52 |
| 5 | 47 | 5,808 | 33 | 5,069 | 13 |
| 6 | 372 | 1,451 | 180 | 1,541 | 44 |
| 7 | 10 | 629 | 8 | 2,545 | 19 |
| 8 | 499 | 88,391 | 505 | 88,391 | 13 |
| 9 | 45 | 7,277 | 29 | 7,499 | 27 |
| 10 | 65 | 1,665 | 17 | 1,716 | 42 |
| 11 | 141 | 27,338 | 186 | 50,634 | 18 |
| 12 | 3 | 2,341 | 5 | 2,498 | 33 |
| 13 | 29 | 17,854 | 27 | 16,913 | 33 |
Assuming a binomial distribution for the number of cases of diagnosed TB in arm k of trial i, fixed and random effects meta-analyses of the number of events (TB diagnosis) in vaccinated and unvaccinated individuals were conducted using the core model presented in Chapter 2 (binomial likelihood with logit link). The code for these analyses is given in Ch8_BCG_Bi_logit_FE.odc and Ch8_BCG_Bi_logit_RE.odc, respectively.
The fixed effects model had a very poor fit to the data (posterior mean of the residual deviance of 191 compared with 26 data points, DIC = 205), so the random effects model was preferred (Table 8.2). However, a large between-study heterogeneity was estimated (posterior median 0.65 with 95% CrI 0.39–1.17), comparable in size to the pooled log odds ratio (OR) of −0.76 (Table 8.2).
Table 8.2 BCG vaccine example: results from the random effects meta-analyses with and without the covariate absolute distance from the equator.
| No covariate | Model with covariatea | |||
| Median | 95% CrI | Median | 95% CrI | |
| b | – | – | −0.03 | (−0.05, −0.01) |
| log OR | −0.76 | (−1.21, −0.33) | −0.76 | (−1.03, −0.52) |
| OR | 0.47 | (0.30, 0.72) | 0.47 | (0.36, 0.59) |
| σ | 0.65 | (0.39, 1.17) | 0.27 | (0.03, 0.74) |
| Model fit | ||||
| resdevb | 26.1 | 30.6 | ||
| pD | 23.6 | 21.4 | ||
| DIC | 49.7 | 52.0 | ||
Posterior median and 95% CrI of the log OR, OR, interaction estimate (b) and posterior median between-trial heterogeneity (standard deviation, σ) for the number of patients diagnosed with TB (log OR < 0 and OR < 1 favour vaccination) and measures of model fit (posterior mean of the residual deviance, resdev, number of parameters, pD and DIC).
a Treatment effects are at the mean value of the covariate: latitude = 33.46°.
b Compare to 26 data points.
The observed log ORs and their 95% confidence intervals (CI) are presented in Figure 8.1 along with the study-specific (shrunken) estimates, the pooled mean log OR (based on the posterior distribution) and the predictive log OR (based on the predictive distribution) and their 95% CrI, obtained from the random effects models (Table 8.2). Focusing only on the solid lines in Figure 8.1, the first thing to note is that there is substantial between-study variability: some studies have shown very positive effects, while others have shown no effect, even suggesting harmful effects. This impacts the width of the 95% CrI for the mean and the predictive effects, with the latter being extremely wide, due to the observed heterogeneity (Figure 8.1).

Figure 8.1 BCG vaccine example: effect of covariate adjustment (absolute distance from the equator). Observed log ORs with 95% CI (black circles, solid lines); posterior median with 95% CrI of the trial-specific log ORs (the ‘shrunken’ estimates) for the random effects models with no covariate (black squares, black dashed lines) and with covariate (grey triangles, grey dashed lines); median with 95% CrI of the posterior (black diamond, solid line) and predictive distribution (open diamond, dashed line) of the pooled treatment effect for the random effects model with no covariates; and median with 95% CrI of the posterior (grey diamond, grey solid line) and predictive distribution (grey open diamond, grey dashed line) of the pooled treatment effect at the mean covariate value for the random effects model with covariate absolute distance from the equator.
8.3.2 Implications of Heterogeneity in Decision Making
In the presence of high levels of heterogeneity, it is critical to consider its impact on decisions. In particular the size of the treatment effect should be interpreted in the context of the estimated between-trial variation. Figure 8.1 portrays a situation where a random effects model has been fitted and the mean effect is clearly different from zero with 95% CrI (−1.21, −0.33). However, given the large heterogeneity, median 0.65 95% CrI (0.39, 1.17) (Table 8.2), what is a reasonable CrI for our prediction of the outcome of a future trial of infinite size? The predictive distribution shown in Figure 8.1 gives the answer: in a model with no covariate adjustment, the 95% predictive interval for a future trial ranges from −2.27 to 0.72, spanning no effect and including a range of harmful effects. This means that while the probability that the vaccine is harmful based on the mean effect is essentially zero, the probability that a new trial would show a harmful effect is much higher at 14%.
This issue has been discussed before (Spiegelhalter et al., 2004; Ades et al., 2005; Welton et al., 2007; Higgins et al., 2009), and it has been proposed that, in the presence of heterogeneity, the predictive distribution, rather than the distribution of the mean treatment effect, better represents our uncertainty about the comparative effectiveness of treatments in a future ‘roll-out’ of a particular intervention. In an MCMC setting, a predictive distribution is easily obtained by drawing further samples from the distribution of effects, as described in Chapter 3. The mean of the predictive distribution, on its linear scale, will be the same as the mean of the distribution of the mean effect. But the implications on the uncertainty in a decision, in cases where there are high levels of unexplained heterogeneity, could be quite profound, and it is therefore important that the degree of heterogeneity is not exaggerated (Higgins et al., 2009). Methods to adjust for factors that cause heterogeneity are therefore important. See Section 5.6.2 for further comments on predictive distributions and alternative characterisation of the treatment effect in a decision-making context and Chapter 9 for bias adjustment methods that can also reduce heterogeneity.
For this example, it has been suggested that the absolute latitude, or distance from the equator, at which the trials were conducted might influence vaccine efficacy (Berkey et al., 1995). The crude ORs obtained from Table 8.1 are plotted (on a log scale) against distance from the equator in Figure 8.2 where, for each study, the size of the plotted bubble is proportional to its precision so that larger, more precise studies have larger diameters. It seems plausible that the effect of the vaccine may differ at varying latitudes according to a linear relationship (on the log OR scale).

Figure 8.2 BCG vaccine example: plot of the crude odds ratios (on a log scale) against absolute distance from the equator in degrees latitude. The size of the circles is proportional to the studies’ precisions, the horizontal line (dashed) represents no treatment effect, the vertical line (dashed) is at the mean covariate value (33.46° latitude), and the solid line is the regression line estimated by the random effects model including degrees latitude as a continuous covariate. Odds ratios below 1 favour the vaccine.
If instead we consider the model with the covariate distance from the equator (for details, see Section 8.4.3.1), we can see that much of the between-study variability is explained (Table 8.2). The posterior and predictive distributions at the mean covariate value (latitude = 33.46°) for the model with the covariate are represented by the grey lines in Figure 8.1. The predictive probability that a new trial, carried out at the mean covariate value, will show harmful effects is now only 3%. However, note that this probability will differ for different values of the covariate. For example, the predictive probability that a new trial conducted at the equator (latitude = 0°) will show harmful effects is 80%; if the trial is instead conducted at 13° or 50° latitude, the predictive probabilities of a harmful effect are 35 and 0.6%, respectively. The estimated relative treatment effects and the width of the credible intervals around them will also differ with different covariate values. There is now a continuum of treatment effects for different covariate values, and this can have major implications when deciding whether or not to recommend the intervention. So while the vaccine seems effective at the mean latitude (Figure 8.1) and far from the equator (Figure 8.2), it has a very small effect at lower latitudes, and this needs to be taken into account by the decision maker who will be interested in a target population at a particular latitude. See Section 8.4 for further details.
8.4 Meta-Regression Models for Network Meta-Analysis
In network meta-analysis, a trial-level covariate can be seen as a variable that interacts with the treatment, but these interactions may be different for every treatment. The hypothesis is that the size of the treatment is different for different values of the covariate and that the relationship is linear on the chosen scale. To model this, we introduce as many interaction terms as there are basic treatment effects, β12, β13, …, β1S. Each of these added terms represents the additional (interaction) treatment effect per unit increase in the covariate value in comparisons of treatments 2, 3, …, S to treatment 1. These terms are exactly parallel to the main effects d12, d13, …, d1S. As with the main effects, for trials comparing, say, treatments 3 and 4, the interaction term would be the difference between the interaction terms on the effects relative to treatment 1, so that β34 = β14 − β13. The generic network meta-analysis model in Chapter 4 with interactions can then be written as
with tik representing the treatment in arm k of trial i; xi the trial-level covariate for trial i, which can represent a subgroup, a continuous covariate or baseline risk; and βck the regression coefficient for the covariate effect in comparisons of treatment k to c, which can be written as the difference in interactions with the reference treatment ![]() . We set
. We set ![]() so that
so that ![]() and note that the treatment and covariate interaction effects (δ and β) only act on the treatment arm, not on the control. In this model δik represent the relative effect of the treatment in arm k compared with the treatment in arm 1 of trial i when the covariate value is zero. Similarly, the pooled effects d1k will be the relative effects of treatments k = 2, …, S compared with the reference treatment when the covariate is zero.
and note that the treatment and covariate interaction effects (δ and β) only act on the treatment arm, not on the control. In this model δik represent the relative effect of the treatment in arm k compared with the treatment in arm 1 of trial i when the covariate value is zero. Similarly, the pooled effects d1k will be the relative effects of treatments k = 2, …, S compared with the reference treatment when the covariate is zero.
The special case of a pairwise (two-treatment) meta-analysis has ![]() and
and ![]() for all included trials, and therefore only one regression coefficient, β12, and one relative treatment effect, d12, are estimated.
for all included trials, and therefore only one regression coefficient, β12, and one relative treatment effect, d12, are estimated.
This model can be used to fit categorical or continuous covariates, although for continuous covariates it is generally advisable to centre the covariate to improve convergence (Draper and Smith, 1998; Welton et al., 2012). Therefore the model becomes
with ![]() as before. Now δik represent the relative effect of the treatment in arm k compared with the treatment in arm 1 of trial i at the centring value mx, which is usually the mean covariate value
as before. Now δik represent the relative effect of the treatment in arm k compared with the treatment in arm 1 of trial i at the centring value mx, which is usually the mean covariate value ![]() , but could be some other value that aids interpretation such as the mean in the decision population of interest. The pooled effects d1k will be the relative effects of treatments k = 2, …, S compared with the reference treatment at the centring value mx. Note that the model in equation (8.1) is exactly equivalent to the model in equation (8.2) when
, but could be some other value that aids interpretation such as the mean in the decision population of interest. The pooled effects d1k will be the relative effects of treatments k = 2, …, S compared with the reference treatment at the centring value mx. Note that the model in equation (8.1) is exactly equivalent to the model in equation (8.2) when ![]() .
.
The treatment effects can be un-centred and transformed to produce treatment effect estimates at any covariate value. The mean treatment effect for treatment c compared with treatment k at covariate value z is
For a random effects model, the trial-specific treatment effects δik in equations (8.1) and (8.2) come from a common distribution as described in Chapter 4 with a common variance. However, we could instead assume that the between-study variances depend on the covariate values, for example, in subgroup analyses, provided there was enough data to inform them or informative prior distributions were used.
For a fixed effects model, we replace δik in equations (8.1) and (8.2) with ![]() . In all models we also set
. In all models we also set ![]() . The likelihood, link function and prior distributions for μi, d1k and the between-study heterogeneity are chosen taking into account the scale of analysis, as detailed in Chapters 2 and 4.
. The likelihood, link function and prior distributions for μi, d1k and the between-study heterogeneity are chosen taking into account the scale of analysis, as detailed in Chapters 2 and 4.
However, in a network meta-analysis context, there are a very large number of models that can be proposed for the interaction terms, β, each with very different implications. Three general meta-regression models can be defined, describing different assumptions for the interactions in a multiple-treatment context:
- Independent, treatment-specific interactions: We assume that there is an interaction effect between the covariate and the treatment, but the interactions are different for every treatment. To model this, we introduce as many interaction terms as there are basic treatment effects, that is, S − 1, and consider them to be entirely unrelated. Thus the interaction effects are given unrelated non-informative prior distributions, such that for treatment k = 2, …, S The interaction effects β1k represent the change in relative effect d1k for each unit increase in the covariate xi. Interaction effects for other treatments can be obtained by subtraction.
- Exchangeable, related, treatment-specific interactions: In this model we assume that the interaction effects for each treatment are exchangeable, that is, they are similar, but not equal. This has the same number of parameters as the previous model, but now the (S − 1) ‘basic’ interaction terms are drawn from a random distribution with a common mean and between-treatment variance, so for treatment k = 2, …, S The mean interaction effect and its variance are estimated from the data. They are given non-informative prior distributions, for example,
 and σb could be given a uniform prior distribution with lower limit at zero and a suitable chosen upper limit, depending on the outcome scale used (Chapters 2 and 4). Informative prior distributions, which limit how similar or different the interaction terms are, could also be used.
and σb could be given a uniform prior distribution with lower limit at zero and a suitable chosen upper limit, depending on the outcome scale used (Chapters 2 and 4). Informative prior distributions, which limit how similar or different the interaction terms are, could also be used. - The same interaction effect for all treatments: In this more restrictive model, there is a single interaction term b that applies to relative effects of all the treatments relative to treatment 1. An important point to note is that the assumption of a common regression term b allows the interaction parameter to be estimated even for comparisons in the network which only have one trial and therefore do not provide information on a regression slope. The model can be expressed, and coded for computer implementation, in many ways. We have chosen to retain the treatment-specific interaction effects but set them all equal to b. This guarantees that the terms cancel out in comparisons of the non-reference treatments against each other. Thus, for all treatments k = 2, …, S, we set A non-informative prior distribution can be given to b, for example,
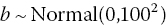 , or an informative prior distribution can be used instead. In this model, the assumption is that the change in treatment effects relative to treatment 1, d12, d13, …, d1S, all increase or decrease by the same amount b, for each unit increase in the covariate xi. However, the effects of treatments 2, 3, …, S relative to each other are exactly the same regardless of the covariate value, because the interaction terms now cancel out. This means that the choice of reference treatment 1 becomes important and the results for models with covariates are sensitive to this choice. In fact, it will only make sense to use this type of model if the reference treatment is somehow different from the others, such as a placebo, an older treatment or ‘standard care’. It is also important to ensure that the data are set up so that treatments are coded in ascending order by arm, as described in Chapter 2, to ensure the desired assumptions are implemented. Readers should be aware of the interpretation of parameters when coding all models, but it is particularly important for models including covariates.
, or an informative prior distribution can be used instead. In this model, the assumption is that the change in treatment effects relative to treatment 1, d12, d13, …, d1S, all increase or decrease by the same amount b, for each unit increase in the covariate xi. However, the effects of treatments 2, 3, …, S relative to each other are exactly the same regardless of the covariate value, because the interaction terms now cancel out. This means that the choice of reference treatment 1 becomes important and the results for models with covariates are sensitive to this choice. In fact, it will only make sense to use this type of model if the reference treatment is somehow different from the others, such as a placebo, an older treatment or ‘standard care’. It is also important to ensure that the data are set up so that treatments are coded in ascending order by arm, as described in Chapter 2, to ensure the desired assumptions are implemented. Readers should be aware of the interpretation of parameters when coding all models, but it is particularly important for models including covariates.
Readers will note that it would be relatively straightforward to build models that incorporated a combination of these assumptions for different treatment comparisons by taking advantage of the modularity of the WinBUGS code. This would be suitable if, for example, treatments belonging to different classes are included in the network and different assumptions apply to different classes of treatments (see also Section 8.7). For example, in a six-treatment network with placebo as the reference, if treatments 2–4 belong to the same class, they may be assumed to have the same interaction effect (equation (8.6)). If treatments 5 and 6 are different from the others and sufficient data are available, a separate interaction effect can be assumed for comparisons of each of these treatments to placebo. The consistency equations on the interaction terms will ensure that the correct relative effects are used each time.
8.4.1 Baseline Risk
A special kind of covariate is the average baseline risk in the trial, defined as the outcome on the reference treatment in that trial, on the chosen scale. This is usually the log odds, probability or rate of an event on the reference treatment, when the outcome is binary, but it can also be the mean outcome on the reference treatment. The baseline risk is often chosen as a proxy for underlying, often unmeasured or unknown, patient-level covariates that are thought to modify the treatment effect, but which cannot be accounted for directly in the model.
The meta-regression model on baseline risk is the same as in equation (8.2), but now ![]() , the trial-specific baseline for the control arm in each trial. Thus, when arm-based data are available, no additional data are required to consider baseline risk in the meta-regression model, since this is already estimated for each trial. An important property of this Bayesian formulation is that it takes the ‘true’ trial-specific baseline (as estimated by the model) as the covariate and automatically takes the uncertainty in each μi into account (McIntosh, 1996; Thompson et al., 1997; Welton et al., 2012). Naïve approaches that regress against the observed baseline risk fail to take into account the correlation between the treatment effect and baseline risk and the consequent regression to the mean phenomenon.
, the trial-specific baseline for the control arm in each trial. Thus, when arm-based data are available, no additional data are required to consider baseline risk in the meta-regression model, since this is already estimated for each trial. An important property of this Bayesian formulation is that it takes the ‘true’ trial-specific baseline (as estimated by the model) as the covariate and automatically takes the uncertainty in each μi into account (McIntosh, 1996; Thompson et al., 1997; Welton et al., 2012). Naïve approaches that regress against the observed baseline risk fail to take into account the correlation between the treatment effect and baseline risk and the consequent regression to the mean phenomenon.
It is important to note that the covariate value μi is on the same scale as the linear predictor (e.g. the logit, log or identity scales – see Chapter 4), and therefore the mean covariate value for centring needs to be on this scale too. For example, when using a logit link function, the covariate should be centred by subtracting the mean of the log odds in the trial-specific baseline arms (k = 1) of each trial that compares treatment 1 from μi. In a network meta-analysis context, the treatment in arm 1 will not always be treatment 1 (the reference treatment). However, for the model in equation (8.6), which assumes the same interaction effect for all treatments compared with treatment 1, the regression terms will cancel for all other comparisons, so no baseline risk adjustment is performed for trials that do not include treatment 1. Fitting one of the other models, care should be taken to ensure that the risk being adjusted for refers to the estimated risk for the reference treatment (treatment 1) that may not have been compared in every trial. This can be done by augmenting the data so that all trials have treatment 1 in arm 1 with missing data when this treatment was not compared. For example, for binary outcomes, an extra arm with treatment 1 should be added to studies that do not already have it, where the number of observed events is zero and the number of individuals is arbitrary, for example, 1. WinBUGS will then generate a prediction for the baseline risk on treatment 1 in those studies based on the model (Dias et al., 2011d) accounting for the full uncertainty in the missing baseline risk. For continuous data a missing observation with arbitrary variance (e.g. 1) should be added (Achana et al., 2013). An alternative is to ensure that the baseline risk considered reflects the expected outcome on treatment 1. This can be done by subtracting the effect of the treatment in arm 1 in study i from μi, ensuring that the baseline risk is corrected using the mean relative effect. See Exercise 8.3 for an illustration and comparison of the two methods.
When considering the different models that allow for effect modification, one of the factors that can influence choice of model is the amount of data available. If a fixed treatment effects model is being considered with a binary covariate (subgroup), the unrelated interaction model, equation (8.4), requires two connected networks, one for each subgroup, including all the treatments, that is, with at least (S − 1) trials in each. With random treatment effects, even more data are required to estimate the common between-trial variance: at least one, but preferably more, treatment comparison has to have multiple trials at the same covariate level if we assume a common between-study heterogeneity across covariate values. If the heterogeneity values are allowed to differ, a lot more data will be required. If a continuous covariate is considered, data need to include a suitable range of covariate values across all treatment comparisons, unless external data, in the form of informative prior distributions, are used.
It may be possible to estimate the exchangeable interaction model in equation (8.5) with less data. However, to use this model, we need to have a clear rationale for exchangeability, and we would suggest that this model is most useful for model checking, for example, to check whether there is evidence that the assumption of a common interaction may not hold. See Section 8.7 for a further discussion of the issues with the different models.
8.4.2 WinBUGS Implementation
The generic WinBUGS code for a random effects network meta-analysis presented in Chapter 4 can be extended to implement the meta-regression model in equation (8.2) simply by adding the extra term containing the regression coefficients multiplied by the centred covariate values to the linear predictor, so that for an appropriate link function (see Chapter 4), we write
# model for linear predictor, covariate effect relative# to treat in arm 1link function <- mu[i] + delta[i,k] + (beta[t[i,k]]- beta[t[i,1]]) * (x[i]-mx)
Values for the covariate vector x and the centring constant mx are given as data. If no centring is required, we set mx=0.
The rest of the generic code remains the same, including the multi-arm adjustment. However, further code needs to be added to implement the chosen assumptions for the interaction terms beta. To implement the assumption of independent, treatment-specific interactions (equation (8.4)), the following code should be added before the final closing brace:
beta[1] <- 0 # covariate effect is zero for reference treatmentfor (k in 2:nt){ # LOOP THROUGH TREATMENTSbeta[k] <- dnorm(0, 0.0001) # independent covariate effects}
To implement the assumption of exchangeable interactions (equation (8.5)), the following code should be added before the final closing brace:
beta[1] <- 0 # covariate effect is zero for reference treatmentfor (k in 2:nt){ # LOOP THROUGH TREATMENTSbeta[k] ~ dnorm(B, tau.B) # exchangeable covariate effects}B ~ dnorm(0,0.0001) # Prior for mean of distribution of regression parameterssd.B ~ dunif(0, appropriate upper bound) # Prior for sd of distr of regression parameterstau.B <- pow(sd.B,-2) # precision of regression parameters
To implement the assumption of equal interactions (equation (8.6)), we instead add the following code before the final closing brace:
beta[1] <- 0 # covariate effect is zero for reference treatmentfor (k in 2:nt){ # LOOP THROUGH TREATMENTSbeta[k] <- B # common covariate effects}B ~ dnorm(0,0.0001) # Prior for common regression parameter
To implement models with adjustment for baseline risk, x[i] is replaced with mu[i] in the definitions of the linear predictor, and the centring constant mx should be on appropriate scale.
Fixed effects models with covariates can also be fitted by adapting the generic code for fixed effects network meta-analysis given in Chapter 4 in the same way.
In addition, code can be added before the final closing brace to estimate the treatment effects relative to the reference treatment for covariate values in vector z of length nz, given as data:
for (k in 1:nt){ # LOOP THROUGH TREATMENTSfor (j in 1:nz) { # LOOP THROUGH COVARIATE VALUESdz[j,k] <- d[k] + (beta[k]-beta[1])*(z[j]-mx) # treatment effect when covariate = z[j]}}
For example, for a meta-regression with two subgroups, a vector z of length two would be added to the list data statement: list(z=c(0,1), nz=2).
Further code can be added to estimate all relative effects and to produce estimates of absolute effects on all treatments, given additional information on the absolute treatment effect on one of the treatments, for given covariate values. For example, if we had chosen to use a logit link, the following code would be added to calculate all relative effects for covariate values in z:
# pairwise ORs and LORs for all possible pairwise# comparisons at covariate=z[j]for (c in 1:(nt-1)) {for (k in (c+1):nt) {for (j in 1:nz) {orz[j,c,k] <- exp(dz[j,k] - dz[j,c])lorz[j,c,k] <- dz[j,k]-dz[j,c]}}}
If a different link function had been used, the code would be adjusted as described in Chapter 4. The absolute effects of each treatment, Tz[], for each treatment can be calculated using the following code:
for (k in 1:nt) { # LOOP THROUGH TREATMENTSfor (j in 1:nz){ # LOOP THROUGH COVARIATE VALUESlogit(Tz[j,k]) <- A + dz[j,k] # logit link function used}}
Note that the only difference in the main expression for T is that we now use the relative effects for each covariate value, given in dz, and have to include a double loop through all the treatments and then through the vector with the covariate values of interest.
Depending on the scale of analysis, the link function may need to be replaced as described in Chapter 4.
Deviance calculations, DIC and predictive distributions at the centring value can be calculated as described in Chapters 3 and 4. Predictive distributions at different values of the covariate can be calculated by adapting the code to implement equation (8.3) for the predictive relative treatment effects.
8.4.3 Meta-Regression with a Continuous Covariate
We will assume that there is a trial-level covariate defined on a continuous scale, which is given in the data as a vector with each term, xi, representing the covariate value for trial i. This covariate could be an average patient characteristic such as the proportion of males in the trial (B2 in Section 8.2.1), or it could be a genuine trial characteristic (B1 in Section 8.2.1), such as distance from the equator, in absolute degrees latitude (Section 8.3.1).
We return to the meta-analysis of trials evaluating the efficacy of a BCG vaccine for preventing TB described in Section 8.3.1, to provide details on the model and interpretation of results, and then present an example with a continuous covariate in a network meta-analysis context.
8.4.3.1 BCG Vaccine Example: Pairwise Meta-Regression with a Continuous Covariate
Assuming a binomial distribution for the number of cases of diagnosed TB in arm k of trial i, and letting xi be the continuous covariate representing absolute degrees latitude, the meta-regression model in equation (8.2) was fitted to the data, with centring at the mean covariate value ![]() latitude. Both fixed and, random treatment effects were considered, but note that since this analysis only involves two treatments, there is only one interaction term. Therefore the models in equations (8.4) and (8.6) are equivalent, and the hierarchical model in equation (8.5) is not relevant.
latitude. Both fixed and, random treatment effects were considered, but note that since this analysis only involves two treatments, there is only one interaction term. Therefore the models in equations (8.4) and (8.6) are equivalent, and the hierarchical model in equation (8.5) is not relevant.
A random treatment effects model with covariate was fitted using the implementation in equation (8.6). The data structure is similar to that presented in Chapter 2, but now we add a column containing the value of covariate x for each trial and the centring value (the mean of the covariate) mx to the list data for centring. In addition we want to calculate all the pairwise log ORs and ORs for covariate values 0, 13 and 50, so a vector z of length three is also added to the data. Initial values will need to be given for B, which requires a single number, as well as for the other parameters, as described in Chapter 2. See Ch8_BCG_Bi_logit_RE-x1.odc for details on the code, data and initial values for this example (results are based on 100,000 iterations from three independent chains after a burn-in of 40,000).
The results of fitting a random effects model with and without the covariate ‘absolute degrees latitude’ are presented in Table 8.2. Note that the treatment effect for the model with covariate adjustment is interpreted as the log OR at the mean value of the covariate (33.46° latitude). The estimated log ORs at different degrees latitude are represented by the solid line in Figure 8.2. See also Section 8.3 for a further discussion of the results.
Comparing the values of the DIC (Table 8.2), it would appear that the models with and without the covariate are not very different; differences of less than 3 are not considered important (Chapter 3). Although the model without covariates has a smaller posterior mean of the residual deviance, the model with the covariate allows for more shrinkage of the random treatment effects, resulting in a smaller effective number of parameters (pD). We can however see that the heterogeneity is considerably reduced when we add the covariate: the posterior medians are 0.65 for the model with no covariate and 0.27 for the model with covariate, and the 95% CrI for the interaction term b does not include zero (Table 8.2). Note also that the model with the covariate has the effect of ‘shrinking’ the study-specific estimates further towards the regression line (Figure 8.1), particularly for studies which were farther from it (Figure 8.2), and the 95% CrI for its predictive distribution no longer crosses the line of no effect. We might now ask whether the covariate has explained all the heterogeneity, in effect allowing us to fit a fixed effects model with the covariate. See Exercise 8.1.
It is important to note that when deciding whether a covariate should be included in a random effects model, the posterior mean of the regression coefficient and the posterior between-trial standard deviation (heterogeneity) should be looked at. Reductions in heterogeneity and a 95% CrI for the regression coefficient that does not include zero are signs that the model with the covariate should be preferred. However model fit may not differ by very much between random effects models with and without a covariate, because random effects models usually fit the data well, at the expense of higher between-trial variation.
8.4.3.2 Certolizumab Example: Network Meta-Regression with Continuous Covariate
A review of trials of certolizumab pegol (CZP) for the treatment of rheumatoid arthritis (RA) in patients who had failed on disease-modifying anti-rheumatic drugs (DMARDs), including methotrexate (MTX), was conducted for a single technology appraisal at NICE (National Institute for Health and Clinical Excellence, 2010). Twelve MTX controlled trials were identified, comparing seven different treatments – placebo plus MTX (coded 1), CZP plus MTX (coded 2), adalimumab plus MTX (coded 3), etanercept plus MTX (coded 4), infliximab plus MTX (coded 5), rituximab plus MTX (coded 6) and tocilizumab plus MTX (coded 7), forming the network presented in Figure 8.3. This type of network, where comparisons are all relative to one common treatment and there are no loops, is often called a ‘star network’.
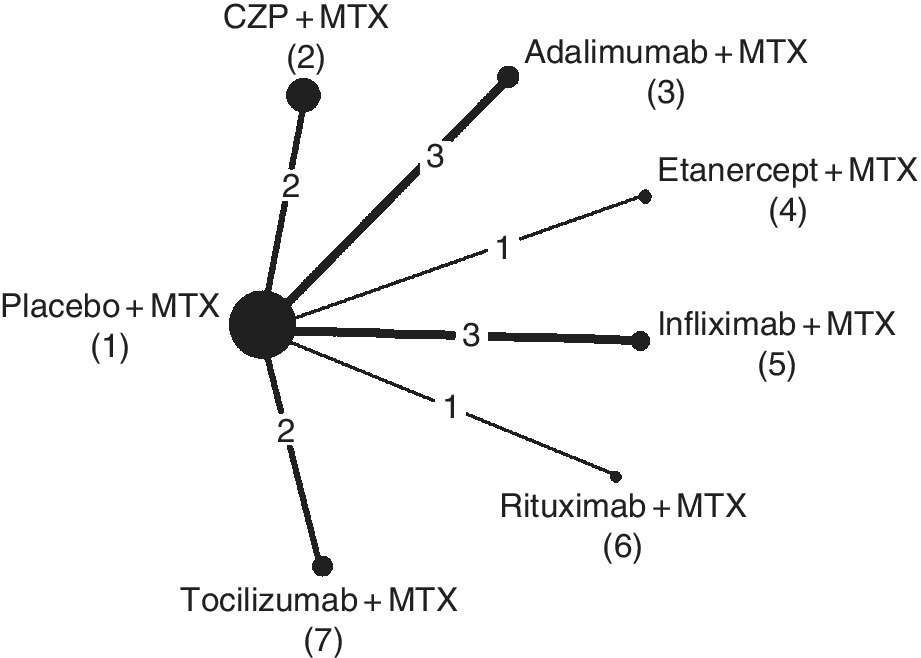
Figure 8.3 Certolizumab example: treatment network. Each circle represents a treatment, and connecting lines indicate pairs of treatments that have been directly compared in randomised trials. The numbers on the lines indicate the numbers of trials making that comparison, and the numbers by the treatment names are the treatment codes used in the modelling. Line thickness is proportional to the number of trials making that comparison, and the width of the circles is proportional to the number of patients randomised to that treatment.
Table 8.3 shows the number of patients achieving ACR-50 at 6 months, that is, the number of patients who have improved by at least 50% on the ACR scale (ACR-50 at 3 months was used when this was not available), rik, out of all included patients, nik, for each arm of the included trials, along with the mean disease duration in years for patients in each trial, xi (i = 1, …, 12; k = 1, 2).
Table 8.3 Certolizumab example: number of patients achieving ACR-50 at 6 months, r, out of the total number of patients, n, in the arms 1 and 2 of the 12 trials and mean disease duration (in years) for patients in trial i, xi.
| Study name | ti1 | ti2 | ri1 | ni1 | ri2 | ni2 | xi |
| RAPID 1 | Placebo | CZP | 15 | 199 | 146 | 393 | 6.15 |
| RAPID 2 | Placebo | CZP | 4 | 127 | 80 | 246 | 5.85 |
| Kim 2007 | Placebo | Adalimumab | 9 | 63 | 28 | 65 | 6.85 |
| DE019 | Placebo | Adalimumab | 19 | 200 | 81 | 207 | 10.95 |
| ARMADA | Placebo | Adalimumab | 5 | 62 | 37 | 67 | 11.65 |
| Weinblatt 1999 | Placebo | Etanercept | 1 | 30 | 23 | 59 | 13 |
| START | Placebo | Infliximab | 33 | 363 | 110 | 360 | 8.1 |
| ATTEST | Placebo | Infliximab | 22 | 110 | 61 | 165 | 7.85 |
| Abe 2006a | Placebo | Infliximab | 0 | 47 | 15 | 49 | 8.3 |
| Strand 2006 | Placebo | Rituximab | 5 | 40 | 5 | 40 | 11.25 |
| CHARISMAa | Placebo | Tocilizumab | 14 | 49 | 26 | 50 | 0.915 |
| OPTION | Placebo | Tocilizumab | 22 | 204 | 90 | 205 | 7.65 |
All trial arms had MTX in addition to the placebo or active treatment.
a ACR-50 at 3 months.
It is thought that mean disease duration can affect relative treatment. The crude ORs from Table 8.3 are plotted (on a log scale) against mean disease duration in Figure 8.4, with the numbers 2–7 representing the OR of that treatment relative to placebo plus MTX (chosen as the reference treatment). Note that due to zero events in one of the treatment arms, for plotting purposes, the crude OR for the Abe 2006 study was calculated by adding 0.5 to each cell. The original zero cell was used in the analysis (see also Chapter 6).

Figure 8.4 Certolizumab example: plot of the crude odds ratios (on a log scale) of the six active treatments relative to placebo plus MTX against mean disease duration (in years). The plotted numbers refer to the treatment being compared with placebo plus MTX, the blobs around the numbers are proportional to the precision of the study, and the lines represent the relative effects of the following treatments (from top to bottom) compared with placebo plus MTX based on a random effects meta-regression model: etanercept plus MTX (treatment 4, dotted line), CZP plus MTX (treatment 2, solid line), tocilizumab plus MTX (treatment 7, short–long dash line), adalimumab plus MTX (treatment 3, dashed line), infliximab plus MTX (treatment 5, dot-dashed line) and rituximab plus MTX (treatment 6, long-dashed line). Odds ratios above 1 favour the plotted treatment, and the horizontal line (thin dashed) represents no treatment effect.
Due to the paucity of data, only the common interaction model described in equation (8.6) will be fitted. The disease duration covariate will be centred at its mean ![]() years. The relative treatment effects obtained are the estimated log ORs at the mean covariate value (8.21 years in this case), which can be transformed to produce the estimate at any covariate value of interest, as described in Section 8.4.2.
years. The relative treatment effects obtained are the estimated log ORs at the mean covariate value (8.21 years in this case), which can be transformed to produce the estimate at any covariate value of interest, as described in Section 8.4.2.
In this network, the generic random effects model with covariate disease duration and a Uniform(0,5) prior distribution for the between-study heterogeneity σ is not identifiable (see Exercise 8.2). This is because there is a trial with a zero cell, not many replicates of each comparison and no indirect evidence on any contrast. Due to the paucity of information from which the between-trial variation can be estimated, in the absence of an informative prior distribution for the between-study heterogeneity, the relative treatment effects for this trial will tend towards infinity. We have therefore used an informative half-normal prior distribution with mean 0.26, which ensures stable computation:
This prior distribution was chosen to ensure that, a priori, 95% of the trial-specific ORs lie approximately within a factor of 2 from the median OR for each comparison – for details, see Appendix B.
This prior distribution should not be used unthinkingly. It should be adapted to ensure it suitably reflects likely values of the heterogeneity for each example. Informative prior distributions allowing wider or narrower ranges of values can be used by changing the value of prec in the previous code. Alternatively, empirically based prior distributions (Turner et al., 2015b) could be used (see Exercise 8.2).
To fit the random effects meta-regression model with the prior distribution in equation (8.7), the line of code annotated as ‘vague prior for between-trial SD’ in the generic network meta-analysis code should be replaced with the following two lines:
sd ~ dnorm(0,prec)I(0,) # prior for between-trial SDprec <- pow(0.32,-2)
The WinBUGS code for the fixed and random effects meta-regression model with covariate disease duration is given in Ch8_CZP_Bi_logit_FE-x1.odc and Ch8_CZP_Bi_logit_RE-x1prior.odc, respectively.
In this example, the posterior distribution obtained for σ differs slightly from the half-normal prior distribution, suggesting there has been some updating based on the data. The range of plausible values for σ does not change much, but the probability of values very close to zero is smaller than that suggested by the prior distribution (Figure 8.5).

Figure 8.5 Certolizumab example: probability density function of (a) Half-Normal(0,0.322) prior distribution simulated in WinBUGS and (b) the posterior distribution for the between-study heterogeneity for the meta-regression model with informative Half-Normal(0,0.322) prior distribution – from WinBUGS.
Table 8.4 shows the results of fitting fixed and random treatment effects network meta-analysis models with and without the covariate disease duration (results are based on 100,000 iterations from three independent chains after a burn-in of 50,000). The WinBUGS code for the fixed and random effects network meta-analysis models without covariate is given in Ch8_CZP_Bi_logit_FE.odc and Ch8_CZP_Bi_logit_RE.odc, respectively.
Table 8.4 Certolizumab example: results from the fixed and random effects models with and without the covariate ‘disease duration’.
| No covariate | Covariate ‘disease duration’ | |||||||
| Fixed effects | Random effectsa | Fixed effects | Random effectsa | |||||
| Median | 95% CrI | Median | 95% CrI | Median | 95% CrI | Median | 95% CrI | |
| b | – | – | – | – | 0.14 | (0.01, 0.26) | 0.14 | (−0.03, 0.32) |
| d 12 | 2.20 | (1.73, 2.72) | 2.27 | (1.53, 3.10) | 2.50 | (1.96, 3.08) | 2.55 | (1.79, 3.44) |
| d 13 | 1.93 | (1.52, 2.37) | 1.96 | (1.33, 2.64) | 1.66 | (1.19, 2.16) | 1.70 | (1.04, 2.41) |
| d 14 | 3.26 | (1.45, 6.74) | 3.28 | (1.26, 6.63) | 2.64 | (0.71, 5.96) | 2.61 | (0.42, 6.01) |
| d 15 | 1.38 | (1.06, 1.72) | 1.46 | (0.90, 2.21) | 1.40 | (1.08, 1.74) | 1.46 | (0.94, 2.16) |
| d 16 | 0.00 | (−1.40, 1.39) | 0.01 | (−1.61, 1.63) | −0.42 | (−1.86, 1.04) | −0.43 | (−2.09, 1.21) |
| d 17 | 1.65 | (1.22, 2.10) | 1.57 | (0.77, 2.28) | 1.98 | (1.45, 2.53) | 1.99 | (1.11, 2.93) |
| σ | – | – | 0.34 | (0.03, 0.77) | – | – | 0.28 | (0.02, 0.73) |
| resdevb | 37.6 | 30.9 | 33.8 | 30.2 | ||||
| pD | 18.0 | 21.1 | 19.0 | 21.2 | ||||
| DIC | 55.6 | 52.0 | 52.8 | 51.3 | ||||
Posterior median and 95% CrI interaction estimate (b), log ORs (dXY) of treatment Y relative to treatment X and between-trial heterogeneity (σ) for the number of patients achieving ACR-50 (dXY < 0 favours the reference treatment) and measures of model fit (posterior mean of the residual deviance, resdev, number of parameters, pD and DIC). Treatment codes are given in Figure 8.3.
a Using informative prior distribution for sd.
b Compare to 24 data points.
The estimated ORs for different durations of disease are represented by the parallel lines in Figure 8.4. The assumption of a common regression term implies that the interaction parameter is estimated even for the comparison of rituximab plus MTX (treatment 6) with placebo plus MTX that only has one trial. The model assumptions imply that a line parallel to the others is drawn through this point (Figure 8.4). This analysis also suggests that adding rituximab to MTX may be of much less benefit to patients than the other treatments and predicts, perhaps implausibly, that it can be harmful for patients with a shorter disease duration.
The DIC and posterior means of the residual deviances for the models in Table 8.4 do not decisively favour a single model. Comparing only the fixed effects models, we can see that the fit is improved by including the covariate interaction term b that also has a 95% CrI, which does not include zero. Looking at the random effects models, although the model with covariate reduces the heterogeneity compared with the model with no covariate (Table 8.4), the 95% CrI for the interaction parameter b includes zero. Thus, the meta-regression models appear reasonable but not strongly supported by the evidence. Nevertheless the finding of smaller treatment effects with a shorter disease duration has been reported with larger sets of studies (Nixon et al., 2007), and the implications of this for the decision model need to be considered. The issue is whether or not the use of biologics should be confined to patients whose disease duration was above a certain threshold. This is not an unreasonable idea, but it would be difficult to determine this threshold on the basis of the regression in Figure 8.4 alone. The slope is largely determined by treatments 3 and 7 (adalimumab and tocilizumab), which are the only treatments trialled at more than one disease duration and which appear to have different effects at each duration. Furthermore, the linearity of relationships is highly questionable, and the prediction of negative effects for treatment 6 (rituximab) is not really credible. This suggests that the meta-regression model used is not plausible and other explorations of the causes of heterogeneity should be undertaken (see also Section 8.4.3.3).
8.4.3.3 Certolizumab Example: Network Meta-Regression on Baseline Risk
Figure 8.6 shows the crude OR obtained from Table 8.3 plotted against the baseline odds of ACR-50 (on a log scale) for the certolizumab example. Numbers 2–7 represent the OR of that treatment relative to placebo plus MTX (chosen as the reference treatment). Due to a zero cell in one arm, for plotting purposes, the crude OR for the Abe 2006 study was calculated by adding 0.5 to each cell, and the baseline log odds were assumed to be 0.01. Figure 8.6 seems to suggest a strong linear relationship between the treatment effect and the baseline risk (on the log scale). The model in equation (8.6) assumes that parallel regression lines are fitted to the points in Figure 8.6, where the differences between the lines represent the true mean treatment effects adjusted for baseline risk.

Figure 8.6 Certolizumab example: plot of the crude odds ratios of the six active treatments relative to placebo plus MTX against odds of baseline response on a log scale. The plotted numbers refer to the treatment being compared with placebo plus MTX, and the lines represent the relative effects of the following treatments (from top to bottom) compared with placebo plus MTX based on a random effects meta-regression model: tocilizumab plus MTX (7, short–long dash line), adalimumab plus MTX (3, dashed line), etanercept plus MTX (4, dotted line), CZP plus MTX (2, solid line), infliximab plus MTX (5, dot-dashed line) and rituximab plus MTX (6, long-dashed line). Odds ratios above 1 favour the plotted treatment, and the horizontal line (dashed) represents no treatment effect.
Both fixed and random treatment effects models with a common interaction term were fitted. The basic parameters d1k and b are given non-informative normal prior distributions Normal(0,1002); the prior distributions for the μi were Normal(0,1000), which have a slightly reduced variance to avoid numerical errors, and σ ~ Uniform(0,5). The WinBUGS code for meta-regression on baseline risk is given in Ch8_CZP_Bi_logit_FE-xbase.odc and Ch8_CZP_Bi_logit_RE-xbase.odc.
The analysis used centred covariate values, achieved by subtracting the mean of the observed log odds on treatment 1, ![]() , from each of the estimated μi. The treatment effects for models with covariate adjustment are interpreted as the effects for patients with a baseline logit probability of ACR-50 of −2.421 that can be converted to a baseline probability of ACR-50 of 0.082 using the inverse logit function (Table 4.1). These treatment effects can be un-centred and transformed to produce estimates at any value of baseline risk, as described in Section 8.4.2.
, from each of the estimated μi. The treatment effects for models with covariate adjustment are interpreted as the effects for patients with a baseline logit probability of ACR-50 of −2.421 that can be converted to a baseline probability of ACR-50 of 0.082 using the inverse logit function (Table 4.1). These treatment effects can be un-centred and transformed to produce estimates at any value of baseline risk, as described in Section 8.4.2.
Table 8.5 shows the results of the interaction models with fixed and random treatment effects, with baseline risk as the covariate (results are based on 100,000 iterations from three independent chains after a burn-in of 60,000).
Table 8.5 Certolizumab example: results from the fixed and random effects models with and without the covariate ‘baseline risk’.
| Fixed effects | Random effects | |||
| Mean | 95% CrI | Median | 95% CrI | |
| b | −0.96 | (−1.03, −0.69) | −0.98 | (−1.10, −0.70) |
| d12 | 1.85 | (1.67, 2.06) | 1.83 | (1.35, 2.29) |
| d13 | 2.13 | (1.90, 2.35) | 2.18 | (1.79, 2.63) |
| d14 | 2.06 | (1.47, 2.80) | 2.03 | (1.19, 2.94) |
| d15 | 1.68 | (1.49, 1.86) | 1.71 | (1.30, 2.16) |
| d16 | 0.39 | (−0.72, 1.26) | 0.39 | (−0.86, 1.45) |
| d17 | 2.20 | (1.92, 2.46) | 2.24 | (1.75, 2.79) |
| σ | – | – | 0.19 | (0.01, 0.70) |
| resdeva | 27.4 | 24.2 | ||
| pDb | 19.0 | 21.6 | ||
| DIC | 46.4 | 45.8 | ||
Posterior median and 95% CrI interaction estimate (b), log ORs dXY of treatment Y relative to treatment X and between-trial heterogeneity (σ) for the number of patients achieving ACR-50 (dXY < 0 favours the reference treatment) and measures of model fit (posterior mean of the residual deviance, resdev, number of parameters, pD and DIC). Treatment codes are given in Figure 8.3.
a Compare to 24 data points.
b pD calculated outside WinBUGS.
Both the fixed and random effects models with covariate have a credible region for the interaction term that is far from zero, suggesting a strong interaction effect between the baseline risk and the treatment effects. The estimated ORs for different durations for the random effects model with baseline risk interaction are represented by the different parallel lines in Figure 8.6. The DIC statistics and the posterior means of the residual deviance favour the models with this covariate over the models without covariate or with disease duration as the covariate (Table 8.4). In fact, we might argue that baseline risk explains all the heterogeneity as a fixed effects model with this covariate is now appropriate.
As noted in Section 8.4.3.2, the assumption of a common regression term b allows the interaction parameter to be estimated for comparisons that only have one trial and gives estimates of treatment effects at values of the baseline risk outside the ranges measured for some comparisons. Again looking at rituximab plus MTX (treatment 6) with placebo plus MTX, the assumptions of parallel lines (common b) (Figure 8.6) predict, perhaps implausibly, that adding rituximab to MTX can be harmful if baseline risk is above 0.15.
The striking support in Figure 8.6 for a single interaction term for all treatments, except maybe treatment 6, has several implications for decision making and for synthesis in practice. Firstly, it clearly suggests a relation between efficacy and baseline risk that needs to be incorporated into cost-effectiveness analysis (CEA) models. Secondly, Figure 8.6 illustrates how variation in effect size due to a covariate will, if not controlled for, introduce severe heterogeneity in pairwise meta-analysis and potential inconsistency in network synthesis. It is clear that both the differences between trials (within treatments) and the differences between drugs are minimal once baseline risk is accounted for.
8.4.4 Subgroup Effects
In the context of treatment effects in RCTs, a subgroup effect can be understood as a categorical trial-level covariate that interacts with the treatment. The hypothesis would be that the size of treatment effect is different in, for example, male and female patients, or that it depends on age group, previous treatment, etc. The simplest way of analysing such data is to carry out separate analyses for each group, using the models described in Chapters 2 and 4, and then examine the estimates of the relative treatment effects. However, this approach has two disadvantages. First, if the models have random treatment effects, having separate analyses means having different estimates of between-trial variation. As there is seldom enough data to estimate the between-trial variation, it may make more sense to assume that it is the same for all subgroups. A second problem is that running separate analyses does not immediately produce a credible interval for the interaction effect. If this credible interval does not cross the value of no interaction (usually zero, depending on scale), it lends statistical support to the inclusion of the covariate when considered in conjunction with the reduction in the between-trial heterogeneity and model fit. The alternative is to run a single integrated analysis with a shared between-trial heterogeneity parameter and an interaction term, β, introduced on the treatment effect, as described in equation (8.1). Different assumptions for the interaction effects can then be used, as described previously.
The WinBUGS code is as described in Section 8.4.2, but care needs to be taken to specify the covariate vector so that it reflects the subgroups under consideration. For a model with two subgroups, these will be coded in a vector, where each element xi will hold the value 0 or 1, depending on which subgroup the trial was conducted on. For a model with a single interaction term β, this will be interpreted as the change in relative effect of all treatments compared with the reference for patients in the subgroup coded 1 over the patients in subgroup coded zero.
These ideas extend naturally, but not necessarily easily, from binary effect modifiers to multiple categories. For example, for trials on patients categorised as mild, moderate and severe, two interaction terms can be introduced: one for moderate compared with mild and the second for severe compared with mild. Alternatively, disease severity can be examined as a continuous covariate (see Section 8.4.3) or as regression on baseline risk (see Section 8.4.3.3).
8.4.4.1 Statins Example: Pairwise Meta-Analysis with Subgroups
A meta-analysis of 19 trials of statins for cholesterol lowering against placebo or usual care (Sutton, 2002; Welton et al., 2012) included some trials on which the aim was primary prevention (patients included had no previous heart disease) and other trials on which the aim was secondary prevention (patients had previous heart disease). Note that in this case the subgroup indicator is a patient-level covariate that applies to all patients in the trials and can thus be considered a trial-level covariate (scenario A2(a) that is also equivalent to A1 (Section 8.2.1)). The outcome of interest is all-cause mortality and the data are presented in Table 8.6. The potential effect modifier, primary versus secondary prevention study, can be considered a subgroup in a pairwise meta-analysis of all the data using the model in equation (8.1), or two separate meta-analyses can be conducted on the two types of study.
Table 8.6 Statins example: data on statins and placebo for cholesterol lowering in patients with and without previous heart disease (Sutton, 2002) – number of deaths due to all-cause mortality in the control and statin arms of 19 RCTs.
| Trial ID | ri1 | ni1 | ri2 | ni2 | xi |
| 1 | 256 | 2223 | 182 | 2221 | Secondary |
| 2 | 4 | 125 | 1 | 129 | Secondary |
| 3 | 0 | 52 | 1 | 94 | Secondary |
| 4 | 2 | 166 | 2 | 165 | Secondary |
| 5 | 77 | 3301 | 80 | 3304 | Primary |
| 6 | 3 | 1663 | 33 | 6582 | Primary |
| 7 | 8 | 459 | 1 | 460 | Secondary |
| 8 | 3 | 155 | 3 | 145 | Secondary |
| 9 | 0 | 42 | 1 | 83 | Secondary |
| 10 | 4 | 223 | 3 | 224 | Primary |
| 11 | 633 | 4520 | 498 | 4512 | Secondary |
| 12 | 1 | 124 | 2 | 123 | Secondary |
| 13 | 11 | 188 | 4 | 193 | Secondary |
| 14 | 5 | 78 | 4 | 79 | Secondary |
| 15 | 6 | 202 | 4 | 206 | Secondary |
| 16 | 3 | 532 | 0 | 530 | Primary |
| 17 | 4 | 178 | 2 | 187 | Secondary |
| 18 | 1 | 201 | 3 | 203 | Secondary |
| 19 | 135 | 3293 | 106 | 3305 | Primary |
The number of deaths in arm k of trial i, rik, is assumed to have a binomial likelihood i = 1, …, 19; k = 1, 2. Defining xi as the trial-level subgroup indicator such that

our interaction model is given in equation (8.1) where the linear predictor is ![]() (Chapter 4). Note that since there are only two treatments, there is only one interaction effect, so we will use the model for a common interaction effect in equation (8.6). In this set-up, μi and δi2 represent the log odds of the outcome in the reference treatment (i.e. the treatment indexed 1) and the trial-specific log ORs of success on the treatment group compared with the reference for primary prevention studies, respectively.
(Chapter 4). Note that since there are only two treatments, there is only one interaction effect, so we will use the model for a common interaction effect in equation (8.6). In this set-up, μi and δi2 represent the log odds of the outcome in the reference treatment (i.e. the treatment indexed 1) and the trial-specific log ORs of success on the treatment group compared with the reference for primary prevention studies, respectively.
The WinBUGS code for the fixed and random effects subgroup meta-regression models is given in Ch8_Statins_Bi_logit_FE-group.odc and Ch8_Statins_Bi_logit_RE-group.odc, respectively.
The results of the two separate analyses and the single analysis using the interaction model for fixed and random treatment effects models are shown in Table 8.7 (results are based on 100,000 iterations from three independent chains after a burn-in of 50,000). Note that in a fixed effects context, the two analyses deliver exactly the same results for the treatment effects in the two groups, while in the random effects analysis, due to the shared variance, treatment effects are not quite the same: they are more precise in the single analysis, particularly for the primary prevention subgroup where there was less evidence available to inform the variance parameter, leading to very wide 95% CrI for all estimates in the separate random effects meta-analysis. However, only the joint analyses offer a 95% CrI for the interaction term β, which, in both cases, includes the possibility of no interaction, although the point estimate is negative, suggesting that statins might be more effective in secondary prevention patients.
Table 8.7 Statins example: results from the fixed and random effects models for primary and secondary prevention groups.
| Fixed effects | Random effects | |||||||
| Primary prevention | Secondary prevention | Primary prevention | Secondary prevention | |||||
| Separate analyses | Separate analyses | |||||||
| Median | 95% CrI | Median | 95% CrI | Median | 95% CrI | Median | 95% CrI | |
| log OR | −0.11 | (−0.30, 0.09) | −0.31 | (−0.42, −0.21) | −0.10 | (−2.01, 1.12) | −0.34 | (−0.72, −0.07) |
| OR | 0.90 | (0.74, 1.09) | 0.73 | (0.66, 0.81) | 0.91 | (0.13, 3.07) | 0.71 | (0.48, 0.94) |
| σ | – | – | – | – | 0.79 | (0.06, 3.90) | 0.16 | (0.01, 0.86) |
| resdev | 16.9a | 29.0b | 11.9a | 28.3b | ||||
| pD | 6.0 | 15.0 | 8.7 | 17.7 | ||||
| DIC | 22.9 | 44.0 | 20.6 | 46.0 | ||||
| Single analysis | Single analysis | |||||||
| Median | 95% CrI | Median | 95% CrI | Median | 95% CrI | Median | 95% CrI | |
| log OR | −0.11 | (−0.30, 0.09) | −0.31 | (−0.42, −0.21) | −0.08 | (−0.48, 0.36) | −0.35 | (−0.72, −0.07) |
| OR | 0.90 | (0.74, 1.09) | 0.73 | (0.66, 0.81) | 0.92 | (0.62, 1.43) | 0.71 | (0.49, 0.94) |
| β | −0.21 | (−0.42, 0.01) | −0.27 | (−0.86, 0.20) | ||||
| σ | – | – | 0.19 | (0.01, 0.76) | ||||
| resdevc | 45.9 | 42.6 | ||||||
| pD | 21.0 | 25.0 | ||||||
| DIC | 66.9 | 67.6 | ||||||
Posterior summaries, mean, standard deviation (sd) and 95% CrI of the log OR, OR and posterior median, sd and 95% CrI between-trial heterogeneity (σ) of all-cause mortality when using statins (log OR < 0 and OR < 1 favour statins) and measures of model fit (posterior mean of the residual deviance, resdev, number of parameters (pD) and (DIC).
a Compare to 10 data points.
b Compare to 28 data points.
c Compare to 38 data points.
8.5 Individual Patient Data in Meta-Regression
IPD meta-analyses have been described as the gold standard (Stewart and Clarke, 1995), and they clearly enjoy certain advantages over syntheses conducted on summary data, including the possibility of standardising analysis methods (Riley et al., 2010). When patient-level covariates are of interest, using the IPD to regress individual patient characteristics on individual patient outcomes will produce a more powerful and reliable analysis (Berlin et al., 2002; Lambert et al., 2002) compared with the use of aggregate outcome and covariate data and can avoid the potential ecological biases (see Section 8.2.1). Furthermore an IPD meta-regression analysis is essential when dealing with a continuous covariate and a continuous outcome.
In meta-analysis of IPD, historically, two broad approaches have been considered, the one- and two-stage approaches (Simmonds et al., 2005). In a two-stage approach, the analyst estimates the effect size(s) of interest from each study, together with a measure of uncertainty (e.g. standard error) in a first step, and then in a second step conducts a meta-analysis in the standard way using this summary data. In the context of exploring heterogeneity, the effect size could relate to a treatment by covariate interaction (Simmonds and Higgins, 2007). In some circumstances, it may be possible to carry out such an IPD analysis even if the analyst does not have access to all the IPD, that is, owners of the data may be willing to calculate and supply such interaction effects when they are not willing to supply the whole IPD dataset. However, such an approach becomes cumbersome/infeasible if multiple covariates are to be considered simultaneously.
IPD random effects pairwise meta-analysis models have been developed for continuous (Goldstein et al., 2000; Higgins et al., 2001), binary (Turner et al., 2000), survival (Tudor Smith et al., 2005) and ordinal (Whitehead et al., 2001) variables, and all allow the inclusion of patient-level covariates. Although most of the models are presented in the single pairwise comparison context, it is possible to extend them to a network meta-analysis context (Higgins et al., 2001; Tudor Smith et al., 2007; Cope et al., 2012). Simmonds and Higgins (2007) consider simple criteria for determining the potential benefits of IPD to assess patient-level covariates, and their work is recommended reading.
Treatment by covariate interactions can be estimated exclusively using between-study information when only summary data are available (meta-regression) and exclusively using within-study (variability) information if IPD are available. However, a subtlety when using IPD is that both between- and within-study coefficients can be estimated (Higgins et al., 2001). This can be achieved by including two covariates: the mean covariate value in that study (i.e. each individual in a study gets the same value – which is the value that would be used if an aggregate meta-regression analysis were being conducted) and a second covariate that is the individual patient response minus the mean value in that study (Riley and Steyerberg, 2010). Note that this applies most naturally to continuous covariates, but it can also be applied to binary covariates (e.g. if the binary covariate is sex, the between-study covariate would be the proportion of women).
There are a number of ways in which these dual effect (within- and between-study interaction) models can be used. The most appealing option is to use the interaction estimate derived exclusively from the within-trial variability, since this is free from ecological/aggregation biases and other potential sources of confounding between studies. Potentially, power could be gained by including the information in the between-trial variability by having the same parameter for within and between covariates. This, of course, comes at the cost of potentially inducing bias. It has been suggested (Riley and Steyerberg, 2010) that a statistical test of the difference between the two estimates could be carried out and the decision of whether to have the same interaction effect for within and between covariates could be based on this test. However, we suspect this test will have very low power in many situations, and further investigation of this approach is required before it can be recommended.
There may be situations where IPD are available from a number of, but not all, relevant studies. In this case, there are three potential options available for exploring heterogeneity. The first is to exclude all trials for which IPD are not available. This keeps the analysis simple, and can be based exclusively on within-study comparisons, but has the obvious disadvantage of not including all of the relevant trials. Furthermore, the analysis could potentially be biased if the reason for not providing IPD is related to the treatment effect. The second is to carry out a meta-regression on the aggregate data. This would potentially mean all trials could be included, but the benefits of having some IPD would be forgone. Finally, it is quite conceivable that IPD may be available for all trials of some comparisons, while none may be available for others. This may be particularly true for single technology appraisals done by industry where a company may have complete access to trial data for their own products, but only aggregate data on competitors’ products (Signorovitch et al., 2012; Phillippo et al., 2016). Models have been developed that allow the incorporation of IPD where available and aggregate data where not (Riley et al., 2007b; Jansen, 2012; Saramago et al., 2012, 2014; Donegan et al., 2013). This approach allows all the data to be included at the most detailed level available from all the studies, but as for an IPD-only analysis, a decision has to be made on whether between-study variability is to be included in the estimation of effects. The difference between the effects using between- and within-study variability can be assessed and used to decide which approach to take, noting that in many contexts there will not be enough data to do this reliably. Models that allow the incorporation of IPD and aggregate data have been described for binary (Riley et al., 2007b; Sutton et al., 2008) and continuous (Riley et al., 2008) outcomes.
As described in Section 8.4, a decision has to be made on whether interaction effects with placebo/usual care are assumed to be the same, exchangeable or different across treatments. Although we have suggested a single interaction parameter for all treatments within the same class, models for all these possibilities can be constructed. Extensions to the dual within- and between-covariate models are possible, and there have been initial explorations of this (Saramago et al., 2011). The availability of IPD for several different treatments would allow a much more thorough investigation of whether patient-level interactions are the same across treatments, as well as linearity of interaction effects for continuous covariates (Donegan et al., 2012; Saramago et al., 2012, 2014).
8.6 Models with Treatment-Level Covariates
When patients are randomised to treatments at different doses, to treatments that belong to classes or to combinations of treatments, we may wish to express the relationship between relative treatment effects through a dose–response model, a class model or a treatment combination model. These models can be particularly useful when networks are sparse as they have fewer basic parameters than the standard network meta-analysis models described in Chapters 2 and 4, in which relative effects of every dose and every treatment and treatment combination compared with the reference are represented as a different basic parameter. This can have a large impact on network connectivity, since reducing the number of basic parameters may lead to a more connected network when data are sparse (Chapter 6) (Soares et al., 2012; Welton et al., 2015). However, as we stress in the following sections, the assumptions being made are strong and generally hard to check statistically and therefore require a high degree of clinical and empirical plausibility.
These types of model have previously been considered as meta-regression problems (Soares et al., 2012; Del Giovani et al., 2013; Fu et al., 2013; Thorlund et al., 2014; Welton et al., 2015), where dose has been added as a covariate. The basic parameters represent the treatment effects at zero or mean dose, requiring care in interpretation.
It should be noted that although similar in structure, these models are different from standard meta-regression models since patients are randomised to treatment with different doses, classes or combinations.
8.6.1 Accounting for Dose
We have previously noted that lumping across drug doses is to be avoided, as it may cause heterogeneity and make the results of any analysis difficult to interpret for decision making (Chapter 1). If each drug/dose combination is considered a different treatment in the network, that is, given its own treatment code, the standard network meta-analysis model on the appropriate scale can be used, as described in Chapters 2 and 4 (Cope et al., 2013; Naci et al., 2013a, 2013b; Alfirevic et al., 2015). This model does not make any assumption about the relationship between doses of the same treatment and is perhaps the least restrictive way of analysing data when patients are randomised to treatments at different doses. We suggest that this should usually be the base-case model. However, separating all the doses can lead to very sparse networks with limited information on the relative effects of each drug/dose combination.
The alternative is to make assumptions about the dose–response relationship within the same drug, thereby estimating fewer parameters, potentially resulting in more precise estimates (Mawdsley et al., 2016). We can think of this model as a model with a special kind of covariate, dose of drug, to which patients have been randomised to.
We begin by defining a treatment to be the actual drugs (compounds) or placebo, without reference to dose, and code these from 1 to S. As for the usual data set-up for the observed outcomes described in Chapter 4, the data structure describing the drug/dose combinations compared in each arm of each trial will consist of a treatment matrix t with elements tik holding the code for the drug compared in arm k of trial i and a dose matrix x with elements xik holding the dose of drug tik in arm k of trial i defined on some continuous scale (e.g. log dose or 1, 2, 3, etc.) that will be assumed linear, although the model could be extended to incorporate other functional forms. If a particular ‘drug’ is a placebo, then its dose should be set to zero (on the appropriate scale) to reflect the effect at zero dose of every drug. For no treatment arms, or for arms comparing treatments that do not really have doses (e.g. psychotherapy, regular monitoring, provide a leaflet), the corresponding element of the dose matrix should be set to a fixed number, say, 1, without loss of generality.
The generic network meta-analysis model described in equation (4.1) is the same, but now the basic parameters are the relative dose effects βk, (k = 1, …, S), reflecting the change in efficacy for a unit increase in the dose of treatment k when compared with placebo (i.e. the treatment at dose zero).
Thus for a linear dose model with random treatment effects, we use equation (4.2) where
and ![]() as before. For a fixed effects model, we write (equation (4.3))
as before. For a fixed effects model, we write (equation (4.3))
The dose effects are given non-informative prior distributions:
The generic WinBUGS code for fixed and random effects introduced in Chapter 4 needs to be changed so that wherever we had d[t[i,k]] - d[t[i,1]] we now write
beta[t[i,k]]*x[i,k] - beta[t[i,1]]*x[i,1]including in the code to correctly account for the correlation in multi-arm trials (see Chapter 2). Relative effects of treatments at different doses can be obtained by noting that the relative effect of drug b at dose Xb compared with the relative effect of treatment c at dose Xc can be written as ![]() . Thus if we wanted the relative effect of drug 3 at dose 100 mg compared with placebo (dose set to zero), we would have
. Thus if we wanted the relative effect of drug 3 at dose 100 mg compared with placebo (dose set to zero), we would have ![]() .
.
Note that whenever the reference drug (coded 1) is not a placebo, β1 will reflect changes per unit increase in dose of drug 1 and will need to be estimated. Thus using this formulation, we estimate (at most) S relative effect parameters, whereas previously we set one of the effects to zero.
In general, to inform the parameters of this type of model, trials comparing several dose/treatment combinations are needed. In addition, trials comparing multiple doses of the same treatment are particularly informative as they provide information on the dose-relationship without being subject to between-study heterogeneity.
Note also that while the dose model proposed here estimates one parameter per drug, the standard network meta-analysis model would estimate one relative effect per dose of drug, compared with the reference treatment, leading to potentially many more parameters to estimate.
Using the dose effects model may greatly reduce the parameter space, which can result in considerable gains in precision of the estimates. However, this comes at the expense of an assumption of linearity (or other functional form) of the dose effects for each treatment on the chosen scale, which should always be validated clinically and empirically where possible (Mawdsley et al., 2016). Assessment of model fit (Chapter 3) may also bring insights into the suitability of the model.
Alternative models could be used, including those that allow for a non-zero intercept. Care is then required when interpreting the results since the intercept would no longer represent the expected effect at zero dose. Such models may be useful when approximate linearity is expected within the range of observed doses, but results cannot then be extrapolated beyond the range of doses observed (viz. to placebo or dose zero).
8.6.2 Class Effects Models
Another type of model with treatment-level classification that appears similar to regression models is a class model (Dominici et al., 1999; Dakin et al., 2011; Haas et al., 2012; Kew et al., 2014; Mayo-Wilson et al., 2014; Soares et al., 2014; Warren et al., 2014). This is where we may have a network with S treatments, but the treatments fall into classes with similar modes of action, making it reasonable to assume that there is a relationship between the effects of treatments in the same class. The extent of this relationship can be defined in several ways. For example, we may assume that the treatments belonging to a class have identical relative effects when compared with treatments in other classes or that the relative effects of treatments with a class are exchangeable, that is, they come from a common distribution. These models allow borrowing of strength across treatments in the same class. Alternatively we may assume that there are in fact no class effects and a standard network meta-analysis model on each separate treatment should be used. It should be noted that these three different assumptions about the class model are very similar to the possible assumptions on the regression parameters described in Section 8.4.
Defining Dk as the class to which treatment k belongs, the generic network meta-analysis model described in equations (4.1) and (4.2) is the same, but now instead of giving non-informative prior distributions to the basic parameters (equation (2.10)), different assumptions are made.
For an exchangeable class effects model, the basic parameters are assumed to come from a distribution with a common mean and variance, if they belong to the same class:
The within-class standard deviations τk should be given suitable prior distributions for the scale under consideration. When fitting an exchangeable class effects model, comparisons of treatments within the same class are particularly valuable as they can inform the within-class variability. Sparse networks with no within-class comparisons and few loops may require informative prior distributions for the within-class variability τk, or further assumptions, for example, that the within-class variability is the same or exchangeable across some or all classes. All these different assumptions can be implemented in WinBUGS by making small changes to the generic network meta-analysis code presented in Chapter 4.
For the model where all treatments in a class are assumed to have the same effects (fixed class effects model), the basic parameters are assumed equal for all treatments in a class ![]() .
.
The within-class mean treatment effects are given vague prior distributions ![]() , k = 1, …, C, where C is the number of classes.
, k = 1, …, C, where C is the number of classes.
Class models can be useful when the main decision is which class of treatment to recommend, or when data are sparse, as they allow different levels of borrowing of strength within classes, depending on the assumptions being made. These models are particularly useful when the number of classes, C, is much lower than the number of treatments, S. Assessment of model fit and model comparison techniques (Chapter 3) should be used to compare models and assess the suitability of assumptions.
8.6.3 Treatment Combination Models
Another type of treatment-level structure that may be encountered is the case where W discrete treatment components A, B, C, D, … are defined, but some trials compare combinations of these, for example, B + D or B + C + D (Melendez-Torre et al., 2015). Examples include psychological intervention with multiple components (Welton et al., 2009b), combinations of drug treatments with different modes of action, designed to supplement each other, in chronic obstructive pulmonary disease (Riemsma et al., 2011; Mills et al., 2012; National Institute for Health and Care Excellence, 2012), interventions to encourage safe behaviours in the home (Cooper et al., 2012; Achana et al., 2015) and smoking cessation (Madan et al., 2014b).
Once again, if each component and combination is considered a different treatment in the network, that is, given its own treatment code, the standard network meta-analysis model on the appropriate scale can be used, as described in Chapters 2 and 4. Thus, if we had c combination interventions, the network would consist of S = W + c treatments. This does not make any assumption on the relationship between combinations of the same intervention but in some cases may lead to very sparse networks with limited information on the relative effects of each treatment.
The alternative is to make an assumption about the relationship between the relative treatment effects of single and combination interventions. A simple assumption might be that they are additive on the linear predictor scale, so that the effect of combining elements B + D compared with the reference treatment is the sum of the individual effects of B and D relative to the reference on a suitable scale (Welton et al., 2009b; Riemsma et al., 2011). The form of this relationship could be extended to include other forms, for example, multiplicative or proportional, although note that additivity on a logistic or log scale implies a multiplicative relationship on the original (e.g. probability) scale.
Defining treatment components 1, 2, …, S as the unique coding of interventions (single or combinations) where the first W treatments are single and the remaining are combinations of the single interventions, the generic network meta-analysis model described in equations (4.1) and (4.2) is the same, but now the non-informative prior distributions for the basic parameters (equation (2.10)) apply only to the first W treatments. The remaining relative effects implement the assumptions about the combination treatments. For example, if treatment W + 1 was a combination of treatments 2 and 4 (W ≥ 4), to implement an additive assumption, we could state that
and similar assumptions could be stated for the remaining combination treatments. These assumptions can be easily coded in WinBUGS by adding suitable expressions to the generic code in Chapter 4 (see Exercise 8.4).
Fitting these models can result in a large reduction in the number of relative effect parameters to estimate (from S − 1 to W − 1), leading to stronger inferences, particularly when there are few comparisons between the S treatments. However, we stress that the assumptions being made are quite strong and need to have clinical and empirical plausibility. Assessment of model fit and model comparison techniques (Chapter 3) should also be used.
8.7 Implications of Meta-Regression for Decision Making
The implications of using the meta-regression models proposed in Section 8.4 for decision making can be quite profound. In practice, there is seldom enough data to fit the independent, treatment-specific interaction models, although related and exchangeable interactions might seem at first sight to offer an attractive approach. The difficulty is that even with ample data, using either of these models in clinical practice or in decision making could lead to recommendations that are counter-intuitive and difficult to defend. The claim made by these models is that there are real differences between the relative efficacies of the treatments included in the synthesis at different covariate values. If the models for interactions in equations (8.4) and (8.5) were used as a basis for treatment recommendation, a strict application of incremental CEA could lead to different treatments being recommended for different values of the covariate. This might be considered perverse, unless the hypothesis of different interaction effects was shown to be statistically robust, which will usually require very large amount of data. More importantly, this hypothesis needs to be clinically plausible, for example, decisions made based on a measure of severity or subgroup (e.g. screened positive for some marker) for which it is clinically plausible that the effects will differ. In addition, definition of cut-points of continuous covariates for changing decisions could be controversial. For these reasons, it has been recommended that only models implementing equation (8.6), which assumes an identical interaction effect across all treatments with respect to the reference treatment, are used (Dias et al., 2011a, 2013b).
However, we do not completely rule out the alternative models with different or exchangeable interaction effects (Nixon et al., 2007; Cooper et al., 2009) as they can have an important role in exploratory analyses or hypothesis-forming exercises. One rationale for departing from the identical interaction effects model could be to allow for the same covariate effect for different treatments within the same class, but different covariate effects across classes (which may or may not be considered exchangeable). So, if treatment 1 is a standard or placebo treatment while the other treatments belong to ‘classes’, and can therefore be assumed similar within a class, we would have different interaction effects for elements of different classes relative to the reference treatment. For example, one might imagine one set of equal interaction terms for aspirin-based treatments for atrial fibrillation relative to placebo and another set of interactions for warfarin-based treatments relative to placebo (Cooper et al., 2009) and a further set of interactions for novel oral anticoagulants relative to placebo.
There are however situations where it is reasonable to propose the more restricted model. Rather than a single interaction term for all active treatments within a class, we could simply have a single interaction term for all active treatments, regardless of class. For example, some treatments are so effective that they can virtually eliminate symptoms. In this case it is almost inevitable that there will be an ‘interaction’ between severity and treatment efficacy, because the extent of improvement is inevitably greater in more severely affected patients. Note however that in such circumstances, choice of analysis scale can be important. In some circumstances use of a log scale may eliminate the need for a covariate (Button et al., 2015). Potential examples might be different classes of biologic therapy for inflammatory arthritis or perhaps certain treatments for pain relief. In these cases the ‘interaction’ may reflect a property of the scale of measurement rather than the pharmacological effects of the treatment. Informed clinical and scientific input to model formulation is, as ever, critical. Model fit should be assessed as described in Chapter 3, and if several candidate models are considered, the preferred model choice can also be chosen according to the methods described in Chapter 3.
Using baseline risk as a covariate also has implications for interpretability as well as decision making. Often it will not be possible to accurately determine the baseline risk attaching to a particular patient, so unless baseline risk can be quantified by measureable patient attributes, these regression models are not very useful for making decisions for individuals. However, a guideline or reimbursement agency, interested in making decisions for a particular population, may have access to information (e.g. from patient registries or hospital statistics) on the baseline risk (e.g. log odds of an event) of the population of interest on the current treatment. If this is the case, and the statistical analysis is sufficiently robust and convincing, results could be used to guide decisions on which treatment to recommend.
When considering models with subgroups, ideally, we would want to include clinically meaningful subgroup terms whether they had a 95% CrI for the interaction term that included zero or not, possibly using informative prior distributions elicited from clinical experts. However, the NICE Methods Guide (National Institute for Health and Clinical Excellence, 2008b) suggests that subgroup effects should be statistically robust if they are to be considered in a cost-effectiveness model, as well as having some a priori justification. In practice, it would be difficult to sustain an argument that a treatment should be accepted or rejected based on a statistically weak interaction; thus models allowing for subgroups should be interpreted with care (see Section 8.4.4).
Models that incorporate treatment-level covariates allow decision makers to appraise treatments across the values of the treatment-defining covariate. For example, dose–response models (Section 8.6.1) allow decision makers to identify the optimal (e.g. most cost-effective) dose, although care has to be taken not to extrapolate beyond the range of doses in the included RCTs, and to consider all outcomes (including adverse events). Some doses may not be licensed, and therefore do not form part of the decision set of treatment options, but can still form part of the evidence set that contributes to the estimation of relative treatment effects.
Class effects models (Section 8.6.2) are appealing when we might expect treatment effects to be similar within class. However, cost effectiveness may differ between treatments within a class, so decisions are usually made at the treatment rather than class level. This can be achieved by using the shrunken treatment effect within class to inform decision models. If there is little variability in costs and adverse event profiles between treatments within a class, then decisions may be made to recommend a class of treatments, leaving it to local commissioners to identify the lowest cost option within a class.
Models for components of complex interventions are helpful for understanding the ‘active ingredients’ that increase efficacy, which can be helpful in the development of new interventions. However, policy decisions need to be for ‘whole’ interventions that can be recommended and rolled out in practice. Treatment combination models (Section 8.6.3) can be used to estimate the overall efficacy of ‘whole’ interventions for use in decision models, although care should be taken to ensure any assumptions (e.g. additivity) are justified.
8.8 Summary and Further Reading
In this chapter we have outlined the basic concepts: trial-level versus patient-level characteristics, continuous versus discrete covariates, subgroups, baseline risk as a covariate and the reasons why IPD is far more valuable than aggregate data for studying interactions. We have shown how the generic network meta-analysis code presented in Chapter 4 should be adapted to perform network meta-regression and which extra modelling assumptions are required.
We have identified models for the treatment effect itself – dose–response models, class models and treatment combination models – as special forms of ‘meta-regression’ with slightly different properties. Rather than add a further regression ‘slope’ coefficient, representing an interaction between treatment effect and the covariate, to a treatment effect parameter that represents the ‘intercept’, these models all represent different assumptions imposed on the treatment effect terms.
Although we have shown that all the models are easy to code in WinBUGS, requiring only small changes to the generic network meta-analysis code presented in Chapter 4, it is nonetheless extremely important to ensure models are coded accurately since small changes in coding and even choice of reference treatment can lead to major changes in the model assumptions and interpretation of results. It is also important to take care to interpret the parameters adequately, noting, for example, whether the covariate was centred and which is the reference treatment.
As usual, the decision-making context has been emphasised. From a statistician’s perspective, models in which slope coefficients associated with different drugs are drawn from a random effects distribution elegantly express the very reasonable idea that similar products should have similar regression terms. However, for decision making in practice, this could create serious anomalies: a drug that is estimated to be the most effective in patients aged 75 might not be the most effective at age 60, and a third product might be best at age 45. One suspects that neither clinicians nor manufacturers would accept recommendations of this sort, unless of course they were supported by strong statistical evidence of real differences in regression slopes and strong a priori clinical plausibility.
Although the majority of work on meta-regression has been devoted to aggregate data, there is little doubt that IPD meta-analysis offers far greater insights. We would recommend to readers a careful look at some of the very fine applied work using IPD meta-analysis to throw light on the existence, or not, of covariate effects in pairwise meta-analyses (Collins et al., 1990; Berlin et al., 2002; Boutitie et al., 2002; Cholesterol Treatment Trialists’ Collaboration, 2010). A listing of pairwise IPD meta-analyses can be found at http://ipdmamg.cochrane.org/ipd-meta-analyses. There is not, as yet, a large body of applied work using IPD meta-regression with network meta-analysis, although there is a review of this area (Veroniki et al., 2015, 2016).
Some RCTs may report results by subgroups or for combinations of subgroups (collapsed categories). The methods described in Section 5.3.4 can be used to address this.
8.9 Exercises
- 8.1 Fit the fixed effects network meta-analysis model with covariate ‘absolute distance from the equator’ to the BCG example. Compare the fit of this model to the random effects models with and without covariate (Table 8.2). Note that the data are given in Ch8_BCG_Bi_logit_RE-x1.odc.
- 8.2 Consider the CZP example presented in Section 8.4.3.2 and the results displayed in Table 8.4. Note that the full data and code are given in Ch8_CZP_Bi_logit_RE-x1prior.odc.
- Fit the network meta-analysis model with covariate disease duration to the CZP example using a Uniform(0,5) prior distribution for the between-study standard deviation. Note the 95% CrI for
sdand compare it to the prior bounds. Note also the posterior density forsd. - Now fit the same model using an empirically based log-normal prior distribution, as suggested in table IV of Turner et al. (2015b). In this example the interventions are pharmacological compared with control, and we will assume the outcome is best categorised as ‘signs/symptoms reflecting continuation/end of condition’ (Turner et al., 2015b). Thus the suggested prior distribution for the between-study varianceis log-Normal(−2.06, 1.512). [If we instead wanted to classify the outcome as ‘general physical health indicators’, we would use log-Normal(−2.29, 1.532) (Turner et al., 2015b).] Note the 95% CrI and posterior density for
sd, model fit statistics and estimated treatment effects and regression coefficient and compare them to the results in a).
- Fit the network meta-analysis model with covariate disease duration to the CZP example using a Uniform(0,5) prior distribution for the between-study standard deviation. Note the 95% CrI for
- 8.3 Achana et al. (2013) fitted network meta-analysis models including baseline risk as a covariate to a dataset comprising 56 studies comparing four analgesics to reduce post-operative morphine consumption following major surgery. The outcome is the amount of morphine consumed over a 24 h period (in milligrams). The treatment network is in Figure 8.7 and the data are given in Ch8_Ex3_AchanaPaindata-original.txt. The augmented data, where treatment 1 arms with missing data are added to the two studies that did not include it, are given in Ch8_Ex3_AchanaPaindata-augmented.txt.
- Adapt the code for the random effects network meta-regression model accounting for baseline risk to incorporate a continuous outcome, which can be assumed to have a normal likelihood. Fit the three interaction models detailed in Section 8.4 (common interaction, exchangeable and independent interactions) to this dataset, ensuring that you predict the missing baseline risk for studies that do not include treatment 1. See if you can replicate the results in table III of Achana et al. (2013), namely, the results referring to models A1, B1 and C1 (Achana et al., 2013). Check that you can interpret the output correctly and that you know how ‘baseline risk’ is defined in this case.
- For comparison, now fit the model with the non-augmented data, ensuring that the baseline risk is corrected using the relative effect of the treatment in arm 1. Compare the results.

Figure 8.7 Pain data example (data from Achana et al., 2013): treatment network. Connecting lines indicate pairs of treatments that have been directly compared in randomised trials. The numbers on the lines indicate the numbers of trials making that comparison, and the numbers by the treatment names are the treatment codes used in the modelling.
- 8.4 Zangrillo et al. (2015) considered the hypothesis that the combination of total intravenous anaesthesia (TIVA) and volatile agents (Volatile) with the application of remote ischaemic preconditioning (Remote) would have an additive effect on survival after cardiac surgery. The outcome of interest was mortality at the longest available follow-up, and there were 26 studies where at least one event occurred, comparing four treatment strategies involving these three interventions. These are presented in the treatment network shown in Figure 8.8. Standard fixed and random effects network meta-analysis models were fitted, and the fixed effects model was preferred on the basis of the DIC. The code to fit this model, with the data included, is given in Ch8_Mort_FE_Bi_logit.odc. Adapt the code to fit a (fixed effects) treatment combination model with the assumption that the log odds ratios of TIVA + Remote and Remote + Volatile compared with TIVA are the sum of the log odds ratios of each component compared with TIVA (see Section 8.6.3). Compare results to those for the standard network meta-analysis code, noting model fit, relative effect estimates and their precision across the two models.

Figure 8.8 Mortality after cardiac surgery example (Zangrillo et al., 2015): treatment network. Connecting lines indicate pairs of treatments that have been directly compared in randomised trials. Solid lines represent two-arm studies, and the connected dotted lines represent a three-arm study. The numbers on the lines indicate the numbers of trials making each comparison, and the numbers by the treatment names are the treatment codes used in the modelling.
http://journals.plos.org/plosone/article?id=10.1371/journal.pone.0134264. Licensed under CC BY 4.0. https://creativecommons.org/licenses/by/4.0/
