Linear algebra is a fundamental set of mathematical tools that has applications in many areas of science and engineering. Consequently, linear algebra (LA) techniques also play an important role in the practice of financial programming, and they are frequently used throughout the area of financial engineering. LA techniques are frequently used in the development of trading strategies.

As C++ programmers, it is important to understand how the traditional methods of linear algebra can be integrated in financial applications. With this goal in mind, I present a few recipes that show how to use some of the most common LA algorithms along with other C++ libraries. In this chapter you will also learn how to integrate existing LA libraries into your code, with special attention to the uBLAS library included with boost.

Following are some topics that we cover in this set of recipes:

• Basic operations of linear algebra: you will learn how to use the fundamental functions of linear algebra in your code.
• BLAS library overview: BLAS is a well-known set of functions that are nowadays the standard for LA implementations. You will learn about the three levels of BLAS support along with their functionality.
• uBLAS: BLAS is function-based library, which has been used in languages such as Fortran and C. To use the higher-level concepts of modern C++, the boost project has created a new implementation . You will learn how the uBLAS library implements the same concepts present on BLAS.
• Computing determinants: calculating the determinant of a matrix is one of the most common tasks when analyzing a set of linear equations. You will learn how to use uBLAS to perform this type of LA computation.
• Converting between standard types and uBLAS types: you will see how to convert standard types such as std::vector into types that are more appropriate for LA computations.

Using Basic Linear Algebra Operations

Create a class that performs basic LA operations such as vector and scalar products.

Solution

Linear algebra has been used to solve a large number of engineering and scientific problems. As such, these concepts are frequently employed as part of financial applications. The basic level of computational linear algebra deals with scalars and vector, and with the operations allowed on these mathematical entities.

A scalar is a quantity that is composed of a single measurement. Normally, it doesn’t require the creation of a separate class, since it can be easily represented as an integer, a floating point, or a double number. Such quantities are also usually stored as a single element. Scalar numbers enjoy the associated traditional properties such as addition, subtraction, multiplication, and division.

The use of scalars needs no special treatment in C++ implementations, although certain classes may treat scalar parameters as a template argument, so that you can later work with different types. For example, the following is common on numeric libraries:

template <class Scalar>
class MyNumericClass {
    void aFunction(Scalar parameter);

public:
    Scalar m_internalVar;
};

In this case, the Scalar type acts as a placeholder for one of the types supported by C++, such as int, float, or long double. In this way, you can easily parameterize the numeric class according to the actual type needed for the computation, and avoid the unnecessary cast between numeric types, which can introduce unexpected errors to the computation.

The next level of LA operations includes the combination of vectors, using vector addition, vector product, and scalar multiplication. Initially, you may think about employing std::vector to perform such operations; however, std::vector is a general-purpose container that is not tuned for mathematical processing.

The traditional solution for LA implementation is using the BLAS (basic linear algebra programs) library. BLAS is a popular package that was originally implemented in Fortran but has since then become the standard for LA computation even for other languages. The C-language version was created with the use of the f2c converter from Fortran. Since many LA packages came to rely on the functionality provided by BLAS, other libraries have been created to emulate it whenever necessary.

In this section, I introduce a C++ library that implements much of the functionality of BLAS. The uBLAS library is part of boost, and can be accessed by including one of the header files such as <boost/numeric/ublas/vector.hpp>.

BLAS and similar libraries are organized according to support levels, ranging from 1 to 3. The BLAS support levels include the following:

• Level 1: support for operations using scalar numbers and vectors. At this level, the library offers support for numeric vectors in one dimension, with common operations such as scalar multiplication and vector product.
• Level 2: at the second level, BLAS-compatible libraries provide functions to perform computations involving vectors and matrices—for example, the common multiplication of a vector v by a matrix A, which can be performed (with different results) as with vA or Av.
• Level 3: the third level of BLAS is defined for matrix-matrix operations. It allows, for example, the multiplication of matrices.

These three levels of BLAS support have been implemented in several libraries inspired in the original BLAS. Such implementations are mostly created to effectively support new programming languages, architectures, and processors, while still maintaining compatibility with the many numeric algorithms that depend on BLAS. The purpose of a boost uBLAS library is to provide the same support levels of BLAS, while taking advantage of the expressive power provided by C++ classes and templates.

In this recipe, you will explore a class called VectorOperations, which is responsible for implementing level 1 BLAS operations. This means that it has to deal with vectors and scalar numbers, as well as the possible transformations allowed between them. From the documentation of BLAS, we have the following categories of operations:

• Swap: switch element from the first vector to the second vector.
• Scale: multiplies all elements of a vector by a single scalar number.
• Copy: performs a copy of elements of a first vector into a second, destination vector.
• Vector addition: returns a vector whose components are the element-wise additions of two input vectors.
• Dot product: performs the mathematical operation of inner vector product, which is defined for two vectors v and w using the following formula:

  

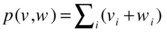
• Norm: the norm of a vector is a way to quantify the length of a vector in a particular direction. A common norm is the two-dimensional distance between two points.

In the implementation of VectorOperations, you will see how some of these operations can be accessed using uBLAS. The first such operation is vector multiplication by a scalar. The method signature is as follows:

std::vector<double> scalarMult(double scalar);

The goal of this method is to return a std::vector object where each member is a scaled version of the elements in the original vector. The implementation shows how to convert between these different vector types.

std::vector<double> VectorOperations::scalarMult(double scalar)
{
    using namespace boost::numeric::ublas;
    vector<double> vx;

    std::copy(m_data.begin(), m_data.end(), vx.end());

    vector<double> res = vx * scalar;

    std::vector<double> v;
    std::copy(res.begin(), res.end(), v.end());

    return v;
}

The first step is to create a vector from the boost::numeric::ublas namespace. Notice that this function employs the using declaration to avoid the boring sequence of namespaces. The next step is to make a copy from the original std::vector into the ublas vector. Finally, the scalar operation is performed using the multiplication operator. To store the result, a new ublas vector, called res, is constructed. The last step is to copy the result into a new vector and return the result.

The previous algorithm creates a lot of temporaries, and therefore it is not efficient for real implementations. However, the fact that we convert from standard vectors to ublas vectors has the advantage of bringing attention to what each vector type is capable of doing. When implementing more complicated LA algorithms, however, we should avoid the creation of any unnecessary temporary variables, since they can occupy a lot of space for large vectors and matrices.

The VectorOperations class presents similar examples for other common operations you will find on BLAS level 1, such as addVector and subtractVector, which use the ublas operators to quickly perform these computations. The dotProduct member function uses the inner_prod function from ublas to implement the dot product, also known as inner product operation between vectors. Finally, we have the example of the norm member function, which returns the length of the vector as defined with the norm_2 function.

Complete Code

The vector operations described in the previous section have been implemented in the VectorOperations class, displayed in Listing 7-1. You should be able to compile the class using any standards-compliant C++ compiler, after you install the boost libraries in your system.

Listing 7-1. VectorOperations.h and VectorOperations.cpp

//
//  VectorOperations.h

#ifndef __FinancialSamples__VectorOperations__
#define __FinancialSamples__VectorOperations__

#include <vector>

// performs operations on std::vector using boost ublas
class VectorOperations {
public:
    VectorOperations(const std::vector<double> &v);
    VectorOperations(const VectorOperations &p);
    ~VectorOperations();
    VectorOperations &operator=(const VectorOperations &p);
    std::vector<double> scalarMult(double scalar);
    std::vector<double> addVector(const std::vector<double> &v);
    std::vector<double> subtractVector(const std::vector<double> &v);
    double dotProd(const std::vector<double> &v);
    double norm();
private:
    std::vector<double> m_data;
};
#endif /* defined(__FinancialSamples__VectorOperations__) */

//
//  VectorOperations.cpp

#include "VectorOperations.h"

#include <boost/numeric/ublas/vector.hpp>

VectorOperations::VectorOperations(const std::vector<double> &p)
: m_data(p)
{
}

VectorOperations::VectorOperations(const VectorOperations &p)
: m_data(p.m_data)
{

}

VectorOperations::~VectorOperations()
{
}

VectorOperations &VectorOperations::operator=(const VectorOperations &p)
{
    if (this != &p)
    {
        m_data = p.m_data;
    }
    return *this;
}

std::vector<double> VectorOperations::scalarMult(double scalar)
{
    using namespace boost::numeric::ublas;
    vector<double> vx;

    std::copy(m_data.begin(), m_data.end(), vx.end());

    vector<double> res = vx * scalar;

    std::vector<double> v;
    std::copy(res.begin(), res.end(), v.end());

    return v;
}

std::vector<double> VectorOperations::addVector(const std::vector<double> &vec)
{
    using namespace boost::numeric::ublas;

    vector<double> v1;
    std::copy(m_data.begin(), m_data.end(), v1.end());

    vector<double> v2;
    std::copy(vec.begin(), vec.end(), v2.end());

    vector<double> v3 = v1 + v2;

    std::vector<double> v;
    std::copy(v3.begin(), v3.end(), v.end());
    return v;
}

double VectorOperations::norm()
{
    using namespace boost::numeric::ublas;

    vector<double> v1;
    std::copy(m_data.begin(), m_data.end(), v1.end());

    double res = norm_2(v1);
    return res;
}

std::vector<double> VectorOperations::subtractVector(const std::vector<double> &vec)
{
    using namespace boost::numeric::ublas;

    vector<double> v1;
    std::copy(m_data.begin(), m_data.end(), v1.end());

    vector<double> v2;
    std::copy(vec.begin(), vec.end(), v2.end());

    vector<double> v3 = v1 - v2;

    std::vector<double> v;
    std::copy(v3.begin(), v3.end(), v.end());
    return v;
}

double VectorOperations::dotProd(const std::vector<double> &v)
{

    using namespace boost::numeric::ublas;

    vector<double> v1;
    std::copy(m_data.begin(), m_data.end(), v1.end());

    vector<double> v2;
    std::copy(v.begin(), v.end(), v2.end());

    double res = inner_prod(v1, v2);
    return res;
}

Using Matrix-Oriented Operations

Create a class to perform matrix operations compatible with BLAS.

Solution

As you learned from Listing 7-1, LA functions are designed to work with linear operators that use scalar numbers, vectors, and matrices. To support these operations, programmers use a set of functions that are compatible with the original BLAS library. In C++, we can have access to a few libraries that implement BLAS, including the uBLAS library from boost, which you have been using so far.

The second level of BLAS is responsible for providing support for matrix-vector operations. In this recipe, you will see how to implement functions that use this level of BLAS. You will use boost uBLAS to access this functionality.

At level 2 of BLAS, the goal is to allow for the combination of vectors and matrices. To make this possible, uBLAS implements a few higher-level classes that incorporate concepts defined in the BLAS framework. Following are some of the most important classes used:

• Vector: this class was already discussed in the last recipe, and it acts as a general container for vector data. Some other classes implement restrictions on the generic functionality of vector.
• Sparse vector: a specialized version of a vector that allows for data represented in a sparse way. It can be used whenever the number of non-zero elements in a vector is small compared to the size of the array.
• Matrix: this is the main class that represents a two-dimensional arrangement of values, which is the traditional representation of a matrix.
• Triangular matrix: this class is used to represent matrices in which data is stored only on or above the main diagonal (for upper triangular matrices). You can also create lower triangular matrices with uBLAS.
• Symmetric matrix: this type of matrix has elements that are symmetric with respect to the diagonal. This class is used to represent this type of matrix on algorithms that take advantage of this property.
• Hermitian matrix: a Hermitian matrix has the property that its elements are complex numbers and there is a symmetry based on the notion of complex conjugate. That is, for each entry at position [i,j], the corresponding elements [j,i] are its complex conjugate.
• Banded matrix: this class represents sparse matrices where the non-zero elements are stored in a narrow band of elements around the main diagonal. The size of the band can be specified when creating the matrix.
• Sparse matrix: a class that represents a generic sparse matrix—that is, a matrix where most elements are zero. By using a sparse matrix, you can avoid the need to store in memory a large number of zero values.

Using these classes, you can easily store the data using the best representation available for the required task. Using the right representation can also give you a great advantage in finding the right algorithm, since uBLAS automatically provides special versions of its operators based on the data types used. For example, if a matrix is known to be triangular, it is possible to speed up some computations when solving a system of equations. This means that using a TriangularMatrix instead of a generic Matrix can result in a substantial speed-up for your code.

To explore the operations available for matrices, I introduce a class called MatrixOperations. This class is able to convert parameters into the classes required by uBLAS. It is also responsible for calling uBLAS operators on these converted parameters. Using this class you have an easy way to test several of the functions that operate on matrix parameters.

Among the main matrix-related functions and operators in uBLAS you will find the following:

• Scalar multiplication: multiplying a matrix by a scalar is a simple process, since it uses the standard multiplication operator in C++. You just need to save the result of the multiplication in a new matrix variable.
• Vector multiplication: Multiplying a matrix by a vector is a common operation. You can do this using the prod function. The product can be performed in two ways: a pre-multiplication requires that the vector be the first argument for the prod function. You can also post-multiply by a vector, in which case the vector enters as the second parameter to the prod function.
• Matrix multiplication: You can also multiply two matrices. This results in a third matrix, which has a size defined by the sizes of the two original matrices. You can perform the multiplication operation using an overridden version of the prod function.
• Element-wise multiplication: this operation performs the multiplication of each corresponding element in the matrix. That is, given matrices A and B, the resulting matrix C is composed of elements C[i,j] = A[i,j] + B[i,j].
• Transposition: the transpose of a matrix is a simple operation where elements A[i,j] and A[j,i] are exchanged. This results in a matrix that is the transposition of the original around the main diagonal.

In the MatrixOperations class you will find examples of each of these operations. The arguments and return values for the member functions of MatrixOperations are given in terms of standard vectors (std::vector) or Matrix objects (which you learned about in Chapter 5). While this kind of conversion should be avoided in high-performance code, you can take it as an example of what is necessary to create objects of the types declared in uBLAS.  Consider for instance the method transpose.

Matrix MatrixOperations::transpose()
{
        using namespace ublas;
        int d1 = m_rows.size();
        int d2 = m_rows[0].size();
        matrix<double> M(d1, d2);

        for (int i = 0; i < d1; ++i)
        {
                for (int j = 0; j < d2; ++j)
                {
                        M(i,j) = m_rows[i][j];
                }
        }

        matrix<double> mp = trans(M);
        return fromMatrix(mp);
}

The first step is to determine the size of the matrix you need to build, which is given by the dimensions d1 and d2. Using this information, you can create a new ublas::matrix object. You will then initialize the matrix using the data stored in the m_rows member variable. Finally, you can call the trans function from uBLAS, which is responsible for doing the transpose of its argument. The last step is to convert from the uBLAS representation into a Matrix object, which is performed by the fromMatrix function.

Complete Code

Listing 7-2 shows the implementation of the class MatrixOperations. The code makes use of the Matrix class implemented in Chapter 5, so you need to add it to your compilation line.

Listing 7-2. MatrixOperations.h and MatrixOperations.cpp

//
//  MatrixOperations.h

#ifndef __FinancialSamples__MatrixOperations__
#define __FinancialSamples__MatrixOperations__

#include <vector>

#include "Matrix.h"

class MatrixOperations {
public:
    MatrixOperations();
    ~MatrixOperations();
    MatrixOperations(const MatrixOperations &p);
    MatrixOperations &operator=(const MatrixOperations &p);

    void addRow(const std::vector<double> &row);
    Matrix multiply(Matrix &m);
    Matrix transpose();
    Matrix elementwiseMultiply(Matrix &m);
    Matrix scalarMultiply(double scalar);
    std::vector<double> preMultiply(const std::vector<double> &v);
    std::vector<double> postMultiply(const std::vector<double> &v);

private:
    std::vector<std::vector<double> > m_rows;
};

#endif /* defined(__FinancialSamples__MatrixOperations__) */

//
//  MatrixOperations.cpp

#include "MatrixOperations.h"

#include <boost/numeric/ublas/matrix.hpp>
#include <boost/numeric/ublas/io.hpp>
#include <boost/numeric/ublas/lu.hpp>

namespace ublas = boost::numeric::ublas;
using std::cout;
using std::endl;

MatrixOperations::MatrixOperations()
{
}

MatrixOperations::~MatrixOperations()
{
}

void MatrixOperations::addRow(const std::vector<double> &row)
{
        m_rows.push_back(row);
}

static Matrix fromMatrix(const ublas::matrix<double> &mp)
{
        using namespace ublas;

        int d1 = mp.size1();
        int d2 = mp.size2();
        Matrix res(d1, d2);
        for (int i = 0; i < d1; ++i)
        {
                for (int j = 0; j < d2; ++j)
                {
                        res[i][j] = mp(i,j);
                }
        }
        return res;
}

Matrix MatrixOperations::elementwiseMultiply(Matrix &m)
{
        using namespace ublas;
        int d1 = m_rows.size();
        int d2 = m_rows[0].size();
        matrix<double> M(d1, d2);

        for (int i = 0; i < d1; ++i)
        {
                for (int j = 0; j < d2; ++j)
                {
                        M(i,j) = m_rows[i][j];
                }
        }

        matrix<double> M2(d1, d2);
        for (int i = 0; i < d1; ++i)
        {
                for (int j = 0; j < d2; ++j)
                {
                        M2(i,j) = m[i][j];
                }
        }

        matrix<double> mp = element_prod(M, M2);
        return fromMatrix(mp);
}

Matrix MatrixOperations::transpose()
{
        using namespace ublas;
        int d1 = m_rows.size();
        int d2 = m_rows[0].size();
        matrix<double> M(d1, d2);

        for (int i = 0; i < d1; ++i)
        {
                for (int j = 0; j < d2; ++j)
                {
                        M(i,j) = m_rows[i][j];
                }
        }

        matrix<double> mp = trans(M);
        return fromMatrix(mp);
}

Matrix MatrixOperations::multiply(Matrix &m)
{
        using namespace ublas;
        int d1 = m_rows.size();
        int d2 = m_rows[0].size();
        matrix<double> M(d1, d2);

        for (int i = 0; i < d1; ++i)
        {
                for (int j = 0; j < d2; ++j)
                {
                        M(i,j) = m_rows[i][j];
                }
        }

        matrix<double> M2(d1, d2);
        for (int i = 0; i < d1; ++i)
        {
                for (int j = 0; j < d2; ++j)
                {
                        M2(i,j) = m[i][j];
                }
        }

    matrix<double> mp = prod(M, M2);
    return fromMatrix(mp);
}

Matrix MatrixOperations::scalarMultiply(double scalar)
{
        using namespace ublas;
        int d1 = m_rows.size();
        int d2 = m_rows[0].size();
        matrix<double> M(d1, d2);

        for (int i = 0; i < d1; ++i)
        {
                for (int j = 0; j < d2; ++j)
                {
                        M(i,j) = m_rows[i][j];
                }
        }

        matrix<double> mp = scalar * M;
        return fromMatrix(mp);
}

std::vector<double> MatrixOperations::preMultiply(const std::vector<double> &v)
{
        using namespace ublas;
        ublas::vector<double> vec;
        std::copy(v.begin(), v.end(), vec.end());

        int d1 = m_rows.size();
        int d2 = m_rows[0].size();
        ublas::matrix<double> M(d1, d2);

        for (int i = 0; i < d1; ++i)
        {
                for (int j = 0; j < d2; ++j)
                {
                        M(i,j) = m_rows[i][j];
                }
        }

        vector<double> pv = prod(vec, M);

        std::vector<double> res;
        std::copy(pv.begin(), pv.end(), res.end());
        return res;
}

std::vector<double> MatrixOperations::postMultiply(const std::vector<double> &v)
{
        using namespace ublas;
        ublas::vector<double> vec;
        std::copy(v.begin(), v.end(), vec.end());

        int d1 = m_rows.size();
        int d2 = m_rows[0].size();
        ublas::matrix<double> M(d1, d2);

        for (int i = 0; i < d1; ++i)
        {
                for (int j = 0; j < d2; ++j)
                {
                        M(i,j) = m_rows[i][j];
                }
        }

        vector<double> pv = prod(M, vec);

        std::vector<double> res;
        std::copy(pv.begin(), pv.end(), res.end());
        return res;
}

int main()
{
    MatrixOperations op;
    for (int i=0; i<5; ++i)
    {
        std::vector<double> row;
        for (int j=0; j<5; ++j)
        {
            row.push_back(sin((double)j+i));
        }
        op.addRow(row);
    }
    op.transpose();
    Matrix res = op.scalarMultiply(12);
    return 0;
}

Running the Application

The code shown in Listing 7-2 can be compiled using any standards-conforming C++ compiler. You need to have boost installed in your system to access uBLAS (I used version 1.55, tested on Windows MingW and Mac OS X). For example, using the gcc compiler on a UNIX system can be done with the following command:

gcc –o matrixOp matrixOperations.cpp

This will result in an application called matrixOp. You can run the resulting application as

./matrixOp

This will run the test main function, which should print out the result of the requested operations. In my system I got the following results:

0 10.0977 10.9116 1.69344 -9.08163
10.0977 10.9116 1.69344 -9.08163 -11.5071
10.9116 1.69344 -9.08163 -11.5071 -3.35299
1.69344 -9.08163 -11.5071 -3.35299 7.88384
-9.08163 -11.5071 -3.35299 7.88384 11.8723

Calculate the Determinant of a Matrix

Write C++ code to calculate the determinant of a matrix using the classes in uBLAS.

Solution

Calculating the determinant of a matrix is one of the .classic problems in LA theory. Among other things, this value is used to determine if a system of equations (as expressed by the matrix of coefficients) has a unique solution.

To be able to easily compute the determinant of a matrix in C++, you can use some of the classes and functions contained in the boost uBLAS library. These functions make use of the matrix class, which is one of the uBLAS internal representations for matrices.

A common solution for this kind of problem uses a simple but elegant algorithm that is taught in any course of linear algebra. The general idea is to use a recursive strategy to calculate the determinant of small submatrices, until you find the determinant of the complete matrix. The algorithm used by the computeDeterminant function, however, is computationally more efficient because it uses the result of lower-upper (LU) decomposition. LU decompositions are a way to factor a matrix into lower and upper triangular components.

The function lu_factorize returns zero if the matrix is non-singular, which means that it can be inverted and its corresponding linear system solved using Gaussian elimination. The matrix is subsequently rearranged using the Gaussian elimination procedure. Additionally, a permutation matrix is used to record the steps of the elimination procedure.

Considering this information, the algorithm for determinant computation is encoded in the function computeDeterminant. It uses the values stored in the main diagonal and the information in the permutation matrix to compute the corresponding determinant for the given matrix. You can see the complete algorithm for this method in the next section.

Complete Code

Listing 7-3 shows you an example for the uBLAS libraries. The function determinantSample uses some of the templates in uBLAS to calculate the determinant of a matrix, as described in the previous section.

Listing 7-3. file Determinant.cpp

//
// Determinant.cpp
#include <boost/numeric/ublas/matrix.hpp>
#include <boost/numeric/ublas/io.hpp>
#include <boost/numeric/ublas/lu.hpp>

namespace ublas = boost::numeric::ublas;
using std::cout;
using std::endl;

// The sign is calculated from a given permutation.
// Just flip the sign for each change in permutation.
int getDeterminantSign(const ublas::permutation_matrix<std::size_t>& pm)
{
    int sign = 1;
    for (int i = 0; i < pm.size(); ++i)
    {
        if (i != pm(i))
        {
            sign *= -1.0;
        }
    }
    return sign;
}

// returns the value of the determinant for matrix m
//
double computeDeterminant(ublas::matrix<double>& m)
{
    ublas::permutation_matrix<std::size_t> pm(m.size1());

    double det = 1.0;
    if (ublas::lu_factorize(m,pm))
    {
        det = 0.0;
    }
    else
    {
        for(int i = 0; i < m.size1(); i++)
        {
            det *= m(i,i);
        }
        det = det * getDeterminantSign(pm);
    }
    return det;
}

void determinantSample()
{
    ublas::matrix<double> M(3, 3);

    for (unsigned i = 0; i < M.size1() ; ++i)
    {
        for (unsigned j = 0; j < M.size2() ; ++j)
        {
            M(i,j) = sin(3 * j);
        }
    }

    double determinant = computeDeterminant(M);

    cout << " determinant value is " << determinant << " for matrix " << M << endl;
}

Conclusion

This chapter includes a few programming recipes for LA computation in C++. One of the goals in this presentation is to show how mathematically oriented code can be used by financial application programmers. Linear algebra is the basis for many of the computational techniques that will be explored in the next few chapters, such as mathematical programming and portfolio optimization.

In this chapter I first introduced some of the important libraries for linear algebra. Since linear algebra is such a specialized area, the best approach for programmers is to use code that contains well-tested components written by experts in the field. The standard for computational mathematics in the area of basic linear algebra is the BLAS library. Although BLAS is a Fortran and C library, its concepts have been translated into many other languages. In this chapter, you have explored uBLAS, a component of the boost libraries that implements the same levels of functionality supported by BLAS. It does it, however, using modern C++ techniques such as classes and templates. This can be viewed as an easier way to achieve the functionality of BLAS while at the same time supporting a high-level C++ interface.

The first example in Listing 7-1 shows how to use uBLAS to implement basic (level 1) operations on vectors and scalars. The class VectorOperations shows how these basic concepts can be invoked using the uBLAS framework.

More advanced operations are available for matrices. The second example (Listing 7-2) contains information and code examples of how to interact with matrices and vectors in uBLAS. Simple operations that can be easily performed by uBLAS include scalar and vector multiplication of matrices, transposition, and matrix-matrix multiplication.

Listing 7-3’s example shows a sample of how these concepts can be used together to calculate the determinant of a matrix. To facilitate the solution of this problem, you can use the LU factorization function provided by uBLAS. This shows how some of the sophisticated algorithms in these LA libraries can be easily used to solve practical problems.

In the next chapter we will continue to explore mathematical tools used in financial applications. I will show you a few recipes about interpolation, a technique that is frequently used to find trends in data sets, including financial data. Along with other computational techniques, interpolation is widely used in the development and analysis of trading strategies.