15
Designing Data Visualizations
Data visualization, when done well, allows you to reveal patterns in your data and communicate insights to your audience. This chapter describes the conceptual and design skills necessary to craft effective and expressive visual representations of your data. In doing so, it introduces skills for each of the following steps in the visualization process:
Understanding the purpose of visualization
Selecting a visual layout based on your question and data type
Choosing optimal graphical encodings for your variables
Identifying visualizations that are able to express your data
Improving the aesthetics (i.e., making it readable and informative)
15.1 The Purpose of Visualization
“The purpose of visualization is insight, not pictures.”1
1Card, S. K., Mackinlay, J. D., & Shneiderman, B. (1999). Readings in information visualization: Using vision to think. Burlington, MA: Morgan Kaufmann.
Generating visual displays of your data is a key step in the analytical process. While you should strive to design aesthetically pleasing visuals, it’s important to remember that visualization is a means to an end. Devising appropriate renderings of your data can help expose underlying patterns in your data that were previously unseen, or that were undetectable by other tests.
To demonstrate how visualization makes a distinct contribution to the data analysis process (beyond statistical tests), consider the canonical data set Anscombe’s Quartet (which is included with the R software as the data set anscombe). This data set consists of four pairs of x and y data: (x1, y1), (xx, y2), and so on. The data set is shown in Table 15.1.
Table 15.1 Anscombe’s Quartet: four data sets with two features each
x1 |
y1 |
x2 |
y2 |
x3 |
y3 |
x4 |
y4 |
|---|---|---|---|---|---|---|---|
10.00 |
8.04 |
10.00 |
9.14 |
10.00 |
7.46 |
8.00 |
6.58 |
8.00 |
6.95 |
8.00 |
8.14 |
8.00 |
6.77 |
8.00 |
5.76 |
13.00 |
7.58 |
13.00 |
8.74 |
13.00 |
12.74 |
8.00 |
7.71 |
9.00 |
8.81 |
9.00 |
8.77 |
9.00 |
7.11 |
8.00 |
8.84 |
11.00 |
8.33 |
11.00 |
9.26 |
11.00 |
7.81 |
8.00 |
8.47 |
14.00 |
9.96 |
14.00 |
8.10 |
14.00 |
8.84 |
8.00 |
7.04 |
6.00 |
7.24 |
6.00 |
6.13 |
6.00 |
6.08 |
8.00 |
5.25 |
4.00 |
4.26 |
4.00 |
3.10 |
4.00 |
5.39 |
19.00 |
12.50 |
12.00 |
10.84 |
12.00 |
9.13 |
12.00 |
8.15 |
8.00 |
5.56 |
7.00 |
4.82 |
7.00 |
7.26 |
7.00 |
6.42 |
8.00 |
7.91 |
5.00 |
5.68 |
5.00 |
4.74 |
5.00 |
5.73 |
8.00 |
6.89 |
The challenge of Anscombe’s Quartet is to identify differences between the four pairs of columns. For example, how does the (x1, y1) pair differ from the (x2, y2) pair? Using a nonvisual approach to answer this question, you could compute a variety of descriptive statistics for each set, as shown in Table 15.2. Given these six statistical assessments, these four data sets appear to be identical. However, if you graphically represent the relationship between each x and y pair, as in Figure 15.1, you reveal the distinct nature of their relationships.
Table 15.2 Anscombe’s Quartet: the (X, Y) pairs share identical summary statistics
Set |
Mean X |
Std. Deviation X |
Mean Y |
Std. Deviation Y |
Correlation |
Linear Fit |
|---|---|---|---|---|---|---|
1 |
9.00 |
3.32 |
7.50 |
2.03 |
0.82 |
y = 3 + 0.5x |
2 |
9.00 |
3.32 |
7.50 |
2.03 |
0.82 |
y = 3 + 0.5x |
3 |
9.00 |
3.32 |
7.50 |
2.03 |
0.82 |
y = 3 + 0.5x |
4 |
9.00 |
3.32 |
7.50 |
2.03 |
0.82 |
y = 3 + 0.5x |

While computing summary statistics is an important part of the data exploration process, it is only through visual representations that differences across these sets emerge. The simple graphics in Figure 15.1 expose variations in the distributions of x and y values, as well as in the relationships between them. Thus the choice of representation becomes paramount when analyzing and presenting data. The following sections introduce basic principles for making that choice.
15.2 Selecting Visual Layouts
The challenge of visualization, like many design challenges, is to identify an optimal solution (i.e., a visual layout) given a set of constraints. In visualization design, the primary constraints are:
The specific question of interest you are attempting to answer in your domain
The type of data you have available for answering that question
The limitations of the human visual processing system
The spatial limitations in the medium you are using (pixels on the screen, inches on the page, etc.)
This section focuses on the second of these constraints (data type); the last two constraints are addressed in Section 15.3 and Section 15.4. The first constraint (the question of interest) is closely tied to Chapter 10 on understanding data. Based on your domain, you need to hone in on a question of interest, and identify a data set that is well suited for answering your question. This section will expand upon the same data set and question from Chapter 10:
“What is the worst disease in the United States?”
As with the Anscombe’s Quartet example, most basic exploratory data questions can be reduced to investigating how a variable is distributed or how variables are related to one another. Once you have mapped from your question of interest to a specific data set, your visualization type will largely depend on the data type of your variables. The data type of each column—nominal, ordinal, or continuous—will dictate how the information can be represented. The following sections describe techniques for visually exploring each variable, as well as making comparisons across variables.
15.2.1 Visualizing a Single Variable
Before assessing relationships across variables, it is important to understand how each individual variable (i.e., column or feature) is distributed. The primary question of interest is often what does this variable look like? The specific visual layout you choose when answering this question will depend on whether the variable is categorical or continuous. To use the disease burden data set as an example, you may want to know what is the range of the number of deaths attributable to each disease.
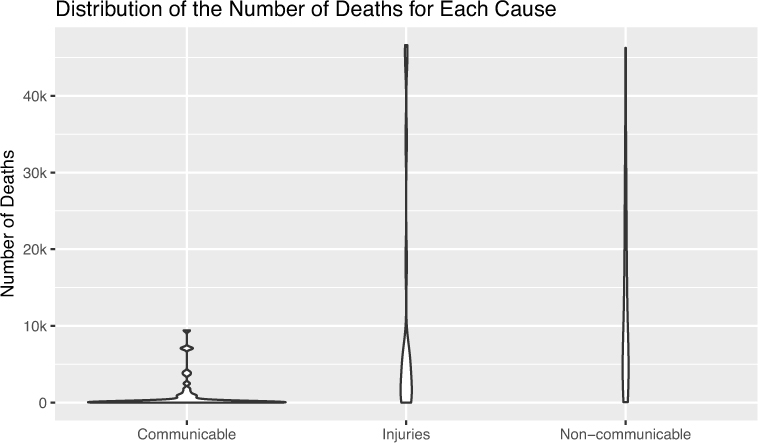
For continuous variables, a histogram will allow you to see the distribution and range of values, as shown in Figure 15.2. Alternatively, you can use a box plot or a violin plot, both of which are shown Figure 15.3. Note that outliers (extreme values) in the data set have been removed to better express the information in the charts.

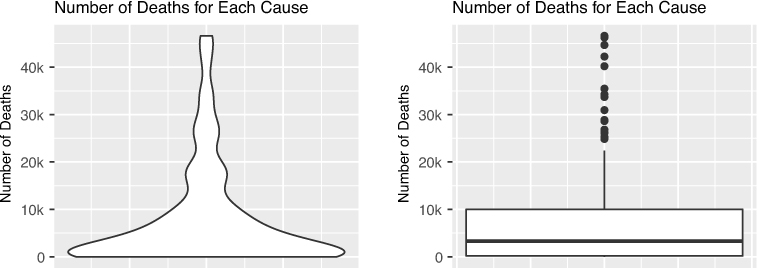
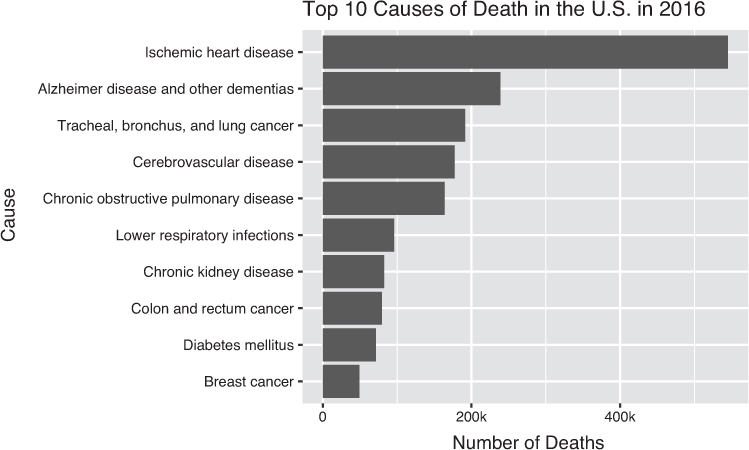
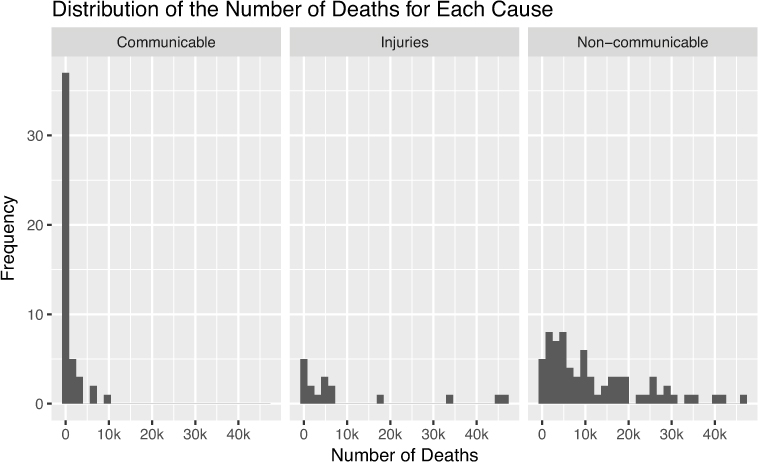
While these visualizations display information about the distribution of the number of deaths by cause, they all leave an obvious question unanswered: what are the names of these diseases? Figure 15.4 uses a bar chart to label the top 10 causes of death, but due to the constraint of the page size, this display is able to express just a small subset of the data. In other words, bar charts don’t easily scale to hundreds or thousands of observations because they are inefficient to scan, or won’t fit in a given medium.
15.2.1.1 Proportional Representations
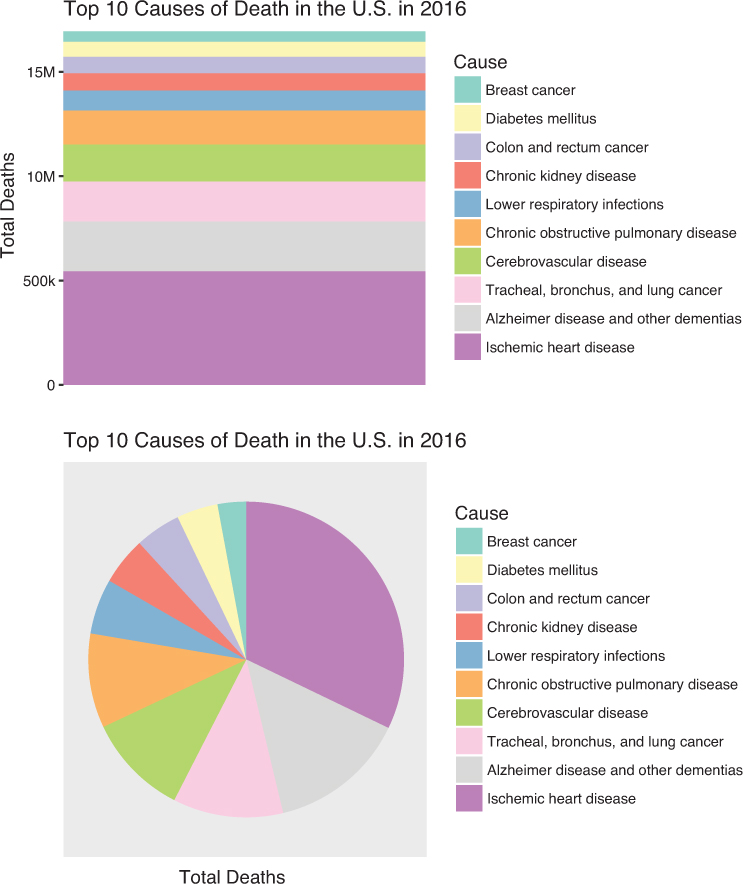
Depending on the data stored in a given column, you may be interested in showing each value relative to the total of the column. For example, using the disease burden data set, you may want to express each value proportional to the total number of deaths. This allows you answer the question, Of all deaths, what percentage is attributable to each disease? To do this, you can transform the data to percentages, or use a representation that more clearly expresses parts of a whole. Figure 15.5 shows the use of a stacked bar chart and a pie chart, both of which more intuitively express proportionality. You can also use a treemap, as shown later in Figure 15.14, though the true benefit of a treemap is expressing hierarchical data (more on this later in the chapter). Later sections explore the trade-offs in perceptual accuracy associated with each of these representations.
If your variable of interest is a categorical variable, you will need to aggregate your data (e.g., count the number of occurrences of different categories) to ask similar questions about the distribution.
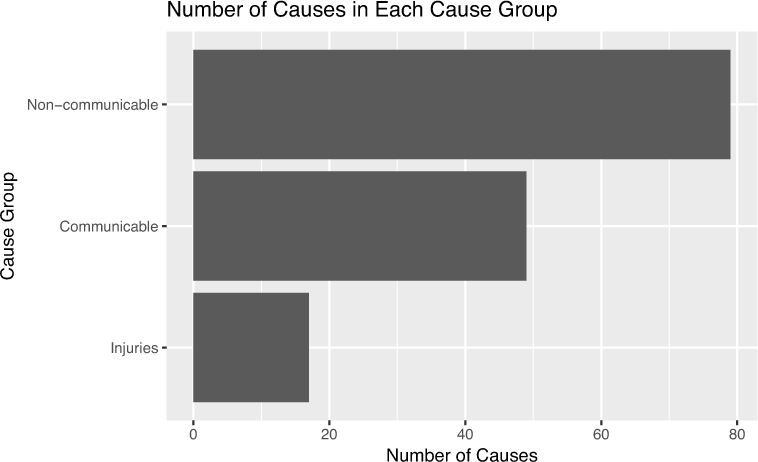
Once doing so, you can use similar techniques to show the data (e.g., bar chart, pie chart, treemap). For example, the diseases in this data set are categorized into three types of diseases: non-communicable diseases, such as heart disease or lung cancer; communicable diseases, such as tuberculosis or whooping cough; and injuries, such as road traffic accidents or self harm. To understand how this categorical variable (disease type) is distributed, you can count the number of rows for each category, then display those quantitative values, as in Figure 15.6.
15.2.2 Visualizing Multiple Variables
Once you have explored each variable independently, you will likely want to assess relationships between or across variables. The type of visual layout necessary for making these comparisons will (again) depend largely on the type of data you have for each variable.
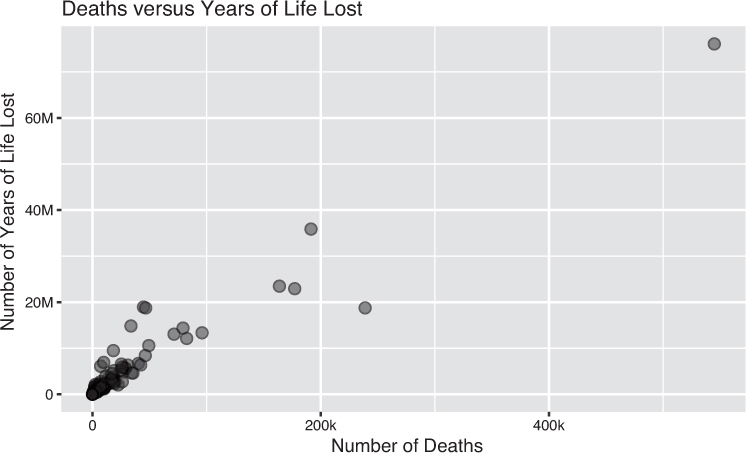
For comparing relationships between two continuous variables, the best choice is a scatterplot. The visual processing system is quite good at estimating the linearity in a field of points created by a scatterplot, allowing you to describe how two variables are related. For example, using the disease burden data set, you can compare different metrics for measuring health loss. Figure 15.7 compares the disease burden as measured by the number of deaths due to each cause to the number of years of life lost (a metric that accounts for the age at death for each individual).
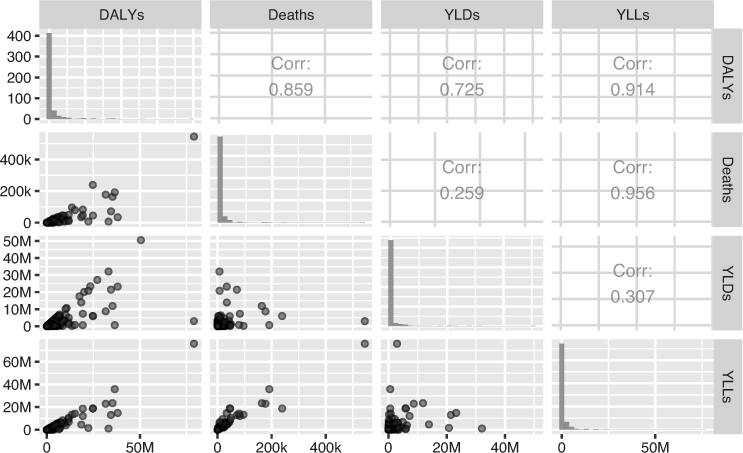
You can extend this approach to multiple continuous variables by creating a scatterplot matrix of all continuous features in the data set. Figure 15.8 compares all pairs of metrics of disease burden, including number of deaths, years of life lost (YLLs), years lived with disability (YLDs, a measure of the disability experienced by the population), and disability-adjusted life years (DALYs, a combined measure of life lost and disability).
When comparing relationships between one continuous variable and one categorical variable, you can compute summary statistics for each group (see Figure 15.6), use a violin plot to display distributions for each category (see Figure 15.9), or use faceting to show the distribution for each category (see Figure 15.10).
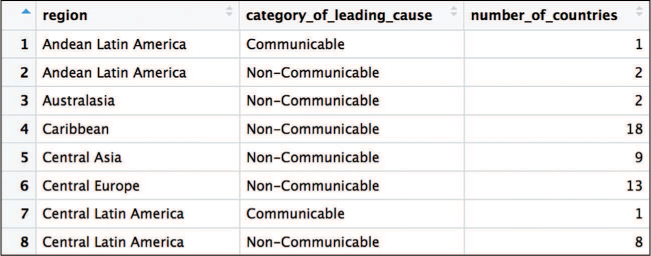
For assessing relationships between two categorical variables, you need a layout that enables you to assess the co-occurrences of nominal values (that is, whether an observation contains both values). A great way to do this is to count the co-occurrences and show a heatmap. As an example, consider a broader set of population health data that evaluates the leading cause of death in each country (also from the Global Burden of Disease study). Figure 15.11 shows a subset of this data, including the disease type (communicable, non-communicable) for each disease, and the region where each country is found.

One question you may ask about this categorical data is:
“In each region, how often is the leading cause of death a communicable disease versus a non-communicable disease?”
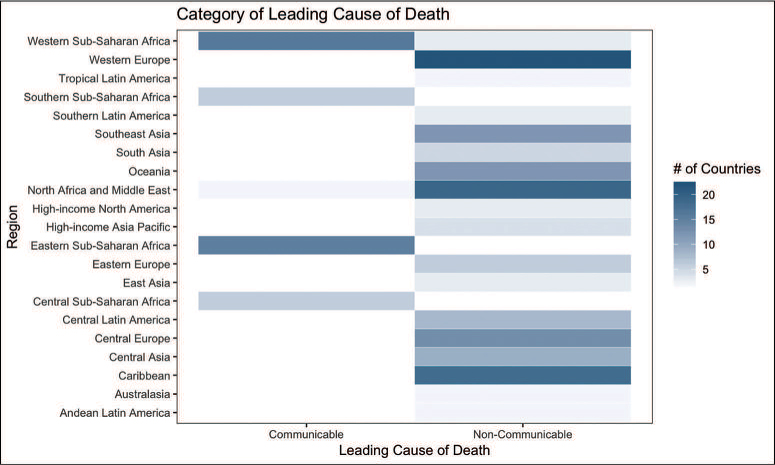
To answer this question, you can aggregate the data by region, and count the number of times each disease category (communicable, non-communicable) appears as the category for the leading cause of death. This aggregated data (shown in Figure 15.12) can then be displayed as a heatmap, as in Figure 15.13.
15.2.3 Visualizing Hierarchical Data
One distinct challenge is showing a hierarchy that exists in your data. If your data naturally has a nested structure in which each observation is a member of a group, visually expressing that hierarchy can be critical to your analysis. Note that there may be multiple levels of nesting for each observation (observations may be part of a group, and that group may be part of a larger group). For example, in the disease burden data set, each country is found within a particular region, which can be further categorized into larger groupings called super-regions. Similarly, each cause of death (e.g., lung cancer) is a member of a family of causes (e.g., cancers), which can be further grouped into overarching categories (e.g., non-communicable diseases). Hierarchical data can be visualized using treemaps (Figure 15.14), circle packing (Figure 15.15), sunburst diagrams (Figure 15.16), or other layouts. Each of these visualizations uses an area encoding to represent a numeric value. These shapes (rectangles, circles, or arcs) are organized in a layout that clearly expresses the hierarchy of information.
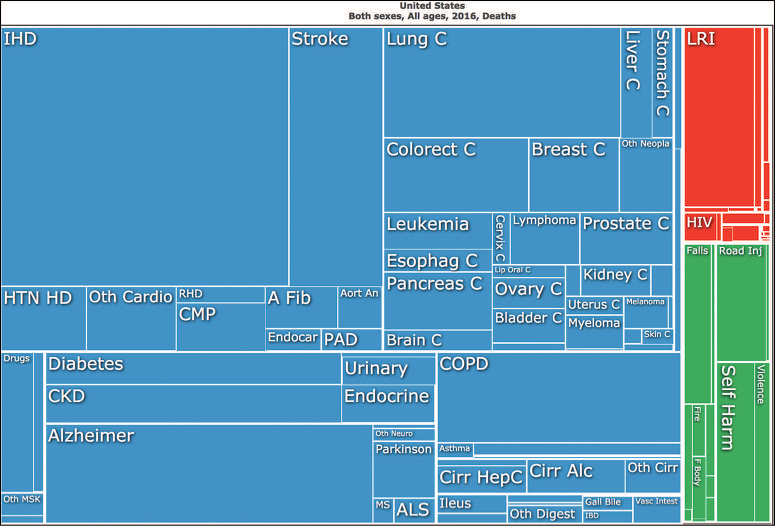
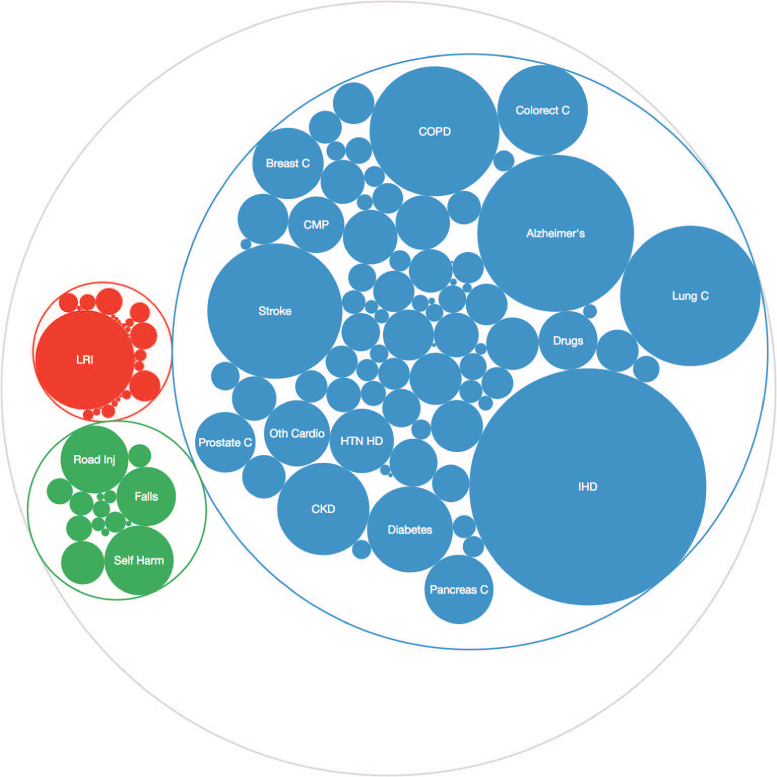
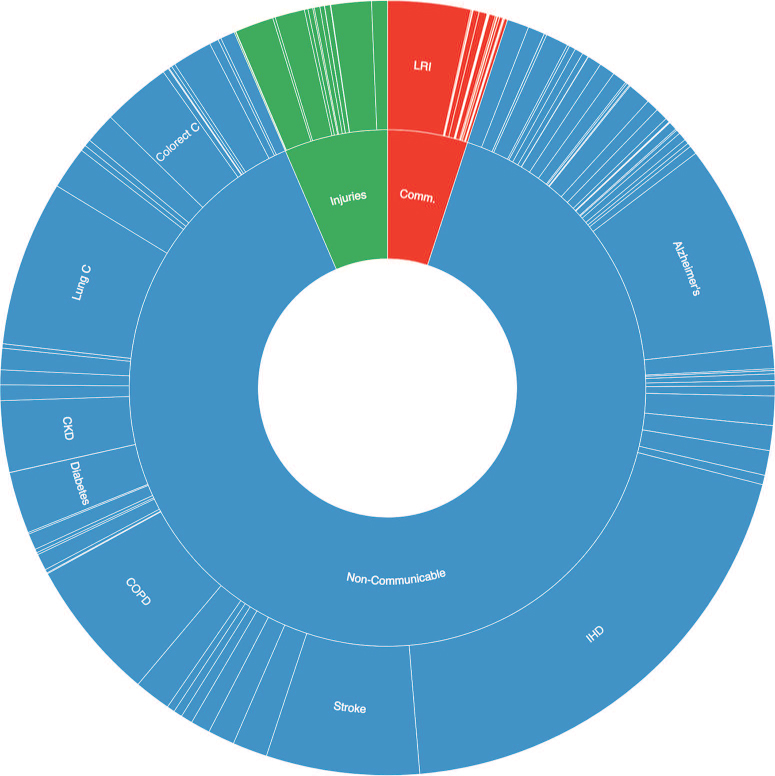
The benefit of visualizing the hierarchy of a data set, however, is not without its costs. As described in Section 15.3, it is quite difficult to visually decipher and compare values encoded in a treemap (especially with rectangles of different aspect ratios). However, these displays provide a great summary overview of hierarchies, which is an important starting point for visually exploring data.
15.3 Choosing Effective Graphical Encodings
While the previously given guidelines for selecting visual layouts based on the data relationship to explore are a good place to start, there are often multiple ways to represent the same data set. Representing data in another format (e.g., visually) is called encoding that data. When you encode data, you use a particular “code” such as color or size to represent each value. These visual representations are then visually decoded by anyone trying to interpret the underlying values.
Your task is thus to select the encodings that are most accurately decoded by users, answering the question:
“What visual form best allows you to exploit the human visual system and available space to accurately display your data values?”
In designing a visual layout, you should choose the graphical encodings that are most accurately visually decoded by your audience. This means that, for every value in your data, your user’s interpretation of that value should be as accurate as possible. The accuracy of these perceptions is referred to as the effectiveness of a graphical encoding. Academic research2 measuring the perceptiveness of different visual encodings has established a common set of possible encodings for quantitative information, listed here in order from most effective to least effective:
Position: the horizontal or vertical position of an element along a common scale
Length: the length of a segment, typically used in a stacked bar chart
Area: the area of an element, such as a circle or a rectangle, typically used in a bubble chart (a scatterplot with differently sized markers) or a treemap
Angle: the rotational angle of each marker, typically used in a circular layout like a pie chart
Color: the color of each marker, usually along a continuous color scale
Volume: the volume of a three-dimensional shape, typically used in a 3D bar chart
2Most notably, Cleveland, W. S., & McGill, R. (1984). Graphical perception: Theory, experimentation, and application to the development of graphical methods. Journal of the American Statistical Association, 79(387), 531–554. https://doi.org/10.1080/01621459.1984.10478080
As an example, consider the very simple data set in Table 15.3. An effective visualization of this data set would enable you to easily distinguish between the values of each group (e.g., between the values 10 and 11). While this identification is simple for a position encoding, detecting this 10% difference is very difficult for other encodings. Comparisons between encodings of this data set are shown in Figure 15.17.
Table 15.3 A simple data set to demonstrate the perceptiveness of different graphical encodings (shown in Figure 15.17). Users should be able to visually distinguish between these values.
group |
value |
a |
1 |
b |
10 |
c |
11 |
d |
7 |
e |
8 |

Thus when a visualization designer makes a blanket claim like “You should always use a bar chart rather than a pie chart,” the designer is really saying, “A bar chart, which uses position encoding along a common scale, is more accurately visually decoded compared to a pie chart (which uses an angle encoding).”
To design your visualization, you should begin by encoding the most important data features with the most accurately decoded visual features (position, then length, then area, and so on). This will provide you with guidance as you compare different chart options and begin to explore more creative layouts.
While these guidelines may feel intuitive, the volume and distribution of your data often make this task more challenging. You may struggle to display all of your data, requiring you to also work to maximize the expressiveness of your visualizations (see Section 15.4).
15.3.1 Effective Colors
Color is one of the most prominent visual encodings, so it deserves special consideration. To describe how to use color effectively in visualizations, it is important to understand how color is measured. While there are many different conceptualizations of color spaces, a useful one for visualization is the hue–saturation–lightness (HSL) model, which defines a color using three attributes:
The hue of a color, which is likely how you think of describing a color (e.g., “green” or “blue”)
The saturation or intensity of a color, which describes how “rich” the color is on a linear scale between gray (0%) and the full display of the hue (100%)
The lightness of the color, which describes how “bright” the color is on a linear scale from black (0%) to white (100%)
This color model can be seen in Figure 15.18, which is an example of an interactive color selector3 that allows you to manipulate each attribute independently to pick a color. The HSL model provides a good foundation for color selection in data visualization.
3HSL Calculator by w3schools: https://www.w3schools.com/colors/colors_hsl.asp

When selecting colors for visualization, the data type of your variable should drive your decisions. Depending on the data type (categorical or continuous), the purpose of your encoding will likely be different:
For categorical variables, a color encoding is used to distinguish between groups. Therefore, you should select colors with different hues that are visually distinct and do not imply a rank ordering.
For continuous variables, a color encoding is used to estimate values. Therefore, colors should be picked using a linear interpolation between color points (i.e., different lightness values).
Picking colors that most effectively satisfy these goals is trickier than it seems (and beyond the scope of this short section). But as with any other challenge in data science, you can build upon the open source work of other people. One of the most popular tools for picking colors (especially for maps) is Cynthia Brewer’s ColorBrewer.4 This tool provides a wonderful set of color palettes that differ in hue for categorical data (e.g., “Set3”) and in lightness for continuous data (e.g., “Purples”); see Figure 15.19. Moreover, these palettes have been carefully designed to be viewable to people with certain forms of color blindness. These palettes are available in R through the RColorBrewer package; see Chapter 16 for details on how to use this package as part of your visualization process.
4ColorBrewer: http://colorbrewer2.org
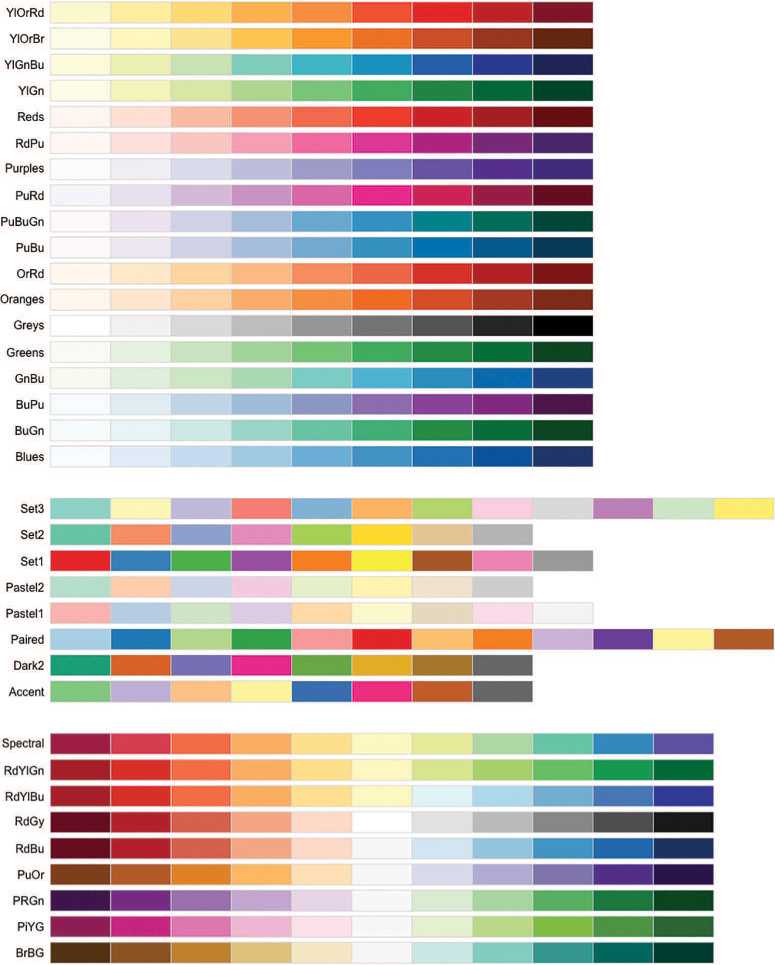
colorbrewer package in R. Run the display. brewer.all() function to see them in RStudio.
Selecting between different types of color palettes depends on the semantic meaning of the data. This choice is illustrated in Figure 15.20, which shows map visualizations of the population of each county in Washington state. The choice between different types of continuous color scales depends on the data:
Sequential color scales are often best for displaying continuous values along a linear scale (e.g., for this population data).
Diverging color scales are most appropriate when the divergence from a center value is meaningful (e.g., the midpoint is zero). For example, if you were showing changes in population over time, you could use a diverging scale to show increases in population using one hue, and decreases in population using another hue.
Multi-hue color scales afford an increase in contrast between colors by providing a broader color range. While this allows for more precise interpretations than a (single hue) sequential color scale, the user may misinterpret or misjudge the differences in hue if the scale is not carefully chosen.
Black and white color scales are equivalent to sequential color scales (just with a hue of gray!) and may be required for your medium (e.g., when printing in a book or newspaper).
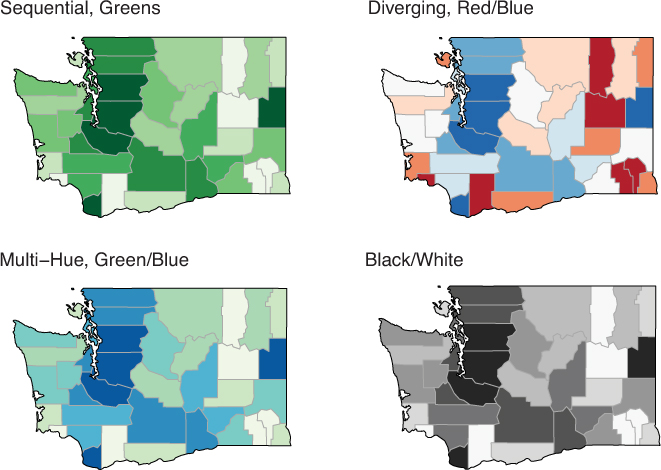
Figure 15.20 Population data in Washington represented with four ColorBrewer scales. The sequential and black/white scales accurately represent continuous data, while the diverging scale (inappropriately) implies divergence from a meaningful center point. Colors in the multi-hue scale may be misinterpreted as having different meanings.
Overall, the choice of color will depend on the data. Your goal is to make sure that the color scale chosen enables the viewer to most effectively distinguish between the data’s values and meanings.
15.3.2 Leveraging Preattentive Attributes
You often want to draw attention to particular observations in your visualizations. This can help you drive the viewer’s focus toward specific instances that best convey the information or intended interpretation (to “tell a story” about the data). The most effective way to do this is to leverage the natural tendencies of the human visual processing system to direct a user’s attention. This class of natural tendencies is referred to as preattentive processing: the cognitive work that your brain does without you deliberately paying attention to something. More specifically, these are the “[perceptual] tasks that can be performed on large multi-element displays in less than 200 to 250 milliseconds.”5 As detailed by Colin Ware,6 the visual processing system will automatically process certain stimuli without any conscious effort. As a visualization designer, you want to take advantage of visual attributes that are processed preattentively, making your graphics as rapidly understood as possible.
5Healey, C. G., & Enns, J. T. (2012). Attention and visual memory in visualization and computer graphics. IEEE Transactions on Visualization and Computer Graphics, 18(7), 1170–1188. https://doi.org/10.1109/TVCG.2011.127. Also at: https://www.csc2.ncsu.edu/faculty/healey/PP/
6Ware, C. (2012). Information visualization: Perception for design. Philadelphia, PA: Elsevier.
As an example, consider Figure 15.21, in which you are able to count the occurrences of the number 3 at dramatically different speeds in each graphic. This is possible because your brain naturally identifies elements of the same color (more specifically, opacity) without having to put forth any effort. This technique can be used to drive focus in a visualization, thereby helping people quickly identify pertinent information.
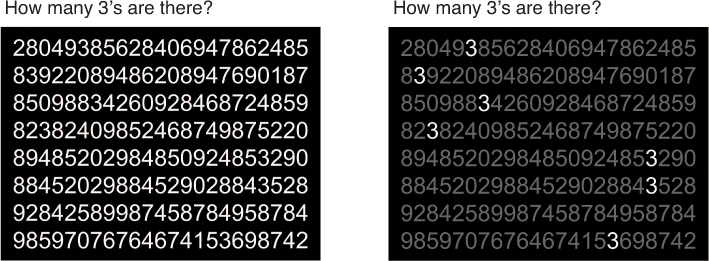
In addition to color, you can use other visual attributes that help viewers preattentively distinguish observations from those around them, as illustrated in Figure 15.22. Notice how quickly you can identify the “selected” point—though this identification happens more rapidly with some encodings (i.e., color) than with others!

As you can see, color and opacity are two of the most powerful ways to grab attention. However, you may find that you are already using color and opacity to encode a feature of your data, and thus can’t also use these encodings to draw attention to particular observations. In that case, you can consider the remaining options (e.g., shape, size, enclosure) to direct attention to a specific set of observations.
15.4 Expressive Data Displays
The other principle you should use to guide your visualization design is to choose layouts that allow you to express as much data as possible. This goal was originally articulated as Mackinlay’s Expressiveness Criteria7 (clarifications added):
7Mackinlay, J. (1986). Automating the design of graphical presentations of relational information. ACM Transactions on Graphics, 5(2), 110–141. https://doi.org/10.1145/22949.22950. Restatement by Jeffrey Heer.
A set of facts [data] is expressible in a language [visual layout] if that language contains a sentence [form] that
encodes all the facts in the set,
encodes only the facts in the set.
The prompt of this expressiveness aim is to devise visualizations that express all of (and only) the data in your data set. The most common barrier to expressiveness is occlusion (overlapping data points). As an example, consider Figure 15.23, which visualizes the distribution of the number of deaths attributable to different causes in the United States. This chart uses the most visually perceptive visual encoding (position), but fails to express all of the data due to the overlap in values.

There are two common approaches to address the failure of expressiveness caused by overlapping data points:
Adjust the opacity of each marker to reveal overlapping data.
Break the data into different groupings or facets to alleviate the overlap (by showing only a subset of the data at a time).
These approaches are both implemented in combination in Figure 15.24.
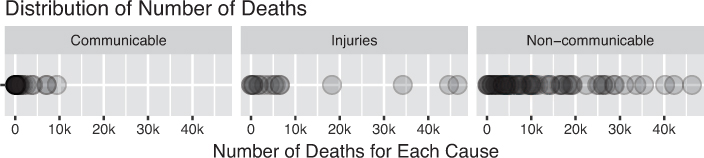
Alternatively, you could consider changing the data that you are visualizing by aggregating it in an appropriate way. For example, you could group your data by values that have similar number of deaths (putting each into a “bin”), and then use a position encoding to show the number of observations per bin. The result of this is the commonly used layout known as a histogram, as shown in Figure 15.25. While this visualization does communicate summary information to your audience, it is unable to express each individual observation in the data (which would communicate more information through the chart).
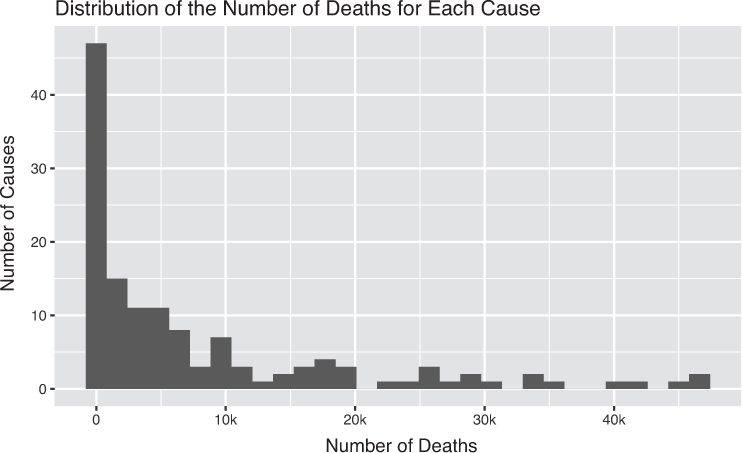
At times, the expressiveness and effectiveness principles are at odds with one another. In an attempt to maximize expressiveness (and minimize the overlap of your symbols), you may have to choose a less effective encoding. While there are multiple strategies for this—for example, breaking the data into multiple plots, aggregating the data, and changing the opacity of your symbols—the most appropriate choice will depend on the distribution and volume of your data, as well as the specific question you wish to answer.
15.5 Enhancing Aesthetics
Following the principles described in this chapter will go a long way in helping you devise informative visualizations. But to gain trust and attention from your potential audiences you will also want to spend time investing in the aesthetics (i.e., beauty) of your graphics.
Tip
Making beautiful charts is a practice of removing clutter, not adding design.
One of the most renowned data visualization theorists, Edward Tufte, frames this idea in terms of the data–ink ratio.8 Tufte argues that in every chart, you should maximize the ink dedicated to displaying the data (and in turn, minimize the non-data ink). This can translate to a number of actions:
8Tufte, E. R. (1986). The visual display of quantitative information. Cheshire, CT: Graphics Press.
Remove unnecessary encodings. For example, if you have a bar chart, the bars should have different colors only if that information isn’t otherwise expressed.
Avoid visual effects. Any 3D effects, unnecessary shading, or other distracting formatting should be avoided. Tufte refers to this as “chart junk.”
Include chart and axis labels. Provide a title for your chart, as well as meaningful labels for your axes.
Lighten legends/labels. Reduce the size or opacity of axis labels. Avoid using striking colors.
It’s easy to look at a chart such as the chart on the left side of Figure 15.26 and claim that it looks unpleasant. However, describing why it looks distracting and how to improve it can be more challenging. If you follow the tips in this section and strive for simplicity, you can remove unnecessary elements and drive focus to the data (as shown on the right-hand side of Figure 15.26).

Luckily, many of these optimal choices are built into the default R packages for visualization, or are otherwise readily implemented. That being said, you may have to adhere to the aesthetics of your organization (or your own preferences!), so choosing an easily configurable visualization package (such as ggplot2, described in Chapter 16) is crucial.
As you begin to design and build visualizations, remember the following guidelines:
Dedicate each visualization to answering a specific question of interest.
Select a visual layout based on your data type.
Choose optimal graphical encodings based on how well they are visually decoded.
Ensure that your layout is able to express your data.
Enhance the aesthetics by removing visual effects, and by including clear labels.
These guidelines will be a helpful start, and don’t forget that visualizations are about insights, not pictures.
