4
BLOCK CIPHERS

During the Cold War, the US and Soviets developed their own ciphers. The US government created the Data Encryption Standard (DES), which was adopted as a federal standard from 1979 to 2005, while the KGB developed GOST 28147-89, an algorithm kept secret until 1990 and still used today. In 2000, the US-based National Institute of Standards and Technology (NIST) selected the successor to DES, called the Advanced Encryption Standard (AES), an algorithm developed in Belgium and now found in most electronic devices. AES, DES, and GOST 28147-89 have something in common: they’re all block ciphers, a type of cipher that combines a core algorithm working on blocks of data with a mode of operation, or a technique to process sequences of data blocks.

This chapter reviews the core algorithms that underlie block ciphers, discusses their modes of operation, and explains how they all work together. It also discusses how AES works and concludes with coverage of a classic attack tool from the 1970s, the meet-in-the-middle attack, and a favorite attack technique of the 2000s—padding oracles.

What Is a Block Cipher?

A block cipher consists of an encryption algorithm and a decryption algorithm:

• The encryption algorithm (E) takes a key, K, and a plaintext block, P, and produces a ciphertext block, C. We write an encryption operation as C = E(K, P).
• The decryption algorithm (D) is the inverse of the encryption algorithm and decrypts a message to the original plaintext, P. This operation is written as P = D(K, C).

Since they’re the inverse of each other, the encryption and decryption algorithms usually involve similar operations.

Security Goals

If you’ve followed earlier discussions about encryption, randomness, and indistinguishability, the definition of a secure block cipher will come as no surprise. Again, we’ll define security as random-lookingness, so to speak.

In order for a block cipher to be secure, it should be a pseudorandom permutation (PRP), meaning that as long as the key is secret, an attacker shouldn’t be able to compute an output of the block cipher from any input. That is, as long as K is secret and random from an attacker’s perspective, they should have no clue about what E(K, P) looks like, for any given P.

More generally, attackers should be unable to discover any pattern in the input/output values of a block cipher. In other words, it should be impossible to tell a block cipher from a truly random permutation, given black-box access to the encryption and decryption functions for some fixed and unknown key. By the same token, they should be unable to recover a secure block cipher’s secret key; otherwise, they would be able to use that key to tell the block cipher from a random permutation. Of course that also implies that attackers can’t predict the plaintext that corresponds to a given ciphertext produced by the block cipher.

Block Size

Two values characterize a block cipher: the block size and the key size. Security depends on both values. Most block ciphers have either 64-bit or 128-bit blocks—DES’s blocks have 64 (2⁶) bits, and AES’s blocks have 128 (2⁷) bits. In computing, lengths that are powers of two simplify data processing, storage, and addressing. But why 2⁶ and 2⁷ and not 2⁴ or 2¹⁶ bits?

For one thing, it’s important that blocks are not too large in order to minimize both the length of ciphertext and the memory footprint. With regard to the length of the ciphertext, block ciphers process blocks, not bits. This means that in order to encrypt a 16-bit message when blocks are 128 bits, you’ll first need to convert the message into a 128-bit block, and only then will the block cipher process it and return a 128-bit ciphertext. The wider the blocks, the longer this overhead. As for the memory footprint, in order to process a 128-bit block, you need at least 128 bits of memory. This is small enough to fit in the registers of most CPUs or to be implemented using dedicated hardware circuits. Blocks of 64, 128, or even 512 bits are short enough to allow for efficient implementations in most cases. But larger blocks (for example, several kilobytes long) can have a noticeable impact on the cost and performance of implementations.

When ciphertexts’ length or memory footprint is critical, you may have to use 64-bit blocks, because these will produce shorter ciphertexts and consume less memory. Otherwise, 128-bit or larger blocks are better, mainly because 128-bit blocks can be processed more efficiently than 64-bit ones on modern CPUs and are also more secure. In particular, CPUs can leverage special CPU instructions in order to efficiently process one or more 128-bit blocks in parallel—for example, the Advanced Vector Extensions (AVX) family of instructions in Intel CPUs.

The Codebook Attack

While blocks shouldn’t be too large, they also shouldn’t be too small; otherwise, they may be susceptible to codebook attacks, which are attacks against block ciphers that are only efficient when smaller blocks are used. The codebook attack works like this with 16-bit blocks:

1. Get the 65536 (2¹⁶) ciphertexts corresponding to each 16-bit plaintext block.

2. Build a lookup table—the codebook—mapping each ciphertext block to its corresponding plaintext block.

3. To decrypt an unknown ciphertext block, look up its corresponding plaintext block in the table.

When 16-bit blocks are used, the lookup table needs only 2¹⁶ × 16 = 2²⁰ bits of memory, or 128 kilobytes. With 32-bit blocks, memory needs grow to 16 gigabytes, which is still manageable. But with 64-bit blocks, you’d have to store 2⁷⁰ bits (a zetabit, or 128 exabytes), so forget about it. Codebook attacks won’t be an issue for larger blocks.

How to Construct Block Ciphers

There are hundreds of block ciphers but only a handful of techniques to construct one. First, a block cipher used in practice isn’t a gigantic algorithm but a repetition of rounds, a short sequence of operations that is weak on its own but strong in number. Second, there are two main techniques to construct a round: substitution–permutation networks (as in AES) and Feistel schemes (as in DES). In this section, we look at how these work, after viewing an attack that works when all rounds are identical to each other.

A Block Cipher’s Rounds

Computing a block cipher boils down to computing a sequence of rounds. In a block cipher, a round is a basic transformation that is simple to specify and to implement, and which is iterated several times to form the block cipher’s algorithm. This construction, consisting of a small component repeated many times, is simpler to implement and to analyze than a construction that would consist of a single huge algorithm.

For example, a block cipher with three rounds encrypts a plaintext by computing C = R₃(R₂(R₁(P))), where the rounds are R₁, R₂, and R₃ and P is a plaintext. Each round should also have an inverse in order to make it possible for a recipient to compute back to plaintext. Specifically, P = iR₁(iR₂(iR₃(C))), where iR₁ is the inverse of R₁, and so on.

The round functions—R₁, R₂, and so on—are usually identical algorithms, but they are parameterized by a value called the round key. Two round functions with two distinct round keys will behave differently, and therefore will produce distinct outputs if fed with the same input.

Round keys are keys derived from the main key, K, using an algorithm called a key schedule. For example, R₁ takes the round key K₁, R₂ takes the round key K₂, and so on.

Round keys should always be different from each other in every round. For that matter, not all round keys should be equal to the key K. Otherwise, all the rounds would be identical and the block cipher would be less secure, as described next.

The Slide Attack and Round Keys

In a block cipher, no round should be identical to another round in order to avoid a slide attack. Slide attacks look for two plaintext/ciphertext pairs (P₁, C₁) and (P₂, C₂), where P₂ = R(P₁) if R is the cipher’s round (see Figure 4-1). When rounds are identical, the relation between the two plaintexts, P₂ = R(P₁), implies the relation C² = R(C₁) between their respective ciphertexts. Figure 4-1 shows three rounds, but the relation C² = R(C₁) will hold no matter the number of rounds, be it 3, 10, or 100. The problem is that knowing the input and output of a single round often helps recover the key. (For details, read the 1999 paper by Biryukov and Wagner called “Advanced Slide Attacks,” available at https://www.iacr.org/archive/eurocrypt2000/1807/18070595-new.pdf)

The use of different round keys as parameters ensures that the rounds will behave differently and thus foil slide attacks.

Figure 4-1: The principle of the slide attack, against block ciphers with identical rounds

Substitution–Permutation Networks

If you’ve read textbooks about cryptography, you’ll undoubtedly have read about confusion and diffusion. Confusion means that the input (plaintext and encryption key) undergoes complex transformations, and diffusion means that these transformations depend equally on all bits of the input. At a high level, confusion is about depth whereas diffusion is about breadth. In the design of a block cipher, confusion and diffusion take the form of substitution and permutation operations, which are combined within substitution–permutation networks (SPNs).

Substitution often appears in the form of S-boxes, or substitution boxes, which are small lookup tables that transform chunks of 4 or 8 bits. For example, the first of the eight S-boxes of the block cipher Serpent is composed of the 16 elements (3 8 f 1 a 6 5 b e d 4 2 7 0 9 c), where each element represents a 4-bit nibble. This particular S-box maps the 4-bit nibble 0000 to 3 (0011), the 4-bit nibble 0101 (5 in decimal) to 6 (0110), and so on.

The permutation in a substitution–permutation network can be as simple as changing the order of the bits, which is easy to implement but doesn’t mix up the bits very much. Instead of a reordering of the bits, some ciphers use basic linear algebra and matrix multiplications to mix up the bits: they perform a series of multiplication operations with fixed values (the matrix’s coefficients) and then add the results. Such linear algebra operations can quickly create dependencies between all the bits within a cipher and thus ensure strong diffusion. For example, the block cipher FOX transforms a 4-byte vector (a, b, c, d) to (a′, b′, c′, d′), defined as follows:

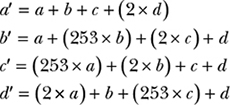
In the above equations, the numbers 2 and 253 are interpreted as binary polynomials rather than integers; hence, additions and multiplications are defined a bit differently than what we’re used to. For example, instead of having 2 + 2 = 4, we have 2 + 2 = 0. Regardless, the point is that each byte in the initial state affects all 4 bytes in the final state.

Feistel Schemes

In the 1970s, IBM engineer Horst Feistel designed a block cipher called Lucifer that works as follows:

1. Split the 64-bit block into two 32-bit halves, L and R.

2. Set L to L ⊕ F(R), where F is a substitution–permutation round.

3. Swap the values of L and R.

4. Go to step 2 and repeat 15 times.

5. Merge L and R into the 64-bit output block.

This construction became known as a Feistel scheme, as shown in Figure 4-2. The left side is the scheme as just described; the right side is a functionally equivalent representation where, instead of swapping L and R, rounds alternate the operations L = L ⊕ F(R) and R = R ⊕ F(L).

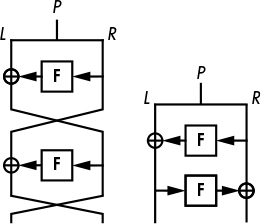
Figure 4-2: The Feistel scheme block cipher construction in two equivalent forms

I’ve omitted the keys from Figure 4-2 to simplify the diagrams, but note that the first F takes a first round key, K₁, and the second F takes another round key, K₂. In DES, the F functions take a 48-bit round key, which is derived from the 56-bit key, K.

In a Feistel scheme, the F function can be either a pseudorandom permutation (PRP) or a pseudorandom function (PRF). A PRP yields distinct outputs for any two distinct inputs, whereas a PRF will have values X and Y for which F(X) = F(Y). But in a Feistel scheme, that difference doesn’t matter as long as F is cryptographically strong.

How many rounds should there be in a Feistel scheme? Well, DES performs 16 rounds, whereas GOST 28147-89 performs 32 rounds. If the F function is as strong as possible, four rounds are in theory sufficient, but real ciphers use more rounds to defend against potential weaknesses in F.

The Advanced Encryption Standard (AES)

AES is the most-used cipher in the universe. Prior to the adoption of AES, the standard cipher in use was DES, with its ridiculous 56-bit security, as well as the upgraded version of DES known as Triple DES, or 3DES.

Although 3DES provides a higher level of security (112-bit security), it’s inefficient because the key needs to be 168 bits long in order to get 112-bit security, and it’s slow in software (DES was created to be fast in integrated circuits, not on mainstream CPUs). AES fixes both issues.

NIST standardized AES in 2000 as a replacement for DES, at which point it became the world’s de facto encryption standard. Most commercial encryption products today support AES, and the NSA has approved it for protecting top-secret information. (Some countries do prefer to use their own cipher, largely because they don’t want to use a US standard, but AES is actually more Belgian than it is American.)

AES Internals

AES processes blocks of 128 bits using a secret key of 128, 192, or 256 bits, with the 128-bit key being the most common because it makes encryption slightly faster and because the difference between 128- and 256-bit security is meaningless for most applications.

Figure 4-3: The internal state of AES viewed as a 4 × 4 array of 16 bytes

Whereas some ciphers work with individual bits or 64-bit words, AES manipulates bytes. It views a 16-byte plaintext as a two-dimensional array of bytes (s = s₀, s₁, . . . , s₁₅), as shown in Figure 4-3. (The letter s is used because this array is called the internal state, or just state.) AES transforms the bytes, columns, and rows of this array to produce a final value that is the ciphertext.

In order to transform its state, AES uses an SPN structure like the one shown in Figure 4-4, with 10 rounds for 128-bit keys, 12 for 192-bit keys, and 14 for 256-bit keys.

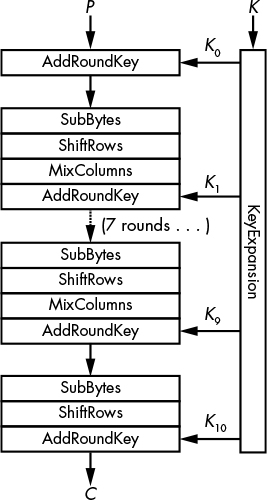
Figure 4-4: The internal operations of AES

Figure 4-4 shows the four building blocks of an AES round (note that all but the last round are a sequence of SubBytes, ShiftRows, MixColumns, and AddRoundKey):

AddRoundKey XORs a round key to the internal state.

SubBytes Replaces each byte (s₀, s₁, . . . , s₁₅) with another byte according to an S-box. In this example, the S-box is a lookup table of 256 elements.

ShiftRows Shifts the ith row of i positions, for i ranging from 0 to 3 (see Figure 4-5).

MixColumns Applies the same linear transformation to each of the four columns of the state (that is, each group of cells with the same shade of gray, as shown on the left side of Figure 4-5).

Remember that in an SPN, the S stands for substitution and the P for permutation. Here, the substitution layer is SubBytes and the permutation layer is the combination of ShiftRows and MixColumns.

The key schedule function KeyExpansion, shown in Figure 4-4, is the AES key schedule algorithm. This expansion creates 11 round keys (K₀, K₁, . . . , K₁₀) of 16 bytes each from the 16-byte key, using the same S-box as SubBytes and a combination of XORs. One important property of KeyExpansion is that given any round key, K_i, an attacker can determine all other round keys as well as the main key, K, by reversing the algorithm. The ability to get the key from any round key is usually seen as an imperfect defense against side-channel attacks, where an attacker may easily recover a round key.

Figure 4-5: ShiftRows rotates bytes within each row of the internal state.

Without these operations, AES would be totally insecure. Each operation contributes to AES’s security in a specific way:

• Without KeyExpansion, all rounds would use the same key, K, and AES would be vulnerable to slide attacks.
• Without AddRoundKey, encryption wouldn’t depend on the key; hence, anyone could decrypt any ciphertext without the key.
• SubBytes brings nonlinear operations, which add cryptographic strength. Without it, AES would just be a large system of linear equations that is solvable using high-school algebra.
• Without ShiftRows, changes in a given column would never affect the other columns, meaning you could break AES by building four 2³²-element codebooks for each column. (Remember that in a secure block cipher, flipping a bit in the input should affect all the output bits.)
• Without MixColumns, changes in a byte would not affect any other bytes of the state. A chosen-plaintext attacker could then decrypt any ciphertext after storing 16 lookup tables of 256 bytes each that hold the encrypted values of each possible value of a byte.

Notice in Figure 4-4 that the last round of AES doesn’t include the MixColumns operation. That operation is omitted in order to save useless computation: because MixColumns is linear (meaning, predictable), you could cancel its effect in the very last round by combining bits in a way that doesn’t depend on their value or the key. SubBytes, however, can’t be inverted without the state’s value being known prior to AddRoundKey.

To decrypt a ciphertext, AES unwinds each operation by taking its inverse function: the inverse lookup table of SubBytes reverses the SubBytes transformation, ShiftRow shifts in the opposite direction, MixColumns’s inverse is applied (as in the matrix inverse of the matrix encoding its operation), and AddRoundKey’s XOR is unchanged because the inverse of an XOR is another XOR.

AES in Action

To try encrypting and decrypting with AES, you can use Python’s crypto­graphy library, as in Listing 4-1.

#!/usr/bin/env python

from cryptography.hazmat.primitives.ciphers import Cipher, algorithms, modes
from cryptography.hazmat.backends import default_backend
from binascii import hexlify as hexa
from os import urandom

# pick a random 16-byte key using Python's crypto PRNG
k = urandom(16)
print "k = %s" % hexa(k)
# create an instance of AES-128 to encrypt a single block
cipher = Cipher(algorithms.AES(k), modes.ECB(), backend = default_backend())
aes_encrypt = cipher.encryptor()

# set plaintext block p to the all-zero string
p = 'x00'*16
# encrypt plaintext p to ciphertext c
c = aes_encrypt.update(p) + aes_encrypt.finalize()
print "enc(%s) = %s" % (hexa(p), hexa(c))
# decrypt ciphertext c to plaintext p
aes_decrypt = cipher.decryptor()
p = aes_decrypt.update(c) + aes_decrypt.finalize()
print "dec(%s) = %s" % (hexa(c), hexa(p))

Listing 4-1: Trying AES with Python’s cryptography library

Running this script produces something like the following output:

$ ./aes_block.py
k = 2c6202f9a582668aa96d511862d8a279
enc(00000000000000000000000000000000) = 12b620bb5eddcde9a07523e59292a6d7
dec(12b620bb5eddcde9a07523e59292a6d7) = 00000000000000000000000000000000

You’ll get different results because the key is randomized at every new execution.

Implementing AES

Real AES software works differently than the algorithm shown in Figure 4-4. You won’t find production-level AES code calling a SubBytes() function, then a ShiftRows() function, and then a MixColumns() function because that would be inefficient. Instead, fast AES software uses special techniques called table-based implementations and native instructions.

Table-Based Implementations

Table-based implementations of AES replace the sequence SubBytes-ShiftRows-MixColumns with a combination of XORs and lookups in tables hardcoded into the program and loaded in memory at execution time. This is possible because MixColumns is equivalent to XORing four 32-bit values, where each depends on a single byte from the state and on SubBytes. Thus, you can build four tables with 256 entries each, one for each byte value, and implement the sequence SubBytes-MixColumns by looking up four 32-bit values and XORing them together.

For example, the table-based C implementation in the OpenSSL toolkit looks like Listing 4-2.

    /* round 1: */
    t0 = Te0[s0 >> 24] ^ Te1[(s1 >> 16) & 0xff] ^ Te2[(s2 >> 8) & 0xff] ^ Te3[s3 & 0xff] ^ rk[ 4];
    t1 = Te0[s1 >> 24] ^ Te1[(s2 >> 16) & 0xff] ^ Te2[(s3 >> 8) & 0xff] ^ Te3[s0 & 0xff] ^ rk[ 5];
    t2 = Te0[s2 >> 24] ^ Te1[(s3 >> 16) & 0xff] ^ Te2[(s0 >> 8) & 0xff] ^ Te3[s1 & 0xff] ^ rk[ 6];
    t3 = Te0[s3 >> 24] ^ Te1[(s0 >> 16) & 0xff] ^ Te2[(s1 >> 8) & 0xff] ^ Te3[s2 & 0xff] ^ rk[ 7];
    /* round 2: */
    s0 = Te0[t0 >> 24] ^ Te1[(t1 >> 16) & 0xff] ^ Te2[(t2 >> 8) & 0xff] ^ Te3[t3 & 0xff] ^ rk[ 8];
    s1 = Te0[t1 >> 24] ^ Te1[(t2 >> 16) & 0xff] ^ Te2[(t3 >> 8) & 0xff] ^ Te3[t0 & 0xff] ^ rk[ 9];
    s2 = Te0[t2 >> 24] ^ Te1[(t3 >> 16) & 0xff] ^ Te2[(t0 >> 8) & 0xff] ^ Te3[t1 & 0xff] ^ rk[10];
    s3 = Te0[t3 >> 24] ^ Te1[(t0 >> 16) & 0xff] ^ Te2[(t1 >> 8) & 0xff] ^ Te3[t2 & 0xff] ^ rk[11];
--snip--

Listing 4-2: The table-based C implementation of AES in OpenSSL

A basic table-based implementation of AES encryption needs four kilobytes’ worth of tables because each table stores 256 32-bit values, which occupy 256 × 32 = 8192 bits, or one kilobyte. Decryption requires another four tables, and thus four more kilobytes. But there are tricks to reduce the storage from four kilobytes to one, or even fewer.

Alas, table-based implementations are vulnerable to cache-timing attacks, which exploit timing variations when a program reads or writes elements in cache memory. Depending on the relative position in cache memory of the elements accessed, access time varies. Timings thus leak information about which element was accessed, which in turn leaks information on the secrets involved.

Cache-timing attacks are difficult to avoid. One obvious solution would be to ditch lookup tables altogether by writing a program whose execution time doesn’t depend on its inputs, but that’s almost impossible to do and still retain the same speed, so chip manufacturers have opted for a radical solution: instead of relying on potentially vulnerable software, they rely on hardware.

Native Instructions

AES native instructions (AES-NI) solve the problem of cache-timing attacks on AES software implementations. To understand how AES-NI works, you need to think about the way software runs on hardware: to run a program, a microprocessor translates binary code into a series of instructions executed by integrated circuit components. For example, a MUL assembly instruction between two 32-bit values will activate the transistors implementing a 32-bit multiplier in the microprocessor. To implement a crypto algorithm, we usually just express a combination of such basic operations—additions, multiplications, XORs, and so on—and the microprocessor activates its adders, multipliers, and XOR circuits in the prescribed order.

AES native instructions take this to a whole new level by providing developers with dedicated assembly instructions that compute AES. Instead of coding an AES round as a sequence of assembly instructions, when using AES-NI, you just call the instruction AESENC and the chip will compute the round for you. Native instructions allow you to just tell the processor to run an AES round instead of requiring you to program rounds as a combination of basic operations.

A typical assembly implementation of AES using native instructions looks like Listing 4-3.

PXOR       %xmm5,  %xmm0
AESENC     %xmm6,  %xmm0
AESENC     %xmm7,  %xmm0
AESENC     %xmm8,  %xmm0
AESENC     %xmm9,  %xmm0
AESENC     %xmm10, %xmm0
AESENC     %xmm11, %xmm0
AESENC     %xmm12, %xmm0
AESENC     %xmm13, %xmm0
AESENC     %xmm14, %xmm0
AESENCLAST %xmm15, %xmm0

Listing 4-3: AES native instructions

This code encrypts the 128-bit plaintext initially in the register xmm0, assuming that registers xmm5 to xmm15 hold the precomputed round keys, with each instruction writing its result into xmm0. The initial PXOR instruction XORs the first round key prior to computing the first round, and the final AESENCLAST instruction performs the last round slightly different from the others (MixColumns is omitted).

Is AES Secure?

AES is as secure as a block cipher can be, and it will never be broken. Fundamentally, AES is secure because all output bits depend on all input bits in some complex, pseudorandom way. To achieve this, the designers of AES carefully chose each component for a particular reason—MixColumns for its maximal diffusion properties and SubBytes for its optimal non-linearity—and they have shown that this composition protects AES against whole classes of cryptanalytic attacks.

But there’s no proof that AES is immune to all possible attacks. For one thing, we don’t know what all possible attacks are, and we don’t always know how to prove that a cipher is secure against a given attack. The only way to really gain confidence in the security of AES is to crowdsource attacks: have many skilled people attempt to break AES and, hopefully, fail to do so.

After more than 15 years and hundreds of research publications, the theoretical security of AES has only been scratched. In 2011 cryptanalysts found a way to recover an AES-128 key by performing about 2¹²⁶ operations instead of 2¹²⁸, a speed-up of a factor four. But this “attack” requires an insane amount of plaintext–ciphertext pairs—about 2⁸⁸ bits worth. In other words, it’s a nice finding but not one you need to worry about.

The upshot is that you should care about a million things when implementing and deploying crypto, but AES security is not one of those. The biggest threat to block ciphers isn’t in their core algorithms but in their modes of operation. When an incorrect mode is chosen, or when the right one is misused, even a strong cipher like AES won’t save you.

Modes of Operation

In Chapter 1, I explained how encryption schemes combine a permutation with a mode of operation to handle messages of any length. In this section, I’ll cover the main modes of operations used by block ciphers, their security and function properties, and how (not) to use them. I’ll begin with the dumbest one: electronic codebook.

The Electronic Codebook (ECB) Mode

Figure 4-6: The ECB mode

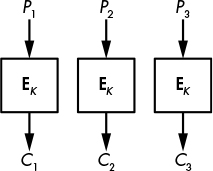
The simplest of the block cipher encryption modes is electronic codebook (ECB), which is barely a mode of operation at all. ECB takes plaintext blocks P₁, P₂, . . . , P_N and processes each independently by computing C₁ = E(K, P₁), C₂ = E(K, P₂), and so on, as shown in Figure 4-6. It’s a simple operation but also an insecure one. I repeat: ECB is insecure and you should not use it!

Marsh Ray, a cryptographer at Microsoft, once said, “Everybody knows ECB mode is bad because we can see the penguin.” He was referring to a famous illustration of ECB’s insecurity that uses an image of Linux’s mascot, Tux, as shown in Figure 4-7. You can see the original image of Tux on the left, and the image encrypted in ECB mode using AES (though the underlying cipher doesn’t matter) on the right. It’s easy to see the penguin’s shape in the encrypted version because all the blocks of one shade of gray in the original image are encrypted to the same new shade of gray in the new image; in other words, ECB encryption just gives you the same image but with different colors.

Figure 4-7: The original image (left) and the ECB-encrypted image (right)

The Python program in Listing 4-4 also shows ECB’s insecurity. It picks a pseudorandom key and encrypts a 32-byte message p containing two blocks of null bytes. Notice that encryption yields two identical blocks and that repeating encryption with the same key and the same plaintext yields the same two blocks again.

#!/usr/bin/env python

from cryptography.hazmat.primitives.ciphers import Cipher, algorithms, modes
from cryptography.hazmat.backends import default_backend
from binascii import hexlify as hexa
from os import urandom

BLOCKLEN = 16
def blocks(data):
    split = [hexa(data[i:i+BLOCKLEN]) for i in range(0, len(data), BLOCKLEN)]
    return ' '.join(split)

k = urandom(16)
print 'k = %s' % hexa(k)

# create an instance of AES-128 to encrypt and decrypt
cipher = Cipher(algorithms.AES(k), modes.ECB(), backend=default_backend())
aes_encrypt = cipher.encryptor()
# set plaintext block p to the all-zero string
p = 'x00'*BLOCKLEN*2

# encrypt plaintext p to ciphertext c
c = aes_encrypt.update(p) + aes_encrypt.finalize()
print 'enc(%s) = %s' % (blocks(p), blocks(c))

Listing 4-4: Using AES in ECB mode in Python

Running this script gives ciphertext blocks like this, for example:

$ ./aes_ecb.py
k = 50a0ebeff8001250e87d31d72a86e46d
enc(00000000000000000000000000000000 00000000000000000000000000000000) =
5eb4b7af094ef7aca472bbd3cd72f1ed 5eb4b7af094ef7aca472bbd3cd72f1ed

As you can see, when the ECB mode is used, identical ciphertext blocks reveal identical plaintext blocks to an attacker, whether those are blocks within a single ciphertext or across different ciphertexts. This shows that block ciphers in ECB mode aren’t semantically secure.

Another problem with ECB is that it only takes complete blocks of data, so if blocks were 16 bytes, as in AES, you could only encrypt chunks of 16 bytes, 32 bytes, 48 bytes, or any other multiple of 16 bytes. There are a few ways to deal with this, as you’ll see with the next mode, CBC. (I won’t tell you how these tricks work with ECB because you shouldn’t be using ECB in the first place.)

The Cipher Block Chaining (CBC) Mode

Cipher block chaining (CBC) is like ECB but with a small twist that makes a big difference: instead of encrypting the ith block, P_i, as C_i = E(K, P_i), CBC sets C_i = E(K, P_i ⊕ C_{i − 1}), where C_{i − 1} is the previous ciphertext block—thereby chaining the blocks C_{i − 1} and C_i. When encrypting the first block, P₁, there is no previous ciphertext block to use, so CBC takes a random initial value (IV), as shown in Figure 4-8.

Figure 4-8: The CBC mode

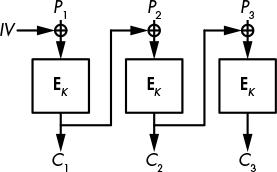
The CBC mode makes each ciphertext block dependent on all the previous blocks, and ensures that identical plaintext blocks won’t be identical ciphertext blocks. The random initial value guarantees that two identical plaintexts will encrypt to distinct ciphertexts when calling the cipher twice with two distinct initial values.

Listing 4-5 illustrates these two benefits. This program takes an all-zero, 32-byte message (like the one in Listing 4-4), encrypts it twice with CBC, and shows the two ciphertexts. The line iv = urandom(16), shown in bold, picks a new random IV for each new encryption.

#!/usr/bin/env python

from cryptography.hazmat.primitives.ciphers import Cipher, algorithms, modes
from cryptography.hazmat.backends import default_backend
from binascii import hexlify as hexa
from os import urandom

BLOCKLEN = 16
# the blocks() function splits a data string into space-separated blocks
def blocks(data):
    split = [hexa(data[i:i+BLOCKLEN]) for i in range(0, len(data), BLOCKLEN)]
    return ' '.join(split)
k = urandom(16)
print 'k = %s' % hexa(k)
# pick a random IV
iv = urandom(16)
print 'iv = %s' % hexa(iv)
# pick an instance of AES in CBC mode
aes = Cipher(algorithms.AES(k), modes.CBC(iv), backend=default_backend()).encryptor()

p = 'x00'*BLOCKLEN*2
c = aes.update(p) + aes.finalize()
print 'enc(%s) = %s' % (blocks(p), blocks(c))
# now with a different IV and the same key
iv = urandom(16)
print 'iv = %s' % hexa(iv)
aes = Cipher(algorithms.AES(k), modes.CBC(iv), backend=default_backend()).encryptor()
c = aes.update(p) + aes.finalize()
print 'enc(%s) = %s' % (blocks(p), blocks(c))

Listing 4-5: Using AES in CBC mode

The two plaintexts are the same (two all-zero blocks), but the encrypted blocks should be distinct, as in this example execution:

$ ./aes_cbc.py
k = 9cf0d31ad2df24f3cbbefc1e6933c872
iv = 0a75c4283b4539c094fc262aff0d17af
enc(00000000000000000000000000000000 00000000000000000000000000000000) =
370404dcab6e9ecbc3d24ca5573d2920 3b9e5d70e597db225609541f6ae9804a
iv = a6016a6698c3996be13e8739d9e793e2
enc(00000000000000000000000000000000 00000000000000000000000000000000) =
655e1bb3e74ee8cf9ec1540afd8b2204 b59db5ac28de43b25612dfd6f031087a

Alas, CBC is often used with a constant IV instead of a random one, which exposes identical plaintexts and plaintexts that start with identical blocks. For example, say the two-block plaintext P₁ || P₂ is encrypted in CBC mode to the two-block ciphertext C₁ || C₂. If P₁ || P₂′ is encrypted with the same IV, where P₂′ is some block distinct from P₂, then the ciphertext will look like C₁ || C₂′, with C₂′ different from C₂ but with the same first block C₁. Thus, an attacker can guess that the first block is the same for both plaintexts, even though they only see the ciphertexts.

With CBC, decryption can be much faster than encryption due to parallelism. While encryption of a new block, P_i, needs to wait for the previous block, C_{i − 1}, decryption of a block computes P_i = D(K, C_i) ⊕ C_{i − 1}, where there’s no need for the previous plaintext block, P_{i − 1}. This means that all blocks can be decrypted in parallel simultaneously, as long as you also know the previous ciphertext block, which you usually do.

How to Encrypt Any Message in CBC Mode

Let’s circle back to the block termination issue and look at how to process a plaintext whose length is not a multiple of the block length. For example, how would we encrypt an 18-byte plaintext with AES-CBC when blocks are 16 bytes? What do we do with the two bytes left? We’ll look at two widely used techniques to deal with this problem. The first one, padding, makes the ciphertext a bit longer than the plaintext, while the second one, ciphertext stealing, produces a ciphertext of the same length as the plaintext.

Padding a Message

Padding is a technique that allows you to encrypt a message of any length, even one smaller than a single block. Padding for block ciphers is specified in the PKCS#7 standard and in RFC 5652, and is used almost everywhere CBC is used, such as in some HTTPS connections.

Padding is used to expand a message to fill a complete block by adding extra bytes to the plaintext. Here are the rules for padding 16-byte blocks:

• If there’s one byte left—for example, if the plaintext is 1 byte, 17 bytes, or 33 bytes long—pad the message with 15 bytes 0f (15 in decimal).
• If there are two bytes left, pad the message with 14 bytes 0e (14 in decimal).
• If there are three bytes left, pad the message with 13 bytes 0d (13 in decimal).

If there are 15 plaintext bytes and a single byte missing to fill a block, padding adds a single 01 byte. If the plaintext is already a multiple of 16, the block length, add 16 bytes 10 (16 in decimal). You get the idea. The trick generalizes to any block length up to 255 bytes (for larger blocks, a byte is too small to encode values greater than 255).

Decryption of a padded message works like this:

1. Decrypt all the blocks as with unpadded CBC.

2. Make sure that the last bytes of the last block conform to the padding rule: that they finish with at least one 01 byte, at least two 02 bytes, or at least three 03 bytes, and so on. If the padding isn’t valid—for example, if the last bytes are 01 02 03—the message is rejected. Otherwise, decryption strips the padding bytes and returns the plaintext bytes left.

One downside of padding is that it makes ciphertext longer by at least one byte and at most a block.

Ciphertext Stealing

Ciphertext stealing is another trick used to encrypt a message whose length isn’t a multiple of the block size. Ciphertext stealing is more complex and less popular than padding, but it offers at least three benefits:

• Plaintexts can be of any bit length, not just bytes. You can, for example, encrypt a message of 131 bits.
• Ciphertexts are exactly the same length as plaintexts.
• Ciphertext stealing is not vulnerable to padding oracle attacks, powerful attacks that sometimes work against CBC with padding (as we’ll see in “Padding Oracle Attacks” on page 74).

In CBC mode, ciphertext stealing extends the last incomplete plaintext block with bits from the previous ciphertext block, and then encrypts the resulting block. The last, incomplete ciphertext block is made up of the first blocks from the previous ciphertext block; that is, the bits that have not been appended to the last plaintext block.

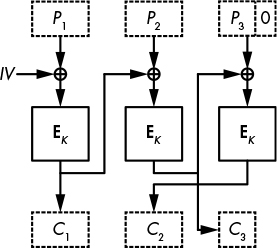
Figure 4-9: Ciphertext stealing for CBC-mode encryption

In Figure 4-9, we have three blocks, where the last block, P₃, is incomplete (represented by a zero). P₃ is XORed with the last bits from the previous ciphertext block, and the encrypted result is returned as C₂. The last ciphertext block, C₃, then consists of the first bits from the previous ciphertext block. Decryption is simply the inverse of this operation.

There aren’t any major problems with ciphertext stealing, but it’s inelegant and hard to get right, especially when NIST’s standard specifies three different ways to implement it (see Special Publication 800-38A).

The Counter (CTR) Mode

To avoid the troubles and retain the benefits of ciphertext stealing, you should use counter mode (CTR). CTR is hardly a block cipher mode: it turns a block cipher into a stream cipher that just takes bits in and spits bits out and doesn’t embarrass itself with the notion of blocks. (I’ll discuss stream ciphers in detail in Chapter 5.)

Figure 4-10: The CTR mode

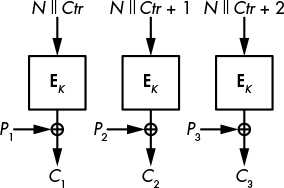
In CTR mode (see Figure 4-10), the block cipher algorithm won’t transform plaintext data. Instead, it will encrypt blocks composed of a counter and a nonce. A counter is an integer that is incremented for each block. No two blocks should use the same counter within a message, but different messages can use the same sequence of counter values (1, 2, 3, . . .). A nonce is a number used only once. It is the same for all blocks in a single message, but no two messages should use the same nonce.

As shown in Figure 4-10, in CTR mode, encryption XORs the plaintext and the stream taken from “encrypting” the nonce, N, and counter, Ctr. Decryption is the same, so you only need the encryption algorithm for both encryption and decryption. The Python script in Listing 4-6 gives you a hands-on example.

#!/usr/bin/env python

from Crypto.Cipher import AES
from Crypto.Util import Counter
from binascii import hexlify as hexa
from os import urandom
from struct import unpack

k = urandom(16)
print 'k = %s' % hexa(k)

# pick a starting value for the counter
nonce = unpack('<Q', urandom(8))[0]
# instantiate a counter function
ctr = Counter.new(128, initial_value=nonce)

# pick an instance of AES in CTR mode, using ctr as counter
aes = AES.new(k, AES.MODE_CTR, counter=ctr)

# no need for an entire block with CTR
p = 'x00x01x02x03'

# encrypt p
c = aes.encrypt(p)
print 'enc(%s) = %s' % (hexa(p), hexa(c))
# decrypt using the encrypt function
ctr = Counter.new(128, initial_value=nonce)
aes = AES.new(k, AES.MODE_CTR, counter=ctr)
p = aes.encrypt(c)
print 'enc(%s) = %s' % (hexa(c), hexa(p))

Listing 4-6: Using AES in CTR mode

The example execution encrypts a 4-byte plaintext and gets a 4-byte ciphertext. It then decrypts that ciphertext using the encryption function:

$ ./aes_ctr.py
k = 130a1aa77fa58335272156421cb2a3ea
enc(00010203) = b23d284e
enc(b23d284e) = 00010203

As with the initial value in CBC, CTR’s nonce is supplied by the encrypter and sent with the ciphertext in the clear. But unlike CBC’s initial value, CTR’s nonce doesn’t need to be random, it simply needs to be unique. A nonce should be unique for the same reason that a one-time pad shouldn’t be reused: when calling the pseudorandom stream, S, if you encrypt P₁ to C₁ = P₁ ⊕ S and P₂ to C₂ = P₂ ⊕ S using the same nonce, then C₁ ⊕ C₂ reveals P₁ ⊕ P₂.

A random nonce will do the trick only if it’s long enough; for example, if the nonce is n bits, chances are that after 2^{N/ 2} encryptions and as many nonces you’ll run into duplicates. Sixty-four bits are therefore insufficient for a random nonce, since you can expect a repetition after approximately 2³² nonces, which is an unacceptably low number.

The counter is guaranteed unique if it’s incremented for every new plaintext, and if it’s long enough; for example, a 64-bit counter.

One particular benefit to CTR is that it can be faster than in any other mode. Not only is it parallelizable, but you can also start encrypting even before knowing the message by picking a nonce and computing the stream that you’ll later XOR with the plaintext.

How Things Can Go Wrong

There are two must-know attacks on block ciphers: meet-in-the-middle attacks, a technique discovered in the 1970s but still used in many cryptanalytic attacks (not to be confused with man-in-the-middle attacks), and padding oracle attacks, a class of attacks discovered in 2002 by academic cryptographers, then mostly ignored, and finally rediscovered a decade later along with several vulnerable applications.

Meet-in-the-Middle Attacks

The 3DES block cipher is an upgraded version of the 1970s standard DES that takes a key of 56 × 3 = 168 bits (an improvement on DES’s 56-bit key). But the security level of 3DES is 112 bits instead of 168 bits, because of the meet-in-the-middle (MitM) attack.

As you can see in Figure 4-11, 3DES encrypts a block using the DES encryption and decryption functions: first encryption with a key, K₁, then decryption with a key, K₂, and finally encryption with another key, K₃. If K₁ = K₂, the first two calls cancel themselves out and 3DES boils down to a single DES with key K₃. 3DES does encrypt-decrypt-encrypt rather than encrypting thrice to allow systems to emulate DES when necessary using the new 3DES interface.

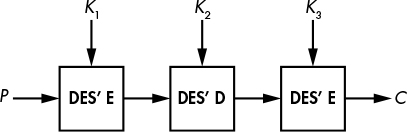
Figure 4-11: The 3DES block cipher construction

Why use triple DES and not just double DES, that is, E(K₁, E(K₂, P))? It turns out that the MitM attack makes double DES only as secure as single DES. Figure 4-12 shows the MitM attack in action.

Figure 4-12: The meet-in-the-middle attack

The meet-in-the-middle attack works as follows to attack double DES:

1. Say you have P and C = E(K₂, E(K₁, P)) with two unknown 56-bit keys, K₁ and K₂. (DES takes 56-bit keys, so double DES takes 112 key bits in total.) You build a key–value table with 2⁵⁶ entries of E(K₁, P), where E is the DES encryption function and K₁ is the value stored.

2. For all 2⁵⁶ values of K₂, compute D(K₂, C) and check whether the resulting value appears in the table as an index (thus as a middle value, represented by a question mark in Figure 4-12).

3. If a middle value is found as an index of the table, you fetch the corresponding K₁ from the table and verify that the (K₁, K₂) found is the right one by using other pairs of P and C. Encrypt P using K₁ and K₂ and then check that the ciphertext obtained is the given C.

This method recovers K₁ and K₂ by performing about 2⁵⁷ instead of 2¹¹² operations: step 1 encrypts 2⁵⁶ blocks and then step 2 decrypts at most 2⁵⁶ blocks, for 2⁵⁶ + 2⁵⁶ = 2⁵⁷ operations in total. You also need to store 2⁵⁶ elements of 15 bytes each, or about 128 petabytes. That’s a lot, but there’s a trick that allows you to run the same attack with only negligible memory (as you’ll see in Chapter 6).

As you can see, you can apply the MitM attack to 3DES in almost the same way you would to double DES, except that the third stage will go through all 2¹¹² values of K₂ and K₃. The whole attack thus succeeds after performing about 2¹¹² operations, meaning that 3DES gets only 112-bit security despite having 168 bits of key material.

Padding Oracle Attacks

Let’s conclude this chapter with one of the simplest and yet most devastating attacks of the 2000s: the padding oracle attack. Remember that padding fills the plaintext with extra bytes in order to fill a block. A plaintext of 111 bytes, for example, is a sequence of six 16-byte blocks followed by 15 bytes. To form a complete block, padding adds a 01 byte. For a 110-byte plaintext, padding adds two 02 bytes, and so on.

A padding oracle is a system that behaves differently depending on whether the padding in a CBC-encrypted ciphertext is valid. You can see it as a black box or an API that returns either a success or an error value. A padding oracle can be found in a service on a remote host sending error messages when it receives malformed ciphertexts. Given a padding oracle, padding oracle attacks record which inputs have a valid padding and which don’t, and exploit this information to decrypt chosen ciphertext values.

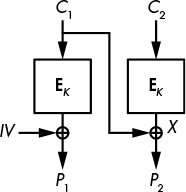
Figure 4-13: Padding oracle attacks recover X by choosing C₁ and checking the validity of padding.

Say you want to decrypt ciphertext block C₂. I’ll call X the value you’re looking for, namely D(K, C₂), and P₂ the block obtained after decrypting in CBC mode (see Figure 4-13). If you pick a random block C₁ and send the two-block ciphertext C₁ || C₂ to the oracle, decryption will only succeed if C₁ ⊕ P₂ = X ends with valid padding—a single 01 byte, two 02 bytes, or three 03 bytes, and so on.

Based on this observation, padding oracle attacks on CBC encryption can decrypt a block C₂ like this (bytes are denoted in array notation: C₁[0] is C₁’s first byte, C₁[1] its second byte, and so on up to C₁[15], C₁’s last byte):

1. Pick a random block C₁ and vary its last byte until the padding oracle accepts the ciphertext as valid. Usually, in a valid ciphertext, C₁[15] ⊕ X[15] = 01, so you’ll find X[15] after trying around 128 values of C₁[15].

2. Find the value X[14] by setting C₁[15] to X[15] ⊕ 02 and searching for the C₁[14] that gives correct padding. When the oracle accepts the ciphertext as valid, it means you have found C₁[14] such that C₁[14] ⊕ X[14] = 02.

3. Repeat steps 1 and 2 for all 16 bytes.

The attack needs on average 128 queries to the oracle for each of the 16 bytes, which is about 2000 queries in total. (Note that each query must use the same initial value.)

Further Reading

There’s a lot to say about block ciphers, be it in how algorithms work or in how they can be attacked. For instance, Feistel networks and SPNs aren’t the only ways to build a block cipher. The block ciphers IDEA and FOX use the Lai–Massey construction, and Threefish uses ARX networks, a combination of addition, word rotations, and XORs.

There are also many more modes than just ECB, CBC, and CTR. Some modes are folklore techniques that nobody uses, like CFB and OFB, while others are for specific applications, like XTS for tweakable encryption or GCM for authenticated encryption.

I’ve discussed Rijndael, the AES winner, but there were 14 other algorithms in the race: CAST-256, CRYPTON, DEAL, DFC, E2, FROG, HPC, LOKI97, Magenta, MARS, RC6, SAFER+, Serpent, and Twofish. I recommend that you look them up to see how they work, how they were designed, how they have been attacked, and how fast they are. It’s also worth checking out the NSA’s designs (Skipjack, and more recently, SIMON and SPECK) and more recent “lightweight” block ciphers such as KATAN, PRESENT, or PRINCE.