11
DIFFIE–HELLMAN

In November 1976, Stanford researchers Whitfield Diffie and Martin Hellman published a research paper titled “New Directions in Cryptography” that revolutionized cryptography forever. In their paper, they introduced the notion of public-key encryption and signatures, though they didn’t actually have any of those schemes; they simply had what they termed a public-key distribution scheme, a protocol that allows two parties to establish a shared secret by exchanging information visible to an eavesdropper. This protocol is now known as the Diffie–Hellman (DH) protocol.

Prior to Diffie–Hellman, establishing a shared secret required performing tedious procedures such as manually exchanging sealed envelopes. Once communicating parties have established a shared secret value with the DH protocol, that secret can be used to establish a secure channel by turning the secret into one or more symmetric keys that are then used to encrypt and authenticate subsequent communication. The DH protocol—and its variants—are therefore called key agreement protocols.

In the first part of this chapter, I review the mathematical foundations of the Diffie–Hellman protocol, including the computational problems that DH relies on to perform its magic. I then describe different versions of the Diffie–Hellman protocol used to create secure channels in the second part of this chapter. Finally, because Diffie–Hellman schemes are only secure when their parameters are well chosen, I conclude the chapter by examining scenarios where Diffie–Hellman can fail.

The Diffie–Hellman Function

In order to understand DH key agreement protocols, you must first understand their core operation, the DH function. The DH function will usually work with groups denoted Z_p^*. Recall from Chapter 9 that these groups are formed of nonzero integer numbers modulo a prime number, denoted p. Another public parameter is the base number, g. All arithmetic operations are performed modulo p.

The DH function involves two private values chosen randomly by the two communicating parties from the group Z_p^*, denoted a and b. A private value a has a public value associated with A = g^a mod p, or g raised to the power a modulo p. This value is sent to the other party through a message that is visible to eavesdroppers. The public value associated with b is B = g^b mod p, or g raised to the power b modulo p, which is sent to the owner of a through a publicly readable message.

DH works its magic by combining either public value with the other private value, such that the result is the same in both cases: A^b = (g^a)^b = g^ab and B ^a = (g^b)^a = g^ba = g^ab. The resulting value, g^ab, is the shared secret; it is then passed to a key derivation function (KDF) in order to generate one or more shared symmetric keys. A KDF is a kind of hash function that will return a random-looking string the size of the desired key length.

And that’s it. Like many great scientific discoveries (gravity, relativity, quantum computing, or RSA), the Diffie–Hellman trick is terribly simple in hindsight.

Diffie–Hellman’s simplicity can be deceiving, however. For one thing, it won’t work with just any prime p or base number g. For example, some values of g will restrict the shared secrets g^ab to a small subset of possible values, whereas you’d expect to have about as many possible values as elements in Z_p^*, and therefore as many possible values for the shared secret. To ensure the highest security, safe DH parameters should work with a prime p such that (p – 1) / 2 is also prime. Such a safe prime guarantees that the group doesn’t have small subgroups that would make DH easier to break. With a safe prime, DH can notably work with g = 2, which makes computations slightly faster. But generating a safe prime p takes more time than generating a totally random prime.

For example, the dhparam command of the OpenSSL toolkit will only generate safe DH parameters, but the extra checks built into the algorithm result increase the execution time considerably, as shown in Listing 11-1.

$ time openssl dhparam 2048
Generating DH parameters, 2048 bit long safe prime, generator 2
This is going to take a long time
--snip--
-----BEGIN DH PARAMETERS-----
MIIBCAKCAQEAoSIbyA9e844q7V89rcoEV8vd/l2svwhIIjG9EPwWWr7FkfYhYkU9
fRNttmilGCTfxc9EDf+4dzw+AbRBc6oOL9gxUoPnOd1/G/YDYgyplF5M3xeswqea
SD+B7628pWTaCZGKZham7vmiN8azGeaYAucckTkjVWceHVIVXe5fvU74k7+C2wKk
iiyMFm8th2zm9W/shiKNV2+SsHtD6r3ZC2/hfu7XdOI4iT6ise83YicU/cRaDmK6
zgBKn3SlCjwL4M3+m1J+Vh0UFz/nWTJ1IWAVC+aoLK8upqRgApOgHkVqzP/CgwBw
XAOE8ncQqroJ0mUSB5eLqfpAvyBWpkrwQwIBAg==
-----END DH PARAMETERS-----
openssl dhparam 2048  154.53s user 0.86s system 99% cpu 2:36.85 total

Listing 11-1: Measuring the execution time of generating 2048-bit Diffie–Hellman parameters with the OpenSSL toolkit

As you can see in Listing 11-1, it took 154.53 seconds to generate the DH parameters using the OpenSSL toolkit. Now, for the sake of comparison, Listing 11-2 shows how long it takes on the same system to generate RSA parameters of the same size (that is, two prime numbers, p and q, each half the size of the p used for DH).

$ time openssl genrsa 2048
Generating RSA private key, 2048 bit long modulus
...................................................+++
.............................................................+++
e is 65537 (0x10001)
-----BEGIN RSA PRIVATE KEY-----
--snip--
-----END RSA PRIVATE KEY-----
openssl genrsa 2048  0.16s user 0.01s system 95% cpu 0.171 total

Listing 11-2: Generating 2048-bit RSA parameters while measuring the execution time

Generating DH parameters took about 1000 times longer than generating RSA parameters of the same security level, mainly due to the extra constraint imposed on the prime generated to create DH parameters.

The Diffie–Hellman Problems

The security of DH protocols relies on the hardness of computational problems, especially on that of the discrete logarithm problem (DLP) introduced in Chapter 9. Clearly, DH can be broken by recovering the private value a from its public value g^a, which boils down to solving a DLP instance. But we don’t care only about the discrete logarithm problem when using DH to compute shared secrets. We also care about two DH-specific problems, as explained next.

The Computational Diffie–Hellman Problem

The computational Diffie–Hellman (CDH) problem is that of computing the shared secret g^ab given only the public values g^a and g^b, and not any of the secret values a or b. The motivation is obviously to ensure that even if an eavesdropper captures g^a and g^b, they should not be able to determine the shared secret g^ab.

If you can solve DLP, then you can also solve CDH; to put it simply, if you can solve DLP, then given g^a and g^b, you’ll be able to derive a and b to compute g^ab. In other words, DLP is at least as hard as CDH. But we don’t know for sure whether CDH is at least as hard as DLP, which would make the problems equally hard. In other words, DLP is to CDH what the factoring problem is to the RSA problem. (Recall that factoring allows you to solve the RSA problem, but not necessarily the converse.)

Diffie–Hellman shares another similarity with RSA in that DH will deliver the same security level as RSA for a given modulus size. For example, the DH protocol with a 2048-bit prime p will get you about the same security that RSA with a 2048-bit modulus n offers, which is about 90 bits. Indeed, the fastest way we know to break CDH is to solve DLP using an algorithm called the number field sieve, a method similar but not identical to the fastest one that breaks RSA by factoring its modulus: the general number field sieve (GNFS).

The Decisional Diffie–Hellman Problem

Sometimes we need something stronger than CDH’s hardness assumption. For example, imagine that an attacker can compute the first 32 bits of g^ab given the 2048-bit values of g^a and g^b, but that they can’t compute all 2048 bits. Although CDH would still be unbroken because 32 bits aren’t enough to completely recover g^ab, the attacker would still have learned something about the shared secret, which might still allow them to compromise an application’s security.

To ensure that an attacker can’t learn anything about the shared secret g^ab, this value needs only to be indistinguishable from a random group element, just as an encryption scheme is secure when ciphertexts are indistinguishable from random strings. The computational problem formalizing this intuition is called the decisional Diffie–Hellman (DDH) problem. Given g^a, g^b, and a value that is either g^ab or g^c for some random c (each of the two with a chance of 1/2), the DDH problem consists of determining whether g^ab (the shared secret corresponding to g^a and g^b) was chosen. The assumption that no attacker can solve DDH efficiently is called the decisional Diffie–Hellman assumption.

If DDH is hard, then CDH is also hard, and you can’t learn anything about g^ab. But if you can solve CDH, you can also solve DDH: given a triplet (g^a, g^b, g^c), you would be able to derive g^ab from g^a and g^b and check whether the result is equal to the given g^c. The bottom line is that DDH is fundamentally less hard than CDH, yet DDH hardness is a prime assumption in cryptography, and one of the most studied. We can be confident that both CDH and DDH are hard when Diffie–Hellman parameters are well chosen.

More Diffie–Hellman Problems

Sometimes cryptographers devise new schemes and prove that they are at least as hard to break as it is to solve some problem related to CDH or DDH but not identical to either of these. Ideally, we’d like to demonstrate that breaking a cryptosystem is as hard as solving CDH or DDH, but this isn’t always possible with advanced cryptographic mechanisms, typically because such schemes involve more complex operations than basic Diffie–Hellman protocols.

For example, in one DH-like problem, given g^a, an attacker would attempt to compute g^{1 / a}, where 1 / a is the inverse of a in the group (typically Z_p^* for some prime p). In another, an attacker might distinguish the pairs (g^a, g^b) from the pairs (g^a, g^{1 / a}) for random a and b. Finally, in what is called the twin Diffie–Hellman problem, given g^a, g^b, and g^c, an attacker would attempt to compute the two values g^ab and g^ac. Sometimes such DH variants turn out to be as hard as CDH or DDH, and sometimes they’re fundamentally easier—and therefore provide lower security guarantees. As an exercise, try to find connections between the hardness of these problems and that of CDH and DDH. (Twin Diffie–Hellman is actually as hard as CDH, but that isn’t easy to prove!)

Key Agreement Protocols

The Diffie–Hellman problem is designed to build secure key agreement protocols—protocols designed to secure communication between two or more parties communicating over a network with the aid of a shared secret. This secret is turned into one or more session keys—symmetric keys used to encrypt and authenticate the information exchanged for the duration of the session. But before studying actual DH protocols, you should know what makes a key agreement protocol secure or insecure, and how simpler protocols work. We’ll begin our discussion with a widely used key agreement protocol that doesn’t rely on DH.

An Example of Non-DH Key Agreement

To give you a sense of how a key agreement protocol works and what it means for it to be secure, let’s look at the protocol used in the 3G and 4G telecommunications standards to establish communication between a SIM card and a telecom operator. The protocol is often referred to as AKA, for authenticated key agreement. It doesn’t use the Diffie–Hellman function, but instead uses only symmetric-key operations. The details are a bit boring, but essentially the protocol works as shown in Figure 11-1.

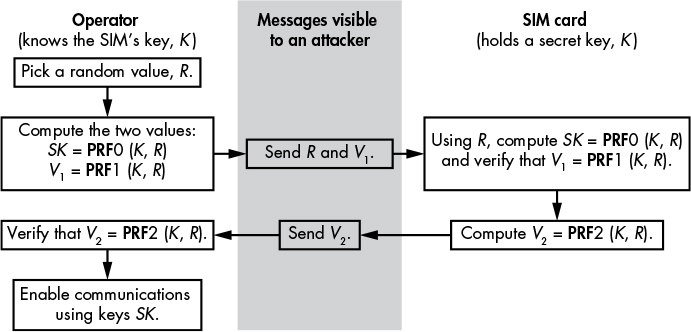
Figure 11-1: The authenticated key agreement protocol in 3G and 4G telecommunication

In this implementation of the protocol, the SIM card has a secret key, K, that the operator knows. The operator begins the session by selecting a random value, R, and then computes two values, SK and V₁, based on two pseudorandom functions, PRF0 and PRF1. Next, the operator sends a message to the SIM card containing the values R and V₁, which are visible to attackers. Once the SIM card has R, it has what it needs in order to compute SK with PRF0, and it does so. The two parties in this session end up with a shared key, SK, that attackers are unable to determine by simply looking at the messages exchanged between the parties, or even by modifying them or injecting new ones. The SIM card verifies that it’s talking to the operator by recomputing V₁ with PRF1, K, and R, and then checking to make sure that the calculated V₁ matches the V₁ sent by the operator. The SIM card then computes a verification value, V₂, with a new function, PRF2, with K and R as input, and sends V₂ to the operator. The operator verifies that the SIM card knows K by computing V₂ and checking that the computed value matches the V₂ it received.

But this protocol is not immune to all kinds of attacks: in principle there’s a way to fool the SIM card with a replay attack. Essentially, if an attacker captures a pair (R, V₁), they may send it to the SIM card and trick the SIM into believing that the pair came from a legitimate operator that knows K. To prevent this attack, the protocol includes additional checks to ensure that the same R isn’t reused.

Problems can also arise if K is compromised. For example, an attacker who compromises K can perform a man-in-the-middle attack and listen to all cleartext communication. Such an attacker could send messages between the two parties while pretending to be both the legitimate SIM card operator and the SIM card. The greater risk is that an attacker can record communications and any messages exchanged during the key agreement, and later decrypt those communications by using the captured R values. An attacker could then determine the past session keys and use them to decrypt the recorded traffic.

Attack Models for Key Agreement Protocols

There is no single definition of security for key agreement protocols, and you can never say that a key protocol is completely secure without context and without considering the attack model and the security goals. You can, for example, argue that the previous 3G/4G protocol is secure because a passive attacker won’t find the session keys, but you could also argue that it’s insecure because once the key K leaks, then all previous and future communications are compromised.

There are different notions of security in key agreement protocols as well as three main attack models that depend on the information the protocol leaks. From weakest to strongest, these are the eavesdropper, the data leak, and the breach:

The eavesdropper This attacker observes the messages exchanged between the two legitimate parties running a key agreement protocol and can record, modify, drop, or inject messages. To protect against an eavesdropper, a key agreement protocol must not leak any information on the shared secret established.

The data leak In this model, the attacker acquires the session key and all temporary secrets (such as SK in the telecom protocol example discussed previously) from one or more executions of the protocol, but not the long-term secrets (like K in that same protocol).

The breach (or corruption) In this model, the attacker learns the long-term key of one or more of the parties. Once a breach occurs, security is no longer attainable because the attacker can impersonate one or both parties in subsequent sessions of the protocol. Nonetheless, the attacker shouldn’t be able to recover secrets from sessions executed before gathering the key.

Now that we’ve looked at the attack models and seen what an attacker can do, let’s explore the security goals—that is, the security guarantees that the protocol should offer. A key agreement protocol can be designed to satisfy several security goals. The four most relevant ones are described here, in order from simplest to most sophisticated.

Authentication Each party should be able to authenticate the other party. That is, the protocol should allow for mutual authentication. Authenticated key agreement (AKA) occurs when a protocol authen­ticates both parties.

Key control Neither party should be able to choose the final shared secret or coerce it to be in a specific subset. The 3G/4G key agreement protocol discussed earlier lacks this property because the operator chooses the value for R that entirely determines the final shared key.

Forward secrecy This is the assurance that even if all long-term secrets are exposed, shared secrets from previous executions of the protocol won’t be able to be computed, even if an attacker records all previous executions or is able to inject or modify messages from previous executions. A forward-secret protocol guarantees that even if you have to deliver your devices and their secrets to some authority or other, they won’t be able to decrypt your prior encrypted communications. (The 3G/4G key agreement protocol doesn’t provide forward secrecy.)

Resistance to key-compromise impersonation (KCI) KCI occurs when an attacker compromises a party’s long-term key and is able to use it to impersonate another party. For example, the 3G/4G key agreement protocol allows trivial key-compromise impersonation because both parties share the same key K. A key agreement protocol should ideally prevent this kind of attack.

Performance

To be useful, a key agreement protocol should be not only secure but also efficient. Several factors should be taken into account when considering a key agreement protocol’s efficiency, including the number of messages exchanged, the length and number of messages, the computational effort to implement the protocol, and whether precomputations can be made to save time. A protocol is generally more efficient if fewer, shorter messages are exchanged, and it’s best if interactivity is kept minimal so that neither party has to wait to receive a message before sending the next one. A common measure of a protocol’s efficiency is its duration in terms of round trips, or the time it takes to send a message and receive a response.

Round-trip time is usually the main cause of latency in protocols, but the amount of computation to be carried out also counts; the fewer the computations required the better, and the more precomputations that can be done in advance, the better.

For example, the 3G/4G key agreement protocol discussed earlier exchanges two messages of a few hundred bits each, which must be sent in a certain order. Pre-computation can be used with this protocol to save time since the operator can pick many values of R in advance; precompute the matching values of SK, V₁, and V₂; and store them all in a database. In this case, precomputation has the advantage of reducing the exposure of the long-term key.

Diffie–Hellman Protocols

The Diffie–Hellman function is the core of most of the deployed public-key agreement protocols. However, there is no single Diffie–Hellman protocol, but rather a variety of ways to use the DH function in order to establish a shared secret. We’ll review three of those protocols in the sections that follow. In each discussion, I’ll stick to the usual crypto placeholder names and call the two parties Alice and Bob, and the attacker Eve. I’ll write g as the basis of the group used for arithmetic operations, a value fixed and known in advance to Alice and Bob.

Anonymous Diffie–Hellman

Anonymous Diffie–Hellman is the simplest of the Diffie–Hellman protocols. It’s called anonymous because it’s not authenticated; the participants have no identity that can be verified by either party, and neither party holds a long-term key. Alice can’t prove to Bob that she’s Alice, and vice versa.

In anonymous Diffie–Hellman, each party picks a random value (a for Alice and b for Bob) to use as a private key, and sends the corresponding public key to the other peer. Figure 11-2 shows the process in a bit more detail.

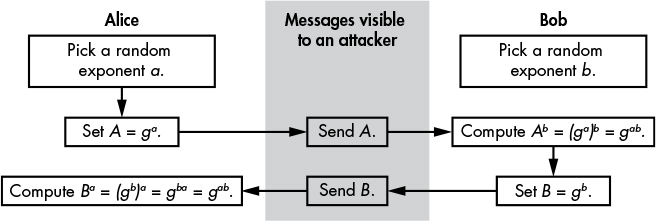
Figure 11-2: The anonymous Diffie–Hellman protocol

As you can see, Alice uses her exponent a and the group basis g to compute A = g^a, which she sends to Bob. Bob receives A and computes A^b, which is equal to (g^a)^b. Bob now obtains the value g^ab and computes B from his random exponent b and the value g. He then sends B to Alice and she uses it to compute g^ab. Alice and Bob end up with the same value, g^ab, after performing similar operations, which involve raising both g and the value received to their private exponent’s power. Pure, simple, but only secure against the laziest of attackers.

Anonymous DH can be taken down with a man-in-the-middle attack. An eavesdropper simply needs to intercept messages and pretend to be Bob (to Alice) and pretend to be Alice (to Bob), as shown in Figure 11-3.

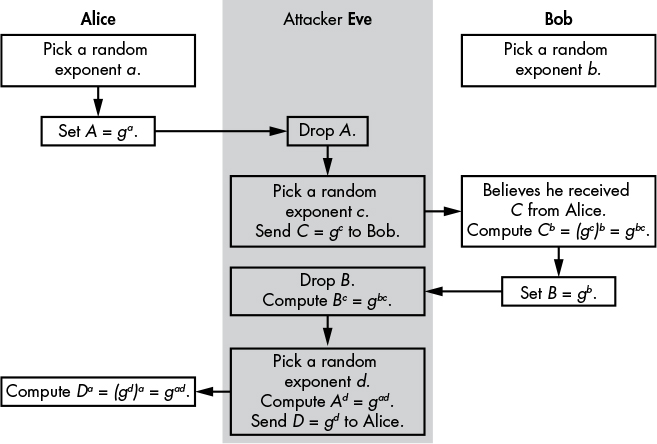
Figure 11-3: A man-in-the-middle attack on the anonymous Diffie–Hellman protocol

As in the previous exchange, Alice and Bob pick random exponents, a and b. Alice now computes and sends A, but Eve intercepts and drops the message. Eve then picks a random exponent, c, and computes C = g^c to send to Bob. Because this protocol has no authentication, Bob believes he is receiving C from Alice and goes on to compute g^bc. Bob then computes B and sends that value to Alice, but Eve intercepts and drops the message again. Eve now computes g^bc, picks a new exponent, d, computes g^ad, computes D from g^d, and sends D to Alice. Alice then computes g^ad as well.

As a result of this attack, the attacker Eve ends up sharing a secret with Alice (g^ad) and another secret with Bob (g^bc), though Alice and Bob believe that they’re sharing a single secret with each other. After completing the protocol execution, Alice will derive symmetric keys from g^ad in order to encrypt data sent to Bob, but Eve will intercept the encrypted messages, decrypt them, and re-encrypt them to Bob using another set of keys derived from g^bc—after potentially modifying the cleartext. All of this happens with Alice and Bob unaware. That is, they’re doomed.

To foil this attack, you need a way to authenticate the parties so that Alice can prove that she’s the real Alice and Bob can prove that he’s the real Bob. Fortunately, there is a way to do so.

Authenticated Diffie–Hellman

Authenticated Diffie–Hellman was developed to address the sort of man-in-the-middle attacks that can affect anonymous DH. Authenticated DH equips the two parties with both a private and a public key, thereby allowing Alice and Bob to sign their messages in order to stop Eve from sending messages on their behalf. Here, the signatures aren’t computed with a DH function, but a public-key signature scheme such as RSA-PSS. As a result, in order to successfully send messages on behalf of Alice, an attacker would need to forge a valid signature, which is impossible with a secure signature scheme.

Figure 11-4 shows how authenticated DH works.

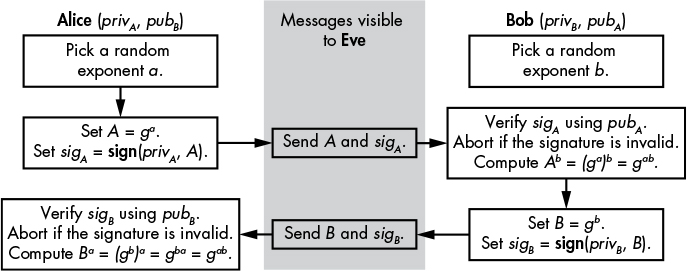
Figure 11-4: The authenticated Diffie–Hellman protocol

The Alice (priv_A, pub_B) label on the first line means that Alice holds her own private key, priv_A, as well as Bob’s public key, pub_B. This sort of priv/pub key pair is called a long-term key because it’s fixed in advance and remains constant through consecutive runs of the protocol. Of course, these long-term private keys should be kept secret, while the public keys are considered to be known to an attacker.

Alice and Bob begin by picking random exponents, a and b, as in anonymous DH. Alice then calculates A and a signature sig_A based on a combination of her signing function sign, her private key priv_A, and A. Now Alice sends A and sig_A to Bob, who verifies sig_A with her public key pub_A. If the signature is invalid, Bob knows that the message didn’t come from Alice, and he discards A.

If the signature is correct, Bob will compute g^ab from A and his random exponent b. He would then compute B and his own signature from a combination of the sign function, his private key priv_B, and B. Now he sends B and sig_B to Alice, who attempts to verify sig_B with Bob’s public key pub_B. Alice will only compute g^ab if Bob’s signature is successfully verified.

Security Against Eavesdroppers

Authenticated DH is secure against eavesdroppers because attackers can’t learn any bit of information on the shared secret g^ab since they ignore the DH exponents. Authenticated DH also provides forward secrecy: even if an attacker corrupts any of the parties at some point, as in the breach attack model discussed earlier, they would learn the private signing keys but not any of the ephemeral DH exponents; hence, they’d be unable to learn the value of any previously shared secrets.

Authenticated DH also prevents any party from controlling the value of the shared secret. Alice can’t craft a special value of a in order to predict the value of g^ab because she doesn’t control b, which influences g^ab as much as a does. (One exception would be if Alice were to choose a = 0, in which case we’d have g^ab = 1 for any b. But 0 isn’t an authorized value and should be rejected by the protocol.)

That said, authenticated DH isn’t secure against all types of attack. For one thing, Eve can record previous values of A and sig_A and replay them later to Bob, in order to pretend to be Alice. Bob will then believe that he’s sharing a secret with Alice when he isn’t, even though Eve would not be able to learn that secret. This risk is eliminated in practice by adding a procedure called key confirmation, wherein Alice and Bob prove to each other that they own the shared secret. For example, Alice and Bob may perform key confirmation by sending respectively Hash(pub_A || pub_B, g^ab) and Hash(pub_B || pub_A, g^ab) for some hash function Hash; when Bob receives Hash(pub_A || pub_B, g^ab) and Alice receives Hash(pub_B || pub_A, g^ab), both can verify the correctness of these hash values using pub_A, pub_B, and g^ab. The different order of public keys (pub_A || pub_B and pub_B || pub_A) ensures that Alice and Bob will send different values, and that an attacker can’t pretend to be Alice by copying Bob’s hash value.

Security Against Data Leaks

Authenticated DH’s vulnerability to data leak attackers is of greater concern. In this type of attack, the attacker learns the value of ephemeral, short-term secrets (namely, the exponents a and b) and uses that information to impersonate one of the communicating parties. If Eve is able to learn the value of an exponent a along with the matching values of A and sig_A sent to Bob, she could initiate a new execution of the protocol and impersonate Alice, as shown in Figure 11-5.

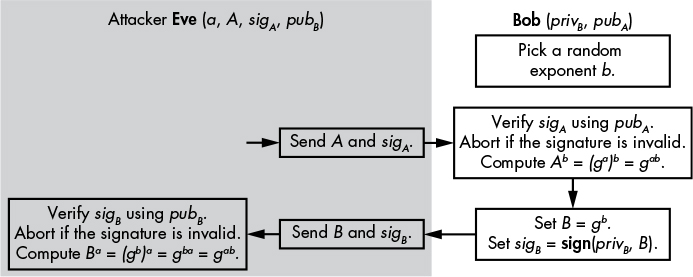
Figure 11-5: An impersonation attack on the authenticated Diffie–Hellman protocol

In this attack scenario, Eve learns the value of an a and replays the corresponding A and its signature sig_A, pretending to be Alice. Bob verifies the signature and computes g^ab from A and sends B and sig_B, which Eve then uses to compute g^ab, using the stolen a. This results in the two having a shared secret. Bob now believes he is talking to Alice.

One way to make authenticated DH secure against the leak of ephemeral secrets is to integrate the long-term keys into the shared secret computation so that the shared secret can’t be determined without knowing the long-term secret.

Menezes–Qu–Vanstone (MQV)

The Menezes–Qu–Vanstone (MQV) protocol is a milestone in the history of DH-based protocols. Designed in 1998, MQV had been approved to protect most critical assets when the NSA included it in its Suite B, a portfolio of algorithms designed to protect classified information. (NSA eventually dropped MQV, allegedly because it wasn’t used. I’ll discuss the reasons why in a bit.)

MQV is Diffie–Hellman on steroids. It’s more secure than authenticated DH, and it improves on authenticated DH’s performance properties. In particular, MQV allows users to send only two messages, independently of each other, in arbitrary order. Other benefits are that users can send shorter messages than they would be able to with authenticated DH, and they don’t need to send explicit signature or verification messages. In other words, you don’t need to use a signature scheme in addition to the Diffie–Hellman function.

As with authenticated DH, in MQV Alice and Bob each hold a long-term private key as well as the long-term public key of the other party. The difference is that the MQV keys aren’t signing keys: the keys used in MQV are composed of a private exponent, x, and a public value, g^x. Figure 11-6 shows the operation of the MQV protocol.

Figure 11-6: The MQV protocol

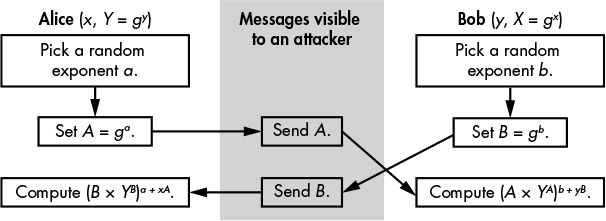
The x and y in Figure 11-6 are Alice and Bob’s respective long-term private keys, and X and Y are their public keys. Bob and Alice start out with their own private keys and each other’s public keys, which are g to the power of a private key. Each chooses a random exponent, and then Alice calculates A and sends it to Bob. Bob then calculates B and sends it to Alice. Once Alice gets Bob’s ephemeral public key B, she combines it with her long-term private key x, her ephemeral private key a, and Bob’s long-term public key Y by calculating the result of (B × Y^B)^{a + xA}, as defined in Figure 11-6. Developing this expression, we obtain the following:

(B × Y^B)^{a + xA} = (g_b × (g^y)^B)^{a + xA} = (g^{b + yB})^{a + xA} = g^{(b + yB)(a + xA)}

Meanwhile, Bob calculates the result of (A × X^A)^{b + yB}, and we can verify that it’s equal to the value calculated by Alice:

(A × X^A)^{b + yB} = (g^a × (g^x)^A)^{b + yB} = (g^{a + xA})^{b + yB} = g^{(a + xA)(b + yB)} = g^{(b + yB)(a + xA)}

As you can see, we get the same value for both Alice and Bob, namely g^{(b + yB)(a + xA)}. This tells us that Alice and Bob share the same secret.

Unlike authenticated DH, MQV can’t be broken by a mere leak of the ephemeral secrets. Knowledge of a or b won’t let an attacker determine the final shared secret because they would need the long-term private keys to compute it.

What happens in the strongest attack model, the breach model, where a long-term key is compromised? If Eve compromises Alice’s long-term private key x, the previously established shared secrets are safe because their computation also involved Alice’s ephemeral private keys.

However, MQV doesn’t provide perfect forward secrecy because of the following attack. Say, for example, that Eve intercepts Alice’s A message and replaces it with her A = g^a for some a that Eve has chosen. In the meantime, Bob sends B to Alice (and Eve records B’s value) and computes the shared key. If Eve later compromises Alice’s long-term private key x, she can determine the key that Bob had computed during this session. This breaks forward secrecy, since Eve has now recovered the shared secret of a previous execution of the protocol. In practice, however, the risk can be eliminated by a key-confirmation step that would have Alice and Bob realize that they don’t share the same key, and they would therefore abort the protocol before deriving any session keys.

Despite its elegance and security, MQV is rarely used in practice. One reason is because it used to be encumbered by patents, which hampered its widespread adoption. Another reason is that it’s harder than it looks to get MQV right in practice. In fact, when weighed against its increased complexity, MQV’s security benefits are often perceived as low in comparison to the simpler authenticated DH.

How Things Can Go Wrong

Diffie–Hellman protocols can fail spectacularly in a variety of ways. I highlight some of the most common ones in the next sections.

Not Hashing the Shared Secret

I’ve alluded to the fact that the shared secret that concludes a DH session exchange (g^ab in our examples) is taken as input to derive session keys but is not a key itself. And it shouldn’t be. A symmetric key should look random, and each bit should either be 0 or 1 with the same probability. But g^ab is not a random string; it’s a random element within some mathematical group whose bits may be biased toward 0 or 1. And a random group element is different from a random string of bits.

Imagine, for example, that we’re working within the multiplicative group Z₁₃^* = {1, 2, 3, . . . , 12} using g = 2 as a generator of the group, meaning that gⁱ spans all values of Z₁₃^* for i in 1, 2, . . . 12: g¹ = 2, g² = 4, g³ = 8, g⁴ = 13, and so on. If g’s exponent is random, you’ll get a random element of Z₁₃^*, but the encoding of a Z₁₃^* element as a 4-bit string won’t be uniformly random: not all bits will have the same probability of being a 0 or a 1. In Z₁₃^*, seven values have 0 as their most significant bit (the numbers from 1 to 7 in the group), but only five have 1 as their most significant bit (from 8 to 12). That is, this bit is 0 with probability 7 / 12 ≈ 0.58, whereas, ideally, a random bit should be 0 with probability 0.5. Moreover, the 4-bit sequences 1101, 1110, and 1111 will never appear.

To avoid such biases in the session keys derived from a DH shared secret, you should use a cryptographic hash function such as BLAKE2 or SHA-3—or, better yet, a key derivation function (KDF). An example of KDF construction is HKDF, or HMAC-based KDF (as specified in RFC 5869), but today BLAKE2 and SHA-3 feature dedicated modes to behave as KDFs.

Legacy Diffie–Hellman in TLS

The TLS protocol is the security behind HTTPS secure websites as well as the secure mail transfer protocol (SMTP). TLS takes several parameters, including the type of Diffie–Hellman protocol it will use, though most TLS implementations still support anonymous DH for legacy reasons, despite its insecurity.

Unsafe Group Parameters

In January 2016, the maintainers of the OpenSSL toolkit fixed a high-severity vulnerability (CVE-2016-0701) that allowed an attacker to exploit unsafe Diffie–Hellman parameters. The root cause of the vulnerability was that OpenSSL allowed users to work with unsafe DH group parameters (namely, an unsafe prime p) instead of throwing an error and aborting the protocol altogether before performing any arithmetic operation.

Essentially, OpenSSL accepted a prime number p whose multiplicative group Z_p^* (where all DH operations happen) contained small subgroups. As you learned at the beginning of this chapter, the existence of small subgroups within a larger group in a cryptographic protocol is bad because it confines shared secrets to a much smaller set of possible values than if it were to use the whole group Z_p^*. Worse still, an attacker can craft a DH exponent x that, when combined with the victim’s public key g^y, will reveal information on the private key y and eventually its entirety.

Although the actual vulnerability is from 2016, the principle the attack used dates back to the 1997 paper “A Key Recovery Attack on Discrete Log-based Schemes Using a Prime Order Subgroup” by Lim and Lee. The fix for the vulnerability is simple: when accepting a prime p as group modulus, the protocol must check that p is a safe prime by verifying that (p – 1) / 2 is prime as well in order to ensure that the group Z_p^* won’t have small subgroups, and that an attack on this vulnerability will fail.

Further Reading

Here’s a rundown of some things that I didn’t cover in this chapter but are useful to learn about.

You can dig deeper into the DH key agreement protocols by reading a number of standards and official publications, including ANSI X9.42, RFC 2631 and RFC 5114, IEEE 1363, and NIST SP 800-56A. These serve as references to ensure interoperability, and to provide recommendations for group parameters.

To learn more about advanced DH protocols (such as MQV and its cousins HMQV and OAKE, among others) and their security notions (such as unknown-key share attacks and group representation attacks), read the 2005 article “HMQV: A High-Performance Secure Diffie–Hellman Protocol” by Hugo Krawczyk (https://eprint.iacr.org/2005/176/) and the 2011 article “A New Family of Implicitly Authenticated Diffie–Hellman Protocols” by by Andrew C. Yao and Yunlei Zhao (https://eprint.iacr.org/2011/035/). You’ll notice in these articles that Diffie–Hellman operations are expressed differently than in this chapter. For example, instead of g^x, you’ll find the shared secret represented as xP. Generally, you’ll find multiplication replaced with addition and exponentiation replaced with multiplication. The reason is that those protocols are usually not defined over groups of integers, but over elliptic curves, as discussed in Chapter 12.