1   Sound waves

Part 1

Some initial knowledge of sound waves is essential if later chapters are going to be fully meaningful. The following is a brief outline of their most important properties. Scientific facts and figures are set out in Part 2 at the end of this chapter for those who may find them useful or interesting.

What are sound waves?

They are described as waves of compression and rarefaction in the air. This means that when sound waves travel past a fixed point the atmospheric pressure at that point goes slightly above and below the steady barometric pressure. But these fluctuations are far too small and far too rapid ever to be registered by a barometer. A microphone, on the other hand, can be thought of as a kind of extra-sensitive electrical barometer capable of detecting these rapid fluctuations in the air pressure, unlike a normal barometer, which can only indicate relatively slow pressure changes. Figure 1.1 shows what a sound wave would look like if we could see it.

There is a compression where the lines are closest together and a rarefaction where they are widely spaced. Waves of this sort are called longitudinal waves. The waves we see in water, for instance, are called transverse waves because the individual bits (molecules) of the water move up and down when the wave goes horizontally. In longitudinal waves, like sound, the air molecules oscillate from side to side.

Figure 1.1 Compression and rarefactions

Despite the fact that sound waves are longitudinal, we always draw them like transverse waves – it's much easier!

Frequency

This is the number of waves emitted, or received, in one second. Up to the 1950s, frequency was expressed in English-speaking countries as so many cycles per second (c.p.s. or c/s), but this has been replaced by the hertz, to commemorate the name of the German physicist, Heinrich Hertz (1857–1894), who was associated with early work in radio waves. The abbreviation is ‘Hz’. This unit is commonly encountered in the home on mains-powered equipment, where the specified frequency of the supply in most of Europe is 50 Hz.

The normal human ear can detect sound wave frequencies in the range from approximately 16 Hz to about 16 kHz (kHz = kilohertz, or thousand hertz – 16 kHz is 16 000 Hz). The ear's response to sound will be dealt with more fully in Chapter 2.

Related to frequency is period – the time duration of one cycle. It is equal to 1/f.

Wavelength

With any wave the distance between corresponding points on successive waves is termed the wavelength. The symbol used for wavelength is the Greek letter λ (pronounced ‘lambda’). Figure 1.2 illustrates wavelength.

Amplitude

This is the ‘height’ of the wave in whatever units are most convenient – in electrical work, for example, the amplitude could be expressed in volts or amperes.

Figure 1.2 Wavelength

The velocity of sound waves

In the air, under normal conditions, sound waves travel at about 340 metres per second (m/s). This is close to 760 miles/hour, or about 1120 feet/second. The velocity varies slightly with air temperature, which is why players of wind instruments need, literally, to warm up their instruments, as the pitch depends on the speed with which sound waves oscillate within the instrument. For most practical purposes, apart from the instance just quoted, the variation in sound wave velocity with temperature is unimportant. Details are given in Part 2 of this chapter. The symbol for sound wave velocity is, in this book, v.

Velocity, frequency and wavelength

These three things are linked by an important, but fortunately simple, formula. A moment's thought will show that if, say, 1000 waves per second are being emitted from a source (i.e. the frequency is 1 kHz) and each has a wavelength of λ, then after one second the first waves emitted will be 1000 × λ away. Or, their velocity is 1000 × λ metres per second.

What we've done is to multiply the frequency by the wavelength to arrive at the velocity:

Frequency × Wavelength = Velocity (or f × λ = v)

Writing this another way:

Wavelength = Velocity/Frequency (or λ = v/f)

Putting 340 m/s as the velocity and 1000 Hz as the frequency we have

Wavelength = 340/1000 metres

= 0.34 metres (or 34 cm)

It should be fairly obvious that if the frequency is doubled (to 2 kHz) then the wavelength is halved (to 17 cm) and so on. Simple calculations along these lines will show that the lowest frequency the normal ear can detect – 16 Hz – corresponds to a wavelength of about 21 m (70 feet), while at the highest frequency, around 16 kHz, the wavelength is about 2 cm, or rather less than one inch.

We shall see in the next two sections that this vast range of wavelengths presents problems in many sound recording situations, as the degree to which sound waves are reflected or bent round obstacles depends critically on the wavelength.

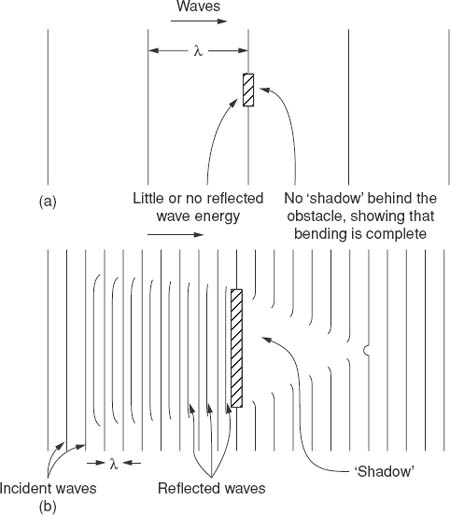
Sound waves and obstacles

Everyone is familiar with echoes – sounds being reflected from a large building or a cliff. What is perhaps not so obvious is that for this reflection to occur to any significant effect the sound wavelength must be smaller than the dimensions of the reflecting object. For example, the side of a building might be 10 m high and 20 m long. Sounds striking this building at right angles will be reflected if their wavelength is less than 10 m – that is, for frequencies greater than about 30 Hz. The most predominant frequencies in the human voice range from roughly 200 Hz to around 500 Hz, so a shout near to this building will be easily reflected.

On the other hand, if the object has dimensions less than wavelength there is no reflection. Instead the waves bend round the object, a process called diffraction, which we shall deal with in the next section.

If sound waves with a short wavelength strike an object and are reflected, there is what is termed a sound shadow behind the object. Figure 1.3 shows what happens in those cases when the wavelength is greater (a) and smaller (b) than the obstacle.

There is no sharp division between reflection and diffraction. For example, and taking simple figures, suppose we have an obstacle which is a rigid board one metre square. A wavelength of one metre corresponds to a frequency of about 340 Hz. What will happen is that sound waves of that frequency will be partially reflected, with partial bending round the board. Frequencies around one third of 340 Hz – about 100 Hz – and the wavelength being about 3 m will be almost totally unreflected. For a wavelength of about 30 cm, there will be almost complete reflection, the frequency in this case being about 3 kHz. A consequence of all this is that in any room or studio being used for sound recording the effect of obstacles can be very difficult to predict, as they will act as reflectors for some frequencies and not for others. And in this context obstacles can mean music stands, people, music cases and even instruments themselves!

The bending of sound waves (diffraction)

This can be thought of as a complementary effect to reflection, in that waves which are not reflected will be bent round an obstacle. If the wavelength is much greater than the obstacle size then there will be marked bending round by the waves (there is then little reflection). If the wavelength is small there will be little diffraction but considerable reflection. Figure 1.3(a) shows almost complete diffraction.

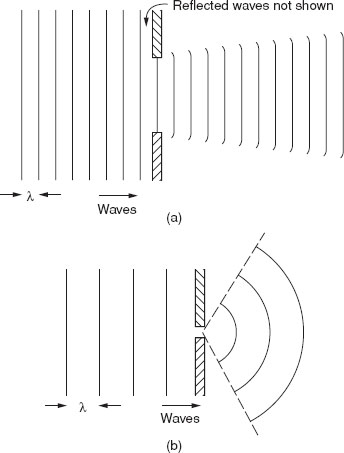
Figure 1.4 shows what happens when sound waves pass through an aperture. Possibly contrary to what one might expect, if the aperture is small compared with wavelength there is considerable spreading of the beam of emerging waves; if it is large then there is little spreading. It is often easy to see effects such as this in water when ripples, or even large waves, meet either obstructions or gaps in, for example, the walls of a quay.

There are many easy-to-perform but highly instructive experiments that the reader can carry out for him/herself. For example, try holding something like a clipboard, or any other conveniently shaped rigid sheet, between your ear and a source of sound. It will be found that the high frequencies from the source are reduced at the ear.

Then angle the board so that sounds are reflected off it into the ear and see what range of frequencies are affected. Notice how the character of the sound varies when an aircraft passes behind a house, trees or other objects.

The range of simple observations is almost endless.

It is worth remarking that all waves, and not just sound waves, undergo reflection and diffraction when the conditions are right. With light, for instance, the wavelengths are so small in relation to the size of everyday objects that virtually 100% reflection occurs almost all the time. Diffraction does occur but the effects are generally not obvious.

Figure 1.3 Sound waves striking an obstacle

Units used in sound

It will be useful to look at ways of expressing the intensity, or power, of sound waves – but not, at the moment, the thing we call ‘loudness’. For various reasons that must come later, in Chapter 2.

Power

This is relatively easy. In all domestic equipment the power required to operate the device is measured in watts (W is the abbreviation) and this will be stated somewhere on it. We are used to 100 W lamps, 3 kW (kilowatt) heaters, and so on.

Since sound waves are a form of energy, we can quite legitimately use watts as units of their power. However, in practice the watt is, in sound wave terms, inconveniently large for most purposes. Or perhaps we should say that the human ear is so sensitive that we need smaller units than watts.

Figure 1.4 Diffraction at an aperture

A much more useful unit is the millionth of a watt, or microwatt. This is usually written μW, μ being a Greek letter called ‘mu’ and generally used to mean ‘one millionth’.

At this point, the reader should not become confused, or possibly even alarmed, by the fact that his or her loudspeakers probably have labels quoting much higher powers than the tiny powers, like millionth of a watt, that the ear can handle. Loudspeakers are often rated at many watts, 50 W or more, for even a modest home system. This power refers to the maximum electrical power that can be fed into the loudspeaker without causing either damage or serious distortion. The sound power that comes out will probably be around 1% or 2% of the electrical power that goes into the loudspeaker – and only a very small fraction of that is likely actually to enter the listener's ear!

Intensity

To many people this word would probably be regarded as being synonymous with loudness. However, in scientific terms it has a different meaning. Intensity is defined as the power falling on, emitted by, or passing through a specific area. The units possibly help to make this more clear, being watts/square metre, or microwatts/square metre, as appropriate. We shall write these as W/m² or μW/m².

Pressure

In scientific terms this is defined as the force acting on a unit area. Many readers will have seen ‘pounds per square inch’ (p.s.i.) as a measurement of pressure. (Car tyre pressures are frequently given in p.s.i.: around 28 p.s.i. is a typical value, although the ‘bar’ is the preferred metric unit.)

Using these units the normal atmospheric pressure at sea level is about 14 p.s.i. Imperial units such as the pound and inch are not recommended for scientific work these days, so we must introduce their metric equivalents. These are, for force, the newton (named after Sir Isaac Newton, 1642–1727) and, for area, the square metre again.

The newton takes a little explaining. It is properly defined as the force which will cause a mass of 1 kilogramme to accelerate at a rate of 1 metre/second every second. This is not an easy definition to visualize. What is easier to grasp, if less precise, is that an average apple (and one remembers the alleged association between Sir Isaac Newton and apples!) held in the hand exerts a downwards force, because of gravity, of roughly 1 N (N = newton).

Thus, sound wave pressures are normally given as so many newtons/square metre, abbreviated to N/m².

To complicate matters further it has become the official practice to remember the French scientist, Blaise Pascal (1623–1662), by calling the N/m² the pascal (Pa for short).

This section on units may seem to have been heavy going. The reader shouldn't worry too much if that is the case, as much of the time in this book we shall be using these units only as a basis for comparison. Familiarity will bring, one hopes, not contempt, but a ready acceptance of them.

Sound intensity and the effect of distance

It hardly needs stating that sounds fall off in loudness the further one gets away from the source of the sound. Here we can be a little more precise and state than intensity (see above) decreases with distance at such a rate that for each doubling of the distance the intensity (I) is quartered.

To help understand this, imagine a partially inflated balloon with a square 1 cm × 1 cm drawn on it. Now if the size of the balloon is doubled the square becomes 2 cm × 2 cm – the sides are doubled but the area has increased four times. The intensity (power per unit area) of a sound wave striking the square is thus a quarter of what it was to start with. (There are important provisos about this law which we shall come to in a moment.) This relationship between intensity and distance is expressed by

I ∝ 1/d² (∝ means ‘is proportional to’)

where d is the distance from the source. For example, suppose that at a distance of 1 m from a sound source the intensity I is 4 W/m². At 2 m the intensity will be 1 W/m² and at 8 m it will be one sixteenth of a W/m², and so on. This relationship is known as The Inverse Square Law.

The important provisos we mentioned above are:

1.   The sound source is small compared with the distances involved (theoretically it should be infinitely small). The Inverse Square Law would not apply half a metre from the bell of a tuba! It would, though, give good approximations a few hundred metres from a full brass band.

2.   There are no reflecting surfaces in the vicinity.

Consequently, the Inverse Square Law rarely applies very precisely in real life. On the other hand, it can often be used as a valuable approximation.

Decibels

The decibel (dB for short) is a most useful unit, but unfortunately it can cause confusion and dread until it is completely understood. For that reason we shall confine ourselves here to no more about the dB than is absolutely necessary, but more about it is given in Part 2 of the chapter.

The decibel is a unit of comparison – basically of two powers, but it is also applicable to sound pressures and electrical voltages. If two powers, two pressures or two voltages are the same then there is 0 (zero) dB difference between them. In the case of sound it so happens that a change of 3 dB in speech or music is just about detectable to the normal ear. And a change of 10 dB represents to most people a doubling or halving of the loudness of a sound. These, then, are practical applications of the idea of the dB being used to compare sound powers or pressures.

It is particularly convenient at times to adopt standard powers, voltages or pressures to give references against which other powers, etc. may be compared. Such standards are basically quite arbitrary, but are chosen nevertheless to be useful. To give an example, the normal ear at its most sensitive can just detect sound wave pressure variations of 0.00002 Pa (of which more later). This particular pressure is taken as a standard and other sound pressures can be quoted as so many dB above 0.00002 Pa. We are then well on the way towards being able to use decibels as units of loudness.

This is the briefest of summaries about decibels but they will occur many times throughout this book. However, gradual and continued exposure to them will steadily make them more meaningful to the reader. Probably without much effort either.