IN THIS CHAPTER

Calculating simple returns

Computing annualized returns

Using the time-weighted return method

Measuring up to the benchmarks

Making changes to your trading plan

Are you a swing trading star or a work in progress? The only way to know is by calculating your portfolio’s returns. You can think of your portfolio returns as the “score” of your performance, and you can think of calculating those returns (usually done monthly or quarterly) as looking up at the scoreboard to know where things stand in the game (if you’re up or down and by how much). Admittedly, calculating returns isn’t the most exciting task. But as a swing trader, you must compute your returns to find out whether you’re doing an amazing job or a lousy one.

Performance calculation can be complicated by several factors, including taxes, commissions, SEC fees, and other expenses. Cash deposits or withdrawals, which I cover later in this chapter, also complicate the process of figuring your returns. Your job is to account for such complications accurately so that your return figures solely reflect your skill. Return miscalculations can lead to unskilled traders thinking they’re hot stuff (see a real-life example of this embarrassment in the Beardstown Ladies sidebar later in this chapter) or skilled traders thinking they aren’t making the grade.

Although some brokers offer performance calculation, many simply report the account balances at month’s end, which fails to remove the distorting effects of cash flows. If your broker computes performance, find out whether the performance figures are time weighted. If they are, you can use them. If not, use the methodology that I describe in this chapter.

Even if your broker provides correct, time-weighted returns for your portfolio, the calculations in this chapter are still important to know. You can use them to calculate the return on an individual security or verify the performance figures you’re shown are correct.

No Additions, No Withdrawals? No Problem!

The simplest return calculation occurs when an account begins at a certain asset level, experiences no withdrawals or deposits, and appreciates or depreciates over time solely due to trading in the account. To calculate your returns in this situation, use the following formula:

Here’s a quick example to illustrate this performance calculation.

On December 31, 2018, Trader Claire’s account value is $86,430. Trader Claire swing trades in the first three months of 2019, buying and selling different stocks every few days. By March 31, 2019, Trader Claire’s account value has reached $92,872. During the first three months, Trader Claire made no deposits or withdrawals from her account. The ending account value reflects all commissions Trader Claire paid in the first three months, but it doesn’t reflect taxes because she’s trading in an Individual Retirement Account (IRA), a tax-deferred investment account. What is Trader Claire’s total return during the period? If you plug these account values into the preceding equation, you find that her return was 7.45 percent:

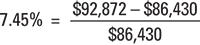
Although this equation is the simplest return calculation equation, swing traders may be depositing and withdrawing assets periodically, which requires adjustments to the formula. To figure out how to calculate your return in such a situation, see the later section “Accounting for Deposits and Withdrawals: The Time-Weighted Return Method.”

Comparing Returns over Different Time Periods: Annualizing Returns

The return calculated in the preceding section represents a return over a specified time period. The return calculation remains the same whether the beginning and ending values are three months apart or three years apart.

However, you can’t really compare a return achieved over three years to one achieved over three months. That’s why the investment management industry usually calculates annualized returns, or returns converted to an annual basis. You can think of annualized returns as an average return. For example, a 50 percent return over a five-year period is roughly equivalent to an annual return of 10 percent.

I say roughly because the actual annualized return is less than 10 percent due to compounding — or the effect of generating earnings on reinvested earnings. I’m just using an average to illustrate the concept. I show you how to calculate the actual annualized return with a tale of two traders who are arguing about who has superior investment skills.

Trader Hot Stuff is convinced his return of 76.23 percent achieved over a five-year period is superior to the return of his friend, Trader Humble, who achieved a return of 52.09 percent over a three-year period. So who’s right? To find out, you must convert both traders’ returns into annual returns, which you can do by completing the following steps:

1. Compute the return over the specified time period.

   Assuming no withdrawals or deposits were made, calculate the return over the time period using the equation shown in the preceding section. (If deposits or withdrawals did occur, use the time-weighted return calculation method I describe in the later section “Accounting for Deposits and Withdrawals: The Time-Weighted Return Method.”)

   In the case of Trader Hot Stuff and Trader Humble, the return has already been calculated over the time period for both traders. The returns are 76.23 percent over five years and 52.09 percent over three years.

2. Add 1 to the return calculated in Step 1.

   Returns are expressed in percentages, so if you want to add 1 to a percentage, you have to convert the percentage into decimal form (because 1 is equal to 100 percent). Trader Hot Stuff had a return of 76.23 percent, which equals 0.7623 in decimal form. Trader Humble had a return of 52.09 percent, which equals 0.5209 in decimal form. Adding 1 to both returns yields 1.7623 for Trader Hot Stuff and 1.5209 for Trader Humble.

3. Determine what time-period conversion fraction you should use to convert the return into an annual return.

   Use the following equation to calculate the fraction:

   

   • The numerator in this fraction will always be either 12 (months), 1 (year), or 4 (quarters). Whether you use 12, 1, or 4 in the numerator depends on what time period the return you computed in Step 1 is measured in.
   • The denominator is equal to the time period covered by the return in Step 1. Make sure that the denominator’s unit of measurement (months, years, or quarters) is equal to the numerator’s unit of measurement.
   For Trader Hot Stuff, the numerator is 1 because the return is in years, and the denominator is 5 because the time period is five years. So Trader Hot Stuff’s time-period conversion fraction is 1⁄5. For Trader Humble, the numerator is 1 because the return is in years, and the denominator is 3 because the time period is three years. So Trader Humble’s time-period conversion fraction is 1⁄3.

4. Raise the figure computed in Step 2 to the fraction calculated in Step 3.

   You need a scientific calculator for this computation. (If you don’t own one but have access to a Windows PC, the computer’s built-in calculator can be used as a scientific calculator by clicking on the Menu and selecting Scientific. For those of you with a Mac, open Calculator from the Applications folder and then click on View and select Scientific.) For Trader Hot Stuff, raising the answer from Step 2 to the fraction from Step 3, you get 1.7623^1⁄5 = 1.11999. For Trader Humble, you get 1.5209^1⁄3 = 1.15000.

5. Subtract 1 from the figures in Step 4 and convert the result into a percentage.

   The final step produces the annualized return that you’re looking for. After you subtract 1, convert the result into a percentage by moving the decimal point two places to the right.

   For Trader Hot Stuff, the calculation looks like this: 1.11999 – 1 = 0.11999 = approximately 12 percent when you move the decimal two places to the right. For Trader Humble, 1.15000 – 1 = 0.15000 = 15 percent.

So Trader Hot Stuff achieved an annualized return of 12 percent over the five-year period, whereas Trader Humble achieved an annualized return of 15 percent over the three-year period. Trader Humble’s annualized return is 3 percent greater, on an annualized basis, than Trader Hot Stuff’s return.

Now that you know how to compute annualized returns, I must throw out this word of caution. Never — ever — annualize a return that spans a time period of less than a year. Doing so can lead to ridiculous returns that don’t reflect what can normally be achieved in a year. For example, a return of 10 percent in a month is equivalent to an annualized return of 214 percent. That’s not exactly a realistic objective.

Accounting for Deposits and Withdrawals: The Time-Weighted Return Method

If you don’t make any deposits to or withdrawals from your investment account, the return calculation is straightforward. Simply determine the positive or negative change in account value and divide that by the initial account value, as I show you in the equation in “No Additions, No Withdrawals? No Problem!” earlier in this chapter. But if you do make deposits and/or withdrawals, the returns on that account are more difficult to measure and require a few more steps to calculate.

For example, if you start with $100,000 in capital, swing trade for a few months, and then deposit an additional $50,000, how do you account for the growth in assets? Part of the growth may be due to your swing trading profits. But part of the growth is also attributable to the additional deposit. If you end the year with an account value of $200,000, you can’t calculate your return simply by backing out the $50,000 deposit and then plugging the other numbers into the formula. Remember, that $50,000 may have grown or declined in value, and that change in value has to be reflected in your return calculation. The nearby Beardstown Ladies sidebar illustrates the perils of failing to properly account for these cash additions.

When deposits and withdrawals occur in an account, you can calculate returns in two ways:

• The time-weighted return method: This method calculates the account’s return independent of any cash flows. Because time-weighted returns are computed irrespective of the timing of cash flows, they’re a better measure of a manager’s skill than money-weighted returns.
• The money-weighted return method: This method figures the return based on the return of the account and the value added due to the timing of cash flows.

In the investment management industry, the time-weighted return method is more widely accepted because it removes the distorting effects that can arise when large cash flows come into or out of an account. For that reason, I devote this section to using that method.

To calculate time-weighted returns, break a portfolio out by the dates of withdrawals and deposits and then calculate the returns for each time period in between these cash flow events using the formula shown in this chapter’s first section. To do this, you need to know the value of the portfolio right before each deposit or withdrawal occurs. After computing the returns for the smaller time periods, you can string together the returns through a process known as geometrically chain-linking the returns. That sounds much worse than it actually is — I promise. I break it all down in the following sections.

Breaking the time period into chunks

The number of deposits and withdrawals you make in an account determines the number of time periods for which you need to calculate returns. You simply take the number of these cash flow events and add 1. So if you have four different deposits and withdrawals, you need to calculate returns for five discrete time periods, as the following example illustrates.

Swing Trader Singh begins the year with $50,000 in his brokerage account. He makes the following deposits and withdrawals from this account:

• $5,000 deposit on February 16 (account value before deposit: $58,500)
• $3,000 withdrawal on April 19 (account value before withdrawal: $61,300)
• $9,000 deposit on June 9 (account value before deposit: $63,780)
• $7,000 withdrawal on December 16 (account value before withdrawal: $72,290)
• Ending value on December 31: $68,350

So what’s the return of this swing trader’s account for the year?

First, split the year into distinct periods in between each deposit and withdrawal, as shown in Figure 13-1. Because the account experienced four different cash flow events, you should come up with five distinct time periods:

• Time Period 1: January 1–February 15
• Time Period 2: February 16–April 18
• Time Period 3: April 19–June 8
• Time Period 4: June 9–December 15
• Time Period 5: December 16–December 31

Comparing Your Returns to an Appropriate Benchmark

After you know how to compute your returns, you should compare them to some benchmark to determine whether you’re outperforming the market. But which benchmark should you use?

If you’re trading stocks, you can look at nine major benchmarks:

• Large Cap Growth (Russell 1000 Growth Index)
• Large Cap Core (Russell 1000 Index)
• Large Cap Value (Russell 1000 Value Index)
• Mid Cap Growth (Russell Mid Cap Growth Index)
• Mid Cap Core (Russell Mid Cap Index)
• Mid Cap Value (Russell Mid Cap Value Index)
• Small Cap Growth (Russell 2000 Growth Index)
• Small Cap Core (Russell 2000 Index)
• Small Cap Value (Russell 2000 Value Index)

You can also compare your returns to international benchmarks. BNY Mellon maintains an excellent compilation of indexes covering international stocks that trade on U.S. markets. Visit www.adrbnymellon.com/indices/adr-index/performance-tables to find out more.

Where do you find the returns for these indexes? The best website I’ve found, hands down, is the FTSE Russell return calculator (www.ftserussell.com/index-series/index-tools/russell-index-performance-calculator). It shows you the returns for indexes covering the aforementioned nine major U.S. equity benchmarks (one of which would be appropriate if you only trade U.S. stocks; if you trade international equities, look at the benchmarks on the BNY Mellon website). It’s free to use and lets you compute returns over specific time periods. The website also annualizes returns automatically when you select time periods that extend beyond one year. Finally, the website shows total returns, which means returns including dividends (as opposed to price returns, which show returns excluding dividends).

Figure 13-2 shows the output from this return calculator for several Russell indexes.

The benchmark you compare yourself to should reflect the type of stocks you are swing trading. If you swing trade large cap companies (generally defined as companies with market capitalizations of $10 billion or more), then one of the Russell 1000 benchmarks would be appropriate. If, on the other hand, you swing trade small cap stocks (generally defined as companies with market capitalizations of $1 billion and lower), then one of the Russell 2000 benchmarks would be appropriate.

After you identify the appropriate benchmark to use, compare your annual return to the benchmark’s annual return. If the return measurement period is less than a year, then compare your unannualized return for the period with the return of the benchmark for the exact same period. Note, the benchmark returns must be total return, meaning inclusive of dividends, and the start and end dates of the portfolio return and benchmark return must be identical. Fortunately, the FTSE Russell return calculator permits you to select a custom time period to ensure you are comparing apples to apples.

If your return is greater than the benchmark, you’re outperforming the average return achieved in your category. This outperformance may be due to one or more of several factors: randomness (otherwise known as luck), trading higher beta securities than your benchmark (see Chapter 10), using cash well (in situations where the market is going down), or adding real value (that is, being a skilled swing trader). Some traders would group the last two categories together, arguing that a skilled trader uses cash to his or her advantage.

To determine whether your outperformance is due to trading higher beta securities, you need to compute a “risk adjusted return” and compare that figure to the risk adjusted return of the benchmark. Common risk adjusted returns include the Sharpe Ratio and the Information Ratio. A simple risk adjusted return ratio can be computed by dividing your total return (preferably over at least a year) by the standard deviation of returns.

For example, if your strategy returned 10 percent during the year with a standard deviation of returns of 5 percent, you’d arrive at a calculated ratio of 2. If the benchmark returned 11 percent with a standard deviation of returns of 6 percent, its calculated ratio is 1.83. The higher the risk adjusted return, the better. In this example, the trader has added value relative to her benchmark because 2 is greater than 1.83.

Ideally, you should have 12 months of returns for your strategy and for the benchmark in order to calculate a simple risk adjusted return.

Calculating standard deviation is outside the scope of this book, but you can do it in Microsoft Excel using the function “=stdev(returns)”. The “returns” should be replaced by the actual cells containing the 12 or more monthly returns. For example, if your returns were in cells A1 through A30, the function above would read “=stdev(A1:A30)” without the quotation marks.

If you don’t have Excel, you can also use the following website to calculate standard deviation: www.calculator.net/standard-deviation-calculator.html.

Express the numerator and denominator in the same time period. If the numerator is an annualized return, then divide by the standard deviation of annualized returns. If the numerator is a monthly return, then divide by the standard deviation of monthly returns. If the numerator is an annualized return and you calculate the standard deviation of monthly returns, you can convert the standard deviation of monthly returns into an annualized standard deviation by multiplying the monthly figure by .

Evaluating Your Trading Plan

After you compute your account’s return and compare it to some benchmark, you can work on improving your trading plan. If your returns exceed the appropriate benchmark, great job! But that doesn’t mean you shouldn’t review your trades and look for ways to refine your plan.

At least monthly, examine your trading journal and review all closed trades (those that you’ve exited) to determine whether you need to make any adjustments to your strategy. If your plan yields subpar returns when compared to the appropriate benchmark, perhaps you can spot a common thread among the losing positions and add a trading rule to avoid similar losses. Conversely, if you’re consistently beating the benchmark, maybe you can identify a common thread among your winning positions and add a trading rule to increase the chances of finding those gainers.

Don’t change your plan too often. Only change it when you’re sure that a tangible benefit exists and that you can address a problem you spot in several trades. If you change your trading plan frequently, you’ll never know whether you have a well-functioning plan because you can’t judge a plan on the basis of a few weeks of data (unless you lose half or all your money, in which case you’re probably not following the risk management techniques I outline in Chapter 10). Apple and Amazon don’t change their corporate strategies weekly, or even yearly. They plan for the long term. Even though you’re swing trading, your trading plan must have a long-term perspective in the sense that it should do well across changing markets and over time.

You’ll never achieve 100 percent success in your trades. A great trading plan may well result in a success rate of 50 percent if the profits from your winners are multiple times larger than the losses from your losers.