Monetary Equilibrium and International Reserve Flows in Australia1
J. RICHARD ZECHER
The balance of payments in an open economy plays an important role in determining changes in the stock of domestic money. International reserve inflows, for example, will increase the domestic stock of money if they are added directly to the money balances of residents, or if they are exchanged for domestic currency at the central bank.2 In Australia, reserve flows are an important factor, and occasionally a dominant one, in determining changes in the domestic stock of money.3 This observation raises the question, what are the major determinants of Australian reserve flows and what role, if any, do policy actions play in affecting reserve flows?
Models of open economies that include a market for money have been developed by R. A. Mundell (1968, 1971), H. G. Johnson (1972), A. B. Laffer (1968), R. Komiya (1969), J. Frenkel (1971), and R. Dornbusch (1971), among others.
These models suggest two equivalent ways of describing a reserve flow. One asserts that reserves flow in when residents demand less goods, services, and non-monetary assets from non-residents than non-residents demand from them, and the converse. The other description says that reserves flow in when residents desire to accumulate money balances faster than the rate at which policy actions and other domestic factors are increasing the stock of money. This highly simplified characterisation implies that reserve flows result from the states of equilibrium in all non-monetary markets or, equivalently, from the state of equilibrium in the money market.
In this chapter the latter, and simpler, approach is taken. Reserve flows are related to factors determining growth in demand for money, and to policy and other domestically determined factors that contribute to growth in the stock of money. This money-market approach to the balance of payments is a slightly modified version of a model developed by H. G. Johnson (1972).
1 INTERNATIONAL RESERVES, MONEY SUPPLY, AND MONEY DEMAND
When the monetary authorities in an open economy are willing to buy or sell international reserves at a fixed price, private citizens and businesses play a central role in determining the amount of high-powered money. If domestic supply of money exceeds demand, outlays rise above receipts, and part of the increased outlays is directed at foreign goods, services, and assets. Residents may acquire the reserve currencies to pay for the increased purchases from foreigners by buying reserves from the central bank in exchange for domestic money, thus generating a decline in the domestic money stock. This process can be formally stated in terms of a money supply identity.
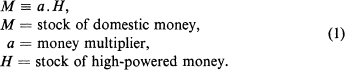
The amount of high-powered money is derived from the consolidated balance sheet of the monetary authorities. In simplified form, this balance sheet contains the following items, in addition to high-powered money:4
Monetary Authorities’ Balance Sheet
![]()
| R | = |
official holdings of international reserves, |
| OA | = |
all other assets of the monetary authorities, such as |
domestic bonds, bank buildings, etc., |
||
| OL | = |
all liabilities of the monetary authorities other than |
high-powered money. |
Define high-powered money in terms of the balance sheet items, such that
![]()
Every change in high-powered money is associated with changes in R and/or changes in all domestic influences on the balance sheet, summarised by the variable D. Substituting (2) into (1) gives the money supply formula
![]()
Demand for money is given the simple form:
![]()
| where | P | = | price index, |
| y | = | permanent income, | |
| i | = | the rate of interest, | |
| e | = | stochastic disturbance term. |
Since demand for money is assumed to be homogeneous of degree one in the price level, (4) may be rewritten as:
![]()
Continuous equilibrium in the money market implies:
![]()
A final set of operations takes the logarithm of (6) and differentiates with respect to time. For simplicity, new notation is introduced such that gX = dlnX/dt, X = a, R, D, y, P, and i. In addition, (R/H)gR is identified as the dependent variable:
![]()
The coefficient (α1) is the income elasticity of demand for money, and therefore it is expected to be positive and in the neighbourhood of unity. For given interest rate, price level, money multiplier, and domestic credit (D), growth in income is associated with reserve inflows, according to the hypothesis. Specifically, a 1 per cent growth in income generates an α1 per cent increase in demand for money, and consequently a reserve inflow just sufficient to result in an α1 per cent increase in nominal and real money stock.5
Increases in the interest rate are associated with reserve outflows in this hypothesis, a result that runs counter to intuition unless the interest rate variable is interpreted in a particular way. Namely, ‘the’ interest rate is viewed as a proxy for world interest rates, and changes in this interest rate are taken to reflect similar movements in rates all around the world. If this assumption is accurate, then estimates of α2 should be negative and within the range that is reasonable for interest elasticities of demand for money. However, if changes in Australian interest rates are dominated by changes relative to the rest of the world, then estimates of α2 are likely to be positive.6
In the regressions reported in the following section, coefficients for gp, ga, and (D/H)gD are estimated, and it may be helpful to consider here the conditions under which they will take the hypothesised values of +1.0 for gP, and –1.0 for both ga and (D/H)gD. In the extreme case where the error terms in equation (5), and hence in equation (7) are everywhere equal to zero, the estimated coefficients for gP, ga, and (D/H)gD would be precisely +1.0, –1.0, and –1.0.
A second extreme case is where demand for money is unrelated to income and the interest rate. Here, the terms α1gy and α2gi drop out of equation (7), and we are left with a regression that makes the contribution of one source of money growth a function of all the other sources. In this case the estimated coefficients for gP, ga, and (D/H)gD can in principle take any value, positive or negative.7 If the demand for money given by equation (5) is reasonably stable, then the estimated coefficients for gP, ga, and (D/H)gD should approach their hypothesised values.
Price changes are assumed to have a positive effect on reserve flows. An X per cent increase in prices will reduce real money balances by X per cent and, other things equal, lead to a reserve inflow just sufficient to restore real money balances to their previous level. As with interest rates, changes in prices are viewed primarily as changes in all world prices rather than as changes in Australian prices relative to the rest of the world prices.
The final two variables reflect all domestic influences on the money stock, and both of these variables are responsive to policy actions by the monetary authorities (McGregor, Burrows, and Zecher, 1972). An increase in either variable tends to increase the stock of money and, other things equal, should lead to an outflow of reserves sufficient to restore money to its previous level.
2 ESTIMATES OF THE MONEY DEMAND EQUATION AND THE RESERVE FLOW EQUATION
Table 1 displays regression results for two equations: the reserve flow equation:
![]()
and the demand for money equation:
![]()
where gm = growth rate of real money balances,
u = stochastic disturbance.
The data are for the period 1950–71.
| y | = | permanent income: a sixteen-quarter weighted average of |
| gross national product, | ||
| R | = | official international reserve holdings of the Australian |
| Reserve Bank, | ||
| i | = | two-year Australian government bond rate, |
| P | = | consumer price index, |
| D | = | H – R: where H is high-powered money, |
| M | = | currency plus all trading bank deposits owned by the public (roughly equivalent to U.S. M2).8 |
A quarterly regression of money demand yields the results shown in the following equation:
![]()
where the numbers in parentheses are t statistics.9 The estimates of both the income and interest rate elasticities of demand for money conform to expectations, but the ![]() shows that much of the variation in real money balances is not systematically related to changes either in income or in the interest rate. Estimation of the reserve flow equation reveals that even on a quarterly basis the demand for money is sufficiently stable to yield the expected results:
shows that much of the variation in real money balances is not systematically related to changes either in income or in the interest rate. Estimation of the reserve flow equation reveals that even on a quarterly basis the demand for money is sufficiently stable to yield the expected results:
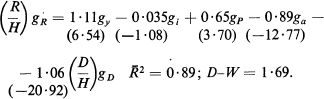
The estimated coefficients of gP, ga, and (D/H)gD are all within two standard errors of their hypothesised values of +1.0 or –1.0.
Expanding the discrete observation period from quarterly to yearly observations yields a much better fit for the money demand equation, and also shows rises in both estimated elasticities:
![]()
Estimation of the reserve flow equation using yearly observations shows that all estimated coefficients continue to conform to values implied by the hypothesis:
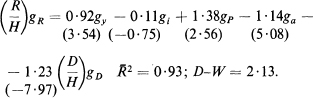
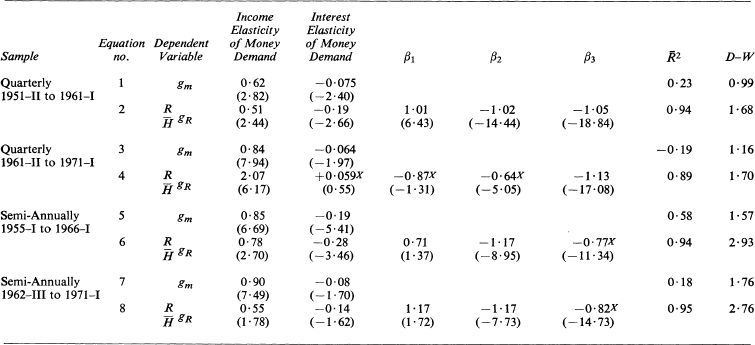
In Table 12.1 the same pairs of regressions are reported for various quarterly and semi-annual subperiods. The most interesting of these are the results in lines 3 and 4, which are based on quarterly data for the period 1961–II through 1971–I. Line 3 shows reasonable estimates of both income and interest rate elasticities, but a negative ![]() . The money market would appear to be far from equilibrium on a quarter-by-quarter basis over this period, at least given this simple money demand formulation. Estimation of the reserve flow equation for the same period, as might be expected, is unsatisfactory in almost every way. The income elasticity estimate is twice its expected value, while the interest elasticity estimate is positive, though not significantly so. The price coefficient is not only more than two standard errors from its hypothesised value, but also has the wrong sign. Estimates of the coefficients of the two domestic money supply variables (ga and (D/H)gD)) are close to their hypothesised values, but
. The money market would appear to be far from equilibrium on a quarter-by-quarter basis over this period, at least given this simple money demand formulation. Estimation of the reserve flow equation for the same period, as might be expected, is unsatisfactory in almost every way. The income elasticity estimate is twice its expected value, while the interest elasticity estimate is positive, though not significantly so. The price coefficient is not only more than two standard errors from its hypothesised value, but also has the wrong sign. Estimates of the coefficients of the two domestic money supply variables (ga and (D/H)gD)) are close to their hypothesised values, but ![]() 2 is slightly more than two standard errors from –1.0. The semi-annual regressions for the same period, reported in lines 7 and 8, showed marked improvement in both equations, and are more consistent with the over-all results.
2 is slightly more than two standard errors from –1.0. The semi-annual regressions for the same period, reported in lines 7 and 8, showed marked improvement in both equations, and are more consistent with the over-all results.
Table 12.1 Semi-Annual and Quarterly Estimates of the Reserve Flow Equation and of the Demand for Money
These results taken together suggest that the Australian reserve flow experience over the period 1950–71, has been broadly in conformity with the monetary approach to the balance of payments. The novel implications of the hypothesis that both economic growth and rises in the price level lead to surpluses are both supported by the evidence. The implication that rises in domestic interest rates lead to deficits, while not finding strong support, is certainly not inconsistent with the results of these regressions. Finally, the two variables reflecting domestic influences on the money stock (ga and (D/H)gD)) appear to have a dependable, negative effect on reserve flows, and also appear to be the dominant influence on short-run fluctuations in reserve flows.
A few comments by way of summary and clarification are in order concerning the independence of the independent variables. In deriving a single equation model of reserve flows, a number of judgments had to be made concerning the dominant factors influencing each of the variables. The resulting hypothesis assumes that (1) Australian reserve flows are dominantly influenced by the state of equilibrium in the market for Australian money, and (2) that the five other variables are dominantly influenced by factors outside the market for Australian money. Growth in real, permanent income is assumed to result primarily from growth in technology and factors of production. Both interest rates and prices are assumed to be dominantly influenced by world market conditions. In addition, Australia being a small part of the world market, conditions in domestic markets should have little influence on these prices and interest rates.
The two remaining variables, the money multiplier and the domestically determined portion of high-powered money, are influenced by a variety of factors, including monetary policy actions. To the extent that policy actions are aimed at offsetting or ‘sterilising’ reserve flows, these two variables will be functionally dependent on reserve flows, thus partly reversing the direction of causation implied by the hypothesis. This objection remains an open question, although I find it unconvincing, particularly during the 1950s when policy actions were carried out by the Commonwealth Bank. After the formation of the Reserve Bank, policy actions were more aggressive, and reserve flows may have become a more important factor in policy decisions.
3 CONCLUSIONS
Australian international reserve flows over the past two decades are consistent with the pattern implied by the monetary approach to the balance of payments. When demand for money grows faster than the supply of money would have grown due to domestic sources alone, international reserves tend to accumulate and to bring actual growth in the money stock closer to desired growth, and the converse. As implied by the hypothesis, growth in output and the price level are associated with balance-of-payments surpluses, while growth in the domestically determined portion of the money stock tends to be associated with deficits and reserve outflows. Effects of the interest rate on reserve flows tend to be weak, but generally conform to the negative relation implied by the hypothesis.
If the present hypothesis captures a significant portion of the systematic factors involved in determining reserve flows in Australia, then the interpretation of reserve flows, and the policy actions required to control reserve flows, are clear. For example, consider the stormy, six-quarter period ending in the August 1971 international monetary crisis. Australian output and Australian (and world) prices rose at historically high rates over this period, while domestic monetary policies were restrictive, contributing little to growth in the domestic money stock. This combination of factors should have led to a rapid rate of reserve accumulation. Such an accumulation did occur, and at a rate sufficient to nearly double official reserve assets in Australia over the six-quarter period.
Two policy implications of the hypothesis concerning this episode are worth mentioning. Firstly, the reserve inflow could have been stemmed or reversed by a more expansionary domestic monetary policy. Secondly, an exchange rate adjustment such as the one in 1971 will at best provide temporary relief from undesirable reserve flows. Once Australian prices adjust to the new international price constellation, the Australian balance of payments will again tend to reflect the difference between growth in demand for money and growth in domestically determined supply of money.
REFERENCES
Dornbusch, Rudiger, ‘Notes on Growth and the Balance of Payments’, Canadian Journal of Economics (August 1971).
Frenkel, J., ‘A Theory of Money, Trade and the Balance of Payments in a Model of Trade and Accumulation’, Journal of International Economics, 1 (May 1971).
Hume, David, ‘Of the Balance of Trade (1752), in his Essays, Moral, Political and Literary, vol. 1 (London, Longmans Green 1898).
Johnson, Harry G., Macroeconomics and Monetary Theory (Chicago, Aldine 1972).
Kindleberger, C. P., ‘Measuring Equilibrium in the Balance of Payments’, Journal of Political Economy, 77, no. 6 (November/December 1969), 873–91.
Komiya, Ryutaro, ‘Economic Growth and the Balance of Payments’, Journal of Political Economy, 77, no. 1 (January/February 1969), 35–48.
Krueger, Anne O., ‘Balance of Payments Theory’, Journal of Economic Literature (March 1969), 1–26.
Laffer, Arthur B., ‘The Anti-Traditional General Equilibrium Theory of the Rate of Growth and the Balance-of-Payments under Fixed Exchange Rates’, unpublished manuscript, University of Chicago (December 1968).
Laidler, David E. W., The Demand for Money: Theories and Evidence (Scranton, Pa., International Textbook Company, 1969).
McGregor, L., Burrows, C, and Zecher, R., ‘Determinants of the Australian Money Supply since 1950’. Presented to the Australian and New Zealand Association for the Advancement of Science, Forty-fourth Congress, Sydney (August 1972).
Meade, J. E., The Balance of Payments (London, Oxford University Press, 1951).
Mundell, Robert A., International Economics (New York, Macmillan, 1968).
Mundell, Robert A., Monetary Theory (Pacific Palisades, Goodyear, 1971).
1 The author is indebted to the Australian Reserve Bank for supplying most of the data used in this study, and to Harry G. Johnson, Arthur B. Laffer, and members of the International Trade Workshop at the University of Chicago during Summer Quarter, 1972, for many helpful comments. Any remaining errors are the author’s.
2 International reserve flows are treated here as equivalent to the balance of payments. For this and other definitions of the balance of payments, see Kindleberger (1969).
3 See McGregor, Burrows, and Zecher (1972).
4 For a detailed discussion of Australian high-powered money, see McGregor, Burrows, and Zecher (1972).
5 This result may appear to be at variance with the absorption theory in which rising income increases imports and generates reserve outflows. However, the absorption theory is concerned with the balance of trade rather than the balance of payments. Whatever the effects on the balance of trade, rapid growth does appear on a causal basis to be associated with reserve inflows (Japan, Germany), and slow growth with reserve outflows (U.S.A., U.K.).
6 That is, increases in Australian rates relative to world rates should attract capital and generate reserve inflows, and the converse.
7 For instance, if gP and ga were always zero, and total money grew at 5 per cent per year, and half of this growth was due to (R/H)gR and half to (D/H)gD, then the estimated coefficients for gp and ga would be zero, and for (D/H)gD, plus one.
8 Readers interested in obtaining these data should contact the author.
9 Sample period is 1951–II through 1971–I.