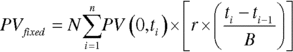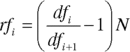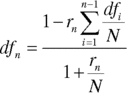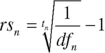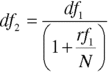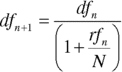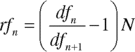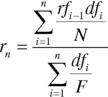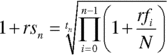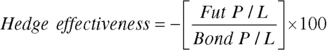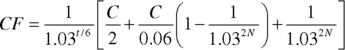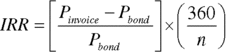CHAPTER 2
Derivative Instruments and Hedging
“The spread of secondary and tertiary education has created a large population of people, often with well‐developed literary and scholarly tastes, who have been educated far beyond their capacity to undertake analytical thought.”
—Peter Medawar, quoted in Richard Dawkins,The Greatest Show on Earth: The Evidence for Evolution, Bantam Press, 2009.
Reiterating our “95–5” rule from Chapter 1, most customer finance requirements – whether long or short of cash – can be met with essentially plain vanilla products. That said, some financial market derivatives have made a positive contribution to society; a good example of this would be the humble interest‐rate swap, without which banks in many countries would not be able to offer fixed‐rate residential mortgages or corporate loans to their customers.
This illustrates the principal reason why derivative instruments are “popular” – they enable an institution to hedge risk exposure. An inability to hedge exposure is the main impediment to a bank offering a customer a desired product such as a fixed‐rate loan. So in this chapter we present previous book extracts that are pertinent to an understanding of the main derivative instruments and the main hedging applications that such products are used for.
The new material in the chapter includes an up‐to‐date discussion on using the asset swap measure to ascertain bond relative value. We also consider the impact of the 2008 crash on the hitherto “standard” pricing principles used for valuing interest‐rate swaps. Swaps have been a collateralised market for some years now, and the previous approach of using solely Libor as the driver of the swap discount factor has had to be modified. The approach described here is important general knowledge for all banks using derivatives in any capacity. Finally, we provide a brief introduction to hedge accounting, again a topic of importance to banks using derivatives.
This extract from Bank Asset and Liability Management (2007)
This extract from Fixed Income Markets, Second Edition (2014)
Swaps
Swaps
Swaps are one of the most important and useful instruments in the debt‐capital markets, indeed the global economy. The main types of swap are interest‐rate swaps, asset swaps, basis swaps, cross‐currency swaps, and currency‐coupon swaps. The market for swaps is organised by the International Swaps and Derivatives Association (ISDA). They are used by a wide range of institutions, including banks, mortgage banks and building societies, corporates, and local authorities. As the market has matured, the instrument has gained wider acceptance, and it is regarded as a plain‐vanilla product in the debt‐capital markets. Virtually all commercial and investment banks will quote swap prices for their customers, and as they are over‐the counter (OTC) instruments, dealt over the telephone, it is possible for banks to tailor swaps to match the precise requirements of individual customers. There is also a close relationship between the bond market and the swap market, and corporate finance teams and underwriting banks keep a close eye on the government yield curve and the swap yield curve, looking out for possibilities regarding new issue of debt.
In this chapter, we review the use of interest‐rate swaps from the point of view of the bond‐market participant; this includes pricing and valuation and its use as a hedging tool. The bibliography lists further reading on important topics such as pricing, valuation, and credit risk.
INTEREST‐RATE SWAPS
Background
Interest‐rate swaps are the most important type of swap in terms of volume of transactions. They are used to manage and hedge interest‐rate risk and exposure, while market makers will also take positions in swaps that reflect their view on the direction of interest rates. An interest‐rate swap is an agreement between two counterparties to make periodic interest payments to one another during the life of the swap, on a predetermined set of dates, based on a notional principal amount. One party is the fixed‐rate payer, and this rate is agreed at the time of trade of the swap; the other party is the floating‐rate payer, the floating rate being determined during the life of the swap by reference to a specific market index. The principal or notional amount is not physically exchanged; hence, the term “off‐balance‐sheet”, but is used merely to calculate the interest payments.1 The fixed‐rate payer receives floating‐rate interest and is said to be “long” or to have “bought” the swap. The long side has conceptually purchased a floating‐rate note (because it receives floating‐rate interest) and issued a fixed‐coupon bond (because it pays out fixed interest at intervals); that is, it has in principle borrowed funds. The floating‐rate payer is said to be “short” or to have “sold” the swap. The short side has conceptually purchased a coupon bond (because it receives fixed‐rate interest) and issued a floating‐rate note (because it pays floating‐rate interest). So an interest‐rate swap is:
- An agreement between two parties
- To exchange a stream of cash flows
- Calculated as a percentage of a notional sum
- Calculated on different interest bases
For example, in a trade between Bank A and Bank B, Bank A may agree to pay fixed semiannual coupons of 10% on a notional principal sum of £1 million, in return for receiving from Bank B the prevailing six‐month sterling Libor rate on the same amount. The known cash flow is the fixed payment of £50,000 every six months by Bank A to Bank B.
Interest‐rate swaps trade in a secondary market, so their value moves in line with market interest rates, in exactly the same way as bonds. If a five‐year interest‐rate swap is transacted today at a rate of 5%, and five‐year interest rates subsequently fall to 4.75%, the swap will have decreased in value to the fixed‐rate payer, and correspondingly increased in value to the floating‐rate payer, who has now seen the level of interest payments fall. The opposite would be true if five‐year rates moved to 5.25%. Why is this? Consider the fixed‐rate payer in an IR swap to be a borrower of funds; if she fixes the interest rate payable on a loan for five years, and then this interest rate decreases shortly afterwards, is she better off? No, because she is now paying above the market rate for the funds borrowed. For this reason, a swap contract decreases in value to the fixed‐rate payer if there is a fall in rates. Equally a floating‐rate payer gains if there is a fall in rates, as he can take advantage of the new rates and pay a lower level of interest; hence, the value of a swap increases to the floating‐rate payer if there is a fall in rates.
A bank swaps desk will have an overall net interest‐rate position arising from all the swaps it has traded that are currently on the book. This position is an interest‐rate exposure at all points along the term structure, out to the maturity of the longest‐dated swap. At the close of business each day, all the swaps on the book will be marked‐to‐market at the relevant tenor interest rate quoted for that day.
A swap can be viewed in two ways; either as a bundle of forward or futures contracts, or as a bundle of cash flows arising from the “sale” and “purchase” of cash‐market instruments. If we imagine a strip of futures contracts, maturing every three or six months out to three years, we can see how this is conceptually similar to a three‐year interest‐rate swap. However, in the author's view it is better to visualise a swap as being a bundle of cash flows arising from cash instruments.
Let us imagine we have only two positions on our book:
- A long position in £100 million of a three‐year floating‐rate note (FRN) that pays six‐month Libor semiannually, and is trading at par
- A short position in £100 million of a three‐year gilt with coupon of 6% that is also trading at par
Being short a bond is the equivalent to being a borrower of funds. Assuming this position is kept to maturity, the resulting cash flows are shown in Table 13.1.
Table 13.1 Three‐Year Cash Flows
| Period (6 mo) | FRN | Gilt | Net Cash Flow |
| 0 | −£100m | +£100m | £0 |
| 1 | +(Libor × 100)/2 | −3 | +(Libor × 100)/2 − 3.0 |
| 2 | +(Libor × 100)/2 | −3 | +(Libor × 100)/2 − 3.0 |
| 3 | +(Libor × 100)/2 | −3 | +(Libor × 100)/2 − 3.0 |
| 4 | +(Libor × 100)/2 | −3 | +(Libor × 100)/2 − 3.0 |
| 5 | +(Libor × 100)/2 | −3 | +(Libor × 100)/2 − 3.0 |
| 6 | +[(Libor × 100)/2] + 100 | −103 | +(Libor × 100)/2 − 3.0 |
| The Libor rate is the six‐month rate prevailing at the time of the setting; for instance, the Libor rate at period 4 will be the rate actually prevailing at period 4. | |||
There is no net outflow or inflow at the start of these trades, as the £100 million purchase of the FRN is netted with receipt of £100 million from the sale of the gilt. The resulting cash flows over the three‐year period are shown in the last column of Table 13.1. This net position is exactly the same as that of a fixed‐rate payer in an (interest‐rate) IR swap. As we had at the start of the trade, there is no cash inflow or outflow on maturity. For a floating‐rate payer, the cash flow would mirror exactly a long position in a fixed‐rate bond and a short position in an FRN. Therefore, the fixed‐rate payer in a swap is said to be short in the bond market; that is, a borrower of funds. The floating‐rate payer in a swap is said to be long the bond market.
Market Terminology
Virtually all swaps are traded under the legal terms and conditions stipulated in the ISDA standard documentation. The trade date for a swap is, not surprisingly, the date on which the swap is transacted. The terms of the trade include the fixed interest rate, the maturity and notional amount of the swap, and the payment bases of both legs of the swap. The date from which floating interest payments are determined is the setting date, which may also be the trade date. Most swaps fix the floating‐rate payments to Libor, although other reference rates that are used include the U.S. Prime rate, the Fed Funds rate, euribor, the Treasury‐bill rate, and the commercial‐paper rate. In the same way as for a forward‐rate agreement (FRA) and for eurocurrency deposits, the rate is fixed two business days before the interest period begins. The second (and subsequent) setting date will be two business days before the beginning of the second (and subsequent) swap periods. The effective date is the date from which interest on the swap is calculated, and this is typically two business days after the trade date. In a forward‐start swap, the effective date will be at some point in the future, specified in the swap terms. The floating interest rate for each period is fixed at the start of the period, so that the interest payment amount is known in advance by both parties (the fixed rate is known, of course, throughout the swap by both parties).
Although for the purposes of explaining swap structures, both parties are said to pay interest payments (and receive them), in practice only the net difference between both payments changes hands at the end of each interest period. This eases the administration associated with swaps and reduces the number of cash flows for each swap. The counterparty that is the net payer at the end of each period will make a payment to the other counterparty. The first payment date will occur at the end of the first interest period, and subsequent payment dates will fall at the end of successive interest periods. The final payment date falls on the maturity date of the swap. The calculation of interest is given by equation (13.1).
where I is the interest amount, M is the nominal amount of the swap, and B is the interest day‐base for the swap. Dollar‐ and euro‐denominated swaps use an actual/360 day‐count, similar to other money‐market instruments in those currencies, while sterling swaps use an actual/365 day‐count basis.
The cash flows in a vanilla interest‐rate swap are illustrated in Figure 13.1.The counterparties in a swap transaction only pay across net cash flows, however, so at each interest payment date only one actual cash transfer will be made, by the net payer. This is shown as Figure 13.1(iii).
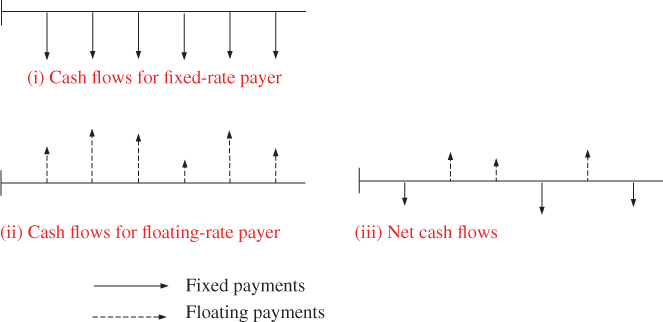
Figure 13.1 Cash Flows for Vanilla Interest‐Rate Swap
Swap Spreads and the Swap Yield Curve
In the market, banks will quote two‐way swap rates on screens or via a dealing system such as Reuters. Brokers will also be active in relaying prices in the market. The convention in the market is for the swap market maker to set the floating leg at Libor and then quote the fixed rate that is payable for that maturity. So for a five‐year swap, a bank's swap desk might be willing to quote the following:
| Floating‐rate payer: | Pay 6‐month‐Libor |
| Receive fixed rate of 5.19% | |
| Fixed‐rate payer: | Pay fixed rate of 5.25% |
| Receive 6‐month Libor |
In this case, the bank is quoting an offer rate of 5.25%, which the fixed‐rate payer will pay, in return for receiving Libor flat. The bid price quote is 5.19%, which is what a floating‐rate payer will receive fixed. The bid‐offer spread in this case is therefore 6 basis points. The fixed‐rate quotes are always at a spread above the government bond yield curve. Let us assume that the five‐year gilt is yielding 4.88%. In this case, then, the five‐year swap bid rate is 31 basis points above this yield. So the bank's swap trader could quote the swap rates as a spread above the benchmark‐bond yield curve, say 37‐31, which is her swap spread quote. This means that the bank is happy to enter into a swap paying fixed 31 basis points above the benchmark yield and receiving Libor, and receiving fixed 37 basis points above the yield curve and paying Libor. The bank's screen on, say, Bloomberg or Reuters might look something like Table 13.2, which quotes the swap rates as well as the current spread over the government‐bond benchmark.
Table 13.2 Swap Quotes
| 1‐yr | 4.50 | 4.45 | +17 |
| 2‐yr | 4.69 | 4.62 | +25 |
| 3‐yr | 4.88 | 4.80 | +23 |
| 4‐yr | 5.15 | 5.05 | +29 |
| 5‐yr | 5.25 | 5.19 | +31 |
| 10‐yr | 5.50 | 5.40 | +35 |
The swap spread is a function of the same factors that influence the spread over government bonds for other instruments. For shorter‐duration swaps of, say, up to three years, there are other yield curves that can be used in comparison, such as the cash‐market curve or a curve derived from futures prices. For longer‐dated swaps, the spread is determined mainly by the credit spreads that prevail in the corporate‐bond market. Because a swap is viewed as a package of long and short positions in fixed‐ and floating‐rate bonds, it is the credit spreads in these two markets that will determine the swap spread. This is logical; essentially, it is the premium for greater credit risk involved in lending to corporates that dictates that a swap rate will be higher than the same maturity government‐bond yield. Technical factors will be responsible for day‐to‐day fluctuations in swap rates, such as the supply of corporate bonds and the level of demand for swaps, plus the cost to swap traders of hedging their swap positions.
We can summarise by saying that swap spreads over government bonds reflect the supply and demand conditions of both swaps and government bonds, as well as the market's view on the credit quality of swap counterparties. There is considerable information content in the swap yield curve, much like that in the government‐bond yield curve. During times of credit concerns in the market, such as the corrections in Asian and Latin American markets in the summer of 1998, and the 2008 bank crash, the swap spread will increase, more so at higher maturities. After the Lehman default in September 2008, the overnight index swap (OIS) spread over Libor widened considerably. The change in swap spreads is shown in Figure 13.2.
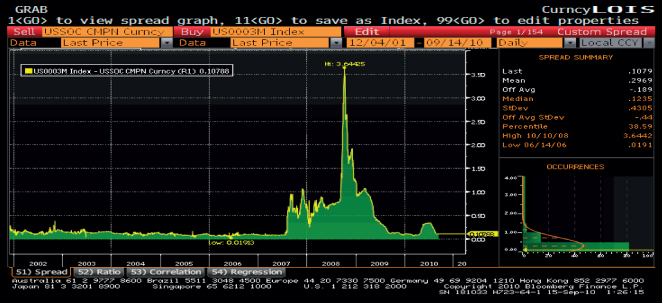
Figure 13.2 Libor‐OIS Spread, 2002–2008
Used with permission of Bloomberg L.P. Copyright© 2014. All rights reserved.
GENERIC SWAP VALUATION
Banks generally use par‐swap (zero‐coupon) swap pricing. We will look at this method in the next section. First, however, we will introduce an intuitive swap valuation method.
Par Swap Pricing
Assume we have a vanilla interest‐rate swap with a notional principal of N that pays n payments during its life, to a maturity date of T. The date of each payment is on ti with i = 1, … n. The present value today of a future payment is denoted by PV(0, t). If the swap rate is r, the value of the fixed‐leg payments is given by (13.2).
where B is the money‐market day base. The term (ti − ti−1) is simply the number of days between the ith and the i −1th payments.
The value of the floating‐leg payments at the date t1 for an existing swap is given by,
where rl is the Libor rate that has been set for the next interest payment. We set the present value of the floating‐rate payment at time 0 as follows:
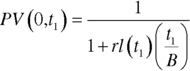
For a new swap, the value of the floating payments is given by
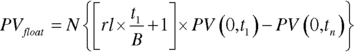
The swap valuation is then given by PVfixed− PVfloat. The swap rate quoted by a market‐making bank is that which sets PVfixed = PVfloat and is known as the par or zero‐coupon swap rate. We consider this next.
Zero‐Coupon Swap Pricing
So far, we have discussed how vanilla swap prices are often quoted as a spread over the benchmark government‐bond yield in that currency, and how this swap spread is mainly a function of the credit spread required by the market over the government (risk‐free) rate. This method is convenient and also logical because banks use government bonds as the main instrument when hedging their swap books. However, because much bank swap trading is now conducted in nonstandard, tailor‐made swaps, this method can sometimes be unwieldy, as each swap needs to have its spread calculated to suit its particular characteristics. Therefore, banks use a standard pricing method for all swaps known as zero‐coupon swap pricing.
In Chapter 3, we referred to zero‐coupon bonds and zero‐coupon interest rates. Zero‐coupon or spot rates, are true interest rates for their particular term to maturity. In zero‐coupon swap pricing, a bank will view all swaps, even the most complex, as a series of cash flows. The zero‐coupon rates that apply now for each of the cash flows in a swap can be used to value these cash flows. Therefore, to value and price a swap, each of the swap's cash flows are present‐valued using known spot rates; the sum of these present values is the value of the swap.
In a swap, the fixed‐rate payments are known in advance, and so it is straightforward to present‐value them. The present value of the floating rate payments is usually estimated in two stages. First, the implied forward rates can be calculated using (13.6). We are quite familiar with this relationship from our reading of Chapter 3
where
| rfi | is the one‐period forward rate starting at time i |
| dfi | is the discount factor for the maturity period i |
| dfi+1 | is the discount factor for the period i + 1 |
| N | is the number of times per year that coupons are paid |
By definition, the floating‐payment interest rates are not known in advance, so the swap bank will predict what these will be, using the forward rates applicable to each payment date. The forward rates are those that are currently implied from spot rates. Once the size of the floating‐rate payments has been estimated, these can also be valued by using the spot rates. The total value of the fixed and floating legs is the sum of all the present values, so the value of the total swap is the net of the present values of the fixed and floating legs.
While the term “zero‐coupon” refers to an interest rate that applies to a discount instrument that pays no coupon and has one cash flow (at maturity), it is not necessary to have a functioning zero‐coupon bond market in order to construct a zerocoupon yield curve. In practice, most financial pricing models use a combination of the following instruments to construct zero‐coupon yield curves:
- Money‐market deposits
- Interest‐rate futures
- FRAs
- Government bonds.
Frequently an overlap in the maturity period of all instruments is used. FRA rates are usually calculated from interest‐rate futures so it is only necessary to use one of either FRA or futures rates.
Once a zero‐coupon yield curve (term structure) is derived, this may be used to value a future cash flow maturing at any time along the term structure. This includes swaps: to price an interest‐rate swap, we calculate the present value of each of the cash flows using the zero‐coupon rates and then sum all the cash flows. As we noted above, while the fixed‐rate payments are known in advance, the floating‐rate payments must be estimated, using the forward rates implied by the zero‐coupon yield curve. The net present value of the swap is the net difference between the present values of the fixed‐ and floating‐rate legs.
Calculating the Forward Rate from Spot‐Rate Discount Factors
Remember that one way to view a swap is as a long position in a fixed‐coupon bond that was funded at Libor, or against a short position in a floating‐rate bond. The cash flows from such an arrangement would be paying floating‐rate and receiving fixed‐rate. In the former arrangement, where a long position in a fixed‐rate bond is funded with a floating‐rate loan, the cash flows from the principals will cancel out, as they are equal and opposite (assuming the price of the bond on purchase was par), leaving a collection of cash flows that mirror an interest‐rate swap that pays floating and receives fixed. Therefore, as the fixed‐rate on an interest‐rate swap is the same as the coupon (and yield) on a bond priced at par, calculating the fixed‐rate on an interest‐rate swap is the same as calculating the coupon for a bond that we wish to issue at par.
The price of a bond paying semiannual coupons is given by (13.7), which may be rearranged for the coupon rate r to provide an equation that enables us to determine the par yield, and hence the swap rate r, given by (13.8).
where rn is the coupon on an n‐period bond with n coupons and M is the maturity payment. Assuming P = 1 and M = 1, it can be shown then that
For annual coupon bonds, there is no denominator for the discount factor, while for bonds paying coupons on a frequency of N we replace the denominator 2 with N.2 The expression in (13.8) may be rearranged again, using F for the coupon frequency, to obtain an equation that may be used to calculate the nth discount factor for an n‐period swap rate, given in (13.9).
The expression in (13.9) is the general expression for the bootstrapping process that we first encountered in Chapter 1. Essentially, to calculate the n‐year discount factor we use the discount factors for the years 1 to n − 1, and the n‐year swap rate or zero‐coupon rate. If we have the discount factor for any period, we may use (13.9) to determine the same period zero‐coupon rate, after rearranging it, shown in (13.10).
Discount factors for spot rates may also be used to calculate forward rates. We know that
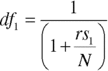
where rs is the zero‐coupon rate. If we know the forward rate we may use this to calculate a second discount rate, shown by (13.12).
where rf1 is the forward rate. This is of no use in itself; however, we may derive from it an expression to enable us to calculate the discount factor at any point in time between the previous discount rate and the given forward rate for the period n to n + 1, shown in (13.13), which may then be rearranged to give us the general expression to calculate a forward rate, given in (13.14).
The general expression for an n‐period discount rate at time n from the previous period forward rates is given by (13.15).
From the above (13.7 to 13.15), we may combine equations (13.8) and (13.14) to obtain the general expression for an n‐period swap rate and zero‐coupon rate, given by (13.16) and (13.17), respectively.
The two expressions do not tell us anything new, as we have already encountered their results in Chapter 3. The swap rate, which we have denoted as rn is shown by (13.16) to be the weighted average of the forward rates. If we consider that a strip of FRAs constitutes an interest‐rate swap, then a swap rate for a continuous period could be covered by a strip of FRAs. Therefore, an average of the FRA rates would be the correct swap rate. As FRA rates are forward rates, we may be comfortable with (13.16), which states that the n‐period swap rate is the average of the forward rates from rf0 to rfn. To be accurate, we must weight the forward rates, and these are weighted by the discount factors for each period. Note that although swap rates are derived from forward rates, interest payments under a swap are paid in the normal way at the end of an interest period, while payments for an FRA are made at the beginning of the period and must be discounted.
Equation (13.17) states that the zero‐coupon rate is calculated from the geometric average of (one plus) the forward rates. The n‐period forward rate is obtained using the discount factors for periods n and n − 1. The discount factor for the complete period is obtained by multiplying the individual discount factors together, and exactly the same result would be obtained by using the zero‐coupon interest‐rate for the whole period to obtain the discount factor.
Illustrating Interest‐Rate Swap Pricing
The rate charged on a newly transacted interest‐rate swap is the one that gives its net present value as zero. The term valuation of a swap is used to denote the process of calculating the net present value of an existing swap, when marking‐to‐market the swap against current market interest rates. Therefore, when we price a swap, we set its net present value to zero; while, when we value a swap, we set its fixed rate at the market rate and calculate the net present value.
To illustrate the basic principle, we price a plain‐vanilla interest‐rate swap with the terms set out below; for simplicity we assume that the annual fixed‐rate payments are the same amount each year, although in practice there would be slight differences. Also assume that we already have our zero‐coupon yields as shown in Table 13.3.
We use the zero‐coupon rates to calculate the discount factors, and then use the discount factors to calculate the forward rates. This is done using equation (13.14). These forward rates are then used to predict what the floating‐rate payments will be at each interest period. Both fixed‐rate and floating‐rate payments are then present‐valued at the appropriate zero‐coupon rate, which enables us to calculate the net present value.
The fixed‐rate for the swap is calculated using equation (13.8) to give us:
or 6.8963%.
The swap terms are:
| Nominal principal | £10 million |
| Fixed rate | 6.8963% |
| Day count fixed | Actual/365 |
| Day count floating | Actual/365 |
| Payment frequency fixed | Annual |
| Payment frequency floating | Annual |
| Trade date | 31st January 2000 |
| Effective date | 2nd February 2000 |
| Maturity date | 2nd February 2005 |
| Term | Five years |
For reference, the Microsoft Excel formulae are shown in Table 13.4. It is not surprising that the net present value is zero, because the zero‐coupon curve is used to derive the discount factors, which are then used to derive the forward rates, which are used to value the swap. As with any financial instrument, the fair value is its break‐even price or hedge cost, and in this case the bank that is pricing the five‐year swap shown in Table 13.3 could hedge the swap with a series of FRAs transacted at the forward rates shown. If the bank is paying fixed and receiving floating, value of the swap to it will rise if there is a rise in market rates, and fall if there is a fall in market rates. Conversely, if the bank was receiving fixed and paying floating, the swap value to it would fall if there was a rise in rates, and vice versa.
Table 13.3 Generic Interest‐Rate Swap
| Period | Zero‐Coupon Rate % | Discount Factor | Forward Rate % | Fixed Payment | Floating Payment | PV Fixed Payment | PV Floating Payment |
| 1 | 5.50 | 0.94 | 5.50 | 689,625 | 550,000.00 | 653,672.98 | 521,327.01 |
| 2 | 6.00 | 0.88 | 6.50 | 689,625 | 650,236.96 | 613,763.79 | 578,708.58 |
| 3 | 6.25 | 0.83 | 6.75 | 689,625 | 675,177.02 | 574,944.84 | 562,899.47 |
| 4 | 6.50 | 0.77 | 7.25 | 689,625 | 725,353.49 | 536,061.43 | 563,834.02 |
| 5 | 7.00 | 0.71 | 9.02 | 689,625 | 902,358.47 | 491,693.09 | 643,369.11 |
| 4.16 | 2,870,137.00 | 2,870,137.00 |
Table 13.4 Generic Interest‐Rate Swap (Excel formulae)
| CELL | C | D | E | F | G | H | I | J |
| 21 | 10000000 | |||||||
| 22 | ||||||||
| 23 | Period | Zero‐Coupon Rate % | Discount Factor | Forward Rate % | Fixed Payment | Floating Payment | PV Fixed Payment | PV Floating Payment |
| 24 | 1 | 5.50 | 0.94 | 5.50 | 689,625 | “(F24*10000000)/100 | “G24/1.055 | “H24/(1.055) |
| 25 | 2 | 6.00 | 0.88 | “((E24/E25)‐1)*100 | 689,625 | “(F25*10000000)/100 | “G24/(1.06)ˆ2 | “H25/(1.06)ˆ2 |
| 26 | 3 | 6.25 | 0.83 | “((E25/E26)‐1)*100 | 689,625 | “(F26*10000000)/100 | “G24/(1.0625)ˆ3 | “H26/(1.0625ˆ3) |
| 27 | 4 | 6.50 | 0.77 | “((E26/E27)‐1)*100 | 689,625 | “(F27*10000000)/100 | “G24/(1.065)ˆ4 | “H27/(1.065)ˆ4 |
| 28 | 5 | 7.00 | 0.71 | “((E27/E28)‐1)*100 | 689,625 | “(F28*10000000)/100 | “G24/(1.07)ˆ5 | “H28/(1.07)ˆ5 |
| “SUM(E24:E28) | 2,870,137.00 | 2,870,137.00 |
This method is used to price any interest‐rate swap, even an exotic one.
Valuation Using Final‐Maturity Discount Factor
A shortcut to valuing the floating‐leg payments of an interest‐rate swap involves using the discount factor for the final maturity period. This is possible because, for the purposes of valuation, an exchange of principal at the beginning and end of the swap is conceptually the same as the floating‐leg interest payments. This holds because, in an exchange of principal, the interest payments earned on investing the initial principal would be uncertain, as they are floating rate, while on maturity the original principal would be returned. The net result is a floating‐rate level of receipts, exactly similar to the floating‐leg payments in a swap. To value the principals, then, we need only the final maturity discount rate.
To illustrate, consider Table 13.3, where the present value of both legs was found to be £2,870,137. The same result is obtained if we use the five‐year discount factor, as shown below.
The first term is the principal multiplied by the discount factor 1; this is because the present value of an amount valued immediately is unchanged (or rather, it is multiplied by the immediate‐payment discount factor, which is 1.0000).
Therefore, we may use the principal amount of a swap if we wish to value the swap. This is, of course, for valuation only, as there is no actual exchange of principal in a swap.
Summary of IR Swap
Let us summarise the chief characteristics of swaps. A plain‐vanilla swap has the following characteristics:
- One leg of the swap is fixed‐rate interest, while the other will be floating‐rate, usually linked to a standard index such as Libor.
- The fixed rate is fixed through the entire life of the swap.
- The floating rate is set in advance of each period (quarterly, semiannually, or annually) and paid in arrears.
- Both legs have the same payment frequency.
- The maturity can be standard whole years up to 30 years, or set to match the customer's requirements.
- The notional principal remains constant during the life of the swap.
Of course, to meet customer demand banks can set up swaps that have variations on any or all of the above standard points. Some of the more common variations are discussed in a following section.
SONIA Swaps
SONIA is the average interest rate of interbank (unsecured) overnight sterling deposit trades undertaken before 1530 hours each day between members of the London Wholesale Money Brokers' Association. Recorded interest rates are weighted by volume. A SONIA swap is a swap contract that exchanges a fixed interest rate (the swap rate) against the geometric average of the overnight interest rates that have been recorded during the life of the contracted. Exchange of interest takes place on maturity of the swap. SONIA swaps are used to speculate on or to hedge against interest rates at the very short end of the sterling yield curve; in other words, they can be used to hedge an exposure to overnight interest rates.7 The swaps themselves are traded in maturities of one week to one year, although two‐year SONIA swaps have also been traded.
Conventional swap rates are calculated off the government bond yield curve and represent the credit premium over government yields of interbank default risk. Essentially they represent an average of the forward rates derived from the government spot (zero‐coupon) yield curve. The fixed rate quoted on a SONIA swap represents the average level of the overnight interest rates expected by market participants over the life of the swap. In practice, the rate is calculated as a function of the Bank of England's repo rate. This is the two‐week rate at which the Bank conducts reverse repo trades with banking counterparties as part of its open market operations. In other words, this is the Bank's base rate. In theory one would expect the SONIA rate to follow the repo rate fairly closely, since the credit risk on an overnight deposit is low. In practice, however, the spread between the SONIA rate and the Bank repo rate is very volatile, and for this reason the swaps are used to hedge overnight exposures.
The daily turnover in SONIA swaps is considerably lower than cash instruments such as gilt repo (£20 billion) or more established derivative instruments such as short sterling (£45 billion); however, it is now a key part of the sterling market. Most trades are between one‐week and three‐month maturity, and the bid‐offer spread has been reported by the BoE as around 2 basis points, which compares favourably with the 1‐basis‐point spread of short sterling.
Figure 13.5 illustrates the monthly average of the SONIA index minus Bank's repo rate during 1999 and 2000, with the exaggerated spread in December 1999 reflecting millenium bug concerns.

Figure 13.5 SONIA Average Rate Minus BoE Repo Rate, 1999–2000
Source: Bank of England.
An illustration of the use of OIS to hedge a funding position is given in Example 13.3.
Example 13.3 Using an OIS swap to hedge a funding requirement
A structured hedge fund derivatives desk at an investment bank offers a leveraged investment product to a client in the form of a participating interest share in a fund of hedge funds. The client's investment is leveraged up by funds lent to it by the investment bank, for which the interest rate charged is overnight Libor plus a spread. (In other words, for instance for each $25 invested by the client, the investment bank puts up $75 to make a total investment of $100. This gives the investor a leveraged investment in the hedge fund of funds. In most cases, the client would also bear the first $15 of loss of the $100 share of the investment.)
Assume that this investment product has an expected life of at least two years, and possibly longer. As part of its routine assetliability management operations, the bank's Treasury desk has been funding this requirement by borrowing overnight each day. It now wishes to match the funding requirement raised by this product by matching asset term structure to the liability term structure. Let us assume that this product creates a USD 1 billion funding requirement for the bank.
The current market deposit rates are shown in Figure 13.6. The Treasury desk therefore funds this requirement in the following way:
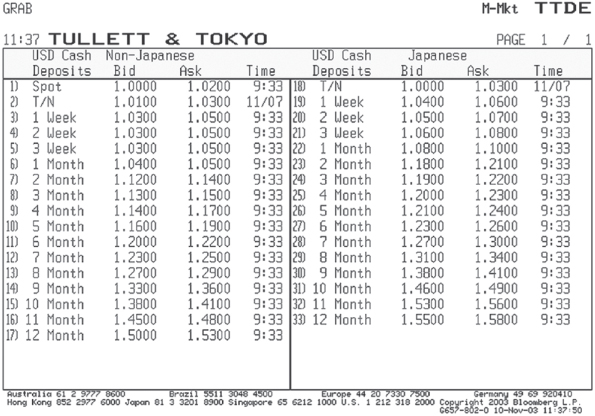
Figure 13.6 Tullet US Dollar Deposit Rates, 10 November 2003
Used with permission of Bloomberg L.P. Copyright© 2014. All rights reserved. © Tullet & Tokyo. Used with permission.
| Assets | $1 billion, > 1‐year term Receiving overnight Libor + 130 bps |
| Liability | $350 million, six‐month loan Pay 1.22% $350 million, 12‐month loan Pay 1.50% $300 million, 15‐month loan Pay 1.70% (not shown in figure 13.6) |
This matches the asset structure more closely to the term structure of the assets; however, it opens up an interest‐rate basis mismatch in that the bank is now receiving an overnight‐Libor‐based income but paying a term‐based liability. To remove this basis mismatch, the Treasury desk transacts an OIS swap to match the amount and term of each of the loan deals, paying overnight floating‐rate interest and receiving fixed‐rate interest. The rates for OIS swaps of varying terms are shown in Figure 13.7, which shows two‐way prices for OIS swaps up to two years in maturity. So for the six‐month OIS the hedger is receiving fixed‐interest at a rate of 1.085% and for the 12‐month OIS he is receiving 1.40%. The difference between what it is receiving in the swap and what it is paying in the term loans is the cost of removing the basis mismatch, but more fundamentally reflects a key feature of OIS swaps versus deposit rates: deposit rates are Libor‐related, whereas U.S. dollar OIS rates are driven by the Fed Funds rate. On average, the Fed Funds rate lies approximately 8–10 bps below the dollar deposit rate, and sometimes as much as 15 bps below cash levels. Note that at the time of this trade, the Fed Funds rate was 1% and the market was not expecting a rise in this rate until at least the second half of 2004. This sentiment would have influenced the shape of the USD OIS curve.
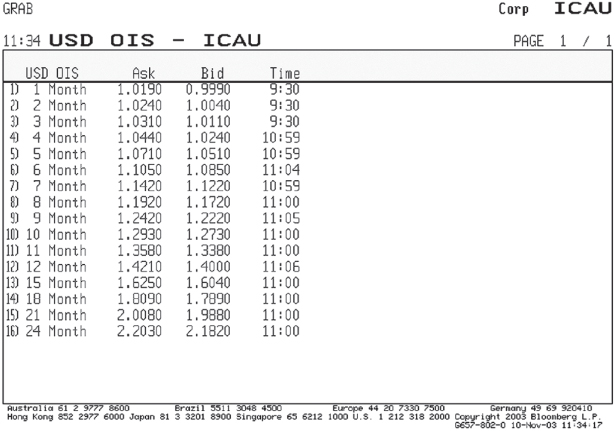
Figure 13.7 Garban ICAP U.S. Dollar OIS Rates, 10 November 2003 Used with permission of Bloomberg L.P.
Copyright© 2014. All rights reserved.
The action taken above hedges out the basis mismatch and also enables the Treasury desk to match its asset profile with its liability profile. The net cost to the Treasury desk represents its hedging costs.
Figure 13.8 illustrates the transaction.

Figure 13.8 Illustration of Interest Basis Mismatch Hedging Using OIS Instrument
OIS Swap Terms
To illustrate OISs further, we give here the terms of one of the OIS executed in Example 13.3, the six‐month swap. The counterparties to the trade are as labelled in Figure 13.8.
| Notional | $350 million |
| Trade date | 10 November 2003 |
| Effective date | 12 November 2003 |
| Termination date | 12 May 2004 |
| Payment terms | The net interest payment is paid as a bullet amount on maturity |
| Fixed Amounts | ||
| Fixed rate payer | OIS swap bank | |
| Fixed rate period end date | 12 May 2004 | |
| Fixed rate | 1.085% | |
| Fixed rate day‐count fraction | Act/360 | |
| Floating Amounts | ||
| Floating rate payer | Treasury desk | |
| Floating rate period end date | 12 May 2004 | |
| Floating rate option | USD‐Fed Funds |
The floating rate is calculated as follows:
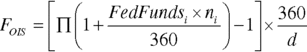
where
| d0 | is the number of New York banking days in the calculation period |
| i | is a series of whole numbers from 1 to d0, each representing a New York banking day |
| FedFundsi | is a reference rate equal to the overnight USD Federal Funds interest rate, as displayed on Telerate page 118 and Bloomberg page BTMM |
| ni | is the number of calendar days in the calculation period on which the rate is FedFundsi |
| d | is the number of days in the calculation period |
| Floating rate day‐count | Act/360 |
| Reset dates | The last day of each calculation period |
| Compounding | Inapplicable |
| Business day convention | Modified following business day |
| Calculation agent | OIS swap bank |
Reproduced from Fixed Income Markets, Second Edition (2014)
This extract from Fixed Income Markets, Second Edition (2014)
Bond Futures Contracts
Bond Futures Contracts
The most widely used risk management instrument in the bond markets is the government‐bond futures contract. This is usually an exchange‐traded standardised contract that fixes the price today at which a specified quantity and quality of a bond will be delivered at a date during the expiry month of the futures contract. Unlike short‐term interest‐rate futures, which only require cash settlement, and which we encountered in the section on money markets, bond futures require the actual physical delivery of a bond when they are settled. In this chapter we review bond futures contracts and their use for trading and hedging purposes.
BACKGROUND
The concept of a bond futures contract is probably easier to grasp intuitively than a short‐dated interest‐rate future. This reflects the fact that a bond futures contract represents an underlying physical asset, the bond itself, and a bond must be delivered on expiry of the contract. In this way, bond futures are similar to commodity futures, which also require physical delivery of the underlying commodity.
A futures contract is an agreement between two counterparties that fixes the terms of an exchange that will take place between them at some future date. They are standardised agreements, as opposed to over‐the‐counter (OTC) ones, when traded on an exchange, so they are also referred to as exchange‐traded futures. In the United Kingdom, financial futures are traded on London International Financial Futures Exchange (LIFFE), which opened in 1982. There are four classes of contract traded on LIFFE: short‐term interest‐rate contracts; long‐term interest‐rate contracts (bond futures); currency contracts; and stock‐index contracts. We discussed interest‐rate futures contracts, which generally trade as part of the money markets, in an earlier chapter. In this section we will look at bond futures contracts, which are an important part of the bond markets; they are used for hedging and speculative purposes. Most futures contracts on exchanges around the world trade at three month maturity intervals, with maturity dates fixed at March, June, September, and December each year. This includes the contracts traded on LIFFE. Therefore, at preset times during the year a contract for each of these months will expire, and a final settlement price is determined for it. The further out one goes, the less liquid the trading is in that contract. It is normal to see liquid trading only in the “front month” contract (the current contract, so that if we are trading in April 2013 the front month is the June 2013 future), and possibly one or two of the next contracts, for most bond futures contracts. The liquidity of contracts diminishes the further one trades out in the maturity range.
When a party establishes a position in a futures contract, it can either run this position to maturity or close out the position between the trade date and maturity. If a position is closed out, the party will have either a profit or loss to book. If a position is held until maturity, the party who is long the future will take delivery of the underlying asset (bond) at the settlement price; the party who is short futures will deliver the underlying asset. This is referred to as physical settlement or sometimes, confusingly, as cash settlement. Figure 12.1 shows the deliverable bonds into the US Treasury futures contract, and the prices of each cash bond at the time.
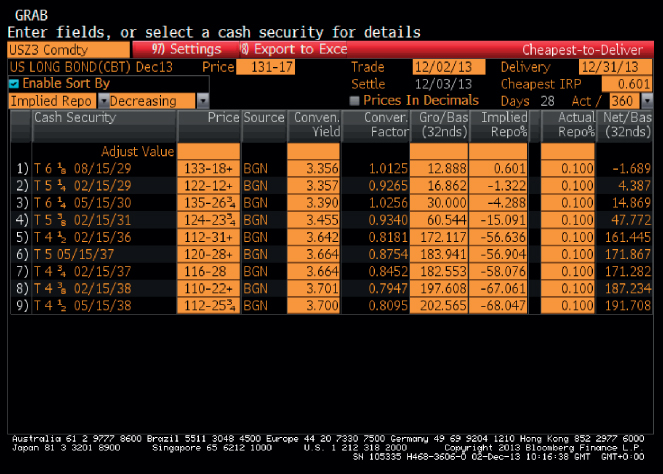
Figure 12.1 Bond Futures Delivery Quotes, Bloomberg Page DLV, 2 December 2013
Used with permission of Bloomberg L.P. Copyright© 2014. All rights reserved.
There is no counterparty risk associated with trading exchange‐traded futures, because of the role of the clearing house, such as the London Clearing House (LCH). This is the body through which contracts are settled. A clearing house acts as the buyer to all contracts sold on the exchange, and the seller to all contracts that are bought. So in the London market, the LCH acts as the counterparty to all transactions, so that settlement is effectively guaranteed. The LCH requires all exchange participants to deposit margin with it, a cash sum that is the cost of conducting business (plus broker's commissions). The size of the margin depends on the size of a party's net open position in contracts (an open position is a position in a contract that is held overnight and not closed out). There are two types of margin, maintenance margin and variation margin. Maintenance margin is the minimum level required to be held at the clearing house; the level is set by the exchange. Variation margin is the additional amount that must be deposited to cover any trading losses and as the size of the net open positions increases. Note that this is not like margin in, say, a repo transaction. Margin in repo is a safeguard against a drop in value of collateral that has been supplied against a loan of cash. The margin deposited at a futures exchange clearing house acts essentially as “good faith” funds, required to provide comfort to the exchange that the futures trader is able to satisfy the obligations of the futures contract that are being traded.
BOND FUTURES CONTRACTS
We have noted that futures contracts traded on an exchange are standardised. This means that each contract represents exactly the same commodity, and it cannot be tailored to meet individual customer requirements. In this section, we describe two very liquid and commonly traded contracts, starting with the U.S. T‐Bond contract traded on the Chicago Board of Trade (CBOT). The details of this contract are given in Table 12.1.
Table 12.1 CBOT U.S. T‐Bond Futures Contract Specifications
| Unit of Trading | U.S. Treasury bond with notional value of $100,000 and a coupon of 8% |
| Deliverable grades | U.S. T‐bonds with a minimum maturity of 15 years from first day of delivery month |
| Delivery months | March, June, September, December |
| Delivery date | Any business day during the delivery month |
| Last trading day | 12:00 noon, seventh business day before last business day of delivery month |
| Quotation | Percent of par expressed as points and thirty‐seconds of a point, e.g., 108–16 is 108 16/32 or 108.50 |
| Minimum price movement | 1/32 |
| Tick value | $31.25 |
| Trading hours | 07.20–14.00 (trading pit) |
| 17.20–20.05 | |
| 22.3006.00 hours (screen trading) |
The terms of this contract relate to a U.S. Treasury bond with a minimum maturity of 15 years and a notional coupon of 8%. We introduced the concept of the notional bond in the chapter on repo markets. A futures contract specifies a notional coupon to prevent delivery and liquidity problems that would arise if there was shortage of bonds with exactly the coupon required, or if one market participant purchased a large proportion of all the bonds in issue with the required coupon. For exchange‐traded futures, a short future can deliver any bond that fits the maturity criteria specified in the contract terms. Of course, a long future would like to be delivered a high‐coupon bond with significant accrued interest, while the short future would want to deliver a low‐coupon bond with low interest accrued. In fact, this issue does not arise because of the way the invoice amount (the amount paid by the long future to purchase the bond) is calculated. The invoice amount on the expiry date is given in equation (12.1).
where
| Invamt | is the invoice amount |
| Pfut | is the price of the futures contract |
| CF | is the conversion factor |
| AI | is the bond accrued interest |
Any bond that meets the maturity specifications of the futures contract is said to be in the delivery basket, the group of bonds that are eligible to be delivered into the futures contract. Every bond in the delivery basket will have its own conversion factor, which is used to equalise coupon and accrued interest differences of all the delivery bonds. The exchange will announce the conversion factor for each bond before trading in a contract begins; the conversion factor for a bond will change over time, but remains fixed for one individual contract. That is, if a bond has a conversion factor of 1.091252, this will remain fixed for the life of the contract. If a contract specifies a bond with a notional coupon of 7%, like the long gilt future on LIFFE, then the conversion factor will be less than 1.0 for bonds with a coupon lower than 7% and higher than 1.0 for bonds with a coupon higher than 7%. A formal definition of conversion factor is given below.
Although conversion factors equalise the yield on bonds, bonds in the delivery basket will trade at different yields, and, for this reason, they are not “equal” at the time of delivery. Certain bonds will be cheaper than others, and one bond will be the cheapest‐to‐deliver bond. The cheapest‐to‐deliver bond is the one that gives the greatest return from a strategy of buying a bond and simultaneously selling the futures contract, and then closing out positions on the expiry of the contract. This so‐called cash‐and‐carry trading is actively pursued by proprietary trading desks in banks. If a contract is purchased and then held to maturity, the buyer will receive, via the exchange's clearing house, the cheapest‐to‐deliver gilt. Traders sometimes try to exploit arbitrage price differentials between the future and the cheapest‐to‐deliver gilt, known as basis trading. This is discussed in Choudhry (2003), where the mathematical calculation of the conversion factor for the gilt future is given in Appendix 12.1.
CONVERSION FACTOR
The conversion factor (or price factor) gives the price of an individual cash bond such that its yield to maturity on the delivery day of the futures contract is equal to the notional coupon of the contract. The product of the conversion factor and the futures price is the forward price available in the futures market for that cash bond (plus the cost of funding, referred to as the gross basis).
We summarise the contract specification of the long gilt futures contract traded on LIFFE in Table 12.2. There is also a medium gilt contract on LIFFE, which was introduced in 1998 (having been discontinued in the early 1990s). This trades a notional five‐year gilt, with eligible gilts being those of four to seven years maturity.
HEDGING USING FUTURES
The Theoretical Position
Bond futures are used for a variety of purposes. Much of one day's trading in futures will be speculative; that is, a punt on the direction of the market. Another main use of futures is to hedge bond positions. In theory, when hedging a cash‐bond position with a bond futures contract, if cash and futures prices move together, then any loss from one position will be offset by a gain from the other. When prices move exactly in lock‐step with each other, the hedge is considered perfect. In practice, the price of even the cheapest‐to‐deliver bond (which one can view as being the bond being traded—implicitly—when one is trading the bond future) and the bond future will not move exactly in line with each other over a period of time. The difference between the cash price and the futures price is called the basis. The risk that the basis will change in an unpredictable way is known as basis risk.
Futures are a liquid and straightforward way of hedging a bond position. By hedging a bond position, the trader or fund manager is hoping to balance the loss on the cash position by the profit gained from the hedge. However, the hedge will not be exact for all bonds except the cheapest‐to‐deliver (CTD) bond, which we can assume is the futures contract underlying bond. The basis risk in a hedge position arises because the bond being hedged is not identical to the CTD bond. The basic principle is that if the trader is long (or net long, where the desk is running long and short positions in different bonds) in the cash market, an equivalent number of futures contracts will be sold to set up the hedge. If the cash position is short, the trader will buy futures. The hedging requirement can arise for different reasons. A market‐maker will wish to hedge positions arising out of client business, when she is unsure when the resulting bond positions will be unwound. A fund manager may, for example, know that she needs to realise a cash sum at a specific time in the future to meet fund liabilities, and sell bonds at that time. The market maker will want to hedge against a drop in value of positions during the time the bonds are held. The fund manager will want to hedge against a rise in interest rates between now and the bond sale date, to protect the value of the portfolio.
When putting on the hedge position, the key is to trade the correct number of futures contracts. This is determined by using the hedge ratio of the bond and the future, which is a function of the volatilities of the two instruments. The number of contracts to trade is calculated using the hedge ratio, which is given by
Therefore one needs to use the volatility values of each instrument. We can see from the calculation that if the bond is more volatile than the hedging instrument, then a greater amount of the hedging instrument will be required. Let us now look in greater detail at the hedge ratio.
THE FUTURES BASIS
The term “basis” is also used to describe the difference in price between the future and the deliverable cash bond. The basis is of considerable significance. It is often used to establish the fair value of a futures contract, as it is a function of the cost of carry. The gross basis is defined (for deliverable bonds only) as follows:
There are different methods available to calculate hedge ratios. The most common ones are the conversion‐factor method, which can be used for deliverable bonds (also known as the price‐factor method) and the modified‐duration method (also known as the basis‐point value method).
Where a hedge is put on against a bond that is in the futures delivery basket, it is common for the conversion factor to be used to calculate the hedge ratio. A conversion‐factor hedge ratio is more useful, as it is transparent and remains constant, irrespective of any changes in the price of the cash bond or the futures contract. The number of futures contracts required to hedge a deliverable bond using the conversion‐factor hedge ratio is determined using the following equation:
where M is the nominal value of the bond or futures contract.
The conversion‐factor method may only be used for bonds in the delivery basket. It is important to ensure that this method is only used for one bond. It is an erroneous procedure to use the ratio of conversion factors of two different bonds when calculating a hedge ratio. This will be considered again later.
Unlike the conversion‐factor method, the modified‐duration hedge ratio may be used for all bonds, both deliverable and nondeliverable. In calculating this hedge ratio the modified duration is multiplied by the dirty price of the cash bond to obtain the basis‐point value (BPV). As we discovered in Chapter 2, the BPV represents the actual impact of a change in the yield on the price of a specific bond. The BPV allows the trader to calculate the hedge ratio to reflect the different price sensitivity of the chosen bond (compared to the CTD bond) to interest‐rate movements. The hedge ratio calculated using BPVs must be constantly updated, because it will change if the price of the bond and/or the futures contract changes. This may necessitate periodic adjustments to the number of lots used in the hedge. The number of futures contracts required to hedge a bond using the BPV method is calculated using the following
where the BPV of a futures contract is defined with respect to the BPV of its CTD bond, as given by equation (12.6).
The simplest hedge procedure to undertake is one for a position consisting of only one bond, the cheapest‐to‐deliver bond. The relationship between the futures price and the price of the CTD given by equation (12.3) indicates that the price of the future will move for moves in the price of the CTD bond; so, therefore, we may set:
where CF is the CTD conversion factor.
The price of the futures contract, over time, does not move tick for tick (although it may on an intraday basis) but rather by the amount of the change divided by the conversion factor. It is apparent, therefore, that to hedge a position in the CTD bond we must hold the number of futures contracts equivalent to the value of bonds held multiplied by the conversion factor. Obviously, if a conversion factor is less than one, the number of futures contracts will be less than the equivalent nominal value of the cash position; the opposite is true for bonds that have a conversion factor greater than one. However, the hedge is not as simple as dividing the nominal value of the bond position by the nominal value represented by one futures contract (!); this error is frequently made by graduate trainees and those new to the desk.
To measure the effectiveness of the hedge position, it is necessary to compare the performance of the futures position with that of the cash‐bond position, and to see how much the hedge instrument mirrored the performance of the cash instrument. A simple calculation is made to measure the effectiveness of the hedge, given by equation (12.8), which is the percentage value of the hedge effectiveness.
Hedging a Bond Portfolio
The principles established above may be applied when hedging a portfolio containing a number of bonds. It is more realistic to consider a portfolio as holding not just bonds that are outside the delivery basket, but are also nongovernment bonds. In this case, we need to calculate the number of futures contracts to put on as a hedge based on the volatility of each bond in the portfolio compared to the volatility of the CTD bond. Note that, in practice, there is usually more than one futures contract that may be used as the hedge instrument. For example, in the sterling market it would be more sensible to use LIFFE's medium gilt contract, whose underlying bond has a notional maturity of four to seven years, if hedging a portfolio of short‐ to medium‐dated bonds. However, for the purposes of illustration we will assume that only one contract, the long gilt, is available.
To calculate the number of futures contracts required to hold as a hedge against any specific bond, we use the expression in equation (12.9).
where M is the nominal value of the bond or future
| Volbond/CTD | is the relative volatility of the bond being hedged compared to that of the CTD bond |
| VolCTD/fut | is the relative volatility of the CTD bond compared to that of the future |
It is not necessarily straightforward to determine the relative volatility of a bond vis‐à‐vis the CTD bond. If the bond being hedged is a government bond, we can calculate the relative volatility using the two bonds' modified duration. This is because the yields of both may be safely assumed to be strongly positively correlated. If, however, the bond being hedged is a corporate bond and/or a nonvanilla bond, we must obtain the relative volatility using regression analysis, as the yields between the two bonds may not be strongly positively correlated. This is apparent when one remembers that the yield spread of corporate bonds over government bonds is not constant and will fluctuate with changes in government‐bond yields. To use regression analysis to determine relative volatilities, historical price data on the bond is required. The daily price moves in the target bond and the CTD bond are then analysed to assess the slope of the regression line. In this section, we will restrict the discussion to a portfolio of government bonds.
If we are hedging a portfolio of government bonds, we can use (12.10) to determine relative volatility values, which are based on the modified duration of each of the bonds in the portfolio.
where MD is the modified duration of the bond being hedged or the CTD bond, as appropriate. This preserves the terminology we introduced in Chapter 2.1
Once we have calculated the relative volatility of the bond being hedged, equation (12.11) (obtained by rearranging (12.7)) tells us that the relative volatility of the CTD bond to that of the futures contract is approximately the same as its conversion factor. We are then in a position to calculate the futures hedge for each bond in a portfolio.
Table 12.3 shows a portfolio of five UK gilts on 20th October 1999. The nominal value of the bonds in the portfolio is £200 million, and the bonds have a market value, excluding accrued interest, of £206.84 million. Only one of the bonds is a deliverable bond, the 5¾% 2009 gilt, which is in fact the CTD bond. For the Dec99 futures contract, the bond had a conversion factor of 0.9124950. The fact that this bond is the CTD explains why it has a relative volatility of 1. We calculate the number of futures contracts required to hedge each position, using the equations listed above. For example, the hedge requirement for the position in the 7% 2002 gilt was calculated as follows:
The volatility of all the bonds is calculated relative to the CTD bond, and the number of futures contracts determined using the conversion factor for the CTD bond. The bond with the highest volatility is, not surprisingly, the 6% 2028, which has the longest maturity of all the bonds and hence the highest modified duration. We note from Table 12.3 that the portfolio requires a hedge position of 2,091 futures contracts. This illustrates how a rough‐and‐ready estimate of the hedging requirement, based on nominal values, would be insufficient, as that would suggest a hedge position of only 2,000 contracts.
Table 12.3 Bond Futures Hedge for Hypothetical Gilt Portfolio, 20 October 1999
| CTD Modified duration Conversion factor Price |
5.75% 2009 7.2345656 0.9124950 99.84 |
||||||
| Bond | Nominal Amount (£m) | Price | Yield % | Duration | Modified Duration | Relative Volatility | Number of Contracts |
| UKT 8% | |||||||
| 2000 | 12 | 102.17 | 5.972 | 1.072 | 1.01158797 | 0.143090242 | 15.67 |
| UKT 7% | |||||||
| 2002 | 5 | 101.50 | 6.367 | 2.388 | 2.24505721 | 0.315483336 | 14.39 |
| UKT 5% | |||||||
| 2004 | 38 | 94.74 | 6.327 | 4.104 | 3.85979102 | 0.50626761 | 175.55 |
| UKT 5.75% | |||||||
| 2009 | 100 | 99.84 | 5.770 | 7.652 | 7.23456557 | 1 | 912.50 |
| UKT 6% | |||||||
| 2028 | 45 | 119.25 | 4.770 | 15.031 | 14.3466641 | 2.368603078 | 972.60 |
| Total | 200 | 2,090.71 | |||||
The effectiveness of the hedge must be monitored over time. No hedge will be completely perfect, however, and the calculation illustrated above, as it uses modified‐duration value, does not take into account the convexity effect of the bonds. The reason why a futures hedge will not be perfect is because, in practice, the price of the futures contract will not move tick for tick with the CTD bond, at least not over a period of time. This is the basis risk that is inherent in hedging cash bonds with futures. In addition, the calculation of the hedge is only completely accurate for a parallel shift in yields, as it is based on modified duration, so as the yield curve changes around pivots, the hedge will move out of line. Finally, the long gilt future is not the appropriate contract to use to hedge three of the bonds in the portfolio, or over 25% of the portfolio by nominal value. This is because these bonds are short‐ or medium‐dated, and so their price movements will not track the futures price as closely as longer‐dated bonds. In this case, the more appropriate futures contract to use would have been the medium gilt contract, or (for the first bond, the 8% 2000) a strip of short sterling contracts. Using shorter‐dated instruments would reduce some of the basis risk contained in the portfolio hedge.
THE MARGIN PROCESS
Institutions buying and selling futures on an exchange deal with only one counterparty at all times, the exchange clearing house. The clearing house is responsible for the settlement of all contracts, including managing the delivery process. A central clearing mechanism eliminates counterparty risk for anyone dealing on the exchange, because the clearing house guarantees the settlement of all transactions. The clearing house may be owned by the exchange itself, such as the one associated with the Chicago Mercantile Exchange (the CME Clearinghouse) or it may be a separate entity, such as the London Clearing House, which settles transactions on LIFFE. The LCH is also involved in running clearing systems for swaps and repo products in certain currencies.
One of the key benefits to the market of the clearing‐house mechanism is that counterparty risk, as it is transferred to the clearing house, is virtually eliminated. The mechanism that enables the clearing house to accept the counterparty risk is the margining process that is employed at all futures exchanges. A bank or local trader must deposit margin before commencing dealing on the exchange; each day a further amount must be deposited or returned, depending on the results of the day's trading activity.
The exchange will specify the level of margin that must be deposited for each type of futures contract that a bank wishes to deal in. The initial margin will be a fixed sum per lot. So, for example, if the margin was £1,000 per lot, an opening position of 100 lots would require margin of £100,000. Once initial margin has been deposited, there is a mark‐to‐market of all positions at the close of business; exchange‐traded instruments are the most transparent products in the market, and the closing price is not only known to everyone, it is also indisputable. The closing price is also known as the settlement price. Any losses suffered by a trading counterparty, whether closed out or run overnight, are entered as a debit on the party's account and must be paid the next day. Trading profits are credited and may be withdrawn from the margin account the next day. This daily process is known as variation margining. Thus, the margin account is updated on a daily basis, and the maximum loss that must be made up on any morning is the maximum price movement that occurred the previous day. It is a serious issue if a trading party is unable to meet a margin call. In such a case, the exchange will order it to cease trading, and will also liquidate all its open positions; any losses will be met out of the firm's margin account. If the level of funds in the margin account is insufficient, the losses will be made good from funds paid out of a general fund run by the clearing house, which is maintained by all members of the exchange.
Payment of margin is made by electronic funds transfer between the trading party's bank account and the clearing house. Initial margin is usually paid in cash, although clearing houses will also accept high‐quality securities, such as T‐bills or certain government bonds, to the value of the margin required. Variation margin is always cash. The advantage of depositing securities rather than cash is that the depositing firm earns interest on its margin. This is not available on a cash margin, and the interest forgone on a cash margin is effectively the cost of trading futures on the exchange. However, if securities are used, there is effectively no cost associated with trading on the exchange (we ignore, of course, infrastructure costs and staff salaries).
The daily settlement of exchange‐traded futures contracts, as opposed to when the contract expires or the position is closed out, is the main reason why futures prices are not equal to forward prices for long‐dated instruments.
Reproduced from Fixed Income Markets, Second Edition (2014)
This extract from The Futures Bond Basis, Second Edition (2006)
The Bond Basis: Basic Concepts
2.3 THE BOND BASIS: BASIC CONCEPTS
2.3.1 Introduction
The previous section introduced the no‐arbitrage forward pricing principle and the concept of the basis. We will look at this again later. So, we know that the price of an asset, including a bond, that is agreed today for immediate delivery is known as its spot price.9 In essence, the forward price of an asset, agreed today for delivery at some specified future date, is based on the spot price and the cost or income of foregoing delivery until the future date. If an asset carries an income stream, with‐holding delivery until, say, 3 months in the future, it would present an opportunity cost to an investor in the asset, so the prospective investor would require a discount on the spot price as the price of dealing in a forward. However, if an asset comes with a holding cost – for example, storage costs – then an investor might expect to pay a premium on the spot price, as he would not be incurring the holding costs that are otherwise associated with the asset.
Commodities such as wheat or petroleum are good examples of assets whose forward delivery is associated with a holding cost. For a commodity whose price is agreed today but for which delivery is taken at a forward date, economic logic dictates that the futures price must exceed the spot price. That is, a commodity basis is usually negative. Financial assets such as bonds have zero storage costs, as they are held in electronic form in a clearing system such as CREST, the settlement system for UK gilts;10 moreover, they provide an income stream that would offset the cost of financing a bond‐holding until a future date. Under most circumstances when the yield curve is positively sloping, the holding of a bond position until delivery at a future date will generate a net income to the holder. For these and other reasons it is common for the bond basis to be positive, as the futures price is usually below the spot price.
As we have noted, bond futures contracts do not specify a particular bond, rather a generic or notional bond. The actual bond that is delivered against an expired futures contract is the one that makes the cost of delivering it as low as possible. The bond that is selected is known as the cheapest‐to‐deliver. Considerable research has been undertaken into the concept of the cheapest‐to‐deliver (CTD) bond. In fact, certain commodity contracts also trade with an underlying CTD. Burghardt et al. (1994) point out that wheat is not an homogenous product, as wheat from one part of the country exhibits different characteristics from wheat from another part of the country, and may have to be transported a longer distance (hence at greater cost) to delivery. Therefore, a wheat contract is also priced based on the designated cheapest‐to‐deliver. There is no physical location factor with government bonds, but futures contracts specify that any bond may be delivered that falls into the required maturity period.
In this section we look at the basic concepts necessary for an understanding of the bond basis, and introduce all the key topics. Basis trading itself is the simultaneous trading of the cash bond and the bond futures contract, an arbitrage trade that seeks to exploit any mis‐pricing of the future against the cash or vice versa.11 In liquid and transparent markets such mis‐pricing is rare, of small magnitude and very short‐lived. The arbitrageur will therefore also try to make a gain from the difference between the costs of holding (or shorting) a bond against that of delivering (or taking delivery of) it at the futures expiry date: essentially, then, the difference between the bond's running yield and its repo financing cost. We'll save the trading principles for Chapter 3. First, let us introduce some basic terminology.
2.3.3 The conversion factor
So, we know that a bond futures contract represents any bond whose maturity date falls in the period described in the contract specifications. During the delivery month, and up to the expiry date, the party that is short the future has the option on which bond to deliver and on what day in the month to deliver it. Let us consider the long gilt contract on LIFFE. If we assume the person that is short the future delivers on the expiry date, for each contract they must deliver to the exchange's clearing house £100,000 nominal of a notional 6% gilt of between ![]() and 13 years' maturity.12 Of course, no such specific bond exists, so the seller delivers a bond from within the delivery basket. However, if the seller delivers a bond of, say, 5% coupon and 9 years' maturity, intuitively we see that the value of this bond is lower than a 6% bond of 13 years' maturity. While the short future may well think, ‘fine by me’, the long future will most certainly think not. There would be the same aggrieved feelings, just reversed, if the seller was required to deliver a bond of 7% coupon. To equalise all bonds, irrespective of which actual bond is delivered, the futures exchange assigns a conversion factor to each bond in the delivery basket. This serves to make the delivery acceptable to both parties. Conversion factors are used in the invoice process to calculate the value of the delivered bond that is equal to that specified by the contract. In some texts the conversion factor is known as the price factor. The concept of the conversion factor was developed by CBOT in the 1970s.
and 13 years' maturity.12 Of course, no such specific bond exists, so the seller delivers a bond from within the delivery basket. However, if the seller delivers a bond of, say, 5% coupon and 9 years' maturity, intuitively we see that the value of this bond is lower than a 6% bond of 13 years' maturity. While the short future may well think, ‘fine by me’, the long future will most certainly think not. There would be the same aggrieved feelings, just reversed, if the seller was required to deliver a bond of 7% coupon. To equalise all bonds, irrespective of which actual bond is delivered, the futures exchange assigns a conversion factor to each bond in the delivery basket. This serves to make the delivery acceptable to both parties. Conversion factors are used in the invoice process to calculate the value of the delivered bond that is equal to that specified by the contract. In some texts the conversion factor is known as the price factor. The concept of the conversion factor was developed by CBOT in the 1970s.
Table 2.3 shows the conversion factors for all gilts that were eligible for delivery for the December 2000 to March 2002 contracts. Notice how the conversion factors exhibit the ‘pull to par’, decreasing towards 1.00 for those with a coupon above the notional 7% and increasing towards 1.00 for bonds with a coupon below 7%. The passage of time also shows bonds falling out of the delivery basket, and the introduction of a new issue into the basket, the 5% gilt maturing 7 March 2012.
TABLE 2.3 Conversion factors for deliverable gilts, Dec00 to Mar02 long gilt contracts.
Source: LIFFE.
| Futures contract | ||||||
| Gilt | Dec00 | Mar01 | Jun01 | Sep01 | Dec01 | Mar02 |
| 5.75% Treasury 2009 | 0.917 472 8 | 0.918 980 2 | ||||
| 6.25% Treasury 2010 | 0.946 747 8 | 0.947 561 1 | 0.948 641 5 | 0.949 495 6 | 0.950 587 4 | |
| 9% Conversion 2011 | 1.147 928 1 | 1.145 557 8 | 1.143 102 6 | 1.140 593 6 | 1.138124 0 | 1.135 585 9 |
| 5% Treasury 2012 | 0.852 8791 | 0.855172 7 | 0.857 727 0 | |||
| 9% Treasury 2012 | 1.157 636 8 | 1.155 551 2 | 1.153 162 6 | |||
| 8% Treasury 2013 | 1.083 567 6 | 1.082 620 6 | 1.081 499 0 | 1.080 511 4 | 1.079 356 0 | 1.078 336 3 |
The yield obtainable on bonds that have different coupons but identical maturities can be equalised by adjusting the price for each bond. This principle is used to calculate the conversion factors for different bonds. The conversion factor for a bond is the price per £1 (or per $1, €1 and so on) at which the bond would give a yield equal to the yield of the notional coupon specified in the futures contract. This is 7% in the case of the long gilt contract, 6% for the Treasury long bond and so on. In other words, the conversion factor for each bond is the price such that every bond would provide an investor with the same yield if purchased; or, the price at which a deliverable bond would trade if its gross redemption yield was 7% (or 6% and so on). The yield calculation is rounded to whole quarters, given the delivery month cycle of futures. Futures exchanges calculate conversion factors effective either on the exact delivery date, where a single date is defined, or (as at LIFFE) on the 1st day of the delivery month if delivery can take place at any time during the delivery month.
The conversion factor is assigned by the exchange to each bond in the delivery basket at the start of trading of each contract. It remains constant throughout the life of the contract. A particular bond that remains in the delivery basket over a length of time will have different conversion factors for successive contracts. For example, the 9% UK Treasury maturing on 13 October 2008 had conversion factors of 1.145 431 7, 1.142 995 5 and 1.140 715 5 for the LIFFE long gilt contracts that matured in June, September and December 1998, respectively.
Other things being equal, bonds with a higher coupon will have larger conversion factors than those with lower coupons. For bonds with the same coupon, maturity has an influence, though this is slightly less obvious. For bonds with coupons below the notional rate defined in the contract description, the conversion factor is smaller for bonds with a longer maturity. The opposite is true for bonds carrying coupons in excess of the notional coupon rate, for which the conversion factor will be larger the longer the maturity. This effect arises from the mathematics of fixed‐interest securities. Bonds with coupon below current market yields will trade at a discount. This discount is larger the longer the maturity, because it is a disadvantage to hold a bond paying a coupon lower than current market rates, and this disadvantage is greater the longer the period to the bond maturing. Conversely, bonds with coupons above current market yields trade at a premium which will be greater the longer the maturity.
To help calculate the invoice price of a bond on delivery, we multiply the price of the final settlement price of the futures contract with its conversion factor. This gives us the converted price. The price payable by the long future on delivery of the bond is the invoice price, and this is the futures settlement price plus accrued interest. This was shown in simple fashion as (2.1). The actual invoice price, calculated once the actual bond being delivered is known, is given by:
where
| Pinv | = | Invoice price; |
| Mfut | = | Nominal value of the delivered bonds as specified in the contract; |
| Pfutsett | = | Futures settlement price. |
Invoice amount
When the bond is delivered, the long pays the short an invoice amount:
The settlement price (or exchange delivery settlement price, EDSP) is the trading price per £100 nominal for the futures contract on the last day of trading, and is confirmed by the exchange. The invoice amount includes accrued interest because the futures contract is traded at a clean price and does not include accrued interest.
Box 2.1 Calculating the invoice price.
A futures contract settles at 102.50. The contract specifies £100,000 nominal of the underlying bond. The delivered bond has a conversion factor of 1.14579 and accrued interest of 0.73973. The settlement price is equal to 1.025% of the nominal value (par value). The invoice price is calculated as:
For the Treasury long bond the conversion factor is calculated using (2.10):
where
| N | = | Complete years to maturity as at the delivery month; |
| t | = | Number of months in excess of the whole N (rounded down to whole quarters). |
The LIFFE conversion factor for the long gilt was given in Appendix 1.A. The formula is actually the same, beginners are invited to explain that this is indeed so. To illustrate (2.10), if a deliverable Treasury bond has a maturity of 19 years and 5 months, t is 3 because the 5 months is rounded down to one quarter or 3 months. Hence, if the maturity is 19 years and 9 months, t is 6.
It is worth summarising what we know so far about conversion factors:
- conversion factors remain constant for a bond from the moment they are assigned to the expiry of the contract;
- conversion factors are different for each bond and for each contract;13 from Table 2.3, which relates to the long gilt contract and its then notional coupon of 7%, we see that conversion factors for bonds with coupons higher than 7% diminish in value for each successive contract month, while those for bonds with coupons lower than 7% rise in value for successive contract months.14 This reflects the ‘pull to par’ effect which for bonds with the higher coupon is falling from a premium and for bonds with the lower coupon is rising from a discount;
- the conversion factor is used to calculate the invoice price of a bond that is delivered into a futures contract;
- bonds with coupons greater than the notional coupon of the futures contract have a conversion factor higher than 1, while bonds with coupons lower than the notional coupon have a conversion factor lower than 1.
Table 2.3 Sample 5‐year CDS premiums, September 2003.
Sources: Morgan Stanley, Bloomberg, Risk.
| Reference name | Mid‐price bps | Moody's/S&P |
| Automobiles | ||
| Ford Motor Co. | 318 | Baa1/BBB2 |
| General Motors | 269 | Baa1/BBB |
| GMAC | 229 | A3/BBB |
| Banks | ||
| Bank of America | 23 | Aa2/A1 |
| Wells Fargo | 33 | Aa2/A1 |
| Asia‐Pacific region | Bid–ask | Moody's/S&P |
| Hutchison Whampoa | 96/106 | A3/A2 |
| PR China | 22/26 | A3/BBB |
| Republic of Korea | 67/74 | A3/A2 |
| NEC | 46/53 | Baa2/BBB2 |
| Qantas | 74/84 | Baa1/BBB1 |
The conversion factor is not a hedge ratio, as has been strongly emphasised by both Burghardt and Kolb,15 and should not be used as such. Certain textbooks and market practitioners have suggested that using the ratio of two bonds' conversion factors can be an effective hedge ratio for hedging a bond position, rather than the traditional approach of using the ratio of basis point values. This is fallacious and will lead to serious errors. The conversion factor of a bond is influenced primarily by its coupon, whereas the modified duration of a bond – from which is derived the Basis Point Value (BPV) – is a function mainly of its term to maturity. Hence, it is not correct to substitute them. If an investor was hedging a position in a long‐dated bond of low coupon, and the current CTD bond was a short‐dated bond of high coupon, the volatility ratio calculated using the respective conversion factors would be lower than unity. However, using respective BPVs would result in a volatility ratio higher than 1. This example illustrates how using a ratio of conversion factors can result in serious hedging errors, and this approach must not be adopted.
Using conversion factors provides an effective system for making all deliverable bonds perfect substitutes for one another. The system is not perfect, of course. Conversion factors are calculated to equalise returns at a single uniform yield, the notional coupon rate specified in the contract specification. In practice though, bonds trade at different yields, resulting in the yield curve. Hence, despite the use of conversion factors, bonds will not be precisely ‘equal at the time of delivery. Some bonds will be relatively more expensive, some cheaper; one particular bond will be the CTD bond. The CTD bond is an important concept in the pricing of bond futures contracts.
2.3.4 The bond basis
Basis trading arises from the difference between the current clean price of a bond and the (implied) forward clean price at which the bond is bought through the purchase of a futures contract. The difference between these two prices is known as the gross basis. This is the bond basis to which the market refers, the difference between the bond's spot cash price and the price implied by the current price of the futures contract. The latter is given by multiplying the futures price by the relevant bond's conversion factor.
The formula for calculating the gross basis is therefore:
From (2.11) we might think that if we sell a futures contract short, in effect this guarantees an ability to deliver the bond at the futures delivery date and receive a known price for the bond. However, the price payable for the bond at delivery is based on the future's final settlement price, and not the trading price of the future at any time beforehand, and so this thinking is erroneous.
In the Treasury market both cash and futures prices are quoted as points and ticks (32nds) per $100 nominal value, and if necessary as half‐ticks or 64ths. A 64th price is indicated by a +.
The gross basis can be explained essentially as the difference between the running yield on the bond and the current repo (money market) rate. However, a residual factor exists due to the delivery option implicit in the design of the futures contract and to the daily marking‐to‐market of the contract, both of which are more difficult to quantify. This residual amount is known as the net basis. Net basis is the gross basis adjusted for net carry. Net carry is the actual coupon income and re‐investment less borrowing expense, which is at the security's actual repo or money market financing rate.
Figure 2.6 is the Bloomberg page DLV of the deliverable bonds for the June 2000 long gilt contract, and shows the conversion factors and gross basis value for each bond in the basket.
FIGURE 2.6 Delivery basket for Jun00 long gilt, Bloomberg page DLV, 15 March 2000.
© Bloomberg L.P. Used with permission. Visit www.bloomberg.com
Box 2.2 The gross basis
Consider the following market details, all relating to one instantaneous point in time:
| Settlement date | 16 March 2000 |
| Futures delivery date | 30 June 2000 |
| Days to delivery | 106 |
| Bond price (UKT 9% 2011) | 131.461 0 |
| Accrued interest | 1.578 082 2 |
| Accrued to delivery | 4.191 780 8 |
| Futures price (M0 LIFFE long gilt) | 112.98 |
| Conversion factor | 1.152 570 5 |
| Cash market repo rate | 6.24% |
We can calculate the gross basis that would apply in a hypothetical cash‐and‐carry trade, where there is a simultaneous purchase of the bond and sale of the futures contract as shown below.
Bond purchase – outflow of funds:
Futures sale – inflow of funds:
The gross basis is:
or 1.243 584 91.
2.3.5 The net basis
We've seen from the previous section that gross basis measures the carry on a bond that applies during the life of the futures contract. Because of other factors associated with the delivery into a futures contract, principally that delivery is at the option of the short future, the gross basis is not the actual carry that would be incurred if a trader put on a cash versus futures trade. This is measured by the net basis. The net basis causes much confusion amongst market participants, but it is a straightforward concept. Burghardt et al. (1994) state that the net basis is the difference between a bond's basis and its total carry to delivery.16 Plona describes net basis as the difference between the implied repo rate (IRR) and the general collateral repo rate. We consider the IRR in Section 2.3.6.17
Both descriptions are good ways in which to consider net basis. Essentially, the net basis is the gross basis adjusted for net carry. Net carry is the actual coupon income (and any re‐investment income) minus borrowing expense, which is at the security's actual repo (money market) rate. The net basis is therefore the true ‘economic basis and measures the net gain from a simultaneous position in the cash bond and the futures contract. A positive value represents a loss or net cost to the long cash/short futures position, and the net basis is the expected profit for the short cash/long futures position (where the actual repo rate used is the reverse repo rate). The opposite is true for negative net basis values.
The net basis is calculated on the assumption that a basis trade is conducted by the arbitrageur borrowing funds to purchase the CTD bond, financing it in the repo market, and shorting the futures contract. It measures the maximum loss that would be suffered by holding this position until the contract expiry date. The net basis should be negative as a loss measure; a positive net basis indicates the potential profit from such a trade.18 On the other hand, a negative net basis theoretically indicates the potential profit from a short bond/long futures position.
To calculate the net basis, we need to make an assumption about the financing rates that would apply to a basis trade.19 This centres on the repo rate that is applicable to the cash bond element of the trade. Analysts use one of two methods:
- the specific repo rate for the cash bond, fixed to the maturity date. This is a logical approach, as it provides an accurate measure of the financing cost associated with running a long position in the bond, and then delivering it into the futures exchange. Calculating net basis under this method provides a measure of the value of the delivery option;
- the overnight general collateral (GC) repo rate, assuming therefore that the bond position is financed on a daily basis. Assuming that the overnight rate will be maintained more or less over the term of the trade is risky.
Box 2.3 illustrates the calculation of the net basis.
Box 2.3 The net basis.
Consider this calculation for the June 1998 long gilt future contract. At this time the ‘special ex’ rule applies to delivery of bonds into the contract, something that no longer applied with the removal of special ex‐trading in August 1998.
| Trade date | 24 April 1998 |
| Settlement date | 25 April 1998 |
| M8 long gilt future price | 109.656 25 |
| CTD bond ( |
106.343 75 |
| Accrued interest | 2.305 48 |
| Accrued to delivery | 3.423 288 2 |
| Dirty price | 108.649 32 |
| Conversion factor ( |
0.967 406 4 |
| Repo rate | 6.36% |
The converted price of the bond (that is, through the futures contract) is:
The market clean price is 106.343 75, therefore the gross basis is:
Due to the special‐ex rule in this case, the last day for delivery of ![]() Treasury 2007 into the futures contract is 12 June. This makes the term 48 days. The total price paid including accrued interest will be 108.649 23. To finance that using repo for 48 days until 12 June will cost £0.908 724 3. The holder of the gilt will however earn 48 days’ accrued interest of £1.117 808 2. Therefore, buying the bond direct gives the owner an income advantage of £0.209 083 9.
Treasury 2007 into the futures contract is 12 June. This makes the term 48 days. The total price paid including accrued interest will be 108.649 23. To finance that using repo for 48 days until 12 June will cost £0.908 724 3. The holder of the gilt will however earn 48 days’ accrued interest of £1.117 808 2. Therefore, buying the bond direct gives the owner an income advantage of £0.209 083 9.
The difference between the gross basis and this income advantage is £0.216 159 – £0.209 083 9, that is £0.0525. It therefore represents the gain by buying the gilt using the futures contract rather than buying directly in the market.
Of course, the long gilt contract gives the futures seller the right to deliver any of the gilts in the delivery basket and on any day of the delivery month. If the CTD is bought through a futures contract the buyer may find that, because of market movements, a different gilt is delivered. The short future in effect holds an option which decreases the value of the futures contract to the long.
For this reason the net basis is usually positive. The futures contract is also marked‐to‐market which means that the gain or loss on the contract is spread over the life of the contract, in contrast to a forward contract. This effect is small but will again lead to the net basis differing from 0.
The net basis is given by:

2.3.6 The implied repo rate
In a basis trade the rate implied by the strategy is known as a repo rate because it is equivalent to a repurchase agreement with the futures market. In effect, the short future lends money to the futures market: the short future agrees to buy a bond with a simultaneous provision to sell it back to the market at a predetermined price and to receive a rate of interest on his money, the repo rate. It is the implied repo rate because it is an expected repo rate gain if the trade was carried out. In some literature it is suggested as a complex and obscure calculation; in fact, the Implied Repo Rate (IRR) is very straightforward to calculate. It is the theoretical return from a basis trade of long cash bond against short future, with the bond delivered into the future on expiry.
The IRR is a measure of return from a basis trade. Consider the cash flows involved when one is long bond/short future. We have:
- a cash outflow from purchasing the bond;
- a cash inflow on delivery into the future, including the accrued interest to the delivery date;
- the cash borrowed to finance the trade.
We simply therefore wish to have the percentage return of the investment over the borrowing cost. That is:
where
| M | = | Day‐base, either 360 or 365; |
| Days | = | Term of the trade. |
There is no need to remember this version though, Burghardt et al. (1994, p. 14) simplify it to:
which is identical to (2.12), with n for the number of days to delivery, and all prices still include accrued interest, at the time of the trade (bond) or to delivery (future). The formula written as (2.13) is easy to explain. The invoice price is the futures invoice price, the amount from the delivery on expiry. Of course, the actual invoice price is a function of the final futures settlement price, but we adjust the current futures price with the conversion factor to allow for this.
Note that Bloomberg quotes the formula in still more simplified fashion, as:

with the 360‐day base associated with the US Treasury market.
Both (2.12) and (2.13) assume that no coupon is paid during the trade. If a coupon is paid during the trade, it is considered as being reinvested, and the cash flow total must therefore include both the coupon and the reinvestment income generated. The re‐investment rate used in the market is one of the following:
- the implied repo rate;
- the bond's yield‐to‐maturity. This is described as being consistent with the bond yield calculation itself, which assumes reinvestment of coupon at the bond yield;
- the overnight repo rate, and rolled over. This is justified on the basis that traders in fact do not reinvest the coupon but use the cash to reduce funding costs.
The first two are assumed to apply to maturity, while the second must be calculated at the prevailing rate each day. If the reinvestment rate is assumed to be the IRR, it is the rate that results in:
where n2 is the number of days between the coupon payment and the futures expiry (delivery) date. Expression (2.15) is then rearranged for the IRR, to give us:
The deliverable bond that has the highest IRR is the cheapest‐to‐deliver bond or CTD. We see from (2.16) that the IRR is a function of the bond price, the value of which is compared to the forward price for the bond implied by futures price. As such the status of the CTD bond reflects the bond's price (in other words, its yield). If the yield of a bond within the delivery basket moves sufficiently vis‐à‐vis the other deliverable bonds, it may become the CTD bond. A change in the cheapest bond is an important development and any such change should be anticipated in advance by good traders.
The bond with the highest IRR will, almost invariably, have the lowest net basis. On rare occasions this will not be observed. When two bonds each have IRRs that are very similar, it is sometimes the case that the bond with the (slightly) lower IRR has a (slightly) lower net basis.
The CTD bond is just that: it is the cheapest bond to deliver into the futures contract in terms of running costs. The short future has the delivery option, and will elect to deliver the CTD bond unless there is a reason it cannot, in which case it will deliver the next cheapest at greater cost to itself. Assuming that a basis trade is put on with the CTD bond against the future, if the CTD changes then the position becomes useless and will be unwound at great loss. The CTD bond is what the market will treat as the actual underlying bond of the futures contract, and it is closely observed. Pricing theory informs us that the futures price will track the CTD bond price; in fact, it is the other way around, with the liquidity and transparency of the futures contract and its price meaning that the CTD bond price tracks that of the future. Under the terms of the long gilt contract, the CTD gilt can be delivered on any business day of the delivery month, but in practice only one of two days are ever used to make delivery: the first (business) day of the delivery month or the last (delivery) day of the month. If the current yield on the CTD gilt exceeds the money market repo rate, the bond will be delivered on the last business day of the month, because the short future earns more by holding on to the bond than by delivering it and investing the proceeds in the money market; otherwise, the bond will be delivered on the first business day of the delivery month. Until very recently a gilt that was eligible for trading special exdividend on any day of the delivery month was not eligible for delivery into that gilt contract. However, from August 1998 the provision for special ex‐dividend trading was removed from gilts, so this consideration no longer applies. Other gilts that are not eligible for delivery are index‐linked, partly paid or convertible gilts.20 For gilts the IRR for all deliverable bonds can be calculated using (2.12) in the normal way. However, if a bond goes ex‐dividend between trade date and delivery date, a modification is required in which the interest accrued is negative during the ex‐dividend period.
Box 2.4 The implied repo rate.
Another way of looking at the concept of the CTD bond is in terms of the IRR. The CTD bond is the bond that gives the highest IRR to the short from a cash‐and‐carry trade; that is, a strategy of buying the bond (with borrowed funds) in the cash market and selling it forward into the futures market. The bond is funded in the repo market, and by selling it forward the trade is in effect a repo with the futures market, hence implied repo rate.
To illustrate we calculate the IRR for the 9% Treasury 2008, a UK gilt, at the time that the ‘front month’ contract was the December 1998 contract. The price of the gilt is 129.083 4. The December 1998 long gilt futures contract is trading at 114.50. The date is 1 October. The money market rate on this date is 7.25%. As the current (or running) yield on the 9% 2008, at 6.972%, is lower than the money market rate, it will be delivered at the beginning of December (that is, in 61 days from now). To identify the CTD bond we would need to calculate the IRR for all eligible bonds. We use the conversion factor for the bond which is 1.140 715, calculated and given out by LIFFE before the futures contract began trading.
The cash outflow in a cash‐and‐carry trade is:
| Bond dirty price | 129.083 4 |
| Interest cost (1 October–1 December) | 129.083 4 × (0.072 5 × (61/365)) |
| Total outflow | 130.647 4 |
The bond (whose price includes 171 days' accrued interest on 1 October) has to be financed at the money market rate of 7.25% for the 61 days between 1 October and 1 December, when the bond (if it is still the CTD) is delivered into the futures market.
The cash inflow per £100 nominal as a result of this trade is:
| Implied clean price of bond on | |
| 1 December (futures price on | |
| 1 October multiplied by | |
| conversion factor) | 114.50 × 1.140 715 5 |
| Accrued interest | |
| 1 October–1 December | £9 × (61/365) |
| Total inflow | 132.11603 |
The implied price of the bond on 1 December equals the futures price on 1 October multiplied by the conversion factor for the bond. Because the futures price is quoted clean, accrued interest has to be added to obtain the implied dirty price on 1 December.
This cash‐and‐carry trade which operates for 61 days from 1 October to 1 December generates a rate of return or IRR of:

Box 2.5 Calculating gross basis, net basis and implied repo rate.
The gross basis is the difference between the actual price of the bond and the forward price of the bond as implied by the price of the futures contract, and represents the carrying cost of the bond. This is the actual difference between the coupon gain and re‐investment minus the carry costs (which is at the actual money market repo rate). A positive net basis represents the loss that would result from a long cash/short futures position, and therefore the theoretical gain from a short cash/long futures trade, where the actual repo rate is the reverse repo rate transacted when covering the short cash position. The IRR is the theoretical return from a long cash/short futures trade, assuming that the trader is short the number of futures equal to the bond's conversion factor for each £100,000 nominal of bonds held. Any coupon payments are assumed to be reinvested at the IRR.
Earlier in this book we presented the formulae for gross basis and IRR. The net basis is given by:

where
| Pbond | = | Bond dirty price; |
| r | = | Actual repo rate (expressed as per cent × 100); |
| Del | = | Days to delivery; |
| Pfut | = | Futures price; |
| CF | = | Bond's conversion factor; |
| AIdel | = | Bond's accrued interest to delivery. |
For net basis calculations in Treasury or euro markets the appropriate 360‐day basis is used.
The calculations are for the CTD bond for the long gilt contract, which was the ![]() 2010 gilt. We use mid prices for the bond. The trade is buying the cash and simultaneously selling the future. Note that gilts accrue on actual/actual basis and there were 184 days in the interest period 25 May–25 November 2001. The accrued interest calculation is therefore (80/184 × (6.25 × 0.5)) for the first date and (126/184 × (6.25 × 0.5)) for the delivery date.
2010 gilt. We use mid prices for the bond. The trade is buying the cash and simultaneously selling the future. Note that gilts accrue on actual/actual basis and there were 184 days in the interest period 25 May–25 November 2001. The accrued interest calculation is therefore (80/184 × (6.25 × 0.5)) for the first date and (126/184 × (6.25 × 0.5)) for the delivery date.
| Settlement date | 13 August 2001 |
| Futures price | 115.94 |
| 110.20 | |
| Conversion factor | 0.949 495 6 |
| Repo rate | 4.90% |
Calculations
Cash out on 13/8/2001:
Cash in on 28/9/2021:

Gross basis
Net basis
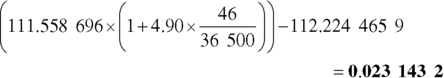
Implied repo rate
These calculations are confirmed by looking at the Bloomberg screens YA and DLV for value on 13 August 2001, as shown in Figures 2.7 and 2.8, respectively. Figure 2.7 is selected for the ![]() 2010 gilt and Figure 2.8 is selected for the front month contract at the time, the Sep01 gilt future. Figure 2.9 shows the change in CTD bond status between the
2010 gilt and Figure 2.8 is selected for the front month contract at the time, the Sep01 gilt future. Figure 2.9 shows the change in CTD bond status between the ![]() 2010 gilt and the 9% 2011 gilt, the second cheapest bond at the time of the analysis, with changes in the futures price. The change of CTD status with changes in the IRR is shown in Figure 2.10. Both are Bloomberg page HCG.
2010 gilt and the 9% 2011 gilt, the second cheapest bond at the time of the analysis, with changes in the futures price. The change of CTD status with changes in the IRR is shown in Figure 2.10. Both are Bloomberg page HCG.

Figure 2.7 Bloomberg YA page for 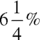 2010 gilt, showing accrued interest for value 13 August 2001.
2010 gilt, showing accrued interest for value 13 August 2001.
© Bloomberg L.P. Used with permission. Visit www.bloomberg.com
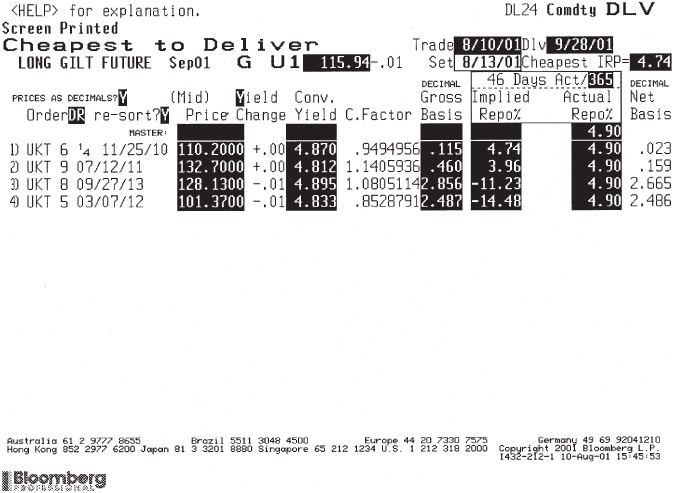
Figure 2.8 Bloomberg DLV page for Sep01 (U1) gilt contract, showing gross basis, net basis and IRR for trade date 12 August 2001.
© Bloomberg L.P. Used with permission. Visit www.bloomberg.com
Figure 2.9 Bloomberg HCG page for Sep01 (U1) gilt contract, showing CTD bond history up to 12 August 2001 with changes in futures price.
© Bloomberg L.P. Used with permission. Visit www.bloomberg.com
Figure 2.10 Bloomberg HCG page for Sep01 (U1) gilt contract, showing CTD bond history up to 12 August 2001, with changes in IRR.
Reproduced from The Futures Bond Basis, Second Edition (2006)
© Bloomberg L.P. Used with permission. Visit www.bloomberg.com
Page DLV on Bloomberg lists deliverable bonds for any selected futures contract. Bonds are listed in order of declining implied repo rate; the user can select in increasing or decreasing order of implied repo rate, basis, yield, maturity, coupon or duration. The user can also select the price source for the bonds (in our example set at ‘Bloomberg Generic’ rather than any specific bank or market maker) and the current cash repo rate.
Credit Risk and Credit Derivatives
CREDIT RISK AND CREDIT DERIVATIVES
Credit derivatives are financial contracts designed to reduce or eliminate credit risk exposure by providing insurance against losses suffered due to credit events. A payout under a credit derivative is triggered by a credit event associated with the credit derivative's reference asset or reference entity. As banks define default in different ways, the terms under which a credit derivative is executed usually include a specification of what constitutes a credit event. The principle behind credit derivatives is straightforward. Investors desire exposure to debt that is not risk‐free because of the higher returns this debt offers. However, such exposure brings with it concomitant credit risk. This can be managed with credit derivatives. At the same time, the exposure itself can be taken on synthetically if, for instance, there are compelling reasons why a cash market position cannot be established. The flexibility of credit derivatives provides users with a number of advantages and as they are over‐the‐counter (OTC) products they can be designed to meet specific user requirements. Some of the most common reasons for which they are used include:
- hedging credit risk: this includes credit default risk, dynamic credit risks and changes in credit quality;
- reducing credit risk with a specific client (obligor) so that lending lines to this client are freed up for other business;
- diversifying investment options; in other words, acquiring credit exposure without having to buy the cash product.
The intense competition among commercial banks, combined with rapid disintermediation, has meant that banks have been forced to evaluate their lending policies, with a view to improving profitability and return on capital. The use of credit derivatives assists banks with restructuring their businesses, because they allow banks to repackage and transfer credit risk, while retaining assets on balance sheet (when required) and thus maintain client relationships. As the instruments isolate certain aspects of credit risk from the underlying loan or bond and transfer them to another entity, it becomes possible to separate the ownership and management of credit risk from the other features of ownership associated with the assets in question. This means that illiquid assets such as bank loans, and illiquid bonds, can have their credit risk exposures transferred—the bank owning the assets can protect against credit loss even if it cannot transfer the assets themselves.5
The same principles apply to the credit risk exposures of portfolio managers. For fixed‐income portfolio managers, some of the advantages of using credit derivatives include the following:
- they can be tailor‐made to meet the specific requirements of the entity buying the risk protection, as opposed to the liquidity or term of the underlying reference asset;
- they can be ‘sold short’ without risk of a liquidity or delivery squeeze, as it is a specific credit risk that is being traded. In the cash market, it is not possible to ‘sell short’ a bank loan for example, but a credit derivative can be used to establish synthetically the economic effect of such a position;
- as they isolate credit risk from other factors such as client relationships and interest rate risk, credit derivatives introduce a formal pricing mechanism to price credit issues only. This means a market is available in credit only, allowing more efficient pricing, and it becomes possible to model a term structure of credit rates;
- they are off‐balance sheet instruments6 and as such incorporate flexibility and leverage, exactly like other financial derivatives. For instance, bank loans are not particularly attractive investments for certain investors because of the administration required in managing and servicing a loan portfolio. However, an exposure to bank loans and their associated return can be achieved using credit derivatives while simultaneously avoiding the administrative costs of actually owning the assets. Hence credit derivatives allow investors access to specific credits while allowing banks access to further distribution for bank loan credit risk.
Thus credit derivatives can be an important instrument for bond portfolio managers as well as commercial banks, who wish to increase the liquidity of their portfolios, gain from the relative value arising from credit pricing anomalies and enhance portfolio returns.
CREDIT DERIVATIVE INSTRUMENTS
Before analysing the main types of credit derivatives, we now consider some generic features of all credit derivatives.
Background
Credit derivative instruments enable participants in the financial market to trade in credit as an asset, as they effectively isolate and transfer credit risk. They also enable the market to separate funding considerations from credit risk. A number of instruments come under the category of credit derivative. In this and the next chapter we consider the most commonly encountered credit derivative instruments. Irrespective of the particular instrument under consideration, all credit derivatives can be described as having the following characteristics:
- the reference entity: which is the asset or name on which credit protection is being bought and sold;7
- the credit event, or events: which indicate that the reference entity is experiencing or about to experience financial difficulty and which act as trigger events for termination of and payments under the credit derivative contract;
- the settlement mechanism for the contract: whether cash settled or physically settled;
- (under physical settlement), the deliverable obligation: that the protection buyer delivers to the protection seller on the occurrence of a trigger event.
Within this broad framework, it is common to see wide variations in detail among specific types of credit derivative instruments.
Funded and Unfunded Contracts
Credit derivatives are grouped into funded and unfunded instruments. In a funded credit derivative, typified by a credit‐linked note (CLN), the investor in the note is the credit‐protection seller and is making an upfront payment to the protection buyer when it buys the note. This upfront payment is the price of the CLN. Thus, the protection buyer is the issuer of the note. If no credit event occurs during the life of the note, the redemption value (par) of the note is paid to the investor on maturity. If a credit event does occur, then on termination (in effect, maturity of the bond), a value less than par will be paid to the investor. This value will be reduced by the nominal value of the reference asset that the CLN is linked to. The exact process will differ according to whether cash settlement or physical settlement has been specified for the note. We will consider this later.
In an unfunded credit derivative, typified by a CDS, the protection seller does not make an upfront payment to the protection buyer. Thus the main difference between funded and unfunded is that in a funded contract, the insurance protection payment is made to the protection buyer at the start of the transaction: if there is no credit event, the payment is returned to the protection seller. In an unfunded contract, the protection payment is made on termination of the contract on occurrence of a triggering credit event. Otherwise it is not made at all. Therefore, when entering into a funded contract transaction, the protection seller (that is, the investor) must find the funds at the start of the trade.
Credit derivatives such as CDS have a number of applications and are used extensively for flow trading of single reference name credit risks or, in portfolio swap form, for trading a basket of reference obligations. CDSs and CLNs are used in structured products, in various combinations, and their flexibility has been behind the growth and wide application of the synthetic collateralised debt obligation (CDO) and other credit hybrid products. We look at these later.
Compared to cash market bonds and loans, an unfunded credit derivative isolates and transfers credit risk only. In other words, its value reflects only the credit quality of the reference entity. Compare this to a fixed‐coupon corporate bond, the value of which is a function of both interest rate risk and credit quality, where the return to the investor depends on the investor's funding costs.8 The interest rate risk element of the bond can be removed by combining the bond with an interest rate swap, to create an asset swap. An asset swap removes the interest rate risk of the bond, leaving only the credit quality and the funding aspects of the bond. With an unfunded credit derivative, the funding aspect is removed as well, leaving only the credit element. This is because no upfront payment is required, resulting in no funding risk to the protection seller. The protection seller, who is the investor, receives a return that is linked only to the credit quality of the reference entity.
This separation of credit risk from other elements of the cash market is shown in Figure 2.5.
Figure 2.5 Credit derivatives isolate credit as an asset class and risk element.
Example 2.1 Reference entity and reference obligation
A reference obligation or reference asset is an obligation issued by a reference entity for which credit protection is required. The reference obligation usually has a pre‐specified seniority, to facilitate ease of determination of the settlement payment. A higher seniority usually leads to a better recovery rate and hence a lower loss rate following a credit event. It is also reflected in a lower price for the credit derivative contract.
Credit Events
The occurrence of a specified credit event will trigger the termination of the credit derivative contract, and result in the transfer of the default protection payment from the protection seller to the protection buyer.
The following may be specified as ‘credit events’ in the legal documentation between counterparties:
- downgrade in S&P and/or Moody's credit rating below a specified minimum level;
- financial or debt restructuring; for example, occasioned under administration or as required under US bankruptcy protection;
- bankruptcy or insolvency of the reference asset obligor;
- default on payment obligations such as bond coupon and continued non‐payment after a specified time period;
- technical default; for example, the non‐payment of interest or coupon when it falls due;
- a change in credit spread payable by the obligor above a specified maximum level.
The International Swap and Derivatives Association (ISDA) compiled standard documentation governing the legal treatment of credit derivative contracts. The standardisation of legal documentation promoted ease of execution and was a factor in the rapid growth of the market. The 1999 ISDA CDS documentation specified bankruptcy, failure to pay, obligation default, debt moratorium and restructuring to be credit events. Note that it does not specify a rating downgrade to be a credit event.9
A summary of the credit events as set forth in the ISDA definitions is given in Appendix 2.1. Note that for North American contracts rate these were affected in 2009, as discussed later in the chapter.
The precise definition of ‘restructuring’ is open to debate and has resulted in legal disputes between protection buyers and sellers. Prior to issuing its 1999 definitions, ISDA had specified restructuring as an event or events that resulted in making the terms of the reference obligation ‘materially less favourable’ to the creditor (or protection seller) from an economic perspective. This definition was open to more than one interpretation and it caused controversy when determining if a credit event had occurred. The 2001 definitions specified more precise conditions, including any action that resulted in a reduction in the amount of principal. In the European market, restructuring is generally retained as a credit event in contract documentation, but in the US market it is less common to see it included. Instead, US contract documentation tends to include as a credit event a form of modified restructuring, the impact of which is to limit the options available to the protection buyer as to the type of assets it could deliver in a physically settled contract. Further clarification was provided in the 2003 ISDA definitions,10 and again as part of the 2009 ISDA ‘Big Bang’.
Comparing Credit Derivatives to Cash Instruments
Both funded and unfunded credit derivatives act as alternatives to cash market products for investors. Funded credit derivatives are similar to cash bonds, but investors will need to assess their requirements more fully when assessing the relative merits of cash versus synthetic products.
RESTRUCTURING, MODIFIED RESTRUCTURING AND MODIFIED‐MODIFIED RESTRUCTURING
The original 1999 ISDA credit definitions defined restructuring among the standard credit events. The five specified definitions included events such as a reduction in the rate of interest payable, a reduction in the amount of principal outstanding and a postponement or deferral of payment. Following a number of high‐profile cases where there was disagreement or dispute between protection buyers and sellers on what constituted precisely a restructuring, the Supplement to the 1999 ISDA limited the term to maturity of deliverable obligations. This was modified restructuring or Mod‐R, which was intended to reduce the difference between the loss suffered by a holder of the actual restructured obligation and the writer of a CDS on that reference name. In practice this has placed a maturity limit on deliverable obligations of 30 months.
The 2003 Definitions presented further clarification and stated that the restructuring event had to be binding on all holders of the restructured debt. The modified‐modified restructuring definition or Mod‐Mod‐R described in the 2003 ISDA defines the modified restructuring term to maturity date as the later of:
- the scheduled termination date;
- 60 months following the restructuring date
in the event that a restructured bond or loan is delivered to the protection seller. If another obligation is delivered, the limitation on maturity is the scheduled maturity date and 30 months following the restructuring date.
Restructuring does not now apply as a credit event in North American contracts.
In certain respects both products offer the same thing. The coupon cash flows of a corporate bond can be replicated using a CDS contract, and an investor can get synthetic access to a particular sovereign or corporate name in this way. In some cases the return can be higher for essentially the same commensurate risk. We can illustrate this with a hypothetical example. Assume a pension fund investor wishes to invest in the bonds of a hypothetical corporate credit, call it Jackfruit Music Limited, which is rated BBB–/Baa3. The investor can buy Jackfruit Music bonds or sell protection on Jackfruit Music instead. Either way, the investor is acquiring risk in Jackfruit Music.
Market makers quote the following for Jackfruit Music:
- 5‐year bonds offered at 250 bps over benchmark government bonds;
- the CDS bid–offer price is 225–230 bps;
- the bond asset swap price is LIBOR + 195 bps (the 5‐year inter‐bank swap spread is 55 bps).
Assume further that the investor is part of a Group entity and funds at LIBOR plus 10 bps.
The alternatives are illustrated in Table 2.1.
Table 2.1 Jackfruit Music Ltd, buying bonds versus selling protection.
| Buy Jackfruit 5‐year bonds | Sell 5‐year protection on Jackfruit |
| Funded position | Unfunded position |
| Earn 195 bps over LIBOR | Earn 225 bps |
| Fund at LIBOR + 10.0 | No funding cost |
| Net return 185 bps | Return 225 bps |
By investing via the synthetic product, the investor earns a yield pick up of 40 bps over the cash position. This sounds too good to be true and in some cases will be; also, in some cases the CDS will be trading below the cash. However it illustrates the key issues. As we will see in Chapter 9, the CDS position in many cases exposes the investor to a greater risk exposure than the cash bond position, which is why the CDS price is in many cases higher. This difference between the CDS price and the cash bond price is known as the basis. The size of the basis is used as an indicator of deteriorating credit quality (or, as significant, potentially deteriorating credit quality) in a reference name.
Table 2.2 shows the key investor considerations for both markets.
Table 2.2 Cash versus synthetic market considerations.
| Buy cash bonds | Sell credit protection |
| Funded position | Unfunded position |
| Investor holds a specific bond and its risk exposure is to that specific bond | Unless written into the contract specifically, investor is selling protection on all obligations of the reference issuer |
| Risk to specific bond that is marked‐to‐market and may be sold in market if buyer is available | In event of credit event, which may not be complete default or full administration, protection seller will settle at par, minus market price of cheapest eligible reference bond (or receive this bond, for which it pays par) |
| Return on bond is net amount of funding cost | Return is CDS bid price |
We now consider the individual credit derivative instruments.
CREDIT DEFAULT SWAPS
We describe first the credit default swap (CDS), the most commonly traded credit derivative instrument.
Structure
The most common credit derivative is the credit default swap, sometimes called the credit swap or default swap.11 This is a bilateral contract that provides protection on the par value of a specified reference asset, with a protection buyer that pays a periodic fixed fee or a one‐off premium to a protection seller, in return for which the seller will make a payment on the occurrence of a specified credit event. The fee is usually quoted as a basis point multiplier of the nominal value. It is usually paid quarterly in arrears. The swap can refer to a specific single asset, known as the reference asset or underlying asset, a basket of assets, or a reference entity. The default payment can be paid in whatever way suits the protection buyer or both counterparties. For example, it may be linked to the change in price of the reference asset or another specified asset, it may be fixed at a pre‐determined recovery rate, or it may be in the form of actual delivery of the reference asset at a specified price. The basic structure is shown in Figure 2.6.
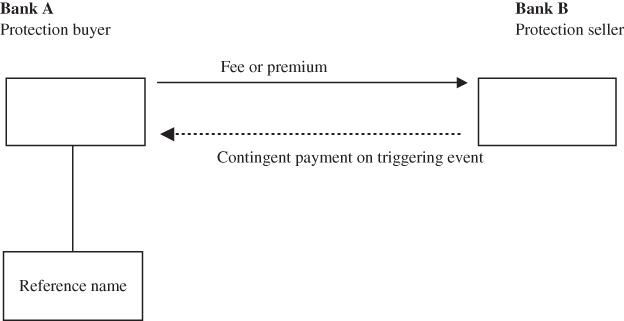
Figure 2.6 Credit default swap (CDS).
The CDS enables one party to transfer its credit risk exposure to another party. Banks may use default swaps to trade sovereign and corporate credit spreads without trading the actual assets themselves; for example, someone who has gone long a default swap (the protection buyer) will gain if the reference asset obligor suffers a rating downgrade or defaults, and can sell the default swap at a profit if they can find a buyer counterparty.12 This is because the cost of protection on the reference asset will have increased as a result of the credit event. The original buyer of the credit default swap need never have shorted the bond issued by the reference asset obligor.
The maturity of the CDS does not have to match the maturity of the reference asset and often does not. On occurrence of a credit event, the swap contract is terminated and a settlement payment is made by the protection seller, or guarantor, to the protection buyer. This termination value is calculated at the time of the credit event, and the exact procedure that is followed to calculate the termination value depends on the settlement terms specified in the contract. This will be either cash settlement or physical settlement. We look at these options later.
For illustrative purposes, Figure 2.7 shows investmentgrade credit default swap levels during 2001 and 2002 for US dollar and euro reference entities (average levels taken), while Table 2.3 shows sample CDS prices during September 2003. We update the latter for December 2008 at Table 2.4.
Figure 2.7 Investment‐grade CDS levels, 2001–2002.
Source: Bloomberg L.P.
Table 2.4 Sample 5‐year CDS premiums, 8 December 2008.
Source: Bloomberg L.P.
| Reference name | Mid‐price bps | Rating: S&P/Moody's/Fitch |
| Automobiles | ||
| Ford Motor Co. | 2508 | CCC+/Caa2/CCC |
| General Motors | 11064 | CCC+/NR/CCC |
| GMAC | 3443 | CC/C/CCC |
| Banks | ||
| Bank of America | 193 | AA−/Aa2/A+ |
| Wells Fargo | 155 | AA−/Aa2/A+ |
| Asia‐Pacific region | Bid‐Ask | S&P/Moody's/Fitch |
| Hutchison Whampoa | 423 | A−/A3/A |
| PR China | 239 | NR/A1/NR |
| Republic of Korea | 419 | A/A2/AA |
| NEC | 195 | BBB/Baa1/BBB |
| Qantas | 348 | BBB+/Baa1/NR |
Example 2.2 Credit default swap example
XYZ plc credit spreads are currently trading at 120 bps over 5‐year government bond maturities and 195 bps over 10‐year government bond maturities. A portfolio manager hedges a $10 million holding of 10‐year paper by purchasing the following CDS, written on the 5‐year bond. This hedge protects for the first five years of the holding, and in the event of XYZ's credit spread widening, will increase in value and may be sold before expiry at profit. The 10‐year bond holding also earns 75 bps over the shorter term paper for the portfolio manager.
| Term: | 5 years |
| Reference credit: | XYZ plc 5‐year bond |
| Credit event: | The business day following occurrence of specified credit event |
| Default payment: | Nominal value of bond × 3 × [100 × 2 × price of bond after credit event] |
| Swap premium: | 3.35% |
Assume that midway into the life of the swap there is a technical default on the XYZ plc 5‐year bond, such that its price now stands at $28. Under the terms of the swap the protection buyer delivers the bond to the seller, who pays $7.2 million to the buyer.
TOTAL RETURN SWAPS
A total return swap (TRS), sometimes known as a total rate of return swap or TR swap, is an agreement between two parties that exchanges the total return from a financial asset between them. This is designed to transfer the credit risk from one party to the other. It is one of the principal instruments used by banks and other financial instruments to manage their credit risk exposure, and as such is a credit derivative. One definition of a TRS is given in Francis et al (1999), which states that a TRS is a swap agreement in which the total return of a bank loan or credit‐sensitive security is exchanged for some other cash flow, usually linked to LIBOR or some other loan or credit‐sensitive security.
The TRS trade itself can be to any maturity term; that is, it need not match the maturity of the underlying security. In a TRS, the total return from the underlying asset is paid to the counterparty in return for a fixed or floating cash flow. This makes it slightly different to other credit derivatives, as the payments between counterparties to a TRS are connected to changes in the market value of the underlying asset, as well as changes resulting from the occurrence of a credit event. So, in other words, TRS cash flows are not solely linked to the occurrence of a credit event—in a TRS the interest rate risk is also transferred. The transaction enables the complete cash flows of a bond to be received without the recipient actually buying the bond, which makes it a synthetic bond product and therefore a credit derivative. An investor may wish to receive such cash flows synthetically for tax, accounting, regulatory capital, external audit or legal reasons. On the other hand, it may be easier to source the reference asset synthetically—via the TRS—than in the cash market. This happens sometimes with illiquid bonds.
In some versions of a TRS, the underlying asset is actually sold to the counterparty, with a corresponding swap transaction agreed simultaneously. In other versions, there is no physical change of ownership of the underlying asset. This makes TRS akin to a synthetic repo transaction. This is discussed in Appendix 2.3.
Figure 2.25 illustrates a generic TRS. The two counterparties are labelled as banks, but the party termed ‘Bank A’ can be another financial institution, including cash‐rich fixed‐income portfolio managers such as insurance companies and hedge funds. In Figure 2.25, Bank A has contracted to pay the ‘total return’ on a specified reference asset, while simultaneously receiving a LIBOR‐based return from Bank B. The reference or underlying asset can be a bank loan such as a corporate loan or a sovereign or corporate bond. The total return payments from Bank A include the interest payments on the underlying loan as well as any appreciation in the market value of the asset. Bank B will pay the LIBOR‐based return and it will also pay any difference if there is a depreciation in the price of the asset. The economic effect is as if Bank B owned the underlying asset, so as such TR swaps are synthetic loans or securities. A significant feature is that Bank A will usually hold the underlying asset on its balance sheet, so that if this asset were originally on Bank B's balance sheet, this is a means by which the latter can have the asset removed from its balance sheet for the term of the TR swap.21 If we assume Bank A has access to LIBOR funding, it will receive a spread on this from Bank B. Under the terms of the swap, Bank B will pay the difference between the initial market value and any depreciation, so it is sometimes termed the ‘guarantor’ while Bank A is the ‘beneficiary’.
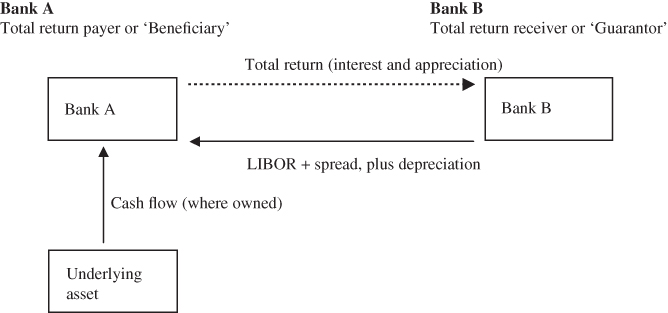
Figure 2.25 Total return swap.
The total return on the underlying asset is the interest payments and any change in the market value if there is capital appreciation. The value of an appreciation may be cash settled, alternatively there may be physical delivery of the reference asset on maturity of the swap, in return for a payment of the initial asset value by the total return ‘receiver’. The maturity of the TR swap need not be identical to that of the reference asset, and in fact it is rare for it to be so.
The swap element of the trade will usually pay on a monthly, quarterly or semi‐annual basis, with the underlying asset being revalued or marked‐to‐market on the re‐fixing dates. The asset price is usually obtained from an independent third party source such as Bloomberg or Reuters, or as the average of a range of market quotes. If the obligor of the reference asset defaults, the swap may be terminated immediately, with a net present value payment changing hands according to what this value is, or it may be continued with each party making appreciation or depreciation payments as appropriate. This second option is only available if there is a market for the asset, which is less likely in the case of a bank loan. If the swap is terminated, each counterparty is liable to the other for accrued interest plus any appreciation or depreciation of the asset. Commonly under the terms of the trade, the guarantor bank has the option to purchase the underlying asset from the beneficiary bank, and then deal directly with loan defaulter.
The TRS can also be traded as a funded credit derivative, and we look at this in the next chapter.
Banks employ a number of methods to price credit derivatives and TR swaps. Essentially the pricing of credit derivatives is linked to that of other instruments; however, the main difference between credit derivatives and other off‐balance sheet products such as equity, currency or bond derivatives is that the latter can be priced and hedged with reference to the underlying asset, which can be problematic when applied to credit derivatives. Credit products pricing uses statistical data on likelihood of default, probability of payout, level of risk tolerance and a pricing model. With a TRS the basic concept is that one party ‘funds’ an underlying asset and transfers the total return of the asset to another party, in return for a (usually) floating return that is a spread to LIBOR. This spread is a function of:
- the credit rating of the swap counterparty;
- the amount and value of the reference asset;
- the credit quality of the reference asset;
- the funding costs of the beneficiary bank;
- any required profit margin;
- the capital charge associated with the TRS.
The TR swap counterparties must consider a number of risk factors associated with the transaction, which include:
- the probability that the TR guarantor or receiver may default while the reference asset has declined in value;
- the reference asset obligor defaults, followed by default of the TR swap receiver before payment of the depreciation has been made to the payer or ‘provider’.
The first risk measure is a function of the probability of default by the TR swap receiver and the market volatility of the reference asset, while the second risk is related to the joint probability of default of both factors as well as the recovery probability of the asset.
Reproduced from Structured Credit Products, Second Edition (2010)
This extract from The Credit Default Swap Basis (2006)
CDS Valuation
We consider now two approaches to pricing a CDS contract, both of which are used in the market. The first we describe is termed the “reduced form” model, developed by Hull and White (2000). The second is a market approach first described by JPMorgan, which extracts a default term structure from bond market prices and is straightforward to apply in practice.
Pricing Methodology Based on Reduced‐Form Model Approach12
A credit default swap, like an interest‐rate swap, consists of two legs—one corresponding to the premium payments, and the other to the contingent default payment. This is illustrated in FIGURE 1.10. The present value (PV) of a default swap can be viewed as the algebraic sum of the present values of its two legs. The market premium is similar to an interest‐rate swap in that the premium makes the current aggregate PV equal to zero.

Figure 1.10 Illustration of cash flows in a default swap
The CDS is priced on the assumption that there is a recovery amount that is a fraction of the recovery rate R of par value, plus any accrued interest.
Because these cash flows may terminate at an unknown time during the life of the deal, their values are computed in a probabilistic sense, using the discounted expected value as calculated under the risk‐neutral method and assumptions.
The theoretical pricing of credit derivatives has attracted attention in the academic literature. Longstaff and Schwartz (1995) present the pricing of credit spread options based on an exogenous mean‐reverting process for credit spreads. Duffie (1999) presents a simple reduced‐form pricing model. Here, we introduce another reduced‐form pricing model developed by Hull and White (2000). Their approach was to calibrate their model based on the traded bonds of the underlying reference name, on a time series of credit default swap prices.
Like most other approaches, their model assumes that there is no counterparty default risk. Default probabilities, interest rates, and recovery rates are independent.
Finally, Hull and White also assume that the claim in the event of default is the face value plus accrued interest. To illustrate, we consider the valuation of a plain vanilla credit default swap with $1 notional principal.
We use the following notation:
| T | is life of credit default swap in years |
| q(t) | is risk‐neutral probability density at time t |
| R | is expected recovery rate on the reference obligation in a risk‐neutral world (independent of the time of default) |
| u(t) | is present value of payments at the rate of $1 per year on payment dates between time zero and time t |
| e(t) | is present value of an accrual payment at time t equal to t − t* where t* is the payment date immediately preceding time t |
| v(t) | is present value of $1 received at time t |
| w | is total payment per year made by credit default swap buyer |
| s | is value of w that causes the value of the credit default swap to have a value of zero |
| π | is the risk‐neutral probability of no credit event during the life of the swap |
| A(t) | is accrued interest on the reference obligation at time t as a percentage of face value |
The value π is one minus the probability that a credit event will occur by time T. This is also referred to as the survival probability, and can be calculated from q(t) as follows:
The payments last until a credit event or until time T, whichever is sooner. If default occurs at t(t<T), the present value of the payment is w[u(t)]. If there is no default prior to time T, the present value of the payment is wu(T). The expected present value of the payment is therefore
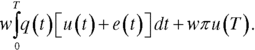
Given the assumption about the claim amount, the risk‐neutral expected payoff from the CDS contract is derived as follows:
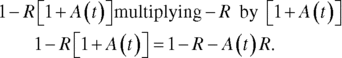
The present value of the expected payoff from the CDS is given as
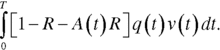
The value of the CDS to the buyer is the present value of the expected payoff minus the present value of the payments made by the buyer, or
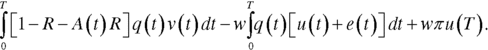
In equilibrium, the present value of each leg of the above equation should be equal. We can now calculate the credit default swap spread s, which is the value of w that makes the equation equal to zero, by simply rearranging the equation, as shown below.
The variable S is referred to as the CDS spread.
The formula at equation (1.5) is simple and intuitive for developing an analytical approach for pricing credit default swaps because of the assumptions used. For example, the model assumes that interest rates and default events are independent; also, the possibility of counterparty default is ignored. The spread s is the payment per year, as a percentage of notional principal, for a newly issued credit default swap.
FIGURE 1.11 shows the CDSW page on the Bloomberg using the modified Hull and White model.13 Certain default parameter inputs (for the DaimlerChrysler five5‐year CDS) are selected. This implementation links the rates observed in the credit‐protection market and the corporate bond market, via probabilities of default of the issuer. The input used to price the CDS contract is selected from a range of market‐observed yield curves, and can include:
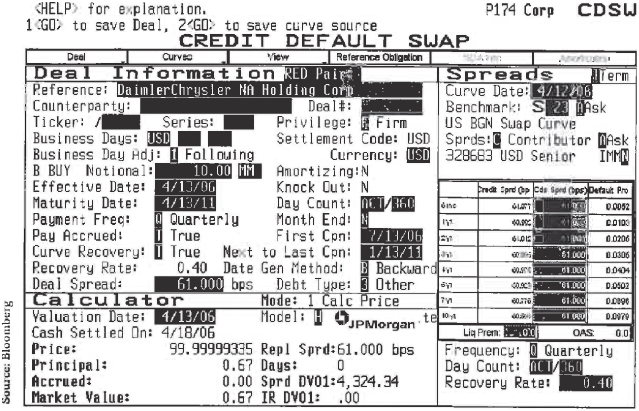
Figure 1.11 Bloomberg page CDSW using modified Hull‐White pricing for selected credit default swap, April 12, 2006
- A curve of CDS spreads
- An issuer (credit‐risky) par yield curve
- A default probability curve (derived from the default probabilities of the underlying reference for each maturity implied by the par credit default swap spreads)
The assumptions based on the independence of recovery rates, default probabilities, and interest rates may not hold completely in practice, since high interest rates may cause companies to experience default or administration. As a result, default probabilities would increase. Hence, a positive relation between interest rates and default probabilities may be associated with high discount rates for the CDS payoffs. This would have the effect of reducing the credit default swap spread. Nevertheless, the modified Hull‐White approach presents a neat and intuitive approach that allows for a closed‐form pricing approach for credit default swaps, using parameter inputs from the market.
Market Pricing Approach14
We now present a discrete form pricing approach that is used in the market, using market‐observed parameter inputs.
We stated earlier that a CDS has two cash‐flow legs; the fee premium leg and the contingent cash‐flow leg. We wish to determine the par spread, or premium, of the CDS, remembering that for a par spread valuation, in accordance with no‐arbitrage principles, the net present value of both legs must be equal to zero (that is, they have the same valuation).
The valuation of the fee leg is given by the following relationship:
which is given by
where
| SN | is the par spread (CDS premium) for maturity N |
| DFi | is the risk‐free discount factor from time T0 to time Ti |
| PNDi | is the no‐default probability from T0 to Ti |
| Ai | is the accrual period from Ti−1 to Ti. |
Note that the value for PND is for the specific reference entity for which a CDS is being priced.
If the accrual fee for the CDS is paid upon default and termination,15 then the valuation of the fee leg is given by the following relationship:
which is given by
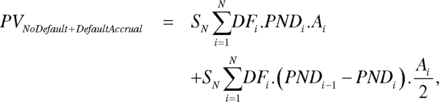
where
(PNDi−1 − PNDi) is the probability of a credit event occurring during the period Ti−1 to Ti
![]() is the average accrual amount from Ti−1 to Ti.
is the average accrual amount from Ti−1 to Ti.
The valuation of the contingent leg is approximated by
which is given by
where R is the recovery rate of the reference obligation.
For a par credit default swap, we know that
and therefore we can set
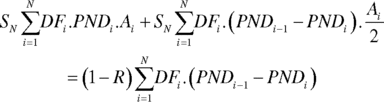
which may be rearranged to give us the formula for the CDS premium s as follows:
In TABLE 1.1, we illustrate an application of the expression in equation (1.10) for a CDS of varying maturities, assuming a recovery rate of the defaulted reference asset of 30% and a given term structure of interest rates. It uses actual/360‐day count convention.
Table 1.1 Example of CDS spread pricing
| MATURITY t | SPOT RATES | DISCOUNT FACTORS DFj | SURVIVAL PROBABILITY PSj | DEFAULT PROBABILITY PDj |
| 0.5 | 3.57% | 0.9826 | 0.9993 | 0.0007 |
| 1.0 | 3.70% | 0.9643 | 0.9983 | 0.0017 |
| 1.5 | 3.81% | 0.9455 | 0.9972 | 0.0028 |
| 2.0 | 3.95% | 0.9254 | 0.9957 | 0.0043 |
| 2.5 | 4.06% | 0.9053 | 0.9943 | 0.0057 |
| 3.0 | 4.16% | 0.8849 | 0.9932 | 0.0068 |
| 3.5 | 4.24% | 0.8647 | 0.9900 | 0.0100 |
| 4.0 | 4.33% | 0.8440 | 0.9886 | 0.0114 |
| 4.5 | 4.42% | 0.8231 | 0.9859 | 0.0141 |
| 5.0 | 4.45% | 0.8044 | 0.9844 | 0.0156 |
| RECOVERY RATE | ||||
| 0.3 |
| PROBABILITY‐WEIGHTED PVs | |||
| PV OF RECEIPTS IF NO DEFAULT | PV OF RECEIPTS IF DEFAULT | DEFAULT PAYMENT IF DEFAULT | CDS PREMIUM s |
| 0.4910 | 0.0002 | 0.0005 | 0.10% |
| 0.9723 | 0.0006 | 0.0016 | 0.17% |
| 1.4437 | 0.0012 | 0.0035 | 0.24% |
| 1.9044 | 0.0022 | 0.0063 | 0.33% |
| 2.3545 | 0.0035 | 0.0099 | 0.42% |
| 2.7939 | 0.0050 | 0.0141 | 0.50% |
| 3.2220 | 0.0072 | 0.0201 | 0.62% |
| 3.6392 | 0.0096 | 0.0269 | 0.74% |
| 4.0450 | 0.0125 | 0.0350 | 0.86% |
| 4.4409 | 0.0156 | 0.0438 | 0.98% |
For readers' reference, we present a fuller explanation of this valuation approach in Appendix II.
We can use CDS prices to extract a market‐implied timing of default. Given that the CDS has a specified fixed term to maturity, it is possible by applying break‐even analysis to extract a market‐implied timing of default for the reference credit in question. This is done by calculating the amount of time that has to elapse before the premium income on the CDS equals the recovery value. By definition therefore, we require an assumed recovery rate to perform this calculation. An illustration of this process is given in Appendix III.
Reproduced from The Credit Default Swap Basis (2006)
ASSET SWAPS AND RELATIVE VALUE
This section can be found in the companion website, in the folder for Chapter 2. Please see Chapter 20 for more details.
This extract from Fixed Income Securities and Derivatives Handbook, Second Edition (2010)
Bond Spreads and Relative Value
Bond Spreads and Relative Value
Return from a holding of fixed‐income securities may be measured in more than one way. The most common approach is to consider the asset‐swap spread. More sophisticated investors also consider the basis spread between the cash bond and the same‐name credit default swap price, which is known as the basis.2 In this chapter we consider the most accessible way to measure bond return.
Bond Spreads
Investors measure the perceived market value, or relative value, of a corporate bond by measuring its yield spread relative to a designated benchmark. This is the spread over the benchmark that gives the yield of the corporate bond. A key measure of relative value of a corporate bond is its swap spread. This is the basis point spread over the interest‐rate swap curve and is a measure of the credit risk of the bond. In its simplest form, the swap spread can be measured as the difference between the yield‐to‐maturity of the bond and the interest rate given by a straight‐line interpolation of the swap curve. In practice, traders use the asset‐swap spread and the Z‐spread as the main measures of relative value. The government bond spread is also used. In addition, now that the market in synthetic corporate credit is well established, using credit derivatives and CDS, investors consider the Cash‐CDS spread as well, which is the basis and which we consider in greater detail later.
The spread that is selected is an indication of the relative value of the bond and a measure of its credit risk. The greater the perceived risk, the greater the spread should be. This is best illustrated by the credit structure of interest rates, which will (generally) show AAA‐ and AA‐rated bonds trading at the lowest spreads and BBB‐ , BB‐ and lower‐bonds trading at the highest spreads. Bond spreads are the most commonly used indication of the risk‐return profile of a bond.
In this section we consider the Treasury spread, asset swap spread, Z‐spread, and basis.
Swap Spread and Treasury Spread
A bond's swap spread is a measure of the credit risk of that bond, relative to the interest‐rate swaps market. Because the swaps market is traded by banks, this risk is effectively the interbank market, so the credit risk of the bond over and above bank risk is given by its spread over swaps. This is a simple calculation to make and is simply the yield of the bond minus the swap rate for the appropriate maturity swap. FIGURE 19.2 shows Bloomberg page IRSB for Pounds sterling as of August 10, 2005. This shows the GBP swap curve on the left‐hand side. The right‐hand side of the screen shows the swap rates' spread over U.K. gilts. It is the spread over these swap rates that would provide the simplest relative value measure for corporate bonds denominated in GBP. If the bond has an odd maturity, say 5.5 years, we would interpolate between the five‐year and six‐year swap rates.
Figure 19.2 Bloomberg Page IRSB for Pounds Sterling, Showing GBP Swap Rates and Swap Spread over U.K. Gilts
Source: © Bloomberg. All rights reserved. Reprinted with permission.
The spread over swaps is sometimes called the I‐spread. It has a simple relationship to swaps and Treasury yields, shown here in the equation for corporate bond yield,
where
| Y | is the yield on the corporate bond |
| I | is the I‐spread or spread over swap |
| S | is the swap spread |
| T | is the yield on the Treasury security (or an interpolated yield). |
In other words, the swap rate itself is given by T + S.
The I‐spread is sometimes used to compare a cash bond with its equivalent CDS price, but for straightforward relative value analysis is usually dropped in favor of the asset‐swap spread, which we look at later in this section.
Of course, the basic relative value measure is the Treasury spread or government bond spread. This is simply the spread of the bond yield over the yield of the appropriate government bond. Again, an interpolated yield may need to be used to obtain the right Treasury rate to use. The bond spread is given by:
Using an interpolated yield is not strictly accurate because yield curves are smooth in shape and so straight‐line interpolation will produce slight errors. The method is still commonly used, though.
Asset‐Swap Spread
An asset swap is a package that combines an interest‐rate swap with a cash bond, the effect of the combined package being able to transform the interest‐rate basis of the bond. Typically, a fixed‐rate bond will be combined with an interest‐rate swap in which the bond holder pays fixed coupon and received floating coupon. The floating coupon will be a spread over LIBOR (see Choudhry et al. 2001). This spread is the asset‐swap spread and is a function of the credit risk of the bond over and above interbank credit risk.3 Asset swaps may be transacted at par or at the bond's market price, usually par. This means that the asset swap value is made up of the difference between the bond's market price and par, as well as the difference between the bond coupon and the swap fixed rate.
The zero‐coupon curve is used in the asset swap valuation. This curve is derived from the swap curve, so it is the implied zero‐coupon curve. The asset swap spread is the spread that equates the difference between the present value of the bond's cash flows, calculated using the swap zero rates, and the market price of the bond. This spread is a function of the bond's market price and yield, its cash flows, and the implied zero‐coupon interest rates.4
FIGURE 19.3 shows the Bloomberg screen ASW for a GBP‐denominated bond, GKN Holdings 7 percent 2012, as of August 10, 2005. We see that the asset‐swap spread is 121.5 basis points. This is the spread over LIBOR that will be received if the bond is purchased in an asset‐swap package. In essence, the asset swap spread measures a difference between the market price of the bond and the value of the bond when cash flows have been valued using zero‐coupon rates. The asset‐swap spread can therefore be regarded as the coupon of an annuity in the swap market that equals this difference.
Figure 19.3 Bloomberg Page ASW for GKN Bond, August 10, 2005
Source: © Bloomberg. All rights reserved. Reprinted with permission.
Z‐Spread
The conventional approach for analyzing an asset swap uses the bond's yield‐to‐maturity (YTM) in calculating the spread. The assumptions implicit in the YTM calculation (see Chapter 2) make this spread problematic for relative analysis, so market practitioners use what is termed the Z‐spread instead. The Z‐spread uses the zero‐coupon yield curve to calculate spread, so is a more realistic, and effective, spread to use. The zero‐coupon curve used in the calculation is derived from the interest‐rate swap curve.
Put simply, the Z‐spread is the basis point spread that would need to be added to the implied spot yield curve such that the discounted cash flows of the bond are equal to its present value (its current market price). Each bond cash flow is discounted by the relevant spot rate for its maturity term. How does this differ from the conventional asset‐swap spread? Essentially, in its use of zero‐coupon rates when assigning a value to a bond. Each cash flow is discounted using its own particular zero‐coupon rate. The bond's price at any time can be taken to be the market's value of the bond's cash flows. Using the Z‐spread we can quantify what the swap market thinks of this value, that is, by how much the conventional spread differs from the Z‐spread. Both spreads can be viewed as the coupon of a swap market annuity of equivalent credit risk of the bond being valued.
In practice, the Z‐spread, especially for shorter‐dated bonds and for better credit‐quality bonds, does not differ greatly from the conventional asset‐swap spread. The Z‐spread is usually the higher spread of the two, following the logic of spot rates, but not always. If it differs greatly, then the bond can be considered to be mispriced.
FIGURE 19.4 is the Bloomberg screen YAS for the same bond shown in Figure 19.3, as of the same date. It shows a number of spreads for the bond. The main spread of 151.00 bps is the spread over the government yield curve. This is an interpolated spread, as can be seen lower down the screen, with the appropriate benchmark bind identified. We see that the asset‐swap spread is 121.6 bps, while the Z‐spread is 118.8 bps. When undertaking relative value analysis, for instance, if making comparisons against cash funding rates or the same company name credit default swap (CDS), it is this lower spread that should be used.5
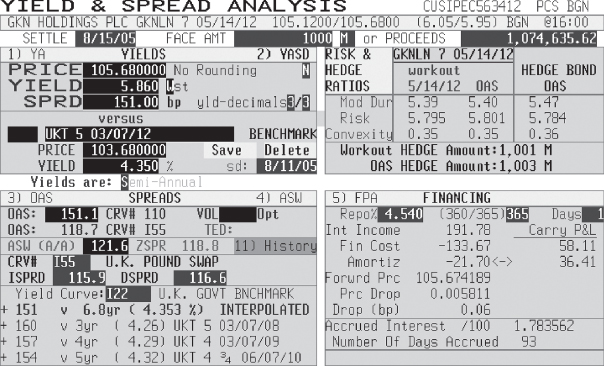
Figure 19.4 Bloomberg Page YAS for GKN Bond, August 10, 2005
Source: © Bloomberg. All rights reserved. Reprinted with permission.
The same screen can be used to check spread history. This is shown at FIGURE 19.5, the Z‐spread graph for the GKN bond for the six months prior to our calculation date.
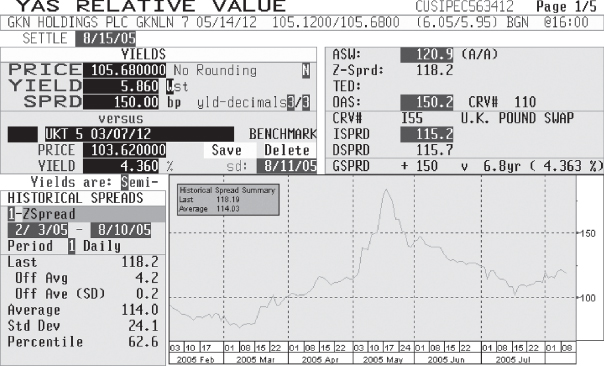
Figure 19.5 Bloomberg Page YAS for GKN Bond, August 10, 2005 Showing Z‐Spread History
Source: © Bloomberg. All rights reserved. Reprinted with permission.
The Z‐spread is closely related to the bond price, as shown by:
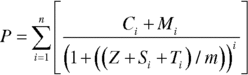
where
| n | is the number of interest periods until maturity |
| P | is the bond price |
| C | is the coupon |
| M | is the redemption payment (so bond cash flow is all C plus M) |
| Z | is the Z‐spread |
| m | is the frequency of coupon payments |
In effect, this is the standard bond price equation with the discount rate adjusted by whatever the Z‐spread is; it is an iterative calculation. The appropriate maturity swap rate is used, which is the essential difference between the I‐spread and the Z‐spread. This is deemed to be more accurate, because the entire swap curve is taken into account rather than just one point on it. In practice, though, as we have seen in the previous example, there is often little difference between the two spreads.
To reiterate, then, using the correct Z‐spread, the sum of the bond's discounted cash flows will be equal to the current price of the bond.
We illustrate the Z‐spread calculation at FIGURE 19.6. This is done using a hypothetical bond, the XYZ PLC 5 percent of June 2008, a three‐year bond at the time of the calculation. Market rates for swaps, Treasury, and CDS are also shown. We require the spread over the swaps curve that equates the present values of the cash flows to the current market price. The cash flows are discounted using the appropriate swap rate for each cash flow maturity. With a bond yield of 5.635 percent, we see that the I‐spread is 43.5 basis points, while the Z‐spread is 19.4 basis points. In practice, the difference between these two spreads is rarely this large.
| Issuer | XYZ PLC | ||||||
| Settlement date | 6/1/2005 | ||||||
| Maturity date | 6/1/2008 | ||||||
| Coupon | 5% | YIELD | 0.05635 | ||||
| Price | 98.95 | [Cell formula = YIELD(C4,C5,C6,C7,C8,C9,C10)] | |||||
| Par | 100 | ||||||
| Semiannual coupon | 2 | PRICE | 98.95000 | ||||
| act/act | 1 | [Cell formula = PRICE(C4,C5,C6,C6,C8,C9,C10)] | |||||
| Bond yield | 5.635% | ||||||
| Sovereign bond yield | 4.880% | ||||||
| Swap rate | 5.200% | ||||||
| 3‐year CDS price | 28 bps | ||||||
| Treasury spread | |||||||
| 5.635 − 4.88 | 55 bps | ||||||
| I‐spread | |||||||
| 5.635−5.20 | 43.5 bps | ||||||
| Z‐spread (Z) | 19.4 bps | 0.00194 | |||||
| The Z‐spread is found using iteration | |||||||
| SUM OF PVS | |||||||
| Cash flow date | 12/1/2005 | 6/1/2006 | 12/1/2006 | 6/1/2007 | 12/1/2007 | 6/1/2008 | |
| Cash flow maturity (years) | 0.50 | 1.00 | 1.50 | 2.00 | 2.50 | 3.00 | |
| 0.5‐year swap rate (S) | 4.31% | 4.84% | 4.99% | 5.09% | 5.18% | 5.20% | |
| Cash flow (CF) | 2.50 | 2.50 | 2.50 | 2.50 | 2.50 | 102.50 | |
| Discount factor | 0.97797598 | 0.951498751 | 0.926103469 | 0.900947692 | 0.875835752 | 0.852419659 | |
| (DF Calculation) | 1/(1+(S+Z)/2)∧1 | 1/(1+(S+Z)/2)∧2 | 1/(1+(S+Z)/2)∧3 | 1/(1+(S+Z)/2)∧4 | 1/(1+(S+Z)/2)∧5 | 1/(1+(S+Z)/2)∧6 | |
| CF present value (PV) | 2.445 | 2.379 | 2.315 | 2.252 | 2.190 | 87.373 | 98.95 |
| A Z‐spread of 19.4 basis points gives us the current bond price, so is the correct one. Using this value, the sum of all the discounted cash flows is equal to the market price. |
|||||||
| CDS Basis | |||||||
| 28 ‐ 19.4 | 8.6 bps | ||||||
| The basis is positive in this example. | |||||||
Figure 19.6 Calculating the Z‐Spread, Hypothetical 5% 2008 Bond Issued by XYZ PLC
For readers' benefit we also show the Excel formula in Figure 19.6. This shows how the Z‐spread is calculated; for ease of illustration, we have assumed that the calculation takes place for value on a coupon date, so that we have precisely an even period to maturity.
Cash‐CDS Basis
The difference between the premium on a CDS contract and the same name (and same tenor) cash bond yield is known as the basis. That is, the basis is the CDS spread minus the ASW spread. Alternatively, it can be the CDS spread minus and the Z‐spread. So the basis is given by
where D is the CDS price. Where D − CashSpread > 0 it is a positive basis; the opposite is a negative basis.
FIGURE 19.7 shows page G <go> on Bloomberg, set up to show the Z‐spread and CDS price history for the GKN 2012 bond, for the period March–September 2005. We can select the “Table” option to obtain the actual values, which can then be used to plot the basis. This is shown at FIGURE 19.8, for the period August 22 to September 22, 2005. Notice how the basis was always negative during August–September; we see from Figure 19.8 that earlier in the year the basis had briefly been positive. Changes in the basis give rise to arbitrage opportunities between the cash and synthetic markets. This is discussed in greater detail in Choudhry (2009).
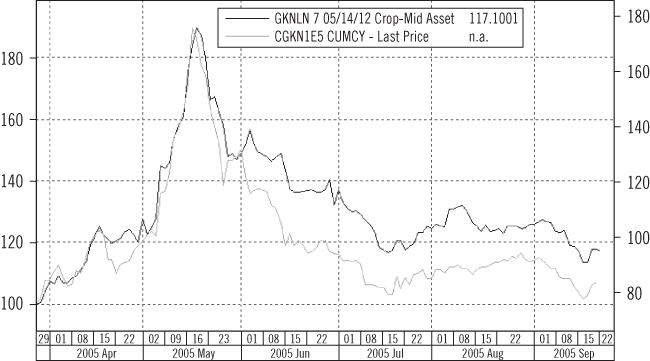
Figure 19.7 Bloomberg Graph Using Screen G <GO>, Plot of Asset‐Swap Spread and CDS Price for GKN Bond, April–September 2005
Source: © Bloomberg. All rights reserved. Reprinted with permission.
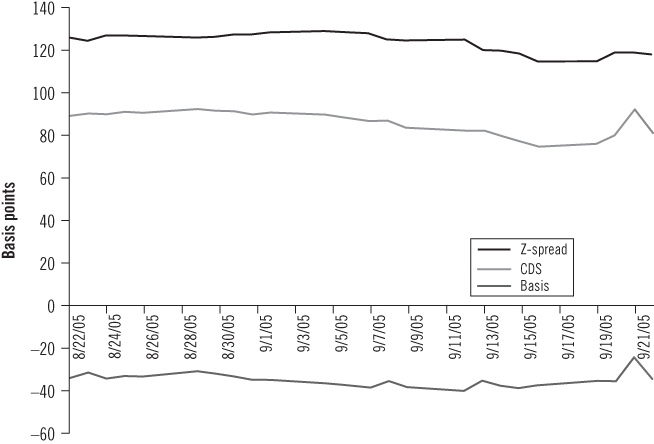
Figure 19.8 GKN Bond, CDS Basis During August–September 2005
Data Source: Bloomberg L.P.
A wide range of factors drive the basis, which are described in detail in Choudhry (2010). The existence of a non‐zero basis has implications for investment strategy. For instance, when the basis is negative, investors may prefer to hold the cash bond, whereas if, for liquidity, supply, or other reasons, the basis is positive, the investor may wish to hold the asset synthetically by selling protection using a credit default swap. Another approach is to arbitrage between the cash and synthetic markets, in the case of a negative basis by buying the cash bond and shorting it synthetically by buying protection in the CDS market. Investors have a range of spreads to use when performing their relative value analysis.
Summary of Fund Managers' Approach to Value Creation
The management of a portfolio of bonds may be undertaken either passively or actively. Passive fund management does not involve any actual analysis or portfolio selection, because the manager merely constructs the bond portfolio to mirror the benchmark or index whose performance he wishes to replicate. As such, passive fund management is more of an administrative function than an analytical or strategic one.
Active fund management involves just that: the manager makes the decision on which bonds to buy and the time at which to buy (and subsequently sell) them. The performance of an actively managed fixed‐income portfolio is still measured against the relevant benchmark or index, because this serves to illustrate how well the manager is doing. If the portfolio does not outperform the index, then the manager has not added value.
What approach is adopted by the active fund manager? Portfolio managers employ four basic strategies to add value over and above the benchmark. We summarize these here:
- Extend duration before a market rally, shorten duration before a market correction: This is the most basic approach, and in its crudest form amounts to “punting” the market. The fund manager basically decides when he or she expects the market to rally and buys longer‐dated bonds ahead of the anticipated move upward, which benefit from such a move more than shorter‐dated bonds. Unfortunately, very few fund managers consistently get such a call right, and this approach is not often adopted, at least not explicitly anyway.
- Yield curve trades: In this approach, the fund manager puts on steepening trades before the yield curve steepens, and flattening trades before the curve flattens. A common approach is to put on barbell and bullet trades; generally the former is adopted for curve flattening trades, while a steepening yield curve tends to favor bullet trades. This strategy has a bit more intellectual cachet than the straight directional “punt” trade, and generally fund managers are given more latitude to put on relative value‐style curve shaping trades compared to directional trades. However, this approach ultimately calls for the manager to call the directional move in the market right.
- Convexity and volatility trades: This strategy also has a directional element to it and involves employing convexity and volatility trades to outperform benchmarks. When there is a mismatch between a manager's view on volatility and the implied volatility of bonds with embedded options, buying or selling convexity before realized volatility increases or decreases can enhance return. An alternative approach is, rather than realized volatility differing from implied volatility, the market as a whole may change its opinion about future volatility and thereby produce a change in implied volatility, which may enhance returns. Convexity and volatility trades can also be effected using barbell and bullet positions, or via derivatives.
- Security selection: Portfolio managers can attempt to outperform benchmarks through security selection. This entails being overweight in “cheap” bonds and underweight in “rich” bonds, which will produce higher total return relative to the benchmark. Security selection requires effective relative value analysis to determine which bonds are cheap compared to their peer group and to the risk‐free benchmark. Such analysis makes use of measures such as the asset‐swap spread. A basic analysis would use this metric and compare it across an (otherwise equivalent) set of bonds. The approach is as follows: after selecting portfolio average duration, and the level of credit risk that is acceptable, purchase the bonds that have the highest asset‐swap spread. The resulting portfolio then represents the best relative value for a given duration target and credit risk exposure. In practice, the asset‐swap spread is nowadays compared also to the same‐name credit default swap premium. The difference between the two measures (the CDS basis) gives another measure of the relative value of the bond, by implying the level of mispricing in either or both of the cash and synthetic markets.
Active fund management, whichever method or combination of methods is adopted, ultimately still requires the manager to have an idea of market direction. If the fund manager gets this right, this makes it more likely that the portfolio will outperform the benchmark.
NOTES
2 For more details on the cash‐CDS basis, see Choudhry (2010).
3 This is because in the interbank market, two banks transacting an interest‐rate swap will be paying/receiving the fixed rate and receiving/paying LIBOR‐flat. See also the “Learning Curve” article on asset swaps available on www.yieldcurve.com.
4 Bloomberg refers to this spread as the Gross Spread.
5 On the date in question, the 10‐year CDS for this reference entity was quoted as 96.8 bps, which is an example of a negative basis, in this case of −22 bps.
Reproduced from Fixed Income Securities and Derivatives Handbook, Second Edition (2010)
POST‐2008 CRASH SWAP DISCOUNTING AND VALUATION PRINCIPLES1
Interest‐rate swaps (IRS) were introduced in the earlier extracts. This section looks at the impact on the swap market of the 2008 bank crash, specifically with respect to pricing and valuation. A large proportion of swaps are now settled via a centralised clearing counterparty (CCP); before that the swap market had become essentially a fully secured market in any case, at least between bank counterparties. The operation of this entailed the mark‐to‐market (MTM) of the swap being passed between the two bilateral counterparties as collateral under the auspices of the credit support annexe (CSA) of the standard ISDA derivatives agreement. Under a CSA, the party that is offside on the swap value (negative MTM) will post collateral to the counterparty equivalent to this MTM value. There is considerable optionality availability in a CSA, which is a legal agreement negotiated between the two parties but if we assume a “gold standard” CSA, which describes (among other things):
- Daily margin, equal to end‐of‐day MTM;
- Margin in the form of cash, in the currency of the IRS;
- No “threshold” amount, so whatever the MTM value the posting takes place at end of day
then this makes the following discussion simpler.
Basic Terms
Herewith some swap basics to ensure everyone is familiar with the key features:
Example definition of an IRS
Notional: 10m EUR
Start Date: 30th August 2016
End Date (Tenor): 30th August 2021 (5 years)
Frequency of payments: Annual fixed, Semi‐annual floating
Fixed Leg accruals: Unadjusted
Floating leg date rolling convention: Modified following (MF)
Floating leg business day calendar for accruals: “Target”
Business day calendar for payments: “Target” for both legs
Business day calendar for resets (floating leg): “Target”
Day count conventions: A/360 floating, 30U/360 fixed
Fixed rate: 1%
Reference for floating rate: 6 month Euribor, reset two days in advance
A “par” swap is defined as a swap with zero mark‐to‐market (MTM). The fixed rate on a par swap can be interpreted as the (discounted) average forward rate over the life of the swap (Figure 2.1).
FIGURE 2.1 Worked example of a Euribor swap
CSA
The CSA is a bilateral agreement governing the collateral posting process. Its most important features describe:
- What instruments can be posted as collateral, or if this can be only cash;
- The interest rate to be paid on collateral;
- Minimum thresholds;
- Minimum transfer amounts (MTA).
In theory, a CSA in place removes all credit risk between the two counterparties. (Except an operational risk, known as margin period of risk, arising out of the fact that the MTM value at close of business yesterday may be different the next day when the bank that has posted collateral defaults and the collateral process is finalised so that the non‐defaulting party now has legal ownership of the collateral. This period is accepted to be about 10 days.) A CSA may require, depending on the credit quality of the counterparty, an initial amount (IA) of margin, a standing value, to be posted by one party to the other. Note that CCPs require IA amounts from all their members.
The CSA sets the risk‐free rate for all transactions between the two counterparties; the “CSA rate” is typically the OIS overnight rate in that currency (OIS USD, SONIA for GBP, and EONIA for EUR)
CSAs introduced additional complexity to the swap market because of the optionality that is inherent in them, although the market generally speaks of a “gold standard” CSA with standard terms. For market‐makers in swaps (dealers), issues arise because some swaps on their book will be under a gold standard CSA, others under non‐standard CSAs and some will be uncollateralised.
CCP
The CCP is the central clearing counterparty. They include for example the London Clearing House (LCH) and the Chicago Mercantile Exchange (CME). Virtually all inter‐bank swaps trade through CCPs. The CCP sets the collateral rate, usually the OIS rate in the swap's payment currency. They also charge risk‐based IAs to all members, as we noted above.
Day Count Conventions (Accrual/Payment basis)
Applied to the accrual dates to calculate the weighting of each payment, also known as the Day Count Fraction (DCF) or Accrual Factor. The principal ones are:
- Actual/x (Act/x, A/x), where x=360 or 365 most commonly;
- (d2 – d1)/x, where di are the accrual start and end dates;
- Number of calendar days in the accrual period, divided by the number of days assumed to be in a year, either 360 or 365;
- 30/360, where [360(Y2 − Y1) + 30(M2 − M1) + (D2 − D1)] / 360.
The ISDA method specifies two further rules:
- If D1 is 31, then change D1 to 30.
- If D2 is 31 and D1 is 30 or 31, then change D2 to 30.
In some cases a convention is denoted as “U”: unadjusted. This is often used with 30/360 to give almost all periods equal weighting.
- Determination of the Main (L)ibor Rates
- Euribor (Euro Interbank Offered Rate) This is set by a panel of 24 banks, determined by the European Banking Federation, that have the highest volume of business in the euro zone money markets. Each bank submits its rate: the top and bottom 15% are eliminated, and the remaining quotes are averaged. Results are published at 11am CET. In theory, Euribor represents the rate at which these banks lend money to each other on unsecured loans. The tenors that are quoted are overnight, 1‐week, 2‐week, 1‐, 2‐, 3‐, 6‐, 9‐ and 12‐month rates.
LIBOR (London Interbank Offer Rate)
This was discussed in Chapter 1.
Note that the reference swaps are very liquid but that not every bank is able to borrow unsecured in the inter‐bank market at Libor‐flat. Some banks, with lower credit ratings, will pay a spread over the relevant term Libor rate for borrowing unsecured, where they have borrowing lines with other banks (again, not every bank has such access).
Alternative Fixing Source: Overnight Indexed Swaps (OIS)
The OIS rate is the average of unsecured overnight lending rates between banks. It is closer to the risk‐free, but of course still contains some credit and liquidity risk. (We assume the risk‐free rate to be the US T‐bill rate.)
The USD OIS swap references the Federal Funds Effective Rate, whereas other currencies references overnight Libor or Euribor. The common currencies are:
- GBP Over‐Night Indexed Average (SONIA);
- EUR Over‐Night Indexed Average (EONIA);
- JPY Over‐Night Indexed Average (TONAR).
The mechanics of OIS swaps are covered elsewhere in this chapter, in the extract from the book Bank Asset Liability Management.
Example Structure Diagrams
Figures 2.2 and 2.3 show a cross‐currency basis swap example and a swap transacted under a CSA agreement.
FIGURE 2.2 Cross‐currency basis swap example
FIGURE 2.3 Swap transacted under a CSA agreement
Discounting
The discount factor represents the present value of a £1 (or $1) unit cash flow paid at a specified future date. The rate is the expected cost of funding the cash flow continuously overnight until maturity.
At the inception of the bilateral OTC swaps market, due to the definition of a swap, banks were already using Libor (or Euribor) in forecasting future cash flows. At that time, swaps were uncollateralised, and the valuation process assumed that all banks could fund at Libor‐flat; hence Libor‐flat would be the rate used to fund swap cash flows. Hence, future cash flows associated with a swap were discounted at the same rate where banks were assumed to fund themselves (Libor‐flat). Of course, in the lead‐up to the 2008 crash and subsequently, many banks were not able to fund themselves at Libor‐flat and instead funded at Libor+spread, hence the origination of the funding value adjustment (FVA), to reflect the actual funding cost of banks. This is very material in a collateralised swap market, as we have now, as banks have to fund the collateral requirement.
Discounting affects the par swap rate. This is not necessarily relevant if every swap transacted by a bank is collateralised under a CSA (although it may be), but given that a swap is funded (in terms of collateral) at the OIS rate, but the floating‐rate re‐fix references the Libor rate showing the UK sovereign curve, GBP vanilla swaps curve, and the SONIA curve) there may be valuation issues especially for longer‐dated swaps. (The Libor and OIS yield curves are different, see Figure 2.4 which is a Bloomberg screen as at 13 September 2016.) To agree the MTM for collateral posting, bilateral swaps would have to agree the discounting curve in order to agree the collateral margin. CCP‐cleared swaps will all value to the CCP convention.
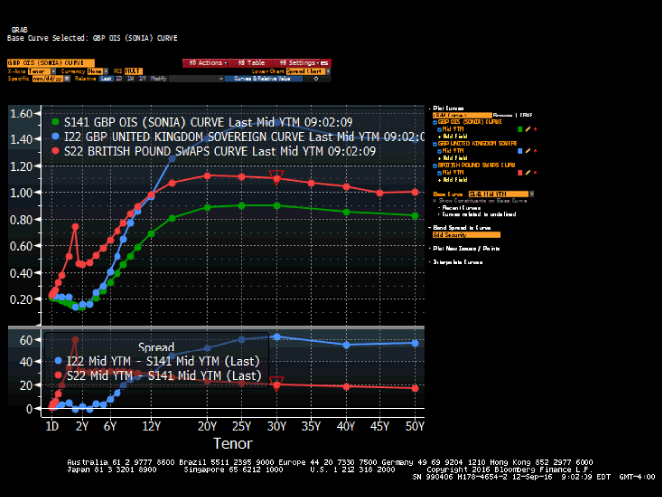
FIGURE 2.4 GBP Swaps and OIS curves, September 2016
Source: © Bloomberg LLP. Reproduced with permission.
Note, typically yield curves are upward‐sloping. A high discount rate reduces the value of longer‐dated cash flows more, and this reduces their weighting in the total PV, causing the par swap rate to fall. If one discounts “wrongly” (such as with Libor), one will misprice steep yield curves and out‐of‐money swaps. A stylised illustration of this effect is shown at Figure 2.5.
FIGURE 2.5 Impact of discount rate on swap NPV
Uncollateralised swaps are discounted at a rate that depends on the credit‐risk of the two counterparties. Bilaterally collateralised swaps are discounted at the CSA rate, and swaps cleared through the CCP are collateralised at a standard OIS rate.
Independent Amounts (IAs) can be charged by banks facing customers. CCPs charge banks IAs which the bank will fund at its specific funding rate.
The relationship between Libor and discount factors is illustrated using Figure 2.6 and expressions below. This shows in effect a dual‐purpose Libor; first a forecasting rate for future cash flows and second a measure for how to discount cash flows.
FIGURE 2.6 Relationship between Libor and discount factors
When pricing a swap on Day 1, we assume that par swap rates have zero net present value (NPV), hence a single swap curve is sufficient both to forecast Libors and determine discount factors. The basic description for this is given in Appendix 2.1.
How Does Collateral Impact the Discount Rate?
Consider the collateralised deal shown at Figure 2.7.
FIGURE 2.7 How collateral impacts the discount rate
At t0 we lend EUR X, to receive EUR 1 at t1. As collateral we immediately receive the mutually agreed NPV which is df(t1) hence it is analogous to a secured loan. Since both parties agree this is the contract NPV, the following must hold:
This implies our net cash position is equal to zero: our portfolio is in balance and there is no need to fund via the money market.
On the collateral cash we have specified an interest rate payable of R, which gives an amount of:
where α is the day‐count accrual factor and the earlier expression is for the notional amount X.
At t1 two cash flows take place.
We receive EUR 1 and we pay the collateral amount back plus interest. Assuming a no‐arbitrage environment these cash flows must be identical and so the following will hold:
It is the interest R on the collateral that determines the discount factor.
Moving to swap valuation, the collateral cash is the swap MTM, so since the collateral rate (generally OIS, SONIA, or EONIA for USD, GBP, and EUR respectively) determines the discounting curve, we need to use two curves to value the swap book. This is shown at Figure 2.8.
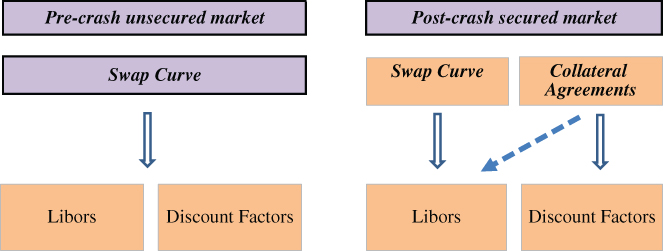
FIGURE 2.8 Separating the forecasting and discounting curve
So when valuing a collateralised swap, we consider both curves. Inter‐bank swap quotes are based on the CSA (or CCP as appropriate) collateral funding rate, generally OIS. The swap curve and the overnight curve forecast Libors, so the forecasting curve is known. The same Libor forecast is used for all secured swaps, irrespective of the actual form of the collateral. Hence, the NPV of a swap is calculated with a discounting curve that is based on the actual posted collateral. As the posted collateral is designed to reflect the swap MTM, the logic is clear.
Figure 2.9 summarises this principle, where the expressions used are again:
| α | the day‐count accrual factor; |
| R | the swap fixed rate; |
| L | Libor. |
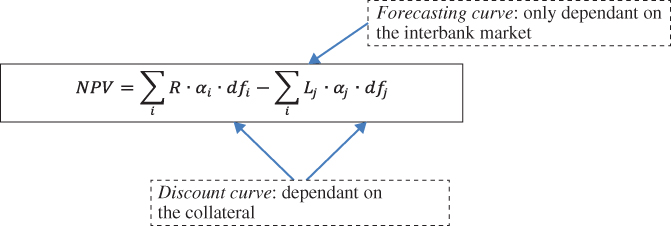
FIGURE 2.9 Valuing a collateralised swap
In practice, banks will use an FVA adjustment to account for their own funding rate (where they are borrowing to post cash collateral) in the swap valuation.
Cross‐Currency Swaps With respect to cross‐currency swaps, in the lead‐up to the Lehman default and subsequently, a cross‐currency basis swap appeared, due to supply/demand, credit, and liquidity. The market had assumed that it could always discount using 3m USD Libor, cross‐currency swapped. For example, euro cash flows would be discounted at 3m Euribor + XCCY basis spread. Post‐Lehman's, the Libor‐OIS spreads blew up, and this assumption failed. (Even pre‐Lehman it was a poor assumption.) At the present time, we know the single currency OIS rates from OIS swaps. The discount factor depends on the trade currency and the collateral type (or lack thereof). Cross‐currency swaps also trade against OIS. The basis spread allows us to calculate our CSA discount factors.
We can use the ratio of two discount rates to calculate the forward FX rate:
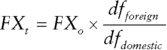
ALM and Hedge Accounting2
A large number of banks around the world employ financial derivative instruments when hedging interest‐rate and FX risk exposure on the balance sheet. Derivatives are treated as “trading book” products requiring daily marking‐to‐market revaluation. This generates a P&L impact, which can be addressed by the application of the “hedge accounting” concept.
In this section, we consider the ALM implications of hedge accounting, as well as the capital reporting issues associated with the trading book.
A banking book exposes a bank to interest rate and credit risks. A banking book may also comprise financial instruments denominated in foreign currency, equities and commodities, exposing the bank to foreign exchange (FX), equity, and commodity risks.
These risks are commonly hedged with derivatives. The international accounting standard that sets out the guidelines to recognise derivatives is IFRS 9. In July 2014, the International Accounting Standards Board (IASB) issued IFRS 9 Financial Instruments, which replaced IAS 39 Financial Instruments: Recognition and Measurement, and included requirements for classification and measurement of financial assets and liabilities, impairment of financial assets, and hedge accounting. IFRS 9 came into force on 2 January 2018.
Derivatives are recognised initially, and are subsequently measured, at fair value, regardless of whether they are held for trading or hedging purposes. Fair values of derivatives are obtained either from quoted market prices or by using valuation techniques. Derivatives are classified as assets when their fair value is positive or as liabilities when their fair value is negative.
Gains and losses from changes in the fair value of derivatives that do not qualify for hedge accounting are reported in “net trading income” (i.e., not reported in “net interest income”).
Accounting Approach
In a hedge accounting relationship there are two elements: the hedged item and the hedging instrument.
- The hedged item is the item that exposes the entity to a market risk(s). It is the element that is designated as being hedged;
- The hedging instrument is the element that hedges the risk(s) to which the hedged item is exposed. Most of the time, the hedging instrument is a derivative.
For example, a bank hedging an issued variable rate bond with a pay‐fixed receive‐floating interest‐rate swap and applying hedge accounting would designate the bond as the hedged item and the swap as the hedging instrument.
Hedge accounting is a technique that modifies the normal basis for recognising gains and losses (or revenues and expenses) associated with a hedged item or a hedging instrument to enable gains and losses on the hedging instrument to be recognised in profit or loss in the same period as offsetting losses and gains on the hedged item.
The application of hedge accounting is voluntary. In other words, were a bank to hedge a specific market risk with a derivative, it is not obliged to apply hedge accounting. However, were a bank willing to apply hedge accounting, it may not be able to do so. To qualify for hedge accounting, these are the three requirements that a hedging relationship must meet:
- The hedging relationship consists only of eligible hedging instruments and eligible hedged items;
- At the inception of the hedging relationship there is formal designation and documentation of the hedging relationship and the entity's risk management objective and strategy for undertaking the hedge. That documentation shall include identification of the hedging instrument, the hedged item, the nature of the risk being hedged and how the entity will assess whether the hedging relationship meets the hedge effectiveness requirements (including its analysis of the sources of hedge ineffectiveness and how it determines the hedge ratio); and
- The hedging relationship meets all the three hedge effectiveness requirements.
The three hedge effectiveness requirements are the following:
- There is an economic relationship between the hedged item and the hedging instrument;
- The effect of credit risk does not dominate the value changes that result from that economic relationship; and
- The weightings of the hedged item and the hedging instrument (i.e., the hedge ratio of the hedging relationship) is the same as that resulting from the quantity of the hedged item that the entity actually hedges and the quantity of the hedging instrument that the entity actually uses to hedge that quantity of hedged item. However, that designation shall not reflect an imbalance between the weightings of the hedged item and the hedging instrument that would create hedge ineffectiveness (irrespective of whether recognised or not) that could result in an accounting outcome that would be inconsistent with the purpose of hedge accounting.
Hedge accounting takes three forms under IFRS 9: fair value hedge, cash flow hedge, and net investment hedge.
Fair Value Hedge
A fair value hedge hedges the change in fair value of a recognised asset or liability or firm commitment.
In the case of interest rate risk hedges, a bank enters into fair value hedges, using primarily interest rate swaps and options, in order to protect itself against movements in the fair value of fixed‐rate financial instruments due to movements in market interest rates.
In a fair value hedge, the changes in the fair value of the hedged asset, liability or unrecognised firm commitment, or a portion thereof, attributable to the risk being hedged, are recognised in the profit or loss statement along with changes in the entire fair value of the derivative. When hedging interest rate risk, any interest accrued or paid on both the derivative and the hedged item is reported in “net interest income”, and the unrealised gains and losses from the hedge accounting fair value adjustments are reported in “net trading income” (i.e., not reported in “net interest income”) in profit or loss.
Let us assume that Megabank provided a fixed‐rate loan to a corporate. Because the fair value of the loan was exposed to changes in interest rates (and the corporate credit spread), Megabank decided to enter into a pay‐fixed receive‐floating interest rate swap. The combination of the loan and the swap resembled an origination of a variable‐rate loan, as shown at Figure 2.10.

FIGURE 2.10 Combined interest flows of the loan and the interest rate swap
Let us assume that Megabank decided not to apply hedge accounting. In such a case, the interest income stemming from the loan and the swap settlement amounts were recognised in profit or loss. The loan was recognised at amortised cost. In contrast, the swap was recognised at fair value through profit or loss, meaning that the changes in fair value of the swap were recognised in profit or loss. Ignoring the loan interest income and the swap settlement amounts, the hedging strategy added volatility to Megabank's profit or loss statement, as shown at Figure 2.11, although the strategy mitigated Megabank's exposure to interest rates stemming from the loan fair value.
FIGURE 2.11 No application of hedge accounting
Let us assume instead that the hedging relationship met the requirements for the application of hedge accounting and that Megabank decided to apply hedge accounting. As in the case of no application of hedge accounting, the interest income stemming from the loan and the swap settlement amounts were recognised in profit or loss. As in the case of no application of hedge accounting, the changes in fair value of the swap were recognised in profit or loss. Through the application of fair value hedge, the loan was fair valued and changes in its fair value due to changes in interest rates were recognised in profit or loss. If the hedge was well constructed, the changes in fair value of the swap would be offset by the changes in fair value of the loan (for changes in interest rates) and, therefore, the hedge would not add volatility in profit or loss, as shown at Figure 2.12 (ignoring the loan interest income and the swap settlement amounts). Therefore, the application of hedge accounting changed the recognition of the loan to align it with the recognition of the swap.
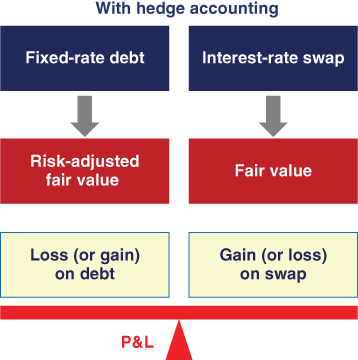
FIGURE 2.12 Application of fair value hedge accounting
Cash Flow Hedge
These are hedges set up to address variability in expected future cash flows that are attributable to a recognised specific asset or liability, or to a future expected transaction.
In the case of interest‐rate risk hedges, a bank enters into cash flow hedges, using primarily interest rate swaps and options, futures, and cross‐currency swaps, in order to protect itself against exposures to variability, due to movements in market interest rates, in future interest cash flows on banking book assets, and liabilities which bear interest at variable rates or which are expected to be re‐funded or reinvested in the future.
In a cash flow hedge, there is no change to the accounting for the hedged item and the derivative is carried at fair value, with changes in value reported initially in other comprehensive income to the extent the hedge is effective. These amounts initially recorded in other comprehensive income are subsequently reclassified into the profit or loss statement in the same periods during which the forecast transaction affects the profit or loss statement. (There is an exception for hedges of equities recognised at fair value though other comprehensive income.) For hedges of interest rate risk, the amounts are amortised into “net interest income” at the same time as the interest is accrued on the hedged transaction.
Hedge ineffectiveness is recorded in “net trading income” in profit or loss and is measured as changes in the excess (if any) in the absolute cumulative change in fair value of the actual hedging derivative over the absolute cumulative change in the fair value of the hypothetically perfect hedge.
Net Investment Hedge
A net investment hedge is a hedge of the net investment in a foreign operation. In other words, it is the hedge of the translation adjustments resulting from translating the functional currency financial statements of the foreign operation into the presentation currency of the parent entity. Imagine that Megabank was a British bank with the GBP as its presentation currency and that it controlled a French bank which reported in EUR. The financial statements of the French subsidiary will be disclosed in EUR and translated into GBP when the group prepares its consolidated financial statements. As a result, Megabank would be exposed to a potential depreciation of the EUR against the GBP. Megabank may hedge such an exposure by entering into, for example, a GBP/EUR FX forward in which the bank receives a fixed amount of GBP in exchange for a fixed amount of EUR.
In a net investment hedge, the portion of the change in fair value of the derivative due to changes in the spot (or forward) foreign exchange rate is recorded as a foreign currency translation adjustment in other comprehensive income to the extent the hedge is effective; the remainder is recorded in “net trading income” in profit or loss.
Changes in fair value of the hedging instrument relating to the effective portion of the hedge are subsequently recognised in profit or loss on disposal of the foreign operations.
APPENDIX 2.A: The Par Asset Swap Spread
We assume we have constructed a market curve of Libor discount factors where Df(t) is the price today of $1 to be paid at time t. From the perspective of the asset swap seller, it sells the bond for par plus accrued interest. The net up‐front payment has a value 100 – P where P is the market price of the bond. If we assume both parties to the swap are inter‐bank credit quality, we can price the cash flows off the Libor curve.
For the calculation we cancel out the principal payments of par at maturity. We assume that cash flows are annual and take place on the same coupon dates. The breakeven asset swap spread A is calculated by setting the present value of all cash flows equal to zero. From the perspective of the asset swap seller, the present value is
There is a 100 – P upfront payment to purchase the asset in return for par. For the interest rate swap we have
for the fixed payments and
for the floating payments, where C equals the bond annual coupon, Li is the Libor rate set at time ti ‐ l and paid at time ti, and Di is the accrual factor in the corresponding basis (day‐count adjustment). We then solve for the asset swap spread A.
SELECTED BIBLIOGRAPHY AND REFERENCES
- Choudhry, M., “An alternative bond relative value measure: determining a fair value of the swap spread using Libor and GC repo rates”, Journal of Asset Management 7 (1), June 2005, pp. 17–21.
- Gale, G., “Using and trading asset‐swaps: interest rate strategy”, Morgan Stanley Fixed Income Research, May 2006.
- O'Kane, D., Sen, S., “Credit spreads explained”, Journal of Credit Risk 1 (2), Spring 2005, pp. 61–78.