The best way to decide between models is to use AIC and BIC. Let's focus mainly on AIC because BIC is very similar. If we have a collection of candidate models, the best model should minimize AIC. We want models to predict data well but adding too many features leads to overfitting. AIC rewards accuracy but punishes complexity, so it helps to choose models that balance these competing desires. So, let's start working with AIC and BIC, and explore how they can help us to predict models.
I'm going to fit another model, which doesn't include the features that are not statistically different from 0. We can do this using the following code:

This results in the following output:
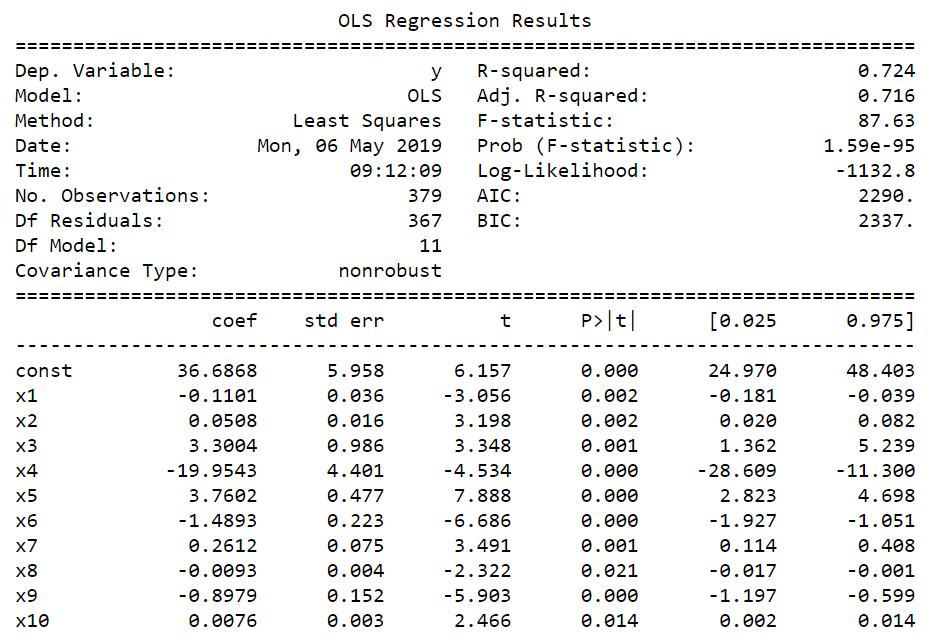
So, here is the new model, where we have a different AIC and BIC. Ideally, we want a smaller AIC. This means that the second model, where we removed the coefficients, might be a better one. Now, there's actually a nice interpretation for a different AIC. You cannot universally compare AIC between completely different problems. However, if you are staying within a localized problem (such as the Boston dataset using linear regression estimated through OLS), you can use these different criteria and make statements, such as which model is more likely to be true; which model is more likely to minimize information loss; and which model is a concept from information theory that's relatively common in statistics and data science, and accounts for not only how well a model is able to predict your target variable, but also how complex your model is.
We want models that are very likely to minimize information loss. We can use the following formula to find out which model is more likely to do so, given two of them:

We can find the performance of model 2 against model 1 as follows:

Then, we can find the performance for model 1 against model 2:

Here, we can see that model 1 is only 0.23 times (so, a number less than 1) more likely to minimize information loss than model 2; whereas, if we take the inverse of this, then model 2 is four times more likely to minimize information loss than model 1. So, by this metric, model 2 is four times better than model 1, which suggests that we should be using model 2 instead of model 1.
So, let's import the mean_squared_error metric and look at the predictions of model 2 on the training data:

This results in the following output:
![]()
This is the MSE for the training data.
Additionally, here is the MSE for the test data:

This results in the following output:
![]()
Here, we can see that the MSE is slightly larger, but not by much.
Now we can compare this to model 1, as follows:

Here, we see that there is not that much of a difference. Technically, model 1 did have a larger MSE than model 2 on the test dataset, so model 2 did perform better. So, this is another way for you to decide between models. It can also help you to decide which features to include in a model and which features to exclude. Additionally, if you wanted to explore different functional forms such as a quadratic term, adding a quadratic term or a cubic term, or interaction terms, then you could use AIC or BIC to decide between the different models. In the next section, we will move away from OLS and discuss its alternatives. We will explore our first alternative to OLS—the Bayesian approach to linear models.
