2

From Elementary Particles to Aerodynamic Flows

Step back for a moment to consider the really big picture and ponder how aerodynamics fits into the whole body of modern physical theory. The tour I'm about to take you on will be superficial, but I hope it will help to put some of the later discussions in perspective.

First, consider some of the qualitative features of the phenomena we commonly deal with in aerodynamics. Even in flows around the simplest body shapes, there is a richness of possible global flow patterns that can be daunting to anyone trying to understand them, and most flows have local features that are staggeringly complex. There are complicated patterns in how the flow attaches itself to the surface of the body and separates from it (Figure 2.1a, b), and these patterns can be different depending on whether you look at the actual time-dependent flow or the “mean” flow with the time variations averaged out. Even in flows that are otherwise steady, the shear layers that form next to the surface and in the wake are often unsteady (turbulent). This shear-layer turbulence contains flow structures that occur randomly in space and time but also display a surprising degree of organization over a wide range of length and time scales. Examples include vortex streets in wakes and the various instability “waves,” “spots,” “eddies,” “bursts,” and “streaks” in boundary layers. Examples are shown in Figure 2.1c–f, and many others can be found in Van Dyke (1982). Such features usually display extreme sensitivity to initial conditions and boundary conditions, so that their apparent randomness is real, for all practical purposes. The “butterfly effect” we've all read about doesn't just apply to the weather; the details of a small eddy in the turbulent boundary layer on the wing of a 747 are just as unpredictable.

How does all this marvelous richness and complexity arise? It is natural to expect that complexity in the flow requires complexity in the basic physics and that complex behavior in the flow must therefore have its origin at a “low level,” in the statistical behavior of the molecules that make up the gas or in the behavior of the particles that make up the molecules. But this natural expectation is wrong. Instead, the complexity we see arises from the aggregate behavior of the fluid represented by the continuum equations. In fact, the essential features of everything we observe in ordinary aerodynamic flows could be predicted from the equations for the continuum viscous flow of a perfect gas, that is, the Navier-Stokes (NS) equations, provided we could solve them in sufficient detail.

But there are two caveats that must accompany this sweeping claim. The first is that although the NS equations are a high-fidelity representation of the real physics, they are not exact. Imagine comparing a real turbulent flow with the corresponding exact solution to the NS equations, starting at an initial instant in which the theoretical flowfield is exactly the same as the real one in every detail. We would find that the NS solution matches the detailed time history of the real flow only for a short time and then gradually diverges from it. Detailed time histories of flows, however, are rarely of much interest in aerodynamics, where a statistical description of the flow nearly always suffices. In a statistical sense, we expect that a real flow and the corresponding NS solution would be practically indistinguishable. The second caveat is that even this less ambitious claim of statistical equivalence is nearly impossible to evaluate quantitatively. For one thing, exact solutions to the NS equations are not practically available for anything but the simplest of flows, and agreement for these simple cases doesn't prove much. For all other flows, especially turbulent flows, we must settle for numerical solutions. Numerical calculations that fully resolve the turbulence down to the last detail have been carried out only for simple flow geometries and relatively low Reynolds numbers. Comparisons of such calculations with the real world, at the level of detailed time histories, would be extremely difficult, if not impossible, and have not yet been attempted. Comparisons of statistical quantities have been encouraging, but for some of the most interesting and revealing quantities, Reynolds stresses, for example, the uncertainties in the experimental measurements are large. Still, in spite of these reservations, I'm confident that the NS equations could in principle predict any phenomenon of interest in practical aerodynamics to an accuracy sufficient for any reasonable engineering purpose. This doesn't mean that they can do so practically, as we'll discuss later in connection with the computational work involved in generating solutions.

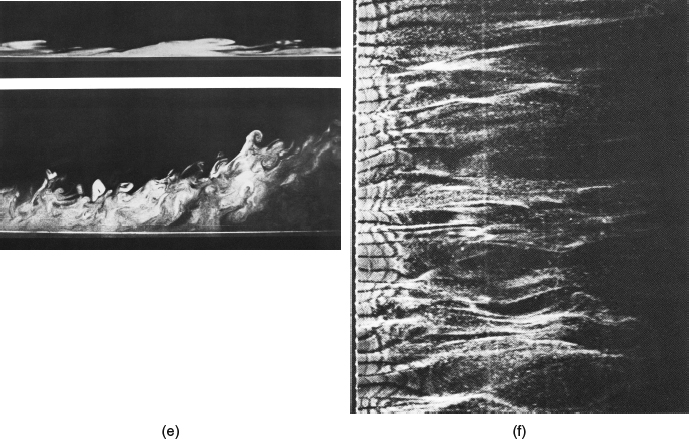
Figure 2.1 Examples of complexity in fluid flows, from Van Dyke (1982). (a) Horseshoe vortices in a laminar boundary layer ahead of a cylinder. Photo by S. Taneda, © SCIPRESS. Used with permission. (b) Rankine ogive at angle of attack. Photo by Werle (1962), courtesy of ONERA. (c) Tollmien-Schlichting waves and spiral vortices on a spinning axisymmetric body, visualized by smoke. From Mueller, et al. (1981). Used with permission. (d) Emmons turbulent spot in a boundary layer transitioning from laminar to turbulent. From Cantwell, et al(1978). Used with permission of Journal of Fluid Mechanics. (e) Eddies of a turbulent boundary layer, as affected by pressure gradients. Top: Eddies stretched in a favorable pressure gradient. Bottom: Boundary layer thickens and separates in adverse pressure gradient. Photos by R. Falco from Head and Bandyopadhyay (1981). Used with permission of Journal of Fluid Mechanics. (f) Streaks in sublayer of a turbulent boundary layer. From Kline, et al(1967). Used with permission of Journal of Fluid Mechanics

The NS equations are, of course, part of a larger system of theory applicable to a hierarchy of physical domains. Figure 2.2 illustrates this by listing the levels of physical phenomena and the corresponding levels of physical theory that deal with them. Here and in the following discussion I use the word “level” both in a conceptual sense, as in levels of physical detail, and in a physical sense, as in levels of physical and temporal scale, from small to large. As already mentioned, the NS equations are an aggregate-level theory applicable to a physical domain separated by several levels from that of the elementary particles that make up the molecules of the fluid. Starting at the lowest level shown and moving upward, each domain or level represents a narrowing of focus, a specialization to a particular situation or class of conditions. We can follow the same logical sequence in deriving the theoretical models, starting with the known properties of elementary particles and eventually reaching the NS equations. The historic development of the theories didn't follow this orderly progression, but the required steps have now been filled in, and the required assumptions and approximations are now understood.

Figure 2.2 Hierarchy of domains of physical theory leading to computational and theoretical aerodynamics

I've already made the claim that the potential for complexity in aerodynamic flows arises at the level of continuum gas flows in Figure 2.2. Is this potential for complexity really independent of what goes on at the lower levels? How can this be? In all of the levels below that of the continuum gas, there is considerable local complexity, and this is reflected in the difficulty of the corresponding mathematical theories. However, adjacent levels are separated by huge gaps in physical scale and very little of the complexity at one level is felt at the next level up. These gaps in scale act a bit like low-pass filters that allow only certain “integrated” effects of the structure at lower levels to be felt at higher levels. For example, the structure of a nitrogen molecule is affected very little by the detailed internal structure of electrons and atomic nuclei. Then, although the electron cloud of a molecule has a complex structure, the details of that internal structure have very little effect on the statistical mechanics of a dilute gas made up of large numbers of molecules. Finally, the continuum properties of gases that really matter to us in aerodynamics are highly insensitive to the details of the molecular motions. For example, the viscous behavior of the fluid under shearing deformation that we assume in the NS equations does not even depend on the fact that the fluid is a gas; it is the same for liquids such as water. As we move up the line toward the NS equations, instead of increasing complexity, we encounter a series of natural simplifications, and surprisingly, these simplifications cost us little loss of physical fidelity for flows that interest us.

So the interesting behavior we see in aerodynamic flows is not inherent in any of the lower levels of the physics. Instead, it emerges in the behavior of the fluid at the continuum level and can be captured in solutions to the NS equations. This is a bit surprising at first, because the physical balances represented by the equations at the local level aren't all that complicated. However, in recent years, studies in the field of complexity science have identified a broad class of seemingly simple systems that can exhibit complex behavior. The NS equations are one example of this kind of system, and solutions (fluid flows) commonly exhibit emergent behavior in which great complexity arises from many simple local interactions. The NS equations are, after all, a set of nonlinear partial-differential field equations in space and time, with multiple, interacting dependent variables, and the space of possible solutions is huge. This, combined with the fact that the possible interactions between flow variables at different points in space are sufficiently rich, makes the emergence of complexity in the solutions a natural outcome.

There is also a much more mundane way in which fluid flows must be considered complex, and that is that even some of the simplest flows are not easy to understand or “explain” even qualitatively in a satisfying way without appealing to mathematics. Why is it so difficult? Remember that we are dealing with multiple, interacting flow quantities (dependent variables) and that if we are to understand a flow properly, the behavior of these quantities must be known over some extended spatial domain. Understanding simultaneous behavior over an extended spatial domain is inherently difficult, and the problem of local physics versus global flow behavior contributes to the difficulty. The basic physical laws impose relationships between flow quantities locally, while global behavior is constrained by the requirement that these laws be satisfied everywhere simultaneously. A flowfield is a global phenomenon in which what happens at one point depends to some extent on what happens everywhere else.

Another major difficulty has to do with assigning cause and effect. Here I'm not referring to the general philosophical difficulties of linking causes and their effects. The NS equations are based on Newtonian mechanics and classical thermodynamics, in which clear physical cause-and-effect relationships are assumed. The problem is that when these physical laws are combined in the NS equations, they define relationships between different flow quantities, but they don't define one-way trains of causation. For example, consider Bernoulli's equation, which relates the pressure to the velocity under certain conditions. In trying to explain a flowfield, do we consider the behavior of the velocity to be known and then use Bernoulli's principle to deduce the behavior of the pressure? Or vice versa? In most situations, the right answer is “neither.” Cause-and-effect relationships in fluid mechanics tend to be circular, or reciprocal, in the sense that A and B cause each other and are caused by each other at the same time, and often at the same point in space. The upshot of this is that linear explanations assigning one-way cause and effect (A causes B, which in turn causes C) are nearly always wrong. Instead, we must seek explanations of the type that begin with a hypothesis and eventually come back around to consistency with the hypothesis. (If A, then B, then C, which is consistent with A.) We will consider the issue of cause and effect in greater detail with regard to basic fluid mechanics in Section 3.5. Later, we will see examples, such as nonmathematical explanations of the lift on a wing or airfoil in Chapter 7, where trying to force one-way causation has led to errors.

So far, we have considered some of the generic characteristics of continuum flows governed by the NS equations. We've seen how the emergence of complexity in the structure of the flows themselves is a natural outcome of the physics, and we've identified some of the reasons why understanding and explaining flows can be difficult. We've looked at how the NS equations fit into the overall body of physical theory, and we've seen that they represent an aggregate-level theory that involves some simplifying approximations. I've also asserted that within their range of validity the NS equations are a highly accurate representation of reality and that they can in principle predict anything of interest in practical aerodynamics.

Given this essentially complete predictive capability of the NS equations, we could say that they represent all of the “hard science” we should need in aerodynamics. But, of course, the NS equations by themselves are not enough, and there is much more to aerodynamics as a science than what we've seen so far on this brief tour. For the foreseeable future, we won't be calculating an NS solution every time we want to predict or understand what will happen in an aerodynamic flow, and until recently in the history of our discipline, we couldn't have done so anyway. The pioneers in the field had to devise other ways of getting answers: higher level theories that provided both intuitive insight and computational tractability. Such theories are usually derivable at least in part from the NS equations using additional simplifying assumptions, but often also depend on conceptual models of the flows in question. These theories therefore tend to be specialized to particular situations and to have more restricted ranges of applicability than the basic equations. The strategies are several and varied, and we'll consider them in some detail in later chapters. In any case, aerodynamic theory carries a considerable superstructure of higher level theoretical models in addition to the basic NS equations.

Considering this body of aerodynamic theory as a whole, what is its status as science? Like everything else on the conceptual or theoretical side of science, it is “just a theory.” This is something the proponents of creationism like to say of Darwinian evolution, implying that it is merely a tentative hypothesis. But of course evolution is much more than a tentative hypothesis, and so is aerodynamic theory. Both have been tested again and again against empirical observations, and have so far always passed the test.

In principle, of course, any theory could be contradicted tomorrow by new evidence and end up needing to be replaced. The NS equations, however, are about as secure as a scientific theory can ever be. In the context of science as a whole, the NS equations purport to be valid only for a narrow range of phenomena, and within this range the NS equations are unlikely ever to be significantly contradicted. The higher level extensions of aerodynamic theory are also not likely ever to be completely overthrown. They, however, typically have even more limited ranges of applicability than the NS equations and are known to be seriously contradicted in common situations that are outside their ranges but still within the realm of aerodynamics. In using the higher level conceptual models of aerodynamics, we must always keep their limitations in mind.

So aerodynamics is on solid ground as a science. But what can we say of its general character? Where does it stand on the deductive/inductive spectrum? In this regard, it has a distinctly split personality. On one hand, we have an all-encompassing theory, the NS equations with a no-slip condition, which is solidly tied to the rest of modern physical theory and from which we can in principle deduce anything of interest in the field. On the other hand, the computational intractability of the equations has greatly limited what we can deduce from first principles in most situations, and much of what we know comes from empirical observations, that is, the inductive approach. This is something we've already discussed in connection with the vital role that phenomenological knowledge plays in our conceptual framework.

The actual physics embodied in our theoretical framework consists of Newtonian mechanics and classical thermodynamics, combined with a mathematical formalism that enables us to bookkeep material properties, forces, and fluxes in a continuous material. Thus when we apply the framework correctly, we are adhering to what I call a Newtonian worldview, in which all effects must have causes that are consistent with Newtonian (or post-Newtonian) scientific principles. As we'll see, some of the errors that can arise in aerodynamic reasoning can be traced to regressions to pre-Newtonian ways of thinking.