Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

Chapter 2 Summary and Review

Study Guide

Key Terms and Concepts	Examples
SECTION 2.1: INCREASING, DECREASING, AND PIECEWISE FUNCTIONS; APPLICATIONS
Increasing, Decreasing, and Constant Functions A function `f` is said to be increasing on an open interval `I` if for all `a` and `b` in that interval, $a < b$ implies $f (a) < f (b)$ . A function `f` is said to be decreasing on an open interval `I` if for all `a` and `b` in that interval, $a < b$ implies $f (a) > f (b)$ . A function `f` is said to be constant on an open interval `I` if for all `a` and `b` in that interval, $f (a) = f (b)$ .	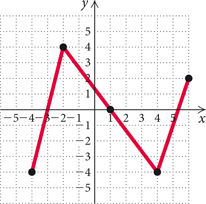Determine the intervals on which the function is (a) increasing; (b) decreasing; (c) constant. As `x`-values increase from −5 to −2, `y`-values increase from −4 to −2; `y`-values also increase as `x`-values increase from −1 to 1. Thus the function is increasing on the intervals (−5, 2) and (−1, 1). As `x`-values increase from −2 to −1, `y`-values decrease from −2 to −3, so the function is decreasing on the interval (−2, −1). As `x`-values increase from 1 to 5, `y` remains 5, so the function is constant on the interval (1, 5).
Relative Maxima and Minima Suppose that `f` is a function for which $f (c)$ exists for some `c` in the domain of `f`. Then: $f (c)$ is a relative maximum if there exists an open interval `I` containing `c` such that $f (c) > f (x)$ for all `x` in `I`, where $x \neq c;$ and $f (c)$ is a relative minimum if there exists an open interval `I` containing `c` such that $f (c) < f (x)$ for all `x` in `I`, where $x \neq c$ .	Determine any relative maxima or minima of the function. We see from the graph that the function has one relative maximum, 4.05. It occurs when $x = - 1.09$ . We also see that there is one relative minimum, −2.34. It occurs when $x = 0.76$ .
Some applied problems can be modeled by functions.	See Examples 3 and 4 on pages 101 and 102.
To graph a function that is defined piecewise, graph the function in parts as defined by its output formulas.	Graph the function defined as $f (x) = {\begin{array}{l} 2 x - 3, & for x < 1, \\ x + 1, & for x \geq 1. \end{array}$ We create the graph in two parts. First, we graph $f (x) = 2 x - 3$ for inputs `x` less than 1. Then we graph $f (x) = x + 1$ for inputs `x` greater than or equal to 1.
Greatest Integer Function $f (x) = 〚 x 〛 =$ the greatest integer less than or equal to `x`.	The graph of the greatest integer function is shown below. Each input is paired with the greatest integer less than or equal to that input.
SECTION 2.2: THE ALGEBRA OF FUNCTIONS
Sums, Differences, Products, and Quotients of Functions If `f` and `g` are functions and `x` is in the domain of each function, then: $(f + g) (x) = f (x) + g (x)$ , $(f - g) (x) = f (x) - g (x)$ , $(f g) (x) = f (x) \cdot g (x)$ , $(f / g) (x) = f (x) / g (x)$ , $provided g (x) \neq 0$ .	Given that $f (x) = x - 4$ and $g (x) = \sqrt{x + 5}$ , find each of the following. $(f + g) (x)$ $(f - g) (x)$ $(f g) (x)$ $(f / g) (x)$ $(f + g) (x) = f (x) + g (x) = x - 4 + \sqrt{x + 5}$ $(f - g) (x) = f (x) - g (x) = x - 4 - \sqrt{x + 5}$ $(f g) (x) = f (x) \cdot g (x) = (x - 4) \sqrt{x + 5}$ $(f / g) (x) = f (x) / g (x) = \frac{x - 4}{\sqrt{x + 5}}, x \neq - 5$
Domains of $f + g$ , $f - g$ , `fg`, and $f / g$ If `f` and `g` are functions, then the domain of the functions $f + g$ , $f - g$ , and `fg` is the intersection of the domain of `f` and the domain of `g`. The domain of $f / g$ is also the intersection of the domain of `f` and the domain of `g`, with the exclusion of any `x`-values for which $g (x) = 0$ .	For the functions `f` and `g` above, find the domains of $f + g$ , $f - g$ , `fg`, and $f / g$ . The domain of $f (x) = x - 4$ is the set of all real numbers. The domain of $g (x) = \sqrt{x + 5}$ is the set of all real numbers for which $x + 5 \geq 0$ , or $x \geq - 5$ , or $[- 5, \infty)$ . Then the domain of $f + g$ , $f - g$ , and `fg` is the set of numbers in the intersection of these domains, or $[- 5, \infty)$ . Since $g (- 5) = 0$ , we must exclude −5. Thus the domain of $f / g$ is $[- 5, \infty)$ excluding −5, or $(- 5, \infty)$ .
The difference quotient for a function $f (x)$ is the ratio $\frac{f (x + h) - f (x)}{h} .$	For the function $f (x) = x^{2} - 4$ , construct and simplify the difference quotient. $\begin{array}{rcll} \frac{f (x + h) - f (x)}{h} & = & \frac{[{(x + h)}^{2} - 4] - (x^{2} - 4)}{h} \\ = & \frac{x^{2} + 2 x h + h^{2} - 4 - x^{2} + 4}{h} \\ = & \frac{2 x h + h^{2}}{h} = \frac{h (2 x + h)}{h} \\ = & 2 x + h \end{array}$
SECTION 2.3: THE COMPOSITION OF FUNCTIONS
The composition of functions, $f \circ g$ , is defined as $(f \circ g) (x) = f (g (x)),$ where `x` is in the domain of `g` and $g (x)$ is in the domain of `f`.	Given that $f (x) = 2 x - 1$ and $g (x) = \sqrt{x}$ , find each of the following. $(f \circ g) (4)$ $(g \circ g) (625)$ $(f \circ g) (x)$ $(g \circ f) (x)$ The domain of $f \circ g$ and the domain of $g \circ f$ $(f \circ g) (4) = f (g (4)) = f (\sqrt{4}) = f (2) = 2 \cdot 2 - 1 = 4 - 1 = 3$ $(g \circ g) (625) = g (g (625)) = g (\sqrt{625}) = g (25) = \sqrt{25} = 5$ $(f \circ g) (x) = f (g (x)) = f (\sqrt{x}) = 2 \sqrt{x} - 1$ $(g \circ f) (x) = g (f (x)) = g (2 x - 1) = \sqrt{2 x - 1}$ The domain and the range of $f (x)$ are both $(- \infty, \infty)$ , and the domain and the range of $g (x)$ are both $[0, \infty)$ . Since the inputs of $f \circ g$ are outputs of `g` and since `f` can accept any real number as an input, the domain of $f \circ g$ consists of all real numbers that are outputs of `g`, or $[0, \infty)$ . The inputs of $g \circ f$ consist of all real numbers that are in the domain of `g`. Thus we must have $2 x - 1 \geq 0$ , or $x \geq \frac{1}{2}$ , so the domain of $g \circ f$ is $[\frac{1}{2}, \infty)$ .
When we decompose a function, we write it as the composition of two functions.	If $h (x) = \sqrt{3 x + 7}$ , find $f (x)$ and $g (x)$ such that $h (x) = (f \circ g) (x)$ . This function finds the square root of $3 x + 7$ , so one decomposition is $f (x) = \sqrt{x}$ and $g (x) = 3 x + 7$ . There are other correct answers, but this one is probably the most obvious.
SECTION 2.4: SYMMETRY
Algebraic Tests of Symmetry x-axis: If replacing `y` with −`y` produces an equivalent equation, then the graph is symmetric with respect to the `x`-axis. y-axis: If replacing `x` with −`x` produces an equivalent equation, then the graph is symmetric with respect to the `y`-axis. Origin: If replacing `x` with −`x` and `y` with −`y` produces an equivalent equation, then the graph is symmetric with respect to the origin.	Test $y = 2 x^{3}$ for symmetry with respect to the `x`-axis, the `y`-axis, and the origin. x-axis: We replace `y` with −`y`: $\begin{array}{rcll} - y & = & 2 x^{3} \\ y & = & - 2 x^{3} . & Multiplying by - 1 \end{array}$ The resulting equation is not equivalent to the original equation, so the graph is not symmetric with respect to the `x`-axis. y-axis: We replace `x` with −`x`: $\begin{array}{rcl} y & = & 2 {(- x)}^{3} \\ y & = & - 2 x^{3} . \end{array}$ The resulting equation is not equivalent to the original equation, so the graph is not symmetric with respect to the `y`-axis. Origin: We replace `x` with −`x` and `y` with −`y`: $\begin{array}{rcl} - y & = & 2 {(- x)}^{3} \\ - y & = & - 2 x^{3} \\ y & = & 2 x^{3} . \end{array}$ The resulting equation is equivalent to the original equation, so the graph is symmetric with respect to the origin.
Even Functions and Odd Functions If the graph of a function is symmetric with respect to the `y`-axis, we say that it is an even function. That is, for each `x` in the domain of `f`, $f (x) = f (- x)$ . If the graph of a function is symmetric with respect to the origin, we say that it is an odd function. That is, for each `x` in the domain of `f`, $f (- x) = - f (x)$ .	Determine whether each function is even, odd, or neither. $g (x) = 2 x^{2} - 4$ $h (x) = x^{5} - 3 x^{3} - x$ We first find $g (- x)$ and simplify: $\begin{array}{rcll} g (- x) & = & 2 {(- x)}^{2} - 4 \\ = & 2 x^{2} - 4. \end{array}$ $g (x) = g (- x)$ , so `g` is even. Since a function other than $f (x) = 0$ cannot be both even and odd and `g` is even, we need not test to see if it is an odd function. We first find $h (- x)$ and simplify: $\begin{array}{rcl} h (- x) & = & {(- x)}^{5} - 3 {(- x)}^{3} - (- x) \\ = & - x^{5} + 3 x^{3} + x . \end{array}$ $h (x) \neq h (- x)$ , so `h` is not even. Next, we find $- h (x)$ and simplify: $\begin{array}{rcl} - h (x) & = & - (x^{5} - 3 x^{3} - x) \\ = & - x^{5} + 3 x^{3} + x . \end{array}$ $h (- x) = - h (x)$ , so h is odd.
SECTION 2.5: TRANSFORMATIONS
Vertical Translation For $b > 0 :$ the graph of $y = f (x) + b$ is the graph of $y = f (x)$ shifted up b units; the graph of $y = f (x) - b$ is the graph of $y = f (x)$ shifted down b units. Horizontal Translation For $d > 0 :$ the graph of $y = f (x - d)$ is the graph of $y = f (x)$ shifted right `d` units; the graph of $y = f (x + d)$ is the graph of $y = f (x)$ shifted left `d` units.	Graph $g (x) = {(x - 2)}^{2} + 1$ . Before doing so, describe how the graph can be obtained from the graph of $f (x) = x^{2}$ . First, note that the graph of $h (x) = {(x - 2)}^{2}$ is the graph of $f (x) = x^{2}$ shifted right 2 units. Then the graph of $g (x) = {(x - 2)}^{2} + 1$ is the graph of $h (x) = {(x - 2)}^{2}$ shifted up 1 unit. Thus the graph of `g` is obtained by shifting the graph of $f (x) = x^{2}$ right 2 units and up 1 unit.
Reflections The graph of $y = - f (x)$ is the reflection of $y = f (x)$ across the `x`-axis. The graph of $y = f (- x)$ is the reflection of $y = f (x)$ across the `y`-axis. If a point (`x`, `y`) is on the graph of $y = f (x)$ , then (`x`, −`y`) is on the graph of $y = - f (x)$ , and (−`x`, `y`) is on the graph of $y = f (- x)$ .	Graph each of the following. Before doing so, describe how each graph can be obtained from the graph of $f (x) = x^{2} - x$ . $g (x) = x - x^{2}$ $h (x) = {(- x)}^{2} - (- x)$ Note that $\begin{array}{rcl} - f (x) & = & - (x^{2} - x) \\ = & - x^{2} + x \\ = & x - x^{2} \\ = & g (x) . \end{array}$ Thus the graph is a reflection of the graph of $f (x) = x^{2} - x$ across the `x`-axis. Note that $f (- x) = {(- x)}^{2} - (- x) = h (x) .$ Thus the graph of $h (x) = {(- x)}^{2} - (- x)$ is a reflection of the graph of $f (x) = x^{2} - x$ across the `y`-axis.
Vertical Stretching and Shrinking The graph of $y = a f (x)$ can be obtained from the graph of $y = f (x)$ by: stretching vertically for $\| a \| > 1$ , or shrinking vertically for $0 < \| a \| < 1$ . For $a < 0$ , the graph is also reflected across the `x`-axis. (The `y`-coordinates of the graph of $y = a f (x)$ can be obtained by multiplying the `y`-coordinates of $y = f (x)$ by `a`.) Horizontal Stretching and Shrinking The graph of $y = f (c x)$ can be obtained from the graph of $y = f (x)$ by: shrinking horizontally for $\| c \| > 1$ , or stretching horizontally for $0 < \| c \| < 1$ . For $c < 0$ , the graph is also reflected across the `y`-axis. (The `x`-coordinates of the graph of $y = f (c x)$ can be obtained by dividing the `x`-coordinates of $y = f (x)$ by `c`.)	A graph of $y = g (x)$ is shown below. Use this graph to graph each of the given equations. $f (x) = g (2 x)$ $f (x) = - 2 g (x)$ $f (x) = \frac{1}{2} g (x)$ $f (x) = g (\frac{1}{2} x)$ Since $\| 2 \| > 1$ , the graph of $f (x) = g (2 x)$ is a horizontal shrinking of the graph of $y = g (x)$ . The transformation divides each `x`-coordinate of `g` by 2. Since $\| - 2 \| > 1$ , the graph of $f (x) = - 2 g (x)$ is a vertical stretching of the graph of $y = g (x)$ . The transformation multiplies each `y`-coordinate of `g` by 2. Since $- 2 < 0$ , the graph is also reflected across the `x`-axis. Since $\| \frac{1}{2} \| < 1$ , the graph of $f (x) = \frac{1}{2} g (x)$ is a vertical shrinking of the graph of $y = g (x)$ . The transformation multiplies each `y`-coordinate of `g` by $\frac{1}{2}$ . Since $\| \frac{1}{2} \| < 1$ , the graph of $f (x) = g (\frac{1}{2} x)$ is a horizontal stretching of the graph of $y = g (x)$ . The transformation divides each `x`-coordinate of `g` by $\frac{1}{2}$ (which is the same as multiplying by 2).
SECTION 2.6: VARIATION AND APPLICATIONS
Direct Variation If a situation gives rise to a linear function $f (x) = k x$ , or $y = k x$ , where `k` is a positive constant, we say that we have direct variation, or that `y` varies directly as `x`, or that `y` is directly proportional to `x`. The number `k` is called the variation constant, or the constant of proportionality.	Find an equation of variation in which `y` varies directly as `x`, and $y = 24$ when $x = 8$ . Then find the value of `y` when $x = 5$ . First, we have $\begin{array}{rcll} y & = & k x & y varies directly as x . \\ 24 & = & k \cdot 8 & Substituting \\ 3 & = & k & Variation constant \end{array}$ The equation of variation is $y = 3 x$ . Now we use the equation to find the value of `y` when $x = 5$ : $\begin{array}{rcll} y & = & 3 x \\ = & 3 \cdot 5 & Substituting \\ = & 15. \end{array}$ When $x = 5$ , the value of `y` is 15.
Inverse Variation If a situation gives rise to a function $f (x) = k / x$ , or $y = k / x$ , where `k` is a positive constant, we say that we have inverse variation, or that `y` varies inversely as `x`, or that `y` is inversely proportional to `x`. The number `k` is called the variation constant, or the constant of proportionality.	Find an equation of variation in which `y` varies inversely as `x`, and $y = 5$ when $x = 0.1$ . Then find the value of `y` when $x = 10$ . First, we have $\begin{array}{rcll} y & = & \frac{k}{x} & y varies inversely as x . \\ 5 & = & \frac{k}{0.1} & Substituting \\ 0.5 & = & k . & Variation constant \end{array}$ The equation of variation is $y = \frac{0.5}{x}$ . Now we use the equation to find the value of `y` when $x = 10 :$ $\begin{array}{rcll} y & = & \frac{0.5}{x} \\ = & \frac{0.5}{10} & Substituting \\ = & 0.05. \end{array}$ When $x = 10$ , the value of `y` is 0.05.
Combined Variation `y` varies directly as the `n`th power of `x` if there is some positive constant `k` such that $y = k x^{n} .$ `y` varies inversely as the `n`th power of `x` if there is some positive constant `k` such that $y = \frac{k}{x^{n}} .$ `y` varies jointly as `x` and `z` if there is some positive constant `k` such that $y = k x z .$	Find an equation of variation in which `y` varies jointly as `w` and the square of `x` and inversely as `z`, and $y = 8$ when $w = 3, x = 2$ , and $z = 6$ . First, we have $\begin{array}{rcll} y & = & k \cdot \frac{w x^{2}}{z} \\ 8 & = & k \cdot \frac{3 \cdot 2^{2}}{6} & Substituting \\ 8 & = & k \cdot \frac{3 \cdot 4}{6} \\ 8 & = & 2 k \\ 4 & = & k . & Variation constant \end{array}$ The equation of variation is $y = 4 \frac{w x^{2}}{z}$ , or $y = \frac{4 w x^{2}}{z}$ .

Key Terms and Concepts

Examples

SECTION 2.1: INCREASING, DECREASING, AND PIECEWISE FUNCTIONS; APPLICATIONS

Increasing, Decreasing, and Constant Functions

A function f is said to be increasing on an open interval I if for all a and b in that interval, $a < b$ implies $f (a) < f (b)$ .

A function f is said to be decreasing on an open interval I if for all a and b in that interval, $a < b$ implies $f (a) > f (b)$ .

A function f is said to be constant on an open interval I if for all a and b in that interval, $f (a) = f (b)$ .

Determine the intervals on which the function is (a) increasing; (b) decreasing; (c) constant.

As x-values increase from −5 to −2, y-values increase from −4 to −2; y-values also increase as x-values increase from −1 to 1. Thus the function is increasing on the intervals (−5, 2) and (−1, 1).
As x-values increase from −2 to −1, y-values decrease from −2 to −3, so the function is decreasing on the interval (−2, −1).
As x-values increase from 1 to 5, y remains 5, so the function is constant on the interval (1, 5).

Relative Maxima and Minima

Suppose that f is a function for which $f (c)$ exists for some c in the domain of f. Then:

$f (c)$ is a relative maximum if there exists an open interval I containing c such that $f (c) > f (x)$ for all x in I, where $x \neq c;$ and

$f (c)$ is a relative minimum if there exists an open interval I containing c such that $f (c) < f (x)$ for all x in I, where $x \neq c$ .

Determine any relative maxima or minima of the function.

We see from the graph that the function has one relative maximum, 4.05. It occurs when $x = - 1.09$ . We also see that there is one relative minimum, −2.34. It occurs when $x = 0.76$ .

Some applied problems can be modeled by functions.

See Examples 3 and 4 on pages 101 and 102.

To graph a function that is defined piecewise, graph the function in parts as defined by its output formulas.

Graph the function defined as

$f (x) = {\begin{array}{l} 2 x - 3, & for x < 1, \\ x + 1, & for x \geq 1. \end{array}$

We create the graph in two parts. First, we graph $f (x) = 2 x - 3$ for inputs x less than 1. Then we graph $f (x) = x + 1$ for inputs x greater than or equal to 1.

Greatest Integer Function

$f (x) = 〚 x 〛 =$ the greatest integer less than or equal to x.

The graph of the greatest integer function is shown below. Each input is paired with the greatest integer less than or equal to that input.

SECTION 2.2: THE ALGEBRA OF FUNCTIONS

Sums, Differences, Products, and Quotients of Functions

If f and g are functions and x is in the domain of each function, then:

$(f + g) (x) = f (x) + g (x)$ ,
$(f - g) (x) = f (x) - g (x)$ ,
$(f g) (x) = f (x) \cdot g (x)$ ,
$(f / g) (x) = f (x) / g (x)$ , $provided g (x) \neq 0$ .

Given that $f (x) = x - 4$ and $g (x) = \sqrt{x + 5}$ , find each of the following.

$(f + g) (x)$
$(f - g) (x)$
$(f g) (x)$
$(f / g) (x)$

$(f + g) (x) = f (x) + g (x) = x - 4 + \sqrt{x + 5}$
$(f - g) (x) = f (x) - g (x) = x - 4 - \sqrt{x + 5}$
$(f g) (x) = f (x) \cdot g (x) = (x - 4) \sqrt{x + 5}$
$(f / g) (x) = f (x) / g (x) = \frac{x - 4}{\sqrt{x + 5}}, x \neq - 5$

Domains of $f + g$ , $f - g$ , fg, and $f / g$

If f and g are functions, then the domain of the functions $f + g$ , $f - g$ , and fg is the intersection of the domain of f and the domain of g. The domain of $f / g$ is also the intersection of the domain of f and the domain of g, with the exclusion of any x-values for which $g (x) = 0$ .

For the functions f and g above, find the domains of $f + g$ , $f - g$ , fg, and $f / g$ .

The domain of $f (x) = x - 4$ is the set of all real numbers. The domain of $g (x) = \sqrt{x + 5}$ is the set of all real numbers for which $x + 5 \geq 0$ , or $x \geq - 5$ , or $[- 5, \infty)$ . Then the domain of $f + g$ , $f - g$ , and fg is the set of numbers in the intersection of these domains, or $[- 5, \infty)$ .

Since $g (- 5) = 0$ , we must exclude −5. Thus the domain of $f / g$ is $[- 5, \infty)$ excluding −5, or $(- 5, \infty)$ .

The difference quotient for a function $f (x)$ is the ratio

$\frac{f (x + h) - f (x)}{h} .$

For the function $f (x) = x^{2} - 4$ , construct and simplify the difference quotient.

$\begin{array}{rcll} \frac{f (x + h) - f (x)}{h} & = & \frac{[{(x + h)}^{2} - 4] - (x^{2} - 4)}{h} \\ = & \frac{x^{2} + 2 x h + h^{2} - 4 - x^{2} + 4}{h} \\ = & \frac{2 x h + h^{2}}{h} = \frac{h (2 x + h)}{h} \\ = & 2 x + h \end{array}$

SECTION 2.3: THE COMPOSITION OF FUNCTIONS

The composition of functions, $f \circ g$ , is defined as

$(f \circ g) (x) = f (g (x)),$

where x is in the domain of g and $g (x)$ is in the domain of f.

Given that $f (x) = 2 x - 1$ and $g (x) = \sqrt{x}$ , find each of the following.

$(f \circ g) (4)$
$(g \circ g) (625)$
$(f \circ g) (x)$
$(g \circ f) (x)$
The domain of $f \circ g$ and the domain of $g \circ f$

$(f \circ g) (4) = f (g (4)) = f (\sqrt{4}) = f (2) = 2 \cdot 2 - 1 = 4 - 1 = 3$
$(g \circ g) (625) = g (g (625)) = g (\sqrt{625}) = g (25) = \sqrt{25} = 5$
$(f \circ g) (x) = f (g (x)) = f (\sqrt{x}) = 2 \sqrt{x} - 1$
$(g \circ f) (x) = g (f (x)) = g (2 x - 1) = \sqrt{2 x - 1}$
The domain and the range of $f (x)$ are both $(- \infty, \infty)$ , and the domain and the range of $g (x)$ are both $[0, \infty)$ . Since the inputs of $f \circ g$ are outputs of g and since f can accept any real number as an input, the domain of $f \circ g$ consists of all real numbers that are outputs of g, or $[0, \infty)$ .

The inputs of $g \circ f$ consist of all real numbers that are in the domain of g. Thus we must have $2 x - 1 \geq 0$ , or $x \geq \frac{1}{2}$ , so the domain of $g \circ f$ is $[\frac{1}{2}, \infty)$ .

When we decompose a function, we write it as the composition of two functions.

If $h (x) = \sqrt{3 x + 7}$ , find $f (x)$ and $g (x)$ such that $h (x) = (f \circ g) (x)$ .

This function finds the square root of $3 x + 7$ , so one decomposition is $f (x) = \sqrt{x}$ and $g (x) = 3 x + 7$ .

There are other correct answers, but this one is probably the most obvious.

SECTION 2.4: SYMMETRY

Algebraic Tests of Symmetry

x-axis: If replacing y with −y produces an equivalent equation, then the graph is symmetric with respect to the x-axis.

y-axis: If replacing x with −x produces an equivalent equation, then the graph is symmetric with respect to the y-axis.

Origin: If replacing x with −x and y with −y produces an equivalent equation, then the graph is symmetric with respect to the origin.

Test $y = 2 x^{3}$ for symmetry with respect to the x-axis, the y-axis, and the origin.

x-axis: We replace y with −y:

$\begin{array}{rcll} - y & = & 2 x^{3} \\ y & = & - 2 x^{3} . & Multiplying by - 1 \end{array}$

The resulting equation is not equivalent to the original equation, so the graph is not symmetric with respect to the x-axis.

y-axis: We replace x with −x:

$\begin{array}{rcl} y & = & 2 {(- x)}^{3} \\ y & = & - 2 x^{3} . \end{array}$

The resulting equation is not equivalent to the original equation, so the graph is not symmetric with respect to the y-axis.

Origin: We replace x with −x and y with −y:

$\begin{array}{rcl} - y & = & 2 {(- x)}^{3} \\ - y & = & - 2 x^{3} \\ y & = & 2 x^{3} . \end{array}$

The resulting equation is equivalent to the original equation, so the graph is symmetric with respect to the origin.

Even Functions and Odd Functions

If the graph of a function is symmetric with respect to the y-axis, we say that it is an even function. That is, for each x in the domain of f, $f (x) = f (- x)$ .

If the graph of a function is symmetric with respect to the origin, we say that it is an odd function. That is, for each x in the domain of f, $f (- x) = - f (x)$ .

Determine whether each function is even, odd, or neither.

$g (x) = 2 x^{2} - 4$
$h (x) = x^{5} - 3 x^{3} - x$

We first find $g (- x)$ and simplify:

$\begin{array}{rcll} g (- x) & = & 2 {(- x)}^{2} - 4 \\ = & 2 x^{2} - 4. \end{array}$

$g (x) = g (- x)$ , so g is even. Since a function other than $f (x) = 0$ cannot be both even and odd and g is even, we need not test to see if it is an odd function.
We first find $h (- x)$ and simplify:

$\begin{array}{rcl} h (- x) & = & {(- x)}^{5} - 3 {(- x)}^{3} - (- x) \\ = & - x^{5} + 3 x^{3} + x . \end{array}$

$h (x) \neq h (- x)$ , so h is not even.

Next, we find $- h (x)$ and simplify:

$\begin{array}{rcl} - h (x) & = & - (x^{5} - 3 x^{3} - x) \\ = & - x^{5} + 3 x^{3} + x . \end{array}$

$h (- x) = - h (x)$ , so h is odd.

SECTION 2.5: TRANSFORMATIONS

Vertical Translation

For $b > 0 :$

the graph of $y = f (x) + b$ is the graph of $y = f (x)$ shifted up b units;
the graph of $y = f (x) - b$ is the graph of $y = f (x)$ shifted down b units.

Horizontal Translation

For $d > 0 :$

the graph of $y = f (x - d)$ is the graph of $y = f (x)$ shifted right d units;
the graph of $y = f (x + d)$ is the graph of $y = f (x)$ shifted left d units.

Graph $g (x) = {(x - 2)}^{2} + 1$ . Before doing so, describe how the graph can be obtained from the graph of $f (x) = x^{2}$ .

First, note that the graph of $h (x) = {(x - 2)}^{2}$ is the graph of $f (x) = x^{2}$ shifted right 2 units. Then the graph of $g (x) = {(x - 2)}^{2} + 1$ is the graph of $h (x) = {(x - 2)}^{2}$ shifted up 1 unit. Thus the graph of g is obtained by shifting the graph of $f (x) = x^{2}$ right 2 units and up 1 unit.

Reflections

The graph of $y = - f (x)$ is the reflection of $y = f (x)$ across the x-axis.

The graph of $y = f (- x)$ is the reflection of $y = f (x)$ across the y-axis.

If a point (x, y) is on the graph of $y = f (x)$ , then (x, −y) is on the graph of $y = - f (x)$ , and (−x, y) is on the graph of $y = f (- x)$ .

Graph each of the following. Before doing so, describe how each graph can be obtained from the graph of $f (x) = x^{2} - x$ .

$g (x) = x - x^{2}$
$h (x) = {(- x)}^{2} - (- x)$

Note that

$\begin{array}{rcl} - f (x) & = & - (x^{2} - x) \\ = & - x^{2} + x \\ = & x - x^{2} \\ = & g (x) . \end{array}$

Thus the graph is a reflection of the graph of $f (x) = x^{2} - x$ across the x-axis.
Note that

$f (- x) = {(- x)}^{2} - (- x) = h (x) .$

Thus the graph of $h (x) = {(- x)}^{2} - (- x)$ is a reflection of the graph of $f (x) = x^{2} - x$ across the y-axis.

Vertical Stretching and Shrinking

The graph of $y = a f (x)$ can be obtained from the graph of $y = f (x)$ by:

stretching vertically for $| a | > 1$ , or
shrinking vertically for $0 < | a | < 1$
.

For $a < 0$ , the graph is also reflected across the x-axis.

(The y-coordinates of the graph of $y = a f (x)$ can be obtained by multiplying the y-coordinates of $y = f (x)$ by a.)

Horizontal Stretching and Shrinking

The graph of $y = f (c x)$ can be obtained from the graph of $y = f (x)$ by:

shrinking horizontally for $| c | > 1$ , or
stretching horizontally for $0 < | c | < 1$
.

For $c < 0$ , the graph is also reflected across the y-axis.

(The x-coordinates of the graph of $y = f (c x)$ can be obtained by dividing the x-coordinates of $y = f (x)$ by c.)

A graph of $y = g (x)$ is shown below. Use this graph to graph each of the given equations.

$f (x) = g (2 x)$
$f (x) = - 2 g (x)$
$f (x) = \frac{1}{2} g (x)$
$f (x) = g (\frac{1}{2} x)$

Since $| 2 | > 1$ , the graph of $f (x) = g (2 x)$ is a horizontal shrinking of the graph of $y = g (x)$ . The transformation divides each x-coordinate of g by 2.
Since $| - 2 | > 1$ , the graph of $f (x) = - 2 g (x)$ is a vertical stretching of the graph of $y = g (x)$ . The transformation multiplies each y-coordinate of g by 2. Since $- 2 < 0$ , the graph is also reflected across the x-axis.
Since $| \frac{1}{2} | < 1$ , the graph of $f (x) = \frac{1}{2} g (x)$ is a vertical shrinking of the graph of $y = g (x)$ . The transformation multiplies each y-coordinate of g by $\frac{1}{2}$ .
Since $| \frac{1}{2} | < 1$ , the graph of $f (x) = g (\frac{1}{2} x)$ is a horizontal stretching of the graph of $y = g (x)$ . The transformation divides each x-coordinate of g by $\frac{1}{2}$ (which is the same as multiplying by 2).

SECTION 2.6: VARIATION AND APPLICATIONS

Direct Variation

If a situation gives rise to a linear function $f (x) = k x$ , or $y = k x$ , where k is a positive constant, we say that we have direct variation, or that y varies directly as x, or that y is directly proportional to x. The number k is called the variation constant, or the constant of proportionality.

Find an equation of variation in which y varies directly as x, and $y = 24$ when $x = 8$ . Then find the value of y when $x = 5$ .

First, we have

$\begin{array}{rcll} y & = & k x & y varies directly as x . \\ 24 & = & k \cdot 8 & Substituting \\ 3 & = & k & Variation constant \end{array}$

The equation of variation is $y = 3 x$ . Now we use the equation to find the value of y when $x = 5$ :

$\begin{array}{rcll} y & = & 3 x \\ = & 3 \cdot 5 & Substituting \\ = & 15. \end{array}$

When $x = 5$ , the value of y is 15.

Inverse Variation

If a situation gives rise to a function $f (x) = k / x$ , or $y = k / x$ , where k is a positive constant, we say that we have inverse variation, or that y varies inversely as x, or that y is inversely proportional to x. The number k is called the variation constant, or the constant of proportionality.

Find an equation of variation in which y varies inversely as x, and $y = 5$ when $x = 0.1$ . Then find the value of y when $x = 10$ .

First, we have

$\begin{array}{rcll} y & = & \frac{k}{x} & y varies inversely as x . \\ 5 & = & \frac{k}{0.1} & Substituting \\ 0.5 & = & k . & Variation constant \end{array}$

The equation of variation is $y = \frac{0.5}{x}$ . Now we use the equation to find the value of y when $x = 10 :$

$\begin{array}{rcll} y & = & \frac{0.5}{x} \\ = & \frac{0.5}{10} & Substituting \\ = & 0.05. \end{array}$

When $x = 10$ , the value of y is 0.05.

Combined Variation

y varies directly as the nth power of x if there is some positive constant k such that

$y = k x^{n} .$

y varies inversely as the nth power of x if there is some positive constant k such that

$y = \frac{k}{x^{n}} .$

y varies jointly as x and z if there is some positive constant k such that

$y = k x z .$

Find an equation of variation in which y varies jointly as w and the square of x and inversely as z, and $y = 8$ when $w = 3, x = 2$ , and $z = 6$ .

First, we have

$\begin{array}{rcll} y & = & k \cdot \frac{w x^{2}}{z} \\ 8 & = & k \cdot \frac{3 \cdot 2^{2}}{6} & Substituting \\ 8 & = & k \cdot \frac{3 \cdot 4}{6} \\ 8 & = & 2 k \\ 4 & = & k . & Variation constant \end{array}$

The equation of variation is $y = 4 \frac{w x^{2}}{z}$ , or $y = \frac{4 w x^{2}}{z}$ .

Review Exercises

Determine whether the statement is true or false.

1. The greatest integer function pairs each input with the greatest integer less than or equal to that input. [2.1]
2. In general, for functions f and g, the domain of $f \circ g =$ the domain of $g \circ f$ . [2.3]
3. The graph of $y = {(x - 2)}^{2}$ is the graph of $y = x^{2}$ shifted right 2 units. [2.5]
4. The graph of $y = - x^{2}$ is the reflection of the graph of $y = x^{2}$ across the x-axis. [2.5]

Determine the intervals on which the function is (a) increasing, (b) decreasing, and (c) constant. [2.1]

Graph the function. Estimate the intervals on which the function is increasing or decreasing and estimate any relative maxima or minima. [2.1]

7. $f (x) = x^{2} - 1$
8. $f (x) = 2 - | x |$
9. Fenced Patio. Syd has 48 ft of rolled bamboo fence to enclose a rectangular patio. The house forms one side of the patio. Suppose two sides of the patio are each x feet. Express the area of the patio as a function of x. [2.1]
10. Inscribed Rectangle. A rectangle is inscribed in a semicircle of radius 2, as shown. The variable $x =$ half the length of the rectangle. Express the area of the rectangle as a function of x. [2.1]
11. Minimizing Surface Area. A container firm is designing an open-top rectangular box, with a square base, that will hold $108 {in}^{3}$ . Let $x =$ the length of a side of the base.
1. Express the surface area as a function of x. [2.1]
2. Find the domain of the function. [2.1]
3. Using the following graph, determine the dimensions that will minimize the surface area of the box. [2.1]

Graph each of the following. [2.1]

12. $f (x) = {\begin{array}{l} - x, & for x \leq - 4, \\ \frac{1}{2} x + 1, & for x > - 4 \end{array}$
13. $f (x) = {\begin{array}{l} x^{3}, & for x < - 2, \\ | x |, & for - 2 \leq x \leq 2, \\ \sqrt{x - 1}, & for x > 2 \end{array}$
14. $f (x) = {\begin{array}{l} \frac{x^{2} - 1}{x + 1}, & for x \neq - 1, \\ 3, & for x = - 1 \end{array}$
15. $f (x) = 〚 x 〛$
16. $f (x) = 〚 x - 3 〛$
17. For the function in Exercise 13, find $f (- 1), f (5), f (- 2)$ , and $f (- 3)$ .
[2.1]
18. For the function in Exercise 14, find $f (- 2), f (- 1), f (0)$ , and $f (4)$ . [2.1]

Given that $f (x) = \sqrt{x - 2}$ and $g (x) = x^{2} - 1$ , find each of the following if it exists. [2.2]

19. $(f - g) (6)$
20. $(f g) (2)$
21. $(f + g) (- 1)$

For each pair of functions in Exercises 22 and 23:

Find the domains of f, g, $f + g, f - g$ , fg, and $f / g$ . [2.2]
Find $(f + g) (x), (f - g) (x), (f g) (x)$ , and $(f / g) (x)$ . [2.2]

22. $f (x) = \frac{4}{x^{2}}, g (x) = 3 - 2 x$
23. $f (x) = 3 x^{2} + 4 x, g (x) = 2 x - 1$
24. Given the total-revenue and total-cost functions $R (x) = 120 x - 0.5 x^{2}$ and $C (x) = 15 x + 6$ , find the total-profit function $P (x)$ . [2.2]

For each function f, construct and simplify the difference quotient. [2.2]

25. $f (x) = 2 x + 7$
26. $f (x) = 3 - x^{2}$
27. $f (x) = \frac{4}{x}$

Given that $f (x) = 2 x - 1, g (x) = x^{2} + 4$ , and $h (x) = 3 - x^{3}$ , find each of the following. [2.3]

28. $(f \circ g) (1)$
29. $(g \circ f) (1)$
30. $(h \circ f) (- 2)$
31. $(g \circ h) (3)$
32. $(f \circ h) (- 1)$
33. $(h \circ g) (2)$
34. $(f \circ f) (x)$
35. $(h \circ h) (x)$

For each pair of functions in Exercises 36 and 37:

Find $(f \circ g) (x)$ and $(g \circ f) (x)$ . [2.3]
Find the domain of $f \circ g$ and the domain of $g \circ f$ . [2.3]

36. $f (x) = \frac{4}{x^{2}}, g (x) = 3 - 2 x$
37. $f (x) = 3 x^{2} + 4 x, g (x) = 2 x - 1$

Find $f (x)$ and $g (x)$ such that $h (x) = (f \circ g) (x)$ . [2.3]

38. $h (x) = \sqrt{5 x + 2}$
39. $h (x) = 4 {(5 x - 1)}^{2} + 9$

Graph the given equation and determine visually whether it is symmetric with respect to the x-axis, the y-axis, and the origin. Then verify your assertion algebraically. [2.4]

40. $x^{2} + y^{2} = 4$
41. $y^{2} = x^{2} + 3$
42. $x + y = 3$
43. $y = x^{2}$
44. $y = x^{3}$
45. $y = x^{4} - x^{2}$

Determine visually whether the function is even, odd, or neither even nor odd. [2.4]

In Exercises 50–55, test whether the function is even, odd, or neither even nor odd. [2.4]

50. $f (x) = 9 - x^{2}$
51. $f (x) = x^{3} - 2 x + 4$
52. $f (x) = x^{7} - x^{5}$
53. $f (x) = | x |$
54. $f (x) = \sqrt{16 - x^{2}}$
55. $f (x) = \frac{10 x}{x^{2} + 1}$

Write an equation for a function that has a graph with the given characteristics. [2.5]

56. The shape of $y = x^{2}$ , but shifted left 3 units
57. The shape of $y = \sqrt{x}$ , but upside down and shifted right 3 units and up 4 units
58. The shape of $y = | x |$ , but stretched vertically by a factor of 2 and shifted right 3 units

A graph of $y = f (x)$ is shown below. No formula for f is given. Graph each of the following. [2.5]

59. $y = f (x - 1)$
60. $y = f (2 x)$
61. $y = - 2 f (x)$
62. $y = 3 + f (x)$

Find an equation of variation for the given situation. [2.6]

63. y varies directly as x, and $y = 100$ when $x = 25$ .
64. y varies directly as x, and $y = 6$ when $x = 9$ .
65. y varies inversely as x, and $y = 100$ when $x = 25$ .
66. y varies inversely as x, and $y = 6$ when $x = 9$ .
67. y varies inversely as the square of x, and $y = 12$ when $x = 2$ .
68. y varies jointly as x and the square of z and inversely as w, and $y = 2$ when $x = 16$ , $w = 0.2$ , and $z = \frac{1}{2}$ .
69. Pumping Time. The time t required to empty a tank varies inversely as the rate r of pumping. If a pump can empty a tank in 35 min at the rate of 800 kL/min, how long will it take the pump to empty the same tank at the rate of 1400 kL/min? [2.6]
70. Test Score. The score N on a test varies directly as the number of correct responses a. Sam answers 29 questions correctly and earns a score of 87. What would Sam’s score have been if he had answered 25 questions correctly? [2.6]
71. Power of Electric Current. The power P expended by heat in an electric circuit of fixed resistance varies directly as the square of the current C in the circuit. A circuit expends 180 watts when a current of 6 amperes is flowing. What is the amount of heat expended when the current is 10 amperes? [2.6]
72. For $f (x) = x + 1$ and $g (x) = \sqrt{x}$ , the domain of $(g \circ f) (x)$ is which of the following? [2.3]
73. For $b > 0$ , the graph of $y = f (x) + b$ is the graph of $y = f (x)$ shifted in which of the following ways? [2.5]
74. The graph of the function f is shown below.

The graph of $g (x) = - \frac{1}{2} f (x) + 1$ is which of the following? [2.5]

Synthesis

75. Prove that the sum of two odd functions is odd. [2.2], [2.4]
76. Describe how the graph of $y = - f (- x)$ is obtained from the graph of $y = f (x)$ . [2.5]

Collaborative Discussion and Writing

77. Given that $f (x) = 4 x^{3} - 2 x + 7$ , find each of the following. Then discuss how each expression differs from the other. [1.2], [2.5]
1. $f (x) + 2$
2. $f (x + 2)$
3. $f (x) + f (2)$
78. Given the graph of $y = f (x)$ , explain and contrast the effect of the constant c on the graphs of $y = f (c x)$ and $y = c f (x)$ . [2.5]
79. Consider the constant function $f (x) = 0$ . Determine whether the graph of this function is symmetric with respect to the x-axis, the y-axis, and/or the origin. Determine whether this function is even or odd. [2.4]
80. Describe conditions under which you would know whether a polynomial function $f (x) = a_{n} x^{n} + a_{n - 1} x^{n - 1} + \dots + a_{2} x^{2} + a_{1} x + a_{0}$ is even or odd without using an algebraic procedure. Explain. [2.4]
81. If y varies directly as $x^{2}$ , explain why doubling x would not cause y to be doubled as well. [2.6]
82. If y varies directly as x and x varies inversely as z, how does y vary with regard to z? Why? [2.6]

2 Chapter Test

1. Determine the intervals on which the function is (a) increasing; (b) decreasing; (c) constant.
2. Graph the function $f (x) = 2 - x^{2}$ . Estimate the intervals on which the function is increasing or decreasing and estimate any relative maxima or minima.
3. Triangular Pennant. A softball team is designing a triangular pennant such that the height is 6 in. less than four times the length of the base b. Express the area of the pennant as a function of b.
4. Graph:

$f (x) = {\begin{array}{l} x^{2}, & for x < - 1, \\ | x |, & for - 1 \leq x \leq 1, \\ \sqrt{x - 1}, & for x > 1. \end{array}$
5. For the function in Exercise 4, find $f (- \frac{7}{8}), f (5)$ , and $f (- 4)$ .

Given that $f (x) = x^{2} - 4 x + 3$ and $g (x) = \sqrt{3 - x}$ , find each of the following, if it exists.

6. $(f + g) (- 6)$
7. $(f - g) (- 1)$
8. $(f g) (2)$
9. $(f / g) (1)$

For $f (x) = x^{2}$ and $g (x) = \sqrt{x - 3}$ , find each of the following.

10. The domain of f
11. The domain of g
12. The domain of $f + g$
13. The domain of $f - g$
14. The domain of fg
15. The domain of $f / g$
16. $(f + g) (x)$
17. $(f - g) (x)$
18. $(f g) (x)$
19. $(f / g) (x)$

For each function, construct and simplify the difference quotient.

20. $f (x) = \frac{1}{2} x + 4$
21. $f (x) = 2 x^{2} - x + 3$

Given that $f (x) = x^{2} - 1, g (x) = 4 x + 3$ , and $h (x) = 3 x^{2} + 2 x + 4$ , find each of the following.

22. $(g \circ h) (2)$
23. $(f \circ g) (- 1)$
24. $(h \circ f) (1)$
25. $(g \circ g) (x)$

For $f (x) = \sqrt{x - 5}$ and $g (x) = x^{2} + 1 :$

26. Find $(f \circ g) (x)$ and $(g \circ f) (x)$ .
27. Find the domain of $(f \circ g) (x)$ and the domain of $(g \circ f) (x)$ .
28. Find $f (x)$ and $g (x)$ such that $h (x) = (f \circ g) (x) = {(2 x - 7)}^{4}$ .
29. Determine whether the graph of $y = x^{4} - 2 x^{2}$ is symmetric with respect to the x-axis, the y-axis, and the origin.
30. Test whether the function

$f (x) = \frac{2 x}{x^{2} + 1}$

is even, odd, or neither even nor odd. Show your work.
31. Write an equation for a function that has the shape of $y = x^{2}$ , but shifted right 2 units and down 1 unit.
32. Write an equation for a function that has the shape of $y = x^{2}$ , but shifted left 2 units and down 3 units.
33. The graph of a function $y = f (x)$ is shown below. No formula for f is given. Graph $y = - \frac{1}{2} f (x)$ .
34. Find an equation of variation in which y varies inversely as x, and $y = 5$ when $x = 6$ .
35. Find an equation of variation in which y varies directly as x, and $y = 60$ when $x = 12$
. [2.6]
36. Find an equation of variation where y varies jointly as x and the square of z and inversely as w, and $y = 100$ when $x = 0.1$ , $z = 10$ , and $w = 5$
. [2.6]
37. The stopping distance d of a car after the brakes have been applied varies directly as the square of the speed r. If a car traveling 60 mph can stop in 200 ft, how long will it take a car traveling 30 mph to stop?
38. The graph of the function f is shown below.

The graph of $g (x) = 2 f (x) - 1$ is which of the following?
Synthesis
39. If (−3, 1) is a point on the graph of $y = f (x)$ , what point do you know is on the graph of $y = f (3 x)$ ?

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for Chapter 2 Summary and Review

Create new playlist

Sign In

Sign Up

Table of Contents for
Chapter 2 Summary and Review