Let’s observe the effect of the constant D in the graphs below.

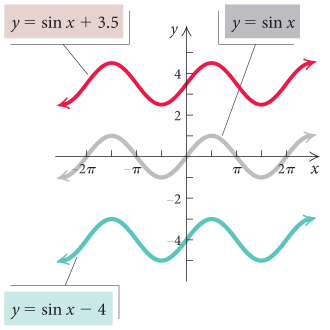
Example 1

Sketch a graph of $y=\text{sin}x+3$.

Solution

The graph of $y=\text{sin}x+3$ is a vertical translation of the graph of $y=\text{sin}x$ up 3 units. One way to sketch the graph is to first consider $y=\text{sin}x$ on an interval of length $2\pi$, say, $[0,2\pi ]$. The zeros of the function and the maximum and minimum values can be considered key points. These are

$$\left(0,0\right),\left({\displaystyle \frac{\pi }{2}},1\right),\left(\pi ,0\right),\left({\displaystyle \frac{3\pi }{2}},-1\right),\left(2\pi ,0\right)\text{.}$$

These key points are transformed up 3 units to obtain the key points of the graph of $y=\text{sin}x+3$. These are

$$\left(0,3\right),\left({\displaystyle \frac{\pi }{2}},4\right),\left(\pi ,3\right),\left({\displaystyle \frac{3\pi }{2}},2\right),\left(2\pi ,3\right)\text{.}$$

The graph of $y=\text{sin}x+3$ can be sketched on the interval $[0,2\pi ]$ and extended to obtain the rest of the graph by repeating the graph on intervals of length $2\pi$,

Next, we consider the effect of the constant A. What can we observe in the following graphs? What is the effect of the constant A on the graph of the basic function when (a)$0<A<1$? (b)$A>1$? (c)$-1<A<0$? (d) $A<-1$

The constant 2 in $y=2\text{cos}x$ has the effect of stretching the graph of $y=\text{cos}x$. vertically by a factor of 2. Since the function values of $y=\text{cos}x$. are such that $-1\le \text{cos}x\le 1$, the function values of $y=2\text{cos}x$ are such that $-2\le 2\text{cos}x\le 2$. The maximum value of $y=2\text{cos}x$ is 2, and the minimum value is $-2$. Thus the amplitude is

We draw the graph of $y=\text{cos}x$ and consider its key points,

on the interval $[0,2\pi ]$

We then multiply the second coordinates by 2 to obtain the key points of $y=2\text{cos}x$. These are

We plot these points and sketch the graph on the interval $[0,2\pi ]$. Then we repeat this part of the graph on adjacent intervals of length $2\pi ,$.

The amplitude of a graph can also be determined by finding $\left|A\right|$ from equations of the form $y=A\text{sin}\left(Bx-C\right)+D$ or $y=A\text{cos}\left(Bx-C\right)+D$. In Example 2, $y=2\text{cos}x$, $A=2$. Thus the amplitude is $\left|2\right|$ or 2.

Solution

The amplitude of the graph is $|-{\displaystyle \frac{1}{2}}|$, or ${\displaystyle \frac{1}{2}}$ The graph of $y=-{\displaystyle \frac{1}{2}}\text{sin}x$ is a vertical shrinking and a reflection of the graph of $y=\sin x$ across the x-axis. In graphing, the key points of $y=\sin x$,

$$\left(0,0\right),\left({\displaystyle \frac{\pi }{2}},1\right),\left(\pi ,0\right),\left({\displaystyle \frac{3\pi }{2}},-1\right),\left(2\pi ,0\right)\text{,}$$

are transformed to

$$\left(0,0\right),\left({\displaystyle \frac{\pi }{2}},-{\displaystyle \frac{1}{2}}\right),\left(\pi ,0\right),\left({\displaystyle \frac{3\pi }{2}},{\displaystyle \frac{1}{2}}\right),\left(2\pi ,0\right)\text{.}$$

Next, let’s consider the effect of the constant B. Changes in the constants A and D do not change the period. But what effect, if any, does a change in B have on the period of the function? Let’s observe the period of each of the following graphs.

Example 4

Sketch a graph of $y=\sin 4x$. What is the period?

Solution

The constant B has the effect of changing the period. The graph of $y=\sin 4x$ is obtained from the graph of $y=\sin x$ by shrinking the graph horizontally. The period of $y=\sin 4x$ is $|2\pi /4|,\text{or}\pi /2$. The new graph is obtained by dividing the first coordinate of each ordered-pair solution of $y=\sin x$ by 4. The key points of $y=\sin x$ are

$$\left(0,0\right),\left({\displaystyle \frac{\pi }{2}},1\right),\left(\pi ,0\right),\left({\displaystyle \frac{3\pi }{2}},-1\right),\left(2\pi ,0\right)\text{.}$$

These are transformed to the key points of $y=\sin 4x$, which are

$$\left(0,0\right),\left({\displaystyle \frac{\pi }{8}},1\right),\left({\displaystyle \frac{\pi }{4}},0\right),\left({\displaystyle \frac{3\pi }{8}},-1\right),\left({\displaystyle \frac{\pi }{2}},0\right)\text{.}$$

We plot these key points and sketch in the graph on the shortened interval $\left[0,\pi /2\right]$.

Then we repeat the graph on other intervals of length $\pi /2$

Next, we examine the effect of the constant C. The curve in each of the following graphs has an amplitude of 1 and a period of $2\pi$ but there are six distinct graphs. What is the effect of the constant C?

Example 5

Sketch a graph of $y=\text{sin}\left(x-{\displaystyle \frac{\pi }{2}}\right)$.

Solution

The amplitude is 1, and the period is $2\pi$. The graph of $y=\text{sin}\left(x-\pi /2\right)$ is obtained from the graph of $y=\text{sin}x$ by translating the graph horizontally—to the right C units if $C>0$ and to the left $\left|C\right|\text{}$ units if $C<0$. The graph of $y=\text{sin}\left(x-\pi /2\right)$ is a translation of the graph of $y=\text{sin}x$ to the right $\pi /2$ units. The value $\pi /2$ is called the phase shift. The key points of $y=\text{sin}x$,

$$\left(0,0\right),\left({\displaystyle \frac{\pi }{2}},1\right),\left(\pi ,0\right),\left({\displaystyle \frac{3\pi }{2}},-1\right),\left(2\pi ,0\right),$$

are transformed by adding $\pi /2$ to each of the first coordinates to obtain the following key points of $y=\text{sin}\left(x-\pi /2\right)$:

$$\left({\displaystyle \frac{\pi }{2}},0\right),\left(\pi ,1\right),\left({\displaystyle \frac{3\pi }{2}},0\right),\left(2\pi ,-1\right),\left({\displaystyle \frac{5\pi }{2}},0\right)\text{.}$$

We plot these key points and sketch the curve on the interval $\left[\pi /2,5\pi /2\right]$. Then we repeat the graph on other intervals of length $2\pi$.

To define phase shift, it is helpful to rewrite

Example 6

Sketch a graph of $y=\text{cos}\left(2x-\pi \right)$.

Solution

The graph of

$$y=\text{cos}\left(2x-\pi \right)$$

is the same as the graph of

$$y=1\cdot \text{cos}\left[2\left(x-{\displaystyle \frac{\pi }{2}}\right)\right]+0\text{.}$$

The amplitude is 1. The factor 2 shrinks the period by half, making the period $|2\pi /2|\text{}$, or $\pi$. The phase shift $\pi /2$ translates the graph of $y=\text{cos}2x$ to the right $\pi /2$ units. Because $D=0$, there is no vertical translation. Thus, to form the graph, we first graph $y=\text{cos}x$, followed by $y=\text{cos}2x$ and then $y=\text{cos}\left[2\left(x-\pi /2\right)\right]$.

Let’s now summarize the effect of the constants. When graphing, we carry out the procedures in the order listed. Be sure that the horizontal stretching or shrinking based on the constant B is done before the translation based on the phase shift $C/B$.

All the graphs in Examples 1–7 can be checked using a graphing calculator. Even though it is faster and more accurate to graph using a calculator, graphing by hand gives us a greater understanding of the effect of changing the constants A, B, C, and D.

Graphing calculators are especially convenient when a period or a phase shift is not a multiple of $\pi /4$.

Example 8

Graph $y=3\text{cos}2\pi x-1$. Find the amplitude, the period, and the phase shift.

Solution

First we note the following:

• $\text{Amplitude}=\left|A\right|\text{}=\left|3\right|\text{}=3$,

• $\text{Period}=\left|{\displaystyle \frac{2\pi }{B}}\right|=\left|{\displaystyle \frac{2\pi }{2\pi }}\right|=\left|1\right|=1$,

• $\text{Phase}\text{shift}={\displaystyle \frac{C}{B}}={\displaystyle \frac{0}{2\pi }}=0$.

There is no phase shift in this case because the constant $C=0$. The graph has a vertical translation of the graph of the cosine function down 1 unit, an amplitude of 3, and a period of 1, so we can use $\left[-4,4,-5,5\right]$ as the viewing window.

Now Try Exercise 31.

The transformation techniques that we learned in this section for graphing the sine and the cosine functions can also be applied in the same manner to the other trigonometric functions. Transformations of this type appear in the synthesis exercises in Exercise Set 6.6.

An oscilloscope is an electronic device that converts electrical signals into graphs like those in the preceding examples. These graphs are often called sine waves. By manipulating the controls of the oscilloscope, we can change the amplitude, the period, and the phase shift of sine waves. The oscilloscope has many applications, and the trigonometric functions play a major role in many of them.