Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

5.3 Logarithmic Functions and Graphs

Find common logarithms and natural logarithms with and without a calculator.
Convert between exponential equations and logarithmic equations.
Change logarithmic bases.
Graph logarithmic functions.
Solve applied problems involving logarithmic functions.

We now consider logarithmic, or logarithm, functions. These functions are inverses of exponential functions and have many applications.

Logarithmic Functions

We have noted that every exponential function (with a>0 $a > 0$ and a≠1 $a \neq 1$ ) is one-to-one. Thus such a function has an inverse that is a function. In this section, we will name these inverse functions logarithmic functions and use them in applications. We can draw the graph of the inverse of an exponential function by interchanging x and y.

Example 1

Graph: x=2y $x = 2^{y}$ .

Solution

Note that x is alone on one side of the equation. We can find ordered pairs that are solutions by choosing values for y and then computing the corresponding x-values.

For y=0, x=20=1 $y = 0, x = 2^{0} = 1$ .
For y=1, x=21=2 $y = 1, x = 2^{1} = 2$ .
For y=2, x=22=4 $y = 2, x = 2^{2} = 4$ .
For y=3, x=23=8 $y = 3, x = 2^{3} = 8$ .
For y=−1, x=2−1=121=12 $y = - 1, x = 2^{- 1} = \frac{1}{2^{1}} = \frac{1}{2}$ .
For y=−2, x=2−2=122=14 $y = - 2, x = 2^{- 2} = \frac{1}{2^{2}} = \frac{1}{4}$ .
For y=−3, x=2−3=123=18 $y = - 3, x = 2^{- 3} = \frac{1}{2^{3}} = \frac{1}{8}$ .

We plot the points and connect them with a smooth curve. Note that the curve does not touch or cross the y-axis. The y-axis is a vertical asymptote.

Note too that this curve is the graph of y=2x $y = 2^{x}$ reflected across the line y=x $y = x$ , as we would expect for an inverse. The inverse of y=2x $y = 2^{x}$ is x=2y $x = 2^{y}$ .

Now Try Exercise 1.

To find a formula for f−1 $f^{- 1}$ when f(x)=2x $f (x) = 2^{x}$ , we use the method discussed in Section 5.1:

1 . Replace f (x) with y : 2 . Interchange x and y : 3 . Solve for y : 4 . Replace y with f - 1 (x) : y x y f - 1 (x) = = = = 2 x 2 y the power to which we raise 2 to get x . the power to which we raise 2 to get x .

$\begin{array}{lrcl} 1. Replace f (x) with y : & y & = & 2^{x} \\ 2. Interchange x and y : & x & = & 2^{y} \\ 3. Solve for y : & y & = & the power to which we raise 2 to get x . \\ 4. Replace y with f^{- 1} (x) : & f^{- 1} (x) & = & the power to which we raise 2 to get x . \end{array}$

Mathematicians have defined a new symbol to replace the words “the power to which we raise 2 to get x.” That symbol is “log2 x $“ \log_{2} x$ ,” read “the logarithm, base 2, of x.”

Thus if f(x)=2x $f (x) = 2^{x}$ , then f−1(x)=log2 x $f^{- 1} (x) = \log_{2} x$ . For example, f−1(8)=log2 8=3 $f^{- 1} (8) = \log_{2} 8 = 3$ , because 3 is the power to which we raise 2 to get 8. Similarly, log2 13 $\log_{2} 13$ is the power to which we raise 2 to get 13. As yet, we have no simpler way to say this other than

“log2 13 $“ \log_{2} 13$ is the power to which we raise 2 to get 13.”

Later, however, we will learn how to approximate this expression using a calculator.

For any exponential function f(x)=ax $f (x) = a^{x}$ , its inverse is called a logarithmic function, base a. The graph of the inverse can be obtained by reflecting the graph of y=ax $y = a^{x}$ across the line y=x $y = x$ , to obtain x=ay $x = a^{y}$ . Then x=ay $x = a^{y}$ is equivalent to y=loga x $y = \log_{a} x$ . We read loga x $\log_{a} x$ as “the logarithm, base a, of x.”

The inverse of f(x)=ax $f (x) = a^{x}$ is given by f−1(x)=logax. $f^{- 1} (x) = \log_{a} x .$

Let’s look at the graphs of f(x)=ax $f (x) = a^{x}$ and f−1(x)=loga x $f^{- 1} (x) = \log_{a} x$ for a>1 $a > 1$ and for 0<a<1 $0 < a < 1$ .

Note that the graphs of f(x) $f (x)$ and f−1(x) $f^{- 1} (x)$ are reflections of each other across the line y=x $y = x$ .

Connecting the Concepts Comparing Exponential Functions and Logarithmic Functions

In the following table, we compare exponential functions and logarithmic functions with bases a greater than 1. Similar statements could be made for a, where 0<a<1 $0 < a < 1$ . It is helpful to visualize the differences by carefully observing the graphs.

EXPONENTIAL FUNCTION

LOGARITHMIC FUNCTION

y=ax $y = a^{x}$

f(x)=ax $f (x) = a^{x}$

a>1 $a > 1$

Continuous

One-to-one

Domain: All positive real numbers, (−∞, ∞) $(- \infty, \infty)$

Range: All real numbers, (0, ∞) $(0, \infty)$

Increasing

Horizontal asymptote is x-axis: (ax→0 as x→−∞) $(a^{x} \to 0 as x \to - \infty)$

y-intercept: (0, 1)

There is no x-intercept.

x=ay $x = a^{y}$

f−1(x)=loga x $f^{- 1} (x) = \log_{a} x$

a>1 $a > 1$

Continuous

One-to-one

Domain: All real numbers, (0, ∞) $(0, \infty)$

Range: All positive real numbers, (−∞, ∞) $(- \infty, \infty)$

Increasing

Vertical asymptote is y-axis: (loga x→−∞ as x→0+) $(\log_{a} x \to - \infty as x \to 0^{+})$

x-intercept: (1, 0)

There is no y-intercept.

Finding Certain Logarithms

Let’s use the definition of logarithms to find some logarithmic values.

Example 2

Find each of the following logarithms.

log10 10,000 $\log_{10} 10,000$
log10 0.01 $\log_{10} 0.01$
log2 8 $\log_{2} 8$
log9 3 $\log_{9} 3$
log6 1 $\log_{6} 1$
log8 8 $\log_{8} 8$

Solution

The exponent to which we raise 10 to obtain 10,000 is 4; thus log10 10,000=4 $\log_{10} 10,000 = 4$ .
We have 0.01=1100=1102=10−2 $0.01 = \frac{1}{100} = \frac{1}{10^{2}} = 10^{- 2}$ . The exponent to which we raise 10 to get 0.01 is −2, so log10 0.01=−2 $\log_{10} 0.01 = - 2$ .
8=23 $8 = 2^{3}$ . The exponent to which we raise 2 to get 8 is 3, so log2 8=3 $\log_{2} 8 = 3$ .
3=9–√=91/2 $3 = \sqrt{9} = 9^{1 / 2}$ . The exponent to which we raise 9 to get 3 is 12 $\frac{1}{2}$ , so log9 3=12 $\log_{9} 3 = \frac{1}{2}$ .
1=60 $1 = 6^{0}$ . The exponent to which we raise 6 to get 1 is 0, so log6 1=0 $\log_{6} 1 = 0$ .
5=51 $5 = 5^{1}$ . The exponent to which we raise 5 to get 5 is 1, so log5 5=1 $\log_{5} 5 = 1$ .

Now Try Exercises 9 and 15.

Examples 2(e) and 2(f) illustrate two important properties of logarithms. The property loga 1=0 $\log_{a} 1 = 0$ follows from the fact that a0=1 $a^{0} = 1$ . Thus, log5 1=0 $\log_{5} 1 = 0$ , log10 1=0 $\log_{10} 1 = 0$ , and so on. The property loga a=1 $\log_{a} a = 1$ follows from the fact that a1=a $a^{1} = a$ . Thus, log5 5=1 $\log_{5} 5 = 1$ , log10 10=1 $\log_{10} 10 = 1$ , and so on.

Converting Between Exponential Equations and Logarithmic Equations

In dealing with logarithmic functions, it is helpful to remember that a logarithm of a number is an exponent. It is the exponent y in x=ay $x = a^{y}$ . You might think to yourself, “the logarithm, base a, of a number x is the power to which a must be raised to get x.”

We are led to the following. (The symbol ↔ means $symbol \leftrightarrow means$ that the two statements are equivalent; that is, when one is true, the other is true. The words “if and only if” can be used in place of ↔ $\leftrightarrow$ .)

Example 3

Convert each of the following to a logarithmic equation.

16=2x $16 = 2^{x}$
10−3=0.001 $10^{- 3} = 0.001$
et=70 $e^{t} = 70$

Solution

10−3=0.001→log10 0.001=−3 $10^{- 3} = 0.001 \to \log_{10} 0.001 = - 3$
et=70→loge 70=t $e^{t} = 70 \to \log_{e} 70 = t$

Now Try Exercise 37.

Example 4

Convert each of the following to an exponential equation.

log2 32=5 $\log_{2} 32 = 5$
loga Q=8 $\log_{a} Q = 8$
x=logt M $x = \log_{t} M$

Solution

loga Q=8→a8=Q $\log_{a} Q = 8 \to a^{8} = Q$
x=logt M→tx=M $x = \log_{t} M \to t^{x} = M$

Now Try Exercise 45.

Finding Logarithms on a Calculator

Before calculators became so widely available, base-10 logarithms, or common logarithms, were used extensively to simplify complicated calculations. In fact, that is why logarithms were invented. The abbreviation log, with no base written, is used to represent common logarithms, or base-10 logarithms. Thus,

log x means log10 x. $\log x means \log_{10} x .$

For example, log 29 $\log 29$ means log10 29 $\log_{10} 29$ . Let’s compare log 29 $\log 29$ with log 10 $\log 10$ and log 100: $\log 100 :$

log 10 = log 10 10 = 1 log 29 = ? log 100 = log 10 100 = 2 ⎫ ⎭ ⎬ ⎪ ⎪ Since 29 is between 10 and 100, it seems reasonable that log 29 is between 1 and 2.

$\begin{array}{r} \log 10 = \log_{10} 10 = 1 \\ \log 29 = ? \\ \log 100 = \log_{10} 100 = 2 \end{array}} \begin{array}{l} \begin{array}{l} Since 29 is between 10 and 100, it seems \\ reasonable that log 29 is between 1 and 2. \end{array} \end{array}$

log 29 \approx 1.462397998 \approx 1.4624

$\log 29 \approx 1.462397998 \approx 1.4624$

rounded to four decimal places. Since 1<1.4624<2 $1 < 1.4624 < 2$ , our answer seems reasonable. This also tells us that 101.4624≈29 $10^{1.4624} \approx 29$ .

Example 5

Find each of the following common logarithms on a calculator. If you are using a graphing calculator, set the calculator in REAL mode. Round to four decimal places.

log 645,778 $\log 645, 778$
log 0.0000239 $\log 0.0000239$
log (−3) $\log (- 3)$

Solution

	FUNCTION VALUE	READOUT	ROUNDED
a)	log 645,778 $\log 645, 778$		5.8101
b)	log 0.0000239 $\log 0.0000239$		−4.6216
c)	log (−3) $\log (- 3)$	^*	Does not exist as a real number

Since 5.810083246 is the power to which we raise 10 to get 645,778, we can check part (a) by finding 105.810083246 $10^{5.810083246}$ . We can check part (b) in a similar manner. In part (c), log (−3) $\log (- 3)$ does not exist as a real number because there is no real-number power to which we can raise 10 to get −3. The number 10 raised to any real-number power is positive. The common logarithm of a negative number does not exist as a real number. Recall that logarithmic functions are inverses of exponential functions, and since the range of an exponential function is (0, ∞) $(0, \infty)$ , the domain of f(x)=loga x is (0, ∞) $f (x) = \log_{a} x is (0, \infty)$ .

Now Try Exercises 57 and 61.

Natural Logarithms

Logarithms, base e, are called natural logarithms. The abbreviation “ln” is generally used for natural logarithms. Thus,

ln x means loge x $\ln x means \log_{e} x$ .

For example, ln 53 means loge 53 $\log_{e} 53$ . On a calculator, the key for natural logarithms is generally marked . Using that key, we find that

ln 53 \approx 3.970291914 \approx 3.9703

$\ln 53 \approx 3.970291914 \approx 3.9703$

rounded to four decimal places. This also tells us that e3.9703≈53 $e^{3.9703} \approx 53$ .

Example 6

Find each of the following natural logarithms on a calculator. If you are using a graphing calculator, set the calculator in REAL mode. Round to four decimal places.

ln 645,778 $\ln 645, 778$
ln 0.0000239 $\ln 0.0000239$
ln (−5) $\ln (- 5)$
ln e $\ln e$
ln 1 $\ln 1$

Solution

	FUNCTION VALUE	READOUT	ROUNDED
a)	ln 645, 778 $\ln 645, 778$		13.3782
b)	ln 0.0000239 $\ln 0.0000239$		−10.6416
c)	ln (−5) $\ln (- 5)$	*	Does not exist
d)	ln e $ln e$		1
e)	ln 1 $\ln 1$		0

Since 13.37821107 is the power to which we raise e to get 645,778, we can check part (a) by finding e13.37821107 $e^{13.37821107}$ . We can check parts (b), (d), and (e) in a similar manner. In parts (d) and (e), note that ln e=loge e=1 $\ln e = \log_{e} e = 1$ and ln 1=loge 1=0 $\ln 1 = \log_{e} 1 = 0$ .

Now Try Exercises 65 and 67.

Changing Logarithmic Bases

Most calculators give the values of both common logarithms and natural logarithms. To find a logarithm with a base other than 10 or e, we can use the following conversion formula.

We will prove this result in the next section.

Example 7

Find log5 8 $\log_{5} 8$ using common logarithms.

Solution

First, we let a=10, b=5 $a = 10, b = 5$ , and M=8 $M = 8$ . Then we substitute into the change-of-base formula:

Since log5 8 $\log_{5} 8$ is the power to which we raise 5 to get 8, we would expect this power to be greater than 1(51=5) $1 (5^{1} = 5)$ and less than 2(52=25) $2 (5^{2} = 25)$ , so the result is reasonable.

Now Try Exercise 69.

We can also use base e for a conversion.

Example 8

Find log5 8 $\log_{5} 8$ using natural logarithms.

Solution

Substituting e for a, 5 for b, and 8 for M, we have

log 5 8 = = log e 8 log e 5 ln 8 ln 5 \approx 1.2920.

$\begin{array}{rcl} \log_{5} 8 & = & \frac{\log_{e} 8}{\log_{e} 5} \\ = & \frac{\ln 8}{\ln 5} \approx 1.2920. \end{array}$

Note that we get the same value using base e for the conversion that we did using base 10 in Example 7.

Now Try Exercise 75.

Graphs of Logarithmic Functions

Let’s now consider graphs of logarithmic functions.

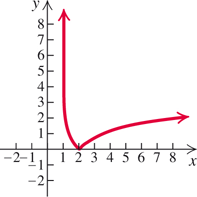
Example 9

Graph: y=f(x)=log5 x $y = f (x) = \log_{5} x$ .

Solution

The equation y=log5 x $y = \log_{5} x$ is equivalent to x=5y $x = 5^{y}$ . We can find ordered pairs that are solutions by choosing values for y and computing the corresponding x-values. We then plot points, remembering that x is still the first coordinate.

For y=0, x=50=1 $y = 0, x = 5^{0} = 1$ .
For y=1, x=51=5 $y = 1, x = 5^{1} = 5$ .
For $y = 2, x = 5^{2} = 25$ .
For $y = 3, x = 5^{3} = 125$ .
For $y = - 1, x = 5^{- 1} = \frac{1}{5}$ .
For $y = - 2, x = 5^{- 2} = \frac{1}{25}$ .

Now Try Exercise 5.

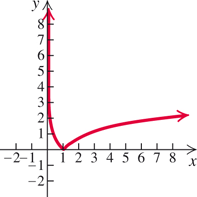
Example 10

Graph: $g (x) = \ln x$ .

Solution

To graph $y = g (x) = \ln x$ , we select values for x and use the key on a calculator to find the corresponding values of $\ln x$ . We then plot points and draw the curve.

`x`	$g (x)$
`x`	$g (x) = \ln x$
0.5	−0.7
1	0
2	0.7
3	1.1
4	1.4
5	1.6

We could also write $g (x) = \ln x$ , or $y = \ln x$ , as $x = e^{y}$ , select values for y, and use a calculator to find the corresponding values of x.

Now Try Exercise 7.

Recall that the graph of $f (x) = \log_{a} x$ , for any base a, has the x-intercept (1, 0). The domain is the set of positive real numbers, and the range is the set of all real numbers. The y-axis is the vertical asymptote.

Example 11

Graph each of the following. Before doing so, describe how each graph can be obtained from the graph of $y = \ln x$ . Give the domain and the vertical asymptote of each function.

$f (x) = \ln (x + 3)$
$f (x) = 3 - \frac{1}{2} \ln x$
$f (x) = | \ln (x - 1) |$

Solution

The graph of $f (x) = \ln (x + 3)$ is a shift of the graph of $y = \ln x$ left 3 units. The domain is the set of all real numbers greater than −3, $(- 3, \infty)$ . The line $x = - 3$ is the vertical asymptote.

`x`	$f (x)$
−2.9	−2.303
−2	0
0	1.099
2	1.609
4	1.946

The graph of $f (x) = 3 - \frac{1}{2} \ln x$ is a vertical shrinking of the graph of $y = \ln x$ , followed by a reflection across the x-axis, and then a translation up 3 units. The domain is the set of all positive real numbers, $(0, \infty)$ . The y-axis is the vertical asymptote.

`x`	$f (x)$
0.1	4.151
1	3
3	2.451
6	2.104
9	1.901

The graph of $f (x) = | \ln (x - 1) |$ is a translation of the graph of $y = \ln x$ right 1 unit. Then the absolute value has the effect of reflecting negative outputs across the x-axis. The domain is the set of all real numbers greater than 1, $(1, \infty)$ . The line $x = 1$ is the vertical asymptote.

`x`	$f (x)$
1.1	2.303
2	0
4	1.099
6	1.609
8	1.946

Now Try Exercise 89.

Applications

Example 12

Walking Speed. In a study by psychologists Bornstein and Bornstein, it was found that the average walking speed w, in feet per second, of a person living in a city of population P, in thousands, is given by the function

$w (P) = 0.37 \ln P + 0.05$

(Source: International Journal of Psychology).

The population of Billings, Montana, is 106,954. Find the average walking speed of people living in Billings.
The population of Chicago, Illinois, is 2,714,856. Find the average walking speed of people living in Chicago.

Solution

Since P is in thousands and $106,954 = 106.954$ thousand, we substitute 106.954 for P:

$\begin{array}{rcll} w (106.954) & = & 0.37 \ln 106.954 + 0.05 & Substituting \\ \approx & 1.8. & Finding the natural logarithm and \\ simplifying \end{array}$

The average walking speed of people living in Billings is about 1.8 ft/sec.
We substitute 2714.856 for P:

$\begin{array}{rcl} w (2714.856) & = & 0.37 \ln 2714.856 + 0.05 & Substituting \\ \approx & 3.0. \end{array}$

The average walking speed of people living in Chicago is about 3.0 ft/sec.

Now Try Exercise 95(d).

Example 13

Earthquake Magnitude. Measured on the Richter scale, the magnitude R of an earthquake of intensity I is defined as

$R = \log \frac{I}{I_{0}},$

where $I_{0}$ is a minimum intensity used for comparison. We can think of $I_{0}$ as a threshold intensity that is the weakest earthquake that can be recorded on a seismograph. If one earthquake is 10 times as intense as another, its magnitude on the Richter scale is 1 greater than that of the other. If one earthquake is 100 times as intense as another, its magnitude on the Richter scale is 2 higher, and so on. Thus an earthquake whose magnitude is 7 on the Richter scale is 10 times as intense as an earthquake whose magnitude is 6. Earthquake intensities can be interpreted as multiples of the minimum intensity $I_{0}$ .

The undersea Tohoku earthquake and tsunami, near the northeast coast of Honshu, Japan, on March 11, 2011, had an intensity of $10^{9.0} \cdot I_{0}$ (Source: earthquake.usgs.gov). They caused extensive loss of life and severe structural damage to buildings, railways, and roads. What was the magnitude on the Richter scale?

Solution

We substitute into the formula:

$R = \log \frac{I}{I_{0}} = \log \frac{10^{9.0} \cdot I_{0}}{I_{0}} = \log 10^{9.0} = 9.0.$

The magnitude of the earthquake was 9.0 on the Richter scale.

Now Try Exercise 97(a).

Visualizing the Graph

Match the equation or function with its graph.

$f (x) = 4^{x}$
$f (x) = \ln x - 3$
${(x + 3)}^{2} + y^{2} = 9$
$f (x) = 2^{- x} + 1$
$f (x) = \log_{2} x$
$f (x) = x^{3} - 2 x^{2} - x + 2$
$x = - 3$
$f (x) = e^{x} - 4$
$f (x) = {(x - 3)}^{2} + 2$
$3 x = 6 + y$

Answers on page A-27

5.3 Exercise Set

Graph.

1. $x = 3^{y}$
2. $x = 4^{y}$
3. $x = {(\frac{1}{2})}^{y}$
4. $x = {(\frac{4}{3})}^{y}$
5. $y = \log_{3} x$
6. $y = \log_{4} x$
7. $f (x) = \log x$
8. $f (x) = \ln x$

Find each of the following. Do not use a calculator.

9. $\log_{2} 16$
10. $\log_{3} 9$
11. $\log_{5} 125$
12. $\log_{2} 64$
13. $\log 0.001$
14. $\log 100$
15. $\log_{2} \frac{1}{4}$
16. $\log_{8} 2$
17. $\ln 1$
18. $\ln e$
19. $\log 10$
20. $\log 1$
21. $\log_{5} 5^{4}$
22. $\log \sqrt{10}$
23. ${log}_{3} \sqrt{3}$
24. $\log 10^{8 / 5}$
25. $\log 10^{- 7}$
26. $\log_{5} 1$
27. $\log_{49} 7$
28. $\log_{3} 3^{- 2}$
29. $\ln e^{3 / 4}$
30. $\log_{2} \sqrt{2}$
31. $\log_{4} 1$
32. $\ln e^{- 5}$
33. $\ln \sqrt{e}$
34. $\log_{64} 4$

Convert to a logarithmic equation.

35. $10^{3} = 1000$
36. $5^{- 3} = \frac{1}{125}$
37. $8^{1 / 3} = 2$
38. $10^{0.3010} = 2$
39. $e^{3} = t$
40. $Q^{t} = x$
41. $e^{2} = 7.3891$
42. $e^{- 1} = 0.3679$
43. $p^{k} = 3$
44. $e^{- t} = 4000$

Convert to an exponential equation.

45. $\log_{5} 5 = 1$
46. $t = \log_{4} 7$
47. $\log 0.01 = - 2$
48. $\log 7 = 0.845$
49. $\ln 30 = 3.4012$
50. $\ln 0.38 = - 0.9676$
51. $\log_{a} M = - x$
52. $\log_{t} Q = k$
53. $\log_{a} T^{3} = x$
54. $\ln W^{5} = t$

Find each of the following using a calculator. Round to four decimal places.

55. $\log 3$
56. $\log 8$
57. $\log 532$
58. $\log 93, 100$
59. $\log 0.57$
60. $\log 0.082$
61. $\log (- 2)$
62. $\ln 50$
63. $\ln 2$
64. $\ln (- 4)$
65. $\ln 809.3$
66. $\ln 0.00037$
67. $\ln (- 1.32)$
68. $\ln 0$

Find the logarithm using common logarithms and the change-of-base formula. Round to four decimal places.

69. $\log_{4} 100$
70. $\log_{3} 20$
71. $\log_{100} 0.3$
72. $\log_{π} 100$
73. $\log_{200} 50$
74. $\log_{5.3} 1700$

Find the logarithm using natural logarithms and the change-of-base formula. Round to four decimal places.

75. $\log_{3} 12$
76. $\log_{4} 25$
77. $\log_{100} 15$
78. $\log_{9} 100$

Graph the function and its inverse using the same set of axes. Use any method.

79. $f (x) = 3^{x}, f^{- 1} (x) = \log_{3} x$
80. $f (x) = \log_{4} x, f^{- 1} (x) = 4^{x}$
81. $f (x) = \log x, f^{- 1} (x) = 10^{x}$
82. $f (x) = e^{x}, f^{- 1} (x) = \ln x$

For each of the following functions, briefly describe how the graph can be obtained from the graph of a basic logarithmic function. Then graph the function. Give the domain and the vertical asymptote of each function.

83. $f (x) = \log_{2} (x + 3)$
84. $f (x) = \log_{3} (x - 2)$
85. $y = \log_{3} x - 1$
86. $y = 3 + \log_{2} x$
87. $f (x) = 4 \ln x$
88. $f (x) = \frac{1}{2} \ln x$
89. $y = 2 - \ln x$
90. $y = \ln (x + 1)$
91. $f (x) = \frac{1}{2} \log (x - 1) - 2$
92. $f (x) = 5 - 2 \log (x + 1)$

Graph the piecewise function.

93. $g (x) = {\begin{array}{l} 5, & for x \leq 0, \\ \log x + 1, & for x > 0 \end{array}$
94. $f (x) = {\begin{array}{l} 1 - x, & for x \leq - 1, \\ \ln (x + 1), & for x > - 1 \end{array}$
95. Walking Speed. Refer to Example 12. Various cities and their populations are given below. Find the average walking speed in each city. Round to the nearest tenth of a foot per second.
1. El Paso, Texas: 672,538
2. Phoenix, Arizona: 1,488,750
3. Birmingham, Alabama: 212,038
4. Milwaukee, Wisconsin: 598,916
5. Honolulu, Hawaii: 345,610
6. Charlotte, North Carolina: 775,202
7. Omaha, Nebraska: 421,570
8. Sydney, Australia: 3,908,643
96. Forgetting. Students in an accounting class took a final exam and then took equivalent forms of the exam at monthly intervals thereafter. The average score $S (t)$ , as a percent, after t months was found to be given by the function

$S (t) = 78 - 15 \log (t + 1), t \geq 0.$
1. What was the average score when the students initially took the test, $t = 0$ ?
2. What was the average score after 4 months? after 24 months?
97. Earthquake Magnitude. Refer to Example 13. Various locations of earthquakes and their intensities are given below. Find the magnitude of each earthquake on the Richter scale.
1. San Francisco, California, 1906: $10^{7.7} \cdot I_{0}$
2. Chile, 1960: $10^{9.5} \cdot I_{0}$
3. Iran, 2003: $10^{6.6} \cdot I_{0}$
4. Turkey, 1999: $10^{7.6} \cdot I_{0}$
5. Peru, 2007: $10^{8.0} \cdot I_{0}$
6. China, 2008: $10^{7.9} \cdot I_{0}$
7. Spain, 2011: $10^{5.1} \cdot I_{0}$
8. Sumatra, 2004: $10^{9.3} \cdot I_{0}$

98. pH of Substances in Chemistry. In chemistry, the pH of a substance is defined as

$pH = - \log [H^{+}],$

where $H^{+}$ is the hydrogen ion concentration, in moles per liter. Find the pH of each substance.

	SUBSTANCE	HYDROGEN ION CONCENTRATION
a)	Pineapple juice 3.8	$1.6 \times 10^{- 4}$
b)	Hair conditioner 2.9	0.0013
c)	Mouthwash 6.2	$6.3 \times 10^{- 7}$
d)	Eggs 7.8	$1.6 \times 10^{- 8}$
e)	Tomatoes 4.2	$6.3 \times 10^{- 5}$

99. Find the hydrogen ion concentration of each substance, given the pH. (See Exercise 98.) Express the answer in scientific notation.

	SUBSTANCE	pH
a)	Tap water	7 $10^{- 7}$
b)	Rainwater	5.4 $4.0 \times 10^{- 6}$
c)	Orange juice	3.2 $6.3 \times 10^{- 4}$
d)	Wine	4.8 $1.6 \times 10^{- 5}$

100. Advertising. A model for advertising response is given by the function

$N (a) = 1000 + 200 \ln a, a \geq 1,$

where $N (a)$ is the number of units sold when a is the amount spent on advertising, in thousands of dollars.
1. How many units were sold after spending $1000 $(a = 1)$ on advertising?
2. How many units were sold after spending $5000?

101. Loudness of Sound. The loudness L, in bels (after Alexander Graham Bell), of a sound of intensity I is defined to be

$L = \log \frac{I}{I_{0}},$

where $I_{0}$ is the minimum intensity detectable by the human ear (such as the tick of a watch at 20 ft under quiet conditions). If a sound is 10 times as intense as another, its loudness is 1 bel greater than that of the other. If a sound is 100 times as intense as another, its loudness is 2 bels greater, and so on. The bel is a large unit, so a subunit, the decibel, is generally used. For L, in decibels, the formula is

$L = 10 \log \frac{I}{I_{0}} .$

Find the loudness, in decibels, of each sound with the given intensity.

	SOUND	INTENSITY
a)	Jet engine at 100 ft	$10^{14} \cdot I_{0}$ 140 decibels
b)	Loud rock concert	$10^{11.5} \cdot I_{0}$ 115 decibels
c)	Bird calls	$10^{4} \cdot I_{0}$ 40 decibels
d)	Normal conversation	$10^{6.5} \cdot I_{0}$ 65 decibels
e)	Thunder	$10^{12} \cdot I_{0}$ 120 decibels
f)	Loudest sound possible	$10^{19.4} \cdot I_{0}$ 194 decibels

Skill Maintenance

Find the slope and the y-intercept of the line. [1.3]

102. $3 x - 10 y = 14$
103. $y = 6$
104. $x = - 4$

Use synthetic division to find the function values. [4.3]

105. $g (x) = x^{3} - 6 x^{2} + 3 x + 10;$ find $g (- 5)$
106. $f (x) = x^{4} - 2 x^{3} + x - 6;$ find $f (- 1)$

Find a polynomial function of degree 3 with the given numbers as zeros. Answers may vary. [4.4]

107. $\sqrt{7}, - \sqrt{7}, 0$
108. $4 i, - 4 i, 1$

Synthesis

Simplify.

109. $\frac{\log_{5} 8}{\log_{5} 2}$
110. $\frac{\log_{3} 64}{\log_{3} 16}$

Find the domain of the function.

111. $f (x) = \log_{5} x^{3}$
112. $f (x) = \log_{4} x^{2}$
113. $f (x) = \ln | x |$
114. $f (x) = \log (3 x - 4)$

Solve.

115. $\log_{2} (2 x + 5) < 0$
116. $\log_{2} (x - 3) \geq 4$

In Exercises 117–120, match the equation with one of the figures (a)–(d) that follow.

117. $f (x) = \ln | x |$
118. $f (x) = | \ln x |$
119. $f (x) = \ln x^{2}$
120. $g (x) = | \ln (x - 1) |$

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 5.3 Logarithmic Functions and Graphs

Create new playlist

Sign In

Sign Up

Table of Contents for
5.3 Logarithmic Functions and Graphs