The examples in this chapter all involve getting a number of people or things across a river under certain constraints. We use them as simple illustrations of “brute-force” search and problem decomposition.
Brute-force search means systematically trying all possibilities. Brute force does not require any skill, but it does require a lot of careful and accurate work. Using brute force is not something human beings are good at; lots of careful, accurate work is something more suited to computers. But brute force is not even practical for implementation on a computer. The amount of work involved explodes as the problem size gets bigger, making it impractical for all but toy problems. Nevertheless, it is useful to know what brute force entails, because it helps to understand the nature of problem solving.
Problem decomposition is something we humans are much better at. Problem decomposition involves exploiting the structure of a problem to break it down into smaller, more manageable problems. Once a problem has been broken down in this way, brute force may be applicable. Indeed, it is often the case that, ultimately, brute force is the only solution method, so we cannot dispense with it. But it is better to explore problem decomposition first, postponing the use of a brute-force search for as long as possible.
All river-crossing problems have an obvious structural property, namely the symmetry between the two banks of the river. The exploitation of symmetry is an important problem-solving technique, but is often overlooked, particularly when using brute force. You may already have seen the problems, or similar ones, elsewhere. As illustrations of brute-force search – which is how their solutions are often presented – they are extremely uninteresting! However, as illustrations of the use of symmetry, combined with problem decomposition, they have startling, hidden beauty.
An important issue that emerges in this chapter is naming the elements of a problem. Deciding on what and how names should be introduced can be crucial to success. We shall see how inappropriate or unnecessary naming can increase the complexity of a problem, making it impossible to solve even with the aid of a very powerful computer.
3.1 PROBLEMS
As in Chapter 2, we begin the chapter by listing a number of problems that will be discussed later. Tackling the problems first before reading on is an aid to a better understanding of their solutions.
1. Goat, Cabbage and Wolf A farmer wishes to ferry a goat, a cabbage and a wolf across a river. However, his boat is only large enough to take one of them at a time, making several trips across the river necessary. The goat should not be left alone with the cabbage (otherwise, the goat would eat the cabbage), and the wolf should not be left alone with the goat (otherwise, the wolf would eat the goat).
How can the farmer achieve the task?
2. The Nervous Couples Three couples (president and bodyguard) wish to cross a river. They have one boat that can carry at most two people, making several trips across the river necessary. The presidents are nervous of the other presidents’ bodyguards so that none is willing to be on a bank or in the boat with another president’s bodyguard unless their own bodyguard is also present.
How can all three couples get across the river?
3. Adults and Children A group of adults and children are on one side of a river. They have one boat that is only big enough to accommodate one adult or two children.
How can all the adults and all the children cross the river? Make clear any assumptions you are obliged to make.
4. Overweight Ann, Bob, Col and Dee are on one side of a river. They have one rowing boat that can carry at most 100 kilos. Ann weighs 46 kilos; Bob, 49; Col, 52; Dee, 100. Bob cannot row.
How can they all get to the other side?
3.2 BRUTE FORCE
3.2.1 Goat, Cabbage and Wolf
The goat–cabbage–wolf problem is often used to illustrate brute-force search. Our main purpose in showing the brute-force solution is to illustrate the pitfalls of poor problem-solving skills. Additionally, we introduce some terminology that is useful when discussing the efficiency of a particular solution to a problem.
A farmer wishes to ferry a goat, a cabbage and a wolf across a river. However, his boat is only large enough to take one of them at a time, making several trips across the river necessary. The goat should not be left alone with the cabbage (otherwise, the goat would eat the cabbage), and the wolf should not be left alone with the goat (otherwise, the wolf would eat the goat).
How can the farmer achieve the task?
The problem involves four individuals, and each is at one of the two river banks. This means that we can represent a state by four variables, each of which has one of two values. We call the variables f (for farmer), g (for goat), c (for cabbage) and w (for wolf), and we call their possible values L (for left) and R (for right). A value of R means “at the right bank”. A value of L means “at the left bank”. Note that the boat is always where the farmer is, so we do not need to introduce a variable to represent its position.
A brute-force search involves constructing a state-transition graph that models all possible states, and ways of changing from one state to another – the state transitions. In the goat–cabbage–wolf problem, a state describes on which bank each of the four individuals can be found. A state transition is a change of state that is allowed by the problem specification. For example, two states between which there is a valid state transition are:
1. All four are at the left bank.
2. The farmer and goat are at the right bank, while the cabbage and wolf are at the left bank.
For the simplest problems, a diagram can be drawn depicting a state-transition graph. The states are drawn as circles, and the state transitions are drawn as lines connecting the circles. The lines have arrows on them if some state transitions are not reversible; if so, the diagram is called a directed graph. If all state transitions are reversible, the arrows are not necessary and the diagram is called an undirected graph. We draw a state-transition graph to demonstrate the brute-force solution to this problem.
If four variables can each have one of two values, there are 24 (i.e. 16) different combinations of values. However, in this problem some of these combinations are excluded. The requirement that the goat cannot be left alone with the cabbage is expressed by the system invariant
f = g = c ![]() g ≠ c.
g ≠ c.
![]() Read Chapter 16 for detailed definitions of directed and undirected graphs. The problems discussed here are all path-finding problems. Chapter 16 formulates such problems algebraically.
Read Chapter 16 for detailed definitions of directed and undirected graphs. The problems discussed here are all path-finding problems. Chapter 16 formulates such problems algebraically.
That is, either the farmer, the goat and the cabbage are all on the same bank (f = g = c), or the goat and cabbage are on different banks (g ≠ c). This excludes cases where g and c are equal, but different from f. Similarly, the requirement that the goat cannot be left alone with the wolf is expressed by the system invariant
f = g = w e ![]() g ≠ w.
g ≠ w.
If we list all states, eliminating the ones that are not allowed, the total reduces to 10. Table 3.1 shows the ten different combinations. (Notice that when f and g are equal all combinations of c and w are allowed; when f and g are different, c and w are required to be equal.)
![]() Table 3.1: Goat–cabbage–wolf problem: allowed states.
Table 3.1: Goat–cabbage–wolf problem: allowed states.
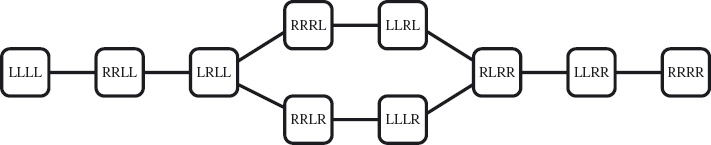
Now, we enumerate all the possible transitions between these states. The graph in Figure 3.1 does just this. The nodes of the graph – the boxes – represent states, and the edges of the graph – the lines connecting the boxes – represent transitions. There are no arrows on the edges because each transition can be reversed.
At the left, the node labelled “LLLL” represents the state where all four are on the left bank. The only allowed transition from this state is to the state where the farmer
![]() Figure 3.1: Goat–cabbage–wolf problem.
Figure 3.1: Goat–cabbage–wolf problem.
and goat are at the right bank, and the cabbage and wolf are at the left bank. This is represented by the line connecting LLLL to RRLL.
From the graph, it is clear that there are two (minimal) solutions to the problem. Each solution is given by a path through the graph from LLLL to RRRR. The upper path gives the following solution:
1. The farmer takes the goat to the right bank and returns alone. This is the path from LLLL to LRLL.
2. The farmer takes the cabbage to the right bank and returns with the goat. This is the path from LRLL to LLRL.
3. The farmer takes the wolf to the right bank and returns alone. This is the path from LLRL to LLRR.
4. The farmer takes the goat to the right bank. This is the path from LLRR to RRRR.
The alternative solution, given by the lower path, interchanges “cabbage” and“wolf” in the second and third steps.
3.2.2 State-Space Explosion
There is often a tendency to apply brute force without thinking when faced with a new problem. However, it should be used only where it is unavoidable. Brute force is useful only for very simple problems. For other problems, the search space quickly becomes much too large. In the jargon used by computing scientists, brute force does not “scale up” to larger problems. The goat–cabbage–wolf problem is not representative; the above – thoughtless! – solution has a manageable number of states, and a manageable number of transitions.
We can see how quickly the search space can grow by analysing what is involved in using brute force to solve the remaining problems in Section 3.1.
In the “overweight” problem, there are four named individuals and no restrictions on their being together on the same side of the bank. So, there are 16 possible states; unlike in the goat–cabbage–wolf problem, no restriction on the size of the state space is possible. Also, from the initial state there are four different transitions; from most other states, there are at least two transitions. So, the total number of transitions is large, too large even for the most diligent problem-solvers.
![]() The mathematical theory used to count the number of states is called combinatorics. Here we are only using very simple combinatorial reasoning. In the “overweight” problem, a state is a function giving, for each individual, which side of the bank that individual is on. Section 12.4.2 discusses how to count the number of functions of a given type.
The mathematical theory used to count the number of states is called combinatorics. Here we are only using very simple combinatorial reasoning. In the “overweight” problem, a state is a function giving, for each individual, which side of the bank that individual is on. Section 12.4.2 discusses how to count the number of functions of a given type.
The situation in an unskilled solution of the “nervous-couples” problem is even worse. Six individuals are involved, each of whom can be on either side of the river bank. If we give each individual a distinct name, the number of states is 26 (i.e. 64). That is an impossible number for most human beings to cope with, and we have not begun to count the number of transitions. In another variation on the nervous-couples problem, there are five couples, and the boat can take three people at a time. That means, if all are named, there are are 210 (i.e. 1024) different states, and a yet larger number of transitions. Take note: these are “toy” problems, not real problems.
The “adults-and-children” problem illustrates another failing of brute force, namely that it can be applied only in specific cases, and not in the general case. The number of adults and children is not specified in this problem. Yet, it is in fact the easiest of all to solve.
The use of a computer to perform a brute-force search shifts the meaning of what is a “small” problem and what is a “large” problem, but not as much as one might expect. The so-called “state-space explosion problem” gets in the way. The river-crossing problems illustrate state-space explosion well. If there are n individuals in such a problem, there are, in principle, 2n different states to be considered. But, even for quite small n, 2n is a very large number. We speak of an “exponential” growth in the number of states (n is the exponent in 2n). Whenever the state space of a class of problems grows exponentially, it means that even the largest and fastest supercomputers can tackle only quite small instances.
Drawing state-transition diagrams is equally ineffective. A diagram can occasionally be used to illustrate the solution of a simple, well-chosen problem. But constructing a diagram is rarely helpful in problem solving. Instead, diagrams quickly become a problem in themselves: apart from the size of paper needed, how are the nodes to be placed on the paper so that the diagram becomes readable?
3.2.3 Abstraction
The state-space explosion is often caused by a failure to properly analyse a problem; a particularly frequent cause is unnecessary or inappropriate naming. The goat–cabbage– wolf problem is a good example.
In the goat–cabbage–wolf problem, distinct names are given to the “farmer”, the “goat”, the “cabbage” and the “wolf”, but do we really need to distinguish between all four? In the discussion of the state space, we remarked on a “similarity” between the wolf and the cabbage. Specifically, the goat cannot be left with either the wolf or the cabbage. This “similarity” also emerged in the solution: two solutions were obtained, symmetrical in the interchange of “wolf” and “cabbage”. Why, then, are the “wolf” and the “cabbage” distinguished by giving them different names?
Let us restate the problem, this time with a naming convention that omits the unnecessary distinction between the wolf and the cabbage. In the restated problem, we call the goat an “alpha” and the cabbage and the wolf “betas”.
A farmer wishes to ferry an alpha and two betas across a river. However, his boat is large enough to take only one of them at a time, making several trips across the river necessary. Also, an alpha should not be left alone with a beta.
How can the farmer achieve the task?
Now the problem becomes much easier to solve. Indeed, there is only one solution: take the alpha across, and then one beta across, returning with the alpha. Then take the second beta across, followed by the alpha. Because there is only one solution, it is easy to discover, and it is unnecessary to construct a state-transition diagram for the problem.
The problem-solving principle that we learn from this example is worth emphasising: avoid unnecessary or inappropriate naming. When elements of a problem are given individual names, it distinguishes them from other elements of the problem, and adds to the size of the state space. The process of omitting unnecessary detail and reducing a problem to its essentials is called abstraction. Poor solutions to problems are ones that fail to “abstract” adequately, making the problem more complicated than it really is. We encounter the importance of appropriate naming time and again in the coming chapters. Bear it in mind as you read.
![]() The crux of this simplification is that the relation “not with” is symmetric. It is the so-called complement (negation) of the relation “with”, which is also symmetric. Indeed, a relation is symmetric exactly when its complement is symmetric. See Section 12.7.2 for more on symmetric relations.
The crux of this simplification is that the relation “not with” is symmetric. It is the so-called complement (negation) of the relation “with”, which is also symmetric. Indeed, a relation is symmetric exactly when its complement is symmetric. See Section 12.7.2 for more on symmetric relations.
We will see more examples where it is useful to spot that a crucial relation is symmetric.
3.3 NERVOUS COUPLES
Often, the inherent structure of a problem facilitates its decomposition into smaller problems. The smaller problems can then be further decomposed until they become sufficiently manageable to be solvable by other means, perhaps even by brute force. Their solutions are then put together to form a solution to the original problem.
The nervous-couples problem is an excellent example. It can be solved by brute force, making it decidedly boring, but it can be solved much more effectively, making use of general problem-solving principles.
Recall its statement:
Three couples (president and bodyguard) wish to cross a river. They have one boat that can carry at most two people, making several trips across the river necessary. The presidents are nervous of the other presidents’ bodyguards so that none is willing to be on a bank or in the boat with another president’s bodyguard unless their own bodyguard is also present.
How can all three couples get across the river?
3.3.1 What Is the Problem?
Let us begin by determining the essence of the problem.
Suppose there is one boat that can carry two “things”, and there are no other restrictions. Then, clearly, it is possible to get any number of “things” across the river: repeat the process of letting two cross from left to right, followed by one returning from right to left, until at most two remain on the left bank.
Now, by replacing “thing” by “couple”, we infer that a boat that can carry two couples at one crossing can be used to ferry an arbitrary number of couples across the river. (After all, couples are not nervous of each other! ) Since a couple is two people, this means that a boat that can carry four people is sufficient to ferry an arbitrary number of couples across the river.
This simple analysis gives us a different slant on the problem. Rather than tackle the problem as stated, we can tackle a related problem, namely, what is the minimum capacity needed to ferry three couples across the river? More generally, what is the minimum capacity needed to ferry n couples across the river? Obviously, the minimum capacity is at least two (since it is not possible to ferry more than one person across a river in a boat that can only carry one person at a time), and we have just shown that the minimum capacity is at most four.
Alternatively, we can specify the capacity of the boat and ask what is the maximum number of couples that can be ferried across with that capacity. If the capacity is one (or less) the maximum number of couples is zero, and if the capacity is four, there is no maximum. So, the question is how many couples can be ferried with a boat of capacity two and how many couples can be ferried with a boat of capacity three.
The new problems look more difficult than the original. In the original problem, we are given the answer – in the case of three couples, a boat with capacity two is needed – and we are required to give a constructive proof that this is the case. But there is often an advantage in not knowing the answer because we can sometimes gain insight by generalising and then first solving simpler instances of the general problem.
3.3.2 Problem Structure
The structure of this problem suggests several ways in which it might be decomposed. First, there are three couples. This suggests seeking a solution that gets each couple across in turn. That is, we decompose the problem into three subproblems: get the first couple across, get the second couple across, and get the third couple across.
Another decomposition is into presidents and bodyguards. We could try first getting all the presidents across, followed by all the bodyguards. Alternatively, we could try first getting all the bodyguards across, followed by all the presidents.
Getting all the presidents across while their bodyguards remain at the left bank turns out to be easy. The reason is that, if the bodyguards all stay in one place, there is no difficulty in transferring the presidents away from them. Getting all the bodyguards across first, while their presidents stay at the left bank, seems much harder. On the other hand, getting the bodyguards to join their presidents may prove to be harder than getting the presidents to join their bodyguards. It is not immediately clear that either strategy will work.
There is, however, one key structural property of the problem that we have not yet considered. It is the symmetry between the left and right banks. The process of getting a group of people from left to right can always be reversed; the result is a process for getting the same group of people from right to left. Perhaps a symmetric solution is possible. If that is the case, we halve our effort, and that is a major saving. This is indeed what we do.
(The state-transition diagram for the goat–cabbage–wolf problem exhibits the left–right symmetry well. The diagram also illustrates the symmetry between the cabbage and wolf. Both symmetries were to be expected from the problem statement; by ignoring them and using brute force, we lost the opportunity of a reduction in effort.)
3.3.3 Denoting States and Transitions
We begin by introducing some local notation to make the solution strategy precise. The introduction of notation involves naming the elements of the problem that we want to distinguish. As discussed earlier, this is a crucial step in finding a solution. Here, we use letters B, P and C to mean bodyguard, president and couple, respectively. These are preceded by a number; for example, 2B means two bodyguards, 3C means three couples and 1C,2B means one couple and two bodyguards. We exploit the notation to distinguish between couples and individuals; for example, 1B,1P means a bodyguard and president who do not form a couple, while 1C means a bodyguard and president who do form a couple. Note that we do not name the individual people as we do, for example, in the “overweight” problem. It is only the numbers of bodyguards, presidents and couples that is relevant to the problem’s solution. Number is an extremely important mathematical abstraction.
We distinguish between states and actions.
A state describes a situation in which each individual (bodyguard or president) is at one of the banks. A state is denoted by two sequences separated by bars. An example is 3B || 3P, which denotes the state in which all three bodyguards are at the left bank, and all three presidents are at the right bank. A second example of a state is 1C,2B || 2P, which denotes the state in which one couple and two bodyguards are at the left bank and two presidents are at the right bank. The starting state is thus 3C || and the required finishing state is || 3C.
An action transports some individuals across the river. An example is 3B |2P| 1P; this denotes the action of transporting two presidents across the river, leaving three bodyguards at the left bank and one president at the right bank.
Note that the notation for states and actions does not specify the position or direction of the boat, and, taken out of context, could be ambiguous. Since the position of the boat must alternate between the left bank and the right bank, this ambiguity is easily resolved.
The notation allows valid and invalid states/actions to be easily identified. For example, 1C,1P || 1C,1B is invalid (because there is a president who is alone on the same side of the river as another president’s bodyguard). Also, 3B |3P| is invalid because the boat can carry at most two people.
In general, a complete, detailed solution to the problem is a sequence, beginning with the state 3C || and ending with the state || 3C, that alternates between valid states and actions.
An action results in a change of state. (In the terminology of state-transition diagrams, an action effects a transition between states.) Additional notation helps to express the result of actions. If p and q denote states, and S denotes a sequence of actions,
{ p }
S
{ q }
is the property that execution of S beginning in state p results in state q. So, for example,
{ 2C,1B || 1P }
3B |2P| 1P
{ 3B || 3P }
is the property that, beginning in the state where two couples and one bodyguard are at the left bank, letting two presidents cross will result in a state in which all three bodyguards are at the left bank, while all three presidents are at the right bank.
Of course, we should always check the validity of such properties. It is easy to make a mistake and make an invalid claim. Care is needed, but the checks are straightforward.
3.3.4 Problem Decomposition
Using this notation we can express our strategy for decomposing the problem. The goal is to construct a sequence of actions S0 satisfying
{ 3C || } S0 {|| 3C }.
Our strategy can be summarised as exploiting two properties of the problem:
- the left–right symmetry;
- the fact that it is easy to get the presidents from one side to the other while their bodyguards remain on one bank.
This strategy is realised by decomposing S0 into three sequences S1, S2 and S3 such that
{ 3C || } S1 { 3B || 3P },
{ 3B || 3P } S2 { 3P || 3B },
{ 3P || 3B } S3 {|| 3C }.
Sequence S1 changes the state from the start state to the state where all the presidents are at the right bank and all the bodyguards are at the left bank. Sequence S2 changes the end state of S1 to the state where the positions of the presidents and bodyguards are reversed. Finally, sequence S3 changes the end state of S2 to the state where everyone is at the right bank. So, doing S1 followed by S2 followed by S3, which we denote by S1; S2; S3, will achieve the objective of changing the state from the start state (everyone is at the left bank) to the final state (everyone is at the right bank).
The decomposition is into three components because we want to exploit symmetry, but, clearly, an odd number of crossings will be necessary. Symmetry is captured by making the function of S3 entirely symmetrical to the function of S1. If we consider the reverse of S3, its task is to transfer all the presidents from the right bank to the left bank. So, if we construct S1, it is a simple task to construct S3 directly from it.
We now have to tackle the problem of constructing S1 and S2.
As mentioned earlier, getting all the presidents across the river, leaving their bodyguards at the left bank is easy. Here is how it is achieved.
{ 3C || }
1C,2B |2P|
; { 1C,2B || 2P }
1C,2B |1P| 1P
; { 2C,1B || 1P }
3B |2P| 1P
{ 3B || 3P }.
That is,
{ 3C || } 1C,2B |2P| ; 1C,2B |1P| 1P ; 3B |2P| 1P { 3B || 3P }.
As discussed above, the sequence S3 is the reverse of S1:
{ 3P || 3B } 1P |2P| 3B ; 1P |1P| 1C,2B ; |2P| 1C,2B {|| 3C }.
We are now faced with the harder task of constructing S2. We seek a solution that is symmetrical about the middle.
Note that, for S2, the starting position of the boat is the right bank, and its finishing position is the left bank. This is a requirement for S2 to follow S1 and be followed by S3. The length of S2 must also be odd.
Again, we look for a decomposition into three subsequences. If the solution is to remain symmetric, the middle action must be 1C |1C| 1C because this is the only action that is symmetric between left and right. That is, the solution must take the following form:
{ 3B || 3P }
T1
; 1C |1C| 1C
; T2
{ 3P || 3B }.
However, the middle action may be a left-to-right crossing or a right-to-left crossing; which is not immediately clear. The task is now to construct the symmetric sequences of actions T1 and T2.
If the middle action is from right to left, the action must be preceded by the state 1C || 2C and results in the state 2C || 1C. Vice versa, if the middle action is from left to right, the action must be preceded by the state 2C || 1C and results in the state 1C || 2C. There is little alternative but to use brute-force search to try to determine which can be achieved, but now the state space is relatively small.
Fortunately, T1 is soon discovered. It consists of just two actions:
{ 3B || 3P }
3B |1P| 2P
; { 1C,2B || 2P }
1C |2B| 2P
{ 1C || 2C }.
Symmetrically, for T2 we have:
{ 2C || 1C }
2P |2B| 1C
; { 2P || 1C,2B }
2P |1P| 3B
{ 3P || 3B }.
Finally, putting everything together, we have the complete solution to the nervous-couples problem:
{ 3C || }
1C,2B |2P| ; 1C,2B |1P| 1P ; 3B |2P| 1P
; { 3B || 3P }
3B |1P| 2P ; 1C |2B| 2P
; { 1C || 2C }
1C |1C| 1C
; { 2C || 1C }
2P |2B| 1C ; 2P |1P| 3B
; { 3P || 3B }
1P |2P| 3B ; 1P |1P| 1C,2B ; |2P| 1C,2B
{ || 3C }.
(In this solution, not all intermediate states are shown. This helps to document the solution, by recording the main steps, but not every step. Too much detail in program documentation can be a hindrance.)
3.3.5 A Review
Pause awhile to review the method used to solve the nervous-couples problem, so that you can fully appreciate how much more effective it is than brute-force search.
The construction seeks at each stage to exploit the symmetry between the left and right banks. Since the number of crossings will inevitably be odd, each decomposition is into three subsequences, where the first and last are “mirror images” in some sense. The middle crossing must be 1C |1C| 1C since this is the only symmetric action, but the direction of crossing is not immediately obvious. Naming the unknown sequences, and formally specifying their function using the { p } S { q } notation, helps to clarify what has to be achieved and to avoid error.
The final solution involves 11 crossings. That is too many to commit to memory. But, because the solution method is well structured, it is easy to remember, making a reconstruction of the solution straighforward. Moreover, the solution to the problem cannot be used in other contexts, but the solution method can. For the proof of the pudding, solve the following related problem:
Exercise 3.1 (Five-Couple Problem) There are five nervous couples, and their boat can carry a maximum of three individuals. Determine how to transport all the couples across the river.
Exercise 3.2 (Four-Couple Problem) Unfortunately, the symmetry between the left and right banks does not guarantee that every river-crossing problem has a symmetric solution. The case of four couples and a three-person boat has a solution, but it is not symmetric. Determine a solution to this problem.
The following hint may be helpful. Four is less than five, and, by now, you will have solved the problem of transporting five couples across the river (Exercise 3.1). Try to modify the solution for five couples to obtain a solution for four. You should be able to find two solutions in this way, one being obtained from the other by reversing left and right.
(In general, individual solutions need not be symmetric, but the set of solutions is symmetric. That is, there is a transformation from solutions to solutions based on reversing left and right. A solution is symmetric if this transformation maps the solution to itself.)
Exercise 3.3 (Project) The goal of this project is to give first-hand experience of the combinatorial explosion that occurs when using brute-force search. This is done by asking you to construct the state-transition diagrams for the three- and five-couple problems – this is feasible because they are not too large – and then asking you to calculate the number of states if all the individuals are named. (It would be entirely infeasible to draw the state diagram.) You are also asked to calculate the number of different ways of getting the couples across, first when individuals are not distinguished and then when they are distinguished. You will need to study Chapter 16, in particular Section 16.4.1, in order to tackle some parts of the project.
(a) How many states are there in the state-transition diagram for the problem of three couples?
How many states are there in the state-transition diagram for the problem of four couples? How many states are there in the state-transition diagram for the problem of five couples?
(b) Construct the state-transition diagram for the problem of five couples with a boat of capacity three.
(c) How many different ways are there of getting three couples across the river in a boat of capacity two using the minimum number of crossings?
How many different ways are there of getting five couples across the river in a boat of capacity three using the minimum number of crossings?
(d) Suppose each president and each bodyguard is named (e.g. Ann and Bob, Con and Dan, etc.) and states are distinguished by the names of the individuals on each side of the river. How many states would there then be in the state-transition diagram for the problem of five couples with a boat of capacity three? How many different ways would there be of getting them all across the river in a boat of capacity three using the minimum number of crossings?
3.4 RULE OF SEQUENTIAL COMPOSITION
The { p } S { q } notation we used for solving the nervous-couples problem is the notation used for specifying and constructing computer programs. It is called a Hoare triple.(The British computing scientist Sir Tony Hoare introduced the notation in his pioneering work on techniques for formally verifying the correctness of computer programs.)
A computer program is specified by a relation between the input values and the output values. The allowed input values are specified by a so-called precondition, p, and the output values are specified by a postcondition, q. Preconditions and postconditions are properties of the program variables.
If S is a program and p and q are properties of the program variables,
{ p } S { q }
means that execution of S begun in a state that satisfies property p is guaranteed to terminate in a state that satisfies property q. For example, a program to compute the remainder r and dividend d after dividing number M by number N would have precondition
N ≠ 0
(since dividing by 0 is not allowed) and postcondition
M = N×d + r ∧ 0 ≤ r < N.
If the program is S, the specification of the program is thus
{ N ≠ 0 } S { M = N×d + r ∧ 0 ≤ r < N }.
Programs are often composed by sequencing; the individual components are executed one after the other. A semicolon is usually used to denote sequencing. Thus, if S1, S2 and S3 are programs, S1; S2; S3 denotes the program that is executed by first executing S1, then executing S2, and then executing S3.This is called the sequential composition of S1, S2 and S3.
A sequential composition is introduced into a program when the problem it solves is decomposed into subproblems. In the case of a decomposition into two components, given a precondition p and a postcondition q, an intermediate condition r, say, is invented. The problem of constructing a program S satisfying the specification
{ p } S { q }
is then resolved by letting S be S1; S2 and constructing S1 and S2 to satisfy the specifications
{ p } S1 { r }
and
{ r } S2 { q }.
The intermediate condition r thus acts as postcondition for S1 and precondition for S2.
If the problem is decomposed into three subproblems, two intermediate conditions are needed. This is what we did in solving the nervous-couples problem. The initial problem statement has precondition 3C || and postcondition || 3C. The intermediate conditions 3B || 3P and 3P || 3B were then introduced in order to make the first decomposition.
There are different ways of using the rule of sequential composition. The structure of the given problem may suggest an appropriate intermediate condition. Alternatively, the problem may suggest an appropriate initial computation S1; the task is then to identify the intermediate condition and the final computation S2. Conversely, the problem may suggest an appropriate final computation S2; then the task becomes one of identifying the intermediate condition r and the initial computation S1. The following exercises provide practice in the technique.
Exercise 3.4 This exercise is about a simple solitaire-like game on a one-dimensional board.
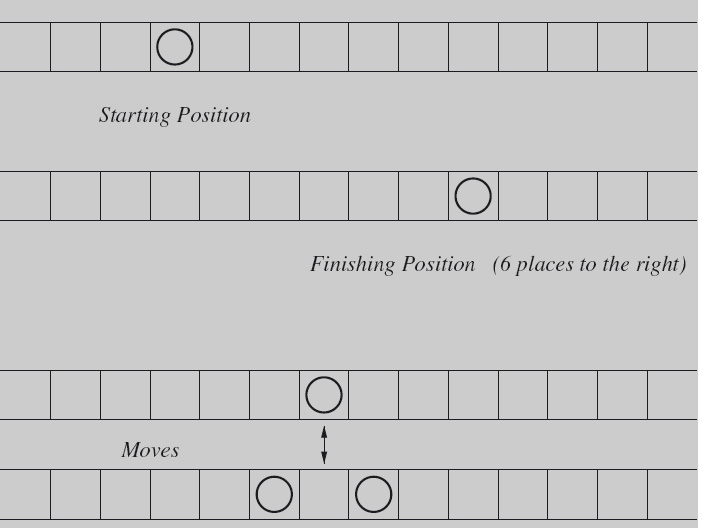
Suppose a long strip of paper has been divided into squares. A single coin is placed on one of the squares. The objective is to displace the coin six places to the right using a sequence of moves, which we now define. The moves are reversible; a move is to replace a single coin on one square by two coins, one on each of the two adjacent squares. The reverse move (which is also allowed) is to replace two coins on squares that are separated by just one square by one coin on the separating square. No other moves are possible, and there are no other restrictions on moves. (The number of coins on any one square is unlimited, and it is not necessary for the separating square in a reverse move to be empty.)
Figure 3.2 shows the starting position, the finishing position and the allowed moves. (The double arrow indicates that the move is reversible.)
![]() Figure 3.2: A one-dimensional game of solitaire.
Figure 3.2: A one-dimensional game of solitaire.
Exploit the insights from this chapter. The moves exhibit a symmetry property, which you should exploit by considering (symmetrical) sequences of moves from the start and finish positions. Also, decompose the problem.
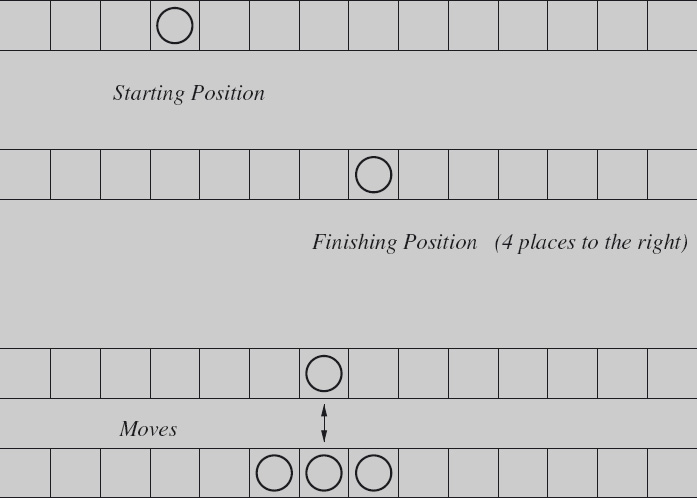
Exercise 3.5 This problem is like the one in Exercise 3.4 but the moves and goal are different. Figure 3.3 illustrates the start and finish positions and the allowed moves.
As in Exercise 3.4, a single coin is placed on one of the squares but this time the objective is to displace it four places to the right. The allowed moves are slightly different. If there is at least one coin on any square, two extra coins can be added in the two adjacent squares. The reverse move is also possible: if there are three adjacent coins, two outer coins can be removed leaving just the middle coin.
![]() Figure 3.3: Another one-dimensional game of solitaire.
Figure 3.3: Another one-dimensional game of solitaire.
The same hint applies to this problem as for Exercise 3.4: exploit symmetry and decompose.
Exercise 3.6 This problem is like the ones in Exercises 3.4 and 3.5 but, again, the moves and goal are different.
As in those problems, a single coin is placed on one of the squares. The allowed moves are slightly different. If there is at least one coin on any square, three extra coins can be added, one in the square itself and one in each of the two adjacent squares. The reverse move is also possible: if there are three adjacent coins, and the middle square has at least two coins, three adjacent coins can be removed.
The question is to find the smallest number m such that it is possible to displace the coin by m spaces.
3.5 THE BRIDGE PROBLEM
Recall the bridge problem posed in Chapter 1:
Four people wish to cross a bridge. It is dark, and it is necessary to use a torch when crossing the bridge, but they have only one torch between them. The bridge is narrow, and only two people can be on it at any one time. The four people take different amounts of time to cross the bridge; when two cross together they proceed at the speed of the slowest. The first person takes 1 minute to cross, the second 2 minutes, the third 5 minutes and the fourth 10 minutes. The torch must be ferried back and forth across the bridge, so that it is always carried when the bridge is crossed.
Show that all four can cross the bridge within 17 minutes.
The problem is reputed to have been used by a major software manufacturer in interviews for software engineers; nowadays its solution is considered to be too well known for such use. In this section, we hypothesise how the interview might proceed assuming the candidate is well acquainted with algorithmic problem-solving techniques. Rather than consider the specific problem above, let us introduce input parameters for the crossing times. In this way, the problem becomes:
Four people wish to cross a bridge. It is dark, and it is necessary to use a torch when crossing the bridge, but they have only one torch between them. The bridge is narrow, and only two people can be on it at any one time. The four people take t.1, t.2, t.3 and t.4 minutes to cross the bridge; when two cross together they proceed at the speed of the slowest. The torch must be ferried back and forth across the bridge, so that it is always carried when the bridge is crossed.
Construct an algorithm that will get all four across the bridge in the shortest possible time.
![]() The notation “t.1” makes clear that t is a function from people to times. The infix dot denotes function application. It is a commonly used notation in computer programs: in a program to solve this problem we might write
The notation “t.1” makes clear that t is a function from people to times. The infix dot denotes function application. It is a commonly used notation in computer programs: in a program to solve this problem we might write time.person or person.time (depending on the programming language and how the variables have been declared). Do not confuse it with multiplication. Other notations that could have been used are subscripts, t1, or t(1). It is advisable to avoid subscripts where they can be complex expressions. The dot notation has been chosen here because the use of subscripts would have led to subscripts of subscripts and the traditional notation t(1) introduces unnecessary parentheses. See Section 12.3.1 for a discussion of the myriad of notations for function application.
We present the interview as a hypothetical dialogue between the interviewer and the interviewee. The interviewer’s questions are indicated by the letter Q and the interviewee’s answers are indicated by the letter A. You might want to use a piece of paper to cover up each answer as the dialogue proceeds, revealing the answer only when you have formulated your own response. We take up the interview from the point at which the interviewee has indicated that he understands the statement of the problem.
Q: Let’s start with an easy question. What is the minimum number of crossings required to get all four across?
A: That will be when, at each step, the maximum number cross and the minimum number return. That is, 2 cross, 1 returns, 2 cross, 1 returns and then 2 cross. That makes 3 forward trips and 2 return trips, 5 in total.
Q: Good. Now, will the shortest time be achieved with the minimum number of crossings?
A: [Thinks: this sounds like a trick question!] Hmm, seems like it but I’m not sure.
Q: It’s good that you are not sure. That’s not such an easy question to answer. Let’s assume the answer is yes. We can return to the question later.
![]() See Exercise 3.15.
See Exercise 3.15.
You said that two return trips are needed. What is the implication for the number of people who make a return trip?
A: At most two make a return trip. [Quickly adds:] And at least one, of course.
Q: Right. So either one or two people make a return trip. Let’s call them “returners”.
What implication does that have for the number of different ways it is possible to get all four across using the minimum number of crossings?
A: Can you explain what you mean by “different”? Do you want me to distinguish each of the four people or not? If you do, it’s going to be a lot and I would need paper and pencil to work it out.
Q: Good question. I was hoping you would ask. The answer is no. Although the people are distinguished by their crossing times, I would like you to ignore that for the moment. You should not need paper and pencil.
![]() Exercise 3.14 asks you to determine the number when the people are all individually named.
Exercise 3.14 asks you to determine the number when the people are all individually named.
A: OK. Then I guess you want me to do a case analysis on whether one or two people return.
[Pauses briefly.] If just one person returns, there is only one way to get all four across: the returner accompanies each of the other three across. All solutions of this form are indistinguishable in the sense that they correspond to permutations of the four people.
Q: Yes, that’s right. We will need that for later. Can you write down the sequence of crossings? I would suggest you introduce π to denote a permutation of the set {1,2,3,4} so that you can give the sequence in its most general form. Also, it might be useful to number the sequence so that we can refer to it later.
![]() Permutations are discussed in Section 16.8.2.
Permutations are discussed in Section 16.8.2.
A: OK. The sequence is: [Writes, simultaneously explaining that “+” indicates a forward trip, “−” a return trip, and π.i is person i in the permutation π.]
+{π.1, π.2} ; −{π.1} ; +{π.1, π.3} ; −{π.1} ; +{π.1, π.4}. (3.7)
Q: That’s correct. Every sequence of crossings in which there is just one returner is obtained by a suitable choice of the permutation π.
Now can you consider the case when two people return? How many different ways are there of this form?
A: Hm. That means that the two returners are π.1 and π.2, say. The issue is at what stage they cross. [Thinks hard for several minutes.] Yes! I think I know the answer. There are just two ways. Either the returners cross twice again immediately, or they do not. Let me write that down. The case where the returners cross again immediately has the form
+{π.1, π.3} ; −{π.1} ; +{π.1, π.2} ; −{π.2} ; +{π.2, π.4}, (3.8)
and the case where they do not has the form
+{π.1, π.2} ; −{π.1} ; +{π.3, π.4} ; −{π.2} ; +{π.1, π.2}. (3.9)
There is no other possibility because each returner must cross twice.
Q: Very good. That is indeed correct. There are just three different ways of getting everyone across: one way if there is one returner and two ways if there are two returners. Many of our candidates make the mistake of naming the individual people; usually they end up making everything grossly over-complicated.
Let’s now take the crossing times into account. For each of the three ways, what is the time taken?
A: When there is one returner, [Writes, simultaneously explaining that “↑” means maximum.]
t.(π.1)↑t.(π.2) + t.(π.1) + t.(π.1)↑t.(π.3) + t.(π.1) + t.(π.1)↑t.(π.4),
when there are two returners who cross again immediately,
t.(π.1)↑t.(π.3) + t.(π.1) + t.(π.1)↑t.(π.2) + t.(π.2) + t.(π.2)↑t.(π.4),
and when there are two returners who do not cross again immediately,
t.(π.1)↑t.(π.2) + t.(π.1) + t.(π.3)↑t.(π.4) + t.(π.2) + t.(π.1)↑t.(π.2).
Q: Good. Let’s consider these in turn. In the case of (3.10) how would you choose the permutation π so as to minimise the time?
A: That’s easy. Just choose person 1 to be the fastest person.
Q: Can you make that precise?
A: Yes. [Picks up paper and pencil again.] Let’s suppose that the people are numbered so that person 1 is the fastest. So, let’s assume that t.1 ≤ t.1 ↓ t.2 ↓ t.3 ↓ t.4 and π is any permutation of the people. Then [writes]
t.1↑t.2 + t.1 + t.1↑t.3 + t.1 + t.1↑t.4
≤ t.(π.1)↑t.(π.2) + t.(π.1) + t.(π.1)↑t.(π.3) + t.(π.1) + t.(π.1)↑t.(π.4)
⇐ { monotonicity of addition }
t.1↑t.2 + t.1 + t.1↑t.3 + t.1↑t.4
≤ t.(π.1)↑t.(π.2) + t.(π.1) + t.(π.1)↑t.(π.3) + t.(π.1)↑t.(π.4)
∧ t.1 ≤ t.(π.1)
= { assumption: t.1 ≤ t.1 ↓ t.2 ↓ t.3 ↓ t.4 }
t.2 + t.1 + t.3 + t.4
≤ t.(π.1)↑t.(π.2) + t.(π.1) + t.(π.1)↑t.(π.3) + t.(π.1)↑t.(π.4)
∧ t.1 ≤ t.(π.1)
= { the assumption implies that t.1 ≤ t.(π.1),
rearranging }
t.1 + t.2 + t.3 + t.4
≤ t.(π.1) + t.(π.1)↑t.(π.2) + t.(π.1)↑t.(π.3) + t.(π.1)↑t.(π.4)
⇐ { transitivity of ≤ }
t.1 + t.2 + t.3 + t.4
≤ t.(π.1) + t.(π.2) + t.(π.3) + t.(π.4)
≤ t.(π.1) + t.(π.1)↑t.(π.2) + t.(π.1)↑t.(π.3) + t.(π.1)↑t.(π.4)
= { first inequality: π is a permutation,
second inequality: [ x ≤ x↑y ] and monotonicity
of addition }
true.
![]() Expressions involving the at-most relation (“≤”) are called inequalities. The cancellation rule and other rules for manipulating inequalities are discussed in Section 15.1. Properties of maximum and minimum are discussed in Section 15.2.
Expressions involving the at-most relation (“≤”) are called inequalities. The cancellation rule and other rules for manipulating inequalities are discussed in Section 15.1. Properties of maximum and minimum are discussed in Section 15.2.
Phew! I didn’t expect the calculation to be quite so long. I had to think hard about the first step. The use of monotonicity of addition seemed to be the obvious thing to do, but there are so many ways to split the five summands on each side of the inequality. Then it seemed obvious: I was aiming to use the fact that π is a permutation (since that is the only thing known about it); that dictated splitting five into four and one. I postponed other more obvious steps because I didn’t want to make the mistake of combining two many steps into one.
![]() The use of the fact that π is a permutation in the final step is an instance of the range-translation rule for quantifications (14.8) discussed in Section 14.2.3. See Section 14.5 for its generalisation to operators other than addition.
The use of the fact that π is a permutation in the final step is an instance of the range-translation rule for quantifications (14.8) discussed in Section 14.2.3. See Section 14.5 for its generalisation to operators other than addition.
Q: Excellent! Although the calculation seems long, it leaves no room for doubt, and it’s good that you document each step. Our company values careful, precise work.
Now let’s look at how to optimise the times when there are two returners. First, compare (3.10) and (3.11); do you spot anything?
A: Oh, yes. The first three terms in each summand are the same. So they can be cancelled leaving the comparison of the last two terms:
t.(π.1) + t.(π.1)↑t.(π.4) ? t.(π.2) + t.(π.2)↑t.(π.4).
Obviously the former is at most the latter if t.(π.1) is at most t.(π.2).
Q: That’s right. So, by choosing person 1 to be the fastest person, method (3.8) (two returners who cross again immediately) can be discounted. It always takes at least the time taken when just the fastest person returns.
What about the case of two returners who do not cross again immediately, method (3.9)? How would you choose π to optimise the time?
A: It looks like persons 1 and 2 should be the fastest and persons 3 and 4 the slowest, but it does not seem so obvious. Can I do the calculation?
Q: Yes, of course. Go ahead. [Hands pencil and paper over again.]
A: Let’s assume t.1↑t.2 ≤ t.3 ↓ t.4. Then, for any permutation π, we have:[Writes.]
t.1↑t.2 + t.1 + t.3↑t.4 + t.2 + t.1↑t.2
≤ t.(π.1)↑t.(π.2) + t.(π.1) + t.(π.3)↑t.(π.4) + t.(π.2) + t.(π.1)↑t.(π.2)
⇐ { by assumption: t.1↑t.2 ≤ t.(π.1)↑t.(π.2),
monotonicity of addition }
t.1 + t.3↑t.4 + t.2
≤ t.(π.1) + t.(π.3)↑t.(π.4) + t.(π.2)
⇐ { by assumption: t.(π.3) ↓ t.(π.4) ≤ t.3 ↓ t.4,
monotonicity of addition }
t.3 ↓ t.4 + t.1 + t.3↑t.4 + t.2
≤ t.(π.3) ↓ t.(π.4) + t.(π.1) + t.(π.3)↑t.(π.4) + t.(π.2)
⇐ { π is a permutation }
true.
Q: That’s another beautiful calculation. I like the way you expanded three terms to four in the two summands, exploiting the symmetry between persons 1 and 2 (the two fastest) and persons 3 and 4 (the two slowest). We call that a “complification” step; it’s clear that your priority is to simplify but sometimes – in the more interesting calculations – it is necessary to complify.
A: [Smiles.] I’ve heard of “simplification” but not of “complification”. Complify: converse of simplify. That’s neat! I wonder why it’s not used elsewhere?
Q: [Tries to hide a smile.] Well, our company is at the forefront of innovation in many ways, but we can’t claim that idea. The word has been in use for at least a quarter of a century among Dutch computing scientists, but the English-speaking world has yet to catch on. But let’s move on. Can you summarise what you have determined so far?
A: Yes. We have determined that there are only two cases to consider. The first case is when the fastest person accompanies each other person across. If we assume that the people have been ordered in such a way that
t.1 ≤ t.1 ↓ t.2 ↓ t.3 ↓ t.4,
the time taken (after simplification) is
t.2 + t.1 + t.3 + t.1 + t.4.
The second case is when two people return and do not cross again immediately. If we assume that the people have been ordered in such a way that
t.1↑t.2 ≤ t.3 ↓ t.4,
the time taken is
t.1↑t.2 + t.1 + t.3 ↑ t.4 + t.2 + t.1↑t.2.
Q: Yes, we are nearly there now. How do you choose between the two?
A: Well, the two conditions on the ordering can be strengthened to
t.1 ≤ t.2 ≤ t.3 ≤ t.4.
Then, with this assumption, it’s simply a matter of determining which (if any) of the two times is smaller.
Q: Can you simplify the comparison?
A: [Looks at what is written.] Looks like it. Is it OK for me to use the assumption to simplify the terms? The simplifications are very elementary.
Q: Yes, go ahead.
A: [Writes]
t.2 + t.1 + t.3 + t.1 + t.4 ≤ t.2 + t.1 + t.4 + t.2 + t.2
= { cancellation }
t.3 + t.1 ≤ 2 × t.2.
So one returner is chosen if t.3+t.1 ≤ 2×t.2 and two returners is chosen if 2×t.2 ≤ t.3+t.1.
Q: Very good. I’ve noticed that you have connected steps in your calculations sometimes by the “if” symbol and sometimes by the equality symbol. Can you explain why you use the equality symbol here rather than the more conventional “if and only if” symbol?
A: That’s simple to explain. The first rule of logic is the rule of substitution of equals for equals. The comparison between the two expressions is to be used in a program and if one boolean expression is to be replaced by another it is vital that they are everywhere equal.
![]() Substitution of equals for equals is a rule that is ubiquitous in mathematical calculations but rarely made explicit. When calculating with boolean expressions, the rule is obscured by the traditional focus on implicational rather than equational reasoning and the use of “if and only if”. See Chapters 5 and 13 for more explanation.
Substitution of equals for equals is a rule that is ubiquitous in mathematical calculations but rarely made explicit. When calculating with boolean expressions, the rule is obscured by the traditional focus on implicational rather than equational reasoning and the use of “if and only if”. See Chapters 5 and 13 for more explanation.
Q: Very good. All that needs to be done now is to write down the algorithm. Can you do that for me?
A: No problem.
[Writes, recalling that “+” indicates a forward trip and “−” a return trip.] order the people
; { t.1 ≤ t.2 ≤ t.3 ≤ t.4 }
if t.3+t.1 ≤ 2×t.2 → +{1,2};−{1};+{1,3};−{1}; +{1,4}
![]() 2×t.2 ≤ t.3+t.1 → +{1,2};−{1};+{3,4}; −{2}; +{1,2}
2×t.2 ≤ t.3+t.1 → +{1,2};−{1};+{3,4}; −{2}; +{1,2}
fi
{ all people are across in the shortest time }
We didn’t resolve the issue of whether the optimal time is always achieved using the minumum number of crossings. We don’t have time for that now but here are some exercises for you to think about later. [Hands over Exercises 3.13, 3.14 and 3.15.]
A: Do I need to complete these exercises before you decide whether or not to offer me a position?
Q: No, you have passed the interview with flying colours. And we will offer you a pay rise immediately. Congratulations!
Exercise 3.13 Construct a single expression that gives the minimal crossing time (assuming that the people are ordered in increasing order of crossing time).
Check that, if the crossing times are 1 minute, 2 minutes, 5 minutes and 10 minutes, the algorithm deduces that the minimal crossing time is 17 minutes.
Construct crossing times for the four people such that it is faster for person 1 to accompany each other person across the bridge rather than let the two slowest cross together.
Exercise 3.14 Suppose all four people are named and a brute-force search is used to solve the problem assuming that an optimal solution uses the minimum number of crossings. This would mean enumerating all the different ways of getting four (individually named) people across the bridge in five trips. How many ways are there?
![]() In the first crossing, two people are chosen from four; in the second step, one person is chosen from two to make the return crossing, and so on. See Section 16.8.2 for how to evaluate the number of such choices.
In the first crossing, two people are chosen from four; in the second step, one person is chosen from two to make the return crossing, and so on. See Section 16.8.2 for how to evaluate the number of such choices.
Exercise 3.15 Suppose there are five people with crossing times 1, 1, 4, 4 and 4 minutes and suppose that three people can cross the bridge together. What is the shortest time needed to get all five across?
What is the minimum number of crossings needed to get all five across, and what is the shortest time to get them across if the minimum number of crossings is used? (Your answer should demonstrate that getting the people across in the minimum number of crossings is not necessarily optimal.)
Show that, if just two people can cross together, it is the case that an optimal solution uses the minimal number of crossings.
Exercise 3.16 A 3×3 chessboard is to be coloured using at most four colours. Two squares on the board touch if they share a side or a corner point. The requirement is that touching squares should be coloured differently. How many different ways are there of colouring the board? Take care to make clear how you differentiate colourings. (Hint: first identify how many different squares there are. You do not need any knowledge of combinatorics.)
3.6 CONDITIONAL STATEMENTS
The solution to the bridge problem uses a so-called conditional statement. A conditional statement chooses between a number of different options according to the value of a number of boolean expressions, called “conditions”. The conditional statement in the bridge problem is recognised by the “if–fi” brackets; one method of getting the four people across is chosen if the boolean expression t.3+t.1 ≤ 2×t.2 has the value true and the second method is chosen if the boolean expression 2×t.2 ≤ t.3+t.1 has the value true. If both have the value true an arbitrary choice is made between the two methods.
In this book, conditional statements always have the form of a (possibly non-deterministic) choice – indicated by the “![]() ” symbol – among a number of guarded commands, bracketed by “if” and “fi”. A guarded command has the form b → S, where b is a boolean expression called the guard and S is a statement called the body. The if–fi statement in the solution to the bridge problem has two guards, but there may be more. A concrete example of a conditional statement with three guards is the following:
” symbol – among a number of guarded commands, bracketed by “if” and “fi”. A guarded command has the form b → S, where b is a boolean expression called the guard and S is a statement called the body. The if–fi statement in the solution to the bridge problem has two guards, but there may be more. A concrete example of a conditional statement with three guards is the following:
if i < j → i := i+1
![]() i = j → skip
i = j → skip
![]() j < i → j := j+1
j < i → j := j+1
fi
(In this example, the choice is deterministic.)
Conditional statements are used to express case analysis. Case analysis is a commonly used problem-solving strategy. Suppose a problem is specified by a precondition P and postcondition Q. Case analysis involves splitting the problem’s solution into several cases, specified by boolean expressions b1 thru1 bk, for some k. The cases must be exhaustive in the sense that
[ P ⇒ ∃i:1 ≤ i ≤ k:bi].
(In words, in every state satisfying the precondition P at least one of the boolean expressions must have the value true.) The problem then becomes to find, for each i, a solution Si to the problem with precondition P ∧ bi and postcondition Q. That is, for each i, Si is constructed so that
{ P ∧ bi } Si { Q }.
![]() The expression “
The expression “![]() ∃i:1 ≤ i ≤ k:bi
∃i:1 ≤ i ≤ k:bi![]() ” is a so-called “existential quantification”. It is read as “there exists an i such that 1 is at most i is at most k such that bi (is true)” or, more informally, “b1 or b2 or dotdotdot bk (is true)”. See Section 14.3.2.
” is a so-called “existential quantification”. It is read as “there exists an i such that 1 is at most i is at most k such that bi (is true)” or, more informally, “b1 or b2 or dotdotdot bk (is true)”. See Section 14.3.2.
These are then combined in a conditional statement to form a solution to the original problem. Specifically, the solution takes the following form:
{ P }
if b1 → S1
![]() ...
...
![]() bk → Sk
bk → Sk
fi
{ Q }
Starting in a given state, a conditional statement is executed by choosing a guarded command whose guard evaluates to true and then executing its body. If several guards evaluate to true, an arbitrary choice of command is made. If none of the guards evaluates to true, execution aborts.2
3.7 SUMMARY
In this chapter, we have contrasted brute-force search with problem decomposition. Brute-force search should be used only as a last resort. Modern computer technology means that some problems that are too large for human beings to solve do become solvable, but the state-space explosion makes the method impractical for realistic problems, even with the most powerful computers. Complexity theory, which is a topic of study in more advanced courses on algorithm design, lends greater force to this argument; no matter how much bigger and faster computers become, they can never compete with the increase in size of the state space caused by modest increases in problem size.
Problem decomposition seeks to exploit the inherent structure of the problem domain. In all river-crossing or similar problems, there is a symmetry between the left and right banks. This suggests tackling the problems by decomposing them into three components, the first and last being symmetrical in some way. This strategy has no guarantee of success, but, if the problems are tackled in this way, they become more manageable, and often have clear, easily remembered and easily reproduced solutions. Most importantly, the solution method can be applied repeatedly, in contrast to the solutions, which are relevant to just one particular problem.
Along the way, the issue of deciding what to name (and what not to name) has emerged as an important problem-solving skill that can have significant impact on the complexity of the problem. The process is called abstraction: from the myriad of details that surround any real-world description of a problem, we abstract the few that are relevant, introducing appropriate, clearly defined mathematical notation to assist in the problem’s solution.
3.8 BIBLIOGRAPHIC REMARKS
The nervous-couples problem is from the 1999 Vierkant Voor Wiskunde calendar. (See Section 2.6 for further information.) For further information on the bridge problem, see Section 10.8. Exercises 3.4 and 3.5 are from the website http://mathlesstraveled.com com where they are called the “nuclear pennies game” and the “thermonuclear pennies game”, respectively. Underlying solitaire-like games is the theory of “polynomials”, which is outside the scope of this text. See [BCaF10] for further information.
The goat–cabbage–wolf problem is reputed to be thousands of years old and is discussed in a great many books. Surprisingly, the symmetry between the cabbage and wolf never seems to be mentioned. The symmetry, and how to exploit it, was pointed out by E.W. Dijkstra (who was a very accomplished problem-solver and a pioneer in mathematical methodology and the formal development of algorithms). Netty van Gasteren [vG90] emphasises the importance of naming in problem solving, using a number of more advanced algorithmic problems as examples.
1We use “thru” when we want to specify an inclusive range of numbers. For example, “1 thru 4” means the numbers 1, 2, 3 and 4. The English expression “1 to 4” is ambiguous about whether the number 4 is included or not. In mathematical expressions, two dots are used as an abbreviation, as in 1..4; the dots are pronounced “thru”.
2If you are already familiar with a conventional programming language, you will be familiar with deterministic conditional statements: if–then–else statements. In such statements, the choice of which of the optional statements should be executed is completely determined by the state of the program variables. In a non-deterministic choice, as used here, the choice is not completely determined.