Solutions to Exercises

Solution 2.1  1233 games must be played. Let k be the number of players who have been knocked out, and let g be the number of games that have been played. Initially, k and g are both equal to 0. Every time a game is played, one more player is knocked out. So, k and g are always equal. To decide the tournament, 1234−1 players must be knocked out. Hence, this number of games must be played.

In general, if there are p players, the tournament consists of p−1 games.

Solution 2.4  Introducing variables b and e as before, filling boxes is modelled by the assignment

b,e := b+k,e+k−1.

The value of (k−1)×b−k×e is invariant. Its initial value is −m. So, when the process of filling boxes is complete,

(k–1)×b–k×n=−m.                                                                      (S.1)

Assuming and simplifying, we get that . For the problem to be well formulated, we require this to be a natural number. That is, we require that n is at least m, k is at least 2 and n−m is a multiple of k−1.

When k is 1, (S.1) simplifies to n=m. That is, the number of empty boxes remains the same. However, the number of boxes cannot be determined.

Solution 2.5  The ball problem is modelled by the choice

b,w := b+1,w−2 b, w := (b−2)+1,w b, w := b−1,w.

In order, the assignments model what happens when two white balls, two black balls and two differently coloured balls are taken out of the urn. Clearly, w either remains unchanged or is decreased by 2. Its parity is thus invariant. That is, the colour of the last ball in the urn is white exactly when the number of white balls in the urn is odd.

For the chessboard problem, let b and w be the number of covered black and white squares, respectively. Placing a domino on the board is modelled by the assignment

b,w := b+1,w+1.

The difference b−w is invariant. Initially it is 0 (since b and w are both 0) and so it remains 0 no matter how many dominoes are placed on the board. But to cover the board completely it must have final value −2 (because the mutilated board has 2 fewer black squares than white squares). This is impossible.

Solution 2.6  f should be symmetric.

Solution 2.7

(a) m mod 3 is invariant.

(b) m mod (j gcd k) is invariant. We have:

(m mod (j gcd k))[m := m+j]

=         {     substitution }

(m+j) mod (j gcd k)

=         {     distributivity of mod through addition }

(m + j mod (j gcd k)) mod (j gcd k)

=         {     j is a multiple of j gcd k, so j mod (j gcd k) = 0 }

m mod (j gcd k).

Similarly, m mod (j gcd k) is an invariant of the assignment m := m+k.

(c) Yes, the answer is valid. For arbitrary j, j gcd 0=j. If k is zero, m mod j is invariant, which is what (b) predicts. This is even the case when j is also zero because m mod 0=m: if both j and k are zero, the statement is equivalent to skip and m is indeed invariant.

Another extreme case is when j gcd k equals 1 (that is, j and k are coprime). Since m mod 1=0 whatever the value of m, we deduce that 0 is an invariant of the choice. This is a case when looking for an invariant does not help.

Solution 2.8  p mod 3 is invariant. This is the only invariant that is dependent on just one of the variables. n−2×m is an invariant of the first assignment and 3×n−p is an invariant of the second assignment. Neither of these is an invariant of the non-deterministic choice but, by combining them,

3×n−p−6×m

is an invariant of the non-deterministic choice. Alternatively, we postulate that A×m + B×n+C×p is an invariant and calculate A, B and C as follows:

A×m + B×n + C×p is an invariant

=         {     definition of an invariant, substitution }

   A×m + B×n + C×p = A×(m+1) + B×(n+2) + C×p

∧ A×m + B×n + C×p = A×m + B×(n+1) + C×(p+3)

=         {     cancellation }

0 = A + B×2 ∧ 0 = B + C×3

=         {     substitution }

A = C×6 ∧ B = −(C×3).

Solution 2.9

(a) The only linear combination that is invariant is the constant 0.

(b) Here is how to construct a suitable linear combination of b, d and l:

A×b + B×d + C×l is an invariant

=         {     definition of an invariant, substitution }

   A×b + B×d + C×l = A×(b+3) + B×(d+1) + C×l

∧ A×b + B×d + C×l = A×(b+1) + B×d + C×(l+1)

=         {     cancellation }

0 = A×3 + B ∧ 0 = A+C

=         {     substitution }

B = −(A×3) ∧ C = −A

⇐        {     substitution }

A = 1 ∧ B = −3 ∧ C = −1.

The invariant b+8×l−3×w is constructed in the same way.

(c) We obtain two equations in the four unknown coefficients. There are lots of solutions of these equations, including the four determined in (b).

Solution 3.1

{ 5C || }

2C,3B |3P| ; 2C,3B |1P| 2P ; 5B |3P| 2P

;     { 5B || 5P }

5B |2P| 3P ; 2C |3B| 3P

;     { 2C || 3C }

2C |1C| 2C

;     { 3C || 2C }

3P |3B| 2C ; 3P |2P| 5B

;     { 5P || 5B }

2P |3P| 5B ; 2P |1P| 2C,3B ; |3P| 2C,3B

{ || 5C }.

Solution 3.2  We modify the solution to the five-couple problem, effectively by leaving one couple behind on the left bank. We get:

{ 4C || }

1C,3B |3P| ; 1C,3B |1P| 2P ; 4B |2P| 2P

;     { 4B || 4P }

4B |2P| 2P ; 2C |2B| 2P

;     { 2C || 2C }

2C |1C| 1C

;     { 3C || 1C }

3P |3B| 1C ; 3P |1P| 4B

;     { 4P || 4B }

2P |2P| 4B ; 2P |1P| 1C,3B ; |3P| 1C,3B

{ || 4C }.

By reversing left and right, we get the second solution:

{ 4C || }

1C,3B |3P| ; 1C,3B |1P| 2P ; 4B |2P| 2P

;     { 4B || 4P }

4B |1P| 3P ; 1C |3B| 3P

;     { 1C || 3C }

1C |1C| 2C

;     { 2C || 2C }

2P |2B| 2C ; 2P |2P| 4B

;     { 4P || 4B }

2P |2P| 4B ; 2P |1P| 1C,3B ; |3P| 1C,3B

{ || 4C }.

Solution 3.4  We exploit left–right symmetry (moving a coin six places to the right is the same as moving a coin six places to the left). We also decompose the problem into first ensuring that there is a coin in the square six places to the right of the starting position (symmetrically, there is a coin in the square six places to the left of the finishing position).

Achieving this first stage is easy. Below we show how it is done. First, six moves are needed to ensure that a coin is added six places to the right of the starting position. (This is shown below using dots to indicate coins on a square. A blank indicates no coin on the square.)

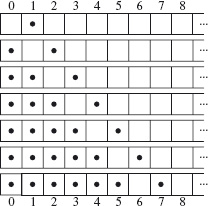
Symmetrically, working from bottom to top, six moves are needed to ensure that a coin is added six places to the left of the finishing position.

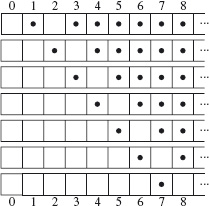
Now the goal is to connect these two intermediate states (the bottom state in the top diagram and the top state in the bottom diagram). An appropriate (symmetrical) sequence of states is as follows. (For the reader’s convenience, the last and first states in the above figures are repeated as the top and bottom states in the figure below.)

The moves to the first and last rows make the number of coins in the leftmost and rightmost positions equal. Then a small amount of creativity is needed to identify the (symmetrical) moves to the (symmetrical) middle position.

Solution 3.5

     1

1   1   1

1   2   1   1

1   2   2   1   1

1   2   2   2   1   1

1   2   2   2   2   1   1

1   1   2   1   2   1   1

1   1   2   2   2   2   1

     1   1   2   2   2   1

          1   1   2   2   1

               1   1   2   1

                    1   1   1

                         1

(Other solutions exploiting the hint are possible. Non-symmetric solutions are also possible.)

Solution 3.6  It is possible to displace the coin by three places. This is one way of doing it.

    1

1  2  1

1  3  2  1

1  3  3  2  1

1  3  3  3  2  1

1  2  2  2  2  1

1  2  3  3  3  1

    1  2  3  3  1

        1  2  3  1

            1  2  1

                1

Solution 3.13  Assuming t.1≤t.2≤t.3≤t.4, the minimum crossing time is

t.1+t.2+t.4+(t.3+t.1)↓(2×t.2).

For the problem as originally stated, the crossing time is 1+2+10+5↓4 (i.e. 17).

Choosing 1, 2, 2 and 2 minutes as the crossing times, the total time is 8 minutes if person 1 is the only one to return, and 9 minutes if persons 1 and 2 both return.

Solution 3.14  If all the people are individually named, there are

(i.e. 108) different ways of getting them across.

Solution 3.15  Using five crossings, the shortest time is 8 minutes. (The three slowest cross together.) The shortest time using three crossings is 9 minutes. (It is not possible for the three slowest to cross together if just three crossings are used.)

See Lemma 10.1 in Chapter 10 for a solution to the second part of this exercise.

Solution 3.16  There are three types of square distinguished by touching: the middle square, the four corner squares and the remaining squares, which we call the edge squares. The middle square touches all other squares. The four corner squares each touch the middle square and two other edge squares. The edge squares each touch the middle square, one corner square and two edge squares.

Because the middle square touches all other squares, one of the four colours must be reserved for this square. Because each edge square touches two other edge squares, it is not possible to use the same colour for all the edge squares; two or three colours must be used. Having chosen the colour of the middle square and the edge squares, there is no choice as to how to colour the corner squares since each corner square touches the middle square and two edge squares all of which touch each other and so must be coloured differently. If two colours are used for the edge squares, there is only one way this can be done: each pair of opposite edge squares must be given the same colour. If three colours are used for the edge squares, there is also only one way this can be done: one pair of opposite edges must be given the same colour. There are thus only two ways to colour the board and all four colours must be used.

Solution 4.1

(a) Naming any day in December, other than 31st December, results in losing. This is forced by the opponent naming 30th November (i.e. the last day of November). Similarly, naming any day in November other than 30th November results in losing, because the opponent can then name 30th November. This is forced by the opponent naming 31st October. In general, the winning strategy is to name the last day of the month. The opponent is then forced to name the 1st of the next month. Whether the year is a leap year or not makes no difference.

(b) In December, the losing positions are the odd-numbered days and the winning positions are the even-numbered days. (Take care: the ‘losing positions’ are the days that the winning player names. This is in line with the terminology of losing and winning positions.) That is, if the last-named day is an odd-numbered day, the player whose turn it is must name an even-numbered day and will eventually lose.

In particular, the player who names 1st December wins. Any day in November is thus a winning position. In October, like December, the odd-numbered days are losing positions, and any day in September is a winning position. Similarly, in August, the odd-numbered days are losing positions, and any day in July is a winning position.

The pattern changes in June, which has an even number of days. The player who names 1st July loses; consequently, any even-numbered day in June is a losing position. This means that every even-numbered day in May is a winning position; also, every even-numbered day in April is a winning position. This means that 31st March is a losing position. Since March has an odd number of days, the pattern we saw for December and November recurs. Every odd-numbered day in March is a losing position, and every day in February is a winning position. Finally, the odd-numbered days in January are losing positions.

We conclude that the second player is guaranteed to win. The strategy is to name the 1st day of the following month when the last-named day is in November, September, July or February. Otherwise, the strategy is to name the next day of the year.

Again, it does not matter if it is a leap year.

Solution 4.2  The first 11 positions are shown in the top three rows in Table S.1. The pattern repeats in the next 11 positions, shown in the bottom three rows.

Table S.1: Winning (W) and losing (L) positions for subtraction set {2, 5, 6}.

Solution 4.3  The squares that are not positions are the ones at the foot of a ladder or at the head of a snake. Positions that cannot be identified as winning or losing positions are attributable to cycles in the positions; a cycle is a sequence of moves that begins and ends at the same position. Labelling of winning and losing positions assumes that every game is guaranteed to terminate no matter how either player moves. If cycles occur this assumption is not valid.

When a game has cycles, the positions are characterised as losing positions, winning positions or stalemate positions. A losing position is one from which every move is to a winning position; a winning position is one from which there is a move to a losing position; and a stalemate position is one from which there is a move to a stalemate position and there are no moves to losing positions.

From a stalemate position the best strategy is to move to a stalemate position since, if there is an alternative of moving to a winning position, this is clearly the wrong thing to do. The opponent will then use the same strategy and the game will continue forever.

Table S.2 shows all positions and the winning move from winning positions. Position 4 is the only stalemate position. From this position, a move to square 6 has the effect of returning the counter to position 4. Any other move from 4 would be to a winning position.

Table S.2: Snakes and ladders. Winning (W), losing (L) and stalemate (S) positions.

Solution 4.5  Consider the simple sum game discussed in Section 4.4.1 where the number of matches in the left and right games is at most 1 and 2, respectively. The sum game has 2×3 positions. As we saw in Section 4.4.1, the position (1, 2) is a winning position and the position (1, 1) is a losing position. Also positions 1 and 2 are both winning positions in the individual games. So, if the operator exists, we would have:

true=winning(1,2)=winning(1)winning(2)=truetrue

and

false=winning(1,1)=winning(1)winning(1)=truetrue.

That is, true=false. This is impossible.

If play begins from a position (l, r) satisfying losing_G(l) ∧ losing_H(r), the perfect player’s strategy is to maintain this property invariant. Starting from such a position, the opponent must either move in the left game, which has the effect of truthifying winning_G(l)∧losing_H(r), or play in the right game, which has the effect of truthifying losing_G(l)∧winning_H(r). By playing in the same game as the one chosen by the opponent, the winner can then truthify losing_G(l)∧losing_H(r) once again.

Solution 4.6

(a) See Table S.3 for the mex numbers up to and including position 10. The mex numbers repeat from here on; that is, the mex number for position m is equal to the mex number for position m mod 11.

Table S.3: The mex numbers for subtraction set {2, 5, 6}.

(b) In the left game, the mex number of position m is m mod 3. Together with the mex numbers for the right game given above, we can complete Table S.4. (Other answers can be given for the winning moves.)

Table S.4: Winning moves.

Solution 4.7

(a) The losing positions are positions 2ⁱ⁺¹−1, where i is a natural number; all other positions are winning positions.

The proof is in two parts: we show that, for all i, every move from position 2ⁱ⁺¹−1 is to a position n where 2ⁱ−1<n<2ⁱ⁺¹−1; also, from a position n where, for all i, n≠2ⁱ⁺¹−1 we show that we can choose i so that there is a move from n to position 2ⁱ−1.

When i equals 0, 2ⁱ⁺¹−1 equals 1. Position 1 is an end position and thus a losing position. When i is greater than 0, every move from position 2ⁱ⁺¹−1 is to a position n where n<2ⁱ⁺¹−1≤2×n. But

          n < 2ⁱ⁺¹−1 ≤ 2×n

=                 {             meaning of continued equalities }

          n < 2ⁱ⁺¹−1 ∧ 2ⁱ⁺¹−1 ≤ 2×n

=                {             integer inequalities, symmetry of ∧ }

          2ⁱ⁺¹−2 < 2×n ∧ n < 2ⁱ⁺¹−1

=                {            monotonicity of 2× }

           2ⁱ−1 < n ∧ n < 2ⁱ⁺¹−1

=                {             meaning of continued equalities }

            2ⁱ−1 < n < 2ⁱ⁺¹−1.

This establishes the first part.

For the second part, suppose that, for all i, n≠2ⁱ⁺¹−1. Let i be the largest number such that 2ⁱ−1<n. Then, by definition of i, n≤2ⁱ⁺¹−1. That is, 2ⁱ−1<n≤2ⁱ⁺¹−1. But then

          there is a move from n to 2ⁱ−1

=                {            definition of legal moves }

         2ⁱ−1 < n ≤ 2×(2ⁱ−1)

=                {             arithmetic }

          2ⁱ−1 < n ≤ 2ⁱ⁺¹−2

=                {              integer inequalities }

           2ⁱ−1 < n < 2ⁱ⁺¹−1

=                {             assumption: for all i, n≠2ⁱ⁺¹−1 }

          2ⁱ−1 < n ≤ 2ⁱ⁺¹−1

=                {              definition of i }

          true.

(b)    Position:              1

    Mex number:       0

    Position:              2 3

    Mex number:       1 0

    Position:              4 5 6 7

    Mex number:       2 1 3 0

    Position:              8 9 10 11 12 13 14 15

    Mex number:       4 2 5 1 6 3 7 0

In general, mex(2×n) equals n and mex(2×n+1) equals mex(n).

(c) See Table S.5.

Table S.5: Solution to rectangle game.

Solution 5.4

          ¬true

=                {                [ p ≡ p ≡ false ] with p := true }

          true ≡ false

=                {                 [ true ≡ p ≡ p ] with p := false }

          false.

Solution 5.5

        ¬¬p

=           {           [ ¬p ≡ p ≡ false ] with p :=¬p }

        ¬ p ≡ false

=          {            [¬p ≡ p ≡ false ] with p := p

                          and symmetry of equivalence }

        p.

Solution 5.7  Let col be the colour of the square, and n be the number of moves. A move is then

col,n :=¬col, n+1.

An invariant of this assignment is

col≡even.n.

An odd number of moves, 63, is needed, but the colour of the square does not change. So, in order to move the knight as required, a change has to be made to col≡even.n, which is impossible.

Solution 5.8  Suppose the number of couples is n. There are 2n people, including the host, who each shake hands with between 0 and 2n−2 people. If 2n−1 of them – everyone but the host – shake hands with a different number of people, there must be someone who shakes hands with k people for each k between 0 and 2n−2 (inclusive).

If n is 1, the only person other than the host is the host’s partner. Since couples do not shake hands, both shake hands 0 times.

Now suppose that n is greater than 1. In this case, there are at least two people other than the host and the host’s partner. Consider the two people who shake hands 0 and 2n−2 times. The person who shakes hands 2n−2 times does so with everyone except their partner (and themself, of course). By the symmetry of the shake-hands relation, it is thus the case that everyone except that person’s partner shakes hands with at least one person. It follows that the two people who shake hands 0 and 2n−2 times are husband and wife. Because neither is the host, it also follows that neither is the host’s partner.

Now suppose we discount this couple. That is, we consider the party consisting of the other n−1 couples. The number of times each person shakes hands is then reduced by one. So, again, all but the host have shaken hands a distinct number of times.

Repeating this process, we eliminate all the couples one by one until the party has been reduced to just the host and the host’s partner. Each time, the number of times the host and the host’s partner shake hands is reduced by one. The host and the host’s partner must therefore have both shaken hands n−1 times.

Solution 5.10

(a) false

(b) false

(c) false

(d) p

(e) false

(f) q   r

(g) p

(h) true

Solution 5.11  The process of decryption after encryption computes a (a b). But,

         a   (a   b)

=                    {               is associative }

         (a   a)   b

=                    {              (a a false) }

         false   b

=                    {              definition of   }

         false ¬b

=                    {              definition of negation: (5.3) }

         b.

Solution 5.12  Let Q be the question. Then, Q≡A≡A B, that is, Q≡¬B. In words, ask A whether B is a knave.

Solution 6.1  It is required that any two lines intersect in a single point. If the lines are not straight and they intersect in a segment of a line, inverting the colours of one of the two regions does not guarantee that the colouring of adjacent regions at the boundary of the left and right regions is satisfactory. This is because, along the line segment, the colours of the adjacent regions are not the same before the inversion takes place, contrary to the assertion made above.

The solution remains valid provided every line cuts the surface in two. A line on a ball does this, whereas a line on a doughnut need not.

The number of colourings is always two no matter how many lines there are. This is clearly the case when there are no lines. When there are n+1 lines, choose any one of the lines. Cut the paper along the chosen line. Assume inductively that, for each half, there are exactly two colourings. Combining these gives four different ways of colouring the entire sheet of paper. However, two of these are unsatisfactory because the colours of regions adjacent at the chosen line must be different. This leaves exactly two ways of colouring the paper with n+1 lines.

Solution 6.2  The base case, n=0, is trivial. The triangle has size 1 and 0 buckets are needed to cover the remaining area.

For the induction step, split a triangle with side of length 2ⁿ⁺¹ into four triangles each of the same size. The topmost triangle of one of these four triangles is covered; by induction, the remainder can be covered with buckets. The remaining three triangles (of size 2ⁿ) have one common corner. Placing a bucket at the corner then leaves three triangles each of size 2ⁿ with one corner covered; by induction, the remainder of the triangles can also be covered by buckets.

Solution 6.3  The base case can be extracted from Figure 6.5: look at the topmost triangle with side of length 3. For the induction step, a triangle with side of length 3(n+1) (where 1≤n) is divided into n triangles each with side of length 3 and one triangle with side of length 3n. This is illustrated for the case where n is 3 in Figure S.1. By induction, all of these triangles can be covered.

Figure S.1: Trapezium problem: sketch of induction step.

Solution 7.1

(a) The base case is when n equals 0. Since 0≤m≤(³−1)/2 equivales 0=m, the algorithm is to do nothing – there are no coins and, hence, no fake coin.

For the induction step, assume the induction hypothesis. Assume the number of coins m is such that 0≤m≤(3ⁿ⁺¹−1)/2. If m≤(3ⁿ−1)/2, the induction hypothesis can be applied directly. So it suffices to consider the case where (3ⁿ−1)/2<m≤(3ⁿ⁺¹−1)/2.

Put (3ⁿ−1)/2 coins aside. Place the remaining m−(3ⁿ−1)/2 coins on the balance, using the supplied genuine coin if necessary to make the number even. Note that the number of coins placed on the balance is at most 3ⁿ (since m≤(3ⁿ⁺¹−1)/2 equivales m−(3ⁿ−1)/2≤3ⁿ).

If the balance tips to one side, mark all the coins on the balance either “possibly heavy” or “possibly light” and apply the solution to part (b). If not, apply the induction hypothesis to the (3ⁿ−1)/2 coins that were left aside. The total number of comparisons is then at most 1+n as required.

(b) The base case is when n equals 0. Since 1≤m≤3⁰ equivales 1=m, the algorithm is to do nothing – the coin is fake and its marking indicates whether it is lighter or heavier than a genuine coin.

For the induction step, assume the induction hypothesis. Assume the number of coins m is such that 1≤m≤3ⁿ⁺¹. If m≤3ⁿ, the induction hypothesis can be applied directly. So it suffices to consider the case where 3ⁿ<m≤3ⁿ⁺¹.

In order to be able to apply the induction hypothesis, it is necessary to divide the coins into three groups each of which has size at most 3ⁿ; also, two of the groups – the coins to be placed on the left and right scales of the balance – must have equal size and contain equal numbers of possibly heavy coins. This can be done as described in Section 7.2.3 by placing coins on the scales two at a time, one on the left and one on the right, always choosing two coins with the same marking. The choice can always be made while there are at least three coins from which to choose; by choosing any three coins, at least two of them will have the same marking. The process of placing coins in this way is continued until each scale has its full complement of 3ⁿ coins, or at most two coins remain.

Once this division process has been completed, there are at most 2×3ⁿ coins on the balance and at most 3ⁿ coins left aside. There are two possibilities that have to be considered. One possibility is that 0 coins have been placed on the balance; this is the case where m equals 2. In this case, one of the coins can be compared with the genuine coin; the outcome clearly determines which of the two coins is fake. The other possibility is that the number of coins on the balance is non-zero. If the balance tips to one side, the fake coin is among the coins whose marking is in agreement with the tip; by the way the coins were placed on the balance, this number is exactly half of the total number of coins on the balance. That is, there are at most 3ⁿ of them and the induction hypothesis can be applied to these coins, giving a total of at most 1+n comparisons. If the balance does not tip to one side, the coins on the balance are all genuine and the induction hypothesis can be applied to the remaining coins (of which there are at most 3ⁿ). In this way, the total number of comparisons is at most 1+n as required.

(c) The basis is when n equals 2 and m equals 3. It is straightforward to determine that 2 comparisons suffice to identify a fake coin (if any). The details are left to the reader. For the induction step, suppose 2≤n and the number of coins is m, where 3≤m<(3ⁿ⁺¹−1)/2. As in parts (a) and (b), it suffices to consider the case where (3ⁿ−1)/2≤m<(3ⁿ⁺¹−1)/2.

Consider two cases: (3ⁿ−1)/2 equal to m and (3ⁿ−1)/2 different from m. In the first case, compare any two coins. If the scales balance, both are genuine and the solution to part (a) can be applied to find the fake coin (if any) among the remaining (3ⁿ−1)/2−2 coins. The total number of comparisons is at most 1+n.

In the second case, (3ⁿ−1)/2<m<(3ⁿ⁺¹−1)/2. Depending on whether m−(3ⁿ−1)/2 is even or odd, place (3ⁿ−1)/2 or (3ⁿ−1)/2−1 coins on the table and divide the remaining coins equally between the scales. If the scales balance, all the coins on the balance are genuine; the solution to part (a) can now be applied to the coins remaining on the table with one of the coins from the balance as the required genuine coin. If the scales tip, the coins on the table are genuine. The coins on the balance can all be marked either ‘possibly heavy’ or ‘possibly light’ and the solution to part (b) applied to them with one of the coins on the table as the required genuine coin. In each case, the total number of comparisons is at most 1+n.

When there are 12 coins, we first note that (3²−1)/2<12<(3³−1)/2. The algorithm begins by dividing the coins into three groups of 4.

If the scales balance, the algorithm proceeds further with the 4 coins on the table and one of the coins from the balance as the genuine coin. After two further comparisons (details of which are left to the reader) the fake coin, if it exists, is determined.

If the scales do not balance, the 8 coins on the scales are marked appropriately and one of the coins on the table is used as the genuine coin. Six of the 8 marked coins are redistributed on the balance (so that each scale gets 2+1 coins, where the ‘2’ coins are from one side of the balance and the ‘1’ coin is from the other side). After this comparison, either two or three marked coins remain (two if the scales balance, three if the scales do not balance). In the case where two remain, the fake coin can be determined by comparing one of the coins with the genuine coin. In the case where three remain, two with the same marking are compared. This one comparison is sufficient to determine which is the fake coin.

Solution 7.2 When m is 0, there is just one object. This is the unique object and 0 (which equals 2×0) comparisons are needed to discover that fact.

Suppose now that m is greater than 0. Split the 3^m objects into three groups each of 3^m−1 objects. One of these three groups will have a different weight than the other two, which will be of equal weight. At most 2 comparisons are needed to determine which of the groups it is. Then, by induction, at most a further 2×(m−1) comparisons are required to find the unique object in that group. This gives a total of 2×(m−1)+2 (i.e. 2×m) comparisons as required by the induction hypothesis.

It is possible to determine whether the unique object is lighter or heavier than the others (although, in the case where there is just one object, the answer is that it is both lighter and heavier than all the rest). It can be decided in the first two comparisons.

Solution 7.3

(a) For n=1, it is clear that 0 comparisons are needed. For the induction step, assume that n−1 comparisons are needed to find the lightest of n objects. To find the lightest of n+1 objects, use n−1 comparisons to find the lightest of n objects, then compare this object with the (n+1)th object. The lightest of the two is the lightest of them all. Also, one extra comparison has been made, making n in total.

(b) For n=2, it is clear that 1 comparison is needed. For the induction step, assume that 2n−3 comparisons are needed to find the lightest and heaviest of n objects. To find the lightest and heaviest of n+1 objects, use 2n−3 comparisons to find the lightest and heaviest of n objects. Call these L and H. Call the (n+1)th object N. The lightest of L and N is the lightest of them all, and the heaviest of H and N is the heaviest of them all. This requires two extra comparisons, making (2n−3)+2, i.e. 2(n+1)−3 in total.

(c) Compare A and C. The lightest of the two is the lightest of the four. Compare B and D. The heaviest of the two is the heaviest of the four.

To weigh four objects, first compare two. Call the lighter one A and the heavier one B. Likewise, compare the remaining two objects and call the lighter one C and the heavier one D. Then proceed as above.

(d) For m=1, it is clear that 1 comparison is needed to find the lightest and heaviest of 2 objects. And 1=3×1−2.

Suppose there are 2(m+1) objects. Select and compare any two of the objects. Let the lightest be A and the heaviest B. By induction, we can find the lightest and heaviest of the remaining 2m objects in 3m−2 comparisons. Let these be C and D, respectively. We now have four objects, A, B, C and D, such that A<B and C<D. By part (c), the lightest and heaviest of these four can be found in 2 further comparisons. These are then the lightest and heaviest of all 2(m+1) objects. And the total number of comparisons is 1+(3m−2)+2 which equals 3(m+1)−2.

Solution 7.4

(a) Distinguishing between left and right scales, each widget can be placed on the left scale, on the right scale, or left aside. For a total of n widgets, this gives 3ⁿ different configurations of the balance. One of these is symmetric between left and right – when no widgets are placed on the scales. All the rest are asymmetric between left and right; from the viewpoint of weighing a fudget, this means that the same configuration is counted twice. The total number of different configurations is thus (3ⁿ−1)/2+1, which simplifies to (3ⁿ+1)/2.

The conclusion is that at most (3ⁿ+1)/2 different fudgets can be weighed using at most n widgets.

(b) Take as induction hypothesis that any fudget of weight w, where 0≤w<(3ⁿ+1)/2, can be weighed by placing it inside s of the balance, and suitably placing at most n widgets of weights 3⁰, 3¹, 3², . . ., at most one of each weight, on the balance.

The basis is when n equals 0. A fudget of weight 0 can be weighed by placing it on scale s of the balance and 0 widgets (arbitrarily) on the two scales.

For the induction step, it suffices to show that it is possible to weigh fudgets of weight w, where (3ⁿ+1)/2≤w<(3ⁿ⁺¹+1)/2, using at most n+1 widgets. Inevitably, the additional widget of weight 3ⁿ will have to be used. A simple calculation shows that

(3ⁿ+1)/2≤w<(3ⁿ⁺¹+1)/2≡−(3ⁿ+1)/2<w−3ⁿ<(3ⁿ+1)/2.

This suggests a case analysis on the sign of w−3ⁿ. If 0≤w−3ⁿ, the induction hypothesis prescribes how to weigh a fudget of weight w−3ⁿ by placing it on side s and suitably placing at most n widgets of weights 3⁰, 3¹, 3², . . ., at most one of each weight, on the balance; by adding the widget of weight 3ⁿ on the opposite side of the balance, the fudget of weight w can be weighed. If, conversely, 0≤−(w−3ⁿ), the induction hypothesis prescribes how to weigh a fudget of weight −(w−3ⁿ) by placing it on side ¬s and suitably placing at most n widgets of weights 3⁰, 3¹, 3², . . ., at most one of each weight, on the balance; by adding the widget of weight 3ⁿ on the opposite side of the balance, the fudget of weight w can be weighed.

Solution 8.1 Formally we have

T₀(d)

=             {        definition of T  }

length(H₀(d))

=             {        definition of H₀(d)  }

length([])

=             {        definition of length  }

0

and

T_n+1(d)

=            {         definition of T  }

length(H_n+1(d))

=            {          definition of H_n+1(d)  }

length(H_n(¬d); n+1, ¬d ; H_n(¬d))

=            {          definition of length  }

length(H_n(¬d)) + length(n+1, ¬d) + length(H_n(¬d))

=            {          definition of T (twice) and length  }

T_n(¬d) + 1 + T_n(¬d).

That is,

                              T_o(d) = 0

                           T_n+1(d) = 2 × T_n(¬d) + 1.

If we expand these equations for n=0,1,2, . . ., just as we did for the equations for H, we discover that T₀(d) is 0, T₁(d) is 1 and T₂(d) is 3 (in each case for all d). This and the form of the equation for T_n+1(d) (in particular the repeated multiplication by 2) suggest that T_n(d) is 2ⁿ−1. The simple inductive proof is omitted.

Solution 8.2 We begin by considering the permissible states that the puzzle may be in. In any state, the discs on any one pole are in order of decreasing size. So, if we want to specify the state of the puzzle we only need to specify which pole each disc is on. For example, suppose there are five discs and suppose we specify that disc 1 is on pole A, disc 2 is on pole B, discs 3 and 4 are on pole A and disc 5 is on pole B. Then disc 4 must be on the bottom of pole A, disc 3 must be on top of it, and disc 1 must be on top of disc 3. Also, disc 5 must be on the bottom of pole B and disc 2 must be on top of it. No other arrangement of the discs satisfies the rule that no disc is above a disc smaller than itself.

The state of an n-disc puzzle can thus be specified by a sequence of n pole names. The first name in the sequence is the location of disc 1, the second is the location of disc 2, and so on. That is, the kth name in the sequence is the location (pole name) of disc k. Since each disc may be on one of three poles, we conclude that there are 3ⁿ different states in the n-disc problem.

We now consider the transitions between states. We consider first the problem where there are no discs, then the 1-disc problem, then the 2-disc problem, and then we consider the general n-disc problem.

When there are no discs there is exactly one state: the state when there are no discs on any of the poles. This is shown in Figure S.2. (You may have difficulty seeing the figure. It consists of a single dot!)

Figure S.2: State-transition diagram for 0-disc problem.

We now explain how to construct the state-transition diagram for the (n+1)-disc problem, for an arbitrary n, given that we have constructed the diagram for the n-disc problem. (See Figure S.3.) Each state is a sequence of n+1 pole names. The first n names specify the location of the smallest n discs and the (n+1)th specifies the location of the largest disc. Thus, each state in the state-transition diagram for the n-disc problem gives rise to 3 states in the state-transition diagram for the (n+1)-disc problem. That is, a state in the state-transition diagram for the (n+1)-disc problem is specified by a sequence of n pole numbers followed by the pole name A, B or C. We split the permissible moves into two sets: those where the largest disc (the disc numbered n+1) is moved and those where a disc other than the largest disc is moved.

Figure S.3: Construction of the state-transition diagram for the (n + 1)-disc problem.

Consider first moving a disc other than the largest disc. When doing so, the largest disc may be on pole A, B or C. But its position does not affect the permissibility or otherwise of a move of a smaller disc. That means that every transition from state s to state t in the n-disc problem is also a valid transition from state sp to state tp in the (n+1)-disc problem, where the pole name p is either A, B or C. The first step in the construction of the state-transition diagram for the (n+1)-disc problem given the state-transition diagram for the n-disc problem is to make three copies of the latter. The pth copy is then modified by simply adding p at the end of each sequence of pole numbers labelling the nodes.

Now consider moving the largest disc, the disc numbered n+1. Being the largest disc, it may only be moved if all the other discs are on one and the same pole different than the pole that the largest disc is on. This gives six possibilities for moving disc n+1, or three edges in the undirected state-transition diagram: an edge connecting the states AⁿB and AⁿC, an edge connecting the states BⁿC and BⁿA and an edge connecting the states CⁿA and CⁿB. The construction is shown schematically in Figure S.3, the three inner triangles representing the set of all moves that do not move disc n+1.

Solution 8.3

(a) Let C_n(d) denote the sequence of discs. The base case, when n equals 0, is the empty sequence.

For the induction step, it is necessary to distinguish two cases: d is clockwise and d is anticlockwise. In the first case, by the inductive hypothesis, it is possible to move the n smallest discs in an anticlockwise direction. By doing so, then moving disc n+1 (clockwise) and, finally, moving the n smallest discs again anticlockwise, the goal of moving n+1 discs in a clockwise direction is achieved. The second case is harder. The key point is that the largest disc must move twice clockwise in order to displace it one position clockwise. As in the first case, begin by moving the n smallest discs anticlockwise followed by moving disc n+1 (clockwise). Then move the n smallest discs clockwise. (This returns the n smallest discs to their original position.) Follow this by moving disc n+1 again. Finally, move the n smallest discs anticlockwise. Formally, the complete algorithm is expressed by the following three equations.

C₀(d) = []

C_n+1(cw) = C_n(aw); [n + 1] ; C_n(aw)

C_n+1(aw) = C_n(aw); [n + 1] ; C_n(cw); [n + 1] ; C_n(aw)

(b) Straightforward generalisation of part (a).

Solution 8.4 Even, because the direction of movement is opposite to that of the smallest disc (which has an odd number).

Solution 8.5 The algorithm is to repeatedly execute the following procedure until it can no longer be executed (i.e. when it is no longer possible to determine k in step 1).

1. Suppose it is possible to move disc k in the direction d′, where k>1. (Recall that disc 1 is the smallest disc.) Set d to odd(k)≡d′.

2. Move disc k (in the direction d′, of course).

3. Move the smallest disc in the direction d.

The correctness is justified as follows. When step 1 is executed, we know that the first k−1 discs are all on the pole in direction ¬d′ from disc k. Progress is made if these k smallest discs can be transferred to the same pole. To do this, it is necessary to move the k−1 smallest discs in the direction ¬d′. The direction that disc 1 has to be moved is thus d, where

even(k−1) ≡ ¬d′ ≡ even(1) ≡ d.

Simplifying, we get that d=(odd(k)≡d′). (In words, the direction that the smallest disc is moved should be the same as the direction that disc k is moved, if k is also odd; otherwise the smallest disc is moved in the opposite direction to disc k.) The correctness of the Tower of Hanoi program then guarantees that this action will initiate a sequence of moves after which all k−1 discs will have been moved onto disc k. During this sequence of moves the smallest disc will continue to move in the same direction. On completion, however, the direction of the smallest disc may or may not be reversed.

The only time that step 1 cannot be executed is when all the discs are on the same pole, as required.

Solution 8.6 The solution is to place the discs in order, starting with the largest and ending with the smallest. Let k denote the number of the discs still to be replaced; so, initially k is N and we are done when k is 0. Each time the value of k is reassigned, we ensure that the k smallest discs are on the same pole.

If the kth disc is on the right pole, decrease k by 1. Otherwise, suppose it needs to be moved in direction d from its current position. Move the smallest k−1 discs in the direction ¬d, then move disc k to its rightful position. Finally, decrease k by 1. Continue this process until k is 0.

Solution 9.4 Clearly, the goal is impossible to reach if the objects are all of the same kind and there is more than one of them. So, as suggested, we assume that there are objects of different kinds. Let m, n and p denote the number of objects of each kind.

The replacement process is modelled by the assignment

m,n,p := m+1,n−1,p−1

and the two assignments obtained by permuting m, n and p.

Noting that increasing/decreasing by 1 flips the parity of a number, we conclude that an invariant of the assignment is: the numbers are all even or the numbers are all odd. Since the goal is to reach a state in which there are two even numbers (two 0s) and one odd number (one 1), that is, the invariant is false, we conclude that the goal is impossible to reach if the invariant is true in the starting state, that is, if initially all the numbers are even or all the numbers are odd.

Let us assume that initially one kind of object has different parity than the other two. For concreteness, assume that even(m)=even(n)≠even(p). The goal becomes to reduce m and n to 0 and p to 1. As mentioned earlier, we assume also that

¬(m=n=0∧p≠1).

Equivalently, we assume that initially

(m≠0∨n≠0∨p=1)∧(even(m)=even(n)≠even(p)).

This is the invariant of the algorithm.

If m or n is zero, p must be odd and hence non-zero. It follows that if m or n is non-zero, there must be two objects of different kinds. Choosing to increase the number of objects of a kind that occurs least frequently maintains the invariant and reduces the number of objects. This is expressed in the algorithm below.

{ Invariant: (m ≠ 0 ∨ n ≠ 0 ∨ p = 1) ∧ (even(m) = even(n) ≠ even(p))

   Measure of progress: m+n+p  }

do m ≠ 0 ∨ n ≠ 0 →    if m ≤ n↓p → m,n,p := m+1, n−1, p−1
                                    n ≤ p↓m → m,n,p := m−1, n+1, p−1
                                    p ≤ m↓n → m,n,p := m−1, n−1, p+1
                                   fi

od

{ m = 0 ∧ n = 0 ∧ p = 1  }

We need to check that the assignments are valid, that is, no attempt is made to decrease a variable when its value is 0. This is where the invariance of

even(m)=even(n)≠even(p)

is relevant. We also need to check that each assignment truthifies

m≠0∨n≠0∨p=1.

The first two truthify m≠0 and n≠0, respectively. The third assignment truthifies p=1 or, if not, maintains m≠0∧n≠0 (note the conjunction rather than disjunction) because m and n are both at least 2 before the assignment.

Solution 9.6 Suppose the number of tumblers is N. Assume the tumblers are numbered from 0 onwards by their position in the line. An algorithm iteratively ensures that the first k tumblers are upside up, so that the measure of progress is N−k. Initially, k is 0. Each iteration ensures that tumbler k is upside up by, if necessary, turning it and tumbler k+1. If N is odd, the fact that there is always an even number of upside-down tumblers ensures that no attempt is made to turn the non-existent tumbler N on the last iteration. Formally, the algorithm is as follows:

{ even(Σi : 0 ≤ i < N ∧ down(i) : 1)  }

k := 0;

{ Invariant: 0 ≤ k ≤ N ∧ even(Σi : k ≤ i < N ∧ down(i) : 1)

    ∧ ∀i : 0 ≤ i < k : up(i)

    Measure of Progress: N–k  }

do k < N →     if down(k) → { 0 ≤ k < k+1 < N  } turn tumblers k and k+1

                          up(k) → skip

                         fi ;

                         k := k+1

od

{ ∀i : 0 ≤ i < N : up(i)  }

Solution 9.7 The system invariant is

That is, either there are no single individuals on either bank, or all bodyguards are on one of the two banks. It is a requirement of any solution that this property is an invariant. (If not, either 0<lB<lP or 0<rB<rP. In words, the presidents outnumber the bodyguards on the left bank or on the right bank. In both cases, the solution is invalid.)

Now, we claim that, under the given assumptions on M and N, either

(a) the boat is on the left bank and

or

(b) the boat is on the right bank and

Property (a) is clearly true initially. (Recall the assumptions about M and N.)

Now, suppose (a) is true and, then, a crossing is made from left to right. Note that lB≠0 both before and after the crossing. (Before the crossing, lB=0 is excluded by the assumption that M<lB. After the crossing, lB=0 is impossible because at most M bodyguards can cross together.) So the invariant (S.2) can be strengthened: the crossing is made starting in a state in which

and must result in a state satisfying this property. Otherwise, the crossing is invalid. Note also that a left-to-right crossing causes lB and/or lP to decrease.

We consider two cases before the crossing: lB=N and (lB=lP)∧(lB≠N).

Since at most N/2 bodyguards can cross together, if lB=N before the crossing, at least N/2 bodyguards are left at the left bank. That is, (b) is true after the crossing.

If (lB=lP)∧(lB≠N) before the crossing, the property lB=lP must be maintained by the crossing. (This is because (S.5) must be maintained and the crossing cannot increase lB.) That is, an equal number of presidents and bodyguards must make the crossing. Since only one couple can cross at one time, the value of lB is decreased by at most 1. But (S.3) is assumed to be true before the crossing; consequently, (S.4) is true after the crossing, and the boat is at the right bank. Thus, (b) is true after the crossing.

In both cases, we have established that, after the crossing, (b) is true.

Now suppose (b) is true and a crossing is made from right to left. A right-to-left crossing causes lB and/or lP to increase. Since lB≠0 before the crossing, and lB does not decrease, lB≠0 after the crossing.

Again, we consider two cases: this time, no bodyguards cross, and some bodyguards cross.

If bodyguards cross, the act of crossing increases lB; so after the crossing M<lB and (of course) the boat is at the left bank. Thus, (a) is true after the crossing.

If only presidents cross, it must be the case that lB=N (because (S.5) must be maintained and, if only presidents cross, it is impossible to maintain that lB=lP). That is, lB is unchanged, and M<lB both before and after the crossing. After the crossing, the boat is, of course, at the left bank. Thus, (a) is true after the crossing.

In both cases, we have established that (a) is true after the crossing.

In summary, property (a) is true initially. Also, if (a) is true and a left-to-right crossing is made, (b) is truthified; vice versa, if (b) is true and a right-to-left crossing is made, (a) is truthified. So, at all times, either (a) or (b) is true. That is, it can never be the case that all bodyguards are at the right bank.

Solution 10.15 Binary search is used to determine when the difference between successive values of the funtion OT changes from being negative to being positive. The search is encoded as follows:

{ 2 ≤ N  }

i,j := 1, N÷2 ;

{ Invariant:

         1 ≤ i ≤ j ≤ N÷2

     ∧ ∀k : 1 ≤ k < i : OT.(k+1) − OT.k ≤ 0

     ∧ ∀k : j ≤ k < N÷2 : 0 ≤ OT.(k+1) − OT.k  }

do i < j →     m := (i+j)÷2 ;

                    if 2 × t.2 ≤ t.1 + t.(N−2m+1) → i := m

                     2 × t.2 ≥ t.1 + t.(N−2m+1) → j := m

                    fi

od

{          1 ≤ j ≤ N÷2

        ∧ ∀k : 1 ≤ k <j : OT.(k+1) − OT.k ≤ 0

        ∧ ∀k : j ≤ k <N÷2 : 0 ≤ OT.(k+1) − OT.k  }.

On termination, j is the multiplicity of {1,2} in an optimal regular bag and OT.j is the required optimal time. Corollary 10.12 specifies the composition of the hard trips and Lemma 10.10 specifies how they are scheduled. The remaining N−2j+2 people are then scheduled to cross in N−2j+1 firm trips as described above.

Solution 10.16

(a) In any state, there are two possible values for the position of each person, and two possible values for the position of the torch. Now, there are 2^N+1 functions from a set of size N+1 to a position. However, if all people are in one position, the torch must be in the same position; this disallows two such functions. Also disallowed are functions that assign the same position to the torch and exactly one person; there are 2×N such functions. The total number of states is thus

2^N+1−(2+2×N).

For N equal to 2, 3, 4, 5 and 6, the number of different states is 2, 8, 22, 52, and 114.

(b) If there are k people at the start, there are ×k×(k−1) ways of choosing the two people to cross. The number k ranges from N down to 2. Thus the number of different ways of composing the forward trips is

If there are k people at the finish, there are k ways of choosing who is to return. The number k ranges from 2 up to N−1. So there are

ways of composing the return trips. The total number of different ways of getting N people across the bridge is the product of these two formulae. This simplifies to

For N equal to 2, 3, 4, 5 and 6, the number of different ways of getting the people across is 1, 6, 108, 4320 and 324 000.

The number of states grows exponentially, the number of different ways grows like the factorial function.

Solution 11.1

(a) The number of moves that have to be made equals the number of squares. After an odd number of moves, the colour of the current square is different from the colour of the starting square. So, after an odd number of moves, it is impossible to return to the starting square.

(b) It’s easy to see that a straight-move circuit of a 2×1 board is possible – starting at one of the squares, move to the other square and then move back again –, but, otherwise, no straight-move circuit is possible. If m is greater than 1, at least one square is two moves from the starting square; it is impossible to visit such a square and return to the starting square without visiting the in-between square more than once.

(c) See (b) for a circuit of a 2×1 board. For n greater than 1, a straight-move circuit of a 2×n board is completed by starting at a corner, moving one-by-one to all the squares in the same row, then returning via the second row.

Solution 11.2 For the 3×3 board, a circuit can be constructed exactly when the omitted square is not adjacent to a corner square. If the squares of the board are coloured black and white as for a chessboard, these are the squares that have a different colour to the corner squares. For larger boards, the same rule applies. Suppose the corner squares are coloured black. (All four corners have the same colour because it is assumed that the board has odd size.) Then the number of black squares exceeds the number of white squares by one. Any circuit comprises an alternating sequence of black and white squares of which the number of black squares equals the number of white squares. If a white square is omitted it is impossible to construct a circuit of all the remaining squares because the number of remaining black squares is greater than the number of remaining white squares.

Suppose the omitted square is black and its coordinates are (m, n). (It doesn’t matter whether numbering starts at zero or one or which corner is taken as the origin.) Then even(m)=even(n).

Figure S.4: Construction of a straight-move circuit omitting one square.

The construction is to split the board into four rectangular boards in such a way that the to-be-omitted square is at a corner of a board with an odd number of squares as shown in Figure S.4. (The to-be-omitted square may thus be the corner square, as shown in the left figure, or one space in from the corner, as shown in the right figure.) The odd-sized board must be at least 3×3 but smaller than the entire board. (This is always possible if the to-be-omitted square is at position (m, n) and even(m)=even(n).) The other three boards each have an even number of squares, and at least one of them has at least one square. Construct circuits of these three boards, and – inductively, with the 3×3 board as the base case – a circuit of the board with the omitted square. Then, connect the circuits together as shown in Figure S.4: the left figure is the case that the distance of the to-be-omitted square from each corner is odd, and the right figure is the case that the distance is even. In the inductive step, moves within a board are replaced by moves between boards as indicated in the figure. (The crucial fact is that the replaced lines must exist because any circuit can only enter and leave each corner square in exactly one way.)

Solution 11.6 See Table S.6.

Table S.6: Sequential composition of flip operations.

Property (11.7) is verified by observing that the table is symmetric about the top-left to bottom-right diagonal. Verification of the associativity property is much more tedious. The case that x, y or z is n can be dealt with simply. This leaves 27 other cases to consider. This is an example of a “tedious, but straightforward” proof!

Solution 11.9 See Table S.7.

Table S.7: Sequential composition of rotation operations.

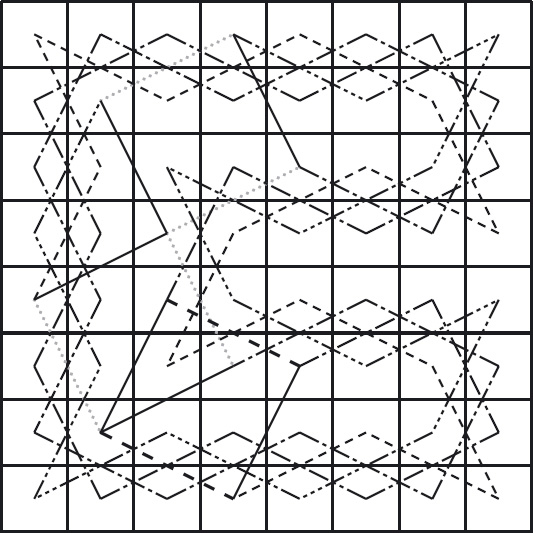
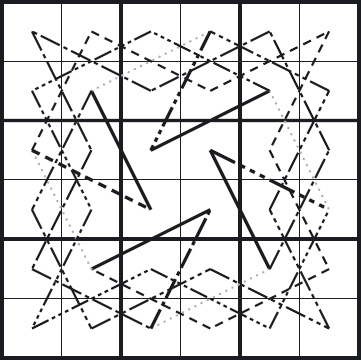
Solution 11.10 See Figure S.5.

The parallel moves used to connect circuits of different colours are indicated by dotted lines depicting the straight moves, and solid black lines, depicting the diagonal moves.

Note how the choice of parallel moves constrains the choice of a circuit of the striped squares. In contrast, there is complete freedom in choosing circuits of the white and shaded-and-striped squares. There is some freedom in choosing a circuit of the shaded squares, but not complete freedom. In this way, a substantial number of circuits can be found all based on the same set of combining parallel moves. In the circuit shown, the “shaded”, “white” and “shaded-and-striped” circuits were constructed by “copying” the striped circuit.

Figure S.5: A knight’s circuit. The circuit is formed from the solid and dashed lines. The two pairs of parallel dotted lines depict straight moves that are replaced. The diagonal moves that replace them are depicted by solid black lines.

Figure S.6: Details of how the four straight-move circuits are combined; the straight moves indicated by dotted lines are replaced by diagonal moves indicated by solid black lines.

Figure S.7: Knight’s circuit of an 8×6 and an 8×8 board. (Dotted lines are not part of the circuit; these are the moves that are replaced by diagonal moves, as detailed in Figure S.6.)

The same set of combining parallel moves can be used to construct a circuit of an 8×6 board; all that is required is to “shorten” the straight-move circuits in order to accommodate the smaller board. (But note that they cannot be used to construct a circuit of a 6×8 board.)

Solution 11.11 Figure S.6 shows details of how the straight-move circuits are combined. Moves indicated by dotted lines are replaced by the diagonal moves indicated by solid black lines.

Figure S.7 shows the circuits obtained in this way. The dotted lines are not part of the circuit; these are the moves that are replaced.

In order to construct a circuit for any board of size 4m×2n, where m is at least 2 and n is at least 3, it suffices to use the technique detailed in Figures 11.2 and 11.3 for extending straight-move circuits to boards of arbitrary size. This construction has to be applied four times, once for each of the straight-move circuits in the solution to the 8×6-board problem.

Solution 11.12 We begin by identifying the moves shown in Figure 11.15. See Figure S.8. (Note the symmetry.)

Figure S.8: Details of combining circuits. Diagonal moves are shown in black. Straight moves are coloured. The dotted lines represent the moves that are replaced. Solid lines represent the moves that replace them.

Now it is easy to fill in the straight-move circuits around the remaining squares. See Figure S.9.

Figure S.9: Knight’s circuit of a 6×6 board. (The dotted lines do not form part of the circuit as detailed in Figure S.8.)

For the general problem, it is easy to extend the straight-move circuits.