Previous chapters used quantitative data to demonstrate important statistical concepts. However, some of the data financial analysts use is qualitative (see Chapter 2 for a discussion of the distinction between qualitative and quantive data). Dummy variables, briefly described in Chapter 2, are a way of turning qualitative variables into quantitative variables. Once the variables are quantitative, then the correlation and regression techniques described in previous chapters can be used. Formally, a dummy variable is a variable that can take on only two values, 0 or 1. We will demonstrate how regression works when some of the explanatory variables are dummies using the following examples.
Once qualitative explanatory variables have been transformed into dummy variables, regression can be carried out in the standard way and all the theory and intuition developed in previous chapters can be used.
Why, then, are we allocating an entire chapter to this topic? There are two answers to this question. First, regression with dummy explanatory variables is quite common and the interpretation of coefficient estimates is somewhat different. For this reason it is worthwhile discussing the interpretation in detail. Second, regression with dummy explanatory variables is closely related to another set of techniques called Analysis of Variance (or ANOVA for short). ANOVA is not used that often by financial researchers (although in the field of corporate finance it is sometimes used), but it is an extremely common tool in other social and physical sciences such as sociology, education, medical statistics and epidemiology.
While most computer software packages such as Excel have ANOVA capabilities, the terminology of ANOVA is quite different from that used by financial analysts, so ANOVA may seem confusing and unfamiliar to you (e.g. the Excel Tools/Data Analysis menu has several ANOVA choices referring to "Single factor", "Two-factor with replication", "Two-factor without replication"). What we should note here, however, is that regression with dummy explanatory variables can do anything ANOVA can. In fact, regression with dummy variables is a more general and more powerful tool than ANOVA. For instance, the terms "Single factor ANOVA" or "Two-factor ANOVA" refer to the number of dummy explanatory variables. Excel (and most common computer packages that perform ANOVA), can handle no more than two. However, Excel allows for up to 16 explanatory variables in its multiple regression facilities and, thus, can handle very complicated ANOVA models. In short, if you know how to use and understand regression, then you have no need to learn about ANOVA.
We begin by considering a regression model with one dummy explanatory variable, D:
If we carry out OLS estimation of the above regression model, we obtain
The straight-line relationship between Y and D gives a fitted value for the ith observation of:
Note, since Di is either 0 or 1, Ŷi =
Example: Explaining house prices (continued from page 111)
Table 7.1 gives computer output from a regression of Y = house prices on D = air conditioning dummy using data from HPRICE.XLS. Note that an examination of the P-value or the confidence interval (i.e. Upper 95%, Lower 95%) shows us that β is strongly significant. Furthermore,
Table 7.1. Regression of house prices on air conditioning dummy.
Coefficient | Standard error | t-stat | P-value | Lower 95% | Upper 95% | |
|---|---|---|---|---|---|---|
Intercept | 59884.85 | 1233.50 | 48.55 | 7.1E – 200 | 57461.84 | 62307.86 |
D | 25995.74 | 2191.36 | 11.86 | 4.9E – 29 | 21691.18 | 30300.32 |
However, there is another, closely related, way of thinking about regression results when the explanatory variable is a dummy. In the case of houses without air conditioning Di = 0 and hence Ŷi = 59,885. In other words, our regression model finds that houses without air conditioning are worth on average $59,885. In the case of houses with air conditioning, Di = 1 and the regression model finds that Ŷi =
To provide more intuition, note that if we had not carried out a regression, but simply calculated the average price for houses with air conditioning, we would have found this figure to be $85,881. If we had then calculated the average price for houses without air conditioning, we would have found them to be worth $59,885. That is, we would have found exactly the same results as in the regression analysis.
Remember, however, the discussion of the omitted variables bias in Chapter 6. The simple regression in this example is omitting many important explanatory variables. We definitely cannot use the results of this simple regression to make statements like "Adding an air conditioner to your house will raise its value by $25,996". Since air conditioners cost a few hundred dollars, the previous statement is clearly ridiculous.
Now, consider the multiple regression model with several dummy explanatory variables:
OLS estimation of this regression model and statistical analysis of the results can be carried out in the standard way. To aid in interpretation, we return to the house-pricing example.
Example: Explaining house prices (continued from page 113)
Consider the case where we have two dummy explanatory variables, D1 = 1 if the house has a driveway (= 0 if not) and D2 = 1 if the house has a recreation room (= 0 if not). These dummy variables implicitly classify the houses in the data set into four different groups:
Houses with a driveway and recreation room (D1 = 1 and D2 = 1).
Houses with a driveway, but no recreation room (D1 = 1 and D2 = 0).
Houses with no driveway, but with a recreation room (D1 = 0 and D2 = 1).
Houses with no driveway and no recreation room (D1 = 0 and D2 = 0).
Keep this classification in mind as we interpret Table 7.3, which contains results from a regression of house price (Y), on D1 and D2.
Table 7.3. Regression of house price on driveway and recreation room dummies.
Coefficient | Standard error | t-stat | P-value | Lower 95% | Upper 95% | |
|---|---|---|---|---|---|---|
Intercept | 47099.08 | 2837.62 | 16.60 | 2.42E – 50 | 41525.02 | 52673.14 |
D1 | 21159.91 | 3062.44 | 6.91 | 1.37E – 11 | 15144.22 | 27175.60 |
D2 | 16023.69 | 2788.63 | 5.75 | 1.52E – 08 | 10545.86 | 21501.51 |
Putting in either 0 or 1 values for the dummy variables, we obtain the fitted values for Y for the four categories of houses:
If D1 = 1 and D2 = 1, then Ŷ =
If D1 = 1 and D2 = 0, then Ŷ =
If D1 = 0 and D2 = 1, then Ŷ =
If D1 0 and D2 = 0, then Ŷ =
In short, multiple regression with dummy variables may be used to classify the houses into different groups and to find average house prices for each group. Alternatively, results may be presented directly as coefficient estimates. For instance,
In the previous discussion, we have assumed that all the explanatory variables are dummies but, in practice, you may often have a mix of different types of explanatory variables. The simplest such case is one where there is one dummy variable (D) and one quantitative explanatory variable (X) in a regression:
The interpretation of results from such a regression can be illustrated in the context of an example.
Example: Explaining house prices (continued from page 115)
If we regress Y = house price on D = air conditioner dummy and X = lot size, we obtain
Here things are not quite so simple since we obtain Ŷi = 52,868 + 5.638 Xi = if Di = 1 (i.e. the ith house has an air conditioner) and Ŷi = 32,693 + 5.638Xi if Di = 0 (i.e. the house does not have an air conditioner). In other words, there are two different regression lines depending on whether the house has an air conditioner or not. Contrast this point with the discussion in example above where we had only one dummy explanatory variable. In that case, the regression implied that the average price of the house differed between houses with and without air conditioners. Here we are saying a wholly different regression line exists. In other words, we cannot simply state (as we did in examples in previous examples in this chapter) what the average value of different groups of houses will be.
We can, however, say that
It is worthwhile to examine more closely the two different regression lines that exist for houses with and without air conditioners. Note that they both have the same slope,
We can extend the previous discussion to the case of many dummy and non-dummy explanatory variables. An example having two dummy and two non-dummy explanatory variables is the following regression model:
The interpretation of results from this regression model combines elements from all the previous examples in this chapter.
Example: Explaining house prices (continued from page 117)
If we regress Y = house price on D1 = dummy variable for driveway, D2 = dummy variable for recreation room, X1 = lot size and X2 = number of bedrooms we obtain:
If D1 = 1 and D2 = 1, then Ŷ =
If D1 = 1 and D2 = 0, then Ŷ = 9,862 + 5.197X1 + 10,562X2. This is the regression line for houses with a driveway but no recreation room.
If D1 = 0 and D2 = 1, then Ŷ = 8,233 + 5.197X1 + 10,562X2. This is the regression line for houses with a recreation room but no driveway.
If D1 = 0 and D2 = 0, then Ŷ = −2,736 + 5.197X1 + 10,562X2. This is the regression line for houses with no driveway and no recreation room.
That is, with two dummy variables we have four different regression lines. All of these lines have the same slopes but different intercepts. The coefficients on the dummy variables,
The following are a few of the types of verbal statements that we can make about the regression results:
"Houses with driveways tend to be worth $12,598 more than similar houses with no driveway".
"If we consider houses with the same number of bedrooms, then adding an extra square foot of lot size will tend to increase the price of a house by $5.20".
"An extra bedroom will tend to add $10,562 to the value of a house, ceteris paribus".
We should stress, however, that all such statements assume that omitted variables bias is not a problem in the regression. Furthermore, statements which imply causality (e.g. "adding an extra square foot of lot size will tend to increase the price of the house by $5.20") are only valid if it is truly the case that the explanatory variable causes the dependent variable (see Chapters 4 and 6 for further discussion of causality in regression).
We used the dummy variables above in a way that allowed for different intercepts in the regression line, but the slope of the regression line was always the same. We can, however, allow for different slopes by interacting dummy and non-dummy variables. To understand this consider the following regression model:
D and X are dummy and non-dummy explanatory variables, as above. However, here we have added a new variable Z into the regression and we define Z = DX.
How do we interpret results from a regression of Y on D, X and Z? This question can be answered by noting that Z is either 0 (for observations with D = 0) or X (for observations with D = 1). If, as before, we consider the fitted regression lines with D = 0 and D = 1 we obtain:
If D = 1 then Ŷ = (
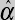
If D = 0, then Ŷ =
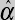
In other words, two different regression lines corresponding to D = 0 and D = 1 exist and have different intercepts and slopes. One implication is that the marginal effect of X on Y is different for D = 0 and D = 1. In a written report, you could write up each of the regression lines separately using the terminology and interpretation of Chapters 4 and 6.
Thus far, we have focussed on the case where the explanatory variables can be dummies. However, in some cases the dependent variable may be a dummy. For instance, a researcher in the field of corporate finance might be interested in investigating why some companies go bankrupt and others do not, or why some raise money by issuing equity and others use debt, etc. An empirical analysis might involve collecting data from many different companies. Potential explanatory variables might include company characteristics such as debt, sales, profit, and so on. The dependent variable, however, would be qualitative (e.g. for each company data would be of the form "It went bankrupt"/"It did not go bankrupt" or "The company expanded through debt financing"/"The company did not use debt to finance its expansion") and the researcher would have to create a dummy dependent variable.
The techniques for working with dummy dependent variables[39] are beyond the scope of this book. However, there are two facts worth noting:
There are some problems with using OLS estimation in this case. However, these problems are not enormous, so that OLS estimation might be adequate in many circumstances.
Nevertheless, there are better estimation methods than OLS. The two main alternatives are termed Logit and Probit. Computer software packages with only basic statistical capabilities (e.g. Excel) do not have the capability to perform these estimation methods. Thus, if you ever need to do extensive work with dummy dependent variable models, you will have to use another software package (e.g. Stata).
Dummy variables can take on a value of either 0 or 1. They are often used with qualitative data.
The statistical techniques associated with the use of dummy explanatory variables are exactly the same as with non-dummy explanatory variables.
A regression involving only dummy explanatory variables implicitly classifies the observations into various groups (e.g. houses with air conditioning and those without). Interpretation of results is aided by careful consideration of what the groups are.
A regression involving dummy and non-dummy explanatory variables implicitly classifies the observations into groups and says that each group will have a regression line with a different intercept. All these regression lines have the same slope.
A regression involving dummy, non-dummy and interaction (i.e. dummy times non-dummy variables) explanatory variables implicitly classifies the observations into groups and says that each group will have a different regression line with a different intercept and slope.
If the dependent variable is a dummy, then other techniques which are not covered in this book should be used.
[39] To introduce some jargon, such models are called "limited dependent variable" models. That is, the dependent variable can take on a limited range of values.