This chapter introduces the basics of data handling. It focuses on four important areas:
A brief discussion of the sources from which data can be obtained.[1]
An illustration of the types of graphs that are commonly used to present information in a data set.
A discussion of simple numerical measures, or descriptive statistics, often presented to summarize key aspects of a data set.
This section introduces common types of data and defines the terminology associated with their use.
Financial researchers are often interested in phenomena such as stock prices, interest rates, exchange rates, etc. This data is collected at specific points in time. In all of these examples, the data are ordered by time and are referred to as time series data. The underlying phenomenon which we are measuring (e.g. stock prices, interest rates, etc.) is referred to as a variable. Time series data can be observed at many frequentcies. Commonly used frequencies are: annual (i.e. a variable is observed every year), quarterly (i.e. four times a year), monthly, weekly or daily.[2]
In this book, we will use the notation Yt to indicate an observation on variable Y (e.g. an exchange rate) at time t. A series of data runs from period t = 1 to t = T. "T" is used to indicate the total number of time periods covered in a data set. To give an example, if we were to use monthly time series data from January 1947 through October 1996 on the UK pound/US dollar exchange – a period of 598 months – then t = 1 would indicate January 1947, t = 598 would indicate October 1996 and T = 598 the total number of months. Hence, Y1 would be the pound/dollar exchange rate in January 1947, Y2 this exchange rate in February 1947, etc. Time series data are typically presented in chronological order.
Working with time series data often requires some special tools, which are discussed in Chapters 8–11.
In contrast to the above, some researchers often work with data that is characterized by individual units. These units might refer to companies, people or countries. For instance, a researcher investigating theories relating to portfolio allocation might collect data on the return earned on the stocks of many different companies. With such cross-sectional data, the ordering of the data typically does not matter (unlike time series data).
In this book, we use the notation Yi to indicate an observation on variable Y for individual i. Observations in a cross-sectional data set run from unit i = 1 to N. By convention, "N" indicates the number of cross-sectional units (e.g. the number of companies surveyed). For instance, a researcher might collect data on the share price of N = 100 companies at a certain point in time. In this case, Y1 will be equal to the share price of the first company, Y2 the share price of the second company, and so on.
It is worthwhile stressing an important distinction between types of data. In the preceding example, the researcher collecting data on share prices will have a number corresponding to each company (e.g. the price of a share of company 1 is $25). This is referred to as quantitative data.
However, there are many cases where data does not come in the form of a single number. For instance, in corporate finance a researcher may be interested in investigating how companies decide between debt or equity financing of new investments. In this case, the researcher might survey companies and obtain responses of the form "Yes, we financed our investment by taking on debt" or "No, we did not finance our investment by taking on debt (instead we raised money by issuing new equity)". Alternatively, in event-study analysis, interest centers on how events (e.g. a company's earning announcement) affects a company's share price. In some cases, the events a researcher is studying come in the form of a simple Good News/Bad News dichotomy.
Data that comes in categories (e.g. Yes/No or Good News/Bad News) are referred to as qualitative. Such data arise often in finance when choices are involved (e.g. the choice to invest or not to invest in a certain stock, to issue new equity or not, etc). Financial researchers will usually convert these qualitative answers into numeric data. For instance, in the debt financing example, we might set Yes = 1 and No = 0. Hence, Y1 = 1 means that the first company financed its investment by taking on debt, Y2 = 0 means that the second company did not. When variables can take on only the values 0 or 1, they are referred to as dummy (or binary) variables. Working with such variables is a topic that will be discussed in detail in Chapter 7.
Some data sets will have both a time series and a cross-sectional component. This data is referred to as panel data. For instance, research involving portfolio choice might use data on the return earned by many companies' shares for many months. Alternatively, financial researchers studying exchange rate behavior might use data from many countries for many months. Thus, a panel data set on Y = the exchange rate for 12 countries would contain the exchange rate for each country in 1950 (N = 12 observations), followed by the exchange rate for the same set of countries in 1951 (another N = 12 observations), and so on. Over a period of T years, there would be T × N observations on Y.[3]
We will use the notation Yit to indicate an observation on variable Y for unit i at time t. In the exchange rate example, Y11 will be the exchange rate in country 1, year 1, Y12 the exchange rate for country 1 in year 2, etc.
In this book, we will mainly assume that the data of interest, Y, is directly available. However, in practice, you may be required to take raw data from one source, and then transform it into a different form for your empirical analysis. For instance, you may take raw time series data on the variables X = company earnings, and W = number of shares, and create a new variable: Y = earnings per share. Here the transformation would be Y = X/W. The exact nature of the transformation required depends on the problem at hand, so it is hard to offer any general recommendations on data transformation. Some special cases are considered in later chapters. Here it is useful to introduce one common transformation that arises repeatedly in finance when using time series data.
To motivate this transformation, note that in many cases we are not interested in the price of an asset, but in the return that an investor would make from purchase of the asset. This depends on how much the price of the asset will change over time. Suppose, for instance, that we have annual data on the price of a share in a particular company for 1950–1998 (i.e. 49 years of data) denoted by Yt for t = 1 to 49. In many empirical projects, this might be the variable of primary interest. We will refer to such series as the level of the share price. However, people are often more interested in the growth of the share price. A simple way to measure growth is to take the share price series and calculate a percentage change for each year. The percentage change in the share price between period t – 1 and t is calculated according to the formula:
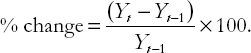
It is worth stressing that a percentage change always has a time scale associated with it (e.g. the percentage change between period t – 1 and t). For instance, with annual data this formula would produce an annual percentage change, with monthly data the formula would produce a monthly percentage change, etc.
As will be discussed in later chapters, it is sometimes convenient to take the natural logarithm, or ln(.) of variables. The definition and properties of logarithms can be found in the Appendix to Chapter 1 or virtually any introductory mathematics textbook. Using the properties of logarithms, it can be shown that the percentage change in a variable is approximately 100 × [ln(Yt) – ln(Yt−1)]. This formula provides an alternative way of calculating a percentage change and is often used in practice.
The percentage change of an asset's price is often referred to as the growth of the price or the change in the price. It can also be referred to as the return if it reflects the return that an investor purchasing the share would earn. However, to interpret the growth of an asset's price as the return an investor would make one has to assume that there are no other income flows coming from holding the asset. For some assets this may be a reasonable assumption. But where it is not reasonable, the formula for a return has to be modified to include all income the investor would receive from holding the asset. For instance, most stocks pay dividends. If we let Dt be the dividend paid between period t – 1 and t then the return (which we denote by Rt) made by an investor (measured as a percentage) would be
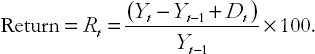
Another concept commonly used in finance is that of the excess return. This is the difference between an asset's return and that of some benchmark asset which is usually defined as a safe, low-risk asset (e.g. the return on a government bond). The concept of an excess return is an important one, since investors will only take on the risk of purchasing a particular asset if it is expected to earn more than a safe asset. For instance, if the expected return on a (risky) company's stock is 5% this might sound like a good return. But if the investor can earn a 6% return by buying (safe) government bonds, then the expected 5% return on the risky asset becomes much less impressive. It is the excess return of holding a share that is important, not the simple return. If the return on a risk-free asset is denoted by R0t, then the excess return (ER), measured as a percentage, on an asset is defined as:
Time series data will be discussed in more detail in Chapters 8–11. It is sufficient for you to note here that we will occasionally distinguish between the level of a variable and its growth rate, and that it is common to work with the returns an investor would make from holding an asset.
Many variables that financial analysts work with come in the form of index numbers. For instance, the common measures of stock price performance reported in the media are indices. The Dow Jones Industrial Average (DJIA) and Standard & Poor's composite share index (S&P500) are stock price indices.
Appendix 2.1, at the end of this chapter, provides a detailed discussion of what these are and how they are calculated. However, if you just want to use an index number in your empirical work, a precise knowledge of how to calculate indices is probably unnecessary. Having a good intuitive understanding of how an index number is interpreted is sufficient. Accordingly, here in the body of the text we provide only an informal intuitive discussion of index numbers.
Suppose you are interested in studying the performance of the stock market as a whole and want a measure of how stock prices change over time. The question arises as to how we measure "prices" in the stock market as a whole. The price of the stock of an individual company (e.g. Microsoft, Ford or Wal-Mart, etc.) can be readily measured, but often interest centers not on individual companies, but on the stock market as a whole. From the point of view of the investor, the relevant price would be the price of a portfolio containing the sorts of shares that a typical investor might buy. The price of this portfolio is observed at regular intervals over time in order to determine how prices are changing in the stock market as a whole. But the price of the portfolio is usually not directly reported. After all, if you are told the price of an individual share (e.g. the price of a share of Microsoft is $2.20), you have been told something informative, but if you are told "the price of a portfolio of representative shares" is $1,400, that statement is not very informative. To interpret this latter number, you would have to know what precisely was in the portfolio and in what quantities. Given the thousands of shares bought and sold in a modern stock market, far too much information would have to be given.
In light of such issues, data often comes in the form of a price index. Indices may be calculated in many ways, and it would distract from the main focus of this chapter to talk in detail about how they are constructed (see Appendix 2.1 for more detail). However, the following points are worth noting at the outset. First, indices almost invariably come as time series data. Second, one time period is usually chosen as a base year and the price level in the base year is set to 100.[4] Third, price levels in other years are measured in percentages relative to the base year.
An example will serve to clarify these issues. Suppose a price index for 4 years exists, and the values are: Y1 = 100, Y2 = 106, Y3 = 109 and Y4 = 111. These numbers can be interpreted as follows: The first year has been selected as a base year and, accordingly, Y1 = 100. The figures for other years are all relative to this base year and allow for a simple calculation of how prices have changed since the base year. For instance, Y2 = 106 means that prices have risen from 100 to 106 – a 6% rise since the first year. It can also be seen that prices have risen by 9% from year 1 to year 3 and by 11% from year 1 to year 4. Since the percentage change in stock prices measures the return (exclusive of dividends), the price index allows the person looking at the data to easily see the return earned from buying the basket of shares which go into making up the index. In other words, you can think of a price index as a way of presenting price data that is easy to interpret and understand.
A price index is very good for measuring changes in prices over time, but should not be used to talk about the level of prices. For instance, it should not be interpreted as an indicator of whether prices are "high" or "low". A simple example illustrates why this is the case. At the time I am writing this, the DJIA is at 10,240 while the S&P500 is at 1,142. This does not mean that the stocks in the DJIA portfolio are worth almost ten times as much as the S&P500 portfolio. In fact, the two portfolios contain shares from many of the same companies. The fact that they are different from one another is due to their having different base years.
In our discussion, we have focussed on stock price indices, and these are indeed by far the most common type of index numbers used in finance. However, it is worth noting that there are many other price indices used in many fields. For example, economists frequently use price indices which measure the prices of goods and services in the economy. The economist faces the same sort of problem that the financial researcher does. The latter has to find ways of combining the information in the stock prices of hundreds of individual companies while the former has to find ways of combining information in the prices of millions of goods in a modern economy. Indices such as the Consumer Price Index (CPI) are the solution and a commonly reported measure of inflation is the change in the CPI. Since inflation plays a role in many financial problems, such economic price indices are also of use to the financial researcher.
Furthermore, other types of indices (e.g. quantity indices) exist and should be interpreted in a similar manner to price indices. That is, they should be used as a basis for measuring how phenomena have changed from a given base year.
This discussion of index numbers is a good place to mention another transformation which is used to deal with the effects of inflation. As an example, consider the interest rate (e.g. the return earned on a savings deposit in a bank or the return on a government bond). In times of high inflation, simply looking at an interest rate can be misleading. If inflation is high (say 10%), then an investor who deposits money in a savings account earning a lower rate of interest (say 5%) will actually lose money on her investment. To be precise, if the investor initially deposits $100 in the savings account, she will have $105 a year from now. But in the meantime the price of the "portfolio of goods" used to construct the CPI will have gone up by 10%. So goods which cost $100 originally will cost $110 a year later. The investor, with only $105 after a year, will actually end up being able to buy fewer goods than she could have originally.
The issues discussed in the previous paragraph lead researchers to want to correct for the effect of inflation. In the case of returns (e.g. the interest rate which measures the return the investor earns on her savings), the way to do this is to subtract the inflation rate from the original return. To introduce some terminology, an interest rate transformed in this way is called a real interest rate. The original interest rate is referred to as a nominal interest rate. This distinction between real and nominal variables is important in many investment decisions. The key things you should remember is that a real return is a nominal return minus inflation and that real returns have the effects of inflation removed from them.
All of the data you need in order to understand the basic concepts and to carry out the simple analyses covered in this book can be downloaded from the website associated with this book (http://www.wiley.com/go/koopafd). However, in the future you may need to gather your own data for an essay, dissertation or report. Financial data come from many different sources and it is hard to offer general comments on the collection of data. Below are a few key points that you should note about common data sets and where to find them.
It is becoming increasingly common for financial researchers to obtain their data over the Internet, and many relevant World Wide Web (www) sites now exist from which data can be downloaded. You should be forewarned that the web is a rapidly growing and changing place, so that the information and addresses provided here might soon be outdated. Appropriately, this section is provided only to give an indication of what can be obtained over the Internet, and as such is far from complete.
Some of the data sets available on the web are free, but many are not. Most university libraries or computer centers subscribe to various databases which the student can use. You are advised to check with your own university library or computer center to see what data sets you have access to. There are many excellent databases of stock prices and accounting information for all sorts of companies for many years. Unfortunately, these tend to be very expensive and, hence, you should see whether your university has a subscription to a financial database. Two of the more popular ones are DataStream by Thompson Financial (http://www.datastream.com/) and Wharton Research Data Services (http://wrds.wharton.upenn.edu/). With regards to free data, a more limited choice of financial data is available through popular Inter-net ports such as Yahoo! (http://finance.yahoo.com). The Federal Reserve Bank of St Louis also maintains a free database with a wide variety of data, including some financial time series (http://research.stlouisfed.org/fred2/). The Financial Data Finder (http://www.cob.ohio-state.edu/fin/osudata.htm), provided by the Fisher College of Business at the Ohio State University is also a useful source. Many academics also make the data sets they have used available on their websites. For instance, Robert Shiller at Yale University has a website which provides links to many different interesting financial data sets (http://aida.econ.yale.edu/%7Eshiller/index.html).
An extremely popular website among economists is "Resources for Economists on the Internet" (http://rfe.wustl.edu/EconFAQ.html). This site contains all sorts of interesting material on a wide range of economic topics, including links to many sorts of financial data. On this site you can also find links to Journal Data Archives. Many journals encourage their authors to make their data publicly available and, hence, in some cases you can get financial data from published academic papers through Journal Data Archives.
The general advice I want to give here is that spending some time searching the Internet can often be very fruitful.
Once you have your data, it is important for you to summarize it. After all, anybody who reads your work will not be interested in the dozens or – more likely – hundreds or more observations contained in the original raw data set. Indeed, you can think of the whole field of financial econometrics as one devoted to the development and dissemination of methods whereby information in data sets is summarized in informative ways. Charts and tables are very useful ways of presenting your data. There are many different types (e.g. bar chart, pie chart, etc.). A useful way to learn about the charts is to experiment with the ChartWizard© in Excel. In this section, we will illustrate a few of the commonly used types of charts.
Since most financial data is either in time series or cross-sectional form, we will briefly introduce simple techniques for graphing both types of data.
Monthly time series data from January 1947 through October 1996 on the UK pound/US dollar exchange rate is plotted using the "Line Chart" option in Excel's ChartWizard© in Figure 2.1 (this data is located in Excel file EXRUK.XLS). Such charts are commonly referred to as time series graphs. The data set contains 598 observations – far too many to be presented as raw numbers for a reader to comprehend. However, a reader can easily capture the main features of the data by looking at the chart. One can see, for instance, the attempt by the UK government to hold the exchange rate fixed until the end of 1971 (apart from large devaluations in September 1949 and November 1967) and the gradual depreciation of the pound as it floated downward through the middle of the 1970s.
With time series data, a chart that shows how a variable evolves over time is often very informative. However, in the case of cross-sectional data, such methods are not appropriate and we must summarize the data in other ways.
A key variable in many studies of international financial development is Gross Domestic Product (GDP) per capita, a measure of income per person. Excel file GDPPC.XLS contains cross-sectional data on real GDP per capita in 1992 for 90 countries.[6]
One convenient way of summarizing this data is through a histogram. To construct a histogram, begin by constructing class intervals or bins that divide the countries into groups based on their GDP per capita. In our data set, GDP per person varies from $408 in Chad to $17,945 in the USA. One possible set of class intervals is 0–2,000, 2,001–4,000, 4,001–6,000, 6,001–8,000, 8,001–10,000, 10,001–12,000, 12,001–14,000, 14,001–16,000 and 16,001 and over (where all figures are in US dollars).
Note that each class interval (with the exception of the 16,001 + category) is $2,000 wide. In other words, the class width for each of our bins is 2,000. For each class interval we can count up the number of countries that have GDP per capita in that interval. For instance, there are seven countries in our data set with real GDP per capita between $4,001 and $6,000. The number of countries lying in one class interval is referred to as the frequency[7] of that interval. A histogram is a bar chart that plots frequencies against class intervals.[8]
Figure 2.2 is a histogram of our cross-country GDP per capita data set that uses the class intervals specified in the previous paragraph. Note that, if you do not wish to specify class intervals, Excel will do it automatically for you. Excel also creates a frequency table, which is located next to the histogram.
The frequency table indicates the number of countries belonging to each class interval (or bin). The numbers in the column labeled "Bin" indicate the upper bounds of the class intervals. For instance, we can read that there are 33 countries with GDP per capita less than $2,000; 22 countries with GDP per capita above $2,000 but less than $4,000; and so on. The last row says that there are 4 countries with GDP per capita above $16,000.
This same information is graphed in a simple fashion in the histogram. Graphing allows for a quick visual summary of the cross-country distribution of GDP per capita. We can see from the histogram that many countries are very poor, but that there is also a "clump" of countries that are quite rich (e.g. 19 countries have GDP per capita greater than $12,000). There are relatively few countries in between these poor and rich groups (i.e. few countries fall in the bins labeled 8,000, 10,000 and 12,000).
Researchers often refer to this clumping of countries into poor and rich groups as the "twin peaks" phenomenon. In other words, if we imagine that the histogram is a mountain range, we can see a peak at the bin labeled 2,000 and a smaller peak at 14,000. These features of the data can be seen easily from the histogram, but would be difficult to comprehend simply by looking at the raw data.
Financial analysts are often interested in the nature of the relationships between two or more variables. For instance: "What is the relationship between capital structure (i.e. the division between debt and equity financing) and firm performance (e.g. profit)?" "What is the relationship between the return on a company's stock and the return on the stock market as a whole?" "What are the effects of financial decisions on the probability that a firm will go bankrupt?" "Are changes in the money supply a reliable indicator of inflation changes?" "Do differences in financial regulation explain why some countries are growing faster than others?"
The techniques described previously are suitable for describing the behavior of only one variable; for instance, the properties of real GDP per capita across countries in Figure 2.2. They are not, however, suitable for examining relationships between pairs of variables.
Once we are interested in understanding the nature of the relationships between two or more variables, it becomes harder to use graphs. Future chapters will discuss regression analysis, which is an important tool used by financial researchers working with many variables. However, graphical methods can be used to draw out some simple aspects of the relationship between two variables. XY-plots (also called scatter diagrams) are particularly useful in this regard.
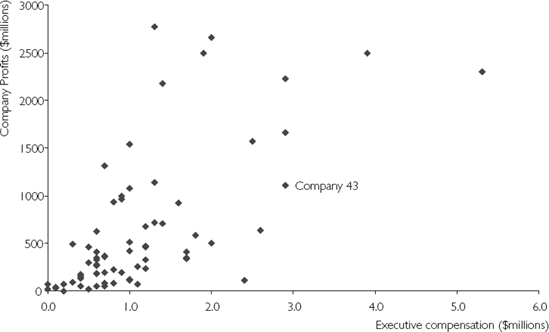
Figure 2.3 is a graph of data on executive compensation (i.e. the salary paid to the chief executive, expressed in millions of dollars) for 70 companies, along with data on the profits of the companies (i.e. profit expressed in millions of dollars). (This data is available in Excel file EXECUTIVE.XLS.) It is commonly thought that there should be a relationship between these two variables, either because more profitable companies can afford to hire better chief executives (and pay them more) or because executive talent leads to higher profits.
Figure 2.3 is an XY-plot of these two variables. Each point on the chart represents a particular company. Reading up the Y-axis (i.e. the vertical one) gives us the compensation of the chief executive in that company. Reading across the X-axis (i.e. the horizontal one) gives us the profit of the company. It is possible to label each point with its corresponding company name. We have not done so here, since labels for 70 companies would clutter the chart and make it difficult to read. However, one company, Company 43, has been labeled. Note that Company 43 paid its chief executive $2.9 million (Y = 2.9) and had profits of $1,113 million (X = 1,113).
The XY-plot can be used to give a quick visual impression of the relationship between profits and executive compensation. An examination of this chart indicates some support for the idea that a relationship between profits and executive compensation does exist. For instance, if we look at companies with relatively low pro-fits (less than $500 million, say), almost all of them compensate their executives at a relatively low level (less than $1 million). If we look at companies with high profits (e.g. over $1,500 million), almost all of them have high levels of executive compensation (more than $2 million). This indicates that there may be a positive relationship between profits and executive compensation (i.e. high values of one variable tend to be associated with high values of the other; and low values, associated with low values). It is also possible to have a negative relationship. This might occur, for instance, if we substituted a measure of losses for profits in the XY-plot. In this case, high levels of losses might be associated with low levels of executive compensation.
It is worth noting that the positive or negative relationships found in the data are only "tendencies", and, as such, do not hold necessarily for every company. That is, there may be exceptions to the general pattern of profit's association with high rates of compensation. For example, on the XY-plot we can observe one company with high profits of roughly $1,300 million, but low executive compensation of only $700,000. Similarly, low profits can also be associated with high rates of compensation, as evidenced by one company with low profits of roughly $150 million, which is paying its chief executive the high amount of almost $2.5 million. As researchers, we are usually interested in drawing out general patterns or tendencies in the data. However, we should always keep in mind that exceptions (in statistical jargon outliers) to these patterns typically exist. In some cases, finding out which companies don't fit the general pattern can be as interesting as the pattern itself.
Graphs have an immediate visual impact that is useful for livening up an essay or report. However, in many cases it is important to be numerically precise. Later chapters will describe common numerical methods for summarizing the relationship between several variables in greater detail. Here we discuss briefly a few descriptive statistics for summarizing the properties of a single variable. By way of motivation, we will return to the concept of distribution introduced in our discussion on histograms.
In our cross-country data set, real GDP per capita varies across the 90 countries. This variability can be seen by looking at the histogram in Figure 2.2, which plots the distribution of GDP per capita across countries. Suppose you wanted to summarize the information contained in the histogram numerically. One thing you could do is to present the numbers in the frequency table in Figure 2.2. However, even this table may provide too many numbers to be easily interpretable. Instead it is common to present two simple numbers called the mean and standard deviation.
The mean is the statistical term for the average. The mathematical formula for the mean is given by:
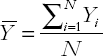
where N is the sample size (i.e. number of countries) and Σ is the summation operator (i.e. it adds up real GDP per capita for all countries). In our case, mean GDP per capita is $5,443.80. Throughout this book, we will place a bar over a variable to indicate its mean (i.e.
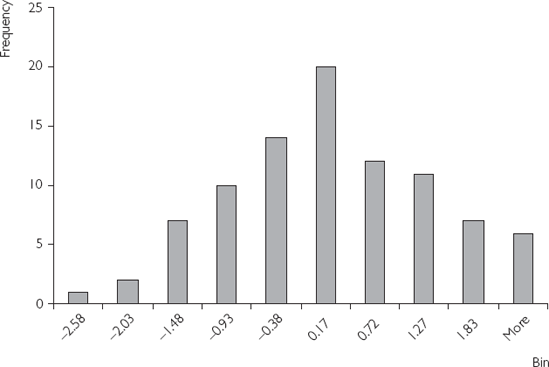
The concept of the mean is associated with the middle of a distribution. For example, if we look at the previous histogram, $5,443.80 lies somewhere in the middle of the distribution. The cross-country distribution of real GDP per capita is quite unusual, having the twin peaks property described earlier. It is more common for distributions of economic variables to have a single peak and to be bell-shaped. Figure 2.4 is a histogram that plots just such a bell-shaped distribution. For such distributions, the mean is located precisely in the middle of the distribution, under the single peak.
Of course, the mean or average figure hides a great deal of variability across countries. Other useful summary statistics, which shed light on the cross-country variation in GDP per capita, are the minimum and maximum. For our data set, minimum GDP per capita is $408 (Chad) and maximum GDP is $17,945 (USA). By looking at the distance between the maximum and minimum we can see how dispersed the distribution is.
The concept of dispersion is quite important in finance and is closely related to the concepts of variability and inequality. For instance, real GDP per capita in 1992 in our data set varies from $408 to $17,945. If poorer countries were, in the near future, to grow quickly, and richer countries to stagnate, then the dispersion of real GDP per capita in, say, 2012, might be significantly less. It may be the case that the poorest country at this time will have real GDP per capita of $10,000 while the richest country will remain at $17,945. If this were to happen, then the cross-country distribution of real GDP per capita would be more equal (less dispersed, less variable). Intuitively, the notions of dispersion, variability and inequality are closely related.
The minimum and maximum, however, can be unreliable guidelines to dispersion. For instance, what if, with the exception of Chad, all the poor countries, experienced rapid economic growth between 1992 and 2012, while the richer countries did not grow at all? In this case, cross-country dispersion or inequality would decrease over time. However, since Chad and the USA did not grow, the minimum and maximum would remain at $408 and $17,945, respectively.
A more common measure of dispersion is the standard deviation. Its mathematical formula is given by:
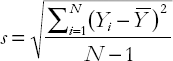
although in practice you will probably never have to calculate it by hand.[9] You can calculate it easily in Excel using either the Tools/Descriptive Statistics or the Functions facility. Confusingly, statisticians refer to the square of the standard deviation as the variance (s2) and it is common to see either terminology used. So it is important to remember this close relationship between the standard deviation and the variance.
These measures have little direct intuition. In our cross-country GDP data set, the standard deviation is $5,369.496 and it is difficult to get a direct feel for what this number means in an absolute sense. However, the standard deviation can be interpreted in a comparative sense. That is, if you compare the standard deviations of two different distributions, the one with the smaller standard deviation will always exhibit less dispersion. In our example, if the poorer countries were to suddenly experience economic growth and the richer countries to stagnate, the standard deviation would decrease over time. As another example, consider the returns of two stocks observed for many months. In some months the stocks earn high returns, in other months they earn low returns. This variability in stock returns is measured by the variance. If one stock has a higher variance than the other stock, then we can say it exhibits more variability. As the variability in stock returns relates to the risk involved in holding the stock, the variance is very important in portfolio management.
In the previous section we talked about means and variances. If this were a statistics textbook, we would actually have called them sample means and sample variances. The word "sample" is added to emphasize that they are calculated using an actual "sample" of data. For instance, in our cross-country GDP data set we took the data we had and calculated (using Excel) exact numbers for
As another example, suppose we have collected data on the return to holding stock in a company for the past 100 months. We can use this data to calculate the mean and variance. However, these numbers are calculated based on the historical performance of the company. In finance, we are often interested in predicting future stock returns. By definition we do not know exactly what these will be, so we cannot calculate sample means and variances as we did above. But a potential investor would be interested in some similar measures. That is, this investor would be interested in the typical return which she might expect. She might also be interested in the risk involved in purchasing the stock. The concept of a typical expected value sounds similar to the ideas we discussed relating to the mean. The concept of riskiness sounds similar to the idea of a variance we discussed above. In short, we need concepts like the sample mean and variance, but for cases when we do not actually have data to calculate them. The relevant concepts are the population mean and population variance.
If this were a statistics book, we would now get into a long discussion of the distinction between population and sample concepts involving probability theory and many equations. However, for the student who is interested in doing financial data analysis, it is enough to provide some intuition and definitions.
A conventional statistics textbook might begin motivating population and sample concepts through an example. Consider, for instance, the height of every individual in the USA. In the population as a whole there is some average height (the population mean height) and some variance of heights (the population variance). This population mean and variance will be unknown, unless someone actually went out and measured the height of every person in the USA.
However, a researcher might have data on the actual heights of 100 people (e.g. a medical researcher might measure the height of each of 100 patients). Using the data for 100 people, the researcher could calculate
Perhaps the previous two paragraphs are enough to intuitively motivate the distinction between sample and population means and variances. To see why financial analysts need to know this distinction (and to introduce some notation), let us use our example of a potential investor interested in the potential return she might make from buying a stock. Let Y denote next month's return on this stock. From the investor's point of view, Y is unknown. The typical return she might expect is measured by the population mean and is referred to as the expected value. We use the notation E(Y) to denote the expected return. Its name accurately reflects the intuition for this statistical concept. The "expected value" sheds light on what we expect will occur.
However, the return on a stock is rarely exactly what is expected [i.e. rarely will you find Y to turn out to be exactly E(Y)]. Stock markets are highly unpredictable, sometimes the return on stocks could be higher than expected, sometimes it could be lower than expected. In other words, there is always risk associated with purchasing a stock. A potential investor will be interested in a measure of this risk. Variance is a common way of measuring this risk. We use the notation var(Y) for this.
To summarize, in the previous section on descriptive statistics we motivated the use of the sample mean and variance,
Suppose you are an investor trying to decide whether to buy a stock based on its return next month. You do not know what this return will be. You are quite confident (say, 70% sure) that the markets will be stable, in which case you will earn a 1% return. But you also know there is a 10% chance the stock market will crash, in which case the stock return will be −10%. There is also a 20% probability that good news will boost the stock markets and you will get a 5% return on your stock.
Let us denote this information using symbols as there being three possible outcomes (good, normal, bad) as 1, 2, 3. So, for instance, Y1 = 0.05 will denote the 5% return if good times occur. We will use the symbol "P" for probability and the same subscripting convention. Thus, P3 = 0.10 will denote the 10% probability of a stock market crash. We can now define the expected return as a weighted average of all the possible outcomes:
In words, the expected return on the stock next month is 0.7% (i.e. a bit less than 1%).
In our example, we have assumed that there are only three possible outcomes next month. In general, if there are K possible outcomes,[10] the formula for the expected value is:
The formula for var(Y) is similar to that for s2 presented in the previous section. It also has a similar lack of intuition and, hence, we shall not discuss it in detail. For the case where we have K possible outcomes, the variance of Y is defined as:
The key thing to remember is that var(Y) is a measure of the dispersion of the possible outcomes which could occur and, thus, is closely related to the concept of risk.
Financial data come in many forms. Common types are time series, cross-sectional and panel data.
Financial data can be obtained from many sources. The Internet is becoming an increasingly valuable repository for many data sets.
Simple graphical techniques, including histograms and XY-plots, are useful ways of summarizing the information in a data set.
Many numerical summaries can be used. The most important are the mean, a measure of the location of a distribution, and the standard deviation, a measure of how spread out or dispersed a distribution is.
If Y is a variable which could have many outcomes, then the expected value, E(Y), is a measure of the typical or expected outcome (e.g. the expected return on a stock next month) and the variance, var(Y), is a measure of the dispersion of possible outcomes (e.g. relating to the riskiness in holding a stock next month).
To illustrate the basic ideas in constructing a stock price index, we use the data shown in Table 2.1.1 on the stock price of three fictitious companies: Megaco, Monstroco and Minico.
We begin by calculating a price index for a single company, Megaco, before proceeding to the calculation of a stock price index. As described in the text, calculating a price index involves first selecting a base year. For our Megaco price index, let us choose the year 2000 as the base year (although it should be stressed that any year can be chosen). By definition, the value of the Megaco price index is 100 in this base year. How did we transform the price of Megaco in the year 2000 to obtain the price index value of 100? It can be seen that this transformation involved taking the price of Megaco in 2000 and dividing by the price of Megaco in 2000 (i.e. dividing the price by itself) and multiplying by 100. To maintain comparability, this same transformation must be applied to the price of Megaco in every year. The result is a stock price index for Megaco (with the year 2000 as the base year). This is illustrated in Table 2.1.2.
From the Megaco stock price index, it can be seen that between 2000 and 2003 the price of stock in Megaco increased by 4.4% and in 1999 the price of Megaco's stock was 97.8%, as high as in 2000.
When calculating the Megaco stock price index (a single company), all we had to look at was the stock price of Megaco. However, if we want to calculate a stock price index (involving several companies), then we have to combine the prices of all stocks together somehow. One thing you could do is simply average the prices of all stock prices together in each year (and then construct a price index in the same manner as for the Megaco stock price index). However, this strategy is usually inappropriate since it implicitly weights all companies equally to one another. Let us suppose, as their names indicate, that Megaco and Monstroco are huge companies with a large amount of stock outstanding, traded on many stock exchanges. In contrast, we suppose Minico to be a tiny company with only a small amount of stock outstanding, traded only rarely on a local stock exchange. A simple average just would add up the stock prices of these three companies and divide by three. In our example (and many real world applications), this equal weighting is unreasonable.[11] An examination of Table 2.1.1 reveals that the stock prices of Megaco and Monstroco are going up only slightly over time (and, in some years, they are not changing or even dropping). However, the price of Minico's stock is going up rapidly over time. Megaco and Monstroco are common stocks purchased frequently by many people, whereas Minico is a small obscure company purchased by a tiny minority of people. In light of this, it is unreasonable to weight all three companies equally when calculating a stock price index. A stock price index which was based on a simple average would reveal stock prices were growing at a fairly rapid rate (i.e. combining the slow growth of Megaco and Monstroco's stocks with the very fast growth of Minico would yield a stock price index which indicates moderately fast growth). However, if the financial analyst were to use such a price index to report "stock prices are increasing at a fairly rapid rate", the vast majority of people would find this report inconsistent with their own experience. That is, the vast majority of people only have shares of Megaco and Monstroco in their portfolios and their prices are growing only slowly over time.
The line of reasoning in the previous paragraph suggests that a stock price index which weights all companies equally will not often be a sensible one. It also suggests how one might construct a sensible stock price index: use a weighted average of the prices of all stocks to construct an index where the weights are chosen so as to reflect the importance of each company. In our stock price index, we would want to attach more weight to Megaco and Monstroco (the big companies) and little weight to the tiny Minico.
There are many different ways of choosing such weights. But most share the idea that stocks should be weighted by the size or importance of the underlying company. The S&P500 weights companies by their market capitalization (i.e. the price per share times the total number of shares outstanding).[12] Sometimes, such indices are referred to as "value-weighted". For empirical work, it is usually acceptable to understand this intuition and a knowledge of the precise calculations performed in calculating a value-weighted stock price index is not necessary. However, for the interested reader, the remainder of Appendix 2.1 describes these calculations in the context of our simple example.
A value-weighted stock price index can be written in terms of a mathematical formula. Let P denote the price of a stock, Q denote the market capitalization and subscripts denote the company and year with Megaco being company 1, Monstroco company 2 and Minico company 3. Thus, for instance, P1,2000, is the stock price of Megaco in the year 2000, Q3,2002 is the market capitalization of Minico in 2002, etc. See the Appendix 1.1 if you are having trouble understanding this subscripting notation or the summation operator used below.
With this notational convention established, a value-weighted price index (PI) in year t (for t = 1999, 2000, 2001, 2002 and 2003) can be written as:
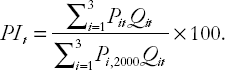
Note that the numerator of this formula takes the price of each stock and multiplies it by the current market capitalization. This ensures that Megaco and Monstroco receive much more weight in the index than Minico. We will not explain the denominator. For the more mathematically inclined, the denominator ensures that the weights in the weighted average sum to one (which is necessary to ensure that it is a proper weighted average) and that 2000 is the base year.
Table 2.1.3 presents the market capitalization (in millions of dollars) for our three companies. Table 2.1.4 shows the calculation of the value-weighted stock price index using the stock price data of Table 2.1.1 and the market capitalization data of Table 2.1.3.
The values from the last column can be interpreted as with any price index. So, for instance, we can say that stock prices rose by 10.4% between 2000 and 2003.
The mean and standard deviation are the most common descriptive statistics but many others exist. The mean is the simplest measure of location of a distribution. The word "location" is meant to convey the idea of the center of the distribution. The mean is the average. Other common measures of location are the mode and median.
To distinguish between the mean, mode and median, consider a simple example. Seven people report their respective incomes in £ per annum as: £18,000, £15,000, £9,000, £15,000, £16,000, £17,000 and £20,000. The mean, or average, income of these seven people is £15,714.
The mode is the most common value. In the present example, two people have reported incomes of £15,000. No other income value is reported more than once. Hence, £15,000 is the modal income for these seven people.
The median is the middle value. That is, it is the value that splits the distribution into two equal halves. In our example, it is the income value at which half the people have higher incomes and half the people have lower incomes. Here the median is £16,000. Note that three people have incomes less than the median and three have incomes higher than it.
The mode and median can also be motivated through consideration of Figures 2.2 and 2.4, which plot two different histograms or distributions. A problem with the mode is that there may not be a most common value. For instance, in the GDP per capita data set (GDPPC.XLS), no two countries have precisely the same values. So there is no value that occurs more than once. For cases like this, the mode is the highest point of the histogram. A minor practical problem with defining the mode in this way is that it can be sensitive to the choice of class intervals (and this is why Excel gives a slightly different answer for the mode for GDPPC.XLS than the one given here). In Figure 2.2, the histogram is highest over the class interval labeled 2,000. Remember, Excel's choice of labeling means that the class interval runs from 0 to 2,000. Hence, we could say that "the class interval 0 to 2,000 is the modal (or most likely) value". Alternatively, it is common to report the middle value of the relevant class interval as the mode. In this case, we could say, "the mode is $1,000". The mode is probably the least commonly used of the three measures of location introduced here.
To understand the median, imagine that all the area of the histogram is shaded. The median is the point on the X-axis which divides this shaded area precisely in half. For Figure 2.4 the highest point (i.e. the mode) is also the middle point that divides the distribution in half (i.e. the median). It turns out it is also the mean. However, in Figure 2.2 the mean ($5,443.80), median ($3,071.50) and mode ($1,000) are quite different.
Other useful summary statistics are based on the notion of a percentile. Consider our GDP per capita data set. For any chosen country, say Belgium, you can ask "how many countries are poorer than Belgium?" or, more precisely, "what proportion of countries are poorer than Belgium?". When we ask such questions we are, in effect, asking what percentile Belgium is at. Formally, the Xth percentile is the data value (e.g. a GDP per capita figure) such that X % of the observations (e.g. countries) have lower data values. In the cross-country GDP data set, the 37th percentile is $2,092. This is the GDP per capita figure for Peru. 37% of the countries in our data set are poorer than Peru.
Several percentiles relate to concepts we have discussed before. The 50th percentile is the median. The minimum and maximum are the 0th and 100th percentile. The percentile divides the data range up into hundredths, while other related concepts use other basic units. Quartiles divide the data range up into quarters. Hence, the first quartile is equivalent to the 25th percentile, the second quartile, the 50th percentile (i.e. the median) and the third quartile, the 75th percentile. Deciles divide the data up into tenths. In other words, the first decile is equivalent to the 10th percentile, the second decile, the 20th percentile, etc.
After the standard deviation, the most common measure of dispersion is the inter-quartile range. As its name suggests, it measures the difference between the third and first quartiles. For the cross-country data set, 75% of countries have GDP per capita less than $9,802 and 25% have GDP per capita less than $1,162. In other words, $1,162 is the first quartile and $9,802 is the third quartile. The inter-quartile range is $9,802-$1,162 = $8,640.
[1] As emphasized in Chapter 1, this is not a book about collecting data. Nevertheless, it is useful to offer a few brief pointers about how to look for data sets.
[2] Some researchers even work with data observed more frequently than this. For instance, in a stock market one can record the price of a stock every time it is traded. Since, for some companies' shares, the time between trades is measured in seconds (or even less) such data is recorded at a very high frequency. Such data sets are useful for investigating market micro-structure. We will not discuss such data sets nor models of market micro-structure in this book. The Econometrics of Financial Markets by Campbell, Lo and MacKinlay has a chapter on this topic.
[3] Another type of data occurs if, say, a researcher carries out a survey of a different set of companies each year. This is not the same as panel data and is referred to as repeated cross-sectional data.
[4] Some indices set the base year value to 1.00, 10 or 1000 instead of 100.
[5] 1954Q1 means the first quarter (i.e. January, February and March) of 1954.
[6] Real GDP per capita in every country has been converted into US dollars using purchasing power parity exchange rates. This allows us to make direct comparisons across countries.
[7] Note that the use of the word "frequency" here as meaning "the number of observations that lie in a class interval" is somewhat different from the use of the word "frequency" in time series analysis (see the discussion of time series data above).
[8] Excel creates the histogram using the Histogram command (in Tools/Data Analysis). It simply plots the bins on the horizontal axis and the frequency (or number of observations in a class) on the vertical axis. Note that most statistics books plot class intervals against frequencies divided by class width. This latter strategy corrects for the fact that class widths may vary across class intervals. In other words, Excel does not calculate the histogram correctly. Provided the class intervals are the same width (or nearly so) this error is not of great practical importance.
[9] In some textbooks, a slightly different formula for calculating the standard deviation is given where the N – 1 in the denominator is replaced by N.
[10] The case where there is a continuity of possible outcomes has similar intuition to the case with K outcomes, but is mathematically more complicated. Since we are only interested in providing intuition, we will not discuss this case.
[11] An exception to this is the DJIA which does equally weight the stock prices of all companies included in making the index. Note, however, that the DJIA is based only on a set of large companies, so the problem of different-sized companies receiving equal weight in a simple average is lessened.
[12] This statement holds for the most commonly reported S&P500 Index, although we note that Standard & Poor's produces many stock price indices, including an S&P500 Equal Weight Index.