In regression analysis, researchers are typically interested in measuring the effect of an explanatory variable or variables on a dependent variable. As mentioned in Chapter 8, this goal is complicated when the researcher uses time series data since an explanatory variable may influence a dependent variable with a time lag. This often necessitates the inclusion of lags of the explanatory variable in the regression. Furthermore, as discussed in Chapter 9, the dependent variable may be correlated with lags of itself, suggesting that lags of the dependent variable should also be included in the regression.
As we shall see, there are also several theories in finance which imply such a regression model. This is not a book which derives financial theories to motivate our regression models. However, to give you a flavor of the kind of things financial researchers do with time series data, it is useful briefly to mention a few classic articles in finance and the time series data sets they use. An influential paper by Campbell and Ahmer called "What moves the stock and bond markets? A variance decomposition for long-term asset returns"[56] used American data on excess stock returns, various interest rates, the yield spread (defined using the difference between long- and short-term interest rates) and the dividend-price ratio. Another influential paper by Lettau and Ludvigson called "Consumption, aggregate wealth and expected stock returns"[57] investigated an important relationship in financial economics using data on excess stock returns, asset wealth, labor income and consumption. In Chapter 8, we presented an example involving the prediction of long-run stock returns using the dividend-price ratio. Such regressions grew out of influential work such as "Stock prices, earnings and expected dividends" by Campbell and Shiller. [58] Examples such as these abound in finance. Exact details about why these researchers chose the particular ular variables they did is not important for present purposes (indeed you need not even worry about precisely what all these variables are). The key thing to note is that important financial theories involve several time series variables and imply models such as the ones discussed in this chapter and the next.
These considerations motivate the commonly used autoregressive distributed lag (or ADL) model:
In this model, the dependent variable, Y, depends on p lags of itself, the current value of an explanatory variable, X, as well as q lags of X. The model also allows for a deterministic trend (t). Since the model contains p lags of Y and q lags of X we denote it by ADL(p, q).[59] In this chapter, we focus on the case where there is only one explanatory variable, X. Note, however, that we could equally allow for many explanatory variables in the analysis.
Estimation and interpretation of the ADL(p, q) model depend on whether the series, X and Y, are stationary or not. We consider these two cases separately here. Note though, that we assume throughout that X and Y have the same stationarity properties; that is, that they either must both be stationary or both have a unit root. Intuitively, regression analysis involves using X to explain Y. If X's properties differ from Y's it becomes difficult for X to explain Y. For instance, it is hard for a stationary series to explain the stochastic trend variation in a unit root series. In practice this means that, before running any time series regression, you should examine the univariate properties of the variables you plan to use. In particular, you should carry out unit root tests along the lines described in Chapter 9 for every variable in your analysis.
When X and Y are stationary, OLS estimation of the ADL(p, q) regression model can be carried out in the standard way described in Chapters 4–8. Testing for the significance of variables can be done using the t-stats and P-values provided by computer packages like Excel. Such tests can in turn be used to select p and q, the number of lags of the dependent and explanatory variables, respectively. You should note, however, that the verbal interpretation of results is somewhat different from the standard case, as elaborated below.
In the case of the AR(p) model in Chapter 9, it proved convenient, both for OLS estimation and interpretation of results, for us to rewrite the model with ΔY as the dependent variable. Similar considerations hold for the ADL(p, q), which can be rewritten as:
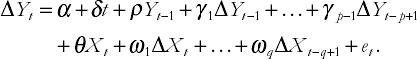
It should be emphasized that this model is the same as that in the original form of the ADL(p, q); it has merely undergone a few algebraic manipulations. Just as we had two different variants of the AR(p) model in Chapter 9, we now have two variants of the ADL(p, q) model. As before, we use new Greek letters for the coefficients in the regression to distinguish them from those in the original variant of the ADL(p, q) model.[60] This model may look complicated, but it is still nevertheless just a regression model. That is, no new mathematical techniques are required for this model, which is, after all, still based on the simple equation of a straight line.
As discussed in Chapter 9, financial time series are often highly correlated with their lags. This implies that the original form of the ADL model frequently runs into multicollinearity problems. With the rewritten form we will typically not encounter such problems. Most importantly, as we shall see, it has a further benefit, one that lies in the interpretation of the coefficients. For these reasons we will work mainly with this second variant of the ADL(p, q) model.
In Chapter 6, we discussed how to interpret regression coefficients, placing special emphasis on ceteris paribus conditions. Recall that we made statements of the form: "The coefficient measures the influence of lot size on the sales price of a house, ceteris paribus". In the ADL(p, q) model, such an interpretation can still be made, but it is not that commonly done. How then can we interpret the coefficients in the ADL model? In economics, a common way is through the concept of a multiplier. The use of multipliers is not that common in finance. However, we introduce the concept anyway since it relates to important concepts we will discuss later.
It is common to focus on the long run or total multiplier, which is what we will do here. To motivate this measure, suppose that X and Y are in an equilibrium or steady state, i.e. are not changing over time. All of a sudden, X changes by one unit, affecting Y, which starts to change, eventually settling down in the long run to a new equilibrium value. The difference between the old and new equilibrium values for Y can be interpreted as the long run effect of X on Y and is the long run multiplier. This multiplier is often of great interest for policymakers who want to know the eventual effects of their policy changes in various areas.
It is worth stressing that the long run multiplier measures the effect of a permanent change in X. That is, the story in the previous paragraph had X being at some value, then X changed permanently to a new level one unit higher than the original value. The long run multiplier measures the effect of this sort of change. In some cases, you might be interested in the effect of a temporary change in X (i.e. X starts at some original level, then increases by one unit for one period before going back to the original level the next). The long run multiplier does not measure the effect of this type of change. We can use the traditional "marginal effect" interpretation of regression coefficients for such temporary changes. The example in Chapter 8, which discussed the effect of news on the stock market, illustrates some ways of reporting the effect of a temporary change in the explanatory variable (e.g. there we were interested in the effect of news in one particular month on market capitalization. We did not discuss the effect of increasing news relating to the stock price of the company permanently as not making sense in that example).
It can be shown, (although we will not prove it here),[61] that the long run multiplier for the ADL(p, q) model is:
In other words, only the coefficients on Xt and Yt−1 in the rewritten ADL model matter for long run behavior. This means that we can easily obtain an estimate of the long run multiplier.
It is worth stressing that we are assuming X and Y are stationary. In Chapter 9, we discussed how ρ = 0 in the AR(p) model implied the existence of a unit root. The ADL model is not the same as the AR model, but to provide some rough intuition, note that if ρ = 0 then the long run multiplier is infinite. In fact, it can be shown that for the model to be stable, then we must have ρ < 0.[62] In practice, if X and Y are stationary, this condition will be satisfied.
In Chapter 8 we described how to create lagged variables in Excel using copy/paste commands. Similar techniques can be used here. Note, however, that when you create ΔYt and ΔXt you will be using formulae. If you want to manipulate ΔYt and ΔXt later, e.g., to create ΔYt−1 and ΔXt−1, you have to be careful to copy and paste the values in the cells and not the formulae. You can do so using the "Paste Special" option in Excel. You are probably noticing by now that Excel is not a very convenient software package for time series analysis. As mentioned previously, there are many other statistical software packages (e.g. Stata, E-views, MicroFit, etc.) which are much more suitable for time series analysis and you might wish to consider learning how to use one of them if you plan on doing extensive work with financial time series.
For the remainder of this chapter, we will assume that Y and X have unit roots. In practice, of course, you would have to test whether this was the case using the Dickey–Fuller test of the previous chapter (or any other unit root test available in your software package). We begin by focussing on the case of regression models without lags, then proceed to similar models to the ADL(p, q) model.
Suppose we are interested in estimating the following regression:
If Y and X contain unit roots, then OLS estimation of this regression can yield results which are completely wrong. For instance, even if the true value of β is 0, OLS
To put it another way: if Y and X have unit roots then all the usual regression results might be misleading and incorrect. This is the so-called spurious regression problem. We do not have the statistical tools to prove that this problem occurs,[64] but it is important to stress the practical implication. With the one exception of cointegration that we note below, you should never run a regression of Y on X if the variables have unit roots.
The one time where you do not have to worry about the spurious regression problem occurs when Y and X are cointegrated. This case not only surmounts the spurious regression problem, but also provides some nice financial intuition. Cointegration has received a great deal of attention recently in the financial literature and many theoretical finance models imply cointegration should occur, so it is worthwhile to discuss the topic in detail here.
Some intuition for cointegration can be obtained by considering the errors in the above regression model: et= Yt – α – βXt. Written in this way, it is clear that the errors are just a linear combination of Y and X. However, X and Y both exhibit nonstationary unit root behavior such that you would expect the error to also exhibit non-stationary behavior. (After all, if you add two things with a certain property together the result generally tends to have that property.) The error does indeed usually have a unit root. Statistically, it is this unit root in the error term that causes the spurious regression problem. However, it is possible that the unit roots in Y and X "cancel each other out" and that the resulting error is stationary. In this special case, called cointegration, the spurious regression problem vanishes and it is valid to run a regression of Y on X. To summarize: if Y and X have unit roots, but some linear combination of them is stationary, then we can say that Y and X are cointegrated.[65]
The intuition behind cointegration is clearest for the case where a = 0 and b = 1. Keep this in mind when you read the following statements. Remember also that variables with unit roots tend to exhibit trend behavior (e.g. they can be increasing steadily over time and therefore can become very large).
If X and Y have unit roots then they have stochastic trends. However, if they are cointegrated, the error does not have such a trend. In this case, the error will not get too large and Y and X will not diverge from one another; Y and X, in other words, will trend together. This fact motivates other jargon used to refer to coin-tegrated time series. You may hear them referred as either having common trends or co-trending.
If we are talking about a financial model involving an equilibrium concept, e is the equilibrium error. If Y and X are cointegrated then the equilibrium error stays small. However, if Y and X are not cointegrated then the equilibrium error will have a trend and departures from equilibrium become increasingly large over time. If such departures from equilibrium occur, then many would hesitate to say that the equilibrium is a meaningful one.
If Y and X are cointegrated then there is an equilibrium relationship between them. If they are not, then no equilibrium relationship exists. (This is essentially just a restatement of the previous point.)
In the real world, it is unlikely that a financial system will ever be in precise equilibrium since shocks and unexpected changes to it will always occur. However, departures from equilibrium should not be too large and there should always be a tendency to return to equilibrium after a shock occurs. Hence, if a financial model which implies an equilibrium relationship exists between Y and X is correct, then we should observe Y and X as being cointegrated.
If Y and X are cointegrated then their trends will cancel each other out.
To summarize: if cointegration is present, then not only do we avoid the spurious regression problem, but we also have important financial information (e.g. that an equilibrium relationship exists or that two series are trending together).
A brief mention of a few theories motivating why cointegration should occur between various financial time series should aid in understanding the importance of this concept.
Common sense tells you that, if two assets are close substitutes for one another, then their prices should not drift too far apart. After all, if one asset becomes much more expensive than a similar asset, then investors will sell the first asset in order to buy the cheaper alternative. But if many investors are selling the expensive asset, then its price should drop. And if many investors are buying the cheap asset its price would rise. Thus, the prices of the expensive and cheap assets would move closer to one another. Many financial theories formalize this intuition to imply different cointegrating relationships.
Cointegration often arises in models of the term structure of interest rates and the yield curve. A detailed discussion of these terms is beyond the scope of this book. However, the basic idea is that bonds can have different maturities or repayment periods. So you can have a bond which promises to pay a fixed interest rate for one year, or two years, or 10 years, etc. The interest rates paid on bonds of different maturities can be different since investors have different time preferences and long maturities are less flexible since they lock the investor in for a longer time period. That is, an investor could either buy a five-year bond, or a sequence of one-year bonds each year for five years. The latter strategy would be more flexible since the investor could always change her mind after each year. Hence, long-term interest rates often tend to be higher than short-term interest rates to compensate the buyer for a loss of flexibility. The exact shape of the relationship between interest rates at different maturities is called the term structure of interest rates or the yield curve (a yield is the return to holding the bond for the entire time until it matures). This provides much useful information about investor's beliefs about the future and is, thus incorporated in many financial theories some of which imply cointegrating relationships. For instance, Campbell, Lo and MacKinlay in their book The Econometrics of Financial Markets (Chapter 10), outline an argument where yield spreads (i.e. the difference between the yield of a bond with an N period maturity and the yield of a bond with a 1 period maturity) are stationary time series variables and show how this implies yields of different maturities should be cointegrated.
In futures markets, theories involving investors having rational expectations tend to imply cointegrating relationships. For instance, in foreign exchange markets you can buy any major currency (e.g. the $ or the £) in the conventional manner (i.e. for immediate delivery at a specified rate). For instance, at the time I am writing this I could purchase $1.90 for £1. This is referred to as the spot exchange rate or spot rate. However, it also possible to agree an exchange rate now, but carry out the actual trade at some future date (e.g. a deal might have the form "I will guarantee that one year from now, I will give you $2.00 for your £1"). Such an exchange rate, agreed now but with the actual trade to be carried out later, is called the forward exchange rate or forward rate. Similar contracts (and much more complicated ones) can be written in stock markets and, indeed, such financial derivatives play a huge role in modern financial markets. Many financial theories, involving market efficiency and rational expectations of investors, imply that forward rates should be good predictors of future spot rates. Empirically, as we have discussed before, it seems that prices of assets (and an exchange rate is a price of an asset) often have unit roots in them (with returns being stationary). If we combine the financial theory with this empirical regularity, it turns out that they imply that spot and forward rates should be cointegrated. In foreign exchange markets, there are many theories which imply such cointegrating relationships. We will not explain them here, but just drop a few of names such as purchasing power parity, uncovered interest parity and covered interest parity.[66]
As we have touched on previously, there are also many financial theories which come out of basic present value relationships which imply cointegration. For instance, one such theory implies that stock prices and dividends should be cointegrated. Another financial theory (the Lettau–Ludvigson paper which we mentioned above and explore below) implies that consumption (c), assets (a) and income (y) should be cointegrated. Such so-called cay relationships have received a great deal of attention in the recent empirical finance literature. Furthermore, theory suggests that the coin-tegrating error from the cay relationship plays a very important role: it should have predictive power for future stock returns.
In short, financial theory suggests cointegrating relationships between many different financial time series should exist. Hence, it is important to test whether cointegration is present (i.e. to see whether financial theory holds in practice) and, if it is present, to estimate models involving cointegrated variables (e.g. to estimate the cointegrating error from the cay relationship). Accordingly, we now address these issues, beginning with an empirical example.
As mentioned above, if Y and X are cointegrated, then the spurious regression problem does not apply; consequently, we can run an OLS regression of Y on X and obtain valid results. Furthermore, the coefficient from this regression is the long run multiplier. Thus, insofar as interest centers on the long run multiplier, then estimation with cointegrated variables is very easy.
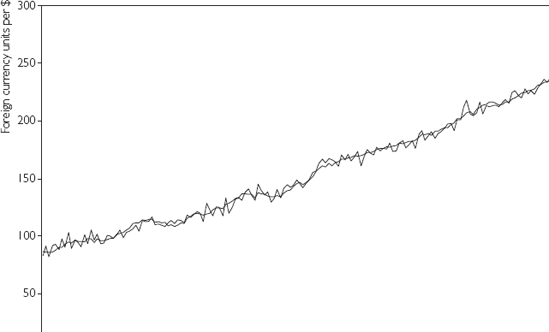
Before using results from this so-called cointegrating regression, it is important to verify that Y and X are in fact cointegrated. Remember that if they are not coin-tegrated, then the spurious regression problem holds and the results you obtain can be completely meaningless. An examination of time series plots like Figure 10.1, can be quite informative, but remember that visual examinations of graphs should not be considered substitutes for a statistical test!
Many tests for cointegration exist and some computer software packages (e.g. Stata and MicroFit) allow you to perform very sophisticated procedures at a touch of the button. We will discuss some of these in the next chapter. However, spreadsheets like Excel do not allow you to carry out these tests. Fortunately, using the regression capabilities of these spreadsheet packages coupled with some data manipulation, we can carry out at least one test for cointegration.
The test for cointegration described here is referred to as the Engle–Granger test, after the two econometricians who developed it. It is based on the regression of Y on X. Remember that, if cointegration occurs, then the errors from this regression will be stationary. Conversely, if cointegration does not occur, then the errors will have a unit root. Given the close relationship between the errors and the residuals,[67] it is reasonable to examine the properties of the residuals in order to investigate the presence of cointegration. In Chapter 9 we discussed testing for a unit root in a time series variable. Here, we test for a unit root in the residuals using the same techniques. In particular, the test for cointegration involves the following steps:
Run the regression of Y on X and save the residuals.[68]
Carry out a unit root test on the residuals (without including a deterministic trend).
If the unit root hypothesis is rejected then conclude that Y and X are cointegrated. However, if the unit root is accepted then conclude cointegration does not occur.
It is worthwhile to stress that the Engle-Granger test is based on a unit root test, so that the problems described at the end of Chapter 9 will arise. In other words, although the cointegration test is based on the t-statistic from a regression (in this case, one involving the residuals from a preliminary regression), you cannot use the P-value printed out by non-specialist packages like Excel. The correct critical values are published in many places (and are slightly different from the critical values for the Dickey–Fuller test). If you are going to do a great deal of work with time series data it is a good idea for you to spend the time to learn more about cointegration testing and look up these correct critical values or use a computer package such as Stata or MicroFit. However, for many purposes it is acceptable to use the same rules of thumb recommended in Chapter 9. A more sophisticated cointegration test, called the Johansen test, is described in Chapter 11. In many cases, the Johansen test performs better than the Engle–Granger test. However, the Johansen test is more complicated and cannot easily be done using a spreadsheet such as Excel.
Note that, when testing for a unit root in the residuals, it is rare to include a deterministic trend. If such a trend were included it could mean the errors could be growing steadily over time. This would violate the idea of cointegration (e.g. the idea that the system always returns to equilibrium and, hence, that errors never grow too big). Hence, we do not consider this case in this book.
In light of these considerations, when carrying out the unit root test on the residuals (see Step 2 above), use −2.89 as a critical value against which to compare the t-statistic. If the t-statistic on ρ in the unit root regression involving the residuals is more negative than −2.89, conclude that the errors do not have a unit root and hence that Y and X are cointegrated.
Note also that in the Dickey–Fuller test, we test the hypothesis that ρ = 0 (i.e. the null hypothesis is the unit root). In the cointegration test, we use the Dickey–Fuller methodology but cointegration is found if we reject the unit root hypothesis for the residuals. In other words, the null hypothesis in the Engle–Granger test is "no cointegration" and we conclude "cointegration is present" only if we reject this hypothesis.
It is also worth stressing that, since the Engle–Granger test is based on the Dickey–Fuller test, it suffers from the difficulties noted at the end of Chapter 9. That is, the Engle–Granger test has low power and can be misleading if structural breaks occur in the data.
In empirical work, it is often vital to establish that Y and X are cointegrated. As emphasized above, cointegration can be related to the idea of Y and X trending together or bearing an equilibrium relationship to each other. A second important task is to estimate the long run multiplier or the long run influence of X on Y. Both cointegration testing and estimation of the long run multiplier can be done using the regression of Y on X. Accordingly, in many empirical projects you may never need to move beyond this simple regression. However, in some cases, you may be interested in understanding short run behavior in a manner that is not possible using only the regression of Y on X. In such cases, we can estimate an error correction model (or ECM for short).
An important theorem, known as the Granger Representation Theorem, says that if Y and X are cointegrated, then the relationship between them can be expressed as an ECM. In this section, we will assume Y and X are cointegrated. Error correction models have a long tradition in time series econometrics, and the Granger Representation Theorem highlights their popularity. In order to understand the properties of ECMs let us begin with the following simple version:
where et−1 is the error obtained from the regression model with Y and X (i.e. et−1 = Yt−1 – α – βXt−1) and εt is the error in the ECM model. Note that, if we knew et−1, then the ECM would be just a regression model (although we introduce some new Greek letters to make sure that the coefficients and error in this model do not get confused with those in other regression models). That is, ΔYt is the dependent variable and et−1 and ΔXt are explanatory variables. Furthermore, we assume that λ < 0.[70]
To aid in interpreting the ECM, consider the implications of ΔYt being its dependent variable. As emphasized throughout this book, the regression model attempts to use explanatory variables to explain the dependent variable. With this in mind, note that the ECM says that ΔY depends on ΔX — an intuitively sensible point (i.e. changes in X cause Y to change). In addition, ΔYt depends on et−1. This latter aspect is unique to the ECM and gives it its name.
Remember that e can be thought of as an equilibrium error (e.g. the difference between the spot and forward rates). If it is non-zero, then the model is out of equilibrium. Consider the case where ΔXt = 0 and et−1 is positive (e.g. the spot rate is higher than the forward rate). The latter implies that Yt−1 is too high to be in equilibrium (i.e.Yt−1 is above its equilibrium level of α + βXt−1). Since λ < 0 the term λet−1 will be negative and so ΔYt will be negative. In other words, if Yt−1 is above its equilibrium level, then it will start falling in the next period and the equilibrium error will be "corrected" in the model; hence the term "error correction model" (e.g. if the spot rate is too much above the forward rate, investors will find it cheap to buy forward driving up the forward rate).[71] In the case where et−1 < 0 the opposite will hold (i.e. Yt−1 is below its equilibrium level, hence λet−1 > 0 which causes ΔYt to be positive, triggering Y to rise in period t).
In sum, the ECM has both long run and short run properties built into it. The former properties are embedded in the et−1 term (remember β is still the long run multiplier and the errors are from the regression involving Y and X). The short run behavior is partially captured by the equilibrium error term, which says that, if Y is out of equilibrium, it will be pulled towards it in the next period. Further aspects of short run behavior are captured by the inclusion of ΔXt as an explanatory variable. This term implies that, if X changes, the equilibrium value of Y will also change, and that Y will also change accordingly. All in all, the ECM has some very sensible properties that are closely related to financial equilibrium concepts.
The ECM also has some nice statistical properties which mean that we do not have to worry about the spurious regression problem. Y and X both have unit roots; hence ΔY and ΔX are stationary. Furthermore, since Y and X are cointegrated, the equilibrium error is stationary. Hence, the dependent variable and all explanatory variables in the ECM are stationary. This property means that we can use OLS estimation and carry out testing using t-statistics and P-values in the standard way described in Chapter 5.
The only new statistical issue in the ECM arises due to the inclusion of et−1 as an explanatory variable. Of course, the errors in a model are not directly observed. This raises the issue of how they can be used as an explanatory variable in a regression. Some sophisticated statistical techniques have been developed to estimate the ECM, but the simplest thing to do is merely to replace the unknown errors by the residuals from the regression of Y on X (i.e. replace et−1 by ut−1). That is, a simple technique based on two OLS regressions proceeds as follows:
Step 1. Run a regression of Y on X and save the residuals.
Step 2. Run a regression of ΔY on ΔX and the residuals from Step 1 lagged one period.
It should be emphasized that before carrying out this two-step estimation procedure for the ECM, you must verify that Y and X have unit roots and are cointegrated.
So far we have discussed the simplest error correction model. In practice, just as the ADL(p, q) model has lags of the dependent and explanatory variables, the ECM may also have lags.[72] It may also have a deterministic trend. Incorporating these features into the ECM yields:
This expression is still in the form of a regression model and can be estimated using the two-step procedure described above. The adjustment to equilibrium intuition also holds for this model. The decisions on whether to include a deterministic trend and on which precise values for p and q are appropriate can be made using t-statistics and P-values in the same manner as for the ADL model. In fact, the ECM is closely related to the ADL model in that it is a restricted version of it.
You may encounter instances where unit root tests indicate that your time series have unit roots, but the Engle–Granger test indicates that the series are not cointegrated. That is, the series may not be trending together and may not have an equilibrium relationship. In these cases, you should not run a regression of Y on X due to the spurious regression problem. The presence of such characteristics suggests that you should rethink your basic model and include other explanatory variables. Instead of working with Y and X themselves, for example, you could difference them. (Remember that if Y and X have one unit root, then ΔY and ΔX should be stationary.)
In this case, you could work with the changes in your time series and estimate the ADL model using the techniques described at the beginning of this chapter. In other words, you may wish to estimate the original ADL model, but with changes in the variables:
For most time series variables, this specification should not suffer from multi-collinearity problems. Alternatively, you may wish to estimate the second variant of the ADL model based on the differenced data. But if you are working with the differences of your time series and then use the variant of the ADL that involves differencing the data you end up with second differenced data:
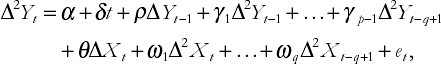
where ΔYt = ΔYt – ΔYt−1. OLS estimation and testing can be done in either of these models in a straightforward way. Whatever route is chosen, it is important to emphasize that the interpretation of regression results will likewise change.
More specifically, let us suppose Y = exchange rates and X = interest rates. If Y and X are cointegrated, or if both are stationary, we can obtain an estimate of the long run effect of a small change in interest rates on exchange rates. If Y and X are neither stationary nor cointegrated and we estimate either of the two preceding equations, we can obtain an estimate of the long run effect of a small change in the change of interest rates on the change in exchange rates. This may or may not be a sensible thing to measure depending on the particular empirical exercise.
Note that, in the example at the beginning of this chapter on the effect of financial liberalization on growth, the variables were already in percentage changes. If we had begun with Y = GDP and X = total stock market capitalization we would have found they had unit roots but were not cointegrated. Hence, we would have run into the spurious regressions problem. This was why we worked with percentage changes.
If all variables are stationary, then an ADL(p, q) model can be estimated using OLS. Statistical techniques are all standard.
A variant on the ADL model is often used to avoid potential multicollinearity problems and provide a straightforward estimate of the long run multiplier.
If all variables are nonstationary, great care must be taken in the analysis due to the spurious regression problem.
If all variables are nonstationary but the regression error is stationary, then cointegration occurs.
If cointegration is present, the spurious regression problem does not occur.
Cointegration is an attractive concept for financial researchers since it implies that an equilibrium relationship exists.
Cointegration can be tested using the Engle–Granger test. This test is a Dickey–Fuller test on the residuals from the cointegrating regression.
If the variables are cointegrated then an error correction model can be used. This model captures short run behavior in a way that the cointegrating regression cannot.
If the variables have unit roots but are not cointegrated, you should not work with them directly. Rather you should difference them and estimate an ADL model using the differenced variables. The interpretation of these models can be awkward.
[56] Campbell, J.Y. and Ammer, J. (1993). "What moves the stock and bond markets? A variance decomposition for long-term asset returns", Journal of Finance, 48, 3–37.
[57] Lettau, M. and Ludvigson, S. (2001). "Consumption, aggregate wealth and expected stock returns", Journal of Finance, 56, 815–49.
[58] Campbell, J. and Shiller, R. (1988). "Stock prices, earnings and expected dividends", Journal of Finance, 43, 661–76.
[59] Formally, we should call this the ADL(p, q) with deterministic trend model. However, we will omit the latter phrase for the sake of simplicity. In practice, you will find that the deterministic trend is often insignificant and will be omitted from the model anyway. Note also that some textbooks abbreviate "autoregressive distributed lag" as ARDL instead of ADL.
[60] The coefficients involving the lags of the dependent variable, ρ, γ1, ..., γp−1 are exactly the same functions of φ1, ..., φp as in Chapter 9. The q + 1 coefficients θ, ω1, ..., ωq are similar functions of β0, β1, ..., βq.
[61] Deriving the long run multiplier from an ADL model is not difficult, and you should try it as an exercise. Here are some hints: assume that the model has been in equilibrium for a long time, and that equilibrium values of X and Y are given by X* and Y*, respectively. Now assume X is increased permanently to X* + 1 and figure out what happens to Y.
[62] "Stable" is a statistical term that we will not formally define in this book. It can, however, be interpreted in a common sense way: if a model is stable, it implies that the time series variables will not be exploding or stochastically trending over time. In essence, it is a very similar concept to stationarity.
[63] It is worth emphasizing that 1.042 is an estimate of the long run multiplier. A confidence interval could be calculated, but this would involve derivations beyond the scope of this book.
[64] You may think that the spurious regression problem occurs as a result of an omitted variable bias when lags are left out of an ADL model. But there is more to it than this. Even when no lags belong in the model, the spurious regression problem arises.
[65] To motivate the word "cointegration", note that if X and Y have unit roots, then it is common jargon to say that they are integrated. Adding the word "co" to emphasize that the unit roots are similar or common in X and Y yields "cointegration".
[66] Chapters 11 through 13 of Quantitative Financial Economics by Keith Cuthbertson (John Wiley & Sons, Ltd) is a good place for further reading on these topics.
[67] Remember that the errors are deviations from the true regression line while residuals are deviations from the estimated regression line (see Chapter 4). Our notation for OLS residuals is ut.
[68] In Excel, you can do it by clicking on the box labeled "Residuals" and following instructions.
[69] If you have done this question correctly, you will find that cointegration does seem to be present for some lag lengths, but not for others. This is a common occurrence in practical applications, so do not be dismayed by it. Financial theory and time series plots of the data definitely indicate that cointegration should occur between Y and X. But the Engle—Granger test does not consistently indicate cointegration. One possible explanation is that the Engle—Granger and Dickey—Fuller tests are known to have low power.
[70] We will not formally prove why this condition must hold except to say that it is a stability condition of the sort discussed in the context of the ADL(p, q) model.
[71] This intuition motivates the stability condition λ < 0, which ensures that equilibrium errors are corrected. If λ is positive then equilibrium errors will be magnified.
[72] Note that we do not include more lags of eti1 as explanatory variables due to an implication of the Granger Representation Theorem, which we will not discuss here.