Statistics is a field of study based on mathematics and probability theory. However, since this book assumes you have little knowledge of these topics, a complete understanding of statistical issues in the regression model will have to await further study.[26] What we will do instead in this chapter is to: (1) discuss what statistical methods in the regression model are designed to do; (2) show how to carry out a regression analysis using these statistical methods and interpret the results obtained; and (3) provide some graphical intuition in order to gain a little insight into where statistical results come from and why these results are interpreted in the manner that they are.
We will begin by stressing a distinction which arose in the previous chapter between the regression coefficients, α and β and the OLS estimates of the regression coefficients,
for i = 1, ..., N observations. As noted previously, α and β measure the relationship between Y and X. We pointed out that we do not know what this relationship is, i.e., what precisely α and β are. We derived so-called ordinary least squares or OLS estimates which we then labeled
These considerations lead us to ask whether we can gauge how accurate these estimates are. Fortunately we can, using statistical techniques. In particular, these techniques enable us to provide confidence intervals for, and to enable us to carry out, hypothesis tests on, our regression coefficients.
To provide some jargon, we say that OLS provides point estimates for β (e.g.
The other major activity of the empirical researcher is hypothesis testing. An example of a hypothesis that a researcher may want to test is β = 0. If the latter hypothesis is true, then this means that the explanatory variable has no explanatory power. Hypothesis testing procedures allow us to carry out such tests.
Both confidence interval and hypothesis testing procedures will be explained further in the rest of this chapter. For expository purposes, we will focus on β since it is usually more important than α in economic problems. However, all the procedures we will discuss for β apply equally well for α.
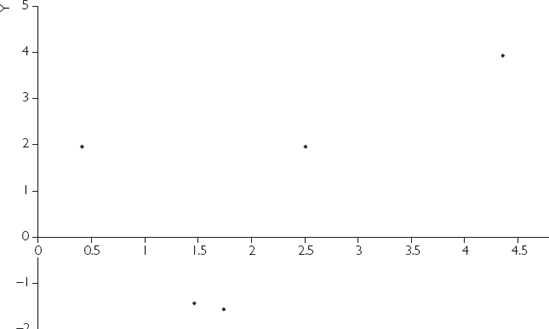
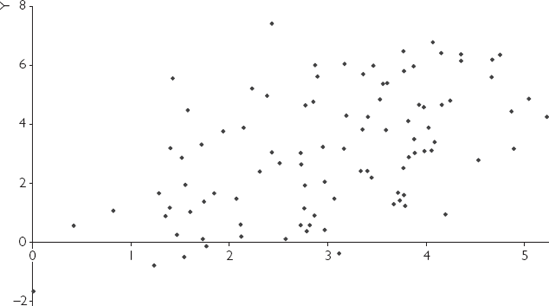
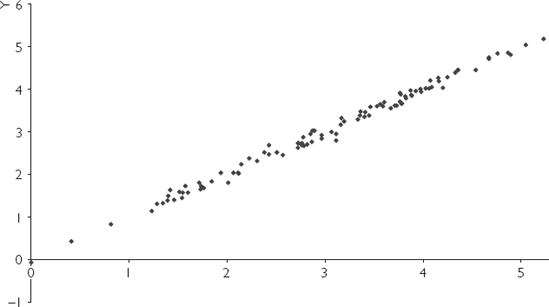
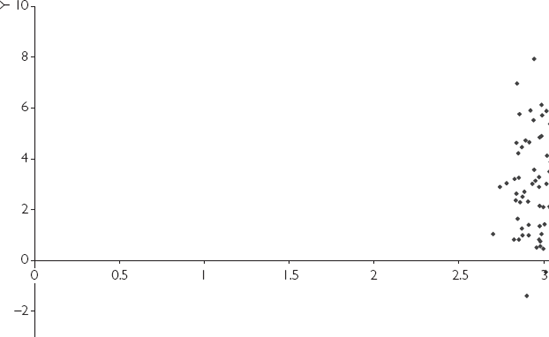
We have artificially created four different data sets for X and Y from regression models with α = 0 and β = 1. XY-plots for these four different data sets are presented in Figures 5.1, 5.2, 5.3 and 5.4. All of these data sets have the same true coefficient values of α = 0 and β = 1, and we hope to obtain
How confident would you feel about the accuracy of the straight line that you have just fitted? It is intuitively straightforward to see that the line fitted for Figure 5.3 would be the most accurate. That is, the straight-line relationship between X and Y "leaps out" in Figure 5.3. Even if a ruler were used and you were to draw a best-fitting line by hand through this XY-plot you would find that the intercept (α) was very close to zero and the slope (β) close to 1. In contrast, you would probably be much less confident about the accuracy of a best-fitting straight line that you drew for Figures 5.1, 5.2 and 5.4.
These figures illustrate three main factors that affect the accuracy of OLS estimates and the uncertainty that surrounds our knowledge of what the true value of β really is:
Having more data points improves accuracy of estimation. This can be seen by comparing Figure 5.1 (N = 5) and Figure 5.3 (N = 100).
Having smaller errors improves accuracy of estimation. Equivalently, if the SSR is small or the variance of the errors is small, the accuracy of the estimation will be improved. This can be seen by comparing Figure 5.2 (large variance of errors) with Figure 5.3 (small variance of errors).[27]
Having a larger spread of values (i.e. a larger variance) of the explanatory variable (X) improves accuracy of estimation. This can be seen by comparing Figure 5.3 (values of the explanatory variable spread all the way from 0 to 6) to Figure 5.4 (values of the explanatory variable all clustered around 3).
The influence of these three factors is intuitively reasonable. With regards to the first two factors, it is plausible that having either more data or smaller errors should increase accuracy of estimation. The third factor is perhaps less intuitive, but a simple example should help you to understand it.
Suppose you are interested in investigating the influence of business education levels (X = years of business education) on the income people receive (Y = income). To understand the nature of this relationship, you will want to go out and interview all types of people (e.g. people with no qualifications, people with an undergraduate degree in business, people with an MBA, people with PhDs in finance, etc.). In other words, you will want to interview a broad spectrum of the population in order to capture as many of these different education levels as possible. In statistical jargon, this means that you will want X to have a high variance. If you do not follow this strategy – for example, were you to interview only those people possessing PhDs in finance – you would get a very unreliable picture of the effect of education on income. In this case, you would not know whether the relationship between education and income was positive. For instance, without collecting data on people who had an MBA you would not know for sure that they are making less income than the PhDs.
Thus, we can summarize by saying that having a large spread of values (i.e. a larger variance) for the explanatory variable, X, is a desirable property in an analysis, whereas having a large spread of values (i.e. a larger variance) for the error, e, is not.
The above three factors are reflected in a commonly used interval estimate for β: the confidence interval. This interval reflects the uncertainty surrounding the accuracy of the estimate
The mathematical formula for the confidence interval for β is:[28]
An equivalent way of expressing the equation above is to say that there is a high level of confidence that the true value of β obeys the following inequality:
The equations above use three numbers that must be calculated:
Below, we discuss each of the three numbers required to calculate a confidence interval, relating them to the issues raised in our discussion of Figures 5.1 through 5.4 on the factors affecting the accuracy of estimation of
First,
Second, sb is the standard deviation of
Large values of sb will imply large uncertainty. In this case,
In other chapters, we have put mathematical formulae in appendices. However, to properly draw out the connections between the formula for the confidence interval and the graphical intuition provided in Figures 5.1–5.4, a small amount of mathematics is required. We present (but do not derive) the following formula for the standard deviation of
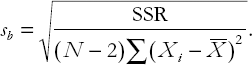
This expression, which measures the variability or uncertainty in
Looking at the formula for the confidence interval, we can see that the larger sb is, the wider the confidence interval is. If we combine this consideration with a careful analysis of the components of the formula for sb, we can say that:
sb and, hence, the width of the confidence interval, varies directly with SSR (i.e. more variable errors/residuals imply wider confidence intervals and, thus, less accurate estimation).
sb and, hence, the width of the confidence interval, vary inversely with N (i.e. more data points imply narrower confidence intervals and, thus, more accurate estimation).
sb and, hence, the width of the confidence interval, vary inversely with Σ(Xi-
)2 (i.e. more variability in X implies more accurate estimation).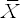
Note that, as described in Chapter 2, Σ(Xi –
We stress that these three factors (i.e. N, SSR and the standard deviation of X), which affect the width of the confidence interval, are the same as those discussed above as affecting the accuracy of the OLS estimate
The third number in the formula for the confidence interval is tb. It is hard to provide much intuition about this number without some knowledge of statistics. For those with some knowledge of statistics, note that tb is a value taken from statistical tables for the Student-t distribution. Appendix 5.1 provides some additional discussion about tb. Some informal intuition for what it means, however, can be obtained from the following example.
Example: Election polls
You may have encountered "point estimates" and something akin to a confidence interval in political polls, which are regularly taken in the weeks and months before an election. These are usually carried out by staffers telephoning a few hundred potential voters and asking them which party they intend to support on election day. Suppose Party A is running in the election. The newspaper reports that 43% of those surveyed will support Party A. This is the newspaper's point estimate of what voters will do on election day. Of course, in reality the actual result on election day will rarely, if ever, be exactly that indicated by the pre-election poll. This discrepancy illustrates a point we stressed earlier in this chapter in the context of the regression model: a point estimate (e.g.
Newspapers typically recognize that their surveys will not be precisely accurate and often add statements to their coverage such as: "This result is accurate to within +/− 2 percentage points." Although they do not explicitly say it, they are getting this result from a confidence interval (usually a 95% confidence interval).[29] An equivalent statement would be: "We are 95% confident that Party A will receive between 41% and 45% of the vote on election day".
This example provides some additional intuition about what confidence intervals are. If you understand this example, you can also see that different confidence levels imply different confidence intervals. As a trivial example, consider the 100% confidence level. We can be certain that Party A is going to receive between 0% and 100% of the vote on election day. A 100% confidence interval for Party A's percentage of the vote would thus be [0, 100].
Now consider the other extreme: how confident can we be that Party A is going to receive almost precisely 43% of the vote? Probably not very confident for, as noted, in reality we rarely find that opinion polls and election day results will match identically. For this reason, a confidence interval right around 43% (e.g. [42.9, 43.1]) will have a very low confidence level (perhaps 10%).
Note that the more confident you wish to be about your interval, the wider it becomes. For instance, 99% confidence intervals will always be wider than 95% confidence intervals. It turns out that the confidence level determines the number tb. If the level of confidence is high (e.g. 99%) tb will be large, while if the level of confidence is low (e.g. 50%) it will be small.
To return to the general statistical theory of regression, we should stress (without explanation beyond that given in the previous example) the following:
tb decreases with N (i.e. the more data points you have the smaller the confidence interval will be).
tb increases with the level of confidence you choose.
Researchers usually present 95% confidence intervals, although other intervals are possible (e.g. 99% or 90% confidence intervals are sometimes presented). A useful (but formally incorrect) intuition for 95% confidence intervals is conveyed by the following statement: "There is a 95% probability that the true value of β lies in the 95% confidence interval". A correct (but somewhat awkward) interpretation of this statement is: "If you repeatedly used (in different data sets) the above formula for calculating confidence intervals, 95% of the confidence intervals constructed would contain the true value for β". Similar statements can be made for 99% or 90% confidence intervals, simply by replacing "95%" with the desired confidence level. Thus, the interpretation of confidence intervals is relatively straightforward (and will be further illustrated in subsequent examples in this chapter).
The preceding material is intended to provide some intuition and motivation for the statistical theory underlying confidence intervals. Even if you do not fully understand this material, confidence intervals can be calculated quite easily in most standard computer software packages. For example, when you run a regression in Excel it automatically calculates the confidence interval and labels the bounds of the 95% confidence interval as "lower 95%" and "upper 95%". Excel also enables you to change the level of confidence, e.g. from 99% to 90%.
Example: Confidence intervals for the data sets in Figures 5.1–5.4
Figures 5.1 through 5.4 contained four different data sets, all of which have α = 0 and β = 1. Remember that the data set used in Figure 5.3 has some very desirable properties, i.e. large sample size, spread-out values for the explanatory variables, and small errors. These properties are missing to varying degrees in the other three data sets. Table 5.1 contains OLS point estimates,
Table 5.1. OLS estimates and confidence intervals.
Data Set | | 90% Confidence interval | 95% Confidence interval | 99% Confidence interval |
|---|---|---|---|---|
0.91 | [−0.92, 2.75] | [−1.57, 3.39] | [−3.64, 5.47] | |
1.04 | [0.75, 1.32] | [0.70, 1.38] | [0.59, 1.49] | |
1.00 | [0.99, 1.01] | [0.99, 1.02] | [0.98, 1.03] | |
1.52 | [−1.33, 4.36] | [−1.88, 4.91] | [−2.98, 6.02] |
The following points are worth emphasizing:
Reading across any row, we can see that as the confidence level gets higher the confidence interval gets wider. The widest interval is the 99% confidence interval for the data set in Figure 5.4. In this case, if you want to be 99% confident, you have to say β could be anywhere between −2.98 and 6.02!
The data set in Figure 5.3 – the one with the most desirable properties of all the data sets – yields an OLS estimate of 1.00 which is equal to the true value to two decimal places (more precisely,
The data set in Figure 5.3 yields confidence intervals which are much narrower than those for Figures 5.1, 5.2 and 5.4. This makes sense since we would expect the OLS estimate using the data set in Figure 5.3 to be more accurate than the other data sets.
The data sets in Figures 5.1, 5.2 and 5.4 yield a variety of results. Figure 5.2 contains a data set of the sort usually found in a well-designed empirical project (rarely does one get a data set as good as Figure 5.3). This data set has mostly desirable properties, but the errors are moderately large, reflecting the measurement error and imperfections in the underlying economic theory which so often occur in practice. For this representative data set,
Exercise 5.1
The data sets used to calculate Figures 5.1, 5.2, 5.3 and 5.4 are in FIG51.XLS, FIG52.XLS, FIG53.XLS and FIG54.XLS.
Calculate the OLS estimates
Calculate confidence intervals for α for the four data sets. Examine how the width of the confidence interval relates to N and the variability of the errors.
Calculate 99% and 90% confidence intervals for the data sets. How do these differ from the 95% confidence intervals in (b)?
Example: The regression of executive compensation on profits
Let us go back to our executive compensation (Y) and profit (X) data set (EXECUTIVE.XLS). We saw in the last chapter that
Example: The regression of lot size on house price
In Chapter 3 we investigated the effect of X = lot size on Y = the sales price of a house, using data on 546 houses sold in Windsor, Canada (see data set HPRICE.XLS). Running a regression of Y on X we obtain the following estimated relationship:
or equivalently,
The 95% confidence interval for β is [5.72, 7.47]. Although the effect of lot size on house price is estimated at $6.59, we are not certain that this figure is exactly correct. However, we are extremely confident (i.e. 95% confident) that the effect of lot size on house is at least $5.72 and at most $7.47. This interval would be enough for a potential buyer or seller to have a good idea of the value of lot size.
Example: The capital asset pricing model
In Chapter 4, we introduced the CAPM, a theory that implied that the excess return on the stock of a particular company should depend on the excess return on the market portfolio. This motivated a regression using monthly data on Y = the excess returns on Company A's stock for the last 10 years on X = excess returns on a stock market index for the same time period. When we ran a regression of Y on X we obtain
Hypothesis testing is another exercise commonly carried out by the empirical researcher. As with confidence intervals, we will not go into the statistical theory that underlies hypothesis testing. Instead we will focus on the practical details of how to carry out hypothesis tests and interpret the results. Classical hypothesis testing involves specifying a hypothesis to test. This is referred to as the null hypothesis, and is labeled as H0. It is compared to an alternative hypothesis, labeled H1. A common hypothesis test is whether β = 0. Formally, we say that this is a test of H0: β = 0 against H1: β # 0.
Note that, if β = 0 then X does not appear in the regression model; that is, the explanatory variable fails to provide any explanatory power whatsoever for the dependent variable. If you think of the kinds of questions of interest to researchers (e.g. "Does a certain characteristic influence the price of an asset or good?", "Will a certain advertising strategy increase sales?", "Does the debt burden of a firm influence its market capitalization?", etc.) you will see that many are of the form "Does the explanatory variable have an effect on the dependent variable?" or "Does β = 0 in the regression of Y on X?". The purpose of the hypothesis test of β = 0 is to answer this question.
The first point worth stressing is that hypothesis testing and confidence intervals are closely related. In fact, one way of testing whether β = 0 is to look at the confidence interval for β and see whether it contains zero. If it does not then we can, to introduce some statistical jargon, "reject the hypothesis that β = 0" or conclude "X has significant explanatory power for Y" or "β is significantly different from zero" or "β is statistically significant". If the confidence interval does include zero then we change the word "reject" to "accept" and "has significant explanatory power" to "does not have significant explanatory power", and so on. This confidence interval approach to hypothesis testing is exactly equivalent to the formal approach to hypothesis testing discussed below.
Just as confidence intervals came with various levels of confidences (e.g. 95% is the usual choice), hypothesis tests come with various levels of significance. If you use the confidence interval approach to hypothesis testing, then the level of significance is 100% minus the confidence level. That is, if a 95% confidence interval does not include zero, then you may say "I reject the hypothesis that β = 0 at the 5% level of significance" (i.e. 100% – 95% = 5%). If you had used a 90% confidence interval (and found it did not contain zero) then you would say: "I reject the hypothesis that β = 0 at the 10% level of significance".
The alternative way of carrying out hypothesis testing is to calculate a test statistic. In the case of testing whether β = 0, the test statistic is known as a t-statistic (or t-ratio or t-stat). It is calculated as:
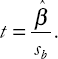
"Large" values (in an absolute value sense) of t indicate that β ≠ 0, while "small" values indicate that β = 0. Mathematical intuition for the preceding sentence is given as: if
If the P-value is less than 5% (usually written as 0.05 by the computer) then t is "large" and we conclude that β ≠ 0.
If the P-value is greater than 5% then t is "small" and we conclude that β = 0.
The preceding test used the 5% level of significance. However, if we were to replace the figure 5% in the above expressions with 1% (i.e. reject β = 0 if the P-value is less than 1%) our hypothesis test would be carried out at the 1% level of significance.
As an aside, it is worth noting that we are focussing on the test of β = 0 partly because it is an important one, but also because it is the test that is usually printed out by computer packages. You can use it without fully understanding the underlying statistics. However, in order to test other hypotheses (e.g. H0: β = 1 or hypotheses involving many coefficients in the multiple regression case in the next chapter) you would need more statistical knowledge than is covered here (see Appendix 5.1 for more details). The general structure of a hypothesis test is always of the form outlined above. That is, (i) specify the hypothesis being tested, (ii) calculate a test statistic and (iii) compare the test statistic to a critical value. The first of these three steps is typically easy, but the second and third can be much harder. In particular, to obtain the test statistic for more complicated hypothesis tests will typically require some extra calculations beyond merely running the regression. Obtaining the critical value will involve the use of statistical tables. Hence, if you wish to do more complicated hypothesis tests you will have to resort to a basic statistics or econometrics textbook (see endnote 1 of this chapter for some suggestions).
As a practical summary, note that regression techniques provide the following information about β:
The 95% confidence interval, which gives an interval where we are 95% confident β will lie.
The standard deviation (or standard error) of
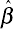
The test statistic, t, for testing β = 0.
The P-value for testing β = 0.
These five components, (
Example: The regression of executive compensation on profits (continued from page 78)
If we regress Y = executive compensation on X = profit using Excel, the following output will be produced (other software packages will provide output of a similar form):
Table 5.2. The regression of executive compensation on profits.
Coefficient | Standard error | t-stat | P-value | Lower 95% | Upper 95% | |
|---|---|---|---|---|---|---|
Intercept | 0.599965 | 0.112318 | 5.341646 | 1.15E – 06 | 0.375837 | 0.824093 |
X-variable | 0.000842 | 0.000117 | 7.227937 | 5.5E – 10 | 0.00061 | 0.001075 |
The row labeled "Intercept" contains results for α, and the row labeled "X-variable", results for β. We will focus discussion on this latter row. The column labeled "Coefficient" presents the OLS estimate and, as we have seen before,
The columns labeled "Standard error" and "t-Stat" indicate that sb = 0.000117 and t = 7.227937. These numbers are not essential to carrying out a hypothesis test of β = 0 when the P-value is given. For most purposes we can ignore these two columns.[30]
The hypothesis test of β = 0 can be done in two equivalent ways. First, we can find a 95% confidence interval for β of [0.00061, 0.001075]. Since this interval does not contain 0, we can reject the hypothesis that β = 0 at the 5% level of significance. In other words, there is strong evidence for the hypothesis that β ≠ 0 and that profit has significant power in explaining executive pay. Second, we can look at the P-value which is 5.5 × 10−10,[31] and much less than 0.05. This means that we can reject the hypothesis that profit has no effect on executive pay at the 5% level of significance. In other words, we have strong evidence that profit does indeed affect executive pay.
Most computer packages which include regression, such as Excel, also print out results for the test of the hypothesis H0: R2 = 0. The definition and interpretation of R2 was given in the previous chapter. Recall that R2 is a measure of how well the regression line fits the data or, equivalently, of the proportion of the variability in Y that can be explained by X. If R2 = 0 then X does not have any explanatory power for Y. The test of the hypothesis R2 = 0 can therefore be interpreted as a test of whether the regression explains anything at all. For the case of simple regression, this test is equivalent to a test of β = 0.
In the next chapter, we will discuss the case of multiple regression (where there are many explanatory variables), in which case this test will be different. To preview our discussion of the next chapter, note that the test of R2 = 0 will be used as a test of whether all of the explanatory variables jointly have any explanatory power for the dependent variable. In contrast, the t-statistic test of β = 0 will be used to investigate whether a single individual explanatory variable has explanatory power.
The strategy and intuition involved in testing R2 = 0 proceed along the same lines as above. That is, the computer software calculates a test statistic which you must then compare to a critical value. Alternatively, a P-value can be calculated which directly gives a measure of the plausibility of the null hypothesis R2 = 0 against the alternative hypothesis, R2 ≠ 0. Most statistical software packages will automatically calculate the P-value and, if so, you don't need to know the precise form of the test statistic or how to use statistical tables to obtain a critical value. For completeness, though, we present the test statistic, the F-statistic,[32] which is calculated as:
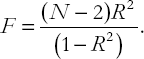
This expression is calculated automatically by Excel and is labeled simply as "F". As before, "large" values of the test statistic indicate R2 ≠ 0 while "small" values indicate R2 = 0. As for the test of β = 0, we use the P-value to decide what is "large" and what is "small" (i.e. whether R2 is significantly different from zero or not). Note, however, that Excel refers to the P-value for this test as "Significance F". The test is performed according to the following strategy:
If Significance F is less than 5% (i.e. 0.05), we conclude R2 ≠ 0.
If Significance F is greater than 5% (i.e. 0.05), we conclude R2 = 0.
The previous strategy provides a statistical test with a 5% level of significance. To carry out a test at the 1% level of significance, merely replace 5% (0.05) by 1% (0.01) in the preceding sentences. Other levels of significance (e.g. 10%) can be calculated in an analogous manner.
Other computer packages might use a slightly different notation than Excel does. For instance, MicroFit labels the F-statistic "F-stat." and puts the P-value in brackets next to F.
The accuracy of OLS estimates depends on the number of data points, the variability of the explanatory variable and the variability of the errors.
The confidence interval provides an interval estimate of β (i.e. an interval in which you can be confident β lies). It is calculated in most computer software packages.
The width of the confidence interval depends on the same factors as affect the accuracy of OLS estimates. In addition, the width of the confidence interval depends on the confidence level (i.e. the degree of confidence you want to have in your interval estimate).
A hypothesis test of whether β = 0 can be used to find out whether the explanatory variable belongs in the regression. The P-value, which is calculated automatically in most spreadsheet or statistical computer packages, is a measure of how plausible the hypothesis is.
If the P-value for the hypothesis test of whether β = 0 is less than 0.05 then you can reject the hypothesis at the 5% level of significance. Hence, you can conclude that X does belong in the regression.
If the P-value for the hypothesis test of whether β = 0 is greater than 0.05 then you cannot reject the hypothesis at the 5% level of significance. Hence, you cannot conclude that X belongs in the regression.
A hypothesis test of whether R2 = 0 can be used to investigate whether the regression helps explain the dependent variable. A P-value for this test is calculated automatically in most spreadsheet and statistical computer packages and can be used in a similar manner to that outlined in points 5 and 6.
The P-value is all that you will need to know in order to test the hypothesis that β = 0. Most computer software packages (e.g. Excel, MicroFit, Stata or SHAZAM) will automatically provide P-values. However, if you do not have such a computer package or are reading a paper which presents the t-statistic, not the P-value, then it is useful to know how to carry out hypothesis testing using statistical tables. Virtually any statistics or econometrics textbook will describe the method in detail and will also provide the necessary statistical table for you to do so. Here we offer only a brief discussion along with a rough rule of thumb which is applicable to the case when the sample size, N, is large.
Remember that hypothesis testing involves the comparison of a test statistic to a number called a critical value. If the test statistic is larger (in absolute value) than the critical value, the hypothesis is rejected. Here, the test statistic is the t-stat given in the body of the chapter. This must be compared to a critical value taken from the Student-t statistical table. It turns out that this critical value is precisely what we have called tb in our discussion of confidence intervals. If N is large and you are using the 5% level of significance, then tb = 1.96. This suggests the following rule of thumb:
If the t-statistic is greater than 1.96 in absolute value (i.e. |t| > 1.96), then reject the hypothesis that β = 0 at the 5% level of significance. If the t-statistic is less than 1.96 in absolute value, then accept the hypothesis that β = 0 at the 5% level of significance.
If the hypothesis that β = 0 is rejected, then we say that "X is significant" or that "X provides statistically significant explanatory power for Y".
This rule of thumb is likely to be quite accurate if the sample size is large. Formally, the critical value equals 1.96 if sample size is infinity. However, even moderately large sample sizes will yield similar critical values. For instance, if N = 120, the critical value is 1.98. If N = 40, it is 2.02. Even the quite small sample size of N = 20 yields a critical value of 2.09 which is not that different from 1.96. However, you should be careful when using this rule of thumb if N is very small or the t-statistic is very close to 2.00. If you look back at the examples included in the body of this chapter you can see that the strategy outlined here works quite well. That is, both the P-value and confidence interval approaches lead to the same conclusion as the approximate strategy described in this appendix.
The previous discussion related to the 5% level of significance. The large sample critical value for the 10% level of significance is 1.65. For the 1% level of significance, it is 2.58.
By far the most common hypothesis to test for is H0: β = 0. Using the techniques outlined in this appendix we can generalize this hypothesis slightly to that of: H0: β = c, where c is some number that may not be zero (e.g. c = 1). In this case, the test statistic changes slightly, but the critical value is exactly the same as for the test of β = 0. In particular, the test statistic becomes:
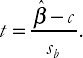
This will not be produced automatically by a computer package, but it can be calculated quite easily in a spreadsheet or on a calculator. That is,
[26] As mentioned previously, a good basic statistics book is Introductory Statistics for Business and Economics by Thomas Wonnacott and Ronald Wonnacott (Fourth edition, John Wiley & Sons, Ltd, 1990). A good introductory econometrics textbook is that by Carter Hill, William Griffiths and George Judge, Undergraduate Econometrics (Second edition, John Wiley & Sons, Ltd, 2000).
[27] If you are having trouble grasping this point, draw a straight line with intercept = 0 and slope = 1 through Figures 5.2 and 5.3 and then look at some of the resulting residuals (constructed as in Figure 4.1). You should see that most of the residuals in Figure 5.2 will be much bigger (in absolute value) than those in Figure 5.3. This will result in a larger SSR (see the formula in Chapter 4) and, since residuals and errors are very similar things, a bigger variance of the errors (see the formula for the standard deviation of a variable in the descriptive statistics section of Chapter 2 and remember that the variance is just the standard deviation squared).
[28] The notation that "β lies between a and b" or "β is greater than or equal to a and less than or equal to b" is expressed mathematically as "β lies in the interval [a, b]". We will use this mathematical notation occasionally in this book.
[29] The choice of a 95% confidence interval is by far the most common one, and whenever a confidence interval is not specified you can assume it is 95%.
[30] In the examples in this book we never use sb and rarely use t. For future reference, the only places we use t are in the Dickey-Fuller and Engle-Granger tests which will be discussed in Chapters 9 and 10, respectively.
[31] Note that 5.5E – 10 is the way most computer packages write 5.5 × 10−10 which can also be written as 0.00000000055.
[32] Formally, the F-statistic is only one in an entire class of test statistics that take their critical values from the so-called "F-distribution". Appendix 11.1 offers some additional discussion of this topic.