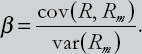Regression is an important tool financial researchers use to understand the relationship among two or more variables. Even when, as done in later chapters, we move beyond regression and use slightly more complicated methods, the intuition provided by regression is of great use. This motivates why we devote this chapter (and the next three) to regression. It is important for the reader to develop the basic tools of regression before proceeding on to more sophisticated methods.
In finance, most empirical work involves time series data. However, as we shall see in the second half of this book, working with time series data requires some specialized tools. Hence, with some exceptions,[18] for the next few chapters you will not see too many examples involving financial time series data. The examples in this chapter will mostly involve cross-sectional data. The reader interested in more traditional applications involving financial time series can be reassured that they will reappear starting in Chapter 8. However, before we get to time series methods, a good understanding of basic regression is required.
Regression is particularly useful for the common case where there are many variables and the interactions between them are complex. All of the examples considered in Chapter 3 really should have involved many variables. For instance, market capitalization likely depends on many characteristics of the firm, such as sales, assets, income, etc. Executive compensation likely does not depend solely on firm profits, but also on other firm characteristics. The price of a house, as well, depends on many characteristics (e.g. number of bedrooms, number of bathrooms, location of house, size of lot, etc.). Many variables must be included in a model seeking to explain why some houses are more expensive than others.
These examples are not unusual. Many problems in finance are of a similar level of complexity. Unfortunately, the basic tool you have encountered so far — simple correlation analysis — cannot handle such complexity. For these more complex cases — that is, those involving more than two variables — regression is the tool to use.
As a way of understanding regression, let us begin with just two variables (Y and X). We refer to this case as simple regression. Multiple regression, involving many variables, will be discussed in Chapter 6. Beginning with simple regression makes sense since graphical intuition can be developed in a straightforward manner and the relationship between regression and correlation can be illustrated quite easily.
Let us return to the XY-plots used previously (e.g. Figure 2.3 which plots profits against executive compensation for many companies or Figure 3.1 which plots lot size against house price). We have discussed in Chapters 2 and 3 how an examination of these XY-plots can reveal a great deal about the relationship between X and Y. In particular, a straight line drawn through the points on the XY-plot provides a convenient summary of the relationship between X and Y. In regression analysis, we formally analyze this relationship.
To start with, we assume that a linear relationship exists between Y and X. As an example, you might consider Y to be the market capitalization variable and X to be the sales variable from data set EQUITY.XLS. Remember that this data set contained the market capitalization of 309 American firms with several characteristics for each firm. It is sensible to assume that the sales of the firm affects its market capitalization.
We can express the linear relationship between Y and X mathematically as:[19]
where α is the intercept of the line and β is the slope. This equation is referred to as the regression line. If in actuality we knew what α and β were, then we would know what the relationship between Y and X was. In practice, of course, we do not have this information. Furthermore, even if our regression model, which posits a linear relationship between Y and X, were true, in the real world we would never find that our data points lie precisely on a straight line. Factors such as measurement error mean that individual data points might lie close to but not exactly on a straight line.
For instance, suppose the price of a house (Y) depends on the lot size (X) in the following manner: Y = 34,000 + 7X (i.e. α = 34,000 and β = 7). If X were 5,000 square feet, this model says the price of the house should be Y = 34,000 + 7 × 5,000 = $69,000. But, of course, not every house with a lot size of 5,000 square feet will have a sales price of precisely $69,000. No doubt in this case, the regression model is missing some important variables (e.g. number of bedrooms) that may affect the price of a house. Furthermore, the price of some houses might be higher than they should be (e.g. if they were bought by irrationally exuberant buyers). Alternatively, some houses may sell for less than their true worth (e.g. if the sellers have to relocate to a different city and must sell their houses quickly). For all these reasons, even if Y = 34,000 + 7X is an accurate description of a straight line relationship between Y and X, it will not be the case that every data point lies exactly on the line.
Our house price example illustrates a truth about regression modeling: the linear regression model will always be only an approximation of the true relationship. The truth may differ in many ways from the approximation implicit in the linear regression model. In many financial applications, the most probable source of error is due to missing variables, usually because we cannot observe them. In our previous example, house prices reflect many variables for which we can easily collect data (e.g. number of bedrooms, number of bathrooms, etc.). But they will also depend on many other factors for which it is difficult if not impossible to collect data (e.g. the number of loud parties held by neighbors, the degree to which the owners have kept the property well-maintained, the quality of the interior decoration of the house, etc.). The omission of these variables from the regression model will mean that the model makes an error.
We call all such errors e. The regression model can now be written as:
In the regression model, Y is referred to as the dependent variable, X the explanatory variable, and α and β, coefficients. It is common to implicitly assume that the explanatory variable "causes" Y, and the coefficient β measures the influence of X on Y. In light of the comments made in the previous chapter about how correlation does not necessarily imply causality, you may want to question the assumption that the explanatory variable causes the dependent variable. There are two responses that can be made to this statement.
First, note that we talk about the regression model. A model specifies how different variables interact. For instance, models of salary determination posit that executive compensation should depend on firm profitability. Such models have the causality "built-in" and the purpose of a regression involving Y = executive compensation and X = profit is to measure the magnitude of the effect of profit on compensation only (i.e. the causality assumption may be reasonable and we do not mind assuming it). Secondly, we can treat the regression purely as a technique for generalizing correlation and interpret the numbers that the regression model produces purely as reflecting the association between variables. (In other words, we can drop the causality assumption if we wish.[20])
In light of the error, e, and the fact that we do not know what α and β are, the first problem in regression analysis is how we can figure approximately, or estimate, what α and β are. It is standard practice to refer to the estimates of α and β as
Before we do this, it is useful to make a distinction between errors and residuals. The error is defined as the distance between a particular data point and the true regression line. Mathematically, we can rearrange the regression model to write ei = Yi – α – βXi. This is the error for the ith observation. However, if we replace α and β by their estimates
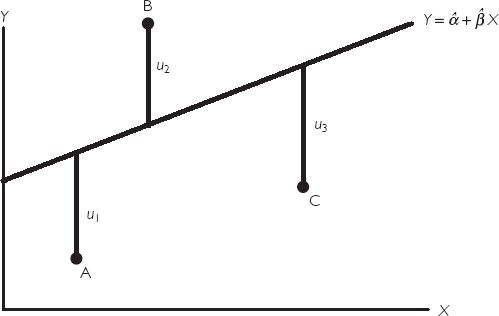
If we return to some basic geometry, note that we can draw one (and only one) straight line connecting any two distinct points. Thus, in the case of two points, there is no doubt about what the best fitting line through an XY-plot is. However, typically we have many points — for instance, our executive compensation/profit example has 70 different companies and the XY-plots 70 points — and there is ambiguity about what is the "best fitting line". Figure 4.1 plots three data points (A, B and C) on an XY graph. Clearly, there is no straight line that passes through all three points. The line I have drawn does not pass through any of them; each point, in other words, is a little bit off the line. To put it another way: the line drawn implies residuals that are labeled u1, u2 and u3. The residuals are the vertical difference between a data point and the line. A good fitting line will have small residuals.
The usual way of measuring the size of the residuals is by means of the sum of squared residuals (SSR), which is given by:
for i = 1, ..., N data points. We want to find the best fitting line which minimizes the sum of squared residuals. For this reason, estimates found in this way are called least squares estimates (or ordinary least squares – OLS – to distinguish them from more complicated estimators which we will not discuss in this book).
In practice, software packages such as Excel can automatically find values for
In the example of the relationship between executive compensation and profits, we obtained OLS estimates for the intercept and slope of the regression line. The question now arises: how should we interpret these estimates? The intercept in the regression model, α, usually has little financial interpretation so we will not discuss it here. However, β is typically quite important. This coefficient is the slope of the best fitting straight line through the XY-plot. In the executive compensation/profits example,
Even if you do not know calculus, the verbal intuition of the previous expression is not hard to provide. Derivatives measure how much Y changes when X is changed by a small (marginal) amount. Hence, β can be interpreted as the marginal effect of X on Y and is a measure of how much X influences Y. To be more precise, we can interpret β as a measure of how much Y tends to change when X is changed by one unit.[22] The definition of "unit" in the previous sentence depends on the particular data set being studied and is best illustrated through examples. Before doing this, it should be stressed that regressions measure tendencies in the data (note the use of the word "tends" in the explanation of β above). It is not necessarily the case that every observation (e.g. company or house) fits the general pattern established by the other observations. In Chapter 2 we called such unusual observations outliers and argued that, in some cases, examining outliers could be quite informative. In the case of regression, outliers are those with residuals that stand out as being unusually large. Hence, examining the residuals from a regression is a common practice. (In Excel you can examine the residuals by clicking on the box labeled "Residuals" in the regression menu.)
In the preceding discussion we learned how to calculate and interpret regression coefficients,
To derive and explain R2, we will begin with some background material. We start by clarifying the notion of a fitted value. Remember that regression fits a straight line through an XY-plot, but does not pass precisely through each point on the plot (i.e. an error is made). In the case of our executive compensation/profits example, this meant that individual companies did not lie on the regression line. The fitted value for observation i is the value that lies on the regression line corresponding to the Xi value for that particular observation (e.g. house, company). In other words, if you draw a straight vertical line through a particular point in the XY-plot, the intersection of this vertical line and the regression line is the fitted value corresponding to the point you chose.
Alternatively, we can think of the idea of a fitted value in terms of the formula for the regression model:
Remember that adding i subscripts (e.g. Yi) indicates that we are referring to a particular observation (e.g. the ith company or the house). If we ignore the error, we can say that the model's prediction of Yi should be equal to α +βXi. If we replace α and β by the OLS estimates
Note that we are using the value of the explanatory variable and the OLS estimates to predict the dependent variable. By looking at actual (Yi) versus fitted (Ŷi) values we can gain a rough impression of the "goodness of fit" of the regression model. Many software packages allow you to print out the actual and fitted values for each observation. An examination of these values not only gives you a rough measure of how well the regression model fits, they allow you to examine individual observations to determine which ones are close to the regression line and which are not. Since the regression line captures general patterns or tendencies in your data set, you can see which observations conform to the general pattern and which do not.
We have defined the residual made in fitting our best fitting line previously. Another way to express this residual is in terms of the difference between the actual and fitted values of Y. That is:
Software packages such as Excel can also plot or list the residuals from a regression model. These can be examined in turn to give a rough impression of the goodness of fit of the regression model. We emphasize that unusually big residuals are outliers and sometimes these outliers are of interest.
To illustrate the kind of information with which residual analysis can provide us, take a look at your computer output from Exercise 4.3 (a). In the Residual Output, observation 39 has a fitted value of 2.93 and a residual of −1.63. By adding these two figures together (or by looking at the original data), you can see that the actual compensation paid to the chief executive by this company is 1.3. What do all these numbers imply? Note that the regression model is predicting a much higher value (2.93) for compensation than actually occurred (1.3) in this company. This means that this company is getting a much cheaper chief executive than the regression model implies.
The ideas of a residual and a fitted value are important in developing an informal understanding of how well a regression model fits. However, we still lack a formal numerical measure of fit. At this stage, we can now derive and motivate such a measure: R2.
Recall that variance is the measure of dispersion or variability of the data. Here we define a closely related concept, the total sum of squares or TSS:
Note that the formula for the variance of Y is TSS/(N – 1) (see Chapter 2). Loosely speaking, the N – 1 term will cancel out in our final formula for R2 and, hence, we ignore it. So think of TSS as being a measure of the variability of Y. The regression model seeks to explain the variability in Y through the explanatory variable X. It can be shown that the total variability in Y can be broken into two parts as:
TSS = RSS + SSR,
where RSS is the regression sum of squares, a measure of the explanation provided by the regression model.[23] RSS is given by:
Remembering that SSR is the sum of squared residuals and that a good fitting regression model will make the SSR very small, we can combine the equations above to yield a measure of fit:
or, equivalently,
Intuitively, the R2 measures the proportion of the total variance of Y that can be explained by X. Note that TSS, RSS and SSR are all sums of squared numbers and, hence, are all non-negative. This implies TSS ≥ RSS and TSS ≥ SSR. Using these facts, it can be seen that 0 ≤ R2 ≤ 1.
Further intuition about this measure of fit can be obtained by noting that small values of SSR indicate that the regression model is fitting well. A regression line which fits all the data points perfectly in the XY-plot will have no errors and hence SSR = 0 and R2 = 1. Looking at the formula above, you can see that values of R2 near 1 imply a good fit and that R2 = 1 implies a perfect fit. In sum, high values of R2 imply a good fit and low values a bad fit.
An alternative source of intuition is provided by the RSS. RSS measures how much of the variation in Y the explanatory variables explain. If RSS is near TSS, then the explanatory variables account for almost all of the variability and the fit will be a good one. Looking at the previous formula you can see that the R2 is near one in this case.
Another property of R2 can be used to link regression and correlation. It turns out that the R2 from the regression of Y on X is exactly equal to the square of the correlation between Y and X. Regression is really just an extension of correlation. Yet, regression also provides you with an explicit expression for the marginal effect (β), which is often important for policy analysis.
So far, we have used the linear regression model and fit a straight line through XY-plots. However, this may not always be appropriate. Consider the XY-plot in Figure 4.2. It looks like the relationship between Y and X is not linear. If we were to fit a straight line through the data, it might give a misleading representation of the relationship between Y and X. In fact, we have artificially generated this data by assuming the relationship between Y and X is of the form:
such that the true relationship is quadratic. A cursory glance at the XY-plots can often indicate whether fitting a straight line is appropriate or not.
What should you do if a quadratic relationship rather than a linear relationship exists? The answer is surprisingly simple: rather than regressing Y on X, regress Y on X2 instead.
Of course, the relationship revealed by the XY-plot may be found to be neither linear nor quadratic. It may appear that Y is related to ln(X) or 1/X or X3 or any other transformation of X. However, the same general strategy holds: transform the X variable as appropriate and then run a regression of Y on the transformed variable. You can even transform Y if it seems appropriate.
A very common transformation, of both the dependent and explanatory variables, is the logarithmic transformation (see Appendix 1.1 for a discussion of logarithms). Even if you are not familiar with logarithms, they are easy to work with in any spreadsheet or econometric software package, including Excel.[25] Often financial researchers work with natural logarithms, for which the symbol is ln. In this book, we will always use natural logarithms and simply refer to them as "logs" for short. It is common to say that: "we took the log of variable X "or that "we worked with log X". The mathematical notation is ln(X). One thing to note about logs is that they are only defined for positive numbers. So if your data contains zeros or negative numbers, you cannot take logs (i.e. the software will display an error message).
Why is it common to use ln(Y) as the dependent variable and ln(X) as the explanatory variable? First, the expressions will often allow us to interpret results quite easily. Second, data transformed in this way often does appear to satisfy the linearity assumption of the regression model.
To fully understand the first point, we need some background in calculus, which is beyond the scope of this book. Fortunately, the intuition can be stated verbally. In the following regression:
ln(Y) = α+ β ln(X)+ e,
β can be interpreted as an elasticity. Recall that, in the basic regression without logs, we said that "Y tends to change by β units for a one unit change in X ". In the regression containing both logged dependent and explanatory variables, we can now say that "Y tends to change by β percent for a one percent change in X". That is, instead of having to worry about units of measurement, regression results using logged variables are always interpreted as elasticities. Logs are convenient for other reasons too. For instance, as discussed in Chapter 2, when we have time series data, the percentage change in a variable is approximately 100 × [ln(Yt) – ln(Yt−1)]. This transformation will turn out to be useful in later chapters in this book.
The second justification for the log transformation is purely practical: With many data sets, if you take the logs of dependent and explanatory variables and make an XY-plot the resulting relationship will look linear. This is illustrated in Figures 4.3 and 4.4. Figure 4.3 is an XY-plot of two data series, Y and X, neither of which has been transformed in any way. Figure 4.4 is an XY-plot of ln(X) and ln(Y). Note that the points in the first figure do not seem to lie along a straight line. Rather the relationship is one of a steep-sloped pattern for small values of X, that gradually flattens out as X increases. This is a typical pattern for data which should be logged. Figure 4.4 shows that, once the data is logged, the XY-plot indicates a linear pattern. An OLS regression will fit a straight line with a high degree of accuracy in Figure 4.4. However, fitting an accurate straight line through Figure 4.3 is a very difficult (and probably not the best) thing to do.
On what basis should you log your data (or for that matter take any other transformation)? There is no simple rule that can be given. Examining XY-plots of the data transformed in various ways is often instructive. For instance, begin by looking at a plot of X against Y. This may look roughly linear. If so, just go ahead and run a regression of Y on X. If the plot does not look linear, it may exhibit some other pattern that you recognize (e.g. the quadratic form of Figure 4.2 or the logarithmic form of Figure 4.3). If so, create an XY-plot of suitable transformed variables (e.g. ln(Y) against ln(X)) and see if it looks linear. Such a strategy will likely work well in a simple regression containing only one explanatory variable. In Chapter 6, we will move on to cases with several explanatory variables. In these cases, the examination of XY-plots may be quite complicated since there are so many possible XY-plots that could be constructed.
Simple regression quantifies the effect of an explanatory variable, X, on a dependent variable, Y. Hence, it measures the relationship between two variables.
The relationship between Y and X is assumed to take the form, Y = α + βX, where α is the intercept and β the slope of a straight line. This is called the regression line.
The regression line is the best fitting line through an XY graph.
No line will ever fit perfectly through all the points in an XY graph. The distance between each point and the line is called a residual.
The ordinary least squares, OLS, estimator is the one which minimizes the sum of squared residuals.
OLS provides estimates of α and β which are labeled
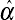
Regression coefficients should be interpreted as marginal effects (i.e. as measures of the effect on Y of a small change in X).
R2 is a measure of how well the regression line fits through the XY graph.
OLS estimates and the R2 are calculated in computer software packages such as Excel.
Regression lines do not have to be linear. To carry out nonlinear regression, merely replace Y and/or X in the regression model by a suitable nonlinear transformation (e.g. ln(Y) or X2).
The OLS estimator defines the best fitting line through the points on an XY-plot. Mathematically, we are interested in choosing
If you have done the previous exercise correctly, you should have obtained the following:
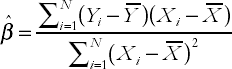
and
where
These equations can be used to demonstrate the consequences of taking deviations from means. By way of explanation, note that we have assumed above that the dependent and explanatory variables, X and Y, are based on the raw data. However, in some cases researchers do not work with just X and Y, but rather with X and Y minus their respective means:
and
Consider using OLS to estimate the regression:
where we have used the symbols a and b to distinguish them from the coefficients α and β in the regression involving Y and X.
It turns out that the relationship between OLS estimates from the original regression and the one where deviations from means have been taken is a simple one. The OLS estimate of b is always exactly the same as
It is not too hard to prove the statements in the previous paragraph and, if you are mathematically inclined, you might be interested in doing so. As a hint, note that the means of y and x are zero.
In Chapter 6, we will consider the case where there are several explanatory variables. In this case, if you take deviations from means of the dependent and all of the explanatory variables, you obtain the same result. That is, the intercept disappears from the regression, but all other coefficient estimates are unaffected.
[18] The regression methods outlined in the next few chapters can be used with time series variables if they are stationary. At this stage, you will not know what the term "stationary" means, but you can be assured that the examples in this chapter and the next involving time series data involve stationary data. The concept of stationarity will be explained in Chapter 9.
[19] Note that, at many places, we will omit multiplication signs for simplicity. For instance, instead of saying Y = α + β × X we will just say Y = α + βX.
[20] Some statistics books draw a dividing line between correlation and regression. They argue that correlation should be interpreted only as a measure of the association between two variables, not the causality. In contrast, regression should be based on causality in the manner of such statements as: "Financial theory tells us that X causes Y". Of course, this division simplifies the interpretation of empirical results. After all, it is conceptually easier to think of your dependent variable — isolated on one side of the regression equation — as being "caused" by the explanatory variables on the other. However, it can be argued that this division is in actuality an artificial one. As we saw in Chapter 3, there are many cases for which correlation does indeed reflect causality. Furthermore, in future chapters we will encounter some cases in which the regressions are based on causality, some in which they are not, and others about which we are unsure. The general message here is that you need to exercise care when interpreting regression results as reflecting causality. The same holds for correlation results. Common sense and financial theory will help you in your interpretation of either.
[21] Some may disagree with this assumption. If the management skills of the chief executive are the key factor in firm profitability, and compensation directly reflects management skills, then one can argue that the executive compensation should be the explanatory variable. But, for reasons of exposition, let us accept that the assumption made in the text is reasonable.
[22] If you cannot see this construct your own numerical example. That is, choose any values for α, β and X, then use the equation Y = α + βX to calculate Y (call this "original Y"). Now increase X by one, leaving α and β unchanged and calculate a new Y. No matter what values you originally chose for α, β and X, you will find new Y minus original Y is precisely β. In other words, β is a measure of the effect on Y of increasing X by one unit.
[23] Excel prints out TSS, RSS and SSR in a table labeled ANOVA. The column labeled "SS" contains these three sums of squares. At this stage, you probably do not know what ANOVA means, but we will discuss it briefly in Chapter 7 (Regression with Dummy Variables).
[24] Any finance textbook will describe the theoretical derivations in this example in detail. See, for instance, Quantitative Financial Economics by Keith Cuthbertson, published by John Wiley & Sons, Ltd.
[25] You can calculate the natural logarithm of any number in Excel by using the formula bar. For instance, if you want to calculate the log of the number in cell D4 move to the formula bar and type "= ln(D4)" then press enter.