4.6. Biometric Authentication Application Examples
SVMs are classifiers, which have demonstrated high generalization capabilities in many different tasks, including the object recognition problem. In Huang et al. [154], SVMs were applied to eye detection, which is often a vital step in face detection. In Popovici and Thiran [281], a method for face class modeling in the eigenfaces space, using a large-margin classifier similar to SVMs, was proposed. The paper also addresses the issue of how to effectively train the SVM to improve generalization. In Heisele et al. [133], a hierarchical SVM classifier is developed by (1) growing image parts by minimizing theoretical bounds on the error probability of an SVM, and (2) then combining component-based face classifiers in a second stage. This represents a new scheme for automatically learning the discriminative components of objects with SVM classifiers. Moreover, experimental results in face classification show considerable robustness against rotations.
In Sadeghi et al. [327], different face identity verification methods on the BANCA database were compared. The SVM classifier was found to be superior when a large enough training set was available. (However, when the training set size is limited, it is outperformed by a normalized correlation method in the LDA space.) In Antonini et al. [9], the effect of representation under the face detection/localization context was studied. An ICA representation and an SVM classification were proposed to extract facial features, with the objective of finding a projection subspace offering better robustness against illumination or other environmental variations. The method was successfully tested on the BANCA database. In Deniz et al. [75], two types of experiments were made on face databases, both achieving a very high recognition rate. In one experiment, SVMs and PCAs were combined, while in another, SVMs and ICA (Independent Component Analysis) were combined for face detection and recognition. The experimental results suggest that SVMs are relatively insensitive to the representation space, as the results using the PCA/SVM combination were not far from the ICA/SVM combination. However, since the training time for ICA is much longer than that of PCA, the paper recommends the best practical combination is PCA with SVM.
Several studies suggest that SVMs can be used for speaker modeling [120, 336, 364, 388]. In these studies, SVMs were used as binary classifiers and were trained to discriminate true-speakers' speech from that of impostors'. Due to an overlap between true-speakers' speech and impostors' speech in the feature space, the training of SVM-based speaker models tended to be computationally intensive. A more interesting way of using SVMs for speaker verification is to classify the dynamic scores derived from GMMs or generative speaker models by a discriminative model [43, 97, 179, 256]. Unlike the classical GMM-based speaker recognition approach, where the kernels (typically Gaussians) characterize frame-level statistics, the SVM-based approach considers the entire sequence of an utterance as a single entity (i.e., the entire sequence is mapped to a single point in a high-dimensional feature space).[8]
[8] In the literature, this type of kernel is referred to as an utterance-based dynamic kernel or a sequence kernel.
The generative model provides an efficient representation of the data, whereas the discriminative model creates the best decision boundary to separate the speaker and the impostor classes. In Fine et al. [97], Fisher scores [160] were obtained from a generative model (GMM), which was plugged into the discriminative SVMs to create a better decision boundary for separating different classes. In Campbell [43], the Fisher kernel was replaced by a linear discriminant kernel; and in Moreno and Ho [256], it was replaced by the exponential of the symmetric Kullback-Leibler divergence. Wan and Renals [365] compared dynamic kernels against static kernels and found that sequence-level discrimination, using the log-likelihood ratio kernel, achieved the best results.
SVMs have also been applied to learn the decision function that aims to classify scores produced by the client and the impostor models on a two-dimensional score plane [23] or a three-dimensional score space [196]. Given an utterance X, state-of-the-art speaker verification systems typically compute the ratio (or log-difference) between the likelihood of the true speaker p(X|spk) and the likelihood of an impostor p(X|imp). Each frame in X then results in a point on the "log p(X|spk)-log p(X|imp)" plane. The Bayes decision rule amounts to finding the best straight line to separate the points on this plane. Instead of using the Bayes decision rule, an SVM with nonlinear kernels can be applied to create a nonlinear decision function to classify data on the plane. Experimental results have demonstrated that decision functions formed by the SVMs are more flexible than Bayes's straight lines, which leads to a lower error rate.
SVMs have also been adopted for the combination of different modalities of identity verification such as face and speakers. It was demonstrated that a combination of modalities did outperform individual modalities; and in particular, the combination of two lowest-performance modules (i.e., Face and VoiceTI) actually outperformed even the best single module (i.e., VoiceTD)—according to the experiments conducted in Ben-Yacoub [21] and Luettin and Ben-Yacoub [218]. In Liu et al. [216], nonstandard SVMs were used to fuse the scores coming from a speaker verifier and a verbal information verifier. It was found that the SVM-based fusion scheme outperforms the conventional combination rule by 50%.
Problems
Suppose that in a two-class problem the class-conditional densities for the two classes can be described by two single Gaussian normal distributions with equal variance but different means. Show that the Fisher projection direction w in Eq. 4.2.9 can be derived by computing the posterior probability using the Bayes theorem.
Show that the Fisher's linear discriminant analysis bears a strong connection to the least-squares error classifier. More precisely,
show that they have the same projection direction;
show that they do not necessarily have the same threshold b.
This problem will show that the Fisher discriminant analysis is not always optimal. The two data points [1, 10], [1, 0] are the centers of two clusters belonging to the first class and [–1, 0], [–1, –10] are the centers of another two clusters belonging to the second class. If the two-dimensional data are projected onto one-dimensional space with projection angle θ (a line with an angle of inclination θ with respect to the horizontal axis of the two-dimensional space), the projected coordinates of these four centers on the one-dimensional space will be cos θ+10 sin θ, cos θ, — cos θ, and - cos θ - 10 sin θ, leading to a classification error rate:
where σ = 3 denotes the cluster variance.
Show that Fisher's linear projection angle is 53° with an error of 21%.
By differentiating the preceding equation with respect to θ, verify that the best projection angle should be 38° and that the minimum error rate is 20%.
Consider the linear separable case (without slack variables). Recall that all support vectors must meet the conditions of Eq. 4.3.5 or Eq. 4.3.6. In your opinion, is the reverse not necessarily true? If not true, show an example in which some training data points satisfying Eq. 4.3.5 or Eq. 4.3.6 are not SVs.
This problem determines how to set the parameter σ in the sigmoidal probability for fuzzy SVM. If the positive-class confidence is expressed as
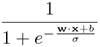
and the marginal support vectors are set to have a confidence level of 2% or 98%, determine the value of σ.
This exercise guides you through the steps to show the scale invariance property of linear SVMs using the dual formulation shown in Eq. 4.4.4. Denote the original training data as xi and the scaled training data as
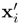such that 
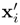= βx where β is a constant. Also denote the Lagrange multipliers and the Lagrangian corresponding to the SVM in the scaled domain as 
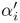and L(
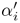), respectively.Show that
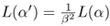if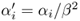 
.Show that the output weights of the linear SVM in the scaled domain is
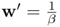w and that the bias term is 
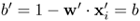.Hence, show that the distance from the origin to the decision plane in the scaled domain is b'/||w'|| = βb/||w||.
Assume that the polynomial kernel of an SVM has the form K(x, xi) = (1 + x · xi)2. When the training data is scaled by a factor β, the kernel function can be changed to K'(x',
) = 
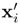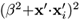, where xi = βxi ∀i.Show that the Lagrangian corresponding to the scaled data is given by L(α') = L(α)/β4, where L(α) is the Lagrangian corresponding to the unscaled data.
Hence, show that the decision boundary of an SVM that uses
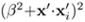as the kernel function will produce a scaled version of the decision boundary given by the SVM that uses (1 + x · xi)2 as the kernel function.Discuss the potential problem of using
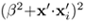as the kernel function, especially when β » 1.Suggest a better polynomial kernel function to address the scaling issue.
Show that SVMs with an RBF-kernel function of the form
are invariant to both scaling and translation if the value of σ can be proportionally scaled. Give the scaling factor for σ if the input data is scaled by β.
Figure 4.16(a) shows a two-class problem in which there are two data points— (0,0) and (0.45, 0.45)—in one class and three data points—(1,0), (0,1), and (1,1)—in the other. Analytically derive the optimal decision boundary and the corresponding SVs for the following SVMs:
Linear
Nonlinear, with second-order polynomial kernels
Nonlinear, with RBF kernels
Figure 4.16. A 5-point problem.
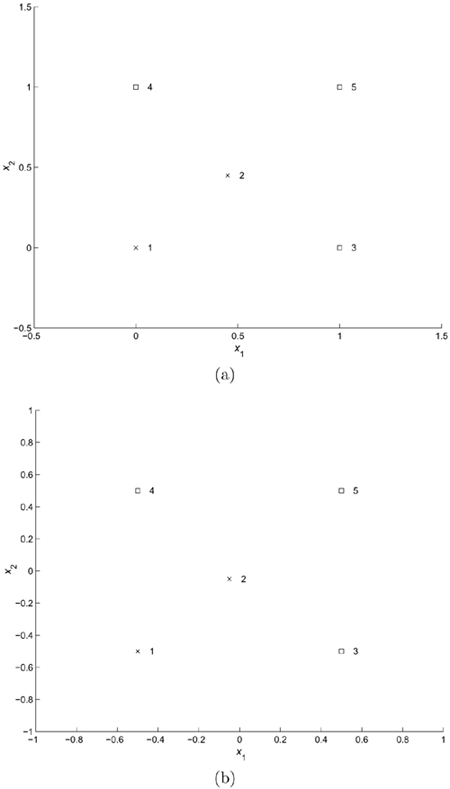
As shown in Figure 4.16(b), which is a shifted version of Figure 4.16(a), there are two data points—(–0.5, –0.5) and (–0.05, –0.05)—for one class and three points for the other—(0.5,–0.5), (–0.5, 0.5), and (0.5, 0.5). Derive the optimal boundary and find the support vectors for the following SVMs:
Linear
Nonlinear, with second-order polynomial kernels
Nonlinear, with RBF kernels
There are two points—(0, 0) and (0, 2)—for one class and two points—(0, –1) and (0,1)—for the other class. Show analytically whether the data patterns can be separated by
Nonlinear SVMs, with RBF kernels
Nonlinear SVMs, with second-order polynomial kernels
Nonlinear SVMs, with higher-order polynomial kernels
Compare your results with those of Problem 10.
Support vectors for clearly separable SVM classifiers. Consider a clearly separable SVM classifier. Let A denote the set of data points with αi > 0 and B denote the set of data points for which yi (xi · w + b) = 1.
Support vectors for fuzzily separable SVM classifiers. Consider a fuzzily separable SVM classifier. Let A the denote the set of data points with αi > 0 and C denote the set of data points such that yi(xi · w + b) = 1 – ξi and ξi > 0. Are the two sets equivalent? If not equivalent, is one set a subset of the other? Explain why?
For two-dimensional training data, suppose that training data points are generically random and that no more than two data points are colinear. What is the maximum number of marginal SVs selected?
Verify that the inner-product kernel is a symmetric function of its arguments, that is,
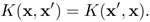
Consider the linear inner-product kernel on a two-dimensional vector space x = [u v]T:
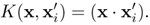
Assuming the lower limit of the integral is b = -a, the eigenfunction decomposition property can be verified by the following equality:
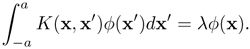
Hint: Note that, for two-dimensional vector space, a double integral must be used:
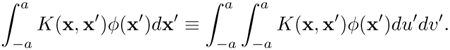
Consider a second-order polynomial kernel on a two-dimensional vector space x = [u v]T:
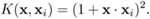
Again assuming the lower limit of the integral is b = –a:
Is φ(x) = u an eigenfunction?
Is φ(x) = u + v an eigenfunction?
Show that φ(x) = u2 is not an eigenfunction.
Under what condition on a will the function φ(x) = u2 be deemed an eigenfunction?
Robust derivation of the threshold b. Once w is fixed, the following methods can be used to determine the threshold b. Which method is more robust? Explain your selection.
Use b=1 - wTxi, where xi is a support vector and yi = 1.
Determine b from the mean value of
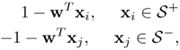
where S+ and S– contain support vectors for which the corresponding target values (yi and yj) are equal to +1 and -1, respectively.
Design a more robust method that makes use of all of the training data (SVs and non-SVs) for determining b [40].