5.3. Multi-Layer Neural Networks

Multi-layer networks are one of the most popular neural-network models. In a multi-layer network, the basis function of each neuron can be a linear basis function (LBF) with the activation function being either the step function or the sigmoidal function. Alternatively, RBF-type neurons can be adopted, which results in the RBF/EBF neural networks.

Multi-layer networks are typically trained by supervised learning, meaning that teacher information is used to train the network parameters. Depending on the nature of the teacher's information, there can be two approaches to supervised learning: One is based on the correctness of the decision and the other is based on the optimization of a training cost criterion. Of the latter, the (least-squares error) approximation-based formulation represents the most important special case. The decision-based and approximation-based formulations differ in the teacher's information that they contain and the ways in which they use it. A brief comparison follows.

Approximation-Based Formulation

An approximation-based formulation can be viewed as an approximation/regression for the trained data set, which is denoted as input/teacher pairs:

where N is the number of training pairs. The desired values at the output nodes corresponding to the input patterns x⁽ⁿ⁾ are assigned as the teacher's values. The objective of network training is to find the optimal weights to minimize the error between the teacher value and actual response. A popular criterion is the minimum-squares error between the teacher's and the actual response. To acquire a more versatile nonlinear approximation capability, multi-layer networks (together with the back-propagation learning rule) are usually adopted.

Decision-Based Formulation

In the decision-based formulation, the teacher only tells the correctness of the classification for each training pattern. The teacher is a set of symbols, T = {t⁽ⁿ⁾}, labeling the correct class for each input pattern. Unlike the approximation formulation, the teacher's exact values are not required. The objective of the training is to find a set of weights that yields the correct classification. In other words, the teacher does not need to know the exact output values of the neurons. This consideration leads to a network structure adopted by the so-called decision-based neural network (DBNN), to be discussed in Chapter 7.

5.3.1. Multi-Layer Neural Models

The most prominent neural models, based on the approximation-based formulation, are the multi-layer networks—also known as the multi-layer perceptrons (MLPs) in the literature. There are basically two types of multi-layer networks: LBF (Eq. 5.2.1) and RBF (Eq. 5.2.2), which are both highly flexible in that they can approximate almost any multivariate distribution function. Generally, a two-layer network should be adequate as a universal approximator of any nonlinear function [138]. Furthermore, it was demonstrated in [213] that, even for extreme situations, a three-layer network suffices to separate any (convex or nonconvex) polyhedral decision region from the background.

Generally, as long as there is an adequate number of nonlinear hidden nodes, a multi-layer network with correctly trained synaptic weights will be able to separate any two classes of data distribution. The synaptic weights can be adaptively trained by the BP learning algorithm. Figure 5.3(b) depicts how the representation space of the hidden-layer can be trained so that the two classes become more linearly separable step by step.

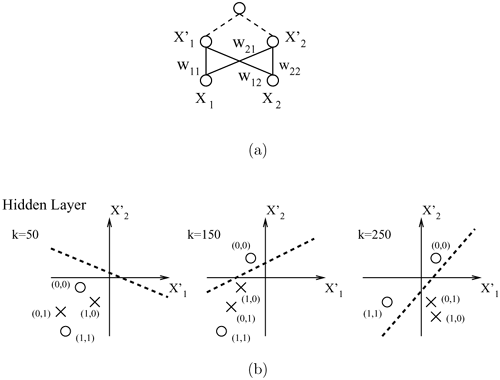
Figure 5.4 depicts the architecture of a three-layer neural network. For training approximation-based networks, the objective is to train the weights {w_ji(l); j = 1, …, M_l; i = 1,…, M_l–1; l = 1, …, L}, where M_l is the number of nodes (including the bias) in the l-th layer and L is the number of layers, so as to minimize the least-squares error between the teacher's and actual responses [326]. More specifically, minimize

Equation 5.3.1

where is the output at node k in the output layer, N is the number of training patterns, and K = ML is the dimension of the output space. The back-propagation algorithm can be applied to any type of energy function, and it offers an effective approach to the computation of the energy gradients.

The input units are represented by x_i ≡ α_i(0) and the output units by y_i ≡ a_i(L), where L is the number of layers. A multi-layer network is characterized by the following feed-forward equations:

Equation 5.3.2

Equation 5.3.3

where w_j(l) = [w_j1(l) … w_j,M_l–1(l)] and a(l – 1) = [a₁(l – 1) … a M_l–1(l – 1)]. The activation function, denoted as f(·), is very often a sigmoid function for LBF neurons or a Gaussian activation function for RBF neurons.

5.3.2. The Classic XOR Problem

The most well-known linearly nonseparable example is the exclusive-or (XOR) problem, the input/output mapping of which is

Equation 5.3.4

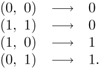
The four input data, labeled by "x" and "o", are depicted in Figure 4.4. Note that the XOR data are not linearly separable because there is no straight line that can separate the two classes. This means that no single-layer network could qualify as an XOR classifier. It is easy to show that a two-layer network, shown in Figure 5.3(a), can solve the XOR problem if the lower weights are set as follows:

Equation 5.3.5

Based on the net function in Eq. 5.2.1 and the neuron function in Eq. 5.2.3 (setting σ → 0 and the threshold θ = 0. 5), the net values and neuron values at the hidden-layer can be derived as follows:

Equation 5.3.6

Thus, by inspection, the mapped data on the hidden-layer have now become linearly separable. Note also that the choice of synaptic weights is highly nonunique. In general, synaptic weights can be adaptively trained by the BP learning algorithm.