Chapter Nine

Our Ten Digits

The idea that language is merely a code seems readily acceptable. Many of us at least attempted to learn a foreign language in high school, so we’re willing to acknowledge that the animal we call a cat in English can also be a gato, chat, Katze, кошка, or γάτα.

Numbers, however, seem less culturally malleable. Regardless of the language we speak and the way we pronounce the numbers, just about everybody we’re likely to come in contact with on this planet writes them the same way:

1   2   3   4   5   6   7   8   9   10

Isn’t mathematics called “the universal language” for a reason?

Numbers are certainly the most abstract codes we deal with on a regular basis. When we see the number

3

we don’t immediately need to relate it to anything. We might visualize 3 apples or 3 of something else, but we’d be just as comfortable learning from context that the number refers to a child’s birthday, a television channel, a hockey score, the number of cups of flour in a cake recipe, or the month of March. Because our numbers are so abstract to begin with, it’s more difficult for us to understand that this number of apples

doesn’t necessarily have to be denoted by the symbol

3

Much of this chapter and the next will be devoted to persuading ourselves that this many apples

can also be indicated by writing

11

Once we’ve reached that point, it will be possible to begin representing numbers in electrical circuits and eventually in computers. But the better we understand how our familiar numbers work, the more prepared we’ll be to make that leap.

From the time our species first began counting, we’ve used our fingers to help. Most civilizations have consequently based their number systems around ten. The only significant exceptions are a few number systems built around five, or 20, or 60, which are all closely related to ten. (The ancient Babylonian number system based on 60 persists in our reckoning of the time in seconds and minutes.) There is nothing inherently special about our number system apart from its relationship to the physiology of the human hand. Had our species developed with eight or twelve fingers, our ways of counting would be a little different. It’s no coincidence that the word digit can refer to fingers or toes as well as to numbers or that the words five and fist have similar roots.

In that sense, using a base-ten, or decimal (from the Latin for ten), number system is completely arbitrary. Yet we endow numbers based on ten with an almost magical significance and give them special names. Ten years is a decade; ten decades is a century; ten centuries is a millennium. A thousand thousands is a million; a thousand millions is a billion. These numbers are all powers of ten:

$\begin{array}{l}{10}^1=10\\ {10}^2=100\\ {10}^3=1000\left(\text{thousand}\right)\\ {10}^4=10,000\\ {10}^5=100,000\\ {10}^6=1,000,000\left(\text{million}\right)\\ {10}^7=10,000,000\\ {10}^8=100,000,000\\ {10}^9=1,000,000,000\left(\text{billion}\right)\end{array}$

Most historians believe that numbers were originally invented to count things, such as people, possessions, and transactions in commerce. For example, if someone owned four ducks, that might be recorded with drawings of four ducks:

Eventually the person whose job it was to draw the ducks thought, “Why do I have to draw four ducks? Why can’t I draw one duck and indicate that there are four of them with, I don’t know, a scratch mark or something?”

And then there came the day when someone had 27 ducks, and the scratch marks got ridiculous:

Someone said, “There’s got to be a better way,” and a number system was born.

Of all the early number systems, only Roman numerals are still in common use. You find them on the faces of clocks and watches, used for dates on monuments and statues, for some chapter and page numbering in books, for some items in an outline, and—most annoyingly—for the copyright notice in movies: The question “What year was this picture made?” can often be answered only if one is quick enough to decipher MCMLIII as the tail end of the credits goes by.

Twenty-seven ducks in Roman numerals is:

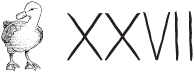
The concept here is easy enough: The X stands for ten scratch marks and the V stands for five scratch marks.

The symbols of Roman numerals that survive today are:

I  V  X  L  C  D  M

The I is a one. This could be derived from a scratch mark or a single raised finger. The V, which is possibly a symbol for a hand, stands for five. Two V’s make an X, which stands for ten. The L is a fifty. The letter C comes from the word centum, which is Latin for a hundred. D is five hundred. Finally, M comes from the Latin word mille, or a thousand. With a thousand left-right paces, you’ll walk about a mile.

Although we might not agree, for a long time Roman numerals were considered to be easy to add and subtract, and that’s why they survived so long in Europe for bookkeeping. Indeed, when adding two Roman numerals, you simply combine all the symbols from both numbers and then simplify the result using just a few rules: Five I’s make a V, two V’s make an X, five X’s make an L, and so forth.

But multiplying and dividing Roman numerals is difficult. Many other early number systems (such as that of the ancient Greeks) are similarly inadequate for working with numbers in a sophisticated manner. The ancient Greeks developed an extraordinary geometry that is still taught virtually unchanged in high schools today, but they aren’t known for their algebra.

The number system we use today is known as the Hindu-Arabic or Indo-Arabic. It is of Indian origin but was brought to Europe by Arab mathematicians. Of particular renown is the Persian mathematician Muhammed ibn Musa al-Khwarizmi (from whose name we have derived the word algorithm) who wrote a book on algebra around 820 CE that used the Hindu system of counting. A Latin translation dates from about 1145 CE and was influential in hastening the transition throughout Europe from Roman numerals to our present Hindu-Arabic system.

The Hindu-Arabic number system differs from previous number systems in three ways:

• The Hindu-Arabic number system is said to be positional, which means that a particular digit represents a different quantity depending on where it is found in the number. Where digits appear in a number is actually more significant than the digits themselves! Both 100 and 1,000,000 have only a single 1 in them, yet we all know that a million is much larger than a hundred.

• Virtually all early number systems have something that the Hindu-Arabic system does not have, and that’s a special symbol for the number ten. In our number system, there’s no special symbol for ten.

• On the other hand, virtually all of the early number systems are missing something that the Hindu-Arabic system has, and which turns out to be much more important than a symbol for ten. And that’s the zero.

Yes, the zero. The lowly zero is without a doubt one of the most important inventions in the history of numbers and mathematics. It supports positional notation because it allows us to immediately see the difference between 25 and 205 and 250. The zero also eases many mathematical operations that are awkward in nonpositional systems, particularly multiplication and division.

The whole structure of Hindu-Arabic numbers is revealed in the way we pronounce them. Take 4825, for instance. We say “four thousand, eight hundred, twenty-five.” That means

four thousands
eight hundreds
two tens and
five.

Or we can write the components like this:

$4825=4000+800+20+5$

Or breaking it down even further, we can write the number this way:

$\begin{array}{ccc}\hfill 4825=4& \times & 1000+\hfill \\ \hfill 8& \times & 100+\hfill \\ \hfill 2& \times & 10+\hfill \\ \hfill 5& \times & 1\hfill \end{array}$

Or, using powers of ten, the number can be written like this:

$\begin{array}{ccc}\hfill 4825=4& \times & {10}^3+\hfill \\ \hfill 8& \times & {10}^2+\hfill \\ \hfill 2& \times & {10}^1+\hfill \\ \hfill 5& \times & {10}^0\hfill \end{array}$

Remember that any number to the 0 power equals 1.

Each position in a multidigit number has a particular meaning. The seven boxes shown here let us represent any number from 0 through 9,999,999:

Since each position corresponds to a power of ten, a special symbol for ten isn’t required, because ten is represented by setting the 1 in a different position and using 0 as a placeholder.

What’s also really nice is that fractional quantities shown as digits to the right of a decimal point follow this same pattern. The number 42,705.684 is

$\begin{array}{ccc}\hfill 4& \times & 10,000+\hfill \\ \hfill 2& \times & 1000+\hfill \\ \hfill 7& \times & 100+\hfill \\ \hfill 0& \times & 10+\hfill \\ \hfill 5& \times & 1+\hfill \\ \hfill 6& ÷& 10+\hfill \\ \hfill 8& ÷& 100+\hfill \\ \hfill 4& ÷& 1000\hfill \end{array}$

Notice that the last three lines use division rather than multiplication. This number can also be written without any division, like this:

$\begin{array}{ccc}\hfill 4& \times & 10,000+\hfill \\ \hfill 2& \times & 1000+\hfill \\ \hfill 7& \times & 100+\hfill \\ \hfill 0& \times & 10+\hfill \\ \hfill 5& \times & 1+\hfill \\ \hfill 6& \times & 0.1+\hfill \\ \hfill 8& \times & 0.01+\hfill \\ \hfill 4& \times & 0.001\hfill \end{array}$

Or, using powers of ten, the number is

$\begin{array}{ccc}\hfill 4& \times & {10}^4+\hfill \\ \hfill 2& \times & {10}^3+\hfill \\ \hfill 7& \times & {10}^2+\hfill \\ \hfill 0& \times & {10}^1+\hfill \\ \hfill 5& \times & {10}^0+\hfill \\ \hfill 6& \times & {10}^{-1}+\hfill \\ \hfill 8& \times & {10}^{-2}+\hfill \\ \hfill 4& \times & {10}^{-3}\hfill \end{array}$

Notice that the exponents go down to zero and then become negative numbers. Our number system is so familiar to us that we don’t often recognize the elegance of its underlying structure.

We know that 3 plus 4 equals 7. Similarly, 30 plus 40 equals 70, 300 plus 400 equals 700, and 3000 plus 4000 equals 7000. This is the beauty of the Hindu-Arabic system. When you add decimal numbers of any length, you follow a procedure that breaks down the problem into steps. Each step involves nothing more complicated than adding pairs of single-digit numbers. That’s why a long time ago someone forced you to memorize an addition table:

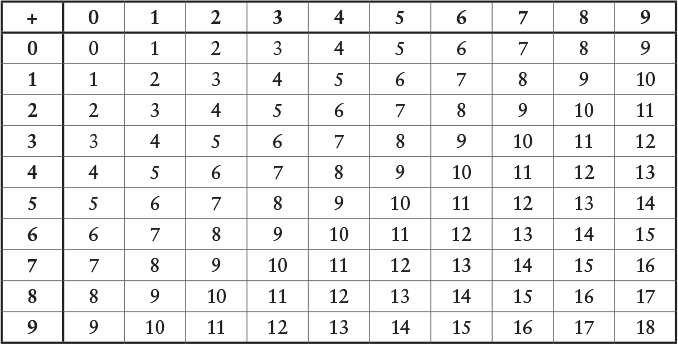
Find the two numbers you wish to add in the top row and the left column. Follow down and across to get the sum. For example, 4 plus 6 equals 10.

Similarly, when you need to multiply two decimal numbers, you follow a somewhat more complicated procedure but still one that breaks down the problem so that you need do nothing more complex than adding or multiplying single-digit decimal numbers. Your early schooling probably also entailed memorizing a multiplication table:

What’s best about the positional system of notation is not how well it works, but how well it works for counting systems not based on ten. Our number system isn’t necessarily appropriate for everyone. One big problem with our base-ten system of numbers is that it doesn’t have any relevance for cartoon characters. Most cartoon characters have only four fingers on each hand (or paw), so they prefer a number system that’s based on eight.

Interestingly enough, much of what we know about decimal numbering can be applied to a number system more appropriate for our friends in cartoons.