Chapter Sixteen

But What About Subtraction?

After you’ve convinced yourself that relays, tubes, or transistors can indeed be wired together to add binary numbers, you might ask, “But what about subtraction?” Rest assured that you’re not making a nuisance of yourself by asking questions like this; you’re actually being quite perceptive. Addition and subtraction complement each other in some ways, but the mechanics of the two operations are quite different. An addition marches consistently from the rightmost column of digits to the leftmost column. Each carry from one column is added to the next column. But we don’t carry in subtraction; instead, we borrow, and that involves an intrinsically different mechanism—a messy back-and-forth kind of thing.

For example, let’s look at a typical borrow-laden subtraction problem:

$\frac{\begin{array}{c}\hfill 253\\ -176\end{array}}{???}$

If you’re like me, as soon as you look at that rightmost column and see that 6 is greater than 3, you say Yuck. You need to borrow from the next column to the left, and that column needs a borrow as well. I won’t go through the gory details, but if you do it correctly (or you’ve made the same mistakes I have), you’ll get an answer of 77:

$\frac{\begin{array}{c}\hfill 253\\ -176\end{array}}{\phantom{00}77}$

Now how are we ever going to persuade a bunch of logic gates to go through the perverse logic necessary to get that result?

Well, we’re not going to try. Instead, we’re going to use a little technique that lets us subtract without borrowing. This might look like a trick at first, but it is a crucial first step for understanding how negative numbers are stored in computers.

You were probably told early on in your education that subtraction is the same as the addition of a negative number. In one sense, this is useless information because it doesn’t make subtraction any easier. But it does mean that we can rewrite that subtraction as a positive number added to a negative number:

$-176+253=$

Now I want to throw another couple of numbers in there—one positive and one negative—so that we’re adding a series of four numbers:

$1000-176+253-1000=$

We’re adding 1000 and then subtracting 1000, so it shouldn’t make any difference to the result. We know that 1000 is 999 plus 1, so instead of starting with 1000, we can start with 999 and then add 1 in later. The string of numbers gets even longer, but it’s still equivalent:

$999-176+253+1-1000=$

This is certainly a lot of clutter, but let’s start working on this from left to right. The first step is a subtraction: 999 minus 176. Amazingly enough, you don’t need to borrow! It’s easy to calculate that 999 minus 176 is 823:

$823+253+1-1000=$

Subtracting a number from a string of 9s results in a number called the nines’ complement. The nines’ complement of 176 is 823. And it works in reverse: The nines’ complement of 823 is 176. What’s nice is this: No matter what the number is, calculating the nines’ complement never requires a borrow.

The next two steps just involve addition. First add 253 to 823 to get the result 1076:

$1076+1-1000=$

Then add 1 and subtract 1000:

$1077-1000=77$

And it’s the same answer as before but accomplished without a single nasty borrow.

Now this is important: When using the nines’ complement to simplify subtraction, you need to know how many digits you’re dealing with. If one or both numbers had four digits, you’ll need to calculate the nines’ complement using 9999 and then subtract 10000 at the end.

But what if you’re subtracting a bigger number from a smaller number? For example, the subtraction problem could be

$\frac{\begin{array}{c}\begin{array}{c}\hfill 176\\ -253\end{array}\end{array}}{???}$

Normally, you would look at this and say, “Hmmm. I see that a bigger number is subtracted from a smaller number, so I have to switch the two numbers around, perform the subtraction, and remember that the result is really a negative number.” You might be able to switch them around in your head and write the answer this way:

$\frac{\begin{array}{c}\begin{array}{c}\hfill 176\\ -253\end{array}\end{array}}{\phantom{0}-77}$

Doing this calculation without borrowing is a little different from the earlier example, but begin by switching the two numbers around, adding 999 at the beginning, and subtracting 999 at the end:

$999-253+176-999=$

You begin as you did before, by subtracting the 253 from 999 to get the nines’ complement:

$746+176-999=$

Now add the nines’ complement to 176:

$922-999=$

At this point in the earlier problem, you were able to add 1 and subtract 1000 to get the final result, but that strategy isn’t going to work well here. Instead, we are left with a positive 922 and a negative 999. If that were a negative 922 and a positive 999, you could just take the nines’ complement of 922. That would be 77. But because we switched the signs to perform this nines’ complement, the answer is really –77. It’s not quite as straightforward as the first example, but again, no borrowing was required.

This same technique can also be used with binary numbers, and it’s actually simpler than with decimal numbers. Let’s see how it works.

The original subtraction problem was

$\frac{\begin{array}{c}\hfill 253\\ -176\end{array}}{\phantom{0}???}$

When these numbers are converted to binary, the problem becomes

$\frac{\begin{array}{c}\hfill \phantom{0}11111101\\ -\phantom{0}10110000\end{array}}{\phantom{00}????????}$

I’m going to first switch these numbers so the problem becomes a positive number added to a negative number. The decimal equivalents are shown underneath the binary numbers:

$\begin{array}{cccc}-10110000& +& 11111101& =\\ -176& +& 253& =\end{array}$

Now let’s add 11111111 (which equals 255 in decimal) at the beginning and later add 00000001 (just 1 in decimal) and subtract 100000000 (which equals 256):

$\begin{array}{cccccccccc}11111111& -& 10110000& +& 11111101& +& 00000001& -& 100000000& =\\ 255& -& 176& +& 253& +& 1& -& 256& =\end{array}$

In binary, that first subtraction requires no carries because the number is being subtracted from 11111111:

$\begin{array}{cccccccc}\underbrace{\begin{array}{c}11111111-10110000\end{array}}& +& 11111101& +& 00000001& -& 100000000& =\\ 01001111& +& 11111101& +& 00000001& -& 100000000& =\end{array}$

When a decimal number is subtracted from a string of nines, the result is called the nines’ complement. With binary numbers, subtracting something from a string of ones is called the ones’ complement. But notice that we don’t really have to do a subtraction to calculate the ones’ complement. Look at these two numbers. The ones’ complement of 10110000 is 01001111, and the ones’ complement of 01001111 is 10110000:

$\begin{array}{cccccccc}1& 0& 1& 1& 0& 0& 0& 0\\ 0& 1& 0& 0& 1& 1& 1& 1\end{array}$

The bits are just inverted: Every 0 bit in a number becomes a 1 bit in the ones’ complement, and every 1 bit becomes a 0 bit. That’s why the ones’ complement is often called the inverse. (At this point, you might recall from Chapter 8 that we built a logic gate called an inverter that changed a 0 to a 1 and a 1 to a 0.)

The problem is now:

$\begin{array}{cccccccc}01001111& +& 11111101& +& 00000001& -& 100000000& =\\ 79& +& 253& +& 1& -& 256& =\end{array}$

Now add the first two numbers:

$\begin{array}{cccccc}\underbrace{\begin{array}{c}01001111+11111101\end{array}}& +& 00000001& -& 100000000& =\\ 101001100& +& 00000001& -& 100000000& =\end{array}$

The result is a 9-bit number, but that’s OK. Now the problem has been reduced to this:

$\begin{array}{cccccc}101001100& +& 000000001& -& 100000000& =\\ 332& +& 1& -& 256& =\end{array}$

Adding the 1 is trivial:

$\begin{array}{cccc}101001101& -& 100000000& =\\ 333& -& 256& =\end{array}$

And now all that’s left is to subtract the binary equivalent of 256, which merely gets rid of the leftmost bit:

$\begin{array}{c}01001101\\ 77\end{array}$

And that final result, you’ll be pleased to know, is the same answer that we got when doing the problem in decimal.

Let’s try it again with the two numbers reversed. In decimal, the subtraction problem is

$\frac{\begin{array}{c}\hfill \phantom{0}176\\ -\phantom{0}253\end{array}}{\phantom{00}???}$

In binary it looks like this:

$\frac{\begin{array}{c}\hfill \phantom{0}10110000\\ -\phantom{0}11111101\end{array}}{\phantom{00}????????}$

Similarly to how this was done with the decimal numbers, let’s switch the order of those numbers. We’ll add 11111111 at the beginning and subtract 11111111 at the end:

$\begin{array}{cccccccc}11111111& -& 11111101& +& 10110000& -& 11111111& =\\ 255& -& 253& +& 176& -& 255& =\end{array}$

The first step is to find the ones’ complement of 11111101:

$\begin{array}{cccccc}\underbrace{\begin{array}{c}11111111-11111101\end{array}}& +& 10110000& -& 11111111& =\\ 00000010& +& 10110000& -& 11111111& =\end{array}$

Add that to the next number:

$\begin{array}{cccc}10110010& -& 11111111& =\\ 178& -& 255& =\end{array}$

Now 11111111 must be subtracted from that result in some way. When subtracting a smaller number from a larger number, you accomplish this task by adding 1 and subtracting 100000000. But you can’t subtract this way without borrowing. So instead, let’s subtract this result from 11111111:

$\begin{array}{ccccc}11111111& -& 10110010& =& 01001101\\ 255& -& 178& =& 77\end{array}$

Again, this strategy really means that we’re just inverting all the bits to get the result. The answer again is the binary equivalent 77, but for this problem, the answer is really −77.

This little quirk that we encounter when subtracting a larger number from a smaller number is a whisper to us that we’re not quite there. We haven’t quite solved this problem.

Regardless, we now have all the knowledge we need to modify the adding machine developed in Chapter 14 so that it can perform subtraction as well as addition. So that this doesn’t become too complex, this new adding and subtracting machine will perform subtractions only when the result is a positive number.

The core of the adding machine was an 8-bit adder assembled from logic gates:

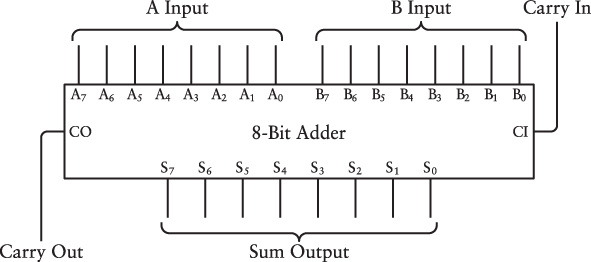
As you probably recall, the inputs A0 through A7 and B0 through B7 were connected to switches that indicated two 8-bit values to be added. The Carry In input was connected to ground, equivalent to a 0 bit. The S0 through S7 outputs were connected to eight lightbulbs that displayed the result of the addition. Because the addition could result in a 9-bit value, the Carry Out output was also connected to a ninth lightbulb.

The control panel looked like this:

In this diagram, the switches are set to add 183 (or 10110111) and 22 (00010110), producing the result of 205, or 11001101 as shown in the row of lightbulbs.

The new control panel for adding and subtracting two 8-bit numbers is just slightly modified. Instead of the big plus sign, it includes an extra switch to indicate whether we want to add or subtract.

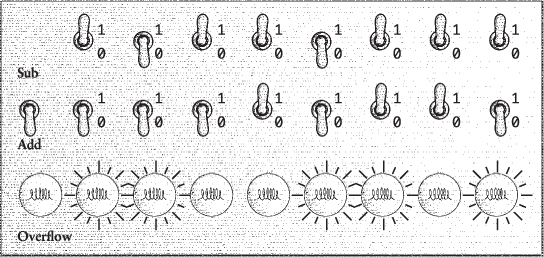
You turn this switch off for addition and on for subtraction, as labeled.

Another difference is that only the rightmost eight lightbulbs are used to display results. The ninth lightbulb is now labeled “Overflow.” This is a term encountered in computer programming in several different contexts, and it almost always indicates a problem. We’ve set up this control panel to add two 8-bit numbers, and in many cases the result will be 8 bits as well. But if the result is 9 bits in length, that’s an overflow. The result is flowing over what we’ve allocated to display it. The overflow can also occur in subtraction if we happen to subtract a larger number from a smaller number. The Overflow light means that the result is negative, but we haven’t adequately accommodated the display of that negative result.

The major addition to the adding machine is some circuitry that calculates a ones’ complement of an 8-bit number. Recall that the ones’ complement is equivalent to inverting bits, so a circuit to calculate the ones’ complement of an 8-bit number might look as simple as eight inverters:

The problem with this circuit is that it always inverts the bits that enter into it. We’re trying to create a machine that does both addition and subtraction, so the circuitry needs to invert the bits only if a subtraction is being performed. A better circuit looks like this:

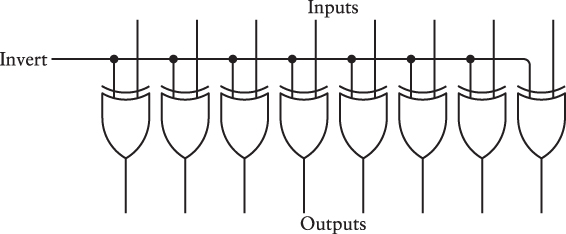
A single signal, labeled Invert, is input to each of eight XOR (exclusive OR) gates. Recall that the XOR exhibits the following behavior:

If the Invert signal is 0, the eight outputs of the XOR gates are the same as the eight inputs. For example, if 01100001 is input, then 01100001 is output. If the Invert signal is 1, the eight input signals are inverted. If 01100001 is input, 10011110 is output.

Let’s package these eight XOR gates in a box labeled Ones’ Complement:

The Ones’ Complement box, the 8-Bit Adder box, and a final exclusive OR gate can now be wired together like this:

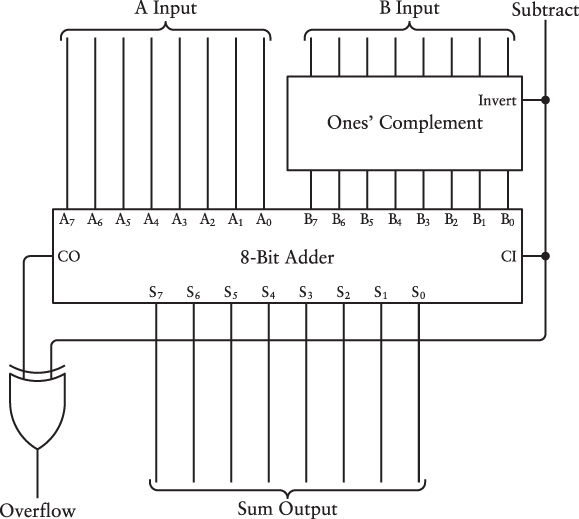
Notice the wire labeled Subtract at the upper-right corner. This comes from the Add/Subtract switch. This signal is 0 if an addition is to be performed and 1 for subtraction. For an addition, the Invert signal to the Ones’ Complement circuit is 0, and the circuit has no effect. The CI input is also 0. It’s the same as a simple addition circuit.

But for a subtraction, the B inputs (the second row of switches in the control panel) are all inverted by the Ones’ Complement circuit before entering the adder. Also for a subtraction, you add 1 to the result of the addition by setting the CI (Carry In) input of the adder to 1.

The Subtract signal and the CO (Carry Out) output of the adder also go into an XOR gate that’s used to light up the Overflow lamp. If the Subtract signal is 0 (which means an addition is being performed), the lightbulb will be lit if the CO output of the adder is 1. This means that the result of the addition is greater than 255.

If a subtraction is being performed and if the B number is smaller than the A number, it’s normal that the CO output from the adder is 1. This represents the 100000000 that must be subtracted in the final step. For subtractions, the Overflow lamp is lit only if the CO output from the adder is 0. This means that we’re trying to subtract a larger number from a smaller number. The machine shown earlier isn’t designed to display negative numbers.

By now you must surely be glad you asked, “But what about subtraction?”

I’ve been talking about negative numbers in this chapter, but I haven’t yet indicated what negative binary numbers look like. You might assume that the traditional negative sign is used with binary just as it is in decimal. For example, −77 is written in binary as −1001101. You can certainly do that, but one of the goals in using binary numbers is to represent everything using 0s and 1s—even tiny symbols such as the negative sign.

Of course, you could simply use another bit for the negative sign. You could make that extra bit a 1 for a negative number and a 0 for a positive number, and let everything else be the same. This would work, but it doesn’t go quite far enough. There’s actually another solution that has become standard for representing negative numbers in computers. The major reason it’s become standard is that it provides a hassle-free method for adding negative and positive numbers together. The biggest drawback is that you must decide ahead of time how many digits are required for all the numbers you might encounter.

Think about this for a moment: The advantage of writing positive and negative numbers the way we normally do is that they can go on forever. We imagine 0 as the middle of an infinite stream of positive numbers going off in one direction and an infinite stream of negative numbers going off in another:

$\begin{array}{ccccccccccc}\cdot \cdot \cdot & -1,000,000-999,999& \cdot \cdot \cdot & -3-2-1& 0& 1& 2& 3& \cdot \cdot \cdot & 999,999& 1,000,000\cdot \cdot \cdot \end{array}$

But suppose we don’t need an infinite number of numbers. Suppose we know at the outset that every number we come across will be within a particular range.

Let’s consider a checking account, which is one place people sometimes see negative numbers. Assume that you never have as much as $500 in the checking account and that the bank has given you a no-bounce checking limit of $500. This means that the balance in your checking account is always a number somewhere between $499 and −$500. Also assume that you never deposit as much as $500, you never write a check for more than $500, and you deal only in dollars and don’t care about cents.

This set of conditions means that the range of numbers you deal with in using your checking account is −500 through 499. That’s a total of 1000 numbers. This restriction implies that you can use just three decimal digits and no negative sign to represent all the numbers you need. The trick is that you really don’t need positive numbers ranging from 500 through 999. That’s because you’ve already established that the maximum positive number you need is 499. So the three-digit numbers from 500 through 999 can actually represent negative numbers. Here’s how it works:

1. To mean –500, use 500.

2. To mean –499, use 501.

3. To mean –498, use 502.

4. (and so forth)

5. To mean –2, use 998.

6. To mean –1, use 999.

7. To mean 0, use 000.

8. To mean 1, use 001.

9. To mean 2, use 002.

10. (and so forth)

11. To mean 497, use 497.

12. To mean 498, use 498.

13. To mean 499, use 499.

In other words, every three-digit number that begins with a 5, 6, 7, 8, or 9 is actually a negative number. Instead of negative and positive numbers extending in two directions from zero, like this:

$\begin{array}{cccccccccccc}-500& -499& -498& \cdot \cdot \cdot & -4-3-2-1& 0& 1& 2& 3& 4& \cdot \cdot \cdot & \begin{array}{cc}497& \begin{array}{cc}498& 499\end{array}\end{array}\end{array}$

They can be written this way:

$\begin{array}{ccccccccccccccccc}500& 501& 502& \cdot \cdot \cdot & 996& 997& 998& 999& 000& 001& 002& 003& 004& \cdot \cdot \cdot & 497& 498& 499\end{array}$

Notice that this forms a circle of sorts. The lowest negative number (500) looks as if it continues from the highest positive number (499). And the number 999 (which is actually −1) is one less than zero. Adding 1 to 999, you’d normally get 1000. But since we’re only dealing with three digits, it’s actually 000.

This type of notation is called ten’s complement. To convert a three-digit negative number to ten’s complement, subtract it from 999 and add 1. In other words, the ten’s complement is the nines’ complement plus one. For example, to write −255 in ten’s complement, subtract it from 999 to get 744 and then add 1 to get 745.

When using ten’s complement, you don’t subtract numbers at all. Everything is addition.

Suppose you have a checking account balance of $143. You write a check for $78. Normally you do the calculation of your new balance like this:

$\frac{\begin{array}{c}\hfill 143\\ -\phantom{0}78\end{array}}{\phantom{00}65}$

It’s a subtraction involving two carries. But in ten’s complement, −78 is written as 999 − 078 + 1, or 922, so it’s just:

$\frac{\begin{array}{c}\hfill 143\\ \mathrm{+}\phantom{0}922\end{array}}{\phantom{00}1065}$

Ignore the overflow and the result is again $65. If you then write a check for $150, you have to add −150, which in ten’s complement equals 850:

$\frac{\begin{array}{c}\hfill 65\\ +\phantom{0}850\end{array}}{\phantom{00}915}$

The result begins with a 9, so it’s a negative number equal to –$85.

The equivalent system in binary is called two’s complement, and it’s the standard way of representing positive and negative numbers in computers.

Let’s assume that we’re working with bytes, so everything is represented by 8-bit numbers. These range from 00000000 to 11111111. Up until now we’ve thought of these numbers as corresponding to decimal numbers 0 through 255. But if you also want to express negative numbers, every 8-bit number that begins with a 1 will actually represent a negative number, as shown in the following table:

The range of numbers that you can represent is now limited to −128 through +127. The most significant (leftmost) bit is known as the sign bit. The sign bit is 1 for negative numbers and 0 for positive numbers.

To calculate the two’s complement, first calculate the ones’ complement and then add 1. This is equivalent to inverting all the digits and adding 1. For example, the decimal number 125 is 01111101. To express −125 in two’s complement, first invert the digits of 01111101 to get 10000010, and then add 1 to get 10000011. You can verify the result using the preceding table. To go backward, do the same thing—invert all the bits and add 1.

The big advantage of this system is that positive and negative numbers can be expressed without using negative signs. Perhaps an even bigger advantage is that it lets us freely add positive and negative numbers using only the rules of addition. For example, let’s add the binary equivalents of −127 and 124. Using the preceding table as a cheat sheet, this is simply

$\frac{\begin{array}{c}\phantom{000}10000001\\ +\phantom{0}01111100\end{array}}{\phantom{00}11111101}$

The result is equivalent to −3 in decimal.

What you need to watch out for here is overflow. That’s when the result of an addition is greater than 127. For example, suppose you add 125 to itself:

$\frac{\begin{array}{c}\phantom{000}01111101\\ +\phantom{0}01111101\end{array}}{\phantom{00}11111010}$

Because the high bit of the sum is set to 1, the result must be interpreted as a negative number, specifically the binary equivalent of −6. Obviously adding two positive numbers cannot make a negative number, but this is exactly what happens. It’s peculiar and obviously incorrect.

Something similar happens when −125 is added to itself:

$\frac{\begin{array}{c}\phantom{000}10000011\\ +\phantom{0}10000011\end{array}}{\phantom{00}100000110}$

This also indicates a problem: We decided at the outset that we’re restricting ourselves to 8-bit numbers, so the leftmost digit of the result must be ignored. The rightmost 8 bits are equivalent to 6, which is a positive number.

In general, the result of an addition involving positive and negative two’s complement numbers is invalid if the sign bits of the two operands are the same, but the sign bit of the result is different. The result is always valid when adding a positive number and a negative number, because the result is always in the range –128 to 127.

Here’s a modified adding machine for adding two 8-bit two’s complement numbers:

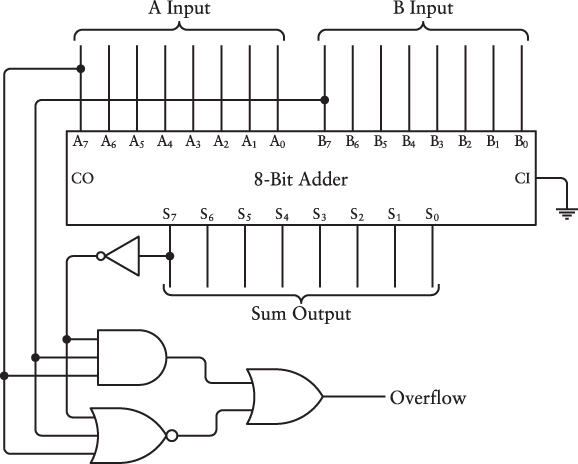
The 8-bit adder is familiar by now. A few gates have been added to detect overflow. Keep in mind that the most significant bits represent the sign of the number: 1 if negative and 0 if positive. On the input side, these sign bits are A₇ and B₇. The sign bit on the sum is S₇. Notice that the sign bit of the sum is inverted before it’s used in the AND gate and the NOR gate.

The AND gate detects an overflow condition for negative numbers. If the sign bits of the A and B inputs are both 1 (indicating two negative numbers) and the sign bit of the Sum is 0 (indicating a positive result), obviously something’s gone wrong. The sum of the two negative numbers is so negative it can’t fit in the 8 bits that we’ve allocated for it.

The NOR gate detects overflow for positive numbers. If the A and B sign bits are both 0 and the sign bit of the Sum is 1, that means that two positive numbers totaled to something so big that it’s represented as a negative number! The three inputs to the NOR gate will all be 0, and the output of the NOR gate will be 1, indicating overflow.

At the outset of this chapter, binary numbers were fairly simple. They corresponded in a very direct way to decimal numbers. An 8-bit binary number could range from 0 to 255. Such binary numbers are called unsigned because they’re always positive.

Two’s complement allows us to work with signed binary numbers. These can be positive or negative. For 8-bit values, they can range from –128 to 127. It’s the same number of numbers (256) but a different range.

The formal mathematical term for what we’ve been working with here is integer—a number that can be positive or negative, but which has no fractional parts. In real life, 8-bit integers are often inadequate for many jobs, and programmers instead use 16-bit integers (which require 2 bytes per number) or 32-bit integers (4 bytes), or even 64-bit integers (8 bytes).

In each case, these can be either signed or unsigned. The following table summarizes the range of decimal values that are possible with these integer sizes:

The ranges are based on powers of 2. For example, 16 bits allow representing 2 to the 16th power, or 65,536, different numbers. Those numbers can range from 0 through 65,535, or from –32,768 through 32,767.

Nothing about the numbers themselves will tell you whether they’re signed or unsigned. For example, suppose someone says, “I have an 8-bit binary number, and the value is 10110110. What’s the decimal equivalent?” You must first inquire, “Is that a signed or an unsigned number? It could be −74 or 182.”

Bits are just 0s and 1s. They don’t tell you anything about themselves. That information must come from the context in which they’re used.