Chapter Twelve

Bytes and Hexadecimal

Individual bits can make big statements: yes or no, true or false, pass or fail. But most commonly, multiple bits are grouped together to represent numbers and, from there, all kinds of data, including text, sound, music, pictures, and movies. A circuit that adds two bits together is interesting, but a circuit that adds multiple bits is on its way to becoming part of an actual computer.

For convenience in moving and manipulating bits, computer systems often group a certain number of bits into a quantity called a word. The length or size of this word—meaning the number of bits that compose the word—becomes crucial to the architecture of the computer because all the computer’s data moves in groups of either one word or multiple words.

Some early computer systems used word lengths that were multiples of 6 bits, such as 12, 18, or 24 bits. These word lengths have a very special appeal for the simple reason that the values are easily represented with octal numbers. As you’ll recall, the octal digits are 0, 1, 2, 3, 4, 5, 6, and 7, which correspond to 3-bit values, as shown in this table:

A 6-bit word can be represented by precisely two octal digits, and the other word sizes of 12, 18, and 24 bits are just multiples of that. A 24-bit word requires eight octal digits.

But the computer industry went in a slightly different direction. Once the importance of binary numbers was recognized, it must have seemed almost perverse to work with word sizes, such as 6, 12, 18, or 24, that are not powers of two and are instead multiples of three.

Enter the byte.

The word byte originated at IBM, probably around 1956. It had its origins in the word bite but was spelled with a y so that nobody would mistake the word for bit. Initially, a byte meant simply the number of bits in a particular data path. But by the mid-1960s, in connection with the development of IBM’s large complex of business computers called the System/360, the word byte came to mean a group of 8 bits.

That stuck; 8 bits to a byte is now a universal measurement of digital data.

As an 8-bit quantity, a byte can take on values from 00000000 through 11111111, which can represent decimal numbers from 0 through 255, or one of 2⁸, or 256, different things. It turns out that 8 is quite a nice bite size of bits, not too small and not too large. The byte is right, in more ways than one. As you’ll see in the chapters ahead, a byte is ideal for storing text because many written languages around the world can be represented with fewer than 256 characters. And where 1 byte is inadequate (for representing, for example, the ideographs of Chinese, Japanese, and Korean), 2 bytes—which allow the representation of 2¹⁶, or 65,536, things—usually works just fine. A byte is also ideal for representing gray shades in black-and-white photographs because the human eye can differentiate approximately 256 shades of gray. For color on video displays, 3 bytes work well to represent the color’s red, green, and blue components.

The personal computer revolution began in the late 1970s and early 1980s with 8-bit computers. Subsequent technical advances doubled the number of bits used within the computer: from 16-bit to 32-bit to 64-bit—2 bytes, 4 bytes, and 8 bytes, respectively. For some special purposes, 128-bit and 256-bit computers also exist.

Half a byte—that is, 4 bits—is sometimes referred to as a nibble (and is sometimes spelled nybble), but this word doesn’t come up in conversation nearly as often as byte.

Because bytes show up a lot in the internals of computers, it’s convenient to be able to refer to their values more succinctly than as a string of binary digits. You can certainly use octal for this purpose: For the byte 10110110, for example, you can divide the bits into groups of three starting at the right and then convert each of these groups to octal using the table shown above:

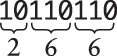
The octal number 266 is more succinct than 10110110, but there’s a basic incompatibility between bytes and octal: Eight doesn’t divide equally by three, which means that the octal representation of a 16-bit number

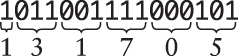
isn’t the same as the octal representations of the 2 bytes that compose the 16-bit number:

In order for the representations of multibyte values to be consistent with the representations of the individual bytes, we need a number system in which each byte is divided into an equal number of bits.

We could divide each byte into four values of 2 bits each. That would be the base four, or quaternary, system described in Chapter 10. But that’s probably not as succinct as we’d like.

Or we could divide the byte into two values of 4 bits each. This would require using the number system known as base 16.

Base 16. Now that’s something we haven’t looked at yet, and for good reason. The base 16 number system is called hexadecimal, and even the word itself is a mess. Most words that begin with the hexa prefix (such as hexagon or hexapod or hexameter) refer to six of something. Hexadecimal is supposed to mean sixteen, or six plus decimal. And even though I have been instructed to make the text of this book conform to the online Microsoft Style Guide, which clearly states, “Don’t abbreviate as hex,” everyone always does and I might sometimes also.

The name of the number system isn’t hexadecimal’s only peculiarity. In decimal, we count like this:

$\begin{array}{cccccccccccc}0& 1& 2& 3& 4& 5& 6& 7& 8& 9& 10& \begin{array}{cc}\begin{array}{c}11\end{array}& 12\dots \end{array}\end{array}$

In octal, we no longer need digits 8 and 9:

$\begin{array}{ccccccccccc}0& 1& 2& 3& 4& 5& 6& 7& 10& 11& 12\dots \end{array}$

But hexadecimal is different because it requires more digits than does decimal. Counting in hexadecimal goes something like this:

$\begin{array}{ccccccccccccccccccc}0& 1& 2& 3& 4& 5& 6& 7& 8& 9& \text{need}& \text{some}& \text{more}& \text{number}& \text{symbols}& \text{here}& 10& 11& 12\end{array}$

where 10 (pronounced one-zero) is actually 16 in decimal. But what do we use for those six missing symbols? Where do they come from? They weren’t handed down to us in tradition like the rest of our number symbols, so the rational thing to do is make up six new symbols, for example:

Unlike the symbols used for most of our numbers, these have the benefit of being easy to remember and identify with the actual quantities they represent. There’s a 10-gallon cowboy hat, an American football (11 players on a team), a dozen donuts, a black cat (associated with unlucky 13), a full moon that occurs about a fortnight (14 days) after the new moon, and a dagger that reminds us of the assassination of Julius Caesar on the ides (the 15th day) of March.

But no. Unfortunately (or perhaps, much to your relief), we really aren’t going to be using footballs and donuts to write hexadecimal numbers. It could have been done that way, but it wasn’t. Instead, the hexadecimal notation in common use ensures that everybody gets really confused and stays that way. Those six missing hexadecimal digits are instead represented by the first six letters of the Latin alphabet, like this:

$\begin{array}{ccccccccccccccccccc}0& 1& 2& 3& 4& 5& 6& 7& 8& 9& \text{A}& \text{B}& \text{C}& \text{D}& \text{E}& \text{F}& 10& 11& 12\dots \end{array}$

The following table shows the conversion between binary, hexadecimal, and decimal:

It’s not pleasant using letters to represent numbers (and the confusion increases when numbers are used to represent letters), but hexadecimal is here to stay. It exists for one reason and one reason only: to represent the values of bytes as succinctly as reasonably possible, and that it does quite well.

Each byte is 8 bits, or two hexadecimal digits ranging from 00 to FF. The byte 10110110 is the hexadecimal number B6, and the byte 01010111 is the hexadecimal number 57.

Now B6 is obviously hexadecimal because of the letter, but 57 could be a decimal number. To avoid confusion, we need some way to easily differentiate decimal and hexadecimal numbers. Such a way exists. In fact, there are about 20 different ways to denote hexadecimal numbers in different programming languages and environments. In this book, I’ll be using a lowercase h following the number, like B6h or 57h.

Here’s a table of a few representative 1-byte hexadecimal numbers and their decimal equivalents:

Like binary numbers, hexadecimal numbers are often written with leading zeros to make clear that we’re working with a specific number of digits. For longer binary numbers, every four binary digits correspond to a hexadecimal digit. A 16-bit value is 2 bytes and four hexadecimal digits. A 32-bit value is 4 bytes and eight hexadecimal digits.

With the widespread use of hexadecimal, it has become common to write long binary numbers with dashes or spaces every four digits. For example, the binary number 0010010001101000101011001110 is a little less frightening when written as 0010 0100 0110 1000 1010 1100 1110 or 0010-0100-0110-1000-1010-1100-1110, and the correspondence with hexadecimal digits becomes clearer:

$\begin{array}{ccccccc}\underbrace{\begin{array}{c}0010\end{array}}& \underbrace{\begin{array}{c}0100\end{array}}& \underbrace{\begin{array}{c}0110\end{array}}& \underbrace{\begin{array}{c}1000\end{array}}& \underbrace{\begin{array}{c}1010\end{array}}& \underbrace{\begin{array}{c}1100\end{array}}& \underbrace{\begin{array}{c}1110\end{array}}\\ 2& 4& 6& 8& \text{A}& \text{C}& \text{E}\end{array}$

That’s the seven-digit hexadecimal number 2468ACE, which is all the even hexadecimal digits in a row. (When cheerleaders chant “2 4 6 8 A C E! Work for that Comp Sci degree!” you know your college is perhaps a little too nerdy.)

If you’ve done any work with HTML, the Hypertext Markup Language used in webpages on the internet, you might already be familiar with one common use of hexadecimal. Each colored dot (or pixel) on your computer screen is a combination of three additive primary colors: red, green, and blue, referred to as an RGB color. The intensity or brightness of each of those three components is given by a byte value, which means that 3 bytes are required to specify a particular color. Often on HTML pages, the color of something is indicated with a six-digit hexadecimal value preceded by a pound sign. For example, the red shade used in the illustrations in this book is the color value #E74536, which means a red value of E7h, a green value of 45h, and a blue value of 36h. This color can alternatively be specified on HTML pages with the equivalent decimal values, like this: rgb (231, 69, 54).

Knowing that 3 bytes are required to specify the color of each pixel on the computer screen, it’s possible to do a little arithmetic and derive some other information: If your computer screen contains 1920 pixels horizontally and 1080 pixels vertically (the standard high-definition television dimensions), then the total number of bytes required to store the image for that display is 1920 times 1080 times 3 bytes, or 6,220,800 bytes.

Each primary color can range from 0 to 255, which means that the total number of combinations can result in 256 times 256 times 256 unique colors, or 16,777,216. In hexadecimal that number is 100h times 100h times 100h, or 1000000h.

In a hexadecimal number, the positions of each digit correspond to powers of 16:

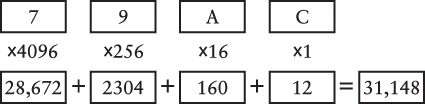
The hexadecimal number 9A48Ch is

$\begin{array}{ccc}\hfill 9\text{A}48\text{Ch}=9& \times & 10000\text{h}+\hfill \\ \hfill \text{A}& \times & 1000\text{h}+\hfill \\ \hfill 4& \times & 100\text{h}+\hfill \\ \hfill 8& \times & 10\text{h}+\hfill \\ \hfill \text{C}& \times & 1\text{h}\hfill \end{array}$

This can be written using powers of 16:

$\begin{array}{ccc}\hfill 9\text{A}48\text{Ch}=9& \times & {16}^4+\hfill \\ \hfill \text{A}& \times & {16}^3+\hfill \\ \hfill 4& \times & {16}^2+\hfill \\ \hfill 8& \times & {16}^1+\hfill \\ \hfill \text{C}& \times & {16}^0\hfill \end{array}$

Or using the decimal equivalents of those powers:

$\begin{array}{ccc}\hfill 9\text{A}48\text{Ch}=9& \times & 65,536+\hfill \\ \hfill \text{A}& \times & 4096+\hfill \\ \hfill 4& \times & 256+\hfill \\ \hfill 8& \times & 16+\hfill \\ \hfill \text{C}& \times & 1\hfill \end{array}$

Notice that there’s no ambiguity in writing the single digits of the number (9, A, 4, 8, and C) without indicating the number base. A 9 by itself is a 9 whether it’s decimal or hexadecimal. And an A is obviously hexadecimal—equivalent to 10 in decimal.

Converting all the digits to decimal lets us actually do the calculation:

$\begin{array}{ccc}\hfill 9\text{A}48\text{Ch}=9& \times & 65,536+\hfill \\ \hfill 10& \times & 4096+\hfill \\ \hfill 4& \times & 256+\hfill \\ \hfill 8& \times & 16+\hfill \\ \hfill 12& \times & 1\hfill \end{array}$

And the answer is 631,948. This is how hexadecimal numbers are converted to decimal.

Here’s a template for converting any four-digit hexadecimal number to decimal:

For example, here’s the conversion of 79ACh. Keep in mind that the hexadecimal digits A and C are decimal 10 and 12, respectively:

Converting decimal numbers to hexadecimal generally requires divisions. If the number is 255 or smaller, you know that it can be represented by 1 byte, which is two hexadecimal digits. To calculate those two digits, divide the number by 16 to get the quotient and the remainder. For example, for the decimal number 182, divide it by 16 to get 11 (which is a B in hexadecimal) with a remainder of 6. The hexadecimal equivalent is B6h.

If the decimal number you want to convert is smaller than 65,536, the hexadecimal equivalent will have four digits or fewer. Here’s a template for converting such a number to hexadecimal:

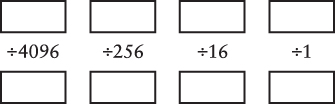
You start by putting the entire decimal number in the box in the upper-left corner:

Divide that number by 4096, but only to get a quotient and remainder. The quotient goes in the first box on the bottom, and the remainder goes in the next box on top:

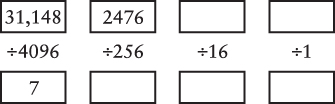
Now divide that remainder by 256, but only to get a quotient of 9 and a new remainder of 172. Continue the process:

The decimal numbers 10 and 12 correspond to hexadecimal A and C, so the result is 79ACh.

Another approach to converting decimal numbers through 65,535 to hexadecimal involves first separating the number into 2 bytes by dividing by 256. Then for each byte, divide by 16. Here’s a template for doing it:

Start at the top. With each division, the quotient goes in the box to the left, and the remainder goes in the box to the right. For example, here’s the conversion of 51,966:

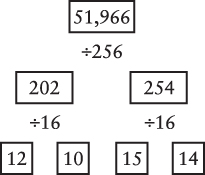
The hexadecimal digits are 12, 10, 15, and 14, or CAFE, which looks more like a word than a number! (And if you go there, you may prefer to order your coffee 56,495.)

As for every other number base, there’s an addition table associated with hexadecimal:

You can use the table and normal carry rules to add hexadecimal numbers:

$\frac{\begin{array}{c}\hfill 4\text{A}3378\text{E}2\\ \hfill +877\text{AB}982\end{array}}{\phantom{0}\text{D}1\text{AE}3264}$

If you prefer not to do these calculations by hand, both the Windows and macOS calculator apps have a Programmer mode that lets you do arithmetic in binary, octal, and hexadecimal, and convert between these number systems.

Or you can build the 8-bit binary adder in Chapter 14.