YORK: Then, York, be still awhile, till time do serve:Watch thou and wake when others be asleep,To pry into the secrets of the state; | ||
| --The Second Part of King Henry the Sixth, I, i, 249–260. | ||
Cryptography is a deep mathematical subject. Because this book focuses on system security, we view cryptography as a supporting tool. Viewed in this context, the reader needs only a brief overview of the major points of cryptography relevant to that use. This chapter provides such an overview.
Cryptographic protocols provide a cornerstone for secure communication. These protocols are built on ideas presented in this chapter and are discussed at length later on.
The word cryptography comes from two Greek words meaning “secret writing” and is the art and science of concealing meaning. Cryptanalysis is the breaking of codes. The basic component of cryptography is a cryptosystem.
Definition 9–1. A cryptosystem is a 5-tuple (E, D, M, K, C), where M is the set of plaintexts, K the set of keys, C is the set of ciphertexts, E: M × K → C is the set of enciphering functions, and D: C × K → M is the set of deciphering functions.
The goal of cryptography is to keep enciphered information secret. Assume that an adversary wishes to break a ciphertext. Standard cryptographic practice is to assume that she knows the algorithm used to encipher the plaintext, but not the specific cryptographic key (in other words, she knows D and E). She may use three types of attacks:
In a ciphertext only attack, the adversary has only the ciphertext. Her goal is to find the corresponding plaintext. If possible, she may try to find the key, too.
In a known plaintext attack, the adversary has the ciphertext and the plaintext that was enciphered. Her goal is to find the key that was used.
In a chosen plaintext attack, the adversary may ask that specific plaintexts be enciphered. She is given the corresponding ciphertexts. Her goal is to find the key that was used.
A good cryptosystem protects against all three types of attacks.
Attacks use both mathematics and statistics. The statistical methods make assumptions about the statistics of the plaintext language and examine the ciphertext to correlate its properties with those assumptions. Those assumptions are collectively called a model of the language. Figure 9-1 presents a character-based, or 1-gram, model of English text; others are 2-gram models (reflecting frequencies of pairs of letters), Markov models, and word models. In what follows, we use the 1-gram model and assume that the characters are chosen independently of one another.
![Table of character frequencies in the English language, from Denning [269], Figure 2.3, p. 65.](http://imgdetail.ebookreading.net/software_development/21/0201440997/0201440997__computer-security-art__0201440997__graphics__09fig01.gif)
Figure 9-1. Table of character frequencies in the English language, from Denning [269], Figure 2.3, p. 65.
Classical cryptosystems (also called single-key or symmetric cryptosystems) are cryptosystems that use the same key for encipherment and decipherment. In these systems, for all Ek ∊ C and k ∊ K, there is a Dk ∊ D such that Dk = Ek–1.
There are two basic types of classical ciphers: transposition ciphers and substitution ciphers.
A transposition cipher rearranges the characters in the plaintext to form the ciphertext. The letters are not changed.
Mathematically, the key to a transposition cipher is a permutation function. Because the permutation does not alter the frequency of plaintext characters, a transposition cipher can be detected by comparing character frequencies with a model of the language. If, for example, character frequencies for 1-grams match those of a model of English, but 2-gram frequencies do not match the model, then the text is probably a transposition cipher.
Attacking a transposition cipher requires rearrangement of the letters of the ciphertext. This process, called anagramming, uses tables of n-gram frequencies to identify common n-grams. The cryptanalyst arranges the letters in such a way that the characters in the ciphertext form some n-grams with highest frequency. This process is repeated, using different n-grams, until the transposition pattern is found.
A substitution cipher changes characters in the plaintext to produce the ciphertext.
A Caesar cipher is susceptible to a statistical ciphertext-only attack.
EXAMPLE: Consider the ciphertext “KHOOR ZRUOG.” We first compute the frequency of each letter in the ciphertext:
G | 0.1 | H | 0.1 | K | 0.1 | O | 0.3 | R | 0.2 | U | 0.1 | Z | 0.1 |
We now apply the character-based model. Let φ(i) be the correlation of the frequency of each letter in the ciphertext with the character frequencies in English (see Figure 9-1). Let f(c) be the frequency of character c (expressed as a fraction). The formula for this correlation for this ciphertext (with all arithmetic being mod 26) is
φ(i) = Σ0 ≤ c ≤ 25 f(c)p(c – i) = 0.1p(6 – i) + 0.1p(7 – i) + 0.1p(10 – i) + 0.3p(14 – i) + 0.2p(17 – i) + 0.1p(20 – i) + 0.1p(25 – i)
This correlation should be a maximum when the key k translates the ciphertext into English. Figure 9-2 shows the values of this function for the values of i. Trying the most likely key first, we obtain as plaintext “EBIIL TLOIA” when i = 6, “AXEEH PHKEW” when i = 10, “HELLO WORLD” when i = 3, and “WTAAD LDGAS” when i = 14.
The example above emphasizes the statistical nature of this attack. The statistics indicated that the key was most likely 6, when in fact the correct key was 3. So the attacker must test the results. The statistics simply reduce the number of trials in most cases. Only three trials were needed, as opposed to 13 (the expected number of trials if the keys were simply tried in order).
A longer key might obscure the statistics. The Vigenère cipher chooses a sequence of keys, represented by a string. The key letters are applied to successive plaintext characters, and when the end of the key is reached, the key starts over. The length of the key is called the period of the cipher. Figure 9-3 shows a tableau, or table, to implement this cipher efficiently. Because this requires several different key letters, this type of cipher is called polyalphabetic.
The index of coincidence measures the differences in the frequencies of the letters in the ciphertext. It is defined as the probability that two randomly chosen letters from the ciphertext will be the same. Let Fc be the frequency of cipher character c, and let N be the length of the ciphertext. It can be shown (see Exercise 7) that the index of coincidence IC is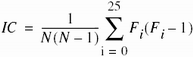 
. Figure 9-4 shows the expected values of IC for several periods. The lower the index of coincidence, the less variation in the characters of the ciphertext and (from our model of English) the longer the period of the cipher.
![Indices of coincidences for different periods. From Denning [269], Table 2.2, p. 78.](http://imgdetail.ebookreading.net/software_development/21/0201440997/0201440997__computer-security-art__0201440997__graphics__09fig04.gif){kind=small}
For many years, the Vigenère cipher was considered unbreakable. Then a Prussian cavalry officer named Kasiski noticed that repetitions occur when characters of the key appear over the same characters in the ciphertext. The number of characters between the repetitions is a multiple of the period.
We examine the ciphertext for multiple repetitions and tabulate their length and the number of characters between successive repetitions. The period is likely to be a factor of the number of characters between these repetitions. From the repetitions, we establish the probable period, using the index of coincidence to check our deduction. We then tabulate the characters for each key letter separately and solve each as a Caesar cipher.
It is worth noting that the Vigenère cipher is easy to break by hand. However, the principles of attack hold for more complex ciphers that can be implemented only by computer. A good example is the encipherments that several older versions of WordPerfect used [79, 83]. These allowed a user to encipher a file with a password. Unfortunately, certain fields in the enciphered file contained information internal to WordPerfect, and these fields could be predicted. This allowed an attacker to derive the password used to encipher the file, and from that the plaintext file itself.
The one-time pad is a variant of the Vigenère cipher. The technique is the same. The key string is chosen at random, and is at least as long as the message, so it does not repeat. Technically, it is a threshold scheme [907], and is provably impossible to break [122] (see also Section 32.3.3, “Perfect Secrecy”). The implementation issues of the pad, including random generation of the key and key distribution, do not concern us here (although a later chapter will touch on them).
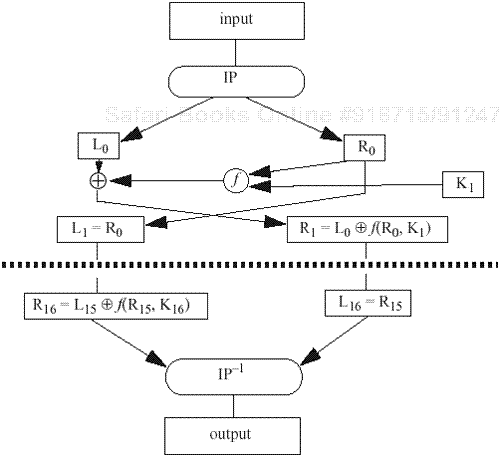
The Data Encryption Standard (DES) [743] was designed to encipher sensitive but nonclassified data. It is bit-oriented, unlike the other ciphers we have seen. It uses both transposition and substitution and for that reason is sometimes referred to as a product cipher. Its input, output, and key are each 64 bits long. The sets of 64 bits are referred to as blocks.
The cipher consists of 16 rounds, or iterations. Each round uses a separate key of 48 bits. These round keys are generated from the key block by dropping the parity bits (reducing the effective key size to 56 bits), permuting the bits, and extracting 48 bits. A different set of 48 bits is extracted for each of the 16 rounds (see Figure 9-5). If the order in which the round keys is used is reversed, the input is deciphered.
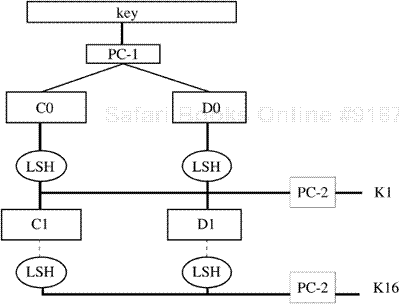
Figure 9-5. DES key schedule generation. PC-1 and PC-2 are permutation tables; LSH is a table of left shifts (rotations).
The rounds are executed sequentially, the input of one round being the output of the previous round. The right half of the input, and the round key, are run through a function f that produces 32 bits of output; that output is then xor'ed into the left half, and the resulting left and right halves are swapped (see Figure 9-6).
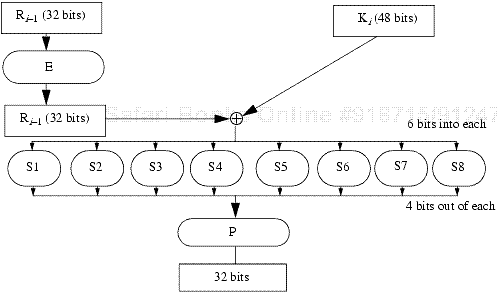
The function f provides the strength of the DES. The right half of the input (32 bits) is expanded to 48 bits, and this is xor'ed with the round key. The resulting 48 bits are split into eight sets of six bits each, and each set is put through a substitution table called the S-box. Each S-box produces four bits of output. They are catenated into a single 32-bit quantity, which is permuted. The resulting 32 bits constitute the output of the f function (see Figure 9-7).
When the DES was first announced, it was criticized as too weak. First, Diffie and Hellman [296] argued that a key length of 56 bits was simply too short, and they designed a machine that could break a DES-enciphered message in a matter of days. Although their machine was beyond the technology of the time, they estimated that it could soon be built for about $20,000,000. Second, the reasons for many of the decisions in the design of the DES—most notably, those involving the S-boxes—were classified. Many speculated that the classification hid “trapdoors,” or ways to invert the cipher without knowing the key.
Some properties of the DES were worrisome. First, it had four weak keys (keys that were their own inverses) and 12 semiweak keys (keys whose inverses were other keys). Second, let 
, 
, and 
be the complement of the key k, the plaintext m, and the ciphertext c, respectively. Let DESk(m) be the encipherment of plaintext m under key k. Then the complementation property states that
Third, some of the S-boxes exhibited irregular properties. The distribution of odd and even numbers was nonrandom, raising concerns that the DES did not randomize the input sufficiently. Several output bits of the fourth S-box seemed to depend on some of the output bits of the third S-box. This again suggested that there was a structure to the S-boxes, and because some of the design decisions underlying the S-boxes were unknown, the reasons for the structure were unknown. The structure made hardware implementation of the DES simpler [1005]. It distributed the dependence of each output bit on each input bit rapidly, so that after five rounds each output bit depended on every key and input bit [701]. It could have been needed to prevent the cipher from being broken easily. It also could enable a trapdoor to allow the cipher to be broken easily. There was considerable speculation that the NSA had weakened the algorithm, although a congressional investigation did not reflect this [63].
In 1990, a breakthrough in cryptanalysis answered many of these questions. Biham and Shamir applied a technique called differential cryptanalysis to the DES [96, 97, 98]. This technique required them to generate 247 pairs of chosen plaintext and ciphertext, considerably fewer than the trial-and-error approach others had used. During the development of this technique, they found several properties of the DES that appeared to answer some of the questions that had been raised.
First, for a known plaintext attack, differential cryptanalysis requires 256 plaintext and ciphertext pairs for a 15-round version of the DES. For the full 16 rounds, 258 known plaintext and ciphertext pairs are needed, which is more than sufficient for a trial-and-error approach. (Matsui subsequently improved this using a variant attack called linear cryptanalysis [663]; this attack requires 243 known plaintext and ciphertext pairs on the average.) Second, small changes in the S-boxes weakened the cipher (so that the required number of chosen plaintext and ciphertext pairs was reduced). Third, making every bit of the round keys independent (for an effective key length of 16 × 48 = 768 bits) did not make the DES resistant to differential cryptanalysis, which suggests that the designers of the DES knew about differential analysis. Coppersmith later confirmed this [234].
The DES is used in several modes [744]. Using it directly is called electronic code book (ECB) mode, and is very rare. Modes in which it can be used to generate a pseudo-one-time pad are cipher feed back (CFB) mode (see Section 11.2.1.2) and output feed back (OFB) mode (see Section 11.2.1.1). Its most common modes of use are cipher block chaining (CBC) mode (see Section 11.2.2), encrypt-decrypt-encrypt (EDE) mode, and triple DES mode (the EDE and triple DES modes are described in Section 11.2.2.1).
The CBC mode is an iterative mode in which a block of ciphertext depends not only on its input but also on the preceding ciphertext block. In addition to a 64-bit key, it requires a 64-bit initialization vector. Figure 9-8 shows this mode. It has the self-healing property. This property says that if one block of ciphertext is altered, the error propagates for at most two blocks. Figure 9-9 shows how a corrupted block affects others.
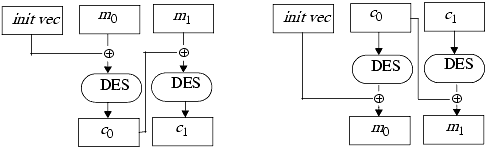
Figure 9-8. Cipher block chaining mode. The left diagram shows encipherment; each ciphertext is “fed back” into the cipher stream. The right diagram shows decipherment.
Figure 9-9. Example of the self-healing property. The ciphertext at the top was stored incorrectly (the italicized 4c should be 4b). Its decipherment is shown next, with the incorrect octets italicized. The plaintext used to create the ciphertext is shown at the bottom.
The EDE mode is used by many financial institutions. It requires two 64bit keys k and k'. The ciphertext c corresponding to some data m is c = DESk (DESk'–1(DESk(m))). Triple DES uses three keys k, k', and k'', and the second step is an encipherment, not a decipherment: c = DESk(DESk'(DESk"(m))).
In 1998, a design for a computer system and software that could break any DES-enciphered message in a few days was published [395]. This design complemented several challenges to break specific DES messages. Those challenges had been solved using computers distributed throughout the Internet. By 1999, it was clear that the DES no longer provided the same level of security as it had 10 years earlier, and the search was on for a new, stronger cipher (to be called the Advanced Encryption Standard, or AES) to fill the needs that the DES no longer filled.
The DES is one of the most important classical cryptosystems in the history of cryptography. It provided the impetus for many advances in the field and laid the theoretical and practical groundwork for many other ciphers. While analyzing it, researchers developed differential and linear cryptanalysis. Cryptographers developed other ciphers to avoid real, or perceived, weaknesses; cryptanalysts broke many of these ciphers and found weaknesses in others. Many of the features of the DES are used in other ciphers. Hence, even though it is nearing the end of its useful lifetime, it is well worth understanding.
In late 2001, the National Institute of Standards and Technology announced the selection of Rijndael as the Advanced Encryption Standard [754], the successor to the DES. Like the DES, the AES is a product cipher. Unlike the DES, the AES can use keys of 128, 192, or 256 bits and operates on blocks of 128 bits. It was specifically designed to withstand the attacks to which the DES showed weaknesses [254]. Time will show how rapidly it supplants the DES, but the lessons learned from the DES have borne fruit.
Several algorithms have been proposed to overcome the weaknesses in the DES. NewDES (which, despite its name, is not a variant of DES but a new algorithm) has a block size of 64 bits and a key length of 120 bits [895]. However, it can be broken using an attack similar to differential cryptanalysis [888]. FEAL is another block cipher, with a block size of 64 bits and a key size of 64 bits [721, 915]. FEAL-4 (FEAL with four rounds) and FEAL-8 (FEAL with eight rounds) fell to differential cryptanalysis with 20 [738] and 10,000 [393] chosen plaintexts, respectively. Biham and Shamir broke FEAL-N, which uses N rounds, for N < 32 by differential crypt-analysis more quickly than by trial-and-error [97]. It was proposed that the key be lengthened to 128 bits, but the 128-bit key proved as easy to break as FEAL-N with the original 64-bit key. REDOC-II [252] has an 80-bit block and a 160-bit key. It has 10 rounds, and although a single round was successfully cryptanalyzed [95], the use of 10 rounds appears to withstand differential cryptanalysis.
LOKI89 [150], proposed as an alternative to the DES, was vulnerable to differential cryptanalysis [95]. Its successor, LOKI91 [151], uses a 64-bit key and a 64-bit block size. Differential cryptanalysis fails to break this cipher [577]. Khufu [699] has a block size of 64 bits and a key size of 512 bits. When used with 24 or 32 rounds, it resists chosen plaintext attacks. Its S-boxes are computed from the keys. Khafre [699], similar in design to Khufu, uses fixed S-boxes, but it has been broken [95].
IDEA is an eight-round cipher that uses 64-bit blocks and 128-bit keys [604]. It uses three operations: exclusive or's, addition modulo 216, and multiplication modulo 216 + 1. It appears to withstand known attacks but is too new for any definitive statement to be made about its security [888]. It is used in noncommercial software—notably, in the electronic mail program PGP [1073]—but is patented and requires licensing for use in commercial software.
In 1976, Diffie and Hellman [295] proposed a new type of cryptography that distinguished between encipherment and decipherment keys.[2] One of the keys would be publicly known; the other would be kept private by its owner. Classical cryptography requires the sender and recipient to share a common key. Public key cryptography does not. If the encipherment key is public, to send a secret message simply encipher the message with the recipient's public key. Then send it. The recipient can decipher it using his private key. (Chapter 10, “Key Management,” discusses how to make public keys available to others.)
Because one key is public, and its complementary key must remain secret, a public key cryptosystem must meet the following three conditions.
It must be computationally easy to encipher or decipher a message given the appropriate key.
It must be computationally infeasible to derive the private key from the public key.
It must be computationally infeasible to determine the private key from a chosen plaintext attack.
The first cipher to meet these requirements generates a shared session key. The second one provides both secrecy and authentication.
The Diffie-Hellman scheme [295] was the first public key cryptosystem proposed, and it is still in use today. A pair of users use this algorithm to generate a common key. It is based on the discrete logarithm problem. This problem is to find a value of k such that n = gk mod p for a given n, g, and prime p. Although solutions are known for small values of p, the difficulty increases exponentially as p increases [605].
In this cryptosystem, all users share a common modulus p and a g other than 0, 1, or p – 1. Each user chooses a private key k and computes a public key K. When two users want to communicate, each enciphers the other's public key using their own private key, and uses the result as the shared secret key S.
Because the users share a common secret key S, the Diffie-Hellman scheme is an example of a symmetric key exchange protocol. Under the assumption that solving the discrete logarithm problem is computationally infeasible, deriving a private key from the corresponding public key is also computationally infeasible. In practice, p must be very large (hundreds of bits) for this assumption to be met.
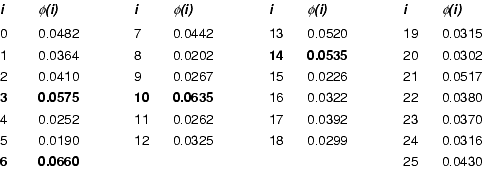
RSA [844] is an exponentiation cipher. Choose two large prime numbers p and q, and let n = pq. The totient φ(n) of n is the number of numbers less than n with no factors in common with n.[3]
Choose an integer e < n that is relatively prime to φ(n). Find a second integer d such that ed mod φ(n) = 1. The public key is (e, n), and the private key is d.
Let m be a message. Then:
c = me mod n
and
m = cd mod n
In addition to confidentiality, RSA can provide data and origin authentication. If Alice enciphers her message using her private key, anyone can read it, but if anyone alters it, the (altered) ciphertext cannot be deciphered correctly.
Providing both confidentiality and authentication requires enciphering with the sender's private key and the recipient's public key.
The recipient uses the recipient's private key to decipher the message and the sender's public key to authenticate it.
The use of a public key system provides a technical type of nonrepudiation of origin. The message is deciphered using Alice's public key. Because the public key is the inverse of the private key, only the private key could have enciphered the message. Because Alice is the only one who knows this private key, only she could have enciphered the message. The underlying assumption is that Alice's private key has not been compromised, and that the public key bearing her name really does belong to her.
In practice, no one would use blocks of the size presented here. The issue is that, even if n is very large, if one character per block is enciphered, RSA can be broken using the techniques used to break classical substitution ciphers (see Sections 9.2.2 and 11.1.3). Furthermore, although no individual block can be altered without detection (because the attacker presumably does not have access to the private key), an attacker can rearrange blocks and change the meaning of the message.
Alice wants to send Bob a message of n bits. She wants Bob to be able to verify that the message he receives is the same one that was sent. So she applies a mathematical function, called a checksum function, to generate a smaller set of k bits from the original n bits. This smaller set is called the checksum or message digest. Alice then sends Bob both the message and the checksum. When Bob gets the message, he recomputes the checksum and compares it with the one Alice sent. If they match, he assumes that the message has not been changed.
Definition 9–2. A cryptographic checksum function (also called a strong hash function or a strong one-way function) h: A → B is a function that has the following properties.
For any x ∊ A, h(x) is easy to compute.
For any y ∊ B, it is computationally infeasible to find x ∊ A such that h(x) = y.
It is computationally infeasible to find x, x' ∊ A, such that x ≠ x' and h(x) = h(x'). (Such a pair is called a collision.)
The third requirement is often stated as:
Given any x ∊ A, it is computationally infeasible to find another x' ∊ A such that x ≠ x' and h(x') = h(x).
However, properties 3 and 4 are subtlely different. It is considerably harder to find an x' meeting the conditions in property 4 than it is to find a pair x and x' meeting the conditions in property 3. To explain why, we need to examine some basics of cryptographic checksum functions.
Given that the checksum contains fewer bits than the message, several messages must produce the same checksum. The best checksum functions have the same number of messages produce each checksum. Furthermore, given any message, the checksum it produces can be determined only by computing the checksum. Such a checksum function acts as a random function.
The size of the output of the cryptographic checksum is an important consideration owing to a mathematical principle called the pigeonhole principle.
Definition 9–3. The pigeonhole principle states that if there are n containers for n + 1 objects, at least one container will hold two objects. To understand its application here, consider a cryptographic checksum function that computes hashes of three bits and a set of files each of which contains five bits. This yields 23 = 8 possible hashes for 25 = 32 files. Hence, at least four different files correspond to the same hash.
Now assume that a cryptographic checksum function computes hashes of 128 bits. The probability of finding a message corresponding to a given hash is 2–128, but the probability of finding two messages with the same hash (that is, with the value of neither message being constrained) is 2–64 (see Exercise 21).
Definition 9–4. A keyed cryptographic checksum function requires a cryptographic key as part of the computation. A keyless cryptographic checksum does not.
Examples of keyless hash functions include MD2 [543]; MD4 [841]; MD5 [842]; the Secure Hash Algorithm (SHA-1) which produces 160-bit checksums [745, 744]; Snefru (either 128-bit or 256-bit checksums) [698]; and HAVAL, which produces checksums of 128, 160, 192, 224, and 256 bits [1071]. Of these, Snefru is vulnerable to differential cryptanalysis if four rounds or fewer are used [98], so Merkle recommends using at least eight passes. Dobbertin devised a method of generating collisions in MD4 [303]; a similar method also works against MD5 but is slower [302].
HMAC is a generic term for an algorithm that uses a keyless hash function and a cryptographic key to produce a keyed hash function [594]. This mechanism enables Alice to validate that data Bob sent to her is unchanged in transit. Without the key, anyone could change the data and recompute the message authentication code, and Alice would be none the wiser.
The need for HMAC arose because keyed hash functions are derived from cryptographic algorithms. Many countries restrict the import and export of software that implements such algorithms. They do not restrict software implementing keyless hash functions, because such functions cannot be used to conceal information. Hence, HMAC builds on a keyless hash function using a cryptographic key to create a keyed hash function.
Let h be a keyless hash function that hashes data in blocks of b bytes to produce a hash l bytes long. Let k be a cryptographic key. We assume that the length of k is no greater than b; if it is, use h to hash it to produce a new key of length b. Let k' be the key k padded with bytes containing 0 to make b bytes. Let ipad be a sequence of bytes containing the bits 00110110 and repeated b times; let opad be a similar sequence with the bits 01011100. The HMAC-h function with key k for message m is
HMAC-h(k, m) = h(k' ⊕ opad || h(k' ⊕ ipad || m))
where ⊕ is exclusive or and || is concatenation.
Bellare, Canetti, and Krawczyk [69] analyze the security of HMAC and conclude that the strength of HMAC depends on the strength of the hash function h. Various HMAC functions are used in Internet security protocols (see Chapter 11).
For our purposes, three aspects of cryptography require study. Classical cryptography uses a single key shared by all involved. Public key cryptography uses two keys, one shared and the other private. Both types of cryptosystems can provide secrecy and origin authentication (although classical cryptography requires a trusted third party to provide both). Cryptographic hash functions may or may not use a secret key and provide data authentication.
All cryptosystems are based on substitution (of some quantity for another) and permutation (scrambling of some quantity). Cryptanalysis, the breaking of ciphers, uses statistical approaches (such as the Kasiski method and differential cryptanalysis) and mathematical approaches (such as attacks on the RSA method). As techniques of cryptanalysis improve, our understanding of encipherment methods also improves and ciphers become harder to break. The same holds for cryptographic checksum functions. However, as computing power increases, key length must also increase. A 56-bit key was deemed secure by many in 1976; it is clearly not secure now.
Cryptography is an exciting area of research, and all aspects of it are being studied. New secret key ciphers incorporate techniques for defeating differential and linear cryptanalysis. New public key ciphers use simple instances of NP-hard problems as their bases, and they cast those instances into the more general framework of the NP-hard problem. Other public key ciphers revisit well-studied, difficult classical problems (such as factoring) and use them so that mathematically breaking the cipher is equivalent to solving the hard problem. Still others are built on the notion of randomness (in the sense of unpredictability).
Cryptanalytic techniques are also improving. From the development of differential cryptanalysis came linear cryptanalysis. The use of NP-hard problems leads to an analysis of the problem underlying the cipher to reduce it to the simpler, solvable case. The use of classical mathematical problems leads to the application of advanced technology to make the specific problem computable; for example, advances in technology have increased the sizes of numbers that can be factored, which in turn lead to the use of larger primes as the basis for ciphers such as RSA.
Advances in both cryptography and cryptanalysis lead to a notion of “provable security.” The issue is to prove under what conditions a cipher is unbreakable. Then, if the conditions are met, perfect secrecy is obtained. Similar issues arise with cryptographic protocols (some of which the next chapters will explore). This leads to the area of assurance and serves as an excellent test base for many assurance techniques.
Cryptography is a vast, rich subject. Kahn's book The Codebreakers [536, 539] is required reading for anyone interested in this field. Kahn has written other excellent historical books on codebreaking during World War II [537, 538]. Helen Fouché Gaines presents techniques for cryptanalysis of many classical ciphers using traditional, pencil-and-paper analysis [378]. Sinkov applies basic mathematics to many of these classical ciphers [929]. Schneier describes many old, and new, algorithms in a clear, easy-to-understand manner [888]; his book is excellent for implementers. The underpinnings of these algorithms, and others, lie in statistics and mathematics. For classical cryptography, Konheim's book [590] is superb once the reader has mastered his notation. Unlike other books, it focuses on cryptanalysis of classical ciphers using statistical attacks. Meyer and Matyas [702] and Biham and Shamir [98] discuss the strengths and weaknesses of the DES. Seberry and Pieprzyk [897] and Simmons [927] discuss modern cryptography and its applications. Koblitz [584], Coutinho [240], and Goldreich [403] discuss modern mathematics, cryptographic theory, and cryptosystems. Menezes, Van Oorschot, and Vanstone's book [695] is a valuable reference. Trapp and Washington [998] present a good overview of AES-128, the version of the AES that uses 128-bit keys.
1: | A cryptographer once stated that cryptography could provide complete security, and that any other computer security controls were unnecessary. Why is he wrong? (Hint: Think of an implementation of a cryptosystem, and ask yourself what aspect(s) of the implementation can cryptography not protect.) |
2: | Decipher the following ciphertext, which was enciphered using the Caesar cipher: TEBKFKQEBZLROPBLCERJXKBSBKQP. |
3: | If one-time pads are provably secure, why are they so rarely used in practice? |
4: | Prove that the DES key consisting of all 0-bits and the DES key consisting of all 1-bits are both weak keys. What are the other two weak keys? (Note: Differences in the parity bits, which the PC-1 permutation drops, do not count; the keys must differ in the 56 bits that are used to generate the key schedule.) |
5: | Prove that the DES cipher satisfies the complementation property (see page 229). |
6: | Let k be the encipherment key for a Caesar cipher. The decipherment key differs; it is 26 – k. One of the characteristics of a public key system is that the encipherment and decipherment keys are different. Why then is the Caesar cipher a classical cryptosystem, not a public key cryptosystem? Be specific. |
7: | The index of coincidence was defined as “the probability that two randomly chosen letters from the ciphertext will be the same.” Derive the formula in Section 9.2.2.1 for the index of coincidence from this definition. |
8: | The following message was enciphered with a Vigenère cipher. Find the key, and decipher it. TSMVM MPPCW CZUGX HPECP RFAUE IOBQW PPIMS FXIPC TSQPK SZNUL OPACR DDPKT SLVFW ELTKR GHIZS FNIDF ARMUE NOSKR GDIPH WSGVL EDMCM SMWKP IYOJS TLVFA HPBJI RAQIW HLDGA IYOUX |
9: | Prove that two users who perform a Diffie-Hellman key exchange will have the same shared key. |
10: | In the example enciphering HELLO WORLD using the RSA cipher (the second example in Section 9.3.2), the modulus was chosen as 77, even though the magnitude of the cleartext blocks is at most 25. What problems in transmission and/or representation might this cause? |
11: | Prove the following:
|
12: | Fermat's Little Theorem says that, for integers a and n such that a and n are relatively prime, aφ(n) mod n = 1. Use this to show that deciphering of an enciphered message produces the original message with the RSA cryptosystem. Does enciphering of a deciphered message produce the original message also? |
13: | Consider the RSA cryptosystem. Show that the ciphertexts corresponding to the messages 0, 1 and n – 1 are the messages themselves. Are there other messages that produce the same ciphertext as plaintext? |
14: | It is often said that breaking RSA is equivalent to factoring the modulus, n.
|
15: | Prove the fundamental laws of modular arithmetic:
|
16: | How would you use the law ab mod n = ((a mod n)(b mod n)) mod n to reduce to 13 the number of multiplications required to compute 3577 mod 83 from 76 multiplications? Can you reduce it any further? |
17: | The section on public key cryptosystems discussed nonrepudiation of origin in the context of public key cryptosystems. Consider a secret key system (in which a shared key is used). Bob has a message that he claims came from Alice, and to prove it he shows both the cleartext message and the ciphertext message. The ciphertext corresponds to the plaintext enciphered under the secret key that Alice and Bob share. Explain why this does not satisfy the requirements of nonrepudiation of origin. How might you modify a classical cryptosystem to provide nonrepudiation? |
18: | Suppose Alice and Bob have RSA public keys in a file on a server. They communicate regularly using authenticated, confidential messages. Eve wants to read the messages but is unable to crack the RSA private keys of Alice and Bob. However, she is able to break into the server and alter the file containing Alice's and Bob's public keys.
|
19: | Is the identity function, which outputs its own input, a good cryptographic checksum function? Why or why not? |
20: | Is the sum program, which exclusive or's all words in its input to generate a one-word output, a good cryptographic checksum function? Why or why not? |
21: | Assume that a cryptographic checksum function computes hashes of 128 bits. Prove that the probability of finding two messages with the same hash (that is, with the value of neither message being constrained) is 2–64. |
22: | The example involving the DES-MAC cryptographic hash function stated that a birthday attack would find collisions given 232 messages. Alice wants to take advantage of this to swindle Bob. She draws up two contracts, one that Bob has agreed to sign and the other that Bob would not sign. She needs to generate a version of each that has the same checksum. Suggest how she might do this. (Hint: Adding blank spaces, or inserting a character followed by a backspace, will not affect the meaning of either contract.) |
[1] This means that in Konheim's sample, 3.05% of the digrams were “HE.”
[2] James Ellis, a cryptographer working for the British government's Communications-Electronics Security Group, said “he showed proof of concept in a January 1970 CESG report titled 'The Possibility of Secure Non-Secret Digital Encryption.'” Two of his colleagues found practical implementations. This work remained classified until 1997 ([271], p. 299).
[3] Our examples will use small numbers for pedagogical purposes. Actual RSA primes should be at least 512 bits each, giving a modulus of at least 1,024 bits. In practice, RSA is combined with cryptographic hash functions to prevent rearrangement of blocks (see Section 11.1.2).