Entropy is an information-theoretic measure of the amount of uncertainty in a variable. Beginning with Shannon's seminal works [908, 909], cryptographers and information theorists used entropy to determine how well transformations on messages obscure their meaning. Entropy has applications in a wide variety of disciplines, including cryptography, compression, and coding theory. This chapter reviews the basics of entropy, which has its roots in probability theory.
Definition 32–1. A random variable is a variable that represents the outcome of an event.
A word about notation. We write p(X = x1) for the probability that the random variable X has value x1. When the specific value does not matter (for example, when all values are equiprobable), we abbreviate this as p(X).
Sometimes the results of two different events are of interest.
Definition 32–2. The joint probability of X and Y, written p(X, Y), is the probability that the random variables X and Y will simultaneously assume particular values.
The example above involves the probability p(X = 6, Y = heads). If the two random variables are independent (that is, if the value of one does not affect the value of the other), then
p(X, Y) = p(X)p(Y)
Now suppose that the two random variables are not independent.
This example shows that if two events are not independent, then the formula for joint probability is more complicated. The next definition captures the notion of dependence.
Definition 32–3. The conditional probability of X given Y (written p(X | Y)) is the probability that X takes on a particular value, given that Y has a particular value.
We can now write the formula for joint probability in terms of conditional probability:
p(X, Y) = p(X | Y)p(Y) = p(X)p(Y | X)
In fact, the formula for joint probability of two independent events is a special case of the formula above. When X and Y are independent random variables,
p(X | Y) = p(X)
Definition 32–4. Let the random variable X take values from some set { x1, ... xn }. The value xi occurs with probability p(X = xi), where
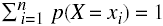= 1.
The entropy, or uncertainty, of x is
H(X) = -
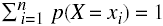lg p(X = xi)
where “lg x” is the base 2 logarithm of x. (For purposes of this definition, we define 0 lg 0 to be 0.)
This definition measures the uncertainty of a message in bits.
EXAMPLE: Suppose the message m is either “yes” or “no,” with either message being equally likely. Because there are two possibilities for the message, intuitively there is 1 bit of uncertainty. The message can be represented as either a 0 or a 1. From the definition above,
H(M) | = |
|
= | – p(M = yes) lg p(M = yes) – p(M = no) lg p(M = no) | |
= | –2–1 lg 2–1 – 2–1 lg 2–1 = 2–1 + 2–1 = 1 |
as expected.
EXAMPLE: Suppose each message is equally likely—that is, p(M = mi) = 1/n. Then
H(M) | = |
|
= |
|
The uncertainty of m is the number of bits needed to represent n.
EXAMPLE: Suppose Ann, Paul, and Pamela are finalists in a game. Ann and Pamela are twice as likely to win as Paul is. Let W be the random variable representing the winner, and let w1 = Ann, w2 = Pamela, and w3 = Paul. Then p(W = w1) = 2/5, p(W = w2) = 2/5, p(W = w3) = 1/5, and
H(W) | = |
|
= | –p(W = w1) lg p(W = w1) – p(W = w2) lg p(W = w2) – p(W = w3) lg p(W = w3) | |
= | – (2/5) lg (2/5) – (2/5) lg (2/5) – (1/5) lg (1/5) = –4/5 + lg 5 Ý 1.52 |
Were all three players equally likely to win, the uncertainty would be lg 3 Ý 1.58, again matching our intuition that the winner is less uncertain if two of the three are more likely to win. To take an extreme case, were Paul 100 times more likely to win than either Ann or Pamela, the uncertainty would be 0.14, considerably lower still.
Joint and conditional entropy are analogous to joint and conditional probability.
Definition 32–5. Let the random variable X take values from some set { x1, ... xn }. The value xi occurs with probability p(X = xi), where
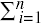p(X = xi) = 1. Let the random variable Y take values from some set { y1, ... ym }. The value yj occurs with probability p(Y = yj), where 
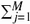p(Y = yj) = 1. The joint entropy of X and Y isH(X, Y) =
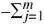
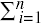p(X = xi, Y = yj) lg p(X = xi, Y = yj)
EXAMPLE: Let X be a random variable representing the roll of one die, and let Y be a random variable representing the flip of a coin. (See the second example in Section 32.1.) Assuming that both die and coin are fair, the entropy of X and Y taken jointly is
H(X, Y) | = |
|
= | –2 [ 6 [ (1/12) lg (1/12) ] ] = lg 12 Ý 3.59 |
Definition 32–6. Let the random variable X take values from some set { x1, ... xn }. The value xi occurs with probability p(X = xi), where
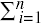p(X = xi) = 1. Let the random variable Y take values from some set { y1, ... ym }. The value yj occurs with probability p(Y = yj), where 
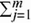p(Y = yj) = 1. The conditional entropy, or equivocation, of X given Y = yj isH(X | Y = yj) =
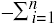p(X = xi | Y = yj) lg p(X = xi | Y = yj)
The conditional entropy of X given Y is
H(X | Y) =
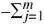p(Y = yj)[ 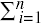p(X = xi | Y = yj) lg p(X = xi | Y = yj)]
The latter is the weighted mean of the conditional entropies of X given Y = yj for the possible values of Y.
EXAMPLE: Let X represent the roll of a red die, and let Y represent the sum of the values from rolling the red die and a blue die. Then the conditional entropy of X given Y = 2 is
H(X | Y = 2) =
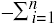p(X = xi | Y = 2) lg p(X = xi | Y = 2) = 0
because p(X = 1 | Y = 2) = 1 and p(X = i | Y = 2) = 0 for i = 2, ..., 6. However, the conditional entropy of X given Y = 7 is
H(X | Y = 7) =
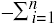p(X = xi | Y = 7) lg p(X = xi | Y = 7) = lg 6 Ý 2.58
Intuitively, these results make sense. If the total of the red and blue dice comes up 2, both must be 1, and so in the first case the conditional entropy is 0 because, given the value of Y, there is no uncertainty in the value of X. In the second case, the red die may take on any of its six possible values, so, assuming that it is fair, the uncertainty corresponds to each possible value of X being equally likely.
The conditional entropy of X given Y is
H(X | Y) | = |
|
= | p(Y = 2)[ |
