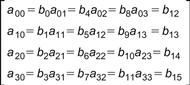Data Encryption
Dr. Bhushan Kapoor and Dr. Pramod Pandya, California State University
The Internet evolved over the years as a means for users to access information and exchange emails. Later, once the bandwidth became available, businesses exploited the Internet’s popularity to reach customers online. In the past few years it has been reported that organizations that store and maintain customers’ private and confidential records were compromised on many occasions by hackers breaking into the data networks and stealing the records from storage media. More recently we have come across headline-grabbing security breaches regarding laptops with sensitive data being lost or stolen, and most recently the Feds have encrypted around 1 million laptops with encryption software loaded to secure data such as names and Social Security numbers. This chapter is about security and the role played by cryptographic technology in data security. Securing data while it is in storage or in transition from an unauthorized access is a critical function of information technology. All forms of ecommerce activities such as online credit card processing, purchasing stocks, and banking data processing would, if compromised, lead to businesses losing billions of dollars in revenues, as well as customer confidence lost in ecommerce.
Keywords
encryption; data encryption; data security; decryption; cryptographic protocols; cryptography; authentication; confidentiality; integrity; nonrepudiation
Data security is not limited to wired networks but is equally critical for wireless communications such as in Wi-Fi and cellular. A very recent case was highlighted when the Indian government requested to Research In Motion (RIM) to share the encryption algorithm used in the BlackBerry cellular device. Of course, RIM refused to share the encryption algorithm. This should demonstrate that encryption is an important technology in all forms of communication. It is hard to accept that secured systems could ever remain secured, since they are designed by us and therefore must be breakable by one of us, given enough time. Every human-engineered system must have a flaw, and it is only a matter of time before someone finds it, thus demanding new innovations by exploring applications from algebraic structures such as groups and rings, elliptic curves, and quantum physics.
Over the past 20 years we have seen classical cryptography evolve to quantum cryptography, a branch of quantum information theory. Quantum cryptography is based on the framework of quantum physics, and it is meant to solve the problem of key distribution, which is an essential component of cryptography that enables us to secure data. The key allows the data to be coded so that to decode it, one would need to know the key that was used to code it. This coding of the given data using a key is known as encryption, and decoding of the encrypted data, the reverse step-by-step process, is known as decryption. At this stage we point out that the encryption algorithm comes in two flavors: symmetric and asymmetric, of which we will get into the details later on. Securing data requires a three-pronged approach: detection, prevention, and response. Data normally resides on storage media that are accessible over a network. This network is designed with a perimeter around it, such that a single access point provides a route for inbound and outbound traffic through a router supplemented with a firewall.
Data encryption prevents data from being exposed to unauthorized access and makes it unusable. Detection enables us to monitor the activities of network users and provides a means to differentiate levels of activities and offers a possible clue to network violations. Response is equally important, since a network violation must not be allowed to be repeated. Thus the three-pronged approach is evolutionary, and therefore systems analysis and design principles must be taken into account when we design a secured data network.
1 Need for Cryptography
Data communication normally takes place over an unsecured channel, as is the case when the Internet provides the pathways for the flow of data. In such a case the cryptographic protocols would enable secured communications by addressing the following.
Authentication
Alice sends a message to Bob. How can Bob verify that the message originated from Alice and not from Eve pretending to be Alice? Authentication is critical if Bob is to believe the message—for example, if the bank is trying to verify your Social Security or account number.
Confidentiality
Alice sends a message to Bob. How can Bob be sure that the message was not read by Eve? For example, personal communications need to be maintained as confidential.
Integrity
Alice sends a message to Bob. How does Bob verify that Eve did not intercept the message and change its contents?
Nonrepudiation
Alice could send a message to Bob and later deny that she ever sent a message to Bob. In such a case, how could Bob ever determine who actually sent him the message?
2 Mathematical Prelude to Cryptography
We will continue to describe Alice and Bob as two parties exchanging messages and Eve as the eavesdropper. Alice sends either a character string or a binary string that constitutes her message to Bob. In mathematical terms we have the domain of the message. The message in question needs to be secured from the eavesdropper Eve—hence it needs to be encrypted.
Mapping or Function
The encryption of the message can be defined as mapping the message from the domain to its range such that the inverse mapping should recover the original message. This mapping is a mathematical construct known as the function.
So we have a domain, and the range of the function is defined such that the elements of the domain will always map to the range of the function, never outside it. If f represents the function, and the message m ∈ the domain, then:
This function can represent, for example, swapping (shifting by k places) the characters positions in the message as defined by the function:
The inverse of this function f must recover the original message, in which case the function is invertible and one-to-one defined. If we were to apply two functions such as f followed by g, the composite function (g 
f) must be defined and furthermore invertible and one-to-one to recover the original message:
We will later see that this function is an algorithm that tells the user in a finite number of ways to disguise (encrypt) the given message. The inverse function, if it does exist, would enable us to recover the original message, which is known as the decryption.
Probability
Information security is the goal of the secured data encryption; hence if the encrypted data is truly randomly distributed in the message space (range), to the hacker the encrypted message is equally likely to be in any one of the states (encrypted). This would amount to maximum entropy, so one could reasonably ask as to the likelihood of a hacker breaking the encrypted message, that is, what is the probability of an insecure event taking place? This is conceptually similar to a system being in statistical equilibrium, when it could be equally likely to be in any one of the states. This could lay the foundations of cryptoanalysis in terms of how secure the encryption algorithm is, and can it be broken in polynomial time?
Complexity
Computational complexity deals with problems that could be solved in polynomial time, for a given input. If a given encryption algorithm is known to be difficult to solve and may have a number of solutions, the hacker would have a surmountable task to solve it. Therefore, secured encryption can be examined within the scope of computational complexity to determine whether a solution exists in polynomial time. There is a class of problems that have solutions in polynomial time for a given input, designated as P. By contrast, NP is the set of all problems that have solutions in polynomial time but the correctness of the problem cannot be ascertained. Therefore, NP is a larger set containing the set P. This is useful, for it leads us to NP-completeness, which reduces the solvability of problems in class P to class NP.
Consider a simple example—a set S={4, 7, 12, 1, 10} of five numbers. We want any three numbers to add to 23. Each of the numbers is either selected once only or not selected. The target is 23. Is there an algorithm for the target 23? If there is one, do we have more than one solution? Let’s explore whether we can add three numbers to reach a target of 25. Is there a solution for a target of 25? Does a solution exist, and can we investigate in polynomial time? We could extend this concept of computational complexity to crack encryption algorithm that is public, but the key used to encrypt and decrypt the message is kept private. So, in essence the cryptoanalysis deals with discovering the key.
3 Classical Cryptography
The conceptual foundation of cryptography was laid out around 3,000 years ago in India and China. The earlier work in cryptology was centered on messages that were expressed using alphanumeric symbols; hence encryption involved simple algorithms such as shifting characters within the string of the message in a defined manner, which is now known as shift cipher. We will also introduce the necessary mathematics of cryptography: integer and modular arithmetic, linear congruence, Euclidean and Extended Euclidean algorithms, Fermat’s theorem, and elliptic curves. We will specify useful notations in context.
Take the set of integers:
For any integers a and n, we say that n divides a if the remainder is zero after the division, or else we write:
The Euclidean Algorithm
Given two positive integers, a and b, find the greatest common divisors of a and b. Let d be the greatest common divisors (gcd) of a and b, then,
Use the following example:
Hence:
The Extended Euclidean Algorithm
Let a and b be two positive integers, then
Use the following example:
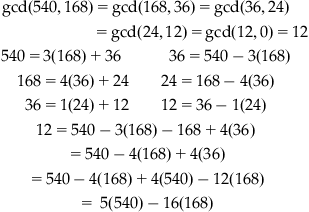
Therefore:
Hence:
Modular Arithmetic
For a given integer a, positive integer m, and the remainder r,
Consider examples:
{divide −18 by 14 leaves −4 as a remainder, then add 14 to −4 so that (−4+14)=10 so the remainder is nonnegative}
A set of residues is a set consisting of remainders obtained by dividing positive integers by a chosen positive number m (modulus).
Take m=7, then
Congruence
In arithmetic we normally use the relational operator, equal (=), to express that the pair of numbers are equal to each other, which is a binary operation. In cryptography we use congruence to express that the residue is the same for a set of integers divided by a positive integer. This essentially groups the positive integers into equivalence classes. Let’s look at some examples:
Hence we say that the set {2, 12, 22} are congruent mod 10.
Residue Class
A residue class is a set of integers congruent mod m, where m is a positive integer.
Take m=7:
Some more useful operations defined in Zm:
Inverses
In everyday arithmetic, it is quite simple to find the inverse of a given integer if the binary operation is either additive or multiplicative, but such is not the case with modular arithmetic.
We will begin with the additive inverse of two numbers a, b∈Zm
That is, the additive inverse of a is b=(m−a).
Given
Verify:
Similarly, the multiplicative inverse of two integers a, b∈Zm if
a has a multiplicative inverse b∈Zm if and only if
in which case (m, a) are relative prime.
We remind the reader that a prime number is any number greater than 1 that is divisible (with a remainder 0) only by itself and 1. For example, {2, 3, 5, 7, 11, 13,…} are prime numbers, and we quote the following theorem for the reader.
Fundamental Theorem of Arithmetic
Each positive number is either a prime number or a composite number, in which case it can be expressed as a product of prime numbers.
Let’s consider a set of integers mod 10 to find the multiplicative inverse of the numbers in the set:
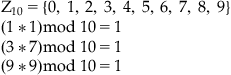
then there are only three pairs (1,1); (3,7); and (9,9):
The numbers {0, 2, 4, 5, 6, 8} have no multiplicative inverse.
Consider a set:
Then,
You will note that Zn* is a subset of Zn with unique multiplicative inverse.
Each member of Zn has a unique additive inverse, whereas each member of Zn* has a unique multiplicative inverse.
Congruence Relation Defined
The a is congruent to b (mod m) if m divides (a−b), that is, the remainder is zero.
Examples: 87 ≡ 27 mod 4, 67 ≡ 1 mod 6.
Next we quote three theorems:
Theorem 1: Suppose that a ≡ c mod m and b ≡=d mod m, then
Theorem 2: Suppose a*b≡a*c (mod m)
Theorem 3: Suppose a*b≡a*c (mod m)
Example to illustrate the use of the theorems just stated:
then
since
therefore,
also
therefore,
Given,
Since
therefore,
you will observe that,
therefore,
and the multiplicative inverse of 7−1 is 4, therefore,
Substitution Cipher
Shift ciphers, also known as additive ciphers, are an example of a monoalphabetic character cipher in which each character is mapped to another character, and a repeated character maps to the same character irrespective of its position in the string. We give a simple example of an additive cipher, where the key is 3, and the algorithm is “add.” We restrict the mapping to {0, 1, ........., 7} (see Table 2.1)—that is, we use mod 8. This is an example of finite domain and the range for mapping, so the inverse of the function can be determined easily from the ciphertext.
Observations:
• The domain of the function is x={0,1,2,3,4,5,6,7}.
The affine cipher has two operations, addition and multiplication, with two keys. Once again the arithmetic is mod m, where m is a chosen positive integer.
where k and b are chosen from integers {0, 1, 2, 3,.........., (m−1)}, and x is the symbol to be encrypted.
The decryption is given as:
where
is the multiplicative inverse of k in Zn*
(—b) is the additive inverse in Zn
Consider,
Then,
In this case, the multiplicative inverse of 5 happens to be 5.
Monoalphabetic substitution ciphers are easily broken, since the key size is small (see Table 2.2).
Transposition Cipher
A transposition cipher changes the location of the character by a given set of rules known as permutation. A cyclic group defines the permutation with a single key to encrypt, and the same key is used to decrypt the ciphered message. Table 2.3 provides an illustration.
4 Modern Symmetric Ciphers
Computers internally represent printable data in binary format as strings of zeros and ones. Therefore any data is represented as a large block of zeros and ones. The processing speed of a computer is used to encrypt the block of zeros and ones. Securing all the data in one go would not be practical, nor would it secure the data; hence the scheme to treat data in chunks of blocks, leading to the concept of block ciphers.
The most common value of a block is 64, 128, 256, or 512 bits. You will observe that these values are powers of 2, since computers process data in binary representation using modular arithmetic with modulus 2. We need an algorithm and a key to encrypt the blocks of binary data such that the ciphered data is confusing and diffusing to the hacker. The algorithm is made public, whereas the key is kept secret from unauthorized users so that hackers could establish the robustness of the cipher by attempting to break the encrypted message. The logic of the block cipher is as follows:
• Each bit of ciphertext should depend on all bits of the key and all bits of the plaintext.
• There should be no evidence of statistical relationship between the plaintext and the ciphertext.
In essence, this is the goal of an encryption algorithm: Confuse the message so that there is no apparent relationship between the ciphertext and the plaintext. This is achieved by the substitution rule (S-boxes) and the key.
If changing one bit in the plaintext has a minimal effect on the encrypted text, it might be possible for the hacker to work backward from the encrypted text to the plaintext by changing the bits. Therefore a minimal change in the plaintext should lead to a maximum change in the ciphertext, resulting in spreading, which is known as diffusion. Permutation or P-boxes implement the diffusion.
The symmetric cipher consists of an algorithm and a key. The algorithm is made public, whereas the key is kept secret and is known only to the parties that are exchanging messages. Of course, this does create a huge problem, since every pair that is going to exchange messages will need a secret key, growing indefinitely in number as the number of pairs increases. We also would need a mechanism by which to manage the secret keys. We will address these issues later on.
The symmetric algorithm would consist of finite rounds of S-boxes and P-boxes. Once the plaintext is encrypted using the algorithm and the key, it would need to be decrypted using the same algorithm and key. The decryption algorithm and the key would need to work backward in some sense to revert the encrypted message to its original message.
So you begin to see that the algorithm must consist of a finite number of combinations of S-boxes and P-boxes; encryption is mapping from message space (domain) to another message space (range), that is, mapping should be a closed operation, a “necessary” condition on the encryption algorithm. This implies that message strings get mapped to message strings, and of course these message strings belong to a set of messages. We are not concerned with the semantics of the message; we leave this to the message sender and receiver. The S-boxes and P-boxes would define a set of operations on the messages or bits that represent the string of messages. Therefore we require that this set of operations should also be able to undo the encryption, that is, mapping must be invertible in the mathematical sense. Hence the set of operations must have definite relationships among them, resulting in some structural and logical connection. In mathematics an example of this is an algebraic structure such as group, ring, and field, which we explore in the next section.
S-Box
The reader should note that an S-box can have a 3-bit input binary string, and its output may be a 2-bit. The S-box may use a key or be keyless. Let S(x) be the linear function computed by the following function [1]:
Such a function is referred to as an S-box. For a given 4-bit block of plaintext x1x2x3x4 and the 3-bit key, k1k2k3, let
where ⊕ represents exclusive OR
Given ciphertext, y1y2y3y4 computed with E and the key, k1k2k3, compute
S-boxes are classified as linear if the number of output bits is the same as the number of input bits, and they’re nonlinear if the number of output bits is different from the number of input bits. Furthermore, S-boxes can be invertible or noninvertible.
P-Boxes
A P-box (permutation box) will permute the bits per specification. There are three different types of P-boxes, as shown in Tables 2.4, 2.5, and 2.6.
In the compression P-box, inputs 2 and 4 are blocked.
The expansion P-box maps elements 1, 2, and 3 only.
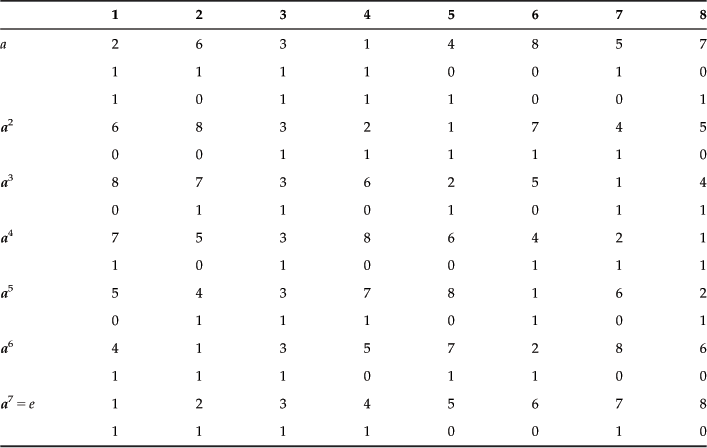
Let’s consider a permutation group with the mapping defined, as shown in Table 2.7.
This group is a cyclic group with elements:
The identity mapping is given by a7=e. The inverse element is a−1.
Table 2.7 shows a permutation of an 8-bit string (11110010).
Product Ciphers
Modern block ciphers are divided into two categories. The first category of the cipher uses both invertible and noninvertible components. A Feistel cipher belongs to the first category, and DES is a good example of a Feistel cipher. This cipher uses the combination of S-boxes and P-boxes with compression and expansion (noninvertible).
The second category of cipher only uses invertible components, and Advanced Encryption Standard (AES) is an example of a non-Feistel cipher. AES uses S-boxes with an equal number of inputs and outputs and a straight P-box that is invertible.
Alternation of substitutions and transpositions of appropriate forms when applied to a block of plaintext can have the effect of obscuring statistical relationships between the plaintext and the ciphertext and between the key and the ciphertext (diffusion and confusion).
5 Algebraic Structure
Modern encryption algorithms such as DES, AES, RSA, and ElGamal, to name a few, are based on algebraic structures such as group theory and field theory as well as number theory. We will begin with a set S, with a finite number of elements and a binary operation (*) defined between any two elements of the set:
that is, if a and b∈S, then a * b∈S. This is important because it implies that the set is closed under the binary operation. We have seen that the message space is finite, and we want to make sure that any algebraic operation on the message space satisfies the closure property. Hence, we want to treat the message space as a finite set of elements. We remind the reader that messages that get encrypted must be finally decrypted by the received party, so the encryption algorithm must run in polynomial time; furthermore, the algorithm must have the property that it be reversible, to recover the original message. The goal of encryption is to confuse and diffuse the hacker to make it almost impossible for the hacker to break the encrypted message. Therefore, encryption must consist of finite number substitutions and transpositions. The algebraic structure classical group facilitates the coding of encryption algorithms.
Next we give some relevant definitions and examples before we proceed to introduce the essential concept of a Galois field, which is central to formulation of a Rijndael algorithm used in the Advanced Encryption Standard.
Definition Group
A definition group (G, •) is a finite set G together with an operation • satisfying the following conditions [2]:
Definitions of Finite and Infinite Groups (Order of a Group)
A group G is said to be finite if the number of elements in the set G is finite; otherwise the group is infinite.
Definition Abelian Group
A group G is abelian if for all a, b∈G, a • b=b • a
The reader should note that in a group, the elements in the set do not have to be numbers or objects; they can be mappings, functions, or rules.
Examples of a Group
The set of integers Z is a group under addition (+), that is, (Z, +) is a group with identity e=0, and inverse of an element a is (−a). This is an additive abelian group, but infinite.
Nonzero elements of Q (rationale), R (reals), and C (complex) form a group under multiplication, with the identity element e=1, and a−1 being the multiplicative inverse.
For any n≥1, the set of integers modulo n forms a finite additive group of n elements.
G=<Zn,+> is an abelian group.
The set of Zn* with multiplication operator, G=<Zn*, x>is also an abelian group.
The set Zn*, is a subset of Zn and includes only integers in Zn that have a unique multiplicative inverse.
Definition: Subgroup
A subgroup of a group G is a non empty subset H of G, which itself is a group under the same operations as that of G. We denote that H is a subgroup of G as H⊆G, and H⊂G is a proper subgroup of G if the set H≠G [2]:
Examples of subgroups:
Under addition, Z⊆Q⊆R⊆C.
H=<Z10,+> is a proper subgroup of G=<Zl2,+>
Definition: Cyclic Group
A group G is said to be cyclic if there exists an element a∈G such that for any b∈G, and i≥0, b=ai. Element a is called a generator of G.
The group G=<Z10*, x>is a cyclic group with generators g=3 and g=7.
The group G=<Z6,+> is a cyclic group with generators g=1 and g=5.
Rings
Let R be a non-empty set with two binary operations addition (+) and multiplication (*). Then R is called a ring if the following axioms are met:
• Under addition, R is an abelian group with zero as the additive identity.
• Under multiplication, R satisfies the closure, the associativity, and the identity axiom; 1 is the multiplicative identity, and that 1≠0.
• For every a and b that belongs to R, a • b=b • a.
• For every a, b, and c that belongs to R, then a• (b+c)=a • b+a • c.
Examples
Z, Q, R, and C are all rings under addition and multiplication. For any n>0, Zn is a ring under addition and multiplication modulo n with 0 as identity under addition, 1 under multiplication.
Definition: Field
If the nonzero elements of a ring form a group under multiplication, the ring is called a field.
Examples
Q, R, and C are all fields under addition and multiplication, with 0 and 1 as identity under addition and multiplication.
Note: Z under integer addition and multiplication is not a field because any nonzero element does not have a multiplicative inverse in Z.
Finite Fields GF(2n)
Construction of finite fields and computations in finite fields are based on polynomial computations. Finite fields play a significant role in cryptography and cryptographic protocols such as the Diffie and Hellman key exchange protocol, ElGamal cryptosystems, and AES.
For a prime number p, the quotient Z/p (or Fp) is a finite field with p number of elements. For any positive integer q, GF(q)=Fq. We define A to be algebraic structure such as a ring, group, or field.
Definition: A polynomial over A is an expression of the form
where n is a nonnegative integer, the coefficient ai∈A, 0≤i≤n, and x ∉ A [2].
Definition: A polynomial f∈A[x] is said to be irreducible in A[x] if f has a positive degree and f=gh for some g, h∈A[x] implies that either g or h is a constant polynomial [2].
The reader should be aware that a given polynomial can be reducible over one structure but irreducible over another.
Definition: Let f, g, q, and r∈A[x] with g ≠ 0. Then we say that r is a remainder of f divided by g:
The set of remainders of all the polynomials in A[x](mod g) denoted as A[x]g.
Theorem: Let F be a field and f be a nonzero polynomial in F[x]. Then F[x]f is a ring and is a field if f is irreducible over F.
Theorem: Let F be a field of p elements, and f be an irreducible polynomial over F. Then the number of elements in the field F[x]f is pn [2].
For every prime p and every positive integer n there exists a finite field of pn number of elements.
For any prime number p, Zp is a finite field under addition and multiplication modulo p with 0 and 1 as the identity under addition and multiplication.
Zp is an additive ring and the nonzero elements of Zp, denoted by Zp*, forms a multiplicative group.
Galois field, GF(pn) is a finite field with number of elements pn, where p is a prime number and n is a positive integer.
Example: Integer representation of a finite field (Rijndael) element.
Polynomial f(x)=x8+x4+x3+x+1 is irreducible over F2.
The set of all polynomials(mod f) over F2 forms a field of 28 elements; they are all polynomials over F2 of degree less than 8. So any element in the field F2[x]f
where b7,b6,b5,b4,b3,b2,b1,b0∈F2 thus any element in this field can represent an 8-bit binary number.
We often use 
field with 256 elements because there exists an isomorphism between Rijndael and 
Data inside a computer is organized in bytes (8 bits) and is processed using Boolean logic, that is, bits are manipulated using binary operations addition and multiplication. These binary operations are implemented using the logical operator XOR, or in the language of finite fields, GF(2). Since the extended ASCII defines 8 bits per byte, an 8-bit byte has a natural representation using a polynomial of degree 8. Polynomial addition would be mod 2, and multiplication would be mod polynomial degree 8. Of course this polynomial degree 8 would have to be irreducible. Hence the Galois field GF(28) would be the most natural tool to implement the encryption algorithm. Furthermore, this would provide a close algebraic formulation.
Consider polynomials over GF(2) with p=2 and n=1.
For polynomials with negative coefficients, −1 is the same as +1 in GF(2). Obviously, the number of such polynomials is infinite. Algebraic operations of addition and multiplication in which the coefficients are added and multiplied according to the rules that apply to GF(2) are sets of polynomials that form a ring.
Modular Polynomial Arithmetic Over GF(2)
The Galois field GF(23): Construct this field with eight elements that can be represented by polynomials of the form
Two choices for a, b, c give 2×2×2=8 polynomials of the form
What is our choice of the irreducible polynomials for this field?
These two polynomials have no factors: (x3+x2+1), (x3+x+1)
So we choose polynomial (x3+x+1). Hence all polynomial arithmetic multiplication and division is carried out with respect to (x3+x+1).
The eight polynomials that belong to GF(23):
You will observe that GF(8)={0,1,2,3,4,5,6,7} is not a field, since every element (excluding zero) does not have a multiplicative inverse such as {2, 4, 6} (mod 8) [2].
Using a Generator to Represent the Elements of GF(2n)
It is particularly convenient to represent the elements of a Galois field with the help of a generator element. If α, is a generator element, then every element of GF(2n), except for the 0 element, can be written as some power of α. A generator is obtained from the irreducible polynomial that was used to construct the finite field. If f(α) is the irreducible polynomial used, then α, is that element that satisfies the equation f(α)=0. You do not actually solve this equation for its roots, since an irreducible polynomial cannot have actual roots in the field GF(2).
Consider the case of GF(23), defined with the irreducible polynomial x3+x+1. The generator α, is that element that satisfies α3+α+1=0. Suppose α is a root in GF(23) of the polynomial p(x)=1+x+x3, that is, p(α)=0, then
All powers of α generate nonzero elements of GF8. The polynomials of GF(23) represent bit strings, as shown in Table 2.8.
Table 2.8
| Polynomial | Bit String |
| 0 | 000 |
| 1 | 001 |
| x | 010 |
| x+1 | 011 |
| X2 | 100 |
| x2+1 | 101 |
| X2+X | 110 |
| x2+x+1 | 111 |
We now consider all polynomials defined over GF(2), modulo the irreducible polynomial x3+x+1. When an algebraic operation (polynomial multiplication) results in a polynomial whose degree equals or exceeds that of the irreducible polynomial, we will take for our result the remainder modulo the irreducible polynomial. For example,
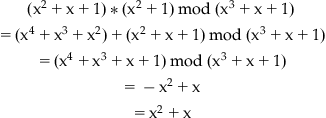
Recall that 1+1=0 in GF(2). With multiplications modulo (x3+x+1), we have only the following eight polynomials in the set of polynomials over GF(2):
We refer to this set as GF(23), where the power of 2 is the degree of the modulus polynomial. The eight elements of Z8 are to be integers modulo 8. Similarly, GF(23) maps all the polynomials over GF(2) to the eight polynomials shown. But you will note the crucial difference between GF(23) and 23: GF(23) is a field, whereas Z8 is not [2].
GF(23) is a Finite Field
We know that GF(23) is an abelian group because the operation of polynomial addition satisfies all the requirements of a group operator and because polynomial addition is commutative. GF(23) is also a commutative ring because polynomial multiplication is a distributive over polynomial addition. GF(23) is a finite field because it is a finite set and because it contains a unique multiplicative inverse for every nonzero element.
GF(2n) is a finite field for every n. To find all the polynomials in GF(2n), we need an irreducible polynomial of degree n. AES arithmetic is based on GF(28). It uses the following irreducible polynomial:
The finite field GF(28) used by AES obviously contains 256 distinct polynomials over GF(2). In general, GF(pn) is a finite field for any prime p. The elements of GF(pn) are polynomials over GF(p) (which is the same as the set of residues Zp).
Next we show how the multiplicative inverse of a polynomial is calculated using the Extended Euclidean algorithm:
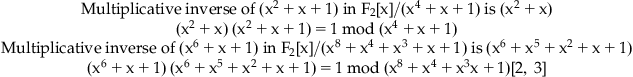
6 The Internal Functions of Rijndael in AES Implementation
Rijndael is a block cipher. The messages are broken into blocks of a predetermined length, and each block is encrypted independently of the others. Rijndael operates on blocks that are 128-bits in length. There are actually three variants of the Rijndael cipher, each of which uses a different key length. The permissible key lengths are 128, 192, and 256 bits. The details of Rijndael may be found in Bennett and Gilles (1984), but we give an overview here [2,3].
Mathematical Preliminaries
Within a block, the fundamental unit operated on is a byte, that is, 8 bits. Bytes can be interpreted in two different ways. A byte is given in terms of its bits as b7b6b5b4b3b2b1b0. We may think of each bit as an element in GF(2), the finite field of two elements (mod 2). First, we may think of a byte as a vector, b7b6b5b4b3b2b1b0 in GF(28). Second, we may think of a byte as an element of GF(28), in the following way: Consider the polynomial ring GF(2)[X]. We may mod out by any polynomial to produce a factor ring. If this polynomial is irreducible and of degree n, the resulting factor ring is isomorphic to GF(2n). In Rijndael, we mod out by the irreducible polynomial X8+X4+X3+X+1 and so obtain a representation for GF(28). The Rijndael algorithm deals with five units of data in the encryption scheme:
State
For our discussion purposes, we will consider a data block of 128 bits with a ky size of 128 bits. The state is 128 bits long. We think of the state as divided into 16 bytes, aij where 0≤i, j≤3. We think of these 16 bytes as an array, or matrix, with 4 rows and 4 columns, such that a00 is the first byte, b0 and so on (see Figure 2.1).
AES uses several rounds (10, 12, or 14) of transformations, beginning with a 128-bit block. A round is made up of four parts: S-box, permutation, mixing, and subkey addition. We discuss each part here [2,3].
The S-Box (SubByte)
S-boxes, or substitution boxes, are common in block ciphers. These are 1-to-l and onto functions, and therefore an inverse exists. Furthermore, these maps are nonlinear to make them immune to linear and differential cryptoanalysis. The S-box is the same in every round, and it acts independently on each byte. Each byte belongs to GF(28) domain with 256 elements. For a given byte we compute the inverse of that byte in the GF(28) field. This sends a byte x to x−1 if x is nonzero and sends it to 0 if it is zero. This defines a nonlinear transformation, as shown in Table 2.9.
Next we apply an affine (over GF(2)) transformation. Think of the byte x as a vector in GF(28). Consider the invertible matrix A, as shown in Figure 2.2.
The structure of matrix A is relatively simple, successively shifting the prior row by 1. If we define the vector v∈GF(28) to be (1, 1, 0, 0, 0, 1, 1, 0), then the second half of the S-box sends byte x to byte y through the affine transformation defined as:
Since the matrix A has an inverse, it is possible to recover x using the following procedure known as the InvSubByte:
We will demonstrate the action of an S-box by choosing an uppercase letter S, for which the hexadecimal representation is 5316 and binary representation is shown in Tables 2.10 and 2.11.
The letter S has a polynomial representation:
The multiplicative inverse of (x6+x4+x+1) is (x7+x6+x3+x), which is derived using the Extended Euclidean algorithm.
Next we multiply the multiplicative inverse x−1 with an invertible matrix A (see Figure 2.3) and add a column vector (b) and get the resulting column vector y (see Table 2.12). This corresponds to SubByte transformation and it is nonlinear [2].
The column vector y represents a character ED16 in hexadecimal representation.
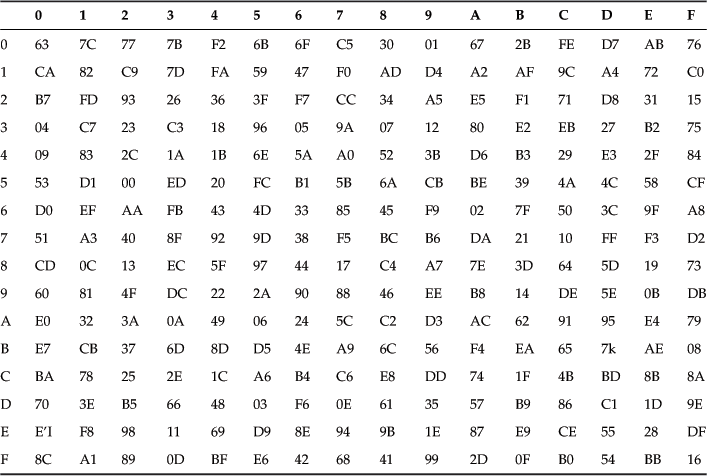
The reader should note that this transformation using the GF(28) field is a pretty tedious computation, so instead we use an AES S-box lookup table (a 17×17 matrix expressed in hexadecimal) to replace the character with a replacement character. This corresponds to the SubByte transformation, and corresponding to the SubByte table there is an InvSubByte table that is the inverse of the SubByte table. The InvSubByte can be found in the references or is readily available on the Internet.
We will work with the following string: QUANTUMCRYPTOGOD, which is 16 bytes long, to illustrate AES (see Table 2.13). The state represents our string as a 4×4 matrix in the given arrangement using a hexadecimal representation of each byte (see Figure 2.4).
Figure 2.4 The state represents a string as a 4×4 matrix in the given arrangement using hexadecimal representation of each byte.
We apply SubByte transformation (see Figure 2.5) using the lookup table, which replaces each byte as defined in Table 2.13.
The next two rounds of ShiftRows and Mixing in the encryption lead to a diffusion process. The ShiftRow is a permutation.
ShiftRows
In the first step, we take the state and apply the following logic. The first row is kept as is. The second row is shifted left by one byte. The third row is shifted left by two bytes, and the last row is shifted left by three bytes. The resulting state is shown in Figure 2.6.
InvShiftRows in decryption shift bytes toward the right, similar to ShiftRows.
Mixing
The second step, the MixColumns transformation, mixes the columns. We interpret the bytes of each column as the coefficients of a polynomial in GF(28)[x]/(x4+1). Then we multiply each column by the polynomial ‘03’ x3+‘02’ x2+‘01’x+‘02’. Multiplication of the bytes is done in GF(28) with mod (x4+1).
The mixing transformation remaps the four bytes to a new four bytes by changing the contents of the individual bytes (see Figure 2.7). The MixColumns transformation is applied to each column of the state, hence each column is multiplied by a constant matrix to obtain a new state, S′0i.
Subkey Addition
From the original key, we produce a succession of 128-bit keys by means of a key schedule. Let’s recap that a word is a group of 32 bits. A 128-bit key is labeled as shown in Table 2.14.
which is then written as a 4×4 matrix (see Figure 2.8), where W0 is the first column, W1 is the second column, W2 is the third column, and W3 is the fourth column.
AES uses a process called key expansion that creates (10+1) round keys from the given cipher key. We start with four words and end with 44 words—four word per round key. Thus
The algorithm to generate 10 round keys is as follows:
The initial cipher key consists of words: W0W1W2W3
The other 10 round keys are made using the following logic:
If (j mod 4)≠0
else
where Z=SubWord(RotWord(Wj−1)⊕RConj/4.
RotWord (rotate word) takes a word as an array of four bytes and shifts each byte to the left with wrapping. SubWord (substitute word) uses the SubByte lookup table to substitute the byte in the word [2,3]. RCon (round constants) is a four-byte value in which the rightmost three bytes are set to zero [2,3].
Let’s work through an example, as shown in Figure 2.9.
Key: 2B 7E 15 16 28 AE D2 A6 AB F7 15 88 09 CF 4F 3C
W0=2B 7E 15 16 W1=28 AE D2 A6 W2=AB F7 15 88 W3=09 CF 4F 3C
Compute W4:
Hence,
Putting it Together
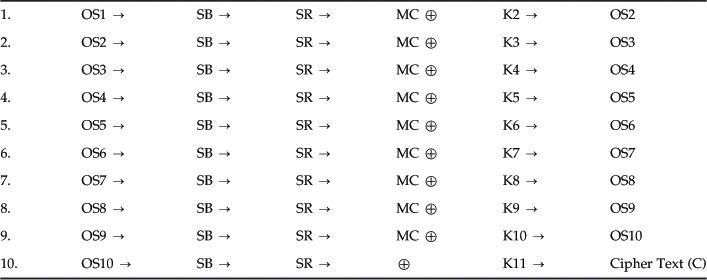
Put the input into the state: XOR is the state with the 0-th round key. We start with this because any actions before the first (or after the last) use of the key are pointless, since they are publicly known and so can be undone by an attacker. Then apply 10 of the preceding rounds, skipping the column mixing on the last round (but proceeding to a final key XOR in that round). The resulting state is the ciphertext. We use the following labels to describe the encryption procedure (see Table 2.15):
Next we cycle through the decryption procedure:
InvSubByte (ISB), InvShiftRows (ISR), InvMixColumns (IMC)
Round
AES is a non-Feistel cipher, hence each set of transformations such as SubByte, ShiftRows, and MixColumns are invertible so that the decryption must consist of steps to recover the plaintext. You will observe that the round keys are used in the reverse order (see Table 2.16).
7 Use of Modern Block Ciphers
DES and AES are designed to encrypt and decrypt data blocks of fixed size. Most practical examples have data blocks of fewer than 64 bits or greater than 128 bits, and to address this issue currently, five different modes of operation have been set up. These five modes of operation are known as Electronic Code Book (ECB), Cipher-Block Chaining (CBC), Output Feedback (OFB), Cipher Feedback (CFB), and Counter (CTR) modes.
The Electronic Code Book (ECB)
In this mode, the message is split into blocks, and the blocks are sequentially encrypted. This mode is vulnerable to attack using the frequency analysis, the same sort used in simple substitution. Identical blocks would get encrypted to the same blocks, thus exposing the key [1].
Cipher-Block Chaining (CBC)
A logical operation is performed on the first block with what is known as an initial vector using the secret key so as to randomize the first block. The output of this step is logically combined with the second block and the key to generate encrypted text, which is then used with the third block and so on [1].
8 Public-Key Cryptography
In this section we cover what is known as asymmetric encryption, which uses a pair of keys rather than one key, as used in symmetric encryption. This single-key encryption between the two parties requires that each party has its secret key, so that as the number of parties increases so does the number of keys. In addition, the distribution of the secret key becomes unmanageable as the number of keys increases. Of course, a longtime use of the same secret key between any pair would make it more vulnerable to cryptoanalysis attack. So, to deal with these inextricable problems, a key distribution facility was born. Symmetric encryption is considered more practical in dealing with vast amounts of data consisting of strings of zeros and ones. Yet another scheme was invented to secure data while in transition, using tools from a branch of mathematics known as number theory. To begin, let’s review the necessary number theory concepts [2,3].
Review: Number Theory
Asymmetric-key encryption uses prime numbers, which are a subset of positive integers. Positive integers are all odd and even numbers, including the number 1, such that some of the numbers are composite, that is, products of numbers therein. This critical fact plays a significant role in generating keys. Next we will go through some statements of fact for the sake of completeness.
Coprimes
Two positive integers are said to be coprime or relatively prime if gcd(a, b)=1.
Cardinality of Primes
The number of primes is infinite. Given a number n, how many prime numbers are smaller than or equal to n? The answer to this question was discovered by Gauss and Lagrange as:
where Π(n) is the number of primes smaller than or equal to n.
Check whether a given number 107 is a prime number. We take the square root of 107 to the nearest whole number, which is 10. Then count the number of primes less than 10, which are 2, 3, 5, 7. Next we check whether any one of these numbers will divide 107. In our example none of these numbers can divide 107, so 107 is a prime number.
Euler’s Phi-Function ϕ(n): Euler’s totient function finds the number of integers that are both smaller than n and coprime to n.
Examples:
Factoring
The fundamental theorem of arithmetic states that every positive integer can be written as a product of prime numbers. There are a number of algorithms to factor large composite numbers.
Fermat’s Little Theorem
In the 1970s, the creators of digital signatures and public-key cryptography realized that the framework for their research was already laid out in the body of work by Fermat and Euler. Generation of a key in public-key cryptography involves exponentiation modulo of a given modulus.
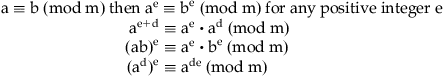
Examples:
Theorem. Let p be a prime number.
Examples:
Theorem: Let p and q be distinct primes.
Example:
Discrete Logarithm
Here we will deal with multiplicative group G=<Zn*x>. The order of a finite group is the number of elements in the group G. Let’s take an example of a group,
that is, 12 elements in the group, and each is coprime to 21.
The order of an element, ord(a) is the smallest integer i such that
where e=1.
Lagrange’s theorem states that the order of an element divides the order of the group. In our example {1, 2, 4} each of them divide 4, therefore we need to check only these powers to find the order of the element.
If a∈G=<Zn*, x>, then aϕ(n)=1 mod n
Euler’s theorem shows that the relationship ai≡1 (mod n) holds whenever the order (i) of an element equals ϕ(n).
Primitive Roots
In the multiplicative group, if G=<Zn*, x> when the order of an element is the same as ϕ(n), then that element is called the primitive root of the group. This property of primitive root is used in ElGamal cryptosystem.
G=<Z8*, x> has no primitive roots. The order of this group is ϕ(8)=4.
1, 2, 4 each divide the order of the group, which is 4.
In this example none of the elements has an order of 4, hence this group has no primitive roots. We will rearrange our data as shown in Table 2.17 [2, 3].
Let’s take another example: G=<Z7*, x>, then ϕ(7)=6, hence the order of the group is 6 with these members {1, 2, 3, 4, 5, 6}, which are all coprime to 7. We note that the order of each of these elements {1, 2, 3, 4, 5, 6} is the smallest integer i such that ai≡1 (mod 7). We note that the order of an element divides the order of the group. Thus the only numbers that divide 6 are {1, 2, 3, 6}:
Since the order of the elements {3, 5} is 6, which is the order of the group, therefore the primitive roots of the group are {3, 5}. In here the smallest integer i=6, ϕ(7)=6.
Solve for x in each of the following:
We can rewrite the above as:
Using the third term in E). we see that x must be equal to 3.
The group G=<Zn*, x> has primitive roots only if n is 2, 4, pt, or 2pt, where p is an odd prime not including 2, and t is an integer.
If the group G=<Zn*, x> has any primitive roots, the number of primitive roots is ϕ(ϕ(n)).
Group G=<Zn*, x> has primitive roots, then it is cyclic, and each of its primitive roots is a generator of the whole group.
Group G=<Z10*, x> has two primitive roots because ϕ(10)=4, and ϕ(ϕ(10))=2. These two primitive roots are {3, 7}.
Group G=<Zp*, x> is always cyclic.
The group G=<Zp*, x> has the following properties:
• Its elements are from 1 to (p−1) inclusive.
• It always has primitive roots.
• It is cyclic, and its elements can be generated using g where x is an integer from 1 to ϕ(n)=p−1.
• The primitive roots can be used as the base of a discrete logarithm.
Now that we have reviewed the necessary mathematical preliminaries, we will focus on the subject matter of asymmetric cryptography, which uses a public and a private key to encrypt and decrypt the plaintext. If Alice wants to send plaintext to Bob, she uses Bob’s public key, which is advertised by Bob, to encrypt the plaintext and then send it to Bob via an unsecured channel. Bob decrypts the data using his private key, which is known to him only. Of course this would appear to be an ideal replacement for the asymmetric-key cipher, but it is much slower, since it has to encrypt each byte; hence it is useful in message authentication and communicating the secret key (see sidebar, “The RSA Cryptosystem”).
The RSA Cryptosystem
Key generation algorithm:
1. Select two prime numbers p and q such that p≠q.
3. Set up a commutative ring R=<Zϕ, +, x> which is public since m is made public.
4. Set up a multiplicative group G=<Zr(m)*, x>which is used to generate public and private keys. This group is hidden from the public since ϕ(m) is kept hidden.
ϕ(m)=(p−1) (q−1)
5. Choose an integer e such that, 1<e<ϕ(m) and e is coprime to ϕ(m).
6. Compute the secret exponent d such that, 1<d<ϕ (m) and that ed≡1 (mod ϕ (m)).
7. The public key is “e” and the private key is “d.” The value of p, q, and ϕ(m) are kept private.
Encryption:
9 Cryptanalysis of RSA
RSA algorithm relies that p and q, the distinct prime numbers, are kept secret, even though m=p×q is made public. So if n is an extremely large number, the problem reduces to find the factors that make up the number n, which is known as the factorization attack.
Factorization Attack
If the middleman, Eve, can factor n correctly, then she correctly guesses p, q, and ϕ(m). Reminding ourselves that the public key e is public, then Eve has to compute the multiplicative inverse of e:
So if the modulus m is chosen to be 1024 bits long, it would take considerable time to break the RSA system unless an efficient factorization algorithm could be found [2,3] (see sidebars “Chosen-Ciphertext Attack” and “The eth Roots Problem”).
Discrete Logarithm Problem
Discrete logarithms are perhaps simplest to understand in the group Zp*, where p is the prime number. Let g be the generator of Zp*, then the discrete logarithm problem reduces to computing a, given (g, p, ga mod p) for a randomly chosen a<(p−1).
Chosen-Ciphertext Attack
Zn is a set of all positive integers from 0 to (n−1). Zn* is a set all integers such that gcd(n,a)=1, where a∈Zn*
Φ(n) calculates the number of elements in Zn* that are smaller than n and coprime to n.
Therefore, the number of integers in ∈Z21* is 12.
Each of which is coprime to 21.
Each of which is coprime to 14.
Example: Choose p=3 and q=7, then m=3×7=21.
Encryption and decryption take place in the ring, R=<Z21,+,x>
Key-Generation Group, G=<Z12*, x>
Alice encrypts the message P using the public key e of Bob and sends the encrypted message C to Bob.
Eve, the middleman, intercepts the message and manipulates the message before forwarding to Bob.
1. Eve chooses a random integer 
(since m is public).
2. Eve calculates Y=C×Xe (mod m).
3. Bob receives Y from Eve, and he decrypts Y using his private key d.
5. Eve can easily discover the plaintext P as follows:
Hence Z=[P×X] (mod m).
Using the Extended Euclidean algorithm, Eve can then compute the multiplicative inverse of X, and thus obtain P:
If we want to find the kth power of one of the numbers in this group, we can do so by finding its kth power as an integer and then finding the remainder after division by p. This process is called discrete exponentiation. For example, consider Z23*. To compute 34 in this group, we first compute 34=81, then we divide 81 by 23, obtaining a remainder of 12. Thus 34=12 in the group Z23*
A discrete logarithm is just the inverse operation. For example, take the equation 3k≡12 (mod 23) for k. As shown above k=4 is a solution, but it is not the only solution. Since 322≡1 (mod 23), it also follows that if n is an integer, then 34+22n≡12×1n≡12 (mod 23). Hence the equation has infinitely many solutions of the form 4+22n. Moreover, since 22 is the smallest positive integer m satisfying 3m≡1 (mod 23), that is, 22 is the order of 3 in Z23* these are all solutions. Equivalently, the solution can be expressed as k≡4 (mod 22) [2,3].
10 Diffie-Hellman Algorithm
The purpose of this protocol is to allow two parties to set up a shared secret key over an insecure communication channel so that they may exchange messages. Alice and Bob agree on a finite cyclic group G and a generating element g in G. We will write the group G multiplicatively [2,3].
1. Alice picks a prime number p, with the base g, exponent a to generate a public key A
3. (g, p, A) are made public, and a is kept private.
4. Bob picks a prime number p, base b, and an exponent b to generate a public key B.
6. (g, p, B) are made public, and b is kept private,
7. Bob using A generates the shared secret key S.
Thus the shared secret key S is established between Bob and Alice.
Example:
Diffie-Hellman Problem
The middleman Eve would know (g, p, A, B) since these are public. So for Eve to discover the secret key S, she would have to tackle the following two congruences:
If Eve had some way of solving the discrete logarithm problem (DLP) in a time-efficient manner, she could discover the shared secret key S; no probabilistic polynomial-time algorithm exists that solves this problem. The set of values:
is called the Diffie-Hellman problem.
If the DLP problem can be efficiently solved, then so can the Diffie-Hellman problem.
11 Elliptic Curve Cryptosystems
For simplicity, we shall restrict our attention to elliptic curves over Zp, where p is a prime greater than 3. We mention, however, that elliptic curves can more generally be defined over any finite field [4]. An elliptic curve E over Zp is defined by an equation of the form
(2.1)
where a, b∈Zp, and 4a3+27b2≠0 (mod p), together with a special point O called the point at infinity. The set E(Zp) consists of all points (x, y), x∈Zp, y∈Zp, which satisfy the defining equation (1), together with O.
An Example
Let p=23 and consider the elliptic curve E: y2=x3+x+1, defined over Z23. (In the notation of Equation 24.1, we have a=1 and b=1.) Note that 4a3+27b2=4+4=8≠0, so E is indeed an elliptic curve. The points in E(Z23) are O and the following are shown in Table 2.18.
Table 2.18
| (0, 1) | (6, 4) | (12, 19) |
| (0, 22) | (6, 19) | (13, 7) |
| (1, 7) | (7, 11) | (13, 16) |
| (1, 16) | (7, 12) | (17, 3) |
| (3, 10) | (9, 7) | (17, 20) |
| (3, 13) | (9, 1 6) | (18, 3) |
| (4, 0) | (11, 3) | (18, 20) |
| (5, 4) | (11, 20) | (19, 5) |
| (5, 19) | (12, 4) | (19, 18) |
Addition Formula
There is a rule for adding two points on an elliptic curve E(Zp) to give a third elliptic curve point. Together with this addition operation, the set of points E(Zp) forms a group with O serving as its identity. It is this group that is used in the construction of elliptic curve cryptosystems. The addition rule, which can be explained geometrically, is presented here as a sequence of algebraic formula [4].
2. If P=(x, y)∈ E(Zp) then (x, y)+(x, −y)=O (The point (x, −y) is denoted by −P, and is called the negative of P; observe that −P is indeed a point on the curve.)
3. Let P=(x1,y1)∈E(Zp) and Q=(x2,y2)∈E(Zp), where Ρ≠−Q. Then P+Q=(x3,y3),
where:
We will digress to modular division: 4/3 mod 11. We are looking for a number, say t, such that 3 * t mod 11=4. We need to multiply the left and right sides by 3−1
Next we use the Extended Euclidean algorithm and get (inverse) 3−1 is 4 (3 * 4=12 mod 11=1).
Hence,
Example of Elliptic Curve Addition
Consider the elliptic curve defined in the previous example. (Also see sidebar, “EC Diffie-Hellman Algorithm.”) [4].
1. Let P=(3, 10) and Q=(9, 7). Then P+Q=(x3, y3) is computed as follows:
x3=112−3−9=6−3−9=−6≡17 (mod 23), and y3=11(3−(–6)) −10=11(9) −10=89≡20(mod 23).
Hence P+Q=(17, 20).
2. Let P=(3,10). Then 2P=P+P=(x3, y3) is computed as follows:
x3=62−6=30≡7 (mod 23), and y3=6 (3−7)−10=−24−10=−11∈12 (mod 23).
Hence 2P=(7, 12).
Consider the following elliptic curve with 
Set p=11 and a=1 and b=2. Take a point P (4, 2) and multiply it by 3; the resulting point will be on the curve with (4, 9).
EC Diffie-Hellman Algorithm
1. Alice has her elliptic curve, and she chooses a secret random number d and computes a number on the curve QA=dA*P[4].
Alice’s public key: (p, a, b, QA)
Alice’s private key: dA
2. Bob has his elliptic curve, and he chooses a secret random number d and computes a number on the curve QB=dB * P:
Bob’s public key: (p, a, b, QB)
Bob’s private key: dB
3. Alice computes the shared secret key as
4. Similarly, Bob computes the shared secret key as
5. The shared secret key computed by Alice and Bob are the same for:
EC Security
Suppose Eve the middleman captures (p, a, b, QA, QB). Can Eve figure out the shared secret key without knowing either (dB, dA)? Eve could use
to compute the unknown dA, which is known as the Elliptic Curve Discrete Logarithm problem [4].
12 Message Integrity and Authentication
We live in the Internet age, and a fair number of commercial transactions take place on the Internet. It has often been reported that transactions on the Internet between two parties have been hijacked by a third party, hence data integrity and authentication are critical if ecommerce is to survive and grow.
This section deals with message integrity and authentication. So far we have discussed and shown how to keep a message confidential. But on many occasions we need to make sure that the content of a message has not been changed by a third party, and we need some way of ascertaining whether the message has been tampered with. Since the message is transmitted electronically as a string of ones and zeros, we need a mechanism to make sure that the count of the number of ones and zeros does not become altered, and furthermore, that zeros and ones are not changed in their position within the string.
We create a pair and label it as message and its corresponding message digest. A given block of messages is run through an algorithm hash function, which has its input the message and the output is the compressed message, the message digest, which is a fixed-size block but smaller in length. The receiver, say, Bob, can verify the integrity of the message by running the message through the hash function (the same hash function as used by Alice) and comparing the message digest with the message digest that was sent along with the message by, say, Alice. If the two message digests agree on their block size, the integrity of the message was maintained in the transmission.
Cryptographic Hash Functions
A cryptographic hash function must satisfy three criteria:
Preimage Resistance
Given a message m and the hash function hash, if the hash value h=hash(m) is given, it should be hard to find any m such that h=hash(m).
Second Preimage Resistance (Weak Collision Resistance)
Given input m1, it should be hard to find another message m2 such that hashing)=hash(m2) and that m1≠m2
Strong Collision Resistance
It ought to be hard to find two messages m1≠m2 such that hash(m1)=hash(m2). A hash function takes a fixed size input n-bit string and produces a fixed size output m-bit string such that m less than n in length. The original hash function was defined by Merkle-Damgard, which is an iterated hash function. This hash function first breaks up the original message into fixed-size blocks of size n. Next an initial vector H0 (digest) is set up and combined with the message block M1 to produce message digest H1, which is then combined with M2 to produce message digest H1, and so on until the last message block produces the final message digest.
Message digest MD2, MD4, and MD5 were designed by Ron Rivest. MD5 as input block size of 512 bits and produces a message digest of 128 bits [1].
Secure Hash Algorithm (SHA) was developed by the National Institute of Standards and Technology (NIST). SHA-1, SHA-224, SHA-256, SHA-384, and SHA-512 are examples of the secure hash algorithm. SHA-512 produces a message digest of 512 bits.
Message Authentication
Alice sends a message to Bob. How can Bob be sure that the message originated from Alice and not someone else pretending to be Alice? If you are engaged in a transaction on the Internet using a Web client, you need to make sure that you are not engaged with a dummy Web site or else you could submit your sensitive information to an unauthorized party. Alice in this case needs to demonstrate that she is communicating and not an imposter.
Alice creates a message digest using the message (M), then using the shared secret key (known to Bob only) she combines the key with a message digest and creates a message authentication code (MAC). She then sends the MAC and the message (M) to Bob over an insecure channel. Bob uses the message (M) to create a hash value and then recreates a MAC using the secret shared key and the hash value. Next he compares the received MAC from Alice with his MAC. If the two match, Bob is assured that Alice was indeed the originator of the message [1].
Digital Signature
Message authentication is implemented using the sender’s private key and verified by the receiver using the sender’s public key. Hence if Alice uses her private key, Bob can verify that the message was sent by Alice, since Bob would have to use Alice’s public key to verify. Alice’s public key cannot verify the signature signed by Eve’s private key [1].
Message Integrity Uses a Hash Function in Signing the Message
Nonrepudiation is implemented using a third party that can be trusted by parties that want to exchange messages with one another. For example, Alice creates a signature from her message and sends the message, her identity, Bob’s identity, and the signature to the third party, who then verifies the message using Alice’s public key that the message came from Alice. Next the third party saves a copy of the message with the sender’s and the recipient’s identity and the time stamp of the message.
The third party then creates another signature using its private key from the message that Alice left behind. The third party then sends the message, the new signature, and Alice’s and Bob’s identity to Bob, who then uses the third party’s public key to ascertain that the message came from the third party [1].
RSA Digital Signature Scheme
Alice and Bob are the two parties that are going to exchange the messages. So, we begin with Alice, who will generate her public and private key using two distinct prime numbers—say, p and q. Next she calculates n=p×q. Using Φ(n)=(p−l)(q−1), picks e and computes d such that e×d=1 mod (Φ(n). Alice declares (e, n) public, keeping her private key d secret.
Signing: Alice takes the message and computes the signature as:
She then sends the message M and the signature S to Bob.
Bob receives the message M and the signature S, and then, using Alice’s public key e and the signature S, recreates the message M′=Se (mod n). Next Bob compares M′ with M, and if the two values are congruent, Bob accepts the message [1].
RSA Digital Signature and the Message Digest
Alice and Bob agree on a hash function. Alice applies the hash function to the message M and generates the message digest, D=hash(M). She then signs the message digest using her private key,
Alice sends the signature S and the message M to Bob. He then uses Alice’s public key, and the signature S recreates the message digest D’=Se (mod n) as well as computes the message digest D= hash(M) from the received message M. Bob then compares D with D’, and if they are congruent modulo n, he accepts the message [1].
Next, let’s take a very very brief look at the Triple Data Encryption Algorithm (TDEA), including its primary component cryptographic engine, the Data Encryption Algorithm (DEA). When implemented, TDEA may be used by organizations to protect sensitive unclassified data. Protection of data during transmission or while in storage may be necessary to maintain the confidentiality and integrity of the information represented by the data.
13 Triple Data Encryption Algorithm (TDEA) Block Cipher
TDEA is made available for use by organizations and Federal agencies within the context of a total security program consisting of physical security procedures, good information management practices, and computer system/network access controls. The TDEA block cipher includes a Data Encryption Algorithm (DEA) cryptographic engine that is implemented as a component of TDEA. TDEA functions incorporating the DEA cryptographic engine are designed in such a way that they may be used in a computer system, storage facility, or network to provide cryptographic protection to binary coded data. The method of implementation will depend on the application and environment. TDEA implementations are subject to being tested and validated as accurately performing the transformations specified in the TDEA algorithm.
Applications
Cryptography is utilized in various applications and environments. The specific utilization of encryption and the implementation of TDEA is based on many factors particular to the computer system and its associated components. In general, cryptography is used to protect data while it is being communicated between two points or while it is stored in a medium vulnerable to physical theft or technical intrusion (hacker attacks). In the first case, the key must be available by the sender and receiver simultaneously during communication. In the second case, the key must be maintained and accessible for the duration of the storage period. The following checklist (see checklist: “An Agenda For Action Of Conformance Requirements For The Installation, Configuration And Use Of TDEA”) lays out an agenda for action for conformance to many of the requirements that are the responsibility of entities installing, configuring or using applications or protocols that incorporate the recommended use of TDEA.
14 Summary
In this chapter we have attempted to cover cryptography from its very simple structure such as substitution ciphers to the complex AES and elliptic curve crypto-systems. There is a subject known as cryptoanalysis that attempts to crack the encryption to expose the key, partially or fully. We briefly discussed this in the section on the discrete logarithm problem. Over the past 10 years, we have seen the application of quantum theory to encryption in what is termed quantum cryptology, which is used to transmit the secret key securely over a public channel. The reader will observe that we did not cover the Public Key Infrastructure (PKI) due to lack of space in the chapter.
Finally, let’s move on to the real interactive part of this Chapter: review questions/exercises, hands-on projects, case projects and optional team case project. The answers and/or solutions by chapter can be found in the Online Instructor’s Solutions Manual.
Chapter Review Questions/Exercises
True/False
1. True or False? Data security is limited to wired networks but is equally critical for wireless communications such as in Wi-Fi and cellular.
2. True or False? Data communication normally takes place over a secured channel, as is the case when the Internet provides the pathways for the flow of data.
3. True or False? The encryption of the message can be defined as mapping the message from the domain to its range such that the inverse mapping should recover the original message.
4. True or False? Information security is the goal of the secured data encryption; hence if the encrypted data is truly randomly distributed in the message space (range), to the hacker the encrypted message is equally unlikely to be in any one of the states (encrypted).
5. True or False? Computational complexity deals with problems that could be solved in polynomial time, for a given input.
Multiple Choice
1. The conceptual foundation of _________ was laid out around 3,000 years ago in India and China.
2. In cryptography we use _________ to express that the residue is the same for a set of integers divided by a positive integer.
3. What is a set of integers congruent mod m, where m is a positive integer?
4. _________________also known as additive ciphers, are an example of a monoalphabetic character cipher in which each character is mapped to another character, and a repeated character maps to the same character irrespective of its position in the string:
5. A transposition cipher changes the location of the character by a given set of rules known as:
Exercise
Problem
How is the DEA cryptographic engine used by TDEA to cryptographically protect (encrypt) blocks of data consisting of 64 bits under the control of a 64-bit key?
Hands-On Projects
Project
Please expand on a discussion of how each TDEA forward and inverse cipher operation is a compound operation of the DEA forward and inverse transformations.
Case Projects
Problem
For all TDEA modes of operation, three cryptographic keys (Key1, Key2, Key3) define a TDEA key bundle. The bundle and the individual keys should do what?
Optional Team Case Project
Problem
There are a few keys that are considered weak for the DEA cryptographic engine. The use of weak keys can reduce the effective security afforded by TDEA and should be avoided. Give an example of Keys that are considered to be weak (in hexadecimal format).
References
1. Barr TH. Invitation to Cryptology Prentice Hall 2002.
2. Mao W. Modern Cryptography, Theory & Practice New York: Prentice Hall; 2004.
3. Forouzan BA. Cryptography and Network Security McGraw-Hill 2008.
4. Jurisic A, Menezes AJ. Elliptic curves and cryptograph. Dr Dobb’s Journals April 01, 1997; http://www.ddj.com/architect/184410167.