Advanced Data Encryption
Pramod Pandya, CSU Fullerton
In this chapter we will explore advanced data encryption algorithms. Every engineered system has a flaw, and it is only a matter of time before someone compromises it, thus demanding new innovations by exploring applications from algebraic structures such as groups and rings, elliptic curves, hyperelliptic curves, lattice-based and quantum physics. Over the last 20 years we have witnessed the evolution of classical cryptography into quantum cryptography, a branch of quantum information theory. Quantum cryptography is based on the framework of quantum physics, and it is meant to solve the problem of key distribution, which is an essential component of cryptography that enables securing the data. The key allows the data to be so coded that to decode the data one would need to know the key that was used to code the data. This coding of the given data using the key is known as the encryption, and decoding of the encryption data, which is the reverse stepby-step process, is known as the decryption. Data encryption prevents data from being exposed to unauthorized access and makes it unusable.
Keywords
mathematics; data encryption; cryptography; public-key cryptography; multiplicative group; discrete logarithm; primitive roots; definition group; definition finite; infinite groups
1 Mathematical Concepts Reviewed
In this section we introduce the necessary mathematics of cryptography: Integer and Modular Arithmetic, Fermat’s Theorem [1]:
Euler’s Phi-Function ϕ(n)
Euler’s totient function finds the number of integers that are both smaller than n and coprime to n:
Examples:
![]()
Fermat’s Little Theorem
In the 1970s, the creators of digital signatures and public-key cryptography realized that the framework for their research was already laid out in the body of work by Fermat and Euler. Generation of a key in public-key cryptography, involves an exponentiation modulo in a given modulus:

Theorem: Let p be a prime number:
Theorem: Let p and q be distinct primes:
Discrete Logarithm
In this section we will deal with multiplicative group G=<Zn*, x>. The order of a finite group is the number of elements in the group G. Let us take an example of a group,
![]()
![]()
The order of an element, ord(a), is the smallest integer i such that
![]()
Find the order of all elements in G=<Z10*, x>
Primitive Roots
In the multiplicative group G=<Zn*, x>, when the order of an element is the same as ϕ(n), then that element is called the primitive root of the group.
G=<Z8*, x> has no primitive roots. The order of this group is, ϕ(8)=4
![]()
1, 2, 4 each divide the order of the group which is 4:

In the example above, none of the elements have an order of 4; hence this group has no primitive roots. The group G=<Zn*, x> has primitive roots only if n is 2, 4, pt, or 2pt, where p is an odd prime not including 2 and t is an integer.
If the group G=<Zn*, x> has any primitive roots, the number of primitive roots is ϕ(ϕ(n)). If a group, G=<Zn*, x> has primitive roots, then it is cyclic, and each of its primitive root is a generator of the whole group.
Group G=<Z10*, x> has two primitive roots because ϕ(10)=4, and ϕ(ϕ(10))=2. These two primitive roots are {3, 7}:
![]()
Group, G=<Zp*, x> is always cyclic.
The group G=<Zp*, x> has the following properties:
1. Its elements are from 1 to (p−1) inclusive.
2. It always has primitive roots.
3. It is cyclic, and its elements can be generated using g where x is an integer from 1 to ϕ(n)=p−1.
4. The primitive roots can be used as the base of logarithm—discrete logarithm.
Modern encryption algorithms such as DES, AES, RSA, and ElGammal to name a few are based on algebraic structures such as Group Theory and Field Theory as well as Number Theory. We will begin with a set S, with finite number of elements, and a binary operation (*) defined between any two elements of the set:
![]()
that is, if a and b∈S, then a*b∈S. This is important, for it implies that the set is closed under the binary operation. We have seen that the message space is finite, and we want to make sure that any algebraic operation on the message space satisfies the closure property. Hence, we want to treat the message space as a finite set of elements. We will remind the reader that messages that get encrypted must be finally decrypted by the received party; thus encryption algorithm must run in polynomial time. Furthermore, the algorithm must have the property that it be reversible to recover the original message. The goal of encryption is to confuse and diffuse the hacker such that it would make it almost impossible for the hacker to break the encrypted message. Therefore, encryption must consist of finite number substitutions and transpositions. The algebraic structure, Classical Group, facilitates the coding of the encryption algorithm. Next we give some relevant definitions and examples before we proceed to introduce the essential concept of a Galois Field, which is central to formulation of the Rijndael algorithm used in the Advanced Encryption Standard (AES).
Definition Group
A group (G, •) is a finite set G together with an operation • satisfying the following conditions:
Definition of Finite and Infinite Groups (Order of a Group)
A group G is said to be finite if the number of elements in the set G is finite. Otherwise, the group is infinite.
Definition of Abelian Group
A group G is abelian if for all a, b∈G, a•b=b•a
The reader should note that in a group, the elements in the set do not have to be a number or objects: They can be mappings, functions, or rules.
Examples of a Group
The set of integers Z is a group under addition (+); that is, (Z, +) is a group with identity e=0, and the inverse of an element a is (−a). This is an additive abelian group, but infinite.
Nonzero elements of Q (rationals), R (reals), and C (complex) form a group under multiplication, with the identity element e=1, and a−1 being the multiplicative inverse. For any n≥1, the set of integers modulo n forms a finite additive group of n elements:
The set of Zn* with multiplication operator, G=<Zn*, x>is also an abelian group. The set Zn*, is a subset of Zn and includes only integers in Zn that have a unique multiplicative inverse:
![]()
Definition Subgroup
A subgroup of a group G is a nonempty subset H of G, which itself is a group under the same operations as that of G. We denote that H is a subgroup of G as H⊆G, and H⊂G is a proper subgroup of G if the set H≠G. Examples of Subgroups:
Under addition, Z⊆Q⊆R⊆C.
H=<Z10, +> is a proper subgroup of G=<Z12, +>
Definition of Cyclic Group
A group G is said to be cyclic if there exists an element a∈G such that for any b∈G, and i≥0, b=ai. Element a is called a generator of G. The group G=<Z10*, x>is a cyclic group with generators g=3 and g=7:
![]()
The group G=<Z6, +> is a cyclic group with generators g=1 and g=5:
![]()
Rings
Let R be a nonempty set with two binary operations: addition (+) and multiplication (*).
Then R is called a ring if the following axioms are met:
1. Under addition, R is an abelian group with zero as the additive identity.
2. Under multiplication, R satisfies the closure, associative, and identity axiom. 1 is the multiplicative identity, and that 1≠0.
3. For every a, and b that belongs to R, a•b=b•a.
4. For every a, b, and c that belongs to R, then a•(b+c)=a•b+a•c
Examples
Z, Q, R, and C are all rings under addition and multiplication. For any n>0, Zn is a ring under addition and multiplication modulo n with 0 as identity under addition, 1 under multiplication.
Definition Field
If the nonzero elements of a ring form a group under multiplication, then the ring is called a field.
Examples
Q, R, and C are all fields under addition and multiplication, with 0 and 1 as identity under addition and multiplication.
[Note that Z under integer addition and multiplication is not a field because any nonzero element does not have a multiplicative inverse in Z.]
Finite Fields GF(2n)
Construction of finite fields and computations in finite fields are based on polynomial computations. Finite fields play a significant role in cryptography and cryptographic protocols such as the Diffie and Hellman key exchange protocol, ElGamal cryptosystems, and Advanced Encryption Standard (AES):
For a prime number p, the quotient Z/p (or Fp) is a finite field with p number of elements. For any positive integer q, GF(q)=Fq
We define A to be algebraic structure such as a ring or a group or a field.
Definition
A polynomial over A is an expression of the form:
![]()
where, n is a nonnegative integer, the coefficient ai∈A, 0≤ i≤n, and x∉A.
Definition
A polynomial f∈A[x] is said to be irreducible in A[x] if f has a positive degree and f=gh for some g, h∈A[x] implies that either g or h is a constant polynomial. The reader should be aware that a given polynomial can be reducible over one structure, but irreducible over another.
Definition
Let f, g, q, and r∈A[x] with g≠0. Then we say that r is remainder of f divided by g:
![]()
The set of remainders of all the polynomials in A[x](mod g) denoted as A[x]g.
Theorem
Let F be a field and f be a non-zero polynomial in F[x]. Then F[x]f is a ring, and is a field iff f is irreducible over F.
Theorem
Let F be field of p elements and f be irreducible polynomial over F. Then the number of elements in the field F[x]f is pn.
For every prime p and every positive integer n there exist a finite field of pn number of elements. For any prime number p, Zp is a finite field under addition and multiplication modulo p, with 0 and 1 as the identity under addition and multiplication.
Zp is an additive ring and nonzero elements of Zp, denoted by Zp* form a multiplicative group. Galois Field, GF(pn) is a finite field with number of elements pn, where p is a prime number and n is a positive integer.
Example
Integer representation of Finite Field (Rijnadel) element. Polynomial f(x)=x8+x4+x3+x+1 is irreducible over F2.
The set of all polynomials (mod f) over F2 forms a field of 28 elements; they are all polynomials over F2 of degree less than 8. So any element in the field F2[x]f
![]()
where, ![]() Thus any element in this field can represent a 8-bit binary number.
Thus any element in this field can represent a 8-bit binary number.
Data inside a computer is organized in bytes (8 bits) and is processed using Boolean logic; that is, bits are manipulated using binary operation addition and multiplication. These binary operations are implemented using the logical operator XOR, or in the language of finite fields, GF(2). Since the extended ASCII defines 8-bit per byte, an 8-bit byte has a natural representation using a polynomial of degree 8. Polynomial addition would be mod 2, and multiplication would be mod polynomial degree 8. Of course this polynomial degree 8 would have to be irreducible. Hence the Galois Field GF(28) would be the most natural tool to implement the encryption algorithm. Furthermore, this would provide a close algebraic formulation. Consider polynomials over GF(2) with p=2 and n=1:
![]()
Polynomials with negative coefficients, −1 is the same as +1 in GF(2). Obviously, the number of such polynomials is infinite. In algebraic operations of addition and multiplication, the coefficients are added and multiplied according to the rules that apply to GF(2). The set of such polynomials forms a ring.
Modular Polynomial Arithmetic over GF(2)
The Galois Field GF(23): Construct this field with eight elements that can be represented by polynomials of the form:
![]()
Two choices for a, b, c gives 2×2×2=8 polynomials of the form:
![]()
What is our choice of the irreducible polynomials for this field?
![]()
These two polynomials have no factors: (x3+x2+1), (x3+x+1). So we choose polynomial (x3+x+1). Hence all polynomial arithmetic multiplication and division is carried out with respect to (x3+x+1). The eight polynomials that belong to GF(23):
![]()
You will observe that GF(8)={0,1,2,3,4,5,6,7} is not a field, since every element (excluding zero) does not have a multiplicative inverse such as {2, 4, 6) (mod 8).
Using a Generator to Represent the Elements of GF(2n)
It is particularly convenient to represent the elements of a Galois Field with the help of a generator element. If α is a generator element, then every element of GF(2n), except for the 0 element, can be written down as some power of α. A generator is obtained from the irreducible polynomial that was used to construct a finite field. If f(α) is the irreducible polynomial used, then α is that element that satisfies the equation f(α)=0. You do not actually solve this equation for its roots since an irreducible polynomial cannot have actual roots in the field GF(2). Consider the case of GF(23) defined with the irreducible polynomial x3+x+1. The generator α is that element which satisfies α3+α+1=0:
Suppose α is a root in GF(23) of the polynomial p(x)=1+x+x3
All powers of α generate nonzero elements of GF8.
We will now consider all polynomials defined over GF(2), modulo the irreducible polynomial x3+x+1. When an algebraic operation (polynomial multiplication) results in a polynomial whose degree equals or exceeds that of the irreducible polynomial, we will take for our result the remainder modulo the irreducible polynomial. For example,

Recall that 1+1=0 in GF(2). With multiplications modulo (x3+x+1), we have only the following eight polynomials in the set of polynomials over GF(2):
![]()
We will refer to this set as GF(23) where the power of 2 is the degree of the modulus polynomial. The eight elements of Z8 are to be integers modulo 8. Similarly, GF(23) maps all of the polynomials over GF(2) to the eight polynomials shown above. But you will note that the crucial difference between GF(23) and 23: GF(23) is a field, whereas Z8 is NOT.
GF(23) is a Finite Field
We know that GF(23) is an Abelian group because the operation of polynomial addition satisfies all of the requirements on a group operator and because polynomial addition is commutative. GF(23) is also a commutative ring because polynomial multiplication is a distributive over polynomial addition. GF(23) is a finite field because it is a finite set and because it contains a unique multiplicative inverse for every nonzero element.
GF(2n) is a finite field for every n. To find all the polynomials in GF(2n), we need an irreducible polynomial of degree n. In general, GF(pn) is a finite field for any prime p. The elements of GF(pn) are polynomials over GF(p) (which is the same as the set of residues Zp). Next we show how the multiplicative inverse of a polynomial is calculated using the Extended Euclidean Algorithm:
2 The RSA Cryptosystem
Now that we have reviewed the necessary mathematical preliminaries, we will focus on the subject matter of Asymmetric Cryptography, which uses a public and a private key to encrypt and decrypt the plaintext. If Alice wants to send plaintext to Bob, then she will use Bob’s public key, which is advertised by Bob, to encrypt the plaintext, and then send it to Bob via an insecured channel. Bob would decrypt the data using his private key, which is known to him only. Of course, this would appear to be an ideal replacement for Symmetric-key cipher, but it is much slower since it has to encrypt each byte; hence it is useful in message authentication and communicating the secret key. See the following Key Generation Algorithm:
1. Select two prime numbers p and q such that p≠q.
3. Set up a commutative ring R=<Zm,+,x> which is public since m is made public.
4. Set up a multiplicative group ![]() which is used to generate public and private keys. This group is hidden from the public since ϕ(m) is kept hidden.
which is used to generate public and private keys. This group is hidden from the public since ϕ(m) is kept hidden.
6. Choose an integer e such that 1<e<ϕ(m) and e is coprime to ϕ(m).
7. Compute the secret exponent d such that, 1<d<ϕ(m) and that ed≡1 (mod ϕ(m)).
Encryption:
1. Alice obtains Bob’s public key (m, e).
2. The plaintext x is treated as a number to lie in the range 1<x<m−1.
Decryption:
Why RSA works
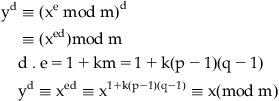
Example:
Choose p=7 and q=11, then m=p×q=7×11=77
R=<Z77,+, x> and ϕ(77)=ϕ(7) ϕ(11)=6×10=60
The corresponding multiplicative group ![]()
Choose e=13 and d=37 from ![]() such that e×d≡1 (mod 60)
such that e×d≡1 (mod 60)
Plaintext=5 y=xe (mod m)=513 (mod 77)=26
Note: 384-bit primes or larger are deemed sufficient to use RSA securely. The prime number e=216+1 is often used in modern RSA implementations.
Factorization Attack
The RSA algorithm relies on the fact that p and q are the distinct prime numbers; and, must be kept secret, even though m = p x q is made public. So if n is an extremely large number, then the problem reduces to finding the factors that make up the number n, which is known as the factorization attack. If the middle man, Eve, can factor n correctly, then she guesses correctly p, q, and ϕ(m). Remind yourselves that if the public key e is public, then Eve has to compute the multiplicative inverse of e:
![]()
So if the modulus m is chosen to be 1024 bits long, then it would take considerable time to break the RSA system unless an efficient factorization algorithm could be found [1][2].
Chosen-Ciphertext Attack
Zn is a set of all positive integers from 0 to (n−1).
![]() is a set all integers such that gcd(n,a)=1, where
is a set all integers such that gcd(n,a)=1, where ![]()
![]()
Φ(n) calculates the number of elements in ![]() that are smaller than n and coprime to n.
that are smaller than n and coprime to n.
![]()
Therefore the number of integers in∈Z21* is 12.
![]()
![]()
![]()
Example:
Choose p=3 and q=7, then m=3×7=21,
Encryption and decryption take place in the ring, R=<Z21, +, x>.
![]()
Key-Generation Group, ![]()
![]()
![]()
Alice encrypts the message P using the public key e of Bob and sends the encrypted message C to Bob:
![]()
Eve the middle man intercepts the message and manipulates the message before forwarding to Bob:
1. Eve chooses a random integer X∈Zm* (since m is public).
2. Eve calculates Y=C x Xe (mod m).
3. Bob receives Y from Eve, and he decrypts Y using his private key d.
5. Eve can easily discover the plaintext P as follows:
Z=Yd (mod m)=[C x Xe]d (mod m)=[Cd x Xed] (mod m)=[Cd x X] (mod m)
Hence Z=[P x X] (mod m)
Eve, using the Extended Euclidean Algorithm, can then compute the multiplicative inverse of X and thus obtain P:
The eth Roots Problem
Given:
Discrete Logarithm Problem
Discrete logarithms are perhaps simplest to understand in the group Zp*, where p is the prime number. Let g be the generator of Zp*; then the discrete logarithm problem reduces to computing a, given (g, p, ga mod p) for a randomly chosen a<(p−1).
If we want to find the kth power of one of the numbers in this group, we can do so by finding its kth power as an integer and then finding the remainder after division by p. This process is called discrete exponentiation. For example, consider Z23*
To compute 34 in this group, we first compute 34=81, and then we divide 81 by 23, obtaining a remainder of 12. Thus 34=12 in the group Z23*
Discrete logarithm is just the inverse operation. For example, take the equation 3k≡12 (mod 23) for k. As shown above k=4 is a solution, but it is not the only solution. Since 322≡1 (mod 23), it also follows that if n is an integer then 34+22n≡12×1n≡12 (mod 23). Hence the equation has infinitely many solutions of the form 4+22n. Since 22 is the smallest positive integer m satisfying 3m≡1 (mod 23), that is, 22 is the order of 3 in Z23*, these are all solutions. Equivalently, the solution can be expressed as k≡4 (mod 22) [1].
In designing public-key cryptosystems, two problems dominate the designs: the integer factorization problem and the discrete logarithm problem. Large instances of these problems are still intractable today.
Discrete logarithms have a natural extension into the realm of elliptic curves and hyperelliptic curves. And Elliptic ElGamal has proved to be a strong cryptosystem using elliptic curves and discrete logarithms. In the next part of the chapter, we will take a look at the discrete logarithm problem and discuss its application to cryptography.
Discrete Logarithm Problem (DLP)
The discrete logarithm problem in group G, given some generator α of a cyclic subgroup G* of G and an element β∈G*, is to find the element x, 0≤x≤(p−2), such that αx=β. The most frequently used cryptosystem utilizing the DLP is ElGamal; we give an elliptic curve variant of ElGamal below [1–3]. For example:
ElGamal Cryptosystem:
Alice wants to talk secretly with Bob.
Setting up: Sometime in the past, Bob has created his keys in the following way:
1. Bob chooses a random large prime p and a generator α of the multiplicative group ![]()
2. Bob chooses a random integer a where 1≤a≤(p−2).
4. The triple eB=(p, α, αa) is the public key, and dB (p, α, a) is the private key.
Alice obtains Bob’s public key from some public key server.
Encryption: Alice wants to encrypt a plaintext M with the cipher eB=(e, d, n). She starts by choosing a random integer k where 1≤k≤(p−2) and then encrypting the plaintext M into the cipher-text C:
![]()
Alice then sends Bob the encrypted message C.
Decryption: Bob then decrypts the cipher-text C=(γ, δ) with the cipher
dB=(e, d, n) in the following manner:
![]()
Lattice-based Cryptography—NTRU
An n-dimensional lattice (see Figure 15.1) is generated using n-linearly independent vectors:
v1,……, vn ε Rn; these vectors are known as the basis of the lattice. There are infinite numbers of such bases that can generate the same lattice.

In group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. A lattice is the symmetry group of discrete translational symmetry in n directions. Two NP-hard problems related to lattices are the shortest vector problem (SVP) and the closest vector problem (CVP; see Figure 15.2). Given an arbitrary basis for a lattice, find the SVP in the lattice or find the CVP to an arbitrary nonlattice vector. In both the quantum and classical computational problems, these problems are hard to solve for high-dimensional lattices (see Figure 15.3). There are a number of lattice-based cryptographic schemes, but the NTRU-based cryptographic algorithm appears to be most practical [4,5].
NTRU Cryptosystem
NTRU is not based on factorization or discrete logarithmic problems. Rather, it is a lattice-based alternative to RSA and ECC and is based on the shortest vector problem in a lattice. NTRU was founded in 1996 by three mathematicians: Jeffrey Hoffstein, Joseph H. Silverman, and Jill Pipher. Later on with the addition of yet another member, Daniel Lieman, to the team, NTRU Cryptosystems was incorporated in Boston. NTRU Cryptosystems was acquired by Security Innovation in 2009.
The NTRU cryptosystem was introduced at the rump session of Crypto’96 and was later published in the proceedings of the ANTS-III conference. NTRU is a ring-based public-key cryptosystem and is therefore quite different from the group-based cryptosystems whose security relies on the integer factorization problem or the discrete logarithm problem. This extra structure can be exploited to obtain a very fast cryptosystem: To encrypt/decrypt a message block of length N, NTRU only requires O(N2) time, whereas the group-based schemes require O(N3) time. Furthermore, NTRU also has a very short key size of O(N) and very low memory requirements, which makes it ideal for constrained devices such as smart cards.
Truncated Polynomial Rings
Consider a polynomial of degree (N−1) having integer coefficients:
![]()
The set of all such polynomials is denoted by R. The arithmetic on the polynomials in R is as follows. Consider two polynomials a and b:
![]()
Suppose N=3 and a=2−X+3X2, b=1+2X−X2
![]()
N=3; hence the polynomial cannot have powers of X more than 2, so we have to truncate powers of X higher than 2 with the following rules:
![]()
![]()
Hence,
![]()
The distributive law also holds for the polynomials
![]()
The inclusion of the above law makes the algebraic structure of polynomials into a ring, the Ring of Truncated Polynomials. This ring R is isomorphic to the quotient ring, Z[X]/(X(N−1)).
Inverses in Truncated Polynomial Ring
The inverse modulo q of a polynomial a is a polynomial a−1 with the property:
![]()
Example:
![]()
![]()
then,
![]()
NTRU Parameters and Keys
N—a polynomial in the ring R with degree N−1, with N being a prime number:
Q—a large modulus to which the coefficient is reduced
P—a small modulus to which each coefficient is reduced
f—a polynomial that is a private key
g—a polynomial that is used to generate the public key h from f
NOTE: g (secret) is discarded later on.
H—a polynomial that is a public key
r—a random binding polynomial (discarded later on, but kept secret.
Key Generation
Consider a truncated polynomial ring with a degree at most N−1:
![]()
1 Choose two small polynomials f and g in the ring R; polynomial f must have an inverse.
2 The inverse of f modulo q and the inverse of f modulo p are computed.
3 Fq=f−1(mod q) and Fp=f−1(mod p)
4 f*Fq=1(mod q) and f*Fp=1(mod p)
6 Alice’s private key: a pair of polynomials f and Fp
Alice chooses: ![]()
![]()
![]()
Private Key
![]()
Public Key
![]()
NTRU Encryption
Alice has a message to transmit:
1. Puts the message in the form of polynomial m whose coefficient is chosen modulo p between −p/2 and p/2 (centered lift).
2. Randomly chooses another small polynomial r (to obscure the message).
![]()
Example of NTRU Encryption
Alice decides to send Bob the message:
![]()
using the random key ![]()
![]()
![]()
![]()
NTRU Decryption
Bob receives a message e from Alice and would like to decrypt it.
Using his private polynomial f, he computes a polynomial
![]()
Bob needs to choose coefficients that lie in an interval of length q. He computes the polynomial b=a(mod p). Bob reduces each of the coefficients of a modulo p. Bob uses the other private polynomial Fp to compute c=Fp*b(modulo p), which is the original message of Alice.
Why Does NTRU Work?
![]()
![]()
![]()
Underlying every public-key cryptosystem lurks an extremely difficult mathematical problem waiting to be solved. There is no direct proof that breaking a cryptosystem is equivalent to solving the mathematical problem. Below we list the public-key cryptosystem and the corresponding mathematical problem.
3 Summary
In this chapter, we reviewed aspects of advanced data encryption security: number theory, group theory, and finite fields relevant to public-key cryptography, as well as advanced data encryption security features (see checklist: An Agenda for Action for Implementing Advanced Data Encryption Security Features). The security of public-key cryptography is determined by what is known as the discrete logarithm problem (DLP), and we gave an example of DLP based on the elliptic curve. In the final section of this chapter, we presented public-key cryptography based on lattice theory—known as the NTRU cryptosystem.
Finally, let’s move on to the real interactive part of this chapter: review questions/exercises, hands-on projects, case projects, and optional team case project. The answers and/or solutions by chapter can be found in the Online Instructor’s Solutions Manual.
Chapter Review Questions/Exercises
True/False
1. True or False? Generation of a key in public-key cryptography involves exponentiation modulo a given modulus.
2. True or False? The order of a finite group is the number of elements in the group H.
3. True or False? In the multiplicative group, H=<Zn*, x>; when the order of an element is the same as ϕ(n), then that element is called the primitive root of the group.
4. True or False? A group H is said to be finite if the number of elements in the set H is finite.
5. True or False? The set of integers Z is a group under addition (+); that is (Z, +) is a group with identity e=0, and inverse of an element a is (−a).
Multiple Choice
1. A subgroup of a group G is a nonempty subset H of G, which itself is a group under the same operations as that of:
2. What group is said to be cyclic if there exists an element a∈G such that for any b∈G, and i≥0, b=ai?
3. Let _________ be a nonempty set with two binary operations addition (+), and multiplication (*).
4. If the nonzero elements of a ring form a group under multiplication, then the ring is called a:
5. Construction of finite fields and computations in finite fields are based on:
Exercise
Problem
How does advanced data encryption work?
Hands-On Projects
Project
What is a key?
Case Projects
Problem
What is the difference between public and private keys?
Optional Team Case Project
Problem
Which types of data can be encrypted.
References
1. Mao W. Modern Cryptography, Theory & Practice Prentice Hall 2004.
2. Forouzan BA. Cryptography and Network Security McGraw-Hill 2008.
3. Jensen PL. Hyperelliptic Curves and Their Application to Cryptography University of Copenhagen 2004.
4. J. Hoffstein, D. Lieman, J. Pipher, J. Silverman, “NTRU”: A Public Key Cyrptosystem, NTRU Cryptosystems, Inc. <www.ntru.com>.
5. J. Hoffstein, J. Pipher, J. Silverman, NTRU—A Ring Based Public Key Cryptosystem.




