CHAPTER 8
Stacks and Queues
In this chapter we introduce two more abstract data types: stacks and queues. Stacks and queues can be modified in only a very limited way, so there are straightforward implementations, that is, data structures, of the corresponding data types. Best of all, stacks and queues have a wide variety of applications. We'll start with stacks because a stack is somewhat easier to implement than a queue.
CHAPTER OBJECTIVES
- Understand the defining properties of stacks and queues, and how these properties are violated by the Java Collections Framework's stack class and Queue interface.
- For both stacks and queues, be able to develop contiguous and linked implementations that do not violate their defining properties.
- Explore the use of stacks in the implementation of recursion and in converting from infix notation to postfix notation.
- Examine the role of queues in computer simulation.
8.1 Stacks
A stack is a finite sequence of elements in which the only element that can be removed is the element that was most recently inserted. That element is referred to as the top element on the stack.
For example, a tray-holder in a cafeteria holds a stack of trays. Insertions and deletions are made only at the top. To put it another way, the tray that was most recently put on the holder will be the next one to be removed. This defining property of stacks is sometimes called "Last In, First Out," or LIFO. In keeping with this view, an insertion is referred to as a push, and a removal as a pop. For the sake of all iteration, a retrieval of the top element is referred to as a peek.
Figure 8.1a shows a stack with three elements and Figures 8.1b, c and d show the effect of two pops and then a push.
In Section 8.1.1, we define the stack class, and note its assets and liabilities.
8.1.1 The Stack Class
The Java Collection Framework's stack class is a legacy class: It was created even before there was a Java Collections Framework. It is a subclass of another legacy class, Vector, which was retrofitted to implement the List interface. In fact, the Vector class is virtually equivalent to the ArrayList class that we studied in Chapter 6.
The stack class's essential methods—push, pop, and peek—were easily defined once the developers decided whether the top of the stack should be at the front or back of the underlying array. Which do you think would be faster for the pop and push methods? For removing the front element in an array, worstTime(n) and averageTime(n) are both linear in n, whereas removing the last element in an array takes only constant time in both the worst and average cases. For inserting at the front of an array, worstTime(n) and averageTime(n) are both linear in n, whereas inserting at the back of an array takes only constant time on average, but linear-in-n time in the worst case (when the array is full). So it is clearly faster for the top element to be at the back of the underlying array. See Figure 8.2.
FIGURE 8.1 A stack through several stages of pops and pushes: 17 and 13 are popped and then 21 is pushed. In each figure, the highest element is the top element

Here are the Stack class's heading and method specifications for the only constructor and the push, pop and peek methods1:
public class Stack<E> extends Vector<E> /** * Creates an empty Stack. */ public Stack() /** * Pushes an element onto the top of this stack. * The worstTime(n) is O(n) and averageTime(n) is constant. * * @param element: the element to be pushed onto this stack. * @return the element argument. */ public E push (E element) /** * Removes the element at the top of this stack and returns that * element. * The worstTime(n) and averageTime(n) are constant. * * @return the element at the top of this stack. * @throws EmptyStackException if this stack is empty. */ public E pop() /** * Returns the element at the top of this stack without removing it * from the stack.
FIGURE 8.2 The effect of three pushes and a pop on the underlying array of an instance of the Java Collection Framework's stack class. The stack class's constructor automatically creates an array of length 10

The worstTime(n) and averageTime(n) are constant.
* @return the element at the top of this stack.
* @throws EmptyStackException if this stack is empty.
*/
public E peek()
The following program utilizes each of the above methods, as well as several List methods you saw in Chapters 6 and 7.
import java.util.*; public class StackExample { public static void main (String[] args) { new StackExample().run(); } // method main public void run() { Stack<Character> myStack = new Stack<Character>(); System.out.println ("push " + myStack.push ('a')); System.out.println ("push " + myStack.push ('b')); System.out.println ("push " + myStack.push ('c')); System.out.println ("pop " + myStack.pop()); System.out.println ("top = " + myStack.peek()); System.out.println ("push " + myStack.push ('d')); System.out.println ("The stack now has " + myStack.size() + " elements."); System.out.println (" Here are the contents of the stack, from top to bottom:"); for (int i = myStack.size() - 1; i >= 0; i-) System.out.println (myStack.get (i)); System.out.println (" Here are the contents of the stack, starting from index 0:"); for (Character c : myStack) System.out.println (c); System.out.println ( " Here are the contents of the stack, from top to bottom, during destruction:"); while (!myStack.isEmpty()) System.out.println (myStack.pop()); System.out.println ("The stack now has " + myStack.size() + " elements."); } // method run } // class StackExample
And here is the corresponding output:
push a push b push c pop c top=b push d The stack now has 3 elements. Here are the contents of the stack, from top to bottom: d b a Here are the contents of the stack, starting at index 0: a b d
Here are the contents of the stack, from top to bottom, during destruction: d b a The stack now has 0 elements.
The first iteration in the above program uses a list index and the get method to access each element, starting at the top of the stack. The second iteration illustrates a curious feature of the stack class: The standard iteration—with an enhanced for statement—accesses the elements starting from the bottom of the stack! The same bottom-up access would apply if you called
system.out.println (mystack);
The third iteration represents destructive access: the top element is repeatedly popped and printed until the stack is empty.
8.1.2 A Fatal Flaw?
The stack class is part of the Java Collections Framework, so that class is always available to you whenever you use the Java language. And the fact that the stack class implements the List interface can occasionally come in handy. For example, as in the above program, you can access each of the elements without removing them, and each access (or modification) takes constant time. Unfortunately, you can also remove an element other than the element that was most recently inserted, and this violates the definition of a stack. For example, you can have the following:
Stack<String> badstack = new Stack<String>();
badstack.push ("Larry");
badstack.push ("Curly");
badstack.push ("Moe");
badstack.remove (1); // removes Curly
We will let the convenience of the stack class override our disapproval of the just noted defect. But if you regard the violation as a fatal flaw, you have (at least) two options, one utilizing inheritance and one utilizing aggregation. For the first option, you can undertake Programming Project 8.4, and create a PureStack class that extends Stack, but throws UnsupportedOperationException for any attempt to remove an element that is not at the top of the stack. And the iterator goes from top to bottom, instead of from bottom to top. This is, essentially, the approach used for the stack class in C#, a member of Microsoft's. NET family of languages.
Another option for a PureStack class is to allow access, modification or removal only of the most recently inserted element. This stringency would allow only a few methods: a default constructor, a copy constructor (so you can non-destructively access a copy of a stack, instead of the original), push, pop, peek, size, and isEmpty. This is the idea behind the stack class in C++, a widely used language. A straightforward way to create such a PureStack class is with aggregation: the only field is a list whose type is ArrayList or LinkedList. For example, the definition of the pop method—in either implementation—is as follows:
public E pop() { return list.remove (list.size() - 1); } // method pop
In fact, all the definitions—in either implementation—are one-liners. See Programming Exercise 8.1 for an opportunity to develop the LinkedList implementation, and Programming Exercise 8.2 for the ArrayList implementation.
Now let's look at a couple of important applications.
8.1.3 Stack Application 1: How Compilers Implement Recursion
We saw several examples of recursive methods in Chapter 5. In adherence to the Principle of Abstraction, we focused on what recursion did and ignored the question of how recursion is implemented by a compiler or interpreter. It turns out that the visual aids—execution frames—are closely related to this implementation. We now outline how a stack is utilized in implementing recursion and the time-space implications for methods, especially recursive methods.
Each time a method call occurs, whether it is a recursive method or not, the return address in the calling method is saved. This information is saved so the computer will know where to resume execution in the calling method after the execution of the called method has been completed. Also, the values of the called method's local variables must be saved. This is done to prevent the destruction of that information in the event that the method is—directly or indirectly—recursive. As we noted in Chapter 5, the compiler saves this method information for all methods, not just the recursive ones (this relieves the compiler of the burden of determining if a given method is indirectly recursive). This information is collectively referred to as an activation record or stack frame.
Each activation record includes:
- the return address, that is, the address of the statement that will be executed when the call has been completed;
- the value of each argument: a copy of the corresponding argument is made (if the type of the argument is reference-to-object, the reference is copied);
- the values of the called method's other local variables;
Part of main memory—the stack—is allocated for a run-time stack onto which an activation record is pushed when a method is called and from which an activation record is popped when the execution of the method has been completed. During the execution of that method, the top activation record contains the current state of the method. For methods that return a value, that value—either a primitive value or a reference—is pushed onto the top of the stack just before there is a return to the calling method.
How does an activation record compare to an execution frame? Both contain values, but an activation record has no code. Of course, the entire method, in bytecode, is available at run-time. So there is no need for a checkmark to indicate the method that is currently executing.
For a simple example of activation records and the run-time stack, let's trace the execution of a getBinary method that invokes the getBin method from Chapter 5. The return addresses have been commented as RA1 and RA2.
/** * * Determines the binary equivalent of a non-negative integer. The worstTime(n) * is O(log n). * * @param n the non-negative integer, in decimal notation. * * @return a String representation of the binary equivalent of n. * * @throws IllegalArgumentException if n is negative. */ public static String getBinary (int n) { if (n < 0) throw new IllegalArgumentException(); return getBin (n); // RA1 } // method getBinary public static String getBin (int n) { if (n <= 1) return Integer.toString (n); return getBin (n / 2) + Integer.toString (n % 2); // RA2 } // method getBin
The getBin method has the formal parameter n as its only local variable, and so each activation record will have two components:
- the return address;
- the value of the formal parameter n.
Also, because the getBin method returns a string reference, a copy of that string reference is pushed onto the stack just before a return is made. For simplicity, we will pretend that the string object itself is pushed.
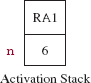
Assume that the value of n is 6. When getBin is called from the getBinary method, an activation record is created and pushed onto the stack, as shown in Figure 8.3.
FIGURE 8.3 The activation stack just prior to getBin's first activation. RA1 is the return address
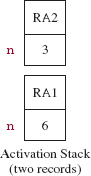
Since n > 1, getBin is called recursively with 3 (that is, 6/2) as the value of the argument. A second activation record is created and pushed onto the stack. See Figure 8.4.
FIGURE 8.4 The activation stack just prior to the second activation of getBin
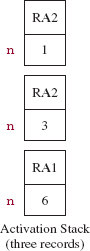
Since n is still greater than 1, getBin is called again, this time with 1 (that is, 3/2) as the value of the argument. A third activation record is created and pushed. See Figure 8.5.
FIGURE 8.5 The activation stack just prior to the third activation of getBin
Since n ≤ 1, the top activation record is popped, the String "1" is pushed onto the top of the stack and a return is made to the address RA2. The resulting stack is shown in Figure 8.6.
The concatenation at RA2 in getBin is executed, yielding the String "1" + Integer.toString (3 % 2), namely, "11". The top activation record on the stack is popped, the String "11" is pushed, and another return to RA2 is made, as shown in Figure 8.7.
FIGURE 8.6 The activation stack just after the completion of the third activation of getBin

FIGURE 8.7 The activation stack just after the completion of the second activation of getBin
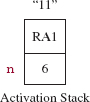
The concatenation at RA2 is "11" + Integer.toString (6 % 2), and the value of that String object is "110". The stack is popped once more, leaving it empty, and "110", the binary equivalent of 6, is pushed. Then a return to RA1—at the end of the getBinary method—is made.
The above discussion should give you a general idea of how recursion is implemented by the compiler. The same stack is used for all method calls. And so the size of each activation record must be saved with each method call. Then the correct number of bytes can be popped. For the sake of simplicity, we have ignored the size of each activation record in the above discussion.
The compiler must generate code for the creation and maintenance, at run time, of the activation stack. Each time a call is made, the entire local environment must be saved. In most cases, this overhead pales to insignificance relative to the cost in programmer time of converting to an iterative version, but this conversion is always feasible.
On those rare occasions when you must convert a recursive method to an iterative method, one option is to simulate the recursive method with an iterative method that creates and maintains its own stack of information to be saved. For example, Project 8.3 requires an iterative version of the (recursive) tryToReachGoal method in the backtracking application from Chapter 5. When you create your own stack, you get to decide what is saved. For example, if the recursive version of the method contains a single recursive call, you need not save the return address. Here is an iterative, stack-based version of the getBinary method (see Programming Exercise 5.1 for an iterative version that is not stack-based, and see Programming Exercise 8.3 for a related exercise).
/** * * Determines the binary equivalent of a non-negative integer. The worstTime(n) * is O(log n). * * @param n the non-negative integer, in decimal notation. * * @return a String representation of the binary equivalent of n. * * @throws IllegalArgumentException if n is negative. */ public static String getBinary (int n) { Stack<Integer> myStack = new Stack<Integer>(); String binary = new String(); if (n < 0) throw new IllegalArgumentException( ); myStack.push (n % 2); while (n > 1) { n /= 2; myStack.push (n % 2); } // pushing while (!myStack.isEmpty()) binary += myStack.pop(); return binary; } // method getBinary
What is most important is that you not overlook the cost, in terms of programmer time, of making the conversion from a recursive method to an iterative method. Some recursive methods, such as the factorial method, can easily be converted to iterative methods. Sometimes the conversion is nontrivial, such as for the move and tryToReachGoal methods of Chapter 5 and the permute method of Lab 9. Furthermore, the iterative version may well lack the simple elegance of the recursive version, and this may complicate maintenance.
You certainly should continue to design recursive methods when circumstances warrant. That is, whenever the problem is such that complex instances of the problem can be reduced to simpler instances of the same form, and the simplest instance(s) can be solved directly. The above discussion on the activation stack enables you to make better-informed tradeoff decisions.
8.1.4 Stack Application 2: Converting from Infix to Postfix
In Section 8.1.3, we saw how a compiler or interpreter could implement recursion. In this section we present another "internal" application: the translation of arithmetic expressions from infix notation into postfix notation. This can be one of the key tasks performed by a compiler as it creates machine-level code, or by an interpreter as it evaluates an arithmetic expression.
In infix notation, a binary operator is placed between its operands. For example, Figure 8.8 shows several arithmetic expressions in infix notation.
FIGURE 8.8 Several arithmetic expressions in infix notation
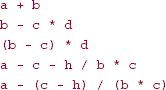
For the sake of simplicity, we initially restrict our attention to expressions with single-letter identifiers, parentheses and the binary operators +, -, *, and /.
The usual rules of arithmetic apply:
- Operations are normally carried out from left to right. For example, if we have
a + b - c
then the addition will be performed first.
- If the current operator is + or - and the next operator is * or /, then the next operator is applied
before the current operator. For example, if we have
b + c * d
then the multiplication will be carried out before the addition. For
a - b + c * d
the subtraction is performed first, then the multiplication and, finally, the addition.
We can interpret this rule as saying that multiplication and division have "higher precedence" than addition and subtraction.
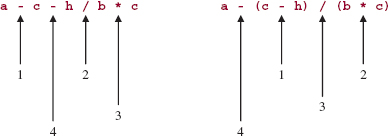
- Parentheses may be used to alter the order indicated by rules 1 and 2. For example, if we have
a - (b+c)
then the addition is performed first. Similarly, with
(a-b) * c
the subtraction is performed first.
Figure 8.9 shows the order of evaluation for the last two expressions in Figure 8.8.
FIGURE 8.9 The order of evaluation for the last two expressions in Figure 8.8
The first widely used programming language was FORTRAN (from FORmula TRANslator), so named because its compiler could translate arithmetic formulas into machine-level code. In early (pre-1960) compilers, the translation was performed directly. But direct translation is awkward because the machine-level code for an operator cannot be generated until both of its operands are known. This requirement leads to difficulties when either operand is a parenthesized subexpression.
8.1.4.1 Postfix Notation
Modern compilers do not translate arithmetic expressions directly into machine-level code. Instead, they can utilize an intermediate form known as postfix notation. In postfix notation, an operator is placed immediately after its operands. For example, given the infix expression a + b, the postfix form is ab +. For a + b * c, the postfix form is abc * + because the operands for + are a and the product of b and c. For (a + b) * c, the postfix form is ab + c *. Since an operator immediately follows its operands in postfix notation, parentheses are unnecessary and therefore not used. Figure 8.10 shows several arithmetic expressions in both infix and postfix notation.
FIGURE 8.10 Several arithmetic expressions in both infix and postfix notation

How can we convert an arithmetic expression from infix notation into postfix notation? Let's view the infix notation as a string of characters and try to produce the corresponding postfix string. The identifiers in the postfix string will be in the same order as they are in the infix string, so each identifier can be appended to the postfix string as soon as it is encountered. But in postfix notation, operators must be placed after their operands. So when an operator is encountered in the infix string, it must be saved somewhere temporarily.
For example, suppose we want to translate the infix string
a-b+c* d
into postfix notation. (The blanks are for readability only—they are not, for now, considered part of the infix expression.) We would go through the following steps:
'a' is appended to postfix, which is now the string "a" '-' is stored temporarily 'b' is appended to postfix, which is now the string "ab"
When '+' is encountered, we note that since it has the same precedence as '-', the subtraction should be performed first by the left-to-right rule (Rule 1, above). So the '-' is appended to the postfix string, which is now "ab-" and ' + ' is saved temporarily. Then 'c' is appended to postfix, which now is "ab-c".
The next operator, must also be saved somewhere temporarily because one of its operands (namely 'd') has not yet been appended to postfix. But ' *' should be retrieved and appended to postfix before ' + ' since multiplication has higher precedence than addition.
When 'd' is appended to postfix, the postfix string is "ab-cd". Then '*' is appended, making the postfix string "ab-cd*". Finally, ' + ' is appended to postfix, and the final postfix representation is
"ab-cd*+"
The temporary storage facility referred to in the previous paragraph is handled conveniently with a stack to hold operators. The rules governing this operatorstack are:
R1. Initially, operatorstack is empty.
R2. For each operator in the infix string,
Loop until the operator has been pushed onto operatorstack:
If operatorStack is empty or the operator has greater precedence than
the operator on the top of operatorStack then
Push the operator onto operatorStack.
else
Pop operatorStack and append that popped operator to the
postfix string.
R3. Once the end of the input string is encountered,
Loop until operatorStack is empty:
Pop operatorstack and append that popped operator to the postfix string.
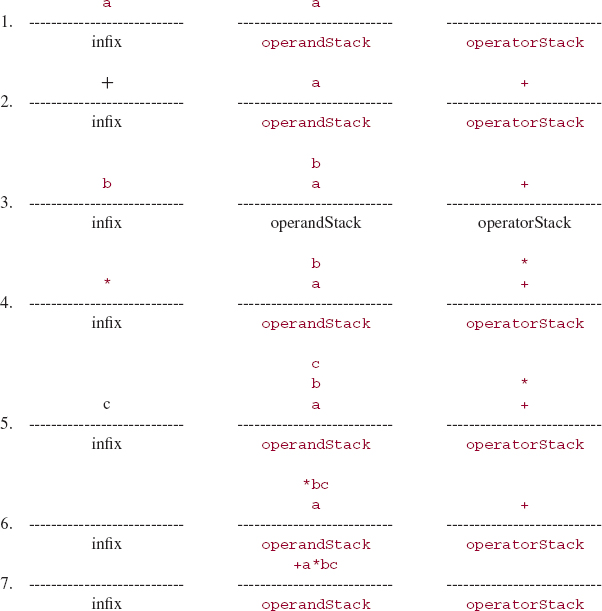
For example, Figure 8.11 shows the history of the operator stack during the conversion of
a + c- h/ b * r
FIGURE 8.11 The conversion of a + c - h/b * r to postfix notation. At each stage, the top of operatorStack is shown as the rightmost element

How are parentheses handled? When a left parenthesis is encountered in the infix string, it is immediately pushed onto operatorStack, but its precedence is defined to be lower than the precedence of any binary operator. When a right parenthesis is encountered in the infix string, operatorStack is repeatedly popped, and the popped element appended to the postfix string, until the operator on the top of the stack is a left parenthesis. Then that left parenthesis is popped but not appended to postfix, and the scan of the infix string is resumed. This process ensures that parentheses will never appear in postfix notation.
For example, when we translate a * (b + c) into postfix, the operators '(', and ' + ' would be pushed and then all would be popped (last-in, first-out) when the right parenthesis is encountered. The postfix form is
a b c + *
For a more complex example, Figure 8.12 (next page) illustrates the conversion of
x - (y * a/ b - (z + d * e) + c) / f into postfix notation.
8.1.4.2 Transition Matrix
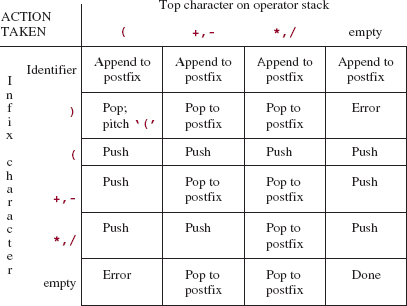
At each step in the conversion process, we know what action to take as long as we know the current character in the infix string and the top character on the operator stack. We can therefore create a matrix to summarize the conversion. The row indexes represent the possible values of the current infix character. The column indexes represent the possible values of the top character on the operator stack. The matrix entries represent the action to be taken. Such a matrix is called a transition matrix because it directs the transition of information from one form to another. Figure 8.13 (page 343) shows the transition matrix for converting a simple expression from infix notation to postfix notation.
The graphical nature of the transition matrix in Figure 8.13 enables us to see at a glance how to convert simple expressions from infix to postfix. We could now design and implement a program to do just that. The program may well incorporate the transition matrix in Figure 8.13 for the sake of extensibility.
FIGURE 8.12 The conversion of x - (y * a/b - (z + d * e) + c)/f from infix to postfix. At each stage, the top of operatorstack is shown as the rightmost element

More complex expressions can be accommodated by expanding the matrix. For the conversion, there would be a switch statement with one case for each matrix entry.
8.1.4.3 Tokens
A program that utilized a transition matrix would probably not work with the characters themselves because there are too many possible (legal) values for each character. For example, a transition matrix that used a row for each legal infix character would need 52 rows just for an identifier. And if we changed the specifications to allow multi-character identifiers, we would need millions of rows!
Instead, the legal characters would usually be grouped together into "tokens." A token is the smallest meaningful unit in a program. Each token has two parts: a generic part that holds its category and a specific part that enables us to recapture the character(s) tokenized. For converting simple infix expressions to postfix, the token categories would be: identifier, rightPar, leftPar, addOp (for ' + ' and multOp (for '*' and V), and empty (for a dummy value). The specific part would contain the index, in the infix string, of the character tokenized. For example, given the infix string
FIGURE 8.13 The transition matrix for converting simple expressions from infix notation to postfix notation
(first + last) / sum
to tokenize "last", we would set its category to identifier and its index to 9.
The structure of tokens varies widely among compilers. Typically, the specific part of a variable identifier's token contains an address into a table, called a symbol table. At that address would be stored the identifier, an indication that it is a variable identifier, its type, initial value, the block it is declared in and other information helpful to the compiler. There is a symbol table in the project of Lab 15, and the creation of a symbol table is the subject of an application in Chapter 14.
In Lab 15, a complete infix-to-postfix project is developed, with tokens and massive input-editing.
You are now prepared to do Lab 15: Converting from Infix to Postfix
8.1.5 Prefix Notation
In Section 8.1.4 we described how to convert an infix expression into postfix notation. Another possibility is to convert from infix into prefix notation, in which each operator immediately precedes its operands2. Figure 8.14 shows several expressions in both infix and prefix notation.
FIGURE 8.14 Several arithmetic expressions in both infix and prefix notation

How can we convert an arithmetic expression from infix to prefix? As in infix-to-postfix, we will need to save each operator until both of its operands have been obtained. But we cannot simply append each identifier to the prefix string as soon as it is encountered. Instead, we will need to save each identifier, in fact, each operand, until its operator has been obtained.
The saving of operands and operators is easily accomplished with the help of two stacks, operand stack and operatorstack. The precedence rules for operatorstack are exactly the same as we saw in converting from infix to postfix. Initially, both stacks are empty. When an identifier is encountered in the infix string, that identifier is pushed onto operandstack. When an operator is encountered, it is pushed onto operatorstack if that stack is empty. Otherwise, one of the following cases applies:
- If the operator is a left parenthesis, push it onto operatorstack (but left parenthesis has lowest precedence).
- If the operator has higher precedence than the top operator on operatorstack, push the operator onto operatorStack.
- If the operator's precedence is equal to or lower than the precedence of the top operator on operatorstack, pop the top operator, opt1, from operatorstack and pop the top two operands, opnd1 and opnd2, from operandstack. Concatenate (join together) opt1, opnd2, and opnd1 and push the result string onto operandstack. Note that opnd2 is in front of opnd1 in the result string because opnd2 was encountered in the infix string—and pushed onto operandstack—before opnd1.
- If the operator is a right parenthesis, treat it as having lower priority than +, -, *, and /. Then Case 3 will apply until a left parenthesis is the top operator on operatorstack. Pop that left parenthesis.
The above process continues until we reach the end of the infix expression. We then repeat the following actions from case 3 (above) until operatorStack is empty:
Pop opt1 from operatorStack.
Pop opnd1 and opnd2 from operandStack.
Concatenate opt1, opnd2 and opnd1 together and push the result onto operandStack.
When operatorstack is finally empty, the top (and only) operand on operandstack will be the prefix string corresponding to the original infix expression.
For example, if we start with
a + b * c
then the history of the two stacks would be as follows:
The prefix string corresponding to the original string is
+a*bc
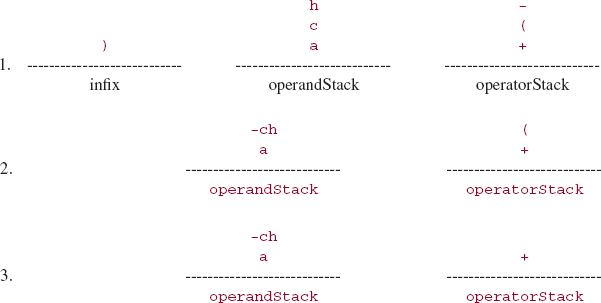
For a more complex example, suppose the infix string is
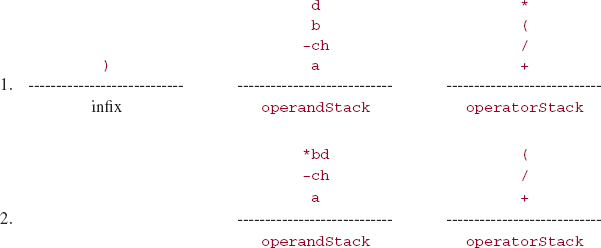
a+(c- h)/(b * d)
Then the elements on the two stacks during the processing of the first right parenthesis would be as follows:
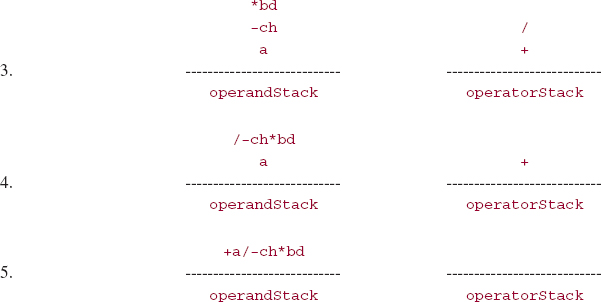
During the processing of the second right parenthesis in the infix string, we would have
The end of the infix expression has been reached, so operatorstack is repeatedly popped.
The prefix string is
+ a/ -ch * bd
8.2 Queues
A queue is a finite sequence of elements in which:
- insertion is allowed only at the back of the sequence;
- removal is allowed only at the front of the sequence.
The term enqueue (or add) is used for inserting an element at the back of a queue, dequeue (or remove) for removing the first element from a queue, and front (or element) for the first element in a queue. A queue imposes a chronological order on its elements: the first element enqueued, at the back, will eventually be the first element to be dequeued, from the front. The second element enqueued will be the second element to be dequeued, and so on. This defining property of queues is sometimes referred to as "First Come, First Served," "First In, First Out," or simply FIFO.
Figure 8.15 shows a queue through several stages of insertions and deletions.
The examples of queues are widespread:
cars in line at a drive-up window
fans waiting to buy tickets to a ball game
customers in a check-out line at a supermarket
airplanes waiting to take off from an airport.
FIGURE 8.15 A queue through several stages of insertions and deletions
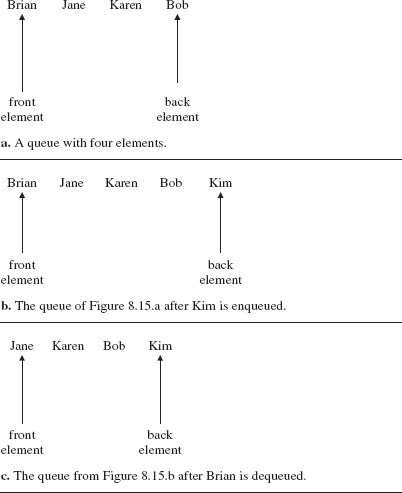
We could continue giving queue examples almost indefinitely. Later in this chapter we will develop an application of queues in the field of computer simulation.
Section 8.2.1 presents the Queue interface—part of the Java Collections Framework.
8.2.1 The Queue Interface
The Queue interface, with type parameter E, extends the Collection interface by specifying remove() and element() methods:
public interface Queue<E> extends Collection<E> { /** * Retrieves and removes the head of this queue. * * @return the head of this queue. * @throws NoSuchElementException if this queue is empty. */ E remove(); /** * Retrieves, but does not remove, the head of this queue. * * @return the head of this queue. * @throws NoSuchElementException if this queue is empty. */ E element(); } // interface Queue
Also, the Queue interface inherits the following add method from the Collection interface:
/**
* Ensures that this collection contains the specified element.
*
* @param element: element whose presence in this collection is to be ensured.
* @return true if this collection changed as a result of the call; otherwise, false.
*
* @throws ClassCastException class of the specified element prevents it
* from being added to this collection.
* @throws NullPointerException if the specified element is null and this
* collection does not support null elements.
*
*/
boolean add (E element);
So the Queue interface includes the essential methods of the queue data type3.
8.2.2 Implementations of the Queue Interface
The LinkedList class, from Chapter 7, implements the Queue interface, with the front of the queue at index 0. Here is the code to create the queue in Figure 8.15:
Queue<String> queue = new LinkedList<String>();
// Figure 8.15.a.
queue.add ("Brian");
queue.add ("Jane");
queue.add ("Karen");
queue.add ("Bob");
// Figure 8.15.b.
queue.add ("Kim");
// Figure 8.15.C
queue.remove();
For the three key methods—add (E element), remove(), and element() —worstTime(n) is constant. That is because in a LinkedList object, insertion at the back and removal or access of the front element take only constant time. And we have the same flaw as we had for the Stack class earlier in this chapter: There are LinkedList methods—such as remove (int index) and add (int index, E element)—that violate the definition of a queue. Whenever a LinkedList object implements the Queue interface, we declare the object with the Queue interface as in the previous example. This is a heads-up to users that insertions should occur only at the back and deletions only at the front.
You can overcome this defective implementation of the Queue interface by extending the LinkedList class to a PureQueue class that throws UnsupportedOperationException for any of the offending methods. Or you can take an austere approach and create a PureQueue class by aggregation: The only field will be a LinkedList (why not ArrayList ?) object, list, and the only methods will be a default constructor, a copy constructor, isEmpty(), size(), add (E element), remove(), and element(). For example, the definition of the remove() method is
/** * Retrieves and removes the head of this queue. * The worstTime(n) is constant and averageTime(n) is constant. * * @return the head of this queue. * @throws NoSuchElementException if this queue is empty. */ public E remove() { return list.removeFirst(); } // method remove()
The definition of each of the other six methods is also a one-liner. Observe that if list were an ArrayList object, worstTime(n) and averageTime(n) for this method would be linear in n.
Now that we have seen several possible implementations of the Queue interface, we turn our attention to applications.
8.2.3 Computer Simulation
A system is a collection of interacting parts. We are often interested in studying the behavior of a system, for example, an economic system, a political system, an ecological system or even a computer system. Because systems are usually complicated, we may utilize a model to make our task manageable. A model, that is, a simplification of a system, is designed so that we may study the behavior of the system.
A physical model is similar to the system it represents, except in scale or intensity. For example, we might create a physical model of tidal movements in the Chesapeake Bay or of a proposed shopping center. War games, spring training, and scrimmages are also examples of physical models. Unfortunately, some systems cannot be modeled physically with currently available technology—there is, as yet, no physical substance that could be expected to behave like the weather. Often, as with pilot training, a physical model may be too expensive, too dangerous, or simply inconvenient.
Sometimes we may be able to represent the system with a mathematical model: a set of assumptions, variables, constants, and equations. Often, a mathematical model is easier to develop than a physical model. For example, such equations as distance = rate * time and the formula for the Pythagorean Theorem can be solved analytically in a short amount of time. But sometimes, this is not the case. For example, most differential equations cannot be solved analytically, and an economic model with thousands of equations cannot be solved by hand with any hope of correctness.
In such cases, the mathematical model is usually represented by a computer program. Computer models are essential in complex systems such as weather forecasting, space flight, and urban planning. The use of computer models is called computer simulation. There are several advantages to working with a computer model rather than the original system:
- Safety. Flight simulators can assail pilot trainees with a welter of dangerous situations such as hurricanes and hijackings, but no one gets hurt.4
- Economy. Simulation games in business-policy courses enable students to run a hypothetical company in competition with other students. If the company goes "belly up," the only recrimination is a lower grade for the students.
- Speed. The computer usually makes predictions soon enough for you to act on them. This feature is essential in almost every simulation, from the stock market to national defense to weather forecasting.
- Flexibility. If the results you get do not conform to the system you are studying, you can change your model. This is an example of feedback: a process in which the factors that produce a result are themselves affected by that result. After the computer model is developed and run, the output is interpreted to see what it says about the original system. If the results are invalid—that is, if the results do not correspond to the known behavior of the original system—the computer model is changed. See Figure 8.16.
The above benefits are so compelling that computer simulation has become a standard tool in the study of complex systems. This is not to say that computer simulation is a panacea for all systems problems. The simplification required to model a system necessarily introduces a disparity between the model and the system. For example, suppose you had developed a computer simulation of the earth's ecosystem 30 years ago. You probably would have disregarded the effects of aerosol sprays and refrigerants that released chlorofluorocarbons. Many scientists now suspect that chlorofluorocarbons may have a significant impact on the ozone layer and thus on all land organisms.
FIGURE 8.16 Feedback in computer simulation
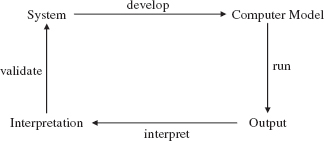
Another disadvantage of computer simulation is that its results are often interpreted as predictions, and prediction is always a risky business. For this reason, a disclaimer such as the following usually precedes the results of a computer simulation: "If the relationships among the variables are as described and if the initial conditions are as described, then the consequences will probably be as follows…"
8.2.4 Queue Application: A Simulated Car Wash
Queues are employed in many simulations. For example, we now illustrate the use of a queue in simulating traffic flow at Speedo's Car Wash.
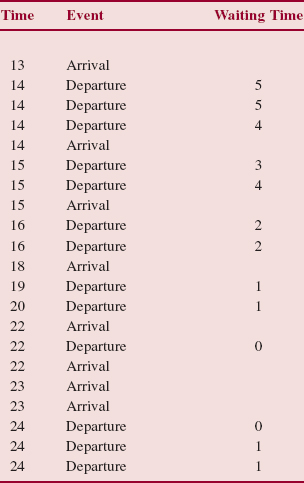
Problem Given the arrival times at the car wash, calculate the average waiting time per car.
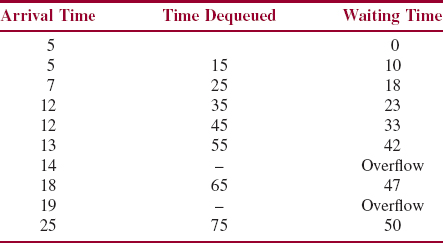
Analysis We assume that there is one station in the car wash, that is, there is one "server." Each car takes exactly ten minutes to get washed. At any time there will be at most five cars waiting —in a queue —to be washed. If an arrival occurs when there is a car being washed and there are five cars in the queue, that arrival is turned away as an "overflow" and not counted. Error messages should be printed for an arrival time that is not an integer, less than zero, greater than the sentinel, or less than the previous arrival time.
The average waiting time is determined by adding up the waiting times for each car and dividing by the number of cars. Here are the details regarding arrivals and departures:
- If an arrival and departure occur during the same minute, the departure is processed first.
- If a car arrives when the queue is empty and no cars are being washed, the car starts getting washed immediately; it is not put on the queue.
- A car leaves the queue, and stops waiting, once the car starts through the ten-minute wash cycle.
The following is a sample list of arrival times:
5 5 7 12 12 13 14 18 19 25 999 (a sentinel)
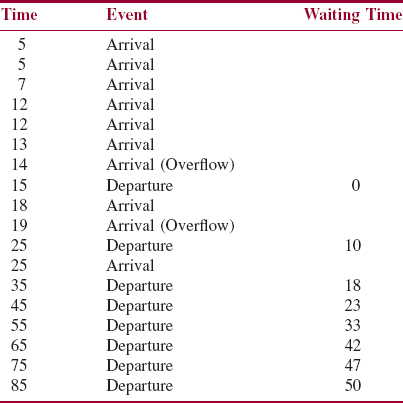
To calculate the waiting time for each car that is washed, we subtract its arrival time from the time when it entered the car wash. The first arrival, at time 5, entered the wash station right away, so its waiting time was 0. For the second arrival, also at time 5, it was enqueued at time 5, and then dequeued and entered the wash station when the first car left the wash station—at time 15. So the waiting time for the second arrival was 10 minutes. Here is the complete simulation:
The sum of the waiting times is 223. The number of cars is 8 (the two overflows at 14 and 19 minutes are not counted), so the average waiting time is 27.875 minutes.
Formally, we supply system tests to specify the expected behavior (that is, in terms of input and output) of the program. The system tests are created before the program is written and provide an indication of the program's correctness. But as we noted in Section 2.4, testing can establish the incorrectness—but not the correctness—of a program. JUnit testing of any class can commence after the class has been designed, that is, after the method specifications have been developed.
System Test 1 (the input is in boldface):
Please enter the next arrival time. The sentinel is 999: 5
Please enter the next arrival time. The sentinel is 999: 5
Please enter the next arrival time. The sentinel is 999: 7
Please enter the next arrival time. The sentinel is 999: 12
Please enter the next arrival time. The sentinel is 999: 12
Please enter the next arrival time. The sentinel is 999: 13
Please enter the next arrival time. The sentinel is 999: 14
Please enter the next arrival time. The sentinel is 999: 18
Please enter the next arrival time. The sentinel is 999: 19
Please enter the next arrival time. The sentinel is 999: 25
Please enter the next arrival time. The sentinel is 999: 999
Here are the results of the simulation:
The average waiting time, in minutes, was 27.875
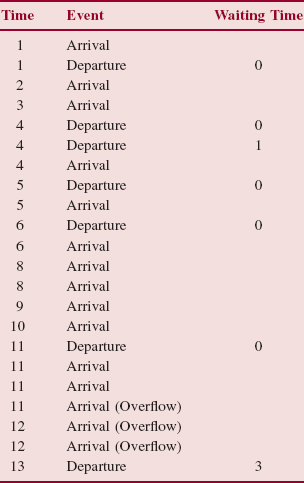
System Test 2 (input is in boldface):
Please enter the next arrival time. The sentinel is 999: -3
java.lang.IllegalArgumentException The input must consist of a non-negative integer less than the sentinel.
Please enter the next arrival time. The sentinel is 999: 5
Please enter the next arrival time. The sentinel is 999: m java.util.InputMismatchException:
Please enter the next arrival time. The sentinel is 999: 3
java.lang.IllegalArgumentException The next arrival time must not be less than the current time.
Please enter the next arrival time. The sentinel is 999: 1000
java.lang.IllegalArgumentException The input must consist of a non-negative integer less than the sentinel.
Please enter the next arrival time. The sentinel is 999: 10
Please enter the next arrival time. The sentinel is 999: 999
Here are the results of the simulation:
The average waiting time, in minutes, was 2.5
8.2.4.1 Program Design and Testing
As usual, we will separate the processing concerns from the input/output concerns, so we will have two major classes: CarWash and CarWashUser. The simulation will be event driven, that is, the pivotal decision in processing is whether the next event will be an arrival or a departure. After each of the next-arrival times has been processed, we need to wash any remaining cars and return the results of the simulation.
For now, four methods can be identified. Here are their specifications
/** * Initializes this CarWash object. * */ public CarWash() /** * Handles all events from the current time up through the specified time for the next * arrival. * * @param nextArrivalTime - the time when the next arrival will occur. * * @throws IllegalArgumentException - if nextArrivalTime is less than the * current time. * * @return - a string that represents the history of the car wash * through the processing of the car at nextArrivalTime. * */ public LinkedList<String> process (int nextArrivalTime) /** * Washes all cars that are still unwashed after the final arrival. * * @return - a string that represents the history of the car wash * after all arrivals have been processed (washed or turned away). */ public LinkedList<String> finishUp() /** * Returns the history of this CarWash object-s arrivals and departures, and the * average waiting time. * * @return the history of the simulation, including the average waiting time. * */ public LinkedList<String> getResults()
The process and finishUp methods return the history of the car wash (times, events, and waiting times), not because that is needed for the definitions of the process and finishUp methods, but for the sake of testing those methods. Recall the maxim from Chapter 2: In general, methods should be designed to facilitate testing.
In the CarWashTest class, carWash is a field, and CarWashTest extends CarWash to enable protected methods in CarWash to be accessed in CarWashTest. Here, for example, are tests for arrivals and overflow:
@Test public void twoArrivalsTest() { carWash.processArrival (5); results = carWash.processArrival (7); assertTrue (results.indexOf ("5 Arrival") != -1); assertTrue (results.indexOf ("7 Arrival") > results.indexOf ("5 Arrival")); } // method twoArrivalsTest @Test public void overflowTest() { carWash.processArrival (5); carWash.processArrival (7); carWash.processArrival (8); carWash.processArrival (12); carWash.processArrival (12); assertTrue (carWash.processArrival (13).toString(). indexOf (CarWash.OVERFLOW) == -1); // no overflow for arrival at 13 assertTrue (carWash.processArrival (14).toString(). indexOf (CarWash.OVERFLOW) > 0); // overflow for arrival at 14 } // method overflowTest
The complete project, including all test classes, is available from the book's website.
8.2.4.2 Fields in the CarWash Class
The next step in the development of the CarWash class is to choose its fields. We'll start with a list of variables needed to solve the problem and then select the fields from this list.
As noted at the beginning of the design stage in Section 8.2.4.1, the essential feature of processing is the determination of whether the next event is an arrival or a departure? We can make this decision based on the values of nextArrivalTime (which is read in) and nextDepartureTime. The variable nextArrivalTime holds the time when the next arrival will occur, and nextDepartureTime contains the time when the washing of the car now being washed will be finished. For example, suppose at some point in the simulation, nextArrivalTime contains 28 and nextDepartureTime contains 24. Then the next event in the simulation will be a departure at time 24. If the two times are the same, the next event will be an arrival (see note 1 of Analysis). What if there is no car being washed? Then the next event will be an arrival. To make sure the next event is an arrival no matter what nextArrivalTime holds, we will set nextDepartureTime to a large number—say 10000—when there is no car being washed.
The cars waiting to be washed should be saved in chronological order, so one of the variables needed will be the queue carQueue. Each element in carQueue is a Car object, so we temporarily suspend development of the CarWash class in order to determine the methods the Car class should have.
When a car leaves the queue to enter the wash station, we can calculate that car's waiting time by subtracting the car's arrival time from the current time. So the Car class will provide, at least, a getArrivalTime() method that returns the arrival time of the car that was just dequeued. Beyond that, all the Car class needs is a constructor to initialize a Car object from nextArrivalTime when a Car object is enqueued. The method specifications for the Car class are:
/** * Initializes this Car object from the specified time of the next arrival. * */ public Car ( int nextArrivalTime) /** * Determines the arrival time of this Car object. * * @return the arrival time of this Car object. * */ public int getArrivalTime()
We now resume the determination of variables in CarWash. As indicated in the previous paragraph, we should have waitingTime and currentTime variables. To calculate the average waiting time, we need numberOfCarsWashed and sumOfWaitingTimes. Finally, we need a variable, results, to hold each line of output of the simulation. We could simply make results a string variable, but then the concatenation operations would become increasingly expensive. Instead, each line will be appended to a linked list:
LinkedList<String> results;
At this point, we have amassed eight variables. Which of these should be fields? A simple heuristic (rule of thumb) is that most of a class's public, non-constructor methods should access most of the class's fields (see Riel, [1996] for more details). Clearly, the process method will need all of the variables. The finishUp method will handle the remaining departures, so that method must have access to carQueue, results, sumOfWaitingTimes, waitingTime, currentTime, and nextDepartureTime; these will be fields. The only other field is numberOfCars, needed by the getResults method. There is no need to make nextArrivalTime a field (it is needed only in the process method). Here are the constant identifiers and fields in the CarWash class:
public final String OVERFLOW = " (Overflow) "; protected final String HEADING = " Time Event Waiting Time "; protected static final int INFINITY = 10000; // indicates no car being washed protected static final int MAX_SIZE = 5; // maximum cars allowed in carQueue protected static final int WASH_TIME = 10; // minutes to wash one car protected Queue<Car> carQueue; protected LinkedList<String> results; // the sequence of events in the simulation protected int currentTime, nextDepartureTime, // when car being washed will finish numberOfCars, waitingTime, sumOfWaitingTimes;
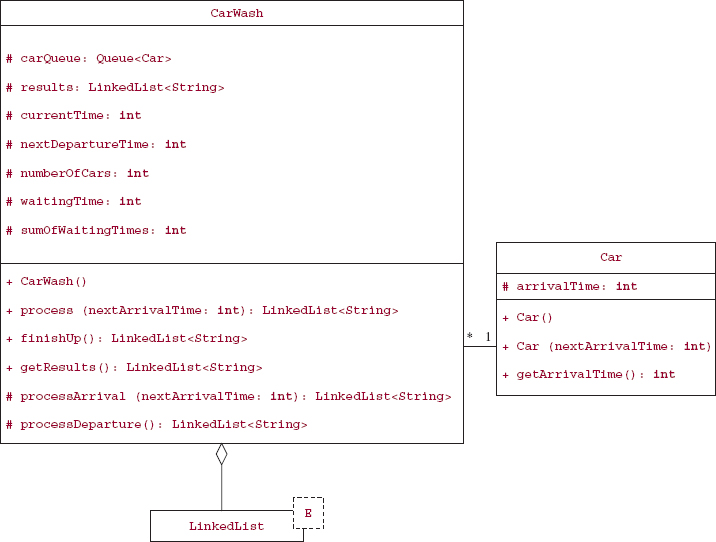
Figure 8.17 has the UML diagrams for the CarWash, Car, and LinkedList classes. For the sake of brevity, the LinkedList fields and methods are not shown, and the Queue interface's methods are not shown because they are implemented by the LinkedList class.
FIGURE 8.17 The class diagrams for CarWash and associated classes
8.2.4.3 Method Definitions of the CarWash Class
We now start on the method definitions of the CarWash class. The constructor is straightforward:
public CarWash()
{
carQueue = new LinkedList<Car>();
results = new LinkedList<String>();
results.add (HEADING);
currentTime = 0;
numberOfCars = 0;
waitingTime = 0;
sumOfWaitingTimes = 0;
nextDepartureTime = INFINITY; // no car being washed
} // constructor
The process method takes the nextArrivalTime read in from the calling method. Then the decision is made, by comparing nextArrivalTime to nextDepartureTime, whether the next event is an arrival or departure. According to the specifications of the problem, we keep processing departures until the next event is an arrival, that is, until nextArrivalTime < nextDepartureTime. Then the arrival at nextArrivalTime is processed. By creating processArrival and processDeparture methods, we avoid getting bogged down in details, at least for now.
public LinkedList<String> process (int nextArrivalTime) { final String BAD_TIME = "The time of the next arrival cannot be less than the current time."; if (nextArrivalTime < currentTime) throw new IllegalArgumentException (BAD_TIME); while (nextArrivalTime >= nextDepartureTime) processDeparture(); return processArrival (nextArrivalTime); } // process
To process the arrival given by nextArrivalTime, we first update currentTime and check for an overflow. If this arrival is not an overflow, numberOfCars is incremented and the car either starts getting washed (if the wash station is empty) or is enqueued on carQueue. Here is the code:
/** * Moves the just arrived car into the car wash (if there is room on the car queue), * or turns the car away (if there is no room on the car queue). * * @param nextArrivalTime - the arrival time of the just-arrived car. * */ protected LinkedList<String> processArrival (int nextArrivalTime) { final String ARRIVAL = " Arrival"; currentTime = nextArrivalTime; results.add (Integer.toString (currentTime) + ARRIVAL); if (carQueue.size() == MAX_SIZE) results.add (OVERFLOW); else { numberOfCars++; if (nextDepartureTime == INFINITY) // if no car is being washed nextDepartureTime = currentTime + WASH_TIME; else carQueue.add (new Car (nextArrivalTime)); results.add (" "); } // not an overflow return results; } // method processArrival
This method reveals how the Car class gets involved: there is a constructor with nextArrivalTime as its argument. Here is the complete definition of the Car class:
public class Car { protected int arrivalTime; /** * Initializes this Car object. * */ public Car() { } // for the sake of subclasses of Car /** * Initializes this Car object from the specified time of the next arrival. * */ public Car (int nextArrivalTime) { arrivalTime = nextArrivalTime; } // constructor with int parameter /** * Determines the arrival time of this Car object. * * @return the arrival time of this Car object. * */ public int getArrivalTime() { return arrivalTime; } // method getArrivalTime } // class Car
For this project, we could easily have avoided the Car class, but a subsequent extension of the project might relate to more information about a car: the number of axles, whether it is a convertible, and so on.
To process a departure, we first update currentTime and results. Note that the waiting time for the departing car was calculated when that car entered the wash station—during the previous call to the processDeparture method. We check to see if there are any cars on carQueue. If so, we dequeue the front car, calculate its waiting time, add that to sumOfWaitingTimes, and begin washing that car. Otherwise, we set waitingTime to O and nextDepartureTime to a large number to indicate that no car is now being washed. Here is the definition:
/** * Updates the simulation to reflect the fact that a car has finished getting washed. * */ protected LinkedList<String> processDeparture() { final String DEPARTURE = " Departure "; int arrivalTime; currentTime = nextDepartureTime; results.add (Integer.toString (currentTime) + DEPARTURE + Integer.toString (waitingTime) + " "); if (!carQueue.isEmpty()) { Car car = carQueue.remove(); arrivalTime = car.getArrivalTime(); waitingTime = currentTime - arrivalTime; sumOfWaitingTimes += waitingTime; nextDepartureTime = currentTime + WASH_TIME; } // carQueue was not empty else { waitingTime = 0; nextDepartureTime = INFINITY; // no car is being washed } // carQueue was empty return results; } // method processDeparture
The finishUp and getResults methods are straightforward:
public LinkedList<String> finishUp() { while (nextDepartureTime < INFINITY) // while there are unwashed cars processDeparture(); return results; } // finishUp public LinkedList<String> getResults() { final String NO_CARS_MESSAGE = "There were no cars in the car wash. "; final String AVERAGE_WAITING_TIME_MESSAGE = " The average waiting time, in minutes, was "; if (numberOfCars == 0) results.add (NO_CARS_MESSAGE); else results.add (AVERAGE_WAITING_TIME_MESSAGE + Double.toString ( (double) sumOfWaitingTimes / numberOfCars)); return results; } // method getResults
8.2.4.4 The CarWashUser Class
The CarWashUser class has a run method and a printResults method (in addition to the usual main method). Here are the method specifications for the run method and the printResults method:
/** * Reads in all of the arrival times, runs the simulation, and calculates the average * waiting time. * */ public void run() /** * Prints the results of the simulation. * */ public void printResults()
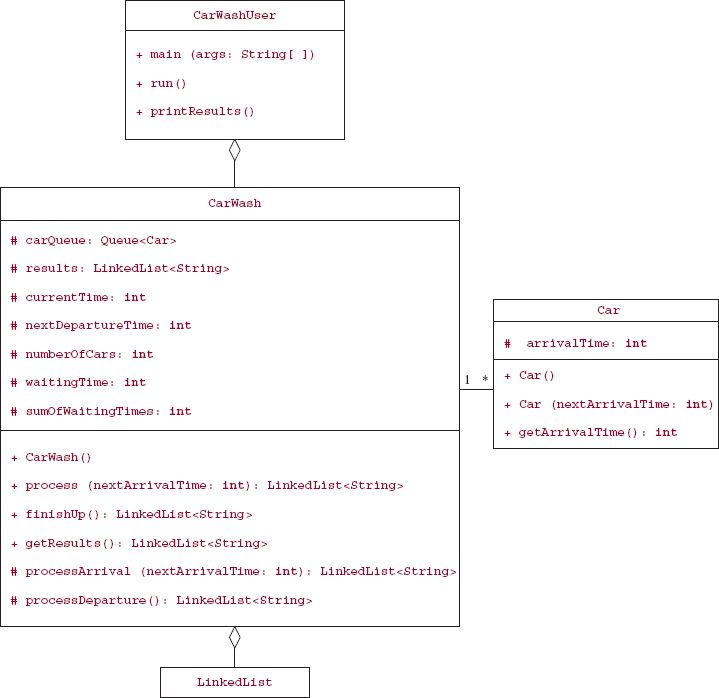
There is no CarWashUserTest class because the CarWashUser class has no testable methods. Figure 8.18 has the UML class diagrams for this project.
The run method repeatedly—until the sentinel is reached—reads in a value for nextArrivalTime. Unless an exception is thrown (for example, if the value is not an int), carWash.process (nextArr ivalTime) is called. When the sentinel is read in, the loop is exited and carWash.finishUp() and printResults (carWash) are called. Here is the code:
public void run() { final int SENTINEL = 999; final String INPUT_PROMPT = " Please enter the next arrival time (or " + SENTINEL + " to quit): "; final String OUT_OF_RANGE = "The input must consist of a non-" + "negative integer less than the sentinel."; CarWash carWash = new CarWash(); Scanner sc = new Scanner (System.in);
FIGURE 8.18 UML class diagrams for the CarWash project
int nextArrivalTime; while (true) { System.out.print (INPUT_PROMPT); try { nextArrivalTime = sc.nextInt(); if (nextArrivalTime == SENTINEL) break; if (nextArrivalTime < 0 || nextArrivalTime > SENTINEL) throw new NumberFormatException (OUT_OF_RANGE); carWash.process (nextArrivalTime); } // try catch (Exception e) { System.out.println(e); sc.nextLine(); } // catch } // while carWash.finishUp(); printResults (carWash); } // method run
The definition of the printResults method needs no explanation:
public void printResults() { final String RESULTS_HEADING = " Here are the results of the simulation: "; LinkedList<String> results = carWash.getResults(); System.out.println (RESULTS_HEADING); for (String s : results) System.out.print (s); } // method printResults
For the run method, worstTime(n) is linear in n, where n is the number of lines of input. There are loops in the definitions of the CarWash methods process and finishUp, but those loops are independent of n; in fact, the number of iterations of either loop is at most 5, the maximum size of the car queue.
8.2.4.5 Randomizing the Arrival Times
It is not necessary that the arrival times be read in. They can be generated by your simulation program, provided the input includes the mean arrival time, that is, the average time between arrivals for the population. In order to generate the list of arrival times from the mean arrival time, we need to know the distribution of arrival times. We now define a function that calculates the distribution, known as the Poisson distribution, of times between arrivals. The mathematical justification for the following discussion is beyond the scope of this book—the interested reader may consult a text on mathematical statistics.
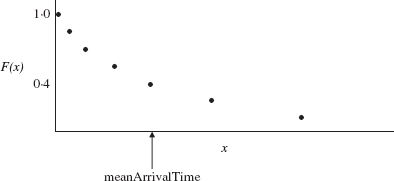
Let x be any time between arrivals. Then F(x), the probability that the time until the next arrival will be at least x minutes from now, is given by
F(x) = exp(-x / meanArrivalTime)
For example, F(0) = exp(0) = 1; that is, it is certain that the next arrival will occur at least 0 minutes from now. Similarly, F(meanArrivalTime) = exp(—1) ~ 0.4.F(10000 * meanArrivalTime) is approximately 0. The graph of the function F is shown in Figure 8.19.
FIGURE 8.19 Graph of the Poisson distribution of interarrival times
To generate the arrival times randomly, we introduce an integer variable called timeTillNext, which will contain the number of minutes from the current time until the next arrival. We determine the value for timeTillNext as follows. According to the distribution function F given previously, the probability that the next arrival will take at least timeTillNext minutes is given by
exp( -timeTillNext / meanArrivalTime)
This expression represents a probability, specifically, a floating point number that is greater than 0.0 and less than or equal to 1.0. To randomize this probability, we associate the expression with the value of a random variable, randomDouble, in the same range. So we set
randomDouble = random.nextDouble();
Then randomDouble contains a double value that is greater than or equal to 0.0 and less than 1.0. So 1—randomDouble will contain a value that is greater than 0.0 and less than or equal to 1.0. This is what we want, so we equate 1—randomDouble with exp(-timeTillNext/meanArrivalTime):
1 -randomDouble = exp (-timeTillNext / meanArrivalTime)
To solve this equation for timeTillNext, we take logs of both sides:
log (1 -randomDouble) = -timeTillNext / meanArrivalTime
Now each side is multiplied by—meanArrivalTime, to yield
timeTillNext = -meanArrivalTime * log (1 -randomDouble)
In Java code, we get:
timeTillNext = (int)Math.round (-meanArrivalTime * Math.log (1 - randomDouble));
We round the result so that timeTillNext will be an integer.
To illustrate how the values would be calculated, suppose that the mean arrival time is 3 minutes and the list of values of 1 - randomDouble starts with 0.715842, 0.28016, and 0.409589. Then the first three, randomized values of timeTillNext will be
1, that is, (int)Math.round (-3 * log (0.715842)), 4, that is, (int)Math.round (-3 * log (0.28016)), and 3, that is, (int)Math.round (-3 * log (0.409589)).
The first car will arrive one minute after the car wash opens and the second car will arrive four minutes later, at minute 5. The third car will arrive three minutes later, at minute 8.
You are now prepared to do Lab 16: Randomizing the Arrival Times
SUMMARY
A stack is a finite sequence of elements in which insertions and deletions can take place only at one end of the sequence, called the top of the stack. Because the most recently inserted element is the next element to be removed, a stack is a last-in-first-out (LIFO) structure. Compilers implement recursion by generating code for pushing and popping activation records onto a run-time stack whose top record holds the state of the method currently being executed. Another stack application occurs in the translation of infix expressions into machine code. With the help of an operator stack, an infix expression can be converted into a postfix expression, which is an intermediate form between infix and machine language. For this conversion, worstTime(n) is linear in n, the size of the infix expression.
A queue is a finite sequence of elements in which insertions can take place only at the back, and removals can take place only at the front. Because the first element inserted will be the first element to be removed, a queue is a first-in-first-out (FIFO) structure. The inherent fairness of this first-come-first-served restriction has made queues important components of many systems. Specifically, queues play a key role in the development of computer models to study the behavior of those systems.
CROSSWORD PUZZLE
| ACROSS | DOWN |
| 3. A two-dimensional array that directs the conversion from infix notation to postfix notation. | 1. The first widely used programming language. |
| 7. The immediate superclass the Stack class. | 2. The smallest meaningful unit in a program. |
| 10. The information saved whenever a method is called. | 4. The area of main memory that is allocated for a run-time stack. |
| 11. A notation in which each operator immediately follows its operands. | 5. The worstTime(n) for the add (E element), remove() and element() methods in the LinkedList implementation of the Queue interface. |
| 6. A process in which the factors that produce a result are themselves affected by that result. | |
| 8. A notation in which each operator immediately precedes its operands. | |
| 9. A simplification of a system. |
CONCEPT EXERCISES
8.1 What advantage was obtained by implementing the List interface before declaring the Stack class?
8.2 Suppose we define:
Queue<Integer> queue = new LinkedList<Integer>();
Show what the LinkedList object (referenced by) queue will look like after each of the following messages is sent:
- queue.add (2000);
- queue, add (1215);
- queue, add (103 5);
- queue, add (2117);
- queue.remove();
- queue, add (1999);
- queue.remove();
8.3 Re-do Exercise 8.2, parts a through g, for a stack instead of a queue. Start with
Stack<Integer> stack = new Stack<Integer>();
stack.push (2000);
8.4 Suppose that elements "a", "b", "c", "d", "e" are pushed, in that order, onto an initially empty stack, which is then popped four times, and as each element is popped, it is enqueued into an initially empty queue. If one element is then dequeued from the queue, what is the next element to be dequeued?
8.5 Use a stack of activation records to trace the execution of the recursive fact method after an initial call of fact (4). Here is the method definition:
<sub>/** /** * Calculates n!. * * @param n the integer whose factorial is calculated. * * @return n!. * */ protected static long fact (int n) { if (n <= 1) return 1; return n * fact (n - 1); } // method fact
8.6 Translate the following expressions into postfix notation:
- x + y * z
- (x + y) * z
- x — y — z * (a + b)
- (a + b) * c — (d + e * f/((g/h + i — j) * k))/ r
Test your answers by running the InfixToPostfix project in Lab 15.
8.7 Translate each of the expressions in Programming Exercise 8.6 into prefix notation.
8.8 An expression in postfix notation can be evaluated at run time by means of a stack. For simplicity, assume that the postfix expression consists of integer values and binary operators only. For example, we might have the following postfix expression:
8 5 4 +* 7 —
The evaluation proceeds as follows: When a value is encountered, it is pushed onto the stack. When an operator is encountered, the first—that is, top—and second elements on the stack are retrieved and popped, the operator is applied (the second element is the left operand, the first element is the right operand) and the result is pushed onto the stack. When the postfix expression has been processed, the value of that expression is the top (and only) element on the stack.
For example, for the preceding expression, the contents of the stack would be as follows:
Convert the following expression into postfix notation and then use a stack to evaluate the expression:
5 + 2 * (30 — 10/5)
PROGRAMMING EXERCISES
8.1 Declare and test the PureStack class (see Section 8.1.2) with a LinkedList field. Hint: Each of the definitions is a one-liner.
8.2 Declare and test the PureStack class (see Section 8.1.2) with an ArrayList field. Hint: For the sake of efficiency, the top of the stack should be at index size() - 1.
8.3 Develop an iterative, stack-based version of the ways method in Programming Exercise 5.7. Test your method with unit testing.
Making the Speedo's Car Wash Simulation More Realistic
Problem Expand the Car Wash Simulation Project with random arrival and service times. Use unit testing of new methods after you have specified those methods.
Analysis The arrival times—with a Poisson distribution—should be generated randomly from the mean arrival time. Speedo has added a new feature: The service time is not necessarily 10 minutes, but depends on what the customer wants done, such as wash only, wash and wax, wash and vacuum, and so on. The service time for a car should be calculated just before the car enters the wash station—that's when the customer knows how much time will be taken until the customer leaves the car wash. The service times, also with a Poisson distribution, should be generated randomly from the mean service time with the same random-number generator used for arrival times.
The input consists of three positive integers: the mean arrival time, the mean service time, and the maximum arrival time. Repeatedly re-prompt until each value is a positive integer.
Calculate the average waiting time and the average queue length, both to one fractional digit5. The average waiting time is the sum of the waiting times divided by the number of customers.
The average queue length is the sum of the queue lengths for each minute of the simulation divided by the number of minutes until the last customer departs. To calculate the sum of the queue lengths, we add, for each minute of the simulation, the total number of customers on the queue during that minute. We can calculate this sum another way: we add, for each customer, the total number of minutes that customer was on the queue. But this is the sum of the waiting times! So we can calculate the average queue length as the sum of the waiting times divided by the number of minutes of the simulation until the last customer departs. And we already calculated the sum of the waiting times for the average waiting time.
Also calculate the number of overflows. Use a seed of 100 for the random-number generator, so the output you get should have the same values as the output from the following tests.
System Test 1: (the input is in boldface)
Please enter the mean arrival time: 3
Please enter the mean service time: 5
Please enter the maximum arrival time: 25
The average waiting time was 11.1 minutes per car.
The average queue length was 1.9 cars per minute.
The number of overflows was 0.
System Test 2: (input in boldface)
Please enter the mean arrival time: 1
Please enter the mean service time: 1
Please enter the maximum arrival time: 23
Here are the results of the simulation:
The average waiting time was 1.7 minutes per car. The average queue length was 1.4 cars per minute. The number of overflows was 3.
Design, Test, and Implement a Program to Evaluate a Condition
Analysis The input will consist of a condition (that is, a Boolean expression) followed by the values—one per line—of the variables as they are first encountered in the condition. For example:
b * a > a + c 6 2 7
The variable b gets the value 6, a gets 2, and c gets 7. The operator * has precedence over >, and + has precedence over >, so the value of the above expression is true (12 is greater than 9).
Each variable will be given as an identifier, consisting of lower-case letters only. All variables will be integer-valued. There will be no constant literals. The legal operators and precedence levels—high to low—are:
* / % + - (that is integer addition and subtraction) >, >=, <=, < ==. != && II <
Parenthesized subexpressions are legal. You need not do any input editing, that is, you may assume that the input is a legal expression.
System Test 1 (Input in boldface):
Please enter a condition, or $ to quit: b * a > a + c
Please enter a value: 6
Please enter a value: 2
Please enter a value: 7
The value of the condition is true.
Please enter a condition, or $ to quit: b * a<a+c
Please enter a value: 2
Please enter a value: 7
The value of the condition is false.
Please enter a condition, or $ to quit: m+j* next == current * (next - previous)
Please enter a value: 6
Please enter a value: 2
Please enter a value: 7
Please enter a value: 5
Please enter a value: 3
The value of the condition is true.
Please enter a condition, or $ to quit: m + j * next ! = current * (next - previous)
Please enter a value: 6
Please enter a value: 2
Please enter a value: 7
Please enter a value: 5
Please enter a value: 3
The value of the condition is false.
Please enter a condition, or $ to quit: a * (b + c / (d -b) *e)> = a + b + c + d + e
Please enter a value: 6
Please enter a value: 2
Please enter a value: 7
Please enter a value: 5
Please enter a value: 3
The value of the condition is true.
Please enter a condition, or $ to quit: a * (b + c / (d -b) *e)< = a + b + c + d + e
Please enter a value: 6
Please enter a value: 2
Please enter a value: 7
Please enter a value: 5
Please enter a value: 3
The value of the condition is false.
Please enter a condition, or $ to quit: $
System Test 2 (Input in boldface):
Please enter a condition, or $ to quit: b<c&&c<a
Please enter a value: 10
Please enter a value: 20
Please enter a value: 30
The value of the condition is true.
Please enter a condition, or $ to quit: b<c&&a<c
Please enter a value: 10
Please enter a value: 20
Please enter a value: 30
The value of the condition is false.
Please enter a condition, or $ to quit: b<c || a<c
Please enter a value: 10
Please enter a value: 20
Please enter a value: 30
The value of the condition is true.
Please enter a condition, or $ to quit: c<b || c> a
Please enter a value: 20
Please enter a value: 30
The value of the condition is true.
Please enter a condition, or $ to quit: b!= a || b < =c && a > =c
Please enter a value: 10
Please enter a value: 20
Please enter a value: 30
The value of the condition is true.
Please enter a condition, or $ to quit: (b ! = a II b<= c)&&a>= c
Please enter a value: 10
Please enter a value: 20
Please enter a value: 30
The value of the condition is false.
Please enter a condition, or $ to quit: a/b* b+a%b == a
Please enter a value: 17
Please enter a value: 5
The value of the condition is true.
Please enter a condition, or $ to quit: $
Hint See Lab 15 on converting infix to postfix, and Concept Exercise 8.8. After constructing the postfix queue, create values, an ArrayList object with Integer elements. The values object corresponds to symbolTable, the ArrayList of identifiers. Use a stack, runTimeStack, for pushing and popping Integer and Boolean elements. Because runTimeStack contains both Integer and Boolean elements, it should not have a type argument.
Programming Project 8.3: Maze-Searching, Revisited
Re-do and re-test the maze-search project in Chapter 5 by replacing tryToReachGoal with an iterative method.
Hint: use a stack to simulate the recursive calls to tryToReachGoal.
The original version of the project is in the Chapter 5 subdirectory on the book's website.
Design, test, and implement a subclass of the stack class, PureStack, that satisfies the definition of a stack. Specifically, PureStack will throw UnsupportedOperationException for any method call that attempts to remove an element that is not the top element on the stack or attempts to insert an element except onto the top of the stack. Furthermore, a forward iteration (using the next() method, either explicitly or implicitly) through a PureStack object will start at the top of the stack and work down to the bottom of the stack. And a reverse iteration will start at the bottom of the stack.
1 Strictly speaking, the pop and peek method headings include the modifier synchronized: a keyword related to concurrent programming, which is beyond the scope of this book and irrelevant to our discussion. For more details on synchronization and concurrent programming, see the Java Tutorials at java.sun.com.
2 Prefix notation was invented by Jan Lukasiewicz, a Polish logician. It is sometimes referred to as Polish Notation. Postfix notation is then called Reverse Polish Notation.
3 The Queue interface also has a poll() method that is equivalent to the remove() method except that poll() returns null if the queue is empty, a peek() method that is equivalent to the element() method except that peek() returns null if the queue is empty, and an offer (E element) method that is equivalent to the add (E element) method except that offer (E element) is better suited if the queue imposes insertion restrictions and a full queue is commonplace.
4 According to legend, a trainee once panicked because one of his simulated engines failed during a simulated blizzard. He "bailed out" of his simulated cockpit and broke his ankle when he hit the unsimulated floor.
5 Given a double d, you can print d rounded to one fractional digit as follows: System.out.println (Math.round (d * 10)/10.0);