Chapter 18. Simplified Linear Transfer Functions
What you will learn in this chapter is to use simplified linear transfer functions to understand the effect of each component on the total variation of a part, an assembly, or a process. In this way you will know each component's contribution to the total variation and know where to focus your attention. Simplified linear transfer functions are used in the Analyze and Improve steps of the DMAIC process. This chapter is primarily for those involved in design, manufacturing, or process work.
Just as with DOEs, there will be some who think that this is too complex for this level of text. But, green belts have used this tool—and with great success.
The method used in simplified linear transfer functions is very similar to the RSS tolerance method we already covered. In fact, this type of transfer function is called the root sum-of-squares (RSS), because it involves squaring and summing the contributing sigmas, as we did for tolerance in the previous chapter. We want to account for all the variation in an assembly or a process by identifying the contributing variation of each component.
NOTE
RSS Linear Transfer Functions
St = the critical sigma of the total assembly or process
s1, s2, s3, s4, etc. are the sigmas of the variables linearly affecting the critical sigma of an assembly or process.
Each variable's influence must be stated in common units consistent with the part, assembly, or process. For example, if we are studying the thickness variation of an injected molded part and one of the contributing variables is the weight of the injected raw material, we need to state that variable's sigma in "thickness variation per sigma," rather than in "weight unit per sigma."
The best way to illustrate this is to tell about an actual project done in a manufacturing plant.
Case Study: Finding Grinding Issue Using Transfer FunctionAmanufacturing plant was manufacturing an item that involved pressing a forming material into a defined cavity. Figure 18-1 is a simplified diagram of this process. Figure 18-1. Diagram of forming process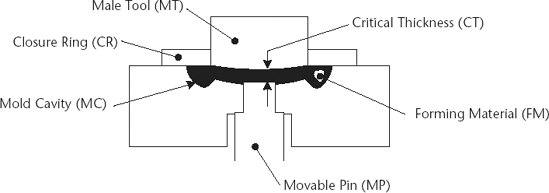
The critical thickness was varying too much and the plant wanted to run tests to see what was causing this excessive variation. First, the team defined the things that could affect this critical thickness: SCT: total sigma on the critical thickness
The formula of the total sigma S would therefore be: The team needed to run the tests such that they changed only one variable at a time. They could then see the effect of each contributing sigma without the effect of the other variables. The only variable they couldn't tightly control was the weight of the forming material, so it was decided to run that test first. Then, on tests for the other variables, they would analyze only product that had an average weight, eliminating weight as a variable on the remaining tests. Test 1: find the sigma SFM of the forming material weight. Product was taken from one mold, where the pin was locked in position to eliminate any influence of the moveable pin. Only one male tool was used. The weight was allowed to vary over its normal range. The critical thickness on the resultant product was measured. From these data it was possible to calculate the effect of a weight change on the critical thickness, with no other variable changing. There were historical data on weight variation, so the sigma in grams was already available. However, to get it into the common units needed, the team used the above data to convert the weight sigma to inches of critical thickness. This was a simple conversion, using the above data on thickness to determine what the equivalent thickness change was at the gram-weight value of the historical weight sigma. The team now had SFM for the weight variation in critical thickness inches. Test 2: find the sigma SMT of the male tool. Product was taken from one mold, where the pin was locked in position to eliminate any influence of the moveable pin. Multiple male tools were run. On products that had weights close to the historic average weight, the critical thickness was measured. In this way the team was able to find SMT in terms of critical thickness inches. Test 3: find the sigma SMC of the mold cavity. Product was taken from multiple molds, where the pins were locked in position to eliminate any influence of the moveable pin. One male tool was used. On products that had weights close to the historic average weight, the critical thickness was measured. In this way the team was able to find SMC in terms of critical thickness inches. Test 4: find the sigma SMP of the moveable pin. Product was taken from the same multiple molds used in the previous test, but the pins were no longer locked in position. One male tool was used. On products that had weights close to the historic average weight, the critical thickness was measured. The sigma was found for each individual mold. This gave a sigma for the moveable pin in that mold. Using the RSS method, the sigma from all the molds was then calculated. This gave the effect of many moveable pins. In this way the team was able to find SMP in terms of critical thickness inches. The total SCT of the critical thickness was already available from historic data. The SAO of the "all other unknown contributing variables" was the variable for which the plant then solved, since all the other variables were known and the SCT equation had only one unknown. If the SAO of the "all other unknown contributing variables" had not been small compared with the other identified contributors, the team would have known that they had missed some important variable(s) and would have had to go back and review their understanding of the process. Here is the resultant RSS equation: 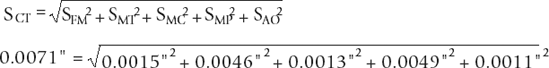 When the team analyzed the elements in the resultant RSS equation, they found that two variables were contributing most of the variation in the critical thickness. The highest, the moveable pin at 0.0049", was no surprise, and the plant already had projects underway to correct this. The sigma on the male tool, which at 0.0046" was almost as large as the moveable pin, was a complete surprise. The male tool, whose surface was periodically reground in the plant, was varying far more than anyone had thought. It was discovered that the check procedures that were supposed to be used to verify that the male tool grinding wheel shape was correct were no longer being followed. This was quickly corrected and almost a third of the problem of critical thickness variation was eliminated within a day, at almost no cost. |
In solving this problem, the team took care to make sure that each sigma contribution related directly to the change in the critical thickness, with the units being consistent with the product effect being measured. In this way comparing the sigmas to see which variable was more critical was valid.
No attempt was made to detail the transfer function to the point that the formula for the "shape" of the male tool was included in the formula. In an ideal world, it would be nice to have the transfer function defined by the geometry and position of parts in space. It just is not normally required or practical!
|

