Chapter 7
Stencil and Recurrence
In this chapter, we discuss a special case of the map pattern, the stencil pattern, which has a regular data access pattern. We will also discuss the recurrence pattern, which is a generalization of the map pattern that supports more complex data dependencies but which can still be efficiently parallelized.
The stencil pattern results when the inputs to every instance of a map pattern are based on regular access to an input data collection using a fixed set of offsets. In other words, every output of a stencil is a function of some neighborhood of elements in an input collection.
Stencils are common in practice. There are also several specific optimizations that can be applied to their implementation. In particular, the neighborhood structure of stencils exposes opportunities for data reuse and optimization of data locality. The regular structure of the memory reads also means that vectorized elemental functions can use shifts, rather than general gathers, for accessing input data. Efficient implementation of multidimensional stencils also requires attention to cache effects.
Stencils access a neighborhood of input data using a set of offsets. Recurrences are similar but access a neighborhood of outputs. Unlike a map, instances of a recurrence can depend on the values computed by other instances. In serial code, recurrences appear as loop-carried dependencies in which iterations of a loop can depend on previous iterations. We limit our discussion to cases where the output dependencies follow a regular pattern based on a set of offsets.
In Chapter 5, we discussed recurrences in one-dimensional loops, which can be parallelized as scans, but only if the instance operations are associative. In this chapter, we show that n-dimensional recurrences with n > 1 (those arising from loop nests) can always be parallelized over n − 1 dimensions whether or not the operations are associative. In fact, you do not require any special properties for the operations in the recurrence. All that matters is that the pattern of data dependencies is regular. In this chapter, we discuss a simple way to parallelize recurrences based on hyperplane sweeps, while in Chapter 8 we discuss another way to parallelize recurrences based on recursive divide-and-conquer.
7.1 Stencil
A stencil is a map in which each output depends on a “neighborhood” of inputs specified using a set of fixed offsets relative to the output position. A defining serial implementation is given in Listing 7.1 and is diagrammed in Figure 7.1. The data access patterns of stencils are regular and can be implemented either using a set of random reads in each elemental function or as a set of shifts, as discussed in Section 7.2.

Listing 7.1 Serial implementation of stencil. This code is generic, so it calls func for doing the actual processing after reading the neighborhood.
Stencils are important in many applications. In image and signal processing, the convolution operation is fundamental to many operations. In a convolution, the input samples are combined using a weighted sum with specific fixed weights associated with each offset input. Convolution is a linear operation but not all stencils are linear. Bilateral filtering is a powerful noise-reduction filter that uses non-linear operations to avoid smoothing over edges [TM98]. It is non-linear but follows the stencil pattern.
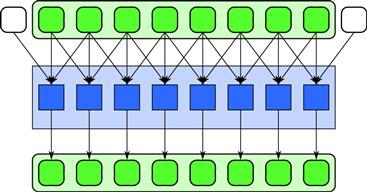
Figure 7.1 Stencil pattern. The stencil pattern combines a local, structured gather with a function to combine the results into a single output for each input neighborhood.
Stencils also arise in solvers for partial differential equations (PDEs) over regular grids. PDE solvers are important in many scientific simulations, in computer-aided engineering, and in imaging. Imaging applications include photography, satellite imaging, medical imaging, and seismic reconstruction. Seismic reconstruction is one of the major workloads in oil and gas exploration.
Stencils can be one dimensional, as shown in Figure 7.1, or multidimensional. Stencils also have different kinds of neighborhoods from square compact neighborhoods to sparse neighborhoods. The special case of a convolution using a square compact neighborhood with constant weights is known as a box filter and there are specific optimizations for it similar to that for the scan pattern. However, these optimizations do not apply to the general case. Stencils reuse samples required for neighboring elements, so stencils, especially multidimensional stencils, can be further optimized by taking cache behavior into account as discussed in Section 7.3. Stencils, like shifts, also require consideration of boundary conditions. When subdivided using the partition pattern, presented in Section 6.6, boundary conditions can result in additional communication between cores, either implicit or explicit.
7.2 Implementing Stencil with Shift
The regular data access pattern used by stencils can be implemented using shifts. For a group of elemental functions, a vector of inputs for each offset in the stencil can be collected by shifting the input by the amount of the offset. This is diagrammed in Figure 7.2.

Figure 7.2 Stencil pattern implemented with shifts. The offsets of a stencil can each be implemented with a shift and then combined.
Implementing a stencil in this way is really only beneficial for one-dimensional stencils or the memory-contiguous dimension of a multidimensional stencil. Also, it does not reduce total memory traffic to external memory since, if random scalar reads are used, data movement from external memory will still be combined into block reads by the cache. Shifts, however, allow vectorization of the data reads, and this can reduce the total number of instructions used. They may also place data in vector registers ready for use by vectorized elemental functions.
7.3 Tiling Stencils for Cache
When parallelizing multidimensional stencils where the data is laid out in a row-by-row fashion, there is a tension between optimizing for cache line data locality and minimizing the size of the working set. Figure 7.3 demonstrates the approach used to optimize stencils for cache known as strip-mining.

Figure 7.3 Tiling stencils for cache using strip-mining. Strips are assigned to each core. The strips are a multiple of a cache line wide, wide enough to avoid too much unused data being read into cache, and the height of the array. Processing goes top to bottom within a strip to minimize the working set and maximize reuse of the data in the cache. The strip alignment with cache lines prevents false sharing between adjacent strips. Reads may come from adjacent input strips, but writes are from separate cores and are always in separate strips.
Assume the data for a two-dimensional array is laid out in a row-by-row fashion so that all data in a row is contiguous in memory. That means that horizontal offsets access data that is close by, but vertical offsets access data that is far away. Therefore, horizontally accessed data will tend to be in the same cache line, but vertically accessed data will tend to be in different cache lines.
When breaking up the work over multiple cores, rectangular regions are assigned to each core. Assigning rows to each core would make good use of horizontal data locality. However, this approach would tend to read data redundantly since each core will need data from adjacent rows, assuming there are vertical offsets in the stencil. Conversely, assigning columns to each core would redundantly read data in the same cache line. Even worse, multiple cores would then write to the same cache line and cause false sharing and less than impressive performance.
If there are a significant number of vertical offsets, the right solution is often to assign a “strip” to each core. The strip is a multiple of cache lines wide, to avoid false sharing on output and to avoid significant redundancy on reads, and the height of the array vertically. Within each core, a strip is processed serially, from top to bottom. This organization of the computation should give good temporal coherence and reuse of data in the cache. The width of the strip should be small enough so that the working set of the stencil for the strip will fit in the cache.
There are two other memory system effects that can occur with memory systems when processing stencils. First, if the row size is a power of two, sometimes data from different rows can map to the same “sets” in set-associative caches, causing false cache conflicts. Whether this happens depends on a number of memory subsystem design issues including the number of sets in the cache and the size of the cache lines. This pathological case, if it occurs, can usually be avoided by padding array rows with unused elements to avoid row lengths that are powers of two. You should also take the strip width and stencil height into account to determine a padding amount that avoids conflicts anywhere in the working set. The second problem is TLB misses. For very large stencils, enough different pages may have to be touched that there are not enough entries in the TLB cache to manage the virtual-to-physical address translation. This can cause TLB cache thrashing, in which constant misses in the TLB cache will severely degrade performance. If the TLB miss rate is high, the data may have to be reorganized into tiles and processing order changed to avoid needing to access more pages at once than are supported by the memory system.
The partition and geometric decomposition patterns, discussed in Section 6.6, are related to strip-mining. When strip-mining, the output partitions are non-overlapping but the input footprints of each partition overlap. That is, the input is a more general geometric decomposition, not a partition.
7.4 Optimizing Stencils for Communication
The stencil pattern is often used inside an iterative loop—for example, in partial differential equation (PDE) solvers. The output of each stencil application is used as the input for the next iteration. In this case, synchronization is required between iterations so that the overlapping regions can be updated. These overlapping regions, often called “ghost cells” in this context, may have to be explicitly communicated between nodes when the pattern is used in a distributed system [KS10]. It is generally better to replicate these ghost cells in each local memory and swap them at the end of each iteration when using an iterated stencil than to try and share the memory for them at a fine-grained level. Fine-grained sharing can lead to increased communication costs.
The set of all ghost cells is sometimes known as a halo. The halo needs to be large enough to contain all the neighbors needed for at least one iteration. It is also possible to reduce communication to only every n th iteration by using a “deep halo” that is n times larger than necessary. However, this does require performing additional redundant computation in each node. This should be used only when the limiting factor is latency of communication, not bandwidth or computation. Optimizations that reduce communication, even when they increase computation, often prove very effective. General trends in computing, toward more processing cores, increasingly favor such optimizations. However, like any program transformation that increases the total amount of work to increase scalability, the code should be carefully analyzed and tested for performance to determine if the transformation is actually beneficial. Many other optimizations are possible in this pattern, including latency hiding, which can be accomplished by doing the interior computations first while simultaneously waiting for ghost cell updates.
In the context of iterative update of stencil computations, there is also the issue of double buffering to consider. For most iterated stencils, it is necessary to make a copy of the input and generate a new output buffer, rather than doing an update in place. However, for some stencils, namely, those that are causal (the offsets to input values can be organized to always point “backward in time” to previously processed samples, for some serial ordering), it is possible to do updates in place. This optimization can reduce memory requirements considerably but assumes a serial processing order. When used with geometric decomposition, ghost cells should still be used to decouple the computations, and some additional memory will still be required for the ghost cells.
Iterated stencils are really a special case of recurrences, discussed in Section 7.5. Thinking about iterated stencils as recurrences exposes the option of space-time blocking, which can significantly improve arithmetic intensity, the ratio of computation to communication.
7.5 Recurrence
When several loops are nested and have data dependencies between them, even though the loop iterations are not independent it is still possible to parallelize the entire loop nest. Consider Figure 7.4. In this figure, the arrows represent data dependencies where each output b[i][j] depends on the outputs from elements to the left and above. Such data dependencies result from the double loop nest shown in Listing 7.2. In the diagram, inputs are only shown at the boundaries (implemented by initializing appropriate elements of b) but in general there could be other inputs at every element, represented in the code with array a, and we also actually have outputs at every element.
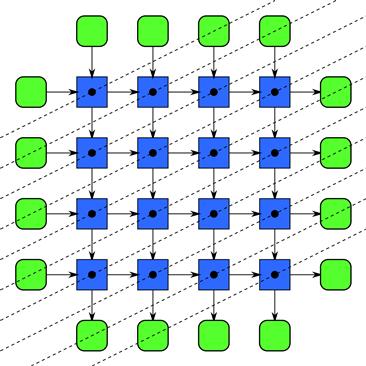
Figure 7.4 Recurrence pattern, definition. A multiply nested loop can be parallelized if the data dependencies are regular by finding a separating hyperplane and sweeping it through the lattice. Here, one possible separating hyperplane sweep is shown using a sequence of dotted lines.

Listing 7.2 Serial 2D recurrence. For syntactic simplicity, the code relies on the C99 feature of variable-length arrays.
You can parallelize such a loop nest even if the function f has no special properties. The trick is to find a plane that cuts through the grid of intermediate results so that all references to previously computed values are on one side of the plane. Such a plane is called a separating hyperplane. You can then sweep (iterate) through the data in a direction perpendicular to this plane and perform all the operations on the plane at each iteration in parallel. This is equivalent to skewing the elements of Figure 7.4 so that all dataflow arrows correctly point downward and forward in time. After you do this, the implementation looks like the diagram in Figure 7.5, where we have also shown all data elements consumed and computed for clarity. Leslie Lamport showed [Lam74] that a hyperplane can always be found if the dependencies are constant offsets. Note that as the plane sweeps through the array, the amount of parallelism is small at first, grows to a maximum value, and then shrinks again. This approach to parallelization can be generalized to higher-dimensional loop nests as well as loop nests whose inner loop bounds depend on indices of outer loops. This generalization is called polyhedral theory [VBC06].
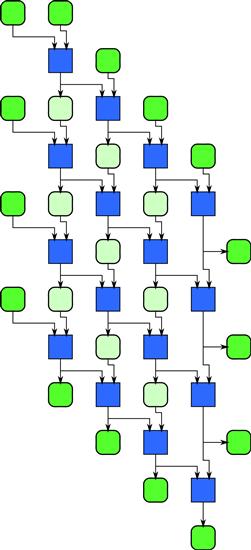
Figure 7.5 Recurrence pattern, implementation. A hyperplane sweep can also be seen as a skew of the elements of the recurrence so that all data dependencies are oriented forward in time.
Such a parallelization can be challenging to implement, especially in higher dimensions, since the transformation of the indices and proper handling of the boundary conditions can get quite complicated. Different choices of the hyperplane can lead to different parallelizations with different performances as well. In the above example, consider the case where the horizontal size h is large and the vertical size v is small, and vice versa. You may want to “slant” the hyperplane in different directions to get optimal performance in these two cases.
Both parallel and serial implementations of recurrences are also often combined with tiling. Tiling is especially beneficial for recurrences since it improves the ratio of data access to computation. In this approach, the recurrence is broken into a grid of tiles, and the data dependencies between the tiles lead to a new recurrence. Within the tiles, however, a serial implementation of the recurrence can be used. Such tiling is often so beneficial that it is useful to convert iterated stencils to recurrences so that this approach can be used. Tiling can be applied using either a static decomposition or a divide-and-conquer strategy under programming models supporting fork–join. The fork–join approach is discussed at greater length in Section 8.12.
Examples of the use of the recurrence pattern include infinite impulse response filters, dynamic programming (such as that used for sequence alignment in the Smith–Waterman algorithm), option pricing by the binomial lattice algorithm, and matrix factorization.
7.6 Summary
In this chapter, we have discussed two related patterns, stencils and recurrences. These are very common in practice, in everything from simulation to image processing. What these two patterns have in common is a regular pattern of communication and data access. To obtain high performance with these patterns, this regularity needs to be used to improve efficiency both by reuse of data (reducing the necessary bandwidth to off-chip memory) and by vectorization.
In both stencil and recurrence, it is possible to convert a set of offset memory accesses to shifts, but this is really only useful if vectorization is also used. Stencils can also use strip-mining to make effective use of the cache.
The other challenge with recurrences in particular (which also arise when stencils are iterated) is implementing space-time tiling. While this is an effective technique, picking the right size of tile involves a tradeoff between higher arithmetic intensity and working set. Chapter 8 introduces a recursive approach to tiling a recurrence, which Chapter 10 elaborates upon in the context of a practical example. The recursive approach tiles the recurrence at many different levels, so that at some level the tiles become the right size to fit in cache.
