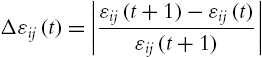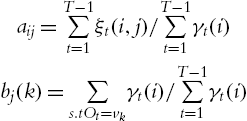10.1 Codebook and key-points generation

The dynamics of a n-link robot in joint space can be written as

$M\left(q\right)\stackrel{\cdot \cdot }{q}+c(q,\stackrel{\cdot }{q})\stackrel{\cdot }{q}+g\left(q\right)+F\left(\stackrel{\cdot }{q}\right)=\tau$

where $q\in {\Re }^n$ denotes the links angles, $\stackrel{\cdot }{q}\in {\Re }^n$ denotes the links velocity, $M(q)\in {\Re }^{n\times n}$ is the inertia matrix, $c(q,\stackrel{\cdot }{q})\in {\Re }^{n\times n}$ is the centripetal and Coriolis matrix, $g(q)\in {\Re }^n$ is the gravity vector, $F\in {\Re }^n$ is the frictional terms, and $\tau \in {\Re }^n$ is the input control vector.

The object is to generate the desired trajectory $q^{⁎}$ from the demonstrations in the joint space $Q={[Q_1\cdots Q_n]}^T$, $Q_i={[X_i^1\cdots X_i^m]}^T$. Here, the trajectory $X_i^r$ defines ith joint and rth trajectory; it is defined as $X_i^r=\left\{q_i\left(l\right)\right\}$, $l=1\cdots T_i^r$, $T_i^r$ is the total sample number of the joint angles. There are m trajectories for each joint. The trajectory number m is not necessary large, because a human cannot repeat the same motion only so many times and this may cause a repeat calculation in HMM. The data length $T_i^r$ is different from one demonstration to another, because of a different speed, and a starting/ending time.

Each joint for each demonstration has its own codebook defined as $C_i$, $i=1\cdots n$. A codebook can be regarded as a $N_i$ dimension vector, i.e., $C_i={[c_{i1}\cdots c_{i{N}_i}]}^T$. The codebook dimension $N_i$ is selected by prior knowledge of the trajectory's geometry.

We use Lloyd's algorithm to train the codebook $C_i\left(t\right)$. Here, t is noted as the training time. The initial codebook is defined as $C_i\left(1\right)$. A bad initial condition may reach local minima. A heuristics method [160] is used to find a better $C_i\left(1\right)$. Since the heuristics method needs a lot time, $C_i\left(1\right)$ can also be selected randomly from $X_i^r$.

The objective of using Lloyd's algorithm to create the codebook is to minimize a quantization error with certain data distribution. We need nearest-neighbor and centroid conditions, which are commonly used in Lloyd's algorithm. For one point $q_i(l_1)$ in the trajectory, we want to find the nearest codebook element by calculating

$\underset{1⩽j⩽N}{\min }|q_i(l_1)-c_{ij}|,l_1=1\cdots T,i=1\cdots n$

If the nearest codebook element is $c_{ik}$, the region $R_{ij}$ ($i=1\cdots n$, $j=1\cdots N_i$) is defined as

$R_{ik}=\{q_i(l_1)\}=[r_{ik1}\cdots r_{ik{p}_{ik}}],k=1\cdots s_i^r$

where $p_{ik}$ is the length of the region $R_{ik}$, $s_i^r$ is the region number of the joint i and the demonstration r.

Obversely, the center of the region $R_{ij}$ should be $c_{ij}$. The new center of $R_{ij}$ can be calculated as

$c_{ij}=\frac{1}{p_{ij}}\sum _{l=1}^{p_{ij}}{r}_{ijl}$

It is the centroid condition. The normal Lloyd's algorithm uses selected points to construct the centers [42]. We calculate the mean value of all points in the region $R_{ij}$. The advantage is that it can be updated online.

With (10.3) and (10.4), we can calculate $c_{ij}\left(t\right)$ recursively. We use the following quantization error to design a stop criterion. The average quantization error for $X_{ij}=\left\{q_i\left(l\right)\right\}$, $l=1\cdots T$, is defined as

${\epsilon }_{ij}\left(t\right)=\frac{1}{T}\sum _{l=1}^T|q_i\left(l\right)-c_{ij}\left(t\right)|$

where t is the recursive calculation times. We define a relative quantization error as

$\mathrm{\Delta }{\epsilon }_{ij}\left(t\right)=\left|\frac{{\epsilon }_{ij}(t+1)-{\epsilon }_{ij}\left(t\right)}{{\epsilon }_{ij}(t+1)}\right|$

The codebook calculation is stopped when the relative error (10.6) is small enough as

$\mathrm{\Delta }{\epsilon }_{ij}\left(t\right)⩽\overline{\epsilon }$

where $\overline{\epsilon }$ is a prior defined upper bound.

In order to train the hidden Markov model, we need key-points and observation symbols. These will be generated from the above codebook. The key-points are the start point, the end point o, and the center point in the time-axis of the codebook. If the time index of $c_{ij}$ in (10.4) is defined as $t_{ij}$ ($i=1\cdots n$, $j=1\cdots N_i$), then the key-points are calculated as

$k_{ij}=t_{ij}+\frac{t_{i(j+1)}-t_{ij}}{2}$

For each demonstration the key-points set are $K_i^r={[k_{i1}\cdots k_{i,v_i^r}]}^T$ ($i=1\cdots n$, $r=1\cdots m$), $v_i^r$ is the key point number in $K_i^r$. Since the key-point is in the center of the $R_{ij}$ and the starting and ending points of the trajectory are also key-points, $v_i^r=s_i^r+2$.

The observation symbols are the joint angles at the time of key-points. When they are less than the codebook, we use the codebook values. $O_i^r={[o_{i1}\cdots o_{i{N}_i}]}^T$ ($i=1\cdots n$, $r=1\cdots m$):

$\{\begin{array}{cc}\hfill o_{ij}(,q)=c_{i,j+1}\hfill & \hfill \text{if }{c}_{ij}⩽q_i^r(k)⩽c_{i,j+1}\hfill \\ \hfill o_{ij}(s,)=j+1\hfill & \hfill \text{otherwise}\hfill \end{array},j=1\cdots N_i,k=1\cdots v_i^r$

where s is the symbol of the observation, q is the value of the codebook.

Lloyd's algorithm allows us to set the dimensions of the key-points and the observation symbols are the same as that of the codebook. We avoid the manual tuning process as in [42,140,152].

We use the following example to explain how to use Lloyd's algorithm to generate the codebook, key-points, and observation symbols.

Example 10.1

A robot draws a circle. The angle of Joint-1 is shown in Fig. 10.1. We first show how the codebook number N will affect the results. The two square waves corresponds to $N=3$ and $N=4$. When $N=3$, there are 3 quantizations in the Y-axis. They generate 5 regions in the trajectory, $s_1^1=5$, $R_{11}\cdots R_{15}$. The key-points are in the center of each segment of the square waves. With the starting point and ending point, the key-point number of $K_1^1$ is 7, $v_1^1=s_1^1+2=7$. When $N=4$, the region number in (10.3) is $s_1^1=7$, and the key-point number is $v_1^1=9$. If there are 3 demonstrations, then $r=1,2,3$; see Fig. 10.2. The velocities are different; usually the dynamic time warping is needed to put them together in the time-axis. Here, we use Lloyd's algorithm; the key-point number of these three demonstrations are the same, $N=3$, $s_1^1=s_1^2=s_1^3=5$. Although the key-points in the time-axis are different, the observation symbols in the Y-axis are similar.

The following algorithm explains the calculation process of the codebook $C_i$, key-points $K_i^r$, and the observation symbols $O_i^r$.

10.2 Joint space trajectory generation with a modified hidden Markov model

After the codebook, key-points, and the observation symbols are generated by Lloyd's algorithm, they are used for training a discrete Hidden Markov Model (HMM). This model can generate a desired trajectory in the joint space as we want; see Fig. 10.3.

A HMM can be understood as a finite state machine where at any instant N, the different states are defined as $S=\{S_1,S_2,S_3...S_N\}$. At regular intervals, the HMM may change its states. The time associated with the changes are denoted by $t=1,2,...$. The changed states are denoted by $h_t$. In the case of process modeling, the change (transition) probabilities only depend on the current state $t_k$ and its previous states $t_{k-1}$, $t_{k-2},\cdots$

$P(h_t=S_j|h_{t-1}=S_k,h_{t-2}=S_k,...)=P(h_t=S_j|h_{t-k}=S_k)$

where $t=1,2,...$, $k=t-1,t-2,...$.

Since the right-hand side of the above equality is independent of t, each transition probability defined $a_{ij}$ as

$a_{ij}=P(h_t=S_j|h_{t-1}=S_i),1⩽i,j⩽N$

Now we define the transition probability distribution matrix as $A=\{a_{ij}\}$. If each state can lead to any other state in a single transition, $a_{ij}>0$.

The number of distinct observation is defined as M. The symbols corresponding to the observable output of the system is defined as

$V=\{v_1,v_2,...,v_M\}$

The distribution of observing the symbol is defined as $B=\{b_j(k)\}$. This probability distribution of the symbol k in state j is

$b_j(k)=P[v_k|h_t=S_j],1<j<N,1<k<M$

A graphical representation of a HMM is Fig. 10.4. This is a graphical representation of the HMM of Fig. 10.2. Here, the codebook number $N_1=4$, the hidden state number $v_1=7$. The configuration of this HMM is the well-known left–right topology.

The probability distribution of the initial state is defined as $\pi =\{{\pi }_i\}$:

${\pi }_i=P[h_1=S_i],1<i<N$

Given suitable for N, M, A, B, and π, a HMM generates a sequence of observations as $O=[O_1,O_2,...O_T]$ according to the following algorithm. Each observation $O_i$ is a symbol of the set V in (10.12):

With the above procedure, a HMM can be represented as

$\lambda =(A,B,\pi )$

For pth joint, the HMM ${\lambda }_i$ can be considered a generalization of the following mixture model [116]:

${\lambda }_p=(A_p,B_p,{\pi }_p)$

Since the difference in joint space is much bigger than task space with respect to motion speed and starting point, and the demonstrations cannot be many. The HMM model (10.16) cannot generate a desired trajectory with good accuracy in the joint space. We modify the HMM (10.16) into the following form:

${\lambda }_p=(A_p,B_p,{\pi }_p,{\hat{q}}_p)$

where ${\hat{q}}_p={[{\hat{q}}_{p1}\cdots {\hat{q}}_{pNp}]}^T$ is the output of the HMM (scaled joint angle), which is defined in (10.1).

The output of HMM ${\hat{q}}_p$ is also regarded as one demonstration, and is sent to HMM again for its training.

The number of states $A_p$ relates to the number of key-points. Although the states in HMM are hidden, and the algorithm of the codebook and key-points generation represents the physical significance of the trajectory. The state of pth joint is defined as $S_p={[s_{p1},...s_{p{v}_p}]}^T$. The hidden state number $v_p$ is the maximum of the key-point number:

$v_p=\underset{1⩽r⩽m}{\max }\left\{v_p^r\right\}$

where m is the demonstration number, $v_p$ is the hidden state number, and $N_p$ is the codebook number.

We use the key-point number $v_p^r$ as the number of states of HMM. Since $v_p^r$ depends on the codebook $C_p$, the m trajectories have the same key-point number, which is defined as $v_p$. The missing points are assigned with the correspond values of the other demonstration. The observation symbols are $O_p={[o_{p1},\cdots o_{p{N}_p}]}^T$ ($p=1\cdots n$).

In order to train the model (10.17) with the data generated the Lloyd's algorithm in the last section, we use the following four steps:

1) Given a sequence of observations $O=O_1{O}_2...O_T$ and the model ${\lambda }_p=(A_p,B_p,{\pi }_p,q_p)$, calculate the probability of the sequence of observations $P(O|{\lambda }_p)$.

The direct way to calculate the probability of $O_1{O}_2...O_T$ with respect to ${\lambda }_p$ is enumerating every possible state sequence of length T (the number of observations). Considering a sequence of fixed states $H=h_1{h}_2...h_T$, the probability of the observation sequence $O=O_1{O}_2...O_T$ for this sequence is

$P(O|H,{\lambda }_p)=\prod _{t=1}^{T}P(O_t|h_t,{\lambda }_p)$

Under the independence assumption for the observations, the joint probability of O and H is

$P(O|H,{\lambda }_p)=b_{h1}(O_1)b_{h2}(O_2)\cdots b_{hT}(O_T)$

The probability of O is calculated by adding this joint probability over all possible state sequences $h_i$:

$\begin{array}{c}\hfill P(O|{\lambda }_p)=\pi a_{h_1{h}_2}{a}_{h_2{h}_3}\cdot \cdot \cdot a_{h_{T-1}{h}_T}\hfill \\ \hfill =\sum _{h_1{h}_2...h_T}{\pi }_i{b}_{h1}(O_1)a_{h_1{h}_2}{a}_{h_2{h}_3}\cdot \cdot \cdot a_{h_{T-1}{h}_T}{b}_{h_T}(O_T)\hfill \end{array}$

We use the following feedforward–feedback process to calculate (10.21).

We define ${\alpha }_t(i)$ as

$\begin{array}{c}\hfill {\alpha }_t(i)=P(O_1,O_2,...O_t,(h_t=S_i|{\lambda }_p))\hfill \\ \hfill {\beta }_t(i)=P(O_{t+1},O_{t+2},...O_T,(h_t=S_i|{\lambda }_p))\hfill \end{array}$

where ${\alpha }_t(i)$ is the probability of the sequence of partial observation (up to time $t<T$) and the state $S_i$. ${\beta }_t(i)$ is the probability of the partial observation sequence from $t+1$.

The feedforward process is as follows: a) start from ${\alpha }_1(i)={\pi }_i{b}_i(O_1)$; then

$a_{t+1}=[\sum _{i=1}^N{\alpha }_t(i)a_{i,j}]b_j(O_1)$

finally, $P(O|{\lambda }_p)\approx \sum _{i=1}^N{\alpha }_t$.

The feedback process is as follows: b) start from ${\beta }_T(i)=1$; then

${\beta }_t(i)=\sum _{j=1}{a}_{ij}{b}_j(O_{t+1}){\beta }_{t+1}(j)$

finally, $P(O|{\lambda }_p)\approx \sum _{j=1}{\beta }_{t+1}(j){\pi }_i{b}_i(O_1)$.

2) Find a sequence $S_i={[s_{i1},...s_{i{v}_i}]}^T$ such that the probability of occurrence of the sequence $O=O_1,O_2,...,O_T$ is an optimal sequence in the sense of

${\delta }_T(i)=\underset{h_1,h_2,...,h_{T-1}}{\max }P(h_1{h}_2...h_T=i,O_1{O}_2...O_T|{\lambda }_p)$

We need the highest probability through a single path. Considering the first t observation:

${\delta }_{t+1}(j)=[\max {\delta }_t(i)a_{ij}]b_j(O_{t+1})$

In order to maximize the equation at each $t,j$, we use the following recursive procedure: a) start from ${\delta }_t(i)={\pi }_i{b}_i(O_1)$; b) then ${\delta }_t(j)=\max [{\delta }_{t-1}(i)a_{ij}]b_j(O_t)$; c) finally,

$S_T^{⁎}=\underset{1⩽i⩽N}{\arg \max }[{\delta }_T(i)]$

This is to find maxim possible state in the codes book, i.e., we want to find

$\underset{1⩽l⩽v_i}{\max }\left\{b_{lj}^i\right\},j=1\cdots N_i$

The index of the maximum $b_{lj}^i$ is $s{c}_j$. Then we obtain the symbol set $\{s{c}_1\cdots s{c}_{N_i}\}$.

3) Use $P(O|{\lambda }_p)$ in Step 1 and the optimal sequence in Step 2 to train the HMM. This means training the ${\lambda }_p$ with $S_p$ to maximize $P[O_p|{\lambda }_p]$.

The value of the state in the instant t is defined as $r\left(t\right)$. The state transition matrix $A_p=\{a_{lj}^p\}$:

$a_{lj}^p=P[r(t+1)=s_{pj}|r\left(t\right)=s_{pl}],1⩽l,j⩽v_p$

(10.25) represents the probability of being in the state $s_{pj}$ at time $t+1$ given the state $s_{il}$ at time t. The initial elements $a_{lj}^i$ of the state transition matrix $A_i\left(1\right)$ is selected as uniform distribution as

$\{\begin{array}{cc}\hfill {\sum }_j{a}_{lj}^i=1\hfill & \hfill l<j\hfill \\ \hfill a_{lj}^i=0\hfill & \hfill \text{otherwise}\hfill \end{array}i=1\cdots n$

The observation probability matrix $B_p=\{b_{lj}^p\}$ is

$b_{lj}^p=P[o_{pl}\text{ at }t|r\left(t\right)=s_{pj}],1⩽l⩽N_p,1⩽j⩽v_p$

This means the states cannot go back, and will jump when the key-points miss from the observed sequences. The initial condition for $b_{lj}^i$ is

$\{\begin{array}{cc}\hfill b_{lj}^i=0\hfill & \hfill o_{il}\text{ is the symbol of the demonstration }l\hfill \\ \hfill b_{lj}^i=P[o_{il}()\text{ at }t|r\left(1\right)=s_{ij}]=1\hfill & \hfill \text{otherwise}\hfill \end{array}$

The initial states distribution ${\pi }_p\left(1\right)=[{\pi }_{p1}\cdots {\pi }_{p{N}_p}]=[1,0\cdots 0]$,

${\pi }_{pj}\left(1\right)=P[r\left(1\right)=s_{pj}],1<j<N_p$

We define

$\begin{array}{c}\hfill {\xi }_t(i,j)=\frac{{\alpha }_t(i)a_{ij}{b}_j(O_{t+1}){\beta }_{t+1}(j)}{P(O|\lambda )}\frac{{\alpha }_t(i)a_{ij}{b}_j(O_{t+1}){\beta }_{t+1}(j)}{\stackrel{N}{\sum _{i=1}}\stackrel{N}{\sum _{j=1}}{\alpha }_t(i)a_{ij}{b}_j(O_{t+1}){\beta }_{t+1}(j)}\hfill \\ \hfill {\gamma }_t(i)=\stackrel{N}{\sum _{j=1}}{\xi }_t(i,j)\hfill \end{array}$

Here, ${\xi }_t(i,j)$ gives the characteristic of a probability measure, and ${\gamma }_t(i)$ is the probability of being $S_T^{⁎}$ given the sequence of observations O.

By the Baum–Welch algorithm [9], the probabilities $P[r(t+1)=s_{ij}|r\left(t\right)=s_{il}]$ and the emission distribution $P[o_{il}\text{ at }t|r\left(t\right)=s_{ij}]$ are

$\begin{array}{c}\hfill a_{ij}=\stackrel{T-1}{\sum _{t=1}}{\xi }_t(i,j)/\stackrel{T-1}{\sum _{t=1}}{\gamma }_t(i)\hfill \\ \hfill b_j(k)=\sum _{s.t{O}_t=v_k}{\gamma }_t(i)/\stackrel{T-1}{\sum _{t=1}}{\gamma }_t(i)\hfill \end{array}$

4) Decode these symbols into values $q_p$.

The output ${\hat{q}}_p$ can be regarded as the decoded values of the observation symbols from the codebook:

${\hat{q}}_p=[{\hat{q}}_{i1}\cdots {\hat{q}}_{iNi}]=[o_{i,s{c}_1}(.,h)\cdots o_{i,s{c}_{N_i}}(.,h)]$

The output of the HMM $\hat{q}$ is a discrete state. In order to generate a smooth trajectory, we use spline interpolation. We use the following third-order (cubic) spline:

$s_t\left(x\right)=a_t{(x-{\hat{q}}_t)}^3+b_t{(x-{\hat{q}}_t)}^2+c_t(x-{\hat{q}}_t)+d_t$

where $t=1,2\cdots T_i$, is the number of the piecewise functions. Since the time index of the output is the key-points $K_i^r$ in (10.8), the total time of the trajectory $\hat{q}$ is

$T_i=\frac{1}{v_i}\sum _{j=1}^{v_i}{k}_{ij},i=1\cdots n$

When the discrete point $x_t$ is the output of the HMM $x_{ij}$, the spline function gives a smooth trajectory ${\hat{q}}^{⁎}\left(t\right)$. After time scale, the desired trajectory is

${\hat{q}}^{⁎}\left(\alpha t\right)$

where α is time scale factor in joint space. Finally, we give the complete scheme of our algorithm; see Fig. 10.5.

10.3 Experiments of learning trajectory

We evaluate the effectiveness of the proposed method with two examples: a two-link revolute joint arm (planar elbow manipulator) and our 4-DoF exoskeleton robot (CINVESRobot-1). The experiments are implemented in Matlab without code optimization. The computer is a PC with Intel Core i3 3.30 GHz processor. We use Kevin Murphy's HMM Toolbox [98] (Baum–Welch algorithm [9]) to train the HMM.

We compare our method (LHMM) with the other two approaches: HMM in task space with the inverse kinematics calculation (THMM), and HMM in joint space with the dynamic time warping (JHMM).

10.3.1 Two-link planar elbow manipulator

We use this example to show our method can learn space and time differences in the demonstrations, and to show how the time difference affects the training results. There are about $8\text{\%}$ (0.1 second) differences.

The definitions of the two-link robot are shown in Fig. 10.6. By direct calculation, the forward kinematic and the inverse kinematics are

$x=l_1\cos q_1+l_2\cos (q_1+q_2),y=l_1\sin q_1+l_2\sin (q_1+q_2)$

(10.30)

$\begin{array}{c}\hfill q_2={\tan }^{-1}\frac{\pm \sqrt{1-D^2}}{D},D=\frac{x^2+y^2-l_1^2-l_2^2}{2l_1{l}_2}\hfill \\ \hfill q_1={\tan }^{-1}\left(\frac{y}{x}\right)-{\tan }^{-1}\left(\frac{l_2\sin q_2}{l_1+l_2\cos q_2}\right)\hfill \end{array}$

(10.31)

1) We first show how our algorithm works with time difference. We draw three similar broken lines in task space with different velocities; see Fig. 10.7. These lines are almost the same in task space. However, in joint space they are different; see Fig. 10.8.

We use $N_1=N_2=100$ as the codebook numbers for the two joints. These values are chosen heuristically to balance computation complexity and the modeling accuracy. The key-point numbers of the joints are obtained from Lloyd's algorithm, for Joint-1, $v_1^1=62$, $v_1^2=63$, $v_1^3=61$; for Joint-2, $v_2^1=76$, $v_2^2=77$, $v_2^3=75$. By (10.18), the state numbers of HMM for each joint are $v_1=63$, $v_2=77$. After the HMM is trained, it generates desired trajectories $q_1^{⁎}$ and $q_2^{⁎}$ with different velocity (10.29). If we select $\alpha =1$, the solid lines Fig. 10.8 are the desired joint angles. We hope that the robot moves two times faster than its demonstrations. We select $\alpha =0.5$, and is shown by the solid lines in Fig. 10.9. It is interesting to see that the corresponding task space trajectory does not change, which is the solid line in Fig. 10.8.

2) The second test is to show how our algorithm works for the space difference. The codebook numbers are also $N_1=N_2=100$. The key-point numbers are $v_1^1=60$, $v_1^2=51$, $v_1^3=55$, $v_2^1=64$, $v_2^2=68$, $v_2^3=71$. The generated trajectory in the task space is the solid line in Fig. 10.10. Their trajectories in joint space are shown in Fig. 10.11.

3) THMM works very well for the speed difference (Fig. 10.8), because the demonstrations in task space are similar, and the inverse kinematics (10.31) are known. However, it does not work well for the space difference (Fig. 10.10), because HMM cannot work well with less demonstrations in task space. On the other hand, our method works in joint space with Lloyd's algorithm. It is not affected by these demonstrations; see Fig. 10.12.

JHMM can work for both speed and space differences. Fig. 10.13 shows the results of the speed difference. The accuracy of JHMM is less than our LHMM; see Fig. 10.10 and Fig. 10.11. The error comes from the dynamic time warping.

The modified HMM (10.17) uses the output, and it can learn the joint space trajectories with small number of demonstrations (three training samples), while the original HMM (10.16) cannot generate the joint space trajectories with three demonstrations.

10.3.2 4-DoF upper limb exoskeleton

The computer control platform for our upper limb exoskeleton is CINVESRobot-1. We first draw a 3-D “O” in the task space three times; see Fig. 10.14. At the same time, the joint angles are saved in the computer as the training trajectories; see Fig. 10.15. Then we use our modified HMM to train a model. Since the drawing speeds are different, the data size of the three demonstration are 629, 576, and 615. We select the codebook numbers $N_1=N_2=N_3=14$. The key-point numbers are $v_1^1=29$, $v_1^2=32$, $v_1^3=30$. (See also Fig. 10.16.) After the HMM is trained, we used it to generate desired trajectories in the joint space; see the solid lines in Fig. 10.17. These trajectories are sent to the lower level controller. The three motors use PID control to follow the trajectories. As a result, the robot draws another “O” in the task space; see the solid line in Fig. 10.18.

An advantage of our joint space method is the time scale of the desired trajectory can be changed such that the “O” in the task space is faster than the demonstrations. The superhuman performance can be realized easily by our modified HMM. Fig. 10.19 shows the trajectory generated by our method is twice as fast as the training demonstrations; here, $\alpha =0.5$ in (10.29).

For this example, we do not compare our method LHMM with THMM, because the task space method THMM does not work with three demonstrations. JHMM can work in joint space for different speeds. Fig. 10.19 shows the result in task space. It is almost “O,” but the accuracy is much less than our LHMM, because the high dimension (3D) approximation of DTW is not good.

10.4 Conclusions

The advantage of programming robot by demonstration in joint space is to avoid the inverse kinematics. The disadvantage is that the demonstrations in joint space are strong time-dependent. Wer uses Lloyd's algorithm and modifies HMM to solve the problems in joint space.

We use Lloyd's algorithm to encode and quantize the input vectors. This approach improves accuracy compared with the dynamic time warping method. The traditional HMM is modified such that it can generate trajectories in joint space. Simulation and experimental results are also proposed. The results show that the proposed method is more effective to generate robot trajectory. Although there are few works in joint space, we believe this direct method can be applied in more robots in the future.