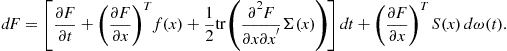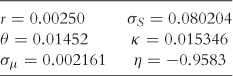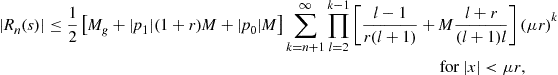On Formulating and Solving Portfolio Decision and Asset Pricing Problems
Yu Chena, Thomas F. Cosimanob and Alex A. Himonasc, aDepartment of Mathematics, Idaho State University, USA, bDepartment of Finance, Mendoza College of Business, University of Notre Dame, USA, cDepartment of Mathematics, University of Notre Dame, USA, [email protected]
Abstract
This chapter discusses computational methods for approximating portfolio and asset pricing problems. Formulation of these problems is usually specified along with components, preferences, payoffs, etc., that are analytic functions. This implies that the solutions to these problems acquire this property, so that these solutions can be accurately approximated by polynomials within a specified region. It is also possible to obtain a uniform upper bound for the approximation error within a subset of this region. Sections 2 and 3 address each problem in discrete time, while Sections 4 and 5 examine these problems in continuous time.
Keywords
Computational methods; Portfolio decisions; Asset pricing problems
JEL Classification Codes
C63; G11; G12
1 Introduction
This chapter discusses the computational methods for portfolio decision and asset pricing problems.1 Financial economists have a common toolkit of assumptions and techniques used to examine portfolio decision and asset pricing problems. For example, in a representative agent model of asset pricing, Menzly et al. (2004) modify a continuous time version of Campbell and Cochrane’s (1999) external habit model by using logarithmic preferences and a linear sensitivity function so that the price-consumption ratio is linear in the state variable. In heterogeneous agent models, Lo and Wang (2006) and Vayanos and Wang (2012) assume a constant absolute risk averse utility and independently and identically distributed shocks to the state variables. The reason is that the equilibrium price and investor’s stock holding are also linear in the state variables. Menzly et al. (2004) and Lo and Wang (2006) motivate their models of marginal utility of wealth using the habit models of Abel (1990) and Campbell and Cochrane (1999). Yet, one can demonstrate that these habit models do not lead to price-dividend functions which are linear in the state variables. For portfolio decision problems, Brennan and Xia (2002, 2005) and Wachter (2002b, 2003) are able to find the closed form solutions to investors’ problems in the face of predictable returns. However, it is well known that these preferences are inconsistent with predictable returns. In each of these papers, the researchers must make a compromise between the needs of the toolkit and realistic financial behavior. In this chapter, we argue that quick and accurate computational methods exist which mitigate the need to make these compromises.
Financial economic problems are usually specified with fundamental components, such as preferences and dividend processes in asset pricing models, that have desirable mathematical properties. Specifically, they are usually assumed to be analytic functions. A function ![]() is analytic on an open interval
is analytic on an open interval ![]() if it can be represented by a power series in some open neighborhood of each
if it can be represented by a power series in some open neighborhood of each ![]() . The radius of convergence,
. The radius of convergence, ![]() , determines the largest interval
, determines the largest interval ![]() in which this power series converges to
in which this power series converges to ![]() . It turns out that the properties of the components of financial models transfer to their solutions for several well-known financial economic problems in both discrete and continuous time. This means that the solutions to these models can be approximated by polynomials within a certain region. In addition, a uniform upper bound for the approximation error can be found in some subset of this region.
. It turns out that the properties of the components of financial models transfer to their solutions for several well-known financial economic problems in both discrete and continuous time. This means that the solutions to these models can be approximated by polynomials within a certain region. In addition, a uniform upper bound for the approximation error can be found in some subset of this region.
The first two sections of this chapter deal with discrete time portfolio decision and asset pricing problems. In discrete time, the models lead to integral equations with unknown functions representing the solutions. As a result, care must be taken to prove that a solution exists within a well-defined vector space. For portfolio decision problems, the integral equations are nonlinear so that there is limited information about the properties of the solutions to these problems. The work of Jin and Judd (2002) can be used to prove that the solutions to these problems are analytic, but little is known about the radii of convergence. As a result, Jin and Judd use polynomial methods, such as the projection method, to approximate the solution. Yet, the error analysis must rely on the relative errors in investor’s Euler equations to assess the accuracy of the approximation.
More is known about the solutions to the representative agent asset pricing problems. In this case, the integral equation is linear in the unknown function. We have shown that several well-known asset pricing models, including Mehra and Prescott (1985), Abel (1990), and Campbell and Cochrane (1999), yield analytic solutions which can be approximated by polynomials in the regions large enough to include any value of interest to financial economists. Having established the radius of convergence about a point of interest, we are able to find a uniform upper bound for the approximation error. The Taylor polynomial approximations to the Mehra and Prescott (1985) and Abel (1990) models can be calculated quickly using Maple. The polynomial approximations to the Campbell and Cochrane (1999) model are more problematic, since the parameter space associated with the existence of a solution restricts the stochastic process for the surplus consumption ratio to be too close to a unit root.2 So, the Taylor polynomial approximations are ill conditioned which suggests the need to use other numerical methods to solve this model. In general, we have found that the Taylor polynomial approximations are accurate representations of solutions to one-dimensional asset pricing models.
Less is known about higher-dimensional asset pricing problems in discrete time. In particular, heterogeneous agent models are a combination of the discrete time portfolio decision and asset pricing problems. In these models, one must solve the decisions of individual agents, which determine the evolution of the distribution of wealth for all investors. Understanding this distribution is essential for solving these models, since investors’ wealth impacts the demand for assets, and subsequently the equilibrium prices of assets. The work by Judd et al. (2000, 2003) has made progress on characterizing when the unique solutions exist for these models. In addition, they rely on alternative polynomial methods to approximate the solutions to these models. As in portfolio decision problems, they use relative errors to determine the accuracy of the approximations.
In the second part of this chapter, we turn to continuous time portfolio decision and asset pricing problems. We start with continuous time portfolio decision problems under stochastic differential utility of Duffie and Epstein (1992a,b) with Kreps and Porteus (1978) functional form, which leads to a second order nonlinear partial differential equation (PDE) depending on the investment horizon and expected return on assets. Currently, this problem is solved for the case of constant relative risk averse utility. Given a solution to the PDE one must check whether this solution satisfies growth conditions. These conditions assure that this solution represents the expected value of the lifetime utility. Given this analysis one must specify the PDE such that it becomes an initial boundary value problem. Consequently, existing methods in mathematics need to be explored to solve and accurately represent the solution to these portfolio problems.
Given the optimal behavior of representative investors we examine asset pricing problems. These problems can be modeled as initial value problems of linear or nonlinear second order differential equations. For this type of problem, the Cauchy-Kovalevsky Theorem can be used to prove that the initial value problem has a unique analytic solution, estimate the radius of convergence, and identify a uniform upper bound on the approximation error. As an example, the one-dimensional asset pricing problem of Campbell and Cochrane (1999) is shown to have an accurate polynomial approximation. The improved behavior, relative to the discrete time Campbell and Cochrane (1999) model, is attributed to two properties of continuous time models. First, the differential equation relies on the local properties rather than the global properties needed for the integral equation. Second, the procedure for calculating the coefficients of the Taylor polynomial approximation is recursive in continuous time, while they have to be determined simultaneously in discrete time. The Cauchy-Kovalevsky Theorem applies to higher-dimensional asset pricing models such as the Wachter (2002a) model which generalizes the Campbell and Cochrane (1999) model. In addition, the Taylor polynomial approximations for the solution to these problems can be calculated quickly. However, additional work needs to be done to bound the approximation error.
We go on to explore the role of initial conditions in the context of the asset pricing problem with stochastic differential utility. In this case the asset pricing problem leads to a differential equation which is mathematically comparable to the investment problem. We first explain how to introduce the initial conditions for this problem when the investor has an infinite investment horizon. We show why the approximation by Campbell et al. (2004) is a first order perturbation of the solution to the original PDE, so that this approximation can be used to estimate initial conditions for the PDE. Given initial conditions it is shown that the Cauchy-Kovalevsky Theorem can be used to quickly and accurately solve the asset pricing problem. This problem can be solved given the initial conditions. Finally, we discuss how one could represent the PDE for the investor’s problem or the asset pricing problem as an initial boundary value problem.
2 Discrete Time Portfolio Decision Making
We follow the development by Chow (1997) for discrete and continuous time dynamic programming. All portfolio decision problems are of the following form: Let ![]() be a vector of
be a vector of ![]() control variables, such as how much to consume and invest in stocks, and
control variables, such as how much to consume and invest in stocks, and ![]() be a vector of
be a vector of ![]() state variables, such as the wealth of the investor and the expected rate of return on stocks. The reward
state variables, such as the wealth of the investor and the expected rate of return on stocks. The reward ![]() of each period is a function of the state and control variables at that time. An example of a reward function is the utility that the investor receives from consuming goods. The problem is to pick
of each period is a function of the state and control variables at that time. An example of a reward function is the utility that the investor receives from consuming goods. The problem is to pick ![]() such that it maximizes the expected present value of future rewards, which formally is stated as:
such that it maximizes the expected present value of future rewards, which formally is stated as:
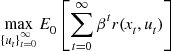 (1)
(1)
![]() (2)
(2)
Here, ![]() is a vector of
is a vector of ![]() random shocks. The actual distributions of these random shocks are specified in the problem.
random shocks. The actual distributions of these random shocks are specified in the problem. ![]() represents the expectation of the reward conditional on information at time
represents the expectation of the reward conditional on information at time ![]() , which in this case would be
, which in this case would be ![]() . The constraint (2) is called the equation of motion for the state variables.
. The constraint (2) is called the equation of motion for the state variables. ![]() determines the expected future value of the state variables given its current value and the control variables.
determines the expected future value of the state variables given its current value and the control variables.
Now introduce a vector ![]() of
of ![]() Lagrange multipliers which are time dependent. The Lagrangian function is
Lagrange multipliers which are time dependent. The Lagrangian function is
 (3)
(3)
Here, the superscript ![]() refers to the transpose of a vector. Take partial derivatives with respect to
refers to the transpose of a vector. Take partial derivatives with respect to ![]() for
for ![]() and
and ![]() for
for ![]() , respectively, and set these derivatives equal to zero, where
, respectively, and set these derivatives equal to zero, where ![]() is the initial state vector. The first order conditions are
is the initial state vector. The first order conditions are
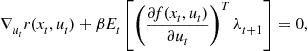 (4)
(4)
and
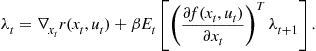 (5)
(5)
Here, ![]() and
and ![]() are the gradient operators with respect to
are the gradient operators with respect to ![]() and
and ![]() , respectively. The first order conditions (4) and (5) are integral equations since
, respectively. The first order conditions (4) and (5) are integral equations since ![]() refers to an integral. As a result, enough structure has to be placed on the problem so that these integral equations have solutions.
refers to an integral. As a result, enough structure has to be placed on the problem so that these integral equations have solutions.
2.1 Investor’s Problem
To illustrate the investor’s problem, let the reward of the investor be the constant relative risk averse utility used by Mehra and Prescott (1985, 2003).
![]() (6)
(6)
where the consumption ![]() is a control variable for the investor. This reward is not a function of the state variable. Assume that the investor can purchase a risk-free bond with constant logarithmic return
is a control variable for the investor. This reward is not a function of the state variable. Assume that the investor can purchase a risk-free bond with constant logarithmic return ![]() or a stock which pays a logarithmic return
or a stock which pays a logarithmic return ![]() . The return on a portfolio of bonds and stocks,
. The return on a portfolio of bonds and stocks, ![]() , is given by
, is given by
![]() (7)
(7)
where the control variable, ![]() , is the percentage of investor’s wealth invested in stocks,
, is the percentage of investor’s wealth invested in stocks, ![]() , and
, and ![]() . The equation of motion for investor’s wealth is
. The equation of motion for investor’s wealth is
![]() (8)
(8)
where ![]() is the current wealth of the investor.
is the current wealth of the investor.
Since Kandel and Stambaugh (1996), the expectation of the logarithm of the return on stocks, ![]() , has been represented by a first order autoregressive process with long run value
, has been represented by a first order autoregressive process with long run value ![]() .
.
![]() (9)
(9)
which is independent of ![]() and
and ![]() .
. ![]() is a random shock to the expected return on stocks. Consequently, the return on stocks is given by
is a random shock to the expected return on stocks. Consequently, the return on stocks is given by
![]() (10)
(10)
Here, it is generally assumed that the correlation between ![]() and
and ![]() is negative based on the evaluation of the data of the return on stocks. In this example, the current wealth
is negative based on the evaluation of the data of the return on stocks. In this example, the current wealth ![]() and the expected return
and the expected return ![]() on stocks are two state variables.
on stocks are two state variables.
In this case, the first order conditions are
![]() (11)
(11)
![]() (12)
(12)
and
![]() (13)
(13)
There is also a transversality or terminal condition at time ![]()
![]() (14)
(14)
In the terminal period, the investor expects to consume all her wealth and any additional wealth in the last period is expected to provide no additional utility.
Combining (11) and (13) yields
![]()
This means that the marginal value of wealth to the investor is equal to the marginal utility of consumption. Substituting this into (13) results in the following equation which determines the consumption by the investor.
 (15)
(15)
The investor compares her loss of utility from consumption today, ![]() , with her gain in utility from payment on the optimal portfolio at a future time,
, with her gain in utility from payment on the optimal portfolio at a future time, ![]() , since she saves part of her initial wealth. Thus, this is just a more sophisticated version of the comparison of present value with future value in which the stochastic discount factor,
, since she saves part of her initial wealth. Thus, this is just a more sophisticated version of the comparison of present value with future value in which the stochastic discount factor, ![]() , is
, is
![]()
Consequently, (15) may be written as
![]() (16)
(16)
In addition, the choice between stocks and bonds in (12) is such that
![]() (17)
(17)
This condition says that the investor chooses the allocation between stocks and bonds so that the expected marginal values of the payoffs from stocks and bonds are identical.
The functional Eqs. (15) and (17) determine the optimal consumption of the investor and the percentage of her wealth allocated to stocks. We seek the functions ![]() and
and ![]() in which
in which ![]() is the current wealth of the investor and
is the current wealth of the investor and ![]() is the expected return on stocks. Once these functions are found, (8) tells us how the wealth of the investor evolves. The equation of motion for the investor’s wealth under this optimal behavior is
is the expected return on stocks. Once these functions are found, (8) tells us how the wealth of the investor evolves. The equation of motion for the investor’s wealth under this optimal behavior is
![]() (18)
(18)
where ![]() refers to the value of wealth at the end of the next period. Here we have used the equations of motion for the return on stocks (10) and its expected value (9). This stochastic difference equation also needs to satisfy the terminal condition (14).
refers to the value of wealth at the end of the next period. Here we have used the equations of motion for the return on stocks (10) and its expected value (9). This stochastic difference equation also needs to satisfy the terminal condition (14).
By assuming a particular cumulative probability distribution for ![]() , say
, say ![]() , we end up with the following integral equation which satisfies the investor’s optimal decisions (15) and (17).
, we end up with the following integral equation which satisfies the investor’s optimal decisions (15) and (17).
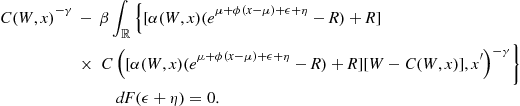 (19)
(19)
As a result, the stochastic discount factor is
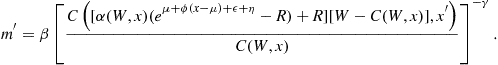
The choice between stocks and bonds is such that
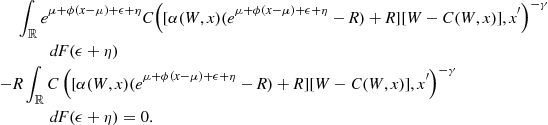 (20)
(20)
We are looking for the investor’s consumption ![]() and allocation
and allocation ![]() to stocks, which satisfy Eqs. (19) and (20). These functions are independent of time so that the path of consumption and allocation to stocks evolves over time as different random shocks to the return on stocks and its expected value impact the stochastic difference equations for the state variables, wealth (18), and the expected return on stocks (9).
to stocks, which satisfy Eqs. (19) and (20). These functions are independent of time so that the path of consumption and allocation to stocks evolves over time as different random shocks to the return on stocks and its expected value impact the stochastic difference equations for the state variables, wealth (18), and the expected return on stocks (9).
Except for certain simple examples, there are no known explicit solutions to these nonlinear integral equations. Altug and Labadie (1994, 2008) provide an analysis of the necessary conditions for the existence of the solution for consumption and allocation to stocks when the support of the probability density function is compact and a general utility function is specified. Researchers appeal to this analysis to suppose that a solution does exist, and immediately proceed to some approximation methods.
2.2 A Survey of Approximation Methods
Campbell (1993), Campbell and Viceira (1999, 2001), and Campbell et al. (2003) use a first order Taylor polynomial approximation of the logarithm of the wealth Eq. (8). In addition, they assume that the return on stocks and consumption growth have a joint log-normal distribution. This transforms the integral equation so that Campbell (1993) can use Euler conditions (15) and (17) to infer the properties of consumption growth. Subsequently, Campbell and Viceira (1999) guess and verify the solution to the approximated problem is log-linear in the state variable for the allocation to stocks and quadratic in the state variable for consumption growth. Campbell and Viceira (2002) use the same method to analyze the investment in long-term bonds. Campbell et al. (2003) extend this work to the case of more than two state variables.
Kandel and Stambaugh (1996) examine a more limited problem in which the investor cares only about the terminal wealth. They use Bayesian priors to specify the probability distribution, ![]() , for the return on stocks. Given the probability distribution, a search is constructed for the optima using a parabolic interpolation. The exact form of this numerical procedure is not specified. The reader is referred to Brent (1973) which is a standard reference on the use of polynomial methods to approximate integrals. Brandt (1999) estimates the first order conditions using the general method of moments.3 For a fixed number of states, he finds the optimal consumption and allocation to stocks in which the Euler conditions (19) and (20) are satisfied. The procedure for finding these fixed states is not specified. Balduzzi and Lynch (1999) and Lynch and Balduzzi (2000) use backward recursion on the value function to find the optimal investment in which the investor cares about only the terminal wealth. Brennan et al. (1997) use finite difference methods to approximate the PDE in the same case. These decisions are being made in the face of transaction cost and predictable return on stocks. The optimal investment choices are the solution to the Bellman equation at discrete points in the interval
, for the return on stocks. Given the probability distribution, a search is constructed for the optima using a parabolic interpolation. The exact form of this numerical procedure is not specified. The reader is referred to Brent (1973) which is a standard reference on the use of polynomial methods to approximate integrals. Brandt (1999) estimates the first order conditions using the general method of moments.3 For a fixed number of states, he finds the optimal consumption and allocation to stocks in which the Euler conditions (19) and (20) are satisfied. The procedure for finding these fixed states is not specified. Balduzzi and Lynch (1999) and Lynch and Balduzzi (2000) use backward recursion on the value function to find the optimal investment in which the investor cares about only the terminal wealth. Brennan et al. (1997) use finite difference methods to approximate the PDE in the same case. These decisions are being made in the face of transaction cost and predictable return on stocks. The optimal investment choices are the solution to the Bellman equation at discrete points in the interval ![]() so that short selling and borrowing are not allowed. They increase the number of discrete points until there is virtually no change in the approximate solution. Barberis (2000) also looks at an investor interested in the terminal wealth. Given a posterior distribution for the return on stocks, he finds the percentage of wealth allocated to stocks among a finite number of points in the interval
so that short selling and borrowing are not allowed. They increase the number of discrete points until there is virtually no change in the approximate solution. Barberis (2000) also looks at an investor interested in the terminal wealth. Given a posterior distribution for the return on stocks, he finds the percentage of wealth allocated to stocks among a finite number of points in the interval ![]() , which maximizes the expected utility of wealth.
, which maximizes the expected utility of wealth.
A similar problem is analyzed in the life-cycle literature. In Carroll (1997) and Gourinchas and Parker (2002), the return on investment is constant and the focus is on permanent labor income so that the second state variable ![]() is expected labor income.4 Both papers use backward induction to calculate the optimal conditions. Carroll (1997) uses a discrete state space and a
is expected labor income.4 Both papers use backward induction to calculate the optimal conditions. Carroll (1997) uses a discrete state space and a ![]() -point cumulative probability distribution function for
-point cumulative probability distribution function for ![]() . Gourinchas and Parker (2002) use Gauss-Hermite quadrature rules from Judd (1998) to form the expectations in (19). They then use a discrete state space to iterate backwards to obtain the optimal consumption rule. Both of these papers provide appendices to explain the algorithms used to find the solution.
. Gourinchas and Parker (2002) use Gauss-Hermite quadrature rules from Judd (1998) to form the expectations in (19). They then use a discrete state space to iterate backwards to obtain the optimal consumption rule. Both of these papers provide appendices to explain the algorithms used to find the solution.
Brandt et al. (2005) provide a more systematic algorithm for solving the optimal consumption and investment problem. First, they use a fourth order Taylor polynomial approximation of the investor’s utility function in the neighborhood of the wealth associated with investing in the risk-free bond and consumption in a deterministic problem.5 Under these circumstances optimal consumption and investment are approximated using the first four moments from the integrals in (19) and (20). The conditional probability distribution for the return on investment is then used to create sample paths for the return and the investor’s information set. Next, they use the sample paths to solve backwards from a terminal date for the optimal consumption and investment decisions of the investor. Finally, they use the parameterized expectations following Den Haan and Marcet (1990) to calculate all the moments in which they use monomials as basis to represent the information set of the investor. To check the accuracy of their method, they rely on the special cases in which the solutions are known. In these circumstances, they can check to see how close their approximate solutions are to the true solutions.
Chacko et al. (2005) use the second order Taylor polynomial approximation to solve the consumption and portfolio problem with CRRA utility and time-varying standard deviation of the return on stocks. They only use the second order Taylor polynomial approximation, since the error of their approximate solution is small for the case in which they know the true solution.
2.3 Polynomial Methods
The projection method of Judd (1992, 1996, 1998) can generalize the approximation method of Chacko et al. (2005) by using orthogonal polynomials. To apply this procedure, we need to assume a probability distribution on the shocks. Suppose that ![]() and
and ![]() are two log-normally distributed random variables, which are consistent with Campbell and Viceira (1999, 2001).6 We then replace the integration with double summation using the Gauss-Hermite quadrature procedure (see Judd, 1998, pp. 261–271). In addition, replace the unknown policy functions for consumption and investment with a linear combination of orthogonal polynomials such as the Chebyshev functions (see Judd, 1998, p. 206):
are two log-normally distributed random variables, which are consistent with Campbell and Viceira (1999, 2001).6 We then replace the integration with double summation using the Gauss-Hermite quadrature procedure (see Judd, 1998, pp. 261–271). In addition, replace the unknown policy functions for consumption and investment with a linear combination of orthogonal polynomials such as the Chebyshev functions (see Judd, 1998, p. 206):
![]() (21)
(21)
and
![]() (22)
(22)
These two functions are only defined in the region ![]() . However, the probability distribution which determines
. However, the probability distribution which determines ![]() and
and ![]() is defined over the entire real line. To account for this possibility we can follow Chen et al. (2008b) by extending
is defined over the entire real line. To account for this possibility we can follow Chen et al. (2008b) by extending ![]() and
and ![]() to
to ![]() .
.
By substituting these hypothesized functions (21) and (22) into the Euler conditions (19) and (20), we end up with two residual equations. These equations are represented by
![]() (23)
(23)
These equations are evaluated at the nodes of Chebyshev polynomials. Newton’s method can then be used to find the vector of coefficients ![]() following
following
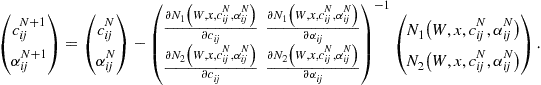 (24)
(24)
Each of the four partial derivatives in (24) are ![]() matrices, where
matrices, where ![]() is the order of the Chebyshev polynomials in (21) and (22). Fortunately, each of these partial derivatives has the same functional form, since they are made up of Chebyshev polynomials and their derivatives. Also, in the implementation of the projection method, the iteration in (24) can be more precise and quicker, since the actual derivatives can be found by using the derivatives of Chebyshev polynomials in (21) and (22).
is the order of the Chebyshev polynomials in (21) and (22). Fortunately, each of these partial derivatives has the same functional form, since they are made up of Chebyshev polynomials and their derivatives. Also, in the implementation of the projection method, the iteration in (24) can be more precise and quicker, since the actual derivatives can be found by using the derivatives of Chebyshev polynomials in (21) and (22).
It is frequently argued that the polynomial method cannot be used in circumstances with occasionally binding constraints such as the cost of security transactions. The Chebyshev parameterized expectation algorithm of Christiano and Fisher (2000) can be used to overcome this problem. Consequently, the above algorithm for solving the investor’s problem can be modified to handle transaction costs. However, the degree of accuracy of such an approximation is still an unresolved problem.
3 Discrete Time Asset Pricing
Another major problem in finance is determining the equilibrium behavior of asset prices. In this problem, it is presumed that investors behave optimally as in the previous section. In addition, this behavior is coordinated within financial markets by the appropriate adjustment of asset prices. To illustrate the problem, suppose that we have a representative investor with utility function (6).7 Previously, we took the return on stocks as given by (10) and chose consumption and the allocation of wealth to stocks. Now suppose that consumption is given and we determine the equilibrium return on stocks. Since there is only one investor and only one asset which pays the dividend ![]() per period, it must be the case in equilibrium that
per period, it must be the case in equilibrium that
![]() (25)
(25)
The problem is to determine the price of a financial asset, ![]() , that yields a random dividend
, that yields a random dividend ![]() each period. The gross return on stocks,
each period. The gross return on stocks, ![]() , is given by the future stock price and dividend relative to the current stock price.
, is given by the future stock price and dividend relative to the current stock price.
![]() (26)
(26)
Combining Eqs. (15), (26), and (25), one finds
![]() (27)
(27)
This equation is rewritten in the form
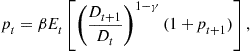 (28)
(28)
where ![]() is the price-dividend function. To complete the model, a stochastic process for dividend is necessary. Let
is the price-dividend function. To complete the model, a stochastic process for dividend is necessary. Let
![]() (29)
(29)
where ![]() , given by (9), is future dividend growth.
, given by (9), is future dividend growth.
Combining (28) with (29) and (9) yields
![]() (30)
(30)
Here, ![]() is the probability density function of the continuous random variable
is the probability density function of the continuous random variable ![]() . The stochastic discount factor in this case is
. The stochastic discount factor in this case is
![]()
where ′ refers to the future value. This integral equation is simpler than that found in the investor’s problem, since this integral equation is linear in the unknown price-dividend function ![]() . This problem was originally specified by Lucas (1978) for a general utility function. Mehra and Prescott (1985) numerically solve this problem for a Bernoulli distributed random variable. Tauchen and Hussey (1991) introduce the quadrature method to approximate the solution of this type of integral equation.
. This problem was originally specified by Lucas (1978) for a general utility function. Mehra and Prescott (1985) numerically solve this problem for a Bernoulli distributed random variable. Tauchen and Hussey (1991) introduce the quadrature method to approximate the solution of this type of integral equation.
3.1 Analytic Method
Calin et al. (2005) introduce the analytic method to solve this problem. The benefit of this method is that it identifies when the solution may be approximated by a polynomial within a certain interval. In addition, the approximation errors can be estimated. In Chen et al. (2008a,b), they apply this method to the more general utility functions developed by Abel (1990) and Campbell and Cochrane (1999), respectively. The analytic method to solve these asset pricing problems may be illustrated with the Mehra and Prescott model.
Step 1: Simplify the integral equation and identify the solution space.
Use the change of variable, ![]() , to rewrite (30).
, to rewrite (30).
![]() (31)
(31)
The advantage of this change of variable is that the properties of the probability density function ![]() are known. For example, Calin et al. (2005) use the Gaussian distribution with mean
are known. For example, Calin et al. (2005) use the Gaussian distribution with mean ![]() and standard deviation
and standard deviation ![]() . The integral equation is
. The integral equation is
![]() (32)
(32)
where ![]() ,
, ![]() , and
, and ![]() . The support of the Gaussian distributed probability density function is not compact, so the usual contraction mapping theorem (see Altug and Labadie, 2008) is not applicable. Yet, once the integral function is written in this form, the price-dividend function cannot grow faster than
. The support of the Gaussian distributed probability density function is not compact, so the usual contraction mapping theorem (see Altug and Labadie, 2008) is not applicable. Yet, once the integral function is written in this form, the price-dividend function cannot grow faster than ![]() . As a result, the solution lies in the following vector space.
. As a result, the solution lies in the following vector space.
Step 2: Verify the existence and uniqueness of the solution to the integral equation (32) in ![]() .
.
Calin et al. construct a linear transformation ![]() given by
given by
![]() (33)
(33)
where ![]() and
and ![]() . The mapping (33) has a unique fixed point in the vector space
. The mapping (33) has a unique fixed point in the vector space ![]() , which turns out to be the solution to the integral equation (32), as long as a new combination of parameters satisfies
, which turns out to be the solution to the integral equation (32), as long as a new combination of parameters satisfies
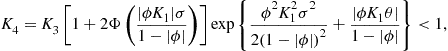
where ![]() . This condition is satisfied for the Mehra and Prescott parameters.
. This condition is satisfied for the Mehra and Prescott parameters.
Step 3: Verify that the solution to the integral equation (32) is analytic.
Whether or not a particular asset pricing problem has an analytic solution relies on the properties of the pricing kernel, the equation of motion for the state variable, and the probability density function. Each of these contributes to the integrand in the integral equation (32) so that the analyticity may be established in some interval. First, a summary of analytic functions is provided.
Analytic functions: To understand analytic functions, a brief introduction to holomorphic functions in one complex variable follows. These properties are also valid in several complex variables with some additional technical complications. Let ![]() be a complex-valued function of
be a complex-valued function of ![]() defined in an open set (domain)
defined in an open set (domain) ![]() of the complex plane
of the complex plane ![]() . Suppose that this function is smooth and it can be expressed as
. Suppose that this function is smooth and it can be expressed as
 (34)
(34)
where ![]() denotes the
denotes the ![]() order complex derivative of
order complex derivative of ![]() at
at ![]() (the usual calculus formulas for real differentiation hold true for complex differentiation, too). Separating this function into its real and imaginary parts
(the usual calculus formulas for real differentiation hold true for complex differentiation, too). Separating this function into its real and imaginary parts ![]() , we obtain
, we obtain
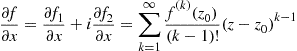
and
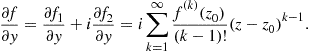
Multiplying the second equation by ![]() and adding it to the first yields8
and adding it to the first yields8
![]() (35)
(35)
This equation is called the Cauchy-Riemann equation, which can also be written in the form:
![]()
This motivates the following definition.
In fact, it can be shown that ![]() is holomorphic in
is holomorphic in ![]() if
if ![]() in the sense of distribution theory (weak derivatives). A proof of this fact can be found in Hörmander (1983, p. 110, Theorem 4.4.1). The basic theory of holomorphic functions can be found in the classical text of Ahlfors (1979) or in Hörmander (1979), where it is presented in the more general context. There, it is proved that a holomorphic function has derivatives of any order, and therefore its Taylor series can be formed. Moreover, for each
in the sense of distribution theory (weak derivatives). A proof of this fact can be found in Hörmander (1983, p. 110, Theorem 4.4.1). The basic theory of holomorphic functions can be found in the classical text of Ahlfors (1979) or in Hörmander (1979), where it is presented in the more general context. There, it is proved that a holomorphic function has derivatives of any order, and therefore its Taylor series can be formed. Moreover, for each ![]() there is a (maximal) number
there is a (maximal) number ![]() , called the radius of convergence for
, called the radius of convergence for ![]() at
at ![]() , such that
, such that ![]() can be represented by its Taylor series, like (34), for
can be represented by its Taylor series, like (34), for ![]() .
.
The “calculus” definition of an analytic function ![]() of a real variable
of a real variable ![]() in an open interval
in an open interval ![]() is that it is in
is that it is in ![]() and at each point
and at each point ![]() the remainder
the remainder ![]() of the
of the ![]() degree Taylor polynomial approximation of
degree Taylor polynomial approximation of ![]() tends to zero as
tends to zero as ![]() when
when ![]() . By complexifying
. By complexifying ![]() to
to ![]() , we obtain a holomorphic function
, we obtain a holomorphic function ![]() in an open subset
in an open subset ![]() of
of ![]() , and we may think of
, and we may think of ![]() as the restriction of
as the restriction of ![]() from
from ![]() to
to ![]() .
.
Using complex variables allows us to determine the precise radius of convergence, ![]() .
.
Now we are ready to show that the solution to the integral equation (32) is analytic in ![]() . Suppose that the function
. Suppose that the function ![]() in the vector space
in the vector space ![]() is the solution to this integral equation. It suffices to show that
is the solution to this integral equation. It suffices to show that
![]() (36)
(36)
is analytic at each ![]() . In this step, we complexify
. In this step, we complexify ![]() so that
so that
![]() (37)
(37)
![]() is analytic if
is analytic if
![]() (38)
(38)
Since ![]() is bounded on any compact set in the complex plane, there exists
is bounded on any compact set in the complex plane, there exists ![]() depending on
depending on ![]() such that
such that
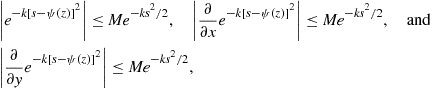 (39)
(39)
where ![]() and
and ![]() . By the Dominated Convergence Theorem (see Folland, 1984, pp. 53–54),
. By the Dominated Convergence Theorem (see Folland, 1984, pp. 53–54), ![]() has continuous partial derivatives with respect to
has continuous partial derivatives with respect to ![]() and
and ![]() , and the partial derivatives can pass through the integral sign in (37). Consequently, we get
, and the partial derivatives can pass through the integral sign in (37). Consequently, we get ![]() for
for ![]() , since
, since
![]() (40)
(40)
Thus, the price-dividend function ![]() is analytic over
is analytic over ![]() .
.
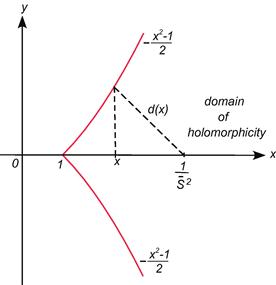
Figure 1 Finding radius of convergence for Example 1.
Step 4: Find the numerical solution to the integral equation (32).
Having established the mathematical properties of the solution to the integral Eq. (32), one can proceed to the numerical approximation of the solution. It is easier to work with a transformed price-dividend function
![]() (41)
(41)
since it reduces the number of summations necessary in the numerical algorithm. As a result, the integral equation (32) is changed to
![]() (42)
(42)
The solution of the integral equation (42) can be approximated by the ![]() order Taylor polynomial around the point
order Taylor polynomial around the point ![]()
![]() (43)
(43)
Alternatively, one could use orthogonal polynomials such as (21) to construct the approximation, which have superior numerical properties. As in the projection method, the polynomial approximation (43) is substituted into the integral equation (42) to yield a system of equations in the undetermined coefficients ![]() , which is given in Calin et al. In this case, the system is linear, since the integral equation (42) is linear in the unknown function.
, which is given in Calin et al. In this case, the system is linear, since the integral equation (42) is linear in the unknown function.
Step 5: Estimate the approximation error.
An important benefit of the analytic method is that one can estimate the difference between the polynomial approximation and the true solution. In particular, Cauchy’s integral formula can be used to bound all the derivatives of the transformed price-dividend function which is used to estimate the approximation error. Let ![]() be the circle of radius
be the circle of radius ![]() centered at
centered at ![]() in the complex plane. Figure 1 provides an example when
in the complex plane. Figure 1 provides an example when ![]() and
and ![]() . Cauchy’s integral formula (see Corollary 5.9 in Conway, 1973) gives
. Cauchy’s integral formula (see Corollary 5.9 in Conway, 1973) gives
![]() (44)
(44)
![]() is the contour integral on the path
is the contour integral on the path ![]() . Each point
. Each point ![]() on
on ![]() satisfies
satisfies ![]() and
and ![]() . The proof of the existence and uniqueness of
. The proof of the existence and uniqueness of ![]() provides an upper bound
provides an upper bound ![]() on
on ![]() where
where ![]() so that
so that
![]() (45)
(45)
Let ![]() be the
be the ![]() order Taylor polynomial of
order Taylor polynomial of ![]() about
about ![]() . Then the Taylor remainder, given by
. Then the Taylor remainder, given by ![]() , satisfies
, satisfies
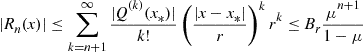 (46)
(46)
for ![]() , where
, where ![]() . Thus, the approximation error is estimated by
. Thus, the approximation error is estimated by
![]() (47)
(47)
Up to now the error in the second summand in (47) has not been calculated. This error occurs because the coefficients ![]() in
in ![]() could be different from the true values of
could be different from the true values of ![]() . In practice, these differences are small when
. In practice, these differences are small when ![]() is small.
is small.
Having estimated the approximation error, we may examine other numerical schemes to learn the tradeoffs of these schemes. For example, Calin et al. solve the Mehra and Prescott model using both the analytic method and Tauchen and Hussey’s (1991) procedure. In the analytic method ![]() is increased to at least
is increased to at least ![]() in (43) for the approximation error to be less than
in (43) for the approximation error to be less than ![]() . Consequently, even for the basic Mehra and Prescott model, a lower degree (
. Consequently, even for the basic Mehra and Prescott model, a lower degree (![]() or
or ![]() ) polynomial is not sufficient to get an accurate representation of the true solution. They also find that using
) polynomial is not sufficient to get an accurate representation of the true solution. They also find that using ![]() for the interval of integration in Tauchen and Hussey’s procedure is not sufficient to obtain an accurate solution. In this case, the price-dividend ratio is about
for the interval of integration in Tauchen and Hussey’s procedure is not sufficient to obtain an accurate solution. In this case, the price-dividend ratio is about ![]() below the true price-dividend ratio, and the interval of integration must increase to
below the true price-dividend ratio, and the interval of integration must increase to ![]() to remove this error. Thus, Tauchen and Hussey’s procedure should use a larger support than what one would expect from intuition.
to remove this error. Thus, Tauchen and Hussey’s procedure should use a larger support than what one would expect from intuition.
3.2 More Complicated Models
Chen et al. (2008a,b) have used the analytic method to study the solution to Abel’s (1990) and Campbell and Cochrane’s (1999) models, respectively. In Abel’s model, (6) is replaced with
 (48)
(48)
where ![]() is the vector of state variables.9 Everything else stays the same as in the Mehra and Prescott (1985) model.
is the vector of state variables.9 Everything else stays the same as in the Mehra and Prescott (1985) model. ![]() represents what you consumed in the past period, while
represents what you consumed in the past period, while ![]() is the consumption of your neighbor. The equations of motion for these two state variables are trivial, i.e.,
is the consumption of your neighbor. The equations of motion for these two state variables are trivial, i.e., ![]() and
and ![]() .10 If
.10 If ![]() , then this reduces to the Mehra and Prescott model.
, then this reduces to the Mehra and Prescott model.
In this case, the integral equation (30) becomes
 (49)
(49)
where ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . The stochastic discount factor is more complicated and is given by
. The stochastic discount factor is more complicated and is given by
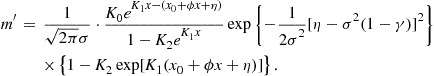
While the integral equation (49) is more complicated, a new transformed price-dividend function is introduced.
![]() (50)
(50)
so that this integral equation becomes
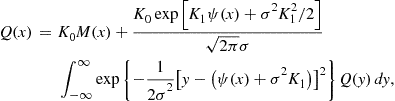 (51)
(51)
where
![]() (52)
(52)
The transformed integral equation (49) is similar to (32) so that the analytic method applies to this model as well. Step 2 leads to an explicit formula for the transformed price-dividend function. In addition, Chen et al. (2008a) show that this explicit solution is an analytic function so that the analytic method is not necessary.
The main lesson from the analysis of the price-dividend function in the Abel model is the importance of the specification of the probability distribution for the future dividend growth.11 Following the Mehra and Prescott model, the probability distribution in (49) is assumed to be a Gaussian distribution; however, the price-dividend function ![]() is only defined on the interval
is only defined on the interval ![]() . This restriction occurs since the marginal utility of consumption
. This restriction occurs since the marginal utility of consumption ![]() is non-positive outside this interval. Consequently, one has to be careful to specify a probability distribution such that the economic properties of the model are sensible. Chen et al. (2008a) show that by restricting to
is non-positive outside this interval. Consequently, one has to be careful to specify a probability distribution such that the economic properties of the model are sensible. Chen et al. (2008a) show that by restricting to ![]() such that
such that ![]() , an error in the numerical approximation is introduced. This error is bounded by
, an error in the numerical approximation is introduced. This error is bounded by ![]() cents out of a million dollars worth of stock for dividend growth within
cents out of a million dollars worth of stock for dividend growth within ![]() , when the parameter values are chosen to match the equity premium.
, when the parameter values are chosen to match the equity premium.
Chen et al. (2008b) solve the model by Campbell and Cochrane (1999). Here the reward function (6) becomes
![]() (53)
(53)
where ![]() is the individual’s consumption at time
is the individual’s consumption at time ![]() is the surplus consumption ratio at time
is the surplus consumption ratio at time ![]() is the average consumption of all individuals at time
is the average consumption of all individuals at time ![]() , and
, and ![]() is their habitual level of consumption at time
is their habitual level of consumption at time ![]() .12
.12
The control variable is now ![]() and the state variable is
and the state variable is ![]() . To maintain positive values for these variables, Campbell and Cochrane define
. To maintain positive values for these variables, Campbell and Cochrane define ![]() and
and ![]() . The equation of motion for the state variable is given as follows: The surplus consumption ratio
. The equation of motion for the state variable is given as follows: The surplus consumption ratio ![]() satisfies the AR(1) process with
satisfies the AR(1) process with ![]() ,
,
![]() (54)
(54)
Consumption growth follows a normal distribution such that
![]() (55)
(55)
To introduce heteroscedasticity of the random shock to the consumption growth, Campbell and Cochrane introduce the sensitivity function:
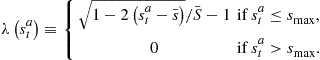 (56)
(56)
Here,13
![]() (57)
(57)
Campbell and Cochrane assume that the dividend growth follows
![]()
As a result, the dividend growth (9) is the same as consumption growth plus a random shock which is correlated with the random shock to consumption growth. The random shock to the dividend growth follows a log-normal distribution.
The integral equation for the price-dividend function is
![]() (58)
(58)
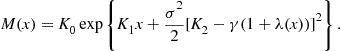 (59)
(59)
Now, the state variable is ![]() and the constants are
and the constants are
![]() (60)
(60)
In this case the stochastic discount factor is
![]()
Thus, each asset pricing model makes the stochastic discount factor more complex, so that it better represents the empirical properties of the price-dividend and asset returns.
The integral equation (58) is similar to that found in the Mehra and Prescott model and the Abel model. The main difference is that the sensitivity function is written as
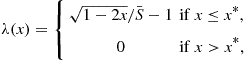 (61)
(61)
where ![]() . This sensitivity function is designed to magnify uncertainty during bad times and to minimize it during good times. The purpose of this modification is to introduce volatility in the return on stocks, which is low (high) during good (bad) times. This mimics the empirical properties of stock returns. Chen et al. (2008b) show that this generates multiple problems in the implementation of the analytic method. On the other hand, it illustrates the ability of the analytic method to handle more complicated integral equations. In step 1 of the analytic method, the form of
. This sensitivity function is designed to magnify uncertainty during bad times and to minimize it during good times. The purpose of this modification is to introduce volatility in the return on stocks, which is low (high) during good (bad) times. This mimics the empirical properties of stock returns. Chen et al. (2008b) show that this generates multiple problems in the implementation of the analytic method. On the other hand, it illustrates the ability of the analytic method to handle more complicated integral equations. In step 1 of the analytic method, the form of ![]() , which measures how much the investors discount the future, determines the conditions for the existence and uniqueness of the price-dividend function.
, which measures how much the investors discount the future, determines the conditions for the existence and uniqueness of the price-dividend function. ![]() has the property that
has the property that ![]() for all
for all ![]() , where
, where
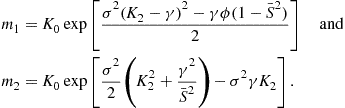 (62)
(62)
As a result, one would seek a solution in the following vector space:
Chen et al. (2008b) show that under the assumptions ![]() , and
, and ![]() , the integral equation (58) has a unique solution in the space
, the integral equation (58) has a unique solution in the space ![]() . The problem is that the parameters of Campbell and Cochrane do not satisfy the condition
. The problem is that the parameters of Campbell and Cochrane do not satisfy the condition ![]() , so that the discounting factor is too big. Given that Campbell and Cochrane want to match the Sharpe ratio, which is the ratio of excess return on stocks relative to its standard deviation. It turns out that the persistence of the surplus consumption ratio must be almost a unit root, i.e.,
, so that the discounting factor is too big. Given that Campbell and Cochrane want to match the Sharpe ratio, which is the ratio of excess return on stocks relative to its standard deviation. It turns out that the persistence of the surplus consumption ratio must be almost a unit root, i.e., ![]() . The problem can be traced to the term
. The problem can be traced to the term ![]() in the exponent of
in the exponent of ![]() . Campbell and Cochrane show that this term is approximately the Sharpe ratio at the steady-state value for the surplus consumption ratio, which is about
. Campbell and Cochrane show that this term is approximately the Sharpe ratio at the steady-state value for the surplus consumption ratio, which is about ![]() per quarter. This value is enough to push the discounting factor above one so that a solution in
per quarter. This value is enough to push the discounting factor above one so that a solution in ![]() cannot be found.
cannot be found.
Chen et al. (2008b) presumed that Campbell and Cochrane did not want dividend growth to be unbounded both above and below. In fact, they explicitly ruled this out in their computer program. As a result, they restricted the price level outside a reasonable range for dividend growth. In this case, the transformed price-dividend function is
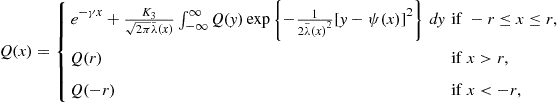 (63)
(63)
where ![]() ,
, ![]() ,
, ![]() , and
, and
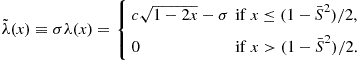 (64)
(64)
Here, ![]() .
.
In the new integral equation (63), one can see why the original integral equation fails to have a solution over the entire real line. In the calculation of the expected transformed price-dividend function, the probability distribution is a Gaussian distribution with mean ![]() and standard deviation
and standard deviation ![]() . The functional form of
. The functional form of ![]() implies that the standard deviation of the transformed price-dividend ratio tends to
implies that the standard deviation of the transformed price-dividend ratio tends to ![]() as the dividend growth approach
as the dividend growth approach ![]() . Consequently, the integral in (63) tends to
. Consequently, the integral in (63) tends to ![]() for extreme negative dividend growth. To avoid this possibility, the new integral equation restricts the transformed price-dividend function to
for extreme negative dividend growth. To avoid this possibility, the new integral equation restricts the transformed price-dividend function to ![]() (
(![]() ) for dividend growth less (more) than
) for dividend growth less (more) than ![]() (
(![]() ). In the calibration of the model,
). In the calibration of the model, ![]() was set at
was set at ![]() per month so that the model applies for all historically observed dividend growth.
per month so that the model applies for all historically observed dividend growth.
This new integral equation for the Campbell and Cochrane model has a unique solution ![]() in the vector space of all continuous and bounded functions defined in
in the vector space of all continuous and bounded functions defined in ![]() when
when ![]() . In addition, the supremum norm of the transformed price-dividend function satisfies
. In addition, the supremum norm of the transformed price-dividend function satisfies
![]() (65)
(65)
Thus, step 2 can be successfully completed for the Campbell and Cochrane model. Consequently, the value of correctly identifying the vector space in step 2 is demonstrated in this model.
The new integral equation (63) does have a solution under the parameter values of Campbell and Cochrane. However, the supremum norm is too small so that the price-dividend function and Sharpe ratio cannot match their historic values. Chen et al. (2008b) demonstrate that a feasible solution, consistent with the Sharpe ratio, can occur for a coefficient of risk aversion ![]() and a persistence of the surplus consumption ratio
and a persistence of the surplus consumption ratio ![]() .
.
Step 3 can also be completed for the Campbell and Cochrane model. In this case, the problem is to find the domain ![]() in the complex plane
in the complex plane ![]() such that
such that
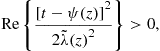 (66)
(66)
where Re refers to real part. This domain is
![]()
As a result, the solution to the transformed price-dividend function is analytic within this domain, since the integral in (63) and its derivative are well defined. The final part of this step is to find the radius of convergence which is the minimum distance ![]() from the point
from the point ![]() on the real line to the boundary of
on the real line to the boundary of ![]() . This problem is illustrated in Figure 2. This is a simple maximization problem which yields a radius of convergence around
. This problem is illustrated in Figure 2. This is a simple maximization problem which yields a radius of convergence around ![]() for
for ![]() . This value is close to the point
. This value is close to the point ![]() at which the sensitivity function (64) becomes non-differentiable. Thus, the analytic method can be applied to this more complicated model.
at which the sensitivity function (64) becomes non-differentiable. Thus, the analytic method can be applied to this more complicated model.
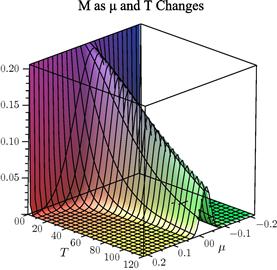
Figure 3 Fundamental solution (121) as time horizon ![]() quarters and expected excess return on stocks
quarters and expected excess return on stocks ![]() , given parameters in Table 1 and
, given parameters in Table 1 and ![]() , and
, and ![]() .
.
Step 4 is also straightforward when one chooses ![]() to satisfy the additional condition:
to satisfy the additional condition:
![]() (67)
(67)
Since the Taylor series of ![]() about the origin converges to
about the origin converges to ![]() for
for ![]() satisfies equation:
satisfies equation:
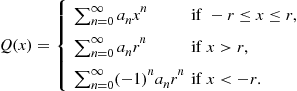 (68)
(68)
Chen et al. (2008b) derive a system of linear equations which solves for the coefficients ![]() in (68). This derivation includes all algebraic manipulations necessary to design an efficient computer program.
in (68). This derivation includes all algebraic manipulations necessary to design an efficient computer program.
Finally, step 5 is completed for the Campbell and Cochrane model as in the Mehra and Prescott model. In this case, the upper bound ![]() in (45) depends on the supremum norm of the transformed price-dividend function (65) and the radius of convergence. Thus, the analytic method can be used to systematically approximate the solution to an asset pricing model as complicated as that posed by Campbell and Cochrane.
in (45) depends on the supremum norm of the transformed price-dividend function (65) and the radius of convergence. Thus, the analytic method can be used to systematically approximate the solution to an asset pricing model as complicated as that posed by Campbell and Cochrane.
Step 2 shows that the persistence of the surplus consumption ratio must be close to a unit root. This means that a large number of coefficients need to be calculated for the solution to be stable. Unfortunately, Chen et al.’s (2008b) Fortran program does not allow for higher precision so that the calculation of the coefficients was not feasible in this case. Their Maple program does allow for higher precision but is too slow to calculate the required number of coefficients.
3.3 Alternative Asset Pricing Models
More recently, Bansal and Yaron (2004) use the recursive preferences of Epstein and Zin (1989, 1990, 1991) and functional form of Kreps and Porteus (1978) to examine the empirical behavior of stock returns. In this case, the reward becomes
![]() (69)
(69)
Here, the utility today, ![]() , depends on the consumption today,
, depends on the consumption today, ![]() , and the utility that the investor expects to receive in the future,
, and the utility that the investor expects to receive in the future, ![]() . As a result, the control variable is
. As a result, the control variable is ![]() and the state variable is
and the state variable is ![]() . The intertemporal rate of substitution,
. The intertemporal rate of substitution, ![]() , measures how much the investor is willing to substitute the consumption today for more utility in the future.
, measures how much the investor is willing to substitute the consumption today for more utility in the future.
For the representative agent economy, in which consumption equals dividends, the equilibrium condition for the price-dividend function becomes
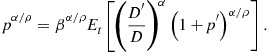 (74)
(74)
This model leads to the integral equation
![]() (75)
(75)
This integral equation is no longer linear in the unknown price-divided function ![]() , since the stochastic discount factor is nonlinear.
, since the stochastic discount factor is nonlinear.
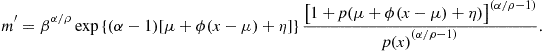
As a result, the analytic method outlined for the Mehra and Prescott model cannot directly be applied to the Epstein and Zin model. In particular, the integral equation (74) is nonlinear as in the portfolio decision problem (19) and (20), so Judd’s (1992) projection method has been used by Bansal and Yaron (2004) to approximate the solution of this model.
In summary, the analytic method can be used to solve most one-dimensional discrete time asset pricing models. In all of these models, the price-dividend ratio and hence the return on stocks (26) can be accurately approximated by a high order polynomial. For example, the order of the polynomial is ![]() in the Mehra and Prescott case. The analytic method also points out the need to use a large support for the probability density function when the Gaussian quadrature procedure of Tauchen and Hussey (1991) is used. In particular, there is an error of
in the Mehra and Prescott case. The analytic method also points out the need to use a large support for the probability density function when the Gaussian quadrature procedure of Tauchen and Hussey (1991) is used. In particular, there is an error of ![]() in the price-dividend ratio when the support is
in the price-dividend ratio when the support is ![]() even though the relative error is driven to zero. To minimize this error, one must consider the support of
even though the relative error is driven to zero. To minimize this error, one must consider the support of ![]() . Chen et al. (2008b) need to use even higher order polynomial approximations to accurately solve the Campbell and Cochrane (1999) model.
. Chen et al. (2008b) need to use even higher order polynomial approximations to accurately solve the Campbell and Cochrane (1999) model.
3.4 A Survey of Log-Linearized Approximations
The conclusion from using the analytic method to solve well-known asset pricing models begs the question: How many anomalies in financial markets are the result of low order polynomial approximations commonly used in the research on financial markets? For example, ever since Campbell and Shiller (1988a,b) it is common to explain the logarithm of the return on stocks in terms of unanticipated changes in the future dividends or discount rate. Campbell and Shiller start with (26) which may be written as
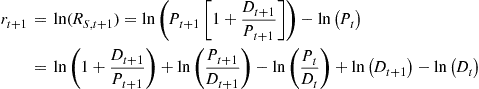 (76)
(76)
Campbell and Shiller do not have the solution to any particular asset pricing model so they do not know ![]() or
or ![]() . As a result, they calculate a first order Taylor’s polynomial approximation of the first term near the point
. As a result, they calculate a first order Taylor’s polynomial approximation of the first term near the point ![]() , where
, where ![]() is the stationary point of dividend growth (9).15
is the stationary point of dividend growth (9).15
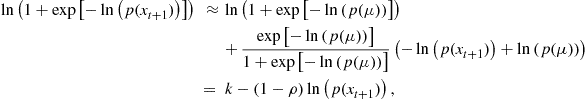
where ![]() and
and ![]() . Substitute this approximation into (76) to yield a first order stochastic difference equation in
. Substitute this approximation into (76) to yield a first order stochastic difference equation in ![]() , which has forcing term
, which has forcing term ![]() , such that
, such that
![]() (77)
(77)
If this difference equation is solved for ![]() and substituted back into (77), then one finds that the unanticipated changes in stock returns are given by
and substituted back into (77), then one finds that the unanticipated changes in stock returns are given by
 (78)
(78)
The first term is the news about future dividend growth, while the second term refers to the news about future rates of return. Campbell (1991), Campbell and Vuolteenaho (2004), and Campbell et al. (2010) among others find that most of the unanticipated changes in the return on stocks may be associated with the news on the future return on stocks rather than the news on the dividend growth. For example, Campbell finds that less than one half of the variation in the return on stocks is due to the news on the dividend growth. Yet, if one has the solution to one of the various models for the price-dividend function ![]() such as Campbell and Cochrane (1999) or Bansal and Yaron (2004), then it is clear from (76) that the unanticipated changes in the return on stocks should only be a function of the unanticipated changes in the state variables
such as Campbell and Cochrane (1999) or Bansal and Yaron (2004), then it is clear from (76) that the unanticipated changes in the return on stocks should only be a function of the unanticipated changes in the state variables ![]() , i.e.,
, i.e., ![]() . Thus, the unanticipated movement in the return on stocks from the news must be associated with a nonlinear relation between the future state variables and return on stocks. Future research should examine how the nonlinear relation between the state variables and the return on stocks color the understanding of what causes the return on stocks to move.
. Thus, the unanticipated movement in the return on stocks from the news must be associated with a nonlinear relation between the future state variables and return on stocks. Future research should examine how the nonlinear relation between the state variables and the return on stocks color the understanding of what causes the return on stocks to move.
Bansal and Yaron (2004) also rely on the Campbell and Shiller (1988a,b) approximation to solve their model with Epstein and Zin preferences. In their model, they separate out the dividend growth from the consumption growth, which they assume is driven by the same state variable, ![]() . This state variable is assumed to be a first order autoregressive process such as (9) with
. This state variable is assumed to be a first order autoregressive process such as (9) with ![]() . As a result, they hypothesize a function for the logarithm of the price-dividend function, which is linear in this state variable. Next, they log-linearize the return on stocks as in Campbell and Shiller. The guess for the price-dividend function and the approximation for the return on stocks are then substituted into the Euler condition (74). They then determine the two coefficients in the guess for the price-dividend function.16 Subsequently, Bansal and Yaron use the projection method to find the approximate solution of the model, which they say is “quite close to” the first order approximation. Yet, they do not say the order of the polynomial approximation used in the projection method.17 Given the close relation between the integral in (75) and that found in the Mehra and Prescott model (32), one would expect the need for at least a 9th order polynomial for an accurate approximation of the solution to the Bansal and Yaron model. Consequently, the long run risk models should also be examined to see whether or not the interpretations and approximation errors are influenced by low order polynomial approximations.
. As a result, they hypothesize a function for the logarithm of the price-dividend function, which is linear in this state variable. Next, they log-linearize the return on stocks as in Campbell and Shiller. The guess for the price-dividend function and the approximation for the return on stocks are then substituted into the Euler condition (74). They then determine the two coefficients in the guess for the price-dividend function.16 Subsequently, Bansal and Yaron use the projection method to find the approximate solution of the model, which they say is “quite close to” the first order approximation. Yet, they do not say the order of the polynomial approximation used in the projection method.17 Given the close relation between the integral in (75) and that found in the Mehra and Prescott model (32), one would expect the need for at least a 9th order polynomial for an accurate approximation of the solution to the Bansal and Yaron model. Consequently, the long run risk models should also be examined to see whether or not the interpretations and approximation errors are influenced by low order polynomial approximations.
An alternative approach to developing log-linearized empirical models of asset returns is illustrated by Gabaix (2009). In this case, he identifies a linear generating process. Here, the stochastic process for dividend growth is found such that the price-dividend ratio is linear in the current state variable. A more sophisticated version of this approach is developed by Le et al. (2010) who incorporate the properties of continuous time affine term structure models into discrete time asset pricing models.18 The idea is to find a probability density function which yields an affine moment generating function under the risk neutral distribution
![]() (79)
(79)
Here ![]() indicates the expectation is with respect to the risk neutral distribution and
indicates the expectation is with respect to the risk neutral distribution and ![]() is now a vector of all state variables. They show that a gamma probability distribution in which the random parameters follow a Poisson probability distribution leads to this affine moment generating function. In this case the functions
is now a vector of all state variables. They show that a gamma probability distribution in which the random parameters follow a Poisson probability distribution leads to this affine moment generating function. In this case the functions ![]() and
and ![]() have explicit formulas so that one can derive the affine bond prices using well-known recursive rules.19 Consequently, the probability distribution under the risk neutral measure,
have explicit formulas so that one can derive the affine bond prices using well-known recursive rules.19 Consequently, the probability distribution under the risk neutral measure, ![]() , has an explicit functional form. One then specifies a market price of risk
, has an explicit functional form. One then specifies a market price of risk ![]() such that the Radon-Nikodym derivative has the functional form
such that the Radon-Nikodym derivative has the functional form
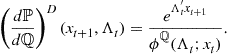 (80)
(80)
Thus, the physical distribution ![]() of the state vector is known and given by
of the state vector is known and given by
![]() (81)
(81)
As a result, the stochastic discount factor is given by
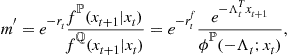 (82)
(82)
since ![]() . Also,
. Also, ![]() is the risk-free interest rate which is assumed to be linear in the current state variables,
is the risk-free interest rate which is assumed to be linear in the current state variables, ![]() . Given the stochastic discount factor one can proceed to price any financial asset.20 To illustrate how this procedure can be applied to a particular asset pricing model Le, Singleton, and Dai specify a stochastic process for the inverse of the surplus consumption ratio in Campbell and Cochrane (1999) and Wachter (2006). This stochastic process has the risk neutral probability distribution with moment generating function (79). In addition, they derive a new sensitivity function for (56) which satisfies the local properties in Campbell and Cochrane’s original model.
. Given the stochastic discount factor one can proceed to price any financial asset.20 To illustrate how this procedure can be applied to a particular asset pricing model Le, Singleton, and Dai specify a stochastic process for the inverse of the surplus consumption ratio in Campbell and Cochrane (1999) and Wachter (2006). This stochastic process has the risk neutral probability distribution with moment generating function (79). In addition, they derive a new sensitivity function for (56) which satisfies the local properties in Campbell and Cochrane’s original model.
This approach establishes a theoretical foundation for the log-linearized asset pricing models. However, the analytic method shows that even the Mehra and Prescott model needs a higher order Taylor polynomial to accurately represent asset returns in this model. Consequently, the stochastic discount factor from the original asset pricing models is not given by (82). Thus, an open question is how close the stochastic discount factor from the original asset pricing models matches the empirical model (82) developed by Le, Singleton, and Dai.
3.5 Heterogeneous Agents
Asset pricing models with heterogeneous characteristics for investors significantly increase the level of complexity of the computational algorithms. The heterogeneity takes many forms including differences in risk aversion, income, beliefs, and access to information. The complexity arises from the need to keep track of the differences among investors, as well as the coordination of their behavior with market equilibrium.
To illustrate these issues, consider the differences among investors’ incomes as in Lucas (1994) and Heaton and Lucas (1996). The budget constraint of the investors (8) now becomes
![]() (83)
(83)
for each individual investor ![]() . The cash in hand for investing,
. The cash in hand for investing, ![]() , includes the initial wealth of the investor,
, includes the initial wealth of the investor, ![]() , plus her labor income,
, plus her labor income, ![]() .
.
Suppose that we still have only two assets as in the representative agent models. The return on the ith investor’s portfolio is found by combining (7), (9), (29), and (26) to yield
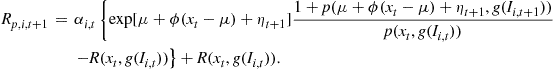 (84)
(84)
Here, the price-dividend ratio depends on the current growth rate of dividends, ![]() . In addition, the distribution of investors’ cash in hand,
. In addition, the distribution of investors’ cash in hand, ![]() , as well as its future value,
, as well as its future value, ![]() , influence investors’ demand for stocks, so that the price of stocks is a function of these distributions. To keep the analysis trackable it is also assumed that this probability distribution has the Markov property as in Heaton and Lucas (1996). The risk-free interest rate depends on the dividend growth and the distribution of investors’ current cash in hand, since they alter investors’ consumption.
, influence investors’ demand for stocks, so that the price of stocks is a function of these distributions. To keep the analysis trackable it is also assumed that this probability distribution has the Markov property as in Heaton and Lucas (1996). The risk-free interest rate depends on the dividend growth and the distribution of investors’ current cash in hand, since they alter investors’ consumption.
The first order conditions (11)–(13), and the terminal condition (14) still hold under the constant relative risk averse utility function (6), where each variable has a subscript to represent investor ![]() .
.
For each agent, we seek functions ![]() and
and ![]() . As a result, the optimal portfolio return is
. As a result, the optimal portfolio return is ![]() , where the optimal investment in stocks,
, where the optimal investment in stocks, ![]() , is substituted into (84). These functions must satisfy the optimal investment decisions for each investor given by
, is substituted into (84). These functions must satisfy the optimal investment decisions for each investor given by
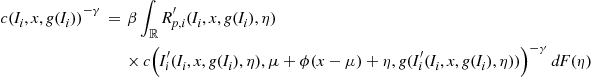 (85)
(85)
and
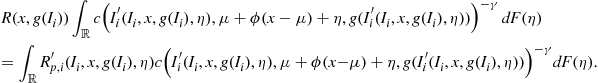 (86)
(86)
Here, the future cash in hand available to the investor, ![]() , is endogenous and is determined by (83), and the optimal decision of investor
, is endogenous and is determined by (83), and the optimal decision of investor ![]() is such that
is such that
![]() (87)
(87)
where ![]() is future labor income.
is future labor income.
Market prices coordinate the behavior of the agents. To illustrate the concept, suppose that there are two agents, i.e., ![]() . Also, assume that there is one share of stock so that the equilibrium in the stock market is given by
. Also, assume that there is one share of stock so that the equilibrium in the stock market is given by
![]() (88)
(88)
where ![]() is the initial level of dividends.21 Note that
is the initial level of dividends.21 Note that ![]() is now the percentage of the cash in hand invested in stocks rather than the percentage of wealth. The market for bonds must be cleared. Usually, it is assumed that these bonds are trading among the investors.
is now the percentage of the cash in hand invested in stocks rather than the percentage of wealth. The market for bonds must be cleared. Usually, it is assumed that these bonds are trading among the investors.
![]() (89)
(89)
This relation means that one investor borrows, i.e., ![]() , and the other lends, i.e.,
, and the other lends, i.e., ![]() .
.
Finally, total labor income each period is given by
![]() (90)
(90)
To complete the model, one needs to specify how labor income and dividend growth move from time to time which determines the evolution of the distribution of the cash in hand from ![]() to
to ![]() following (87).
following (87).
Asset pricing models with heterogeneous agents are more complicated for two reasons. First, both the optimal portfolio decisions and the equilibrium prices must be determined simultaneously. Second, one must keep track of the distribution of the cash in hand across agents. A standard way to circumvent the second issue is to assume a utility function which is an exponential function of consumption and that returns have a normal distribution. These assumptions make investors’ decisions independent of wealth. It generally leads to a linear pricing function for equity. Such models of financial markets are common in the study of the impact of information on stock prices (see Wang, 1994, Easley and O’Hara, 2004, Lo and Wang, 2006).
If one does not make these assumptions, then a tractable mechanism to keep track of investors’ cash in hand is essential in avoiding the curse of dimensionality. Constantinides and Duffie (1996) provide a clever way to reverse engineer the distribution of income such that the reduced form is mathematically the same as the representative agent model (30), albeit with different parameters. Consequently, it may be solved using the same procedure outlined above. Lucas (1994) and Heaton and Lucas (1996) assume finite states for aggregate income growth ![]() . In addition, investors’ share of labor income is given by
. In addition, investors’ share of labor income is given by ![]() so that
so that ![]() following (90). As a result, the exogenous behavior of investors’ income may be represented by two state variables,
following (90). As a result, the exogenous behavior of investors’ income may be represented by two state variables, ![]() . In addition, it is assumed that these two state variables follow a finite state Markov chain.
. In addition, it is assumed that these two state variables follow a finite state Markov chain.
These assumptions make it easier to keep track of the distribution of investors’ cash in hand, ![]() . Given the possible finite realizations of
. Given the possible finite realizations of ![]() , one can calculate the income levels of each individual
, one can calculate the income levels of each individual ![]() so that (87) determines the realizations of cash in hand with probabilities of these realizations dictated by the Markov chain. Thus, the distribution of investors’ cash in hand is incorporated into the calculations of expectations in (85) and (86).
so that (87) determines the realizations of cash in hand with probabilities of these realizations dictated by the Markov chain. Thus, the distribution of investors’ cash in hand is incorporated into the calculations of expectations in (85) and (86).
In principle, the same five steps used in the representative agent models would be followed for developing a computer algorithm for solving the heterogeneous agent models with incomplete markets. Kubler and Schmedders (2003) develop a proof of the existence of an equilibrium for a heterogeneous agent model with collateral constraints on debt. In their model, the exogenous Markov shocks determine both the wage income and dividend growth of assets. They develop a Markov equilibrium concept which modifies Duffie et al. (1994). Their state space includes both the exogenous Markov process and all possible endogenous variables such as cash in hand. The Markov equilibrium consists of a correspondence of expectations which determines the evolution of the state from one period to the next subject to all the conditions for equilibrium including (85), (86), and (88)–(90). In addition, there are correspondences of equilibrium policy which determine all the endogenous variables in the state space. They are able to prove the existence of an equilibrium; however, the properties, including the uniqueness, are not known.23 Following tradition in computational economics, they proceed to define an ![]() -Markov equilibrium in which the optimal conditions (85) and (86) for all investors are satisfied within an arbitrarily small relative error. They are able to prove the existence and uniqueness of the
-Markov equilibrium in which the optimal conditions (85) and (86) for all investors are satisfied within an arbitrarily small relative error. They are able to prove the existence and uniqueness of the ![]() -Markov equilibrium. Subsequently, Kubler and Schmedders (2005) show how to interpret such an approximate equilibrium as an equilibrium for an economy with close by endowments or preferences. As a result, they are able to complete steps 1 and 2 outlined in the representative agent models. Step 3 is not analyzed in the heterogeneous agent models, since the analysis of equilibrium has been limited to general utility functions rather than specific functional forms such as (6). Whether or not step 3 can be successfully undertaken in a heterogeneous agent model is an open question.
-Markov equilibrium. Subsequently, Kubler and Schmedders (2005) show how to interpret such an approximate equilibrium as an equilibrium for an economy with close by endowments or preferences. As a result, they are able to complete steps 1 and 2 outlined in the representative agent models. Step 3 is not analyzed in the heterogeneous agent models, since the analysis of equilibrium has been limited to general utility functions rather than specific functional forms such as (6). Whether or not step 3 can be successfully undertaken in a heterogeneous agent model is an open question.
Heaton and Lucas (1996) consider a recursive equilibrium concept similar to Kubler and Schmedders. However, very little was known at that time about conditions which lead to the existence of such an equilibrium. Heaton and Lucas use Monte Carlo simulations to calculate the expected returns rather than the polynomial approximations. They then use what they call an auctioneer algorithm to search for the equilibrium. They start with an initial guess of the optimal consumption and investment decision for each agent. Given these choices, one can calculate the equilibrium price and interest rates, as well as each agent’s marginal value of the assets. If an agent’s marginal value of a security is not consistent with the equilibrium price and interest rates, then investors’ optimal decisions are modified such that each buys more of the assets which they value higher. This process is continued until there is no discrepancy between the market and investors’ valuation of securities.
Given the state of the literature, Judd et al. (2000) choose to find an ![]() -Markov equilibrium which determines the consumption, investment, and pricing functions that satisfy all the conditions of the model. Under the specification of the Markov stochastic process for the labor income and dividend growth, one can specify equilibrium functions for the price-dividend ratio and risk-free interest rates as a function of dividend growth and the state variable
-Markov equilibrium which determines the consumption, investment, and pricing functions that satisfy all the conditions of the model. Under the specification of the Markov stochastic process for the labor income and dividend growth, one can specify equilibrium functions for the price-dividend ratio and risk-free interest rates as a function of dividend growth and the state variable ![]() .
.
![]() (91)
(91)
and
![]() (92)
(92)
The distribution for investors’ wealth is incorporated into the unknown parameters ![]() and
and ![]() of these functions, since the parameters of the Markov chain are incorporated into the expectations found in (85) and (86). As a result, only the current state
of these functions, since the parameters of the Markov chain are incorporated into the expectations found in (85) and (86). As a result, only the current state ![]() is relevant for the equilibrium prices. Given these price functions, the consumption and investment decision of each individual can be given by (21) and (22), respectively. Here, these functions are dependent on individuals’ cash in hand,
is relevant for the equilibrium prices. Given these price functions, the consumption and investment decision of each individual can be given by (21) and (22), respectively. Here, these functions are dependent on individuals’ cash in hand, ![]() , and the current state
, and the current state ![]() .24
.24
With regard to the polynomial approximations, Judd et al. do not use orthogonal polynomials, since the equilibriums exhibit high curvature on the boundary of the state space. To improve the accuracy of approximations they use the cubic splines ![]() in
in ![]() , which is a third order polynomial on each subinterval
, which is a third order polynomial on each subinterval ![]() with
with ![]() . These subintervals partition the domain of the spline at the knots
. These subintervals partition the domain of the spline at the knots ![]() , where the function to be approximated
, where the function to be approximated ![]() is evaluated. A basis for the cubic splines can be constructed using B-splines (see Judd, 1998, p. 227 and Stoer and Bulirsch, 2002, pp. 97–121). In this case, the approximation functions (21), (22), (91), and (92) are constructed by replacing the Chebyshev polynomials with the B-splines. If the functions being approximated have a uniform bound on the interval
is evaluated. A basis for the cubic splines can be constructed using B-splines (see Judd, 1998, p. 227 and Stoer and Bulirsch, 2002, pp. 97–121). In this case, the approximation functions (21), (22), (91), and (92) are constructed by replacing the Chebyshev polynomials with the B-splines. If the functions being approximated have a uniform bound on the interval ![]() for its continuous fourth order derivatives, then an accurate solution can be found by choosing a fine enough partition of the domain of the functions. Since step 3 has not been undertaken for the heterogeneous agent models, these conditions for a bound on the error have not been verified. Consequently, Judd et al. (2000) rely on the
for its continuous fourth order derivatives, then an accurate solution can be found by choosing a fine enough partition of the domain of the functions. Since step 3 has not been undertaken for the heterogeneous agent models, these conditions for a bound on the error have not been verified. Consequently, Judd et al. (2000) rely on the ![]() -Markov equilibrium concept to represent the accuracy of their algorithm.
-Markov equilibrium concept to represent the accuracy of their algorithm.
Proceeding to step 4, the approximations (21), (22), (91), and (92) are substituted into each investor’s optimal conditions (85) and (86) using the equilibrium conditions (88) and (90). Judd et al. (2000) find that solving this system of equations for the coefficients of the approximation functions is problematic since the system is ill-conditioned. As a result, they adopt the following iterative scheme based on economic intuition. Start with an initial guess for the coefficients of the approximation functions. Use these approximate coefficients only for the future decisions and prices in the optimal conditions (85) and (86) subject to the equilibrium conditions (91) and (92). Then choose a new set of coefficients for the approximation functions so that the conditions (85) and (86) are satisfied. Proceeding in this fashion, the algorithm is continued until there are no further changes in the coefficients.
Each iteration in the algorithm in Judd et al. (2000) requires the solution of a system of nonlinear equations for the coefficients of the approximation functions. The numerical solution of this system using Newton’s method is sensitive to initial values for the coefficients of the approximation functions. Consequently, they use the homotopy method of Schmedders (1999) to locate reasonable initial values for Newton’s method. The homotopy method introduces a marginal penalty to the optimal conditions of each investor (21) and (22) which disappears if the homotopy parameter is set to zero. This procedure helps to mitigate the problems associated with possible discontinuities in the equilibrium solution. After running the homotopy procedure a few times, they switch back to Newton’s method to speed up the convergence to the solution. The procedure stops when the relative error in the optimal conditions for investors’ decisions is within some given tolerance level.
The approach for solving the heterogeneous agent models with incomplete asset markets should follow the same five steps outlined in the representative agent model. Up to now, we are not aware of a heterogeneous agent model which has completed all five steps. In particular, step 3 is bypassed. Our experience with the representative agent models suggests working out the details of the existence and uniqueness of equilibrium for specific examples can yield a better understanding of the equilibrium for model. Under these specific examples it is more likely that step 3 could be successful. Alternatively, enough information about the equilibrium can be found so that the conditions for a bound on the approximation error can be found.
4 Continuous Time Portfolio Decision Problem
We now turn to the investor’s problems under continuous time stochastic environment.25 These problems lead to nonlinear differential equations subject to initial (terminal) conditions rather than linear differential equations. The initial value problem arises since an investor wants to target an optimal amount of wealth at some terminal time in which time has been reversed. As of now only the cases which lead to a linear differential equation have been solved, yet little progress has been made on the nonlinear case. Given the perturbation method the solution to the nonlinear PDE can be approximated but the mathematical properties of this approximation have not been established.
We first start out with a generic optimization problem following Chow (1997). In continuous time, the discrete time problem (1) subject to (2) becomes
![]() (93)
(93)
subject to
![]() (94)
(94)
where ![]() is a vector of
is a vector of ![]() Brownian motions. The instantaneous change of mean in the state vector
Brownian motions. The instantaneous change of mean in the state vector ![]() is
is ![]() . The vector of
. The vector of ![]() control variables is
control variables is ![]() . The instantaneous variance-covariance matrix is denoted by
. The instantaneous variance-covariance matrix is denoted by ![]() . The value of the objective is
. The value of the objective is ![]() , when the optimal policy is always followed.
, when the optimal policy is always followed.
To derive the differential equation for the continuous time version of this optimization problem, we use Ito’s lemma, which is stated here for the reader’s convenience. First, the stochastic process for the n-dimensional state vector is
![]() (95)
(95)
where ![]() is the instantaneous mean of the state variable
is the instantaneous mean of the state variable ![]() and
and ![]() is a vector of
is a vector of ![]() Brownian motions so that the
Brownian motions so that the ![]() matrix
matrix ![]() provides the instantaneous impact of these random shocks on the state variables. Consequently,
provides the instantaneous impact of these random shocks on the state variables. Consequently, ![]() is the instantaneous variance-covariance matrix for the vector of state variables,
is the instantaneous variance-covariance matrix for the vector of state variables, ![]() .
.
Now consider the problem of finding the optimal control vector ![]() over a small time interval from
over a small time interval from ![]() to
to ![]() , so that
, so that
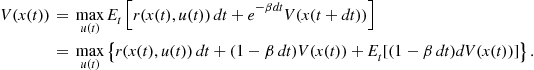 (97)
(97)
In the second step, use ![]() 27 and
27 and ![]() . Applying Ito’s lemma (Lemma 4.1) to
. Applying Ito’s lemma (Lemma 4.1) to ![]() to find
to find
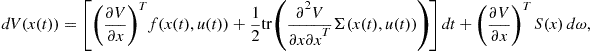 (98)
(98)
so that ![]() . Consequently, the stochastic optimal control problem is given by
. Consequently, the stochastic optimal control problem is given by
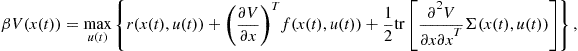 (99)
(99)
which is called the Hamilton-Jacobi-Bellman (HJB) equation.
The usual approach to solving this problem is to find first order conditions of (99) with respect to the control variables ![]() .
.
 (100)
(100)
These equations are solved for ![]() in terms of the value function. If the optimal control vector is substituted into the HJB equation (99), then the value function is the solution to the PDE
in terms of the value function. If the optimal control vector is substituted into the HJB equation (99), then the value function is the solution to the PDE
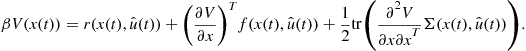 (101)
(101)
This PDE is nonlinear. Specifically, the optimal decisions (100) are a function of the partial derivatives of the solution, so that the PDE (101) involves nonlinear functions of the solution and its derivatives.
This PDE is subject to terminal conditions, called the transversality condition (see Duffie, 2001), which is necessary for the convergence of the improper integral in (93). In the infinite horizon case, this condition is
![]() (102)
(102)
Under a finite horizon ![]() , this boundary condition is given by
, this boundary condition is given by
![]() (103)
(103)
where ![]() is the terminal value of the vector of state variables (see Cox and Huang, 1989, p. 61). When time is reversed such that the investment horizon is
is the terminal value of the vector of state variables (see Cox and Huang, 1989, p. 61). When time is reversed such that the investment horizon is ![]() , then the terminal value in the finite horizon case becomes an initial value. Thus, any generic economic problem in continuous time leads to a nonlinear initial value problem (101) and (103), whose solution is necessary to determine the optimal decisions (100).
, then the terminal value in the finite horizon case becomes an initial value. Thus, any generic economic problem in continuous time leads to a nonlinear initial value problem (101) and (103), whose solution is necessary to determine the optimal decisions (100).
4.1 Optimal Investment Decisions in Continuous Time
To illustrate the optimal investment decisions, we follow Schroder and Skiadas (1999, 2002, 2003, 2005, 2008), Wachter (2002b), Campbell et al. (2004), Liu (2007), Sangvinatsos and Wachter (2005), and Wachter (2010) who use the preferences of Duffie and Epstein (1992a,b) with the particular functional form of Kreps and Porteus (1978). These preferences are the continuous time version of Epstein and Zin (1989, 1990, 1991), (69). The investor chooses the percentage of wealth ![]() consumed,
consumed, ![]() , and invested in stocks,
, and invested in stocks, ![]() , each period so as to maximize
, each period so as to maximize
![]() (104)
(104)
where
 (105)
(105)
Let ![]() . From now on we use the notation
. From now on we use the notation ![]() rather than
rather than ![]() to cut down on space. The measure of the investor’s aversion to risk is
to cut down on space. The measure of the investor’s aversion to risk is ![]() . The bequest function is
. The bequest function is ![]() . In particular, one could choose the
. In particular, one could choose the ![]() of the form
of the form
![]() (106)
(106)
The parameter ![]() measures how much weight the investor places on the welfare of some future person or institution, such as, the investor’s children or a charitable organization. If
measures how much weight the investor places on the welfare of some future person or institution, such as, the investor’s children or a charitable organization. If ![]() , then the weight is the same as if it is herself. If
, then the weight is the same as if it is herself. If ![]() , then no weight is put on this future person.28
, then no weight is put on this future person.28
The investor’s optimization of lifetime utility (104) is subject to the stochastic process for her wealth
![]() (107)
(107)
The risk-free interest rate ![]() for bonds is assumed to be constant. The expected equity premium,
for bonds is assumed to be constant. The expected equity premium, ![]() , has a stationary value
, has a stationary value ![]() while the standard deviation for the equity premium is
while the standard deviation for the equity premium is ![]() . The equity premium randomly changes following the standard Brownian motion
. The equity premium randomly changes following the standard Brownian motion ![]() .
.
The empirical characteristics of the equity premium are based on the work of Campbell and Viceira (1999, 2002) in which the expected excess return on stocks is dependent on the price-dividend ratio.
![]() (108)
(108)
Here ![]() is the price of equity and
is the price of equity and ![]() is the price of the risk-free bond. The expected equity premium follows
is the price of the risk-free bond. The expected equity premium follows
![]() (109)
(109)
The risk-free interest rate ![]() for bonds is assumed to be constant.
for bonds is assumed to be constant. ![]() is also a standard Brownian motion. The shocks to the expected equity premium,
is also a standard Brownian motion. The shocks to the expected equity premium, ![]() , and the equity premium,
, and the equity premium, ![]() , are negatively correlated so that
, are negatively correlated so that ![]()
![]() . The expected equity premium has the solution for any
. The expected equity premium has the solution for any ![]()
![]() (110)
(110)
where the integral has a normal probability distribution following Shreve (2004).29
 (111)
(111)
This specification captures the empirical properties demonstrated in Campbell and Cochrane (1999) and summarized in Lettau and Ludvigson (2010). In particular, when stock prices increase from a higher surplus consumption ratio in Figure 4, the expected return on stocks falls in Figure 5.
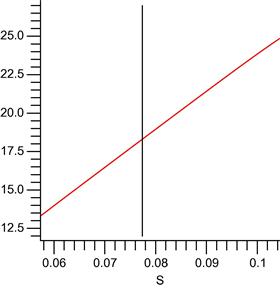
Figure 4 The price-dividend function for the Campbell and Cochrane model. The parameter values are ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . The
. The ![]() -axis gives the surplus consumption ratio on the support of the distribution
-axis gives the surplus consumption ratio on the support of the distribution ![]() . The
. The ![]() -axis records the price-dividend ratio.
-axis records the price-dividend ratio.
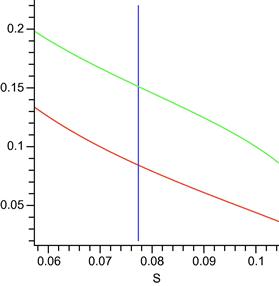
Figure 5 The equity premium and standard deviation of equity in the continuous time model of Campbell and Cochrane. The parameter values are ![]() , and
, and ![]() . The
. The ![]() -axis gives the surplus consumption ratio on the support of the distribution
-axis gives the surplus consumption ratio on the support of the distribution ![]() . The
. The ![]() -axis records the equity premium and standard deviation of stock returns. The equity premium is the solid line, while the dotted line represents the standard deviation.
-axis records the equity premium and standard deviation of stock returns. The equity premium is the solid line, while the dotted line represents the standard deviation.
Following the analysis of Schroder and Skiadas (1999, 2002, 2003, 2005, 2008) one can show that the lifetime utility of the investor is separable between the current value of wealth ![]() and the current expected equity premium
and the current expected equity premium ![]() . This separation is given by
. This separation is given by
![]() (112)
(112)
where ![]() with
with ![]() . One also needs
. One also needs ![]() and
and ![]() , so that
, so that ![]() . Finally, (112) is true at the terminal time
. Finally, (112) is true at the terminal time ![]() , so that the terminal condition (106) has the same form as (112).
, so that the terminal condition (106) has the same form as (112).
Using the dynamic programming procedure following Fleming and Soner (2006) one can derive the optimal consumption and investment decisions
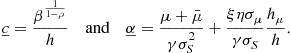 (113)
(113)
For the solution to have a unique critical point, the restrictions ![]() , and
, and ![]() must hold. Given that these critical points are unique,
must hold. Given that these critical points are unique, ![]() must satisfy the initial value problem
must satisfy the initial value problem
 (114)
(114)
The constants are defined by30

This initial value problem can be derived from the backward stochastic differential equation of Schroder and Skiadas (2003) for the investor’s problem (104)–(111). If there are multiple expected excess rates of returns and investment alternatives, ![]() becomes a vector. For the higher-dimensional problem
becomes a vector. For the higher-dimensional problem ![]() and
and ![]() are replaced by positive definite matrices, since they correspond to variance-covariance matrices for the expected excess returns and actual returns.31
are replaced by positive definite matrices, since they correspond to variance-covariance matrices for the expected excess returns and actual returns.31
The solution to the initial value problem does not guarantee that the investor’s problem is solved. One must also show that the integrals in (104) are well defined. Proceeding formally apply Ito’s lemma to the utility of wealth from (112) using the stochastic process for wealth (107). Then use the optimal conditions (113) and the PDE (114) to obtain the following expression for the expected utility of wealth in the terminal period.
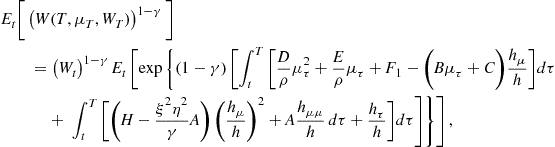 (115)
(115)
where ![]() .32 This expected utility of wealth is a stochastic exponential of a semi-martingale
.32 This expected utility of wealth is a stochastic exponential of a semi-martingale ![]() . For (115) to be well defined, Theorem (45) of Protter (2005, p.141) implies that the lifetime utility is a locally integrable martingale when
. For (115) to be well defined, Theorem (45) of Protter (2005, p.141) implies that the lifetime utility is a locally integrable martingale when
![]() (116)
(116)
We can now discuss the procedure for assuring the lifetime utility (104) is well defined. From (110) and (111) the future expected equity premium ![]() increases (decreases) monotonically to
increases (decreases) monotonically to ![]() for
for ![]() (
(![]() ) as
) as ![]() . In addition, the variance of
. In addition, the variance of ![]() increases monotonically to
increases monotonically to ![]() . Thus, one can establish a bound on the normal probability distribution used to calculate the expected value in (115) and (116) such that33
. Thus, one can establish a bound on the normal probability distribution used to calculate the expected value in (115) and (116) such that33
![]() (117)
(117)
where ![]() is the probability that at time
is the probability that at time ![]() the state
the state ![]() becomes
becomes ![]() at time
at time ![]() . In addition, the constant
. In addition, the constant ![]() and
and ![]() is a locally bounded function of the current expected excess returns on stocks.
is a locally bounded function of the current expected excess returns on stocks.
It is known that the normal probability distribution has the property
![]() (118)
(118)
as long as ![]() . Since the integrands in (115) and (116) are the product of the transition density (117) and some combination of the first and second derivatives of the solution (114),
. Since the integrands in (115) and (116) are the product of the transition density (117) and some combination of the first and second derivatives of the solution (114), ![]() , these combinations must grow more slowly than the bound on the transition density (117). This leads to sufficient conditions on the solution to the IVP (114) for the integrals in (115) and (116) to be bounded.34 For example, one can explicitly calculate a bound for the expectation of the integral
, these combinations must grow more slowly than the bound on the transition density (117). This leads to sufficient conditions on the solution to the IVP (114) for the integrals in (115) and (116) to be bounded.34 For example, one can explicitly calculate a bound for the expectation of the integral
![]() (119)
(119)
in (115) as long as ![]() does not grow faster than
does not grow faster than ![]() in (117). In particular, suppose
in (117). In particular, suppose ![]() , then one can use (110) and (111) and recognize
, then one can use (110) and (111) and recognize ![]() has a normal probability distribution with given mean and variance, as in Hugonnier et al. (2012 Lemma F.1), so that a bound for (119) can be determined.
has a normal probability distribution with given mean and variance, as in Hugonnier et al. (2012 Lemma F.1), so that a bound for (119) can be determined.
The investor’s lifetime utility (104) is also related to the IVP solution, ![]() , through (112). From the application of Ito’s lemma to the lifetime utility function (112), the optimal conditions (113), and the solution to IVP (114) given by
, through (112). From the application of Ito’s lemma to the lifetime utility function (112), the optimal conditions (113), and the solution to IVP (114) given by ![]() yields the integral equation
yields the integral equation
![]() (120)
(120)
If one uses the change of variable ![]() , then the conditions for (120) to be well defined are the same as the growth conditions applied to (115). Thus, the solution to the IVP problem needs to satisfy growth conditions for this solution to satisfy the investor’s problem (104)–(111).
, then the conditions for (120) to be well defined are the same as the growth conditions applied to (115). Thus, the solution to the IVP problem needs to satisfy growth conditions for this solution to satisfy the investor’s problem (104)–(111).
4.2 Solutions
Solutions to the investor’s problem have been published by Kim and Omberg (1996), Wachter (2002b), Schroder and Skiadas (2003), Sangvinatsos and Wachter (2005), and Liu (2007). Wachter (2002b) examines the case in which ![]() , while the others are in
, while the others are in ![]() dimensions. These solution procedures work when the IVP (114) is linear, i.e.,
dimensions. These solution procedures work when the IVP (114) is linear, i.e., ![]() . One case, in which this occurs, is the constant relative risk averse case,
. One case, in which this occurs, is the constant relative risk averse case, ![]() , with
, with ![]() and markets are complete
and markets are complete ![]() . However, any other combination of parameters such that
. However, any other combination of parameters such that ![]() would also lead to the same mathematical problem. In addition, the solution applies for the case
would also lead to the same mathematical problem. In addition, the solution applies for the case ![]() , as long as the solution satisfies bounds like (119). These conditions may not hold, since the constant in (119) switches sign as
, as long as the solution satisfies bounds like (119). These conditions may not hold, since the constant in (119) switches sign as ![]() changes to
changes to ![]() .
.
In all these papers the procedure is the same. First assume the fundamental solution ![]() , when
, when ![]() and
and ![]() , has the Gaussian functional with time-varying mean and variance:
, has the Gaussian functional with time-varying mean and variance:
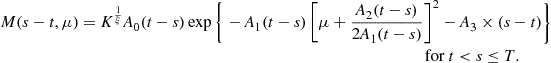 (121)
(121)
Here, ![]() for
for ![]() are functions of the investment horizon
are functions of the investment horizon ![]() for
for ![]() with initial conditions
with initial conditions ![]() for
for ![]() , and the constant
, and the constant ![]() . These initial conditions assure that the solution converges to its terminal value as
. These initial conditions assure that the solution converges to its terminal value as ![]() .
. ![]() is the endogenous discount rate for future values which assures the integrals over time in (115) and (116) imply a present value less than future payments. This along with the stationarity of the stochastic process for the expected equity premium (110) and (111),
is the endogenous discount rate for future values which assures the integrals over time in (115) and (116) imply a present value less than future payments. This along with the stationarity of the stochastic process for the expected equity premium (110) and (111), ![]() , is needed to assure that the integrals over time in (115), (116), and (120) exist even when the time horizon tends to infinity.
, is needed to assure that the integrals over time in (115), (116), and (120) exist even when the time horizon tends to infinity.
One then calculates the derivatives of the hypothesized solution (121) and substitute them into the IVP. By equating the coefficients on ![]() , and
, and ![]() one obtains ordinary differential equations in the investment horizon for each of the coefficients. The remaining terms are used to obtain an ordinary differential equation for
one obtains ordinary differential equations in the investment horizon for each of the coefficients. The remaining terms are used to obtain an ordinary differential equation for ![]() .35 These equations are known as the Riccati equations and their solutions can be quickly and accurately calculated in computer programs.
.35 These equations are known as the Riccati equations and their solutions can be quickly and accurately calculated in computer programs.
After finding the fundamental solution to the IVP (114) one must make sure that conditions like (119) are true. In the case ![]() this condition is true, since
this condition is true, since ![]() is negative so that (118) can be used to calculate the expectation in (119).36 In this case the solution has the form of a Gaussian probability density function so that the expected values in (115), (116), and (120) are well defined. One can see this by looking at Figure 3 which plots the solution (121) for the parameters in Table 1 with
is negative so that (118) can be used to calculate the expectation in (119).36 In this case the solution has the form of a Gaussian probability density function so that the expected values in (115), (116), and (120) are well defined. One can see this by looking at Figure 3 which plots the solution (121) for the parameters in Table 1 with ![]() and
and ![]() . These parameters are updated following Campbell and Viceira (1999) and Campbell et al. (2004) for the US from 1947 to 2006.37
. These parameters are updated following Campbell and Viceira (1999) and Campbell et al. (2004) for the US from 1947 to 2006.37
When ![]() the sign of
the sign of ![]() is positive so that (119) is not necessarily true. In this case Figure 3 would be the inverse of the previous case so that
is positive so that (119) is not necessarily true. In this case Figure 3 would be the inverse of the previous case so that ![]() as
as ![]() for each
for each ![]() . As a result, the convergence of the integrals over
. As a result, the convergence of the integrals over ![]() in (115), (116), and (120) becomes more delicate. In particular, the positive growth of
in (115), (116), and (120) becomes more delicate. In particular, the positive growth of ![]() must be less than the decline in the bound on the normal distribution (117) as
must be less than the decline in the bound on the normal distribution (117) as ![]() . This case is important since Bansal and Yaron (2004), and Bansal et al. (2007, 2009) argue that the elasticity of intertemporal substitution is greater than one, which corresponds to the case of
. This case is important since Bansal and Yaron (2004), and Bansal et al. (2007, 2009) argue that the elasticity of intertemporal substitution is greater than one, which corresponds to the case of ![]() , and
, and ![]() .38
.38
Once the fundamental solution is found, the non-homogeneous linear IVP, i.e., ![]() and
and ![]() , can be found using Duhamel’s principle:
, can be found using Duhamel’s principle:
![]() (122)
(122)
so that the solution to the linear IVP (114) with ![]() is a combination of the fundamental solution (121) at different time to maturities.
is a combination of the fundamental solution (121) at different time to maturities.
The nonlinear case has not been solved and there is limited information about the solution. If one uses the transformation
![]() (123)
(123)
then the fundamental solution can be found for the case ![]() in which there is no intermediate consumption. The solution has the same form as (121) with different constants in the IVP (114). In the general case
in which there is no intermediate consumption. The solution has the same form as (121) with different constants in the IVP (114). In the general case ![]() and
and ![]() one cannot use Duhamel’s principle, since this principle does not hold for nonlinear differential equations. In addition, the Cauchy-Kovalevsky Theorem cannot be used, since the highest derivatives with respect to each variable must be the same. This condition is violated for the IVP (114).
one cannot use Duhamel’s principle, since this principle does not hold for nonlinear differential equations. In addition, the Cauchy-Kovalevsky Theorem cannot be used, since the highest derivatives with respect to each variable must be the same. This condition is violated for the IVP (114).
For the infinite investor’s horizon case one would want to let ![]() once one obtains a solution to the finite horizon case. For example, the functions
once one obtains a solution to the finite horizon case. For example, the functions ![]() , and
, and ![]() in Wachter’s (2002a) solution converge to constants
in Wachter’s (2002a) solution converge to constants ![]() , and
, and ![]() . One can see this behavior of the solution in Figure 3 in that the curve in the
. One can see this behavior of the solution in Figure 3 in that the curve in the ![]() dimension stabilizes as
dimension stabilizes as ![]() gets larger. In addition, the value of the fundamental solution (121) converges as
gets larger. In addition, the value of the fundamental solution (121) converges as ![]() because
because ![]() . Thus, one needs to make sure the final solution (122) converges for
. Thus, one needs to make sure the final solution (122) converges for ![]() .
.
Some approximations for the nonlinear IVP Campbell and Viceira (2002), Campbell et al. (2004), and Chacko and Viceira (2005) approximate the PDE (114) in the case ![]() and
and ![]() by setting
by setting ![]() and replacing
and replacing ![]() with a logarithm approximation around a known solution in which
with a logarithm approximation around a known solution in which ![]() . This leads to a solution to an approximate PDE. However, it is not clear what the relation is with the solution to the original PDE as
. This leads to a solution to an approximate PDE. However, it is not clear what the relation is with the solution to the original PDE as ![]() . Thus, the solution to the infinite horizon problem is not complete and is dependent on the characterization of the finite horizon problem.
. Thus, the solution to the infinite horizon problem is not complete and is dependent on the characterization of the finite horizon problem.
For the case ![]() little is known about the solution to the IVP (114). One could use a traditional procedure, used by scientist and engineers, such as the perturbation method as in Bender and Orszag (1999). This method breaks the nonlinear PDE into an infinite number of linear PDEs which can be solved recursively. In these linear PDEs the nonlinear term in (114) is replaced by an independent function of the solutions to previous linear PDEs. The solution to the IVP (114) is then the sum of the solutions to all these linear PDEs. The mathematical problem is that one does not know whether or not this sum converges and whether it converges to the true solution of (114). Finally, one needs to check whether or not the condition (119) is true such that the integrals over
little is known about the solution to the IVP (114). One could use a traditional procedure, used by scientist and engineers, such as the perturbation method as in Bender and Orszag (1999). This method breaks the nonlinear PDE into an infinite number of linear PDEs which can be solved recursively. In these linear PDEs the nonlinear term in (114) is replaced by an independent function of the solutions to previous linear PDEs. The solution to the IVP (114) is then the sum of the solutions to all these linear PDEs. The mathematical problem is that one does not know whether or not this sum converges and whether it converges to the true solution of (114). Finally, one needs to check whether or not the condition (119) is true such that the integrals over ![]() in (115), (116), and (120) exist. Thus, there is still substantial work that needs to be done before the investor’s IVP (114) is fully characterized.
in (115), (116), and (120) exist. Thus, there is still substantial work that needs to be done before the investor’s IVP (114) is fully characterized.
5 Continuous Time Asset Pricing
As in the discrete time asset pricing models, the equilibrium prices of assets in continuous time are determined through the coordination of the optimal behavior of all investors such that the demand and supply of assets are in balance and all resources in the economy are allocated. To make the problem manageable Cox and Huang (1989) among others use the martingale approach to characterize how assets are priced. Here, a pricing kernel or stochastic discount factor ![]() is a stochastic process such that for a security with payoff
is a stochastic process such that for a security with payoff ![]() at each instant
at each instant ![]() , the value of the security,
, the value of the security, ![]() is given by
is given by
![]() (124)
(124)
where ![]() stands for the maturity of the security. A positive pricing kernel is unique if and only if there are complete markets and no arbitrage opportunities. If markets are incomplete, then the pricing kernel is not unique.39
stands for the maturity of the security. A positive pricing kernel is unique if and only if there are complete markets and no arbitrage opportunities. If markets are incomplete, then the pricing kernel is not unique.39
An example of a pricing kernel can be found from the optimal investment problem (104)–(111) in which the reward per period is the aggregator (105) for the stochastic differential utility model of Duffie and Epstein. Duffie and Epstein (1992b), and Duffie and Skiadas (1994) prove that the pricing kernel is given by40
![]() (125)
(125)
In the case of the additively separable utility the pricing kernel reduces to ![]() , since
, since ![]() . Consequently, the pricing kernel in discrete time
. Consequently, the pricing kernel in discrete time ![]() becomes
becomes ![]() for
for ![]() in continuous time. This pricing kernel is derived under the assumption of a representative investor who solves problem (104)–(111) and that there is a given stochastic process for the payout,
in continuous time. This pricing kernel is derived under the assumption of a representative investor who solves problem (104)–(111) and that there is a given stochastic process for the payout, ![]() , for the asset. Consequently, the same analysis as in Section 3 is used, but conducted under continuous time.
, for the asset. Consequently, the same analysis as in Section 3 is used, but conducted under continuous time.
The alternative approach to the martingale method is to use the optimal decisions for the investor’s problem (104)–(111) to determine the demand and supply for each asset. One then assures that the equilibrium conditions are satisfied such that demand and supply agree and all resources are used. Following Sections 3 and 4 we consider only one-dimensional although all these methods can be extended to multiple dimensions. As in the discrete time model one represents the investor using the solution to the investor’s problem for the percentage of wealth invested in stocks (113). In equilibrium the total demand for stocks ![]() , where
, where ![]() is the wealth of the representative investor, must be equal to the supply. The supply of the stock and the wealth of the representative investor are set equal to one for convenience, so that
is the wealth of the representative investor, must be equal to the supply. The supply of the stock and the wealth of the representative investor are set equal to one for convenience, so that ![]() . One can then solve for the expected return on stocks, which is given by
. One can then solve for the expected return on stocks, which is given by
![]() (126)
(126)
where ![]() is the representative investor’s investment horizon and
is the representative investor’s investment horizon and ![]() is the instantaneous variance of the expected excess return on the market portfolio.41 In this expression
is the instantaneous variance of the expected excess return on the market portfolio.41 In this expression ![]() is the state variable, and
is the state variable, and ![]() is the covariance between the state variable and the excess return on stocks. This state variable is not necessarily the same as the expected excess return on stocks,
is the covariance between the state variable and the excess return on stocks. This state variable is not necessarily the same as the expected excess return on stocks, ![]() , but it must have the same functional form as (109) to yield the same IVP problem (114).42
, but it must have the same functional form as (109) to yield the same IVP problem (114).42
The second term for the expected return on stocks in (126) is dependent on the response of the expected lifetime utility for the representative investor to changes in the state variable,
![]()
from Eq. (112). Thus, one needs the solution to the IVP (114) for the investor’s problem to understand the asset pricing problem.43
For the case in which the state variable is equal to the expected return on equity, ![]() and
and ![]() , we know the solution to the investor’s problem from Section 4.2. Consequently,
, we know the solution to the investor’s problem from Section 4.2. Consequently,
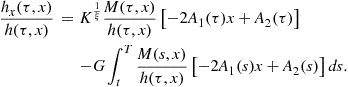 (127)
(127)
Thus, the expected return on stocks (126) is a nonlinear function of the state variable ![]() , which determines the payoff on the stocks.44 Consequently, the expected return is an affine function of the state variable as in Duffie and Kan (1996) and Duffie et al. (2000) only if
, which determines the payoff on the stocks.44 Consequently, the expected return is an affine function of the state variable as in Duffie and Kan (1996) and Duffie et al. (2000) only if ![]() , so that there is no intermediate consumption by the representative investor. For the more general case in which
, so that there is no intermediate consumption by the representative investor. For the more general case in which ![]() , there is an inconsistency between the investor’s problem (104)–(111) and the affine asset pricing problem. In particular, the former presumes a linear stochastic process for the expected return on stocks (109), while the latter implies a nonlinear stochastic process.45
, there is an inconsistency between the investor’s problem (104)–(111) and the affine asset pricing problem. In particular, the former presumes a linear stochastic process for the expected return on stocks (109), while the latter implies a nonlinear stochastic process.45
If one wanted to examine asset prices under the more general case in which ![]() , then one would have to rely on an approximation to
, then one would have to rely on an approximation to ![]() such as the perturbation method discussed in the Section 4.2. This impact of the state variable on the lifetime utility of the representative investor would then determine the expected return on assets using (126). Thus, further progress in understanding the behavior of asset prices is dependent on knowing the properties of the solution to the IVP problem (114) and/or its approximations.
such as the perturbation method discussed in the Section 4.2. This impact of the state variable on the lifetime utility of the representative investor would then determine the expected return on assets using (126). Thus, further progress in understanding the behavior of asset prices is dependent on knowing the properties of the solution to the IVP problem (114) and/or its approximations.
5.1 One-Dimensional Asset Pricing Model Under Infinite Horizon
Given the limited knowledge of the solution to the IVP problem (114), we initially focus on the infinite horizon case in which there is a single risky asset and a risk-free bond under a representative investor. This problem leads to a time independent differential equation, whose solution leads to the price-dividend function, the expected return on stocks, and the risk-free return. This problem can be quickly and accurately approximated using a high order Taylor polynomial using results from and extensions of the Cauchy-Kovalevsky Theorem. The main issue with this approach is that one must specify two conditions for the solution of the differential equation problem. Below we discuss several ways to establish these conditions using an empirical approach or approximations of the solution at the stationary point of the state variable to determine initial conditions. We then discuss the possibility of using boundary values rather than initial conditions to set the conditions on the differential equation. Which procedure best represents the economic problem is an open question, however the mathematical properties can be established once these conditions are known.
5.1.1 Campbell and Cochrane (1999) in Continuous Time
We start with the empirical approach in the context of the continuous time version of the Campbell and Cochrane (1999) external habit model. Let a share of equity pay instantaneous dividends ![]() , so that the payoff at each instant is
, so that the payoff at each instant is ![]() . In this situation, the stock price satisfies46
. In this situation, the stock price satisfies46
![]() (128)
(128)
An equilibrium stock price, which satisfies the Eq. (128), is the solution of the initial value problem of a second order linear differential equation. Such an equilibrium price depends on the specification of the pricing kernel, dividend process, and equilibrium conditions. To illustrate this relation, assume that the pricing kernel is the same as in Campbell and Cochrane’s asset pricing model. Following Cox and Huang (1989), this pricing kernel is the marginal utility of investor’s wealth, which the investor equates with the marginal utility of consumption each period. In this case,
![]() (129)
(129)
The consumption growth in discrete time (55) becomes a random walk in continuous time with drift ![]() , so that
, so that
![]() (130)
(130)
where the random shock to the consumption growth, ![]() , is a standard Brownian motion. The equation of motion for the surplus consumption ratio (54) becomes47
, is a standard Brownian motion. The equation of motion for the surplus consumption ratio (54) becomes47
![]() (131)
(131)
where the sensitivity function (56) and definition of the steady-state surplus consumption ratio (57) stay the same. To keep the model simple, it is assumed that the dividends and consumption growth are identical.
Chen et al. (2010) use Ito’s Lemma 4.1 to derive the ordinary differential equation (ODE) whose solution yields the equilibrium price-dividend function. They first apply Ito’s Lemma 4.1 to the pricing kernel (129) subject to the stochastic process for the consumption growth (130) and the surplus consumption ratio (131). Second, they assume that the price-dividend function is only dependent on the surplus consumption ratio, since consumption growth is constant. A stochastic process for the price-dividend ratio ![]() can then be found using Ito’s Lemma 4.1 and the stochastic process for the surplus consumption ratio (131). Finally, the stochastic process for the pricing kernel, the consumption (dividend) growth (130), and the price-dividend function are substituted into the fundamental pricing relation (128). These calculations yield the ODE for the price-dividend function
can then be found using Ito’s Lemma 4.1 and the stochastic process for the surplus consumption ratio (131). Finally, the stochastic process for the pricing kernel, the consumption (dividend) growth (130), and the price-dividend function are substituted into the fundamental pricing relation (128). These calculations yield the ODE for the price-dividend function
![]() (132)
(132)
where ![]() is measured relative to its steady-state value
is measured relative to its steady-state value ![]() . The coefficients are
. The coefficients are
![]() (133)
(133)
where
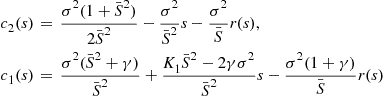
and
![]()
Here, ![]() , and
, and
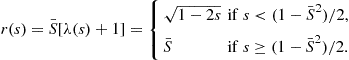
Such a differential equation (132) yields a general solution which is dependent on two conditions. A terminal condition such as in (114) is not useful for determining these conditions. This follows from the independence of the solution, such as (122), of the terminal value, since ![]() . Also notice that the transversality condition (102) holds. Thus, one must use information other than the terminal condition as in (114) to determine the solution to the ODE (132).
. Also notice that the transversality condition (102) holds. Thus, one must use information other than the terminal condition as in (114) to determine the solution to the ODE (132).
5.1.2 Initial Conditions: Empirical Approach
In the empirical approach we use the empirical values of financial ratios to determine the initial conditions for the ODE (132),
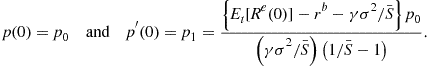 (134)
(134)
Chen et al. (2010) derive the second initial condition from the no-arbitrage condition between stocks and bonds, where ![]() is the expected equity premium at the initial price-dividend ratio
is the expected equity premium at the initial price-dividend ratio ![]() .
.
Chen et al. (2010) show how to use the analytic method to solve an ODE such as (132) subject to initial conditions (134). This initial value problem is a special case of those dealt with in the Cauchy-Kovalevsky Theorem. The linear ODE version of this theorem is.
The radius of convergence for the coefficients (133) is
![]() (135)
(135)
For the parameters used by Campbell and Cochrane, ![]() , which is large enough to contain any value for the surplus consumption ratio of interest to financial economists. As a result, the solution to the initial value problem for the Campbell and Cochrane model can be represented by a power series such as (34). Steps 1 through 3 outlined in the discrete time asset pricing Section 3 are completed by applying the Cauchy-Kovalevsky Theorem.
, which is large enough to contain any value for the surplus consumption ratio of interest to financial economists. As a result, the solution to the initial value problem for the Campbell and Cochrane model can be represented by a power series such as (34). Steps 1 through 3 outlined in the discrete time asset pricing Section 3 are completed by applying the Cauchy-Kovalevsky Theorem.
In step 4, Chen et al. (2010) use a Taylor polynomial approximation (43) to represent the solution ![]() of the initial value problem. Since all the coefficients (133) are analytic at
of the initial value problem. Since all the coefficients (133) are analytic at ![]() , one can write
, one can write
![]() (136)
(136)
and choose ![]() such that
such that ![]() . Since
. Since ![]() is smaller than the radius of convergence for
is smaller than the radius of convergence for ![]() , and
, and ![]() , there exist non-negative constants
, there exist non-negative constants ![]() , and
, and ![]() such that
such that
![]() (137)
(137)
Here, ![]() , and
, and ![]() are determined by bounding the sensitivity function (56) in the complex plane and using the Cauchy integral formula (44). Finally, the coefficients of the power series solution
are determined by bounding the sensitivity function (56) in the complex plane and using the Cauchy integral formula (44). Finally, the coefficients of the power series solution ![]() can be computed by substituting the power series,
can be computed by substituting the power series, ![]() , and
, and ![]() into the ODE (132).
into the ODE (132).
Step 5 in the analytic method is completed using the following corollary to Theorem 5.1, which establishes an upper bound on the Taylor remainder (46) within a certain interval:
Thus, the analytic method can be used to solve the asset pricing models as complicated as the Campbell and Cochrane model. Chen et al. (2010) demonstrate that the approximate solution to the Campbell and Cochrane model may be calculated in less than 10 s.48 The error of the approximate solution is less than one in a billion dollars when one considers a reasonable range for the surplus consumption ratio and a sufficient number of coefficients.49
The price-dividend function for the continuous time version of the Campbell and Cochrane model is portrayed in Figure 4 for the parameter values found in the Campbell and Cochrane paper. It is not surprising that the price-dividend function matches the historic average at ![]() , since the initial value
, since the initial value ![]() was chosen to assure this. However, this price-dividend function matches the one found in the original Campbell and Cochrane paper over the whole domain of this function. This result is surprising, since the original Campbell and Cochrane paper used a simulation of the discrete time version of their external habit asset pricing model for which Chen et al. (2008b) could not prove the existence of the solution. As discussed in Section 3.2, this result follows from the behavior of the sensitivity function for extreme negative values for the consumption (dividend) growth. Yet, the approximate solution of the ODE in the continuous time Campbell and Cochrane model does not depend on such extreme values. Thus, the issues identified in the discrete time version of the Campbell and Cochrane model do not show up in the continuous time version of their model.50
was chosen to assure this. However, this price-dividend function matches the one found in the original Campbell and Cochrane paper over the whole domain of this function. This result is surprising, since the original Campbell and Cochrane paper used a simulation of the discrete time version of their external habit asset pricing model for which Chen et al. (2008b) could not prove the existence of the solution. As discussed in Section 3.2, this result follows from the behavior of the sensitivity function for extreme negative values for the consumption (dividend) growth. Yet, the approximate solution of the ODE in the continuous time Campbell and Cochrane model does not depend on such extreme values. Thus, the issues identified in the discrete time version of the Campbell and Cochrane model do not show up in the continuous time version of their model.50
Once the price-dividend function is known, it is straightforward to calculate the expected equity premium and the volatility of stock returns. Figure 5 from Chen et al. (2010) provides a graph of the equity premium (the lower curve) and the volatility of stock returns (the upper curve). The equity premium also matches the historic pattern found in the original Campbell and Cochrane model. Being able to pin down the value of the expected equity premium at ![]() follows from the choice of the initial condition
follows from the choice of the initial condition ![]() in (134). In addition, the expected equity premium is highest during bad times. The same pattern is followed by the volatility of stock returns. Thus, the continuous time version of the Campbell and Cochrane model delivers the empirical properties that they want to match.51
in (134). In addition, the expected equity premium is highest during bad times. The same pattern is followed by the volatility of stock returns. Thus, the continuous time version of the Campbell and Cochrane model delivers the empirical properties that they want to match.51
Asset pricing in continuous time usually leads to differential equations such as (132). Up to now, most of the models assume affine stochastic discount factors so that the coefficients in the ODE (132) are affine as well (see Duffie and Kan, 1996, Duffie et al., 2000, Dai and Singleton, 2000). Cochrane (2005, Chapter 19) demonstrates how affine models are the generalizations of earlier work by Vasicek (1977) and Cox et al. (1985). See Piazzesi (2010) for a survey of this work. Researchers have been able to guess and verify the solutions to these models. Constantinides (1990) is an exception to this rule; yet, he is also able to find a closed form solution. Menzly et al. (2004) are able to find a closed form solution to a continuous time version of Campbell and Cochrane’s model by assuming that ![]() and the sensitivity function (56) is affine. If one wants to approximate the solutions of the ODEs such as (132) numerically, Judd (1998, Chapters 10 and 11) and Stoer and Bulirsch (2002, Chapter 7) demonstrate how to use the finite difference method and the projection method to solve them.
and the sensitivity function (56) is affine. If one wants to approximate the solutions of the ODEs such as (132) numerically, Judd (1998, Chapters 10 and 11) and Stoer and Bulirsch (2002, Chapter 7) demonstrate how to use the finite difference method and the projection method to solve them.
5.2 Multi-Dimensional Asset Pricing Models
The analytic method may be extended to higher-dimensional continuous time asset pricing models. However, up to now the error analysis for polynomial approximations is not done. To illustrate the issues, consider the two-dimensional extension of the Campbell and Cochrane model by Wachter (2002a, 2006).52 Wachter (2002a) changes the specification of consumption growth from a random walk (130) to
![]() (139)
(139)
where ![]() is the long run growth of consumption,
is the long run growth of consumption, ![]() . As in Bansal and Yaron (2004) this long run growth follows a stochastic process like (109) in which
. As in Bansal and Yaron (2004) this long run growth follows a stochastic process like (109) in which ![]() would be the correlation of consumption growth with the long run risk variable, and
would be the correlation of consumption growth with the long run risk variable, and ![]() is its standard deviation.
is its standard deviation.
Chen et al. (2011) use the methods in Chen et al. (2010) to show that the external habit model subject to long run risk leads a price-dividend function ![]() which is the solution to the IVP:
which is the solution to the IVP:
![]() (140)
(140)
![]() (141)
(141)
where the coefficients are analytic functions near ![]() . In addition, they are similar to (133) in which
. In addition, they are similar to (133) in which ![]() in
in ![]() is replaced by
is replaced by ![]() . In addition, the initial conditions (141) must be analytic near
. In addition, the initial conditions (141) must be analytic near ![]() . Chen et al. (2011) relate these initial conditions to the analytic solution for the Campbell and Cochrane model, since the stationary mean for the long run risk variable is
. Chen et al. (2011) relate these initial conditions to the analytic solution for the Campbell and Cochrane model, since the stationary mean for the long run risk variable is ![]() . As a result, they use the Cauchy-Kovalevsky Theorem to prove that the solution to the PDE (140) subject to the initial conditions (141) is an analytic price-dividend function
. As a result, they use the Cauchy-Kovalevsky Theorem to prove that the solution to the PDE (140) subject to the initial conditions (141) is an analytic price-dividend function
 (142)
(142)
Here, ![]() is the solution to the continuous time Campbell and Cochrane model (132). In addition, they provide a bound on the relative error between the Taylor polynomial approximation and the analytic solution (142) within a region of convergence. This region is
is the solution to the continuous time Campbell and Cochrane model (132). In addition, they provide a bound on the relative error between the Taylor polynomial approximation and the analytic solution (142) within a region of convergence. This region is ![]() and
and ![]() . Unlike the one-dimensional case, obtaining the maximum region of convergence in multiple dimensions is a well-known challenging mathematical problem. For our model we expect that the maximum region of convergence is larger than the one obtained rigorously, since our numerical simulations indicate a convergence within the rectangle
. Unlike the one-dimensional case, obtaining the maximum region of convergence in multiple dimensions is a well-known challenging mathematical problem. For our model we expect that the maximum region of convergence is larger than the one obtained rigorously, since our numerical simulations indicate a convergence within the rectangle ![]() and
and ![]() . For example, in this region a comparison of the Taylor polynomial of order
. For example, in this region a comparison of the Taylor polynomial of order ![]() with one of order
with one of order ![]() yields a relative error less than 6 in 10 million.
yields a relative error less than 6 in 10 million.
The evidence from the Wachter model demonstrates that it is feasible to use the analytic method in multi-dimensional continuous time asset pricing models, although additional work still has to be done on the analysis of the approximation error. However, one must think carefully about how to choose appropriate initial conditions (141). In addition, these initial conditions will become more demanding as the dimension of the problem increases. For example, one could introduce learning about the underlying volatility of the dividend growth as in Wang (1993, 1994) and Lo et al. (2004). In this case, the variation in the conditional variance ![]() or
or ![]() under the continuous time Kalman filter is an ODE with analytic coefficients (see Eq. (A.4) of Wang, 1994). Consequently, the coefficients in the PDE (140) would still be analytic. Bhamra and Uppal (2010) take advantage of this property to analyze a dynamic general equilibrium model in which agents have heterogeneous beliefs and subjective rates of discount. The introduction of such a learning mechanism into Wachter’s model would add a third state variable. In this case, the initial conditions (141) would freeze one of the variables, presumably the conditional variance of dividend growth, so that these conditions would be an analytic function of two variables, the consumption growth and the surplus consumption ratio, i.e., the solution (142) of the Wachter model. Of course, one would also face the same curse of dimensionality problems observed in the discrete time asset pricing models, so that steps have to be taken to minimize the curse. Finally, one could use orthogonal polynomials rather than Taylor polynomials to improve the efficiency of the computer algorithm which implements the analytic method in continuous time asset pricing models.
under the continuous time Kalman filter is an ODE with analytic coefficients (see Eq. (A.4) of Wang, 1994). Consequently, the coefficients in the PDE (140) would still be analytic. Bhamra and Uppal (2010) take advantage of this property to analyze a dynamic general equilibrium model in which agents have heterogeneous beliefs and subjective rates of discount. The introduction of such a learning mechanism into Wachter’s model would add a third state variable. In this case, the initial conditions (141) would freeze one of the variables, presumably the conditional variance of dividend growth, so that these conditions would be an analytic function of two variables, the consumption growth and the surplus consumption ratio, i.e., the solution (142) of the Wachter model. Of course, one would also face the same curse of dimensionality problems observed in the discrete time asset pricing models, so that steps have to be taken to minimize the curse. Finally, one could use orthogonal polynomials rather than Taylor polynomials to improve the efficiency of the computer algorithm which implements the analytic method in continuous time asset pricing models.
5.3 Stochastic Differential Utility: Choosing Initial Conditions
To illustrate the second approach for setting the initial conditions Chen et al. (2013) consider the stochastic differential utility model, when consumption follows a stochastic process for consumption. This process mimics the long run growth model of Bansal and Yaron (2004). Chen et al. (2013) also consider a simpler model following Ai (2010) in which the standard deviation of the state variable is constant. To illustrate the initial value problem for infinite horizon problems we use the Ai model, which can be aligned with the investor’s problem in Section 4.
In the Ai (2010) model the long run risk variable of Bansal and Yaron is represented by investor’s estimates of the persistent component of technological shocks to production, ![]() , by firms in the economy. Ai uses a representative investor with an infinite investment horizon, so that the investor’s problem is given by (104)–(111) as
, by firms in the economy. Ai uses a representative investor with an infinite investment horizon, so that the investor’s problem is given by (104)–(111) as ![]() and the state variable is
and the state variable is ![]() rather than
rather than ![]() . Following Duffie and Lions (1992) the solution to this equation is time independent as a result, and the nonlinear differential equation (114) for Ai’s model is given by53
. Following Duffie and Lions (1992) the solution to this equation is time independent as a result, and the nonlinear differential equation (114) for Ai’s model is given by53
![]() (143)
(143)
As in the Campbell and Cochrane (1999) model one must specify two initial conditions for the existence of a solution to this ODE. The coefficients of this ODE are simpler than those found in the Campbell and Cochrane (1999) model. However, this ODE is nonlinear as long as ![]() , which corresponds to the case in which
, which corresponds to the case in which ![]() or
or ![]() in Ai’s model. From the Cauchy-Kovalevsky Theorem we know that the solution is analytic so that the solution can be represented as a power series within the radius of convergence. However, the error analysis for the Campbell and Cochrane model in Corollary 5.2 had to be modified to account for the nonlinear term in the ODE (143). Chen et al. (2013) carry out this analysis and establish a bound on the error between the solution to (143),
in Ai’s model. From the Cauchy-Kovalevsky Theorem we know that the solution is analytic so that the solution can be represented as a power series within the radius of convergence. However, the error analysis for the Campbell and Cochrane model in Corollary 5.2 had to be modified to account for the nonlinear term in the ODE (143). Chen et al. (2013) carry out this analysis and establish a bound on the error between the solution to (143), ![]() , and its
, and its ![]() order Taylor polynomial approximation within a known radius of convergence. A bound is also established for the derivative of the solution within a fraction of the same radius of convergence. Thus, they obtain an accurate solution to the nonlinear ODE when the initial conditions are given.
order Taylor polynomial approximation within a known radius of convergence. A bound is also established for the derivative of the solution within a fraction of the same radius of convergence. Thus, they obtain an accurate solution to the nonlinear ODE when the initial conditions are given.
Ai (2010) uses the procedure developed by Campbell and Viceira (2002), Campbell et al. (2004), and Chacko and Viceira (2005) which was discussed in Section 4.2. This approximation takes the form
![]() (144)
(144)
where ![]() and
and ![]() are known functions of the parameters in the original ODE (143). This is the actual solution to the approximate ODE, not the original ODE from Ai (143), so there is some unknown approximation error in this procedure.
are known functions of the parameters in the original ODE (143). This is the actual solution to the approximate ODE, not the original ODE from Ai (143), so there is some unknown approximation error in this procedure.
One way to think about this problem is to examine the case ![]() , which has the solution (121) and (122). Suppose all the unknown coefficients converge to constants as the investment horizon converges to infinity,
, which has the solution (121) and (122). Suppose all the unknown coefficients converge to constants as the investment horizon converges to infinity, ![]() . In this case, the first term in (122) approaches zero, as long as
. In this case, the first term in (122) approaches zero, as long as ![]() . Consequently, the terminal value in (122) provides no information about the solution to the ODE in the infinite horizon case. However, the integral does converge to
. Consequently, the terminal value in (122) provides no information about the solution to the ODE in the infinite horizon case. However, the integral does converge to
 (145)
(145)
which corresponds to (144) with the appropriate definition of constants ![]() and
and ![]() . Thus, the Ai approximation and the solutions agree, when
. Thus, the Ai approximation and the solutions agree, when ![]() and the investor has an infinite horizon.
and the investor has an infinite horizon.
Given the approximation by Ai the initial conditions for the original ODE (143) can be taken as
![]() (146)
(146)
To understand the impact of this choice of initial conditions, consider the perturbation method for ![]() and the state variable is
and the state variable is ![]() . Also notice that the solution to the first ODE (143) when
. Also notice that the solution to the first ODE (143) when ![]() , corresponds to the Ai approximation (144). Thus the initial conditions (146) are ignoring the terms associated with the subsequent ODEs in the perturbation method which was discussed in Section 4.2. While the approximation (144) can be shown to satisfy the bounds (119), we do not know if the actual solution does, since the error in using (146) rather than their true values is unknown.
, corresponds to the Ai approximation (144). Thus the initial conditions (146) are ignoring the terms associated with the subsequent ODEs in the perturbation method which was discussed in Section 4.2. While the approximation (144) can be shown to satisfy the bounds (119), we do not know if the actual solution does, since the error in using (146) rather than their true values is unknown.
For the parameter values in Ai (2010) and Chen et al. (2013) approximate the function ![]() for the lifetime utility of the representative investor. The initial conditions are
for the lifetime utility of the representative investor. The initial conditions are ![]() and
and ![]() where
where ![]() is the stationary point for the probability distribution for
is the stationary point for the probability distribution for ![]() . Here,
. Here, ![]() is the estimate for the radius of convergence. The relative error between the
is the estimate for the radius of convergence. The relative error between the ![]() and
and ![]() polynomial approximation is less than one in a million within this radius of convergence. In Figure 6, the solution to the approximate ODE (144) is plotted along with the
polynomial approximation is less than one in a million within this radius of convergence. In Figure 6, the solution to the approximate ODE (144) is plotted along with the ![]() order polynomial approximation using the analytic method. Again this shows that high order approximations make a significant difference given the same initial conditions. This difference is more pronounced in Figure 7 in which the expected excess return on wealth (126) is plotted. The Ai approximation yields a constant expected excess return on wealth, since the elasticity of the exponential function is constant. On the other hand the
order polynomial approximation using the analytic method. Again this shows that high order approximations make a significant difference given the same initial conditions. This difference is more pronounced in Figure 7 in which the expected excess return on wealth (126) is plotted. The Ai approximation yields a constant expected excess return on wealth, since the elasticity of the exponential function is constant. On the other hand the ![]() order approximation yields an expected excess return on wealth which is low (high) when technological progress is high (low). This conforms with the empirical behavior found in the Campbell and Cochrane model (see Figure 5).54
order approximation yields an expected excess return on wealth which is low (high) when technological progress is high (low). This conforms with the empirical behavior found in the Campbell and Cochrane model (see Figure 5).54
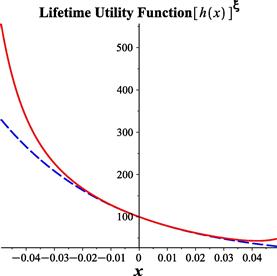
Figure 6 The lifetime utility for the production economy of Ai (2010). The parameters are the same as in Ai (2010).
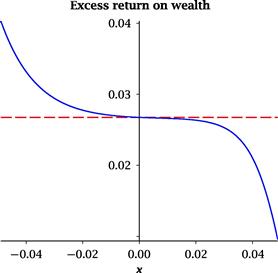
Figure 7 The risk premium on wealth for the production economy of Ai (2010). The parameters are the same as in Ai (2010).
Using initial boundary value problem (I-BVP) rather than IVP An alternative way to place conditions on the differential equation (143) would be to establish boundary conditions on the solution to (143) as the state variable becomes arbitrarily large. An example of such an approach is the solution to the Black-Sholes-Merton European call option pricing problem.55 Consider the case ![]() . Given the functional form of the fundamental solution to the investor’s problem (104) to (111), (121) and Figure 3, the solution should have the following property:
. Given the functional form of the fundamental solution to the investor’s problem (104) to (111), (121) and Figure 3, the solution should have the following property:
![]() (147)
(147)
Given the parameter values this would be the case in Ai (2010) when ![]() and
and ![]() or
or ![]() and
and ![]() .56 Given these properties of the fundamental solution, as well as the intuition from the Black-Scholes-Merton and heat diffusion one can specify the IVP as an I-BVP problem using (147) as boundary conditions on the PDE in (114) for the general case
.56 Given these properties of the fundamental solution, as well as the intuition from the Black-Scholes-Merton and heat diffusion one can specify the IVP as an I-BVP problem using (147) as boundary conditions on the PDE in (114) for the general case ![]() . One could then examine the asset pricing problem by letting the investor’s time horizon go to infinity.
. One could then examine the asset pricing problem by letting the investor’s time horizon go to infinity.
The idea is that the investment horizon is far enough into the future so that the fundamental solution (121) does not change much for longer time horizons. In addition, the investor switches to an environment or preferences such that ![]() at the end of the investment horizon. This approach would be consistent with the strategy for identifying the terminal conditions in the standard neoclassical growth theory (see Acemoglu, 2009, Chapter 8). Once the I-BVP problem is solved, one can analyze how the solution behaves as
at the end of the investment horizon. This approach would be consistent with the strategy for identifying the terminal conditions in the standard neoclassical growth theory (see Acemoglu, 2009, Chapter 8). Once the I-BVP problem is solved, one can analyze how the solution behaves as ![]() becomes arbitrarily large. By using the tools of I-BVP one would study whether the mathematical problem is well posed. In particular, one would want to know how sensitive the solution is to the initial data
becomes arbitrarily large. By using the tools of I-BVP one would study whether the mathematical problem is well posed. In particular, one would want to know how sensitive the solution is to the initial data ![]() in (145). In addition, numerical methods can be structured to accurately solve both the investor’s problem (104)–(111), and the asset pricing problem (124)–(126).
in (145). In addition, numerical methods can be structured to accurately solve both the investor’s problem (104)–(111), and the asset pricing problem (124)–(126).
6 Conclusion
This chapter has laid out how to use the analytic method to formulate and solve portfolio decision and asset pricing problems. While advances have been made in both discrete and continuous time models using this method, continuous time models yield solutions to more complicated problems. In addition, the computer algorithms are quicker. The ability to handle more complicated problems arises from the mathematics of integral versus differential equations. First, the chain rule of differentiation means that the unknown solution tends to be separated from the known functions from the components of the model, such as the pricing kernel. For some cases in the discrete time models, we are able to use change of variables to create this separation, but it is not possible in more complicated models such as the portfolio decision problem. Second, the procedures for calculating the coefficients of the Taylor polynomial approximations are easier to implement for the continuous time models. In discrete time, the coefficients must be calculated simultaneously; while under continuous time, the coefficients are calculated sequentially. Given these benefits, it is currently easier to model these financial problems in continuous time, yet there is still substantial room for improvements.
Acknowledgments
We would like to acknowledge the constructive discussion of these problems with Peter Kelly, Sebastian Roelands, and Adam Speight. We also benefited from feedback from two anonymous referees and the editors Ken Judd and Karl Schmedders. Any remaining errors are our responsibility.
References
1. Abel AB. Asset prices under habit formation and catching up with the Jonees. American Economic Review. 1990;80:38–42.
2. Abel AB. Equity premia with benchmark levels of consumption: closed-form results. In: Mehra Rajnish, ed. Handbook of the Equity Risk Premium. Amsterdam: North Holland; 2007.
3. Acemoglu D. Introduction to Modern Economic Growth. Princeton: Princeton University Press; 2009.
4. Ahlfors LV. Complex Analysis: An Introduction to the Theory of Analytic Functions of One Complex Variable. New York: McGraw-Hill; 1979.
5. Ahlfors LV. Complex Analysis. third ed. New York: McGraw-Hill; 1979.
6. Ai H. Information quality and long-run risk: asset pricing implications. Journal of Finance. 2010;65:1333–1367.
7. Ai, H., Croce, M.M., Li, K., 2012. Toward a quantitative equilibrium asset pricing model with intangible capital. Working Paper Fugua School of Business, Duke University.
8. Altug S, Labadie P. Dynamic Choice and Asset Markets. New York: Academic Press; 1994.
9. Altug S, Labadie P. Asset Pricing for Dynamic Economies. Cambridge, U.K.: Cambridge Press; 2008;
10. Anderson R, Raimondo R. Equilibrium in continuous-time financial markets: endogenously dynamically complete markets. Econometrica. 2008;76:841–907.
11. Balduzzi P, Lynch A. Transaction costs and predictability: some utility cost calculation. The Journal of Financial Economics. 1999;52:47–58.
12. Bansal R, Yaron A. Risks for the long run: a potential resolution of asset pricing puzzles. Journal of Finance. 2004;59:1481–1509.
13. Bansal, R., Kiku, D., Yaron, A., 2007. Risks for the long-run: estimation and inference. Working paper Fuqua School of Business, Duke University, Durham, USA.
14. Bansal, R., Kiku, D., Yaron, A., 2009. An empirical evaluation of the long-run risks model for asset prices. Working paper Fuqua School of Business, Duke University, Durham, USA.
15. Barberis N. Investing for the long run when returns are predictable. Journal of Finance. 2000;60:225–264.
16. Bender CM, Orszag SA. Advanced Methods for Scientists and Engineers I: Asymptotic Methods and Perturbation Theory. Berlin: Springer; 1999.
17. Bernardo AE, Judd KL. Asset market equilibrium with general tastes, returns, and information asymmetries. Journal of Financial Markets. 2000;2:17–43.
18. Bhamra, H.S., Uppal, R., 2010. Asset prices with heterogeneity in preferences and beliefs. Working Paper, EDHEC Business School, London.
19. Brandt M. Estimating portfolio and consumption choice: a conditional Euler equations approach. The Journal of Finance. 1999;54:1609–1646.
20. Brandt M. Portfolio choice problems. In: Aït-Sahalia Yacine, Peter Hansen Lars, eds. Handbook of Financial Econometrics. Amsterdam: North Holland; 2010.
21. Brandt MW, Goyal A, Santa-Clara P, Stroud JR. A simulation approach to dynamic portfolio choice with an application to learning about return predictability. Review of Financial Studies. 2005;18:831–873.
22. Brennan M, Schwartz ES, Lagnado R. Strategic asset allocation. Journal of Economics, Dynamics and Control. 1997;21:1377–1403.
23. Brennan M, Xia Y. Stochastic interest rates and Bond-Stock mix. Journal of Finance. 2002;57:1201–1238.
24. Brennan, M., Xia, Y., 2005. Persistence, predictability, and portlolio planning. Working Paper Inquire Europe.
25. Brent RP. Algorithms for Minimization Without Derivatives. Englewood Cliffs, NJ: Prentice-Hall; 1973.
26. Calin OL, Chen Y, Cosimano TF, Himonas AA. Solving asset pricing models when the price-dividend function is analytic. Econometrica. 2005;73:961–982.
27. Campbell JY. A variance decomposition for stock returns. Economic Journal. 1991;101:157–179.
28. Campbell JY. Intertemporal asset pricing without consumption data. American Economic Review. 1993;83:487–512.
29. Campbell JY, Chacko G, Rodriquez J, Viceira LM. Strategic asset allocation in a continuous-time VAR model. Journal of Economics, Dynamics and Control. 2004;28:2195–2214.
30. Campbell JY, Chan Y, Viceira LM. A multivariate model of strategic asset allocation. Journal of Financial Economics. 2003;67:41–80.
31. Campbell JY, Cochrane J. By force of habit, a consumption-based explanation of aggregate stock market behavior. Journal of Political Economy. 1999;107:205–251.
32. Campbell JY, Polk C, Vuolteenaho T. Growth or glamour? Fundamentals and systematic risk in stock returns. Review of Financial Studies. 2010;23:305–344.
33. Campbell JY, Shiller RJ. Stock prices, earnings, and expected dividends. Journal of Finance. 1988a;43:661–676.
34. Campbell JY, Shiller RJ. The dividend-price ratio and expectations of future dividends and discount factors. Review of Financial Studies. 1988b;1:195–228.
35. Campbell JY, Viceira LM. Consumption and portfolio decisions when expected returns are time varying. Quarterly Journal of Economics. 1999;114:433–495.
36. Campbell JY, Viceira LM. Who should Buy Long-Term Bonds? American Economic Review. 2001;91:99–127.
37. Campbell JY, Viceira LM. Strategic Asset Allocation: Portfolio Choice for Long-Term Investors. New York: Oxford University Press; 2002.
38. Campbell JY, Vuolteenaho T. Bad beta, good beta. American Economic Review. 2004;94:1249–1275.
39. Carroll CD. Buffer-stock saving and the life cycle/permanent income hypothesis. Quarterly Journal of Economics. 1997;112:1–55.
40. Carroll CD. Precautionary saving and the marginal propensity to consume out of permanent income. Journal of Monetary Economics. 2009;56:780–790.
41. Chacko G, Viceira LM. Dynamic consumption and portfolio choice with stochastic volatility in incomplete markets. Review of Financial Studies. 2005;18:1369–1402.
42. Chen Y, Cosimano TF, Himonas AA. Solving an asset pricing model with hybrid internal and external habits, and autocorrelated Gaussian shocks. Annals of Finance. 2008a;4:305–344.
43. Chen Y, Cosimano TF, Himonas AA. Analytic solving of asset pricing models: the by force of habit case. Journal of Economic Dynamics & Control. 2008b;32:3631–3660.
44. Chen Y, Cosimano TF, Himonas AA. Continuous time one-dimensional asset pricing models with analytic price-dividend functions. Economic Theory. 2010;42:461–503.
45. Chen, Y., Cosimano, T.F., Himonas, A.A., 2011. An external habit model subject to long run risk in continuous time: a multi-dimensional asset pricing model. Working Paper, University of Notre Dame.
46. Chen Y, Cosimano TF, Himonas AA, Kelly P. An analytic approach for stochastic differential utility for endowment and production economies Computational Economics. Berlin: Springer; 2013.
47. Chow GC. Dynamic Economics: Optimization by The Lagrange Method. New York: Oxford University Press; 1997.
48. Christiano LJ, Fisher JDM. Algorithms for solving dynamic models with occasionally binding constraints. Journal of Economics Dynamics & Control. 2000;24:1179–1232.
49. Cochrane JH. Asset Pricing. revised ed. Princeton: Princeton University Press; 2005.
50. Cochrane, J.H., 2007. Portfolio theory. Working Paper, Booth School of Business, University of Chicago.
51. Constantinides G. Habit formation: a resolution of the equity premium puzzle. Journal of Political Economy. 1990;98:519–543.
52. Constantinides GM, Duffie D. Asset pricing with heterogenous consumers. Journal of Political Economy. 1996;104:219–240.
53. Conway JB. Functions of One Complex Variable. New York: Springer-Verlag; 1973.
54. Cox JC, Huang CF. Optimal consumption and portfolio policies when asset prices follow a diffusion process. Journal of Economic Theory. 1989;49:33–83.
55. Cox JC, Ingersoll JE, Ross SA. A theory of the term structure of interest rates. Econometrica. 1985;53:385–407.
56. Croce, M.M., 2012. Long-run productivity risk: a new hope for production-based asset pricing. Working Paper, Kenan-Flagler Business School, University of North Carolina.
57. Croce, M.M., Lettau, M., Ludvigson, S.C., 2007. Investor information, long-run risk, and the duration of risky cash flows. Working Paper, New York University.
58. Dai Q, Singleton KJ. Specification analysis of affine term structure models. Journal of Finance. 2000;55:1943–1978.
59. Den Haan W, Marcet A. Solving the stochastic growth model by parameterizing expectations. Journal of Business and Economics Statistics. 1990;8:31–34.
60. Duffie DJ. Dynamic Asset Pricing Theory. third ed. Princeton: Princeton University Press; 2001.
61. Duffie DJ, Epstein LG. Stochastic differential utility. Econometrica. 1992a;60:353–394.
62. Duffie DJ, Epstein LG. Asset pricing with stochatic differential utility. Review of Financial Studies. 1992b;5:411–436.
63. Duffie DJ, Kan R. A yield-factor model of interest rates. Mathematical Finance. 1996;6:379–406.
64. Duffie DJ, Lions P-L. PDE solutions of stochastic differential utility. Journal of Mathematical Economics. 1992;21:577–606.
65. Duffie DJ, Skiadas C. Continuous-time security pricing: a utility gradient approach. Journal of Mathematical Economics. 1994;23:107–131.
66. Duffie D, Geanakoplos J, Mas-Colell A, McLennan A. Stationary Markov equilibria. Econometrica. 1994;62:745–781.
67. Duffie D, Pan J, Singleton KJ. Transform analysis and asset pricing for affine jump-diffusions. Econometrica. 2000;68:1343–1376.
68. Easley D, O’Hara M. Information and the cost of capital. Journal of Finance. 2004;59:1553–1584.
69. Epstein LG, Zin SE. Substitution, risk aversion, and the temporal behavior of consumption and asset returns: a theoretical framework. Econometrica. 1989;57:937–969.
70. Epstein LG, Zin SE. First-order risk aversion and the equity premium puzzle. Journal of Monetary Economics. 1990;26:387–407.
71. Epstein LG, Zin SE. Substitution, risk aversion, and the temporal behavior of consumption and asset returns: an empirical analysis. Journal of Political Economy. 1991;99:263–286.
72. Feigenbaum J. Information shocks and precautionary saving. Journal of Economic Dynamics & Control. 2007;31:3917–3938.
73. Fleming WH, Soner HM. Controlling Markov Processes and Viscosity Solutions. Berlin: Springer-Verlag; 2006.
74. Folland GB. Real Analysis. New York: John Wiley & Sons; 1984.
75. Gabaix, X., 2009. Linearity-generating processes: a modelling tool yielding closed forms for asset prices. Working Paper, NBER.
76. Gourinchas PO, Parker JA. Consumption over the life cycle. Econometrica. 2002;70:47–89.
77. Grimmett G, Stirzaker D. Probability and Random Processes. third ed. New York: Oxford University Press; 2001.
78. Heaton J, Lucas DJ. Evaluating the effects of incomplete markets on risk sharing and asset pricing. Journal of Political Economy. 1996;104:443–487.
79. Hörmander L. An Introduction to Complex Analysis in Several Variables. Amsterdam: Elsevier; 1979.
80. Hörmander L. The Analysis of Linear Partial Differential Operators I. Berlin: Springer-Verlag; 1983.
81. Hugonnier J, Malamud S, Trubowitz E. Endogenous completeness of diffusion driven equilibrium markets. Econometrica. 2012;80:1249–1270.
82. Intriligator MD. Mathematical Optimatization and Economic Theory. Englewood Cliff, NJ: Prentice-Hall; 1971.
83. Jin, H., Judd, K.L., 2002. Perturbation methods for general dynamic stochastic models. Working Paper, Stanford University.
84. Judd KL. Projection methods for solving aggregate growth models. Journal of Economic Theory. 1992;58:410–452.
85. Judd KL. Approximation, perturbation, and projection methods in economic analysis. In: Amman HM, Kendrick DA, Rust J, eds. Handbook of Computational Economics. Amsterdam: North Holland; 1996.
86. Judd KL. Numerical Methods in Economics. Cambridge, MA: MIT Press; 1998.
87. Judd KL, Kubler F, Schmedders K. Computing equilibria in infinite-horizon finance economies: the case of one asset. Journal of Economic Dynamics & Control. 2000;24:1047–1078.
88. Judd KL, Kubler F, Schmedders K. Asset trading volume with dynamically complete markets and heterogeneous agents. Journal of Finance. 2003;63:2203–2217.
89. Kaltenbrunner G, Lochstoer LA. Long-run risk through consumption smoothing. Review of Financial Studies. 2010;28:3190–3224.
90. Kandel S, Stambaugh RF. On the predictability of stock returns: an asset-allocation perspective. Journal of Finance. 1996;51:385–424.
91. Karatzas I, Shreve SE. Brownian Motion and Stochastic Calculus. Berlin: Springer-Verlag; 1991.
92. Kim TS, Omberg E. Dynamic nonmyopic portfolio behavior. Review of Financial Studies. 1996;9:141–161.
93. Kreps D, Porteus E. Temporal resolution of uncertainty and dynamic choice theory. Econometrica. 1978;46:185–200.
94. Kubler F, Schmedders K. Stationary equilibria in asset-pricing models with incomplete markets and collateral. Econometrica. 2003;71:1767–1793.
95. Kubler F, Schmedders K. Approximate versus exact equilibria in dynamic economies. Econometrica. 2005;73:1205–1235.
96. Le A, Singleton KJ, Dai Q. Discrete-time ![]() term structure models with generalized market prices of risk. Review of Financial Studies. 2010;23:2184–2227.
term structure models with generalized market prices of risk. Review of Financial Studies. 2010;23:2184–2227.
97. Lettau M, Ludvigson S. Consumption, aggregate wealth, and expected stock returns. Journal of Finance. 2001a;56:815–849.
98. Lettau M, Ludvigson S. Resurrecting the (C)CAPM: a cross-sectional test when risk premia are time-varying. Journal of Political Economy. 2001b;109:1238–1287.
99. Lettau M, Ludvigson S. Expected returns and expected dividend growth. Journal of Financial Economics. 2005;76:583–626.
100. Lettau M, Ludvigson SC. Measuring and modeling variation in the risk-return trade-off. In: Aït-Sahalia A, Hansen LP, eds. Hanbook of Financial Econometrics. Amsterdam: North Holland; 2010.
101. Lettau M, Wachter JA. The term structures of equity and interest rates. Journal of Financial Economics. 2011;10:90–113.
102. Lettau M, Ludvigson S, Wachter JA. The declining equity premium: what role does macroeconomic risk play? and appendix. Review of Financial Studies. 2008;21:1653–1687.
103. Liu J. Portfolio selection in stochastic environments. Review of Financial Studies. 2007;20:1–39.
104. Lo A, Wang J. Trading volume: implications of an intertemporal consumption asset pricing model. Journal of Finance. 2006;61:2805–2840.
105. Lo A, Mamaysky H, Wang J. Asset pricing and trading volume under fixed transactions costs. Journal of Political Economy. 2004;112:1054–1090.
106. Lucas Jr RE. Asset prices in a pure exchange economy. Econometrica. 1978;46:1429–1445.
107. Lucas DJ. Asset pricing with undiversifiable income risk and short sales constraints: deepening the equity premium puzzle. Journal of Monetary Economics. 1994;34:325–341.
108. Lynch A, Balduzzi P. Predictability and transaction costs: the impact on rebalancing rules and behavior. Journal of Finance. 2000;60:2285–2309.
109. Malin, B., Krueger, D., Kubler, F., 2007. Computing stochastic dynamic economic models with a large number of state variables: a description and application of a Smolyak-collocation method. Working Paper, University of Pennsylvania.
110. Mehra R, Prescott EC. The equity premium: a puzzle. Journal of Monetary Economics. 1985;15:145–161.
111. Mehra R, Prescott EC. The equity premium in retrospect. In: Constantinides George M, Harris Milton, Stulz René, eds. Handbook of the Economics of Finance. Amsterdam: North Holland; 2003.
112. Menzly L, Santos T, Veronesi P. Understanding predictability. Journal of Political Economy. 2004;112:1–47.
113. Merton RC. Lifetime portfolio selection under uncertainty: the continuous time case. Review of Economics & Statisitics. 1969;51:247–257.
114. Merton RC. Continuous-Time Finance. Oxford: Blackwell Publishers; 1990.
115. Mood AM, Graybill FA, Boes DC. Introduction to the Theory of Statistics. New York, USA: McGraw Hill; 1974.
116. Piazzesi M. Affine term structure models. In: Aït-Sahalia A, Hansen LP, eds. Hanbook of Financial Econometrics. Amsterdam: North Holland; 2010.
117. Protter PE. Stochastic Integration and Differential Equations. New York: Springer-Verlag; 2005.
118. Samuelson PA. The fundamental approximation theorem of portfolio analysis in terms of means, variance, and higher moments. Review of Economic Studies. 1970;37:537–542.
119. Sangvinatsos A, Wachter JA. Does the failure of the expectations hypothesis matter for long-term investors. Journal of Finance. 2005;60:179–230.
120. Schmedders K. Computing equilibria in the general equilibrium model with incomplete asset markers. Journal of Economic Dynamics & Control. 1999;22:1375–1401.
121. Schroder M, Skiadas C. Optimal consumption and portfolio selection with stochastic differential utility. Journal of Economic Theory. 1999;89:68–126.
122. Schroder M, Skiadas C. An isomorphism between assets pricing models with and without linear habit formation. Review of Financial Studies. 2002;15:1189–1221.
123. Schroder M, Skiadas C. Optimal lifetime consumption-portfolio strategies under trading constraints and nontradeable income. Stochastic Processes and Their Applications. 2003;155:1–30.
124. Schroder M, Skiadas C. Lifetime consumption-portfolio choice under trading constraints and generalized recursive preferences. Stochastic Processes and Their Applications. 2005;108:155–202.
125. Schroder M, Skiadas C. Optimality and state pricing in constrained financial markets with recursive utility under continuous and discontinuous information. Mathematical Finance. 2008;18:199–238.
126. Shreve SE. Stochastic Caculus for Finance II Continuous-Time Models. third ed. Berlin: Springer-Verlag; 2004.
127. Stoer J, Bulirsch R. Introduction to Numerical Analysis. third ed. Berlin: Springer-Verlag; 2002.
128. Tauchen G, Hussey R. Quadrature-based methods for obtaining approximate solutions to the integral equations of nonlinear rational expectations models. Econometrica. 1991;59:371–396.
129. Vasicek OA. An equilibrium characterization of the term structure. Journal of Financial Economics. 1977;5:177–188.
130. Vayanos D, Wang J. Liquidity and asset returns under asymmetric information and imperfect competition. Review of Financial Studies. 2012;25:1339–1365.
131. Wachter, J.A., 2002a. Habit formation and returns on bonds and stocks. Working Paper, New York University.
132. Wachter JA. Portfolio and consumption decisions under mean-reverting returns: an exact solution for complete markets. Journal of Financial and Quantitative Analysis. 2002b;37:63–91.
133. Wachter JA. Risk aversion and allocation to long-term bonds. Journal of Economic Theory. 2003;112:325–333.
134. Wachter JA. A consumption model of the term structure of interest rates. Journal of Financial Economics. 2006;79:365–399.
135. Wachter JA. Asset allocation. Annual Reviews of Financial Economics. 2010;2:175–206.
136. Wang J. A model of intertemporal asset prices under asymmetric information. Review of Economic Studies. 1993;60:249–282.
137. Wang J. A model of competitive stock trading volume. Journal of Political Economy. 1994;102:127–168.
1Option pricing problems are dealt with in a separate chapter.
2A unit root means that at least one eigenvalue of the stochastic process is one.
3Brandt (2010) provides a recent survey of portfolio research.
4Carroll (2009) is a more recent example of this strand of the literature.
5In the life-cycle literature, Feigenbaum (2007) uses a similar method with a second order Taylor approximation. However, he can explicitly find the formulas for the first and second moments.
6To account for the correlation between ![]() and
and ![]() , we can make a transformation of variables based on the conditional densities from Mood et al. (1974, p.167).
, we can make a transformation of variables based on the conditional densities from Mood et al. (1974, p.167).
7It turns out that if all investors have the same utility function (6), then you can treat the behavior of all investors with one utility function (see Altug and Labadie, 1994, pp. 22–26 for proof).
9Abel (2007) provides the generalizations of this model.
10While one keeps track of the difference between ![]() and
and ![]() in each period to derive the appropriate first order condition. In equilibrium the individual consumption has to be the same as the aggregate consumption in each period, since there is only one representative individual. Finally, consumption and dividends are the same since there is no other source of income for the consumer.
in each period to derive the appropriate first order condition. In equilibrium the individual consumption has to be the same as the aggregate consumption in each period, since there is only one representative individual. Finally, consumption and dividends are the same since there is no other source of income for the consumer.
11Samuelson (1970) initially addressed this problem in a static portfolio problem. See also Jin and Judd (2002) for a discussion of this issue when using the perturbation method.
12Cochrane (2005, Chapter 23) provides a discussion concerning how this model explains the aggregate behavior of the return on stocks.
13Campbell and Cochrane (1999) set ![]() so that the short-term interest rate is constant. Later, when the Wachter (2002a, 2006) model is discussed,
so that the short-term interest rate is constant. Later, when the Wachter (2002a, 2006) model is discussed, ![]() so that this short-term rate responds to the surplus consumption ratio.
so that this short-term rate responds to the surplus consumption ratio.
14See Intriligator (1971). Also note that the Cobb-Douglas production function is a special case in which ![]() .
.
15Lettau and Ludvigson (2001a,b, 2005) use a similar procedure applied to the budget constraint (8) to relate their CAY variable to the news about future return on stocks or consumption growth.
16Bansal and Yaron also consider a more general model in which the variance of the state variable is a first order autoregressive process. This adds a second state variable, the current variance of the state variable, to the linear function for the logarithm of the price-dividend ratio.
17In Croce et al. (2007) and Lettau et al. (2008), models similar to Bansal and Yaron are solved with alternative information structure. Croce, Lettau, and Ludvigson use a third order polynomial for their model with one state variable and second order for their model with two state variables. They do not provide an estimate for the error in their approximation. More recently, Kaltenbrunner and Lochstoer (2010), Croce (2012), and Ai et al. (2012) introduce production models into the Bansal and Yaron setup. They continue to use low order polynomial approximations to simulate their models. For example, Ai, Croce, and Li use a second order approximation.
18See Duffie et al. (2000) for the development of these models.
19See the survey of term structure models by Piazzesi (2010).
20See Lettau and Wachter (2011) for an example in which the state variable, ![]() , is one dimensional.
, is one dimensional.
21D is present because we have been using ![]() for the price-dividend ratio. Consequently,
for the price-dividend ratio. Consequently, ![]() is the dollar value of stocks when there is one unit of the stock.
is the dollar value of stocks when there is one unit of the stock.
22Judd et al. (2003) provide such a model in which markets are complete.
23One problem pointed out by Schmedders (1999) is that the demand for stocks and the consumption may be discontinuous, since the vector space spanned by the assets in an incomplete market may change dimensions as market prices change, altering the constraints faced by investors.
24Bernardo and Judd (2000) introduce heterogeneity into a two-period economy by allowing each group of investors to choose whether or not to acquire information about the dividend process at a fixed cost ![]() . They use complete polynomials which only consider the polynomials in which the sum of the exponents is finite,
. They use complete polynomials which only consider the polynomials in which the sum of the exponents is finite, ![]() , rather than each polynomial having the same finite exponent. This is one way to reduce the number of coefficients which must be found. The sparse grid methods for solving multi-dimensional polynomials introduced into stochastic growth models by Malin et al. (2007) have not been used in asset pricing problems.
, rather than each polynomial having the same finite exponent. This is one way to reduce the number of coefficients which must be found. The sparse grid methods for solving multi-dimensional polynomials introduced into stochastic growth models by Malin et al. (2007) have not been used in asset pricing problems.
25This problem was first considered by Merton (1969, 1990).
26![]() refers to the trace of the matrix
refers to the trace of the matrix ![]() .
.
27Higher order terms disappear as ![]() in (99). At this point one does not know
in (99). At this point one does not know ![]() but it is chosen given the current value of the state variable. This problem is called a controlled Markov process and is analyzed by Fleming and Soner (2006).
but it is chosen given the current value of the state variable. This problem is called a controlled Markov process and is analyzed by Fleming and Soner (2006).
28Note that it is conceivable that the parameters in ![]() are different for her children.
are different for her children.
29See Karatzas and Shreve (1991, p. 358) for the covariance between ![]() and
and ![]() for
for ![]() .
.
30The notation indicates the dependence of the coefficients on the preference parameters ![]() ,
, ![]() , and
, and ![]() . Also notice that some researchers specify the function
. Also notice that some researchers specify the function ![]() in terms of the time to maturity
in terms of the time to maturity ![]() rather than current time
rather than current time ![]() . This involves a change of variable which switches the sign on the partial derivative with respect to time.
. This involves a change of variable which switches the sign on the partial derivative with respect to time.
31Anderson and Raimondo (2008) and Hugonnier et al. (2012) develop conditions for financial markets to be dynamically complete, so that these matrices would be positive definite.
32We use subscripts to represent the derivatives of the function and suppress the dependence of ![]() on
on ![]() .
.
33Hugonnier et al. (2012 Lemma F.1) establish these properties of the transition density for the n-dimensional state vector of the stochastic process (109).
34These conditions are the same as the conditions found in Schroder and Skiadas (2003) for the investor’s problem (104)–(111).
35See Schroder and Skiadas (2003) or Liu (2007) for these equations in the most general cases.
36See Eq. (25) of Wachter (2002b), for example.
37One can use ![]() as long as
as long as ![]() . This means
. This means ![]() .
.
38Bansal and Yaron argue that ![]() in addition to
in addition to ![]() but the solution to the investor’s problem is not known in this case.
but the solution to the investor’s problem is not known in this case.
39See Duffie (2001) and Cox and Huang (1989) for complete specification of the underlying stochastic processes. Hugonnier et al. (2012) show that markets are endogenously complete when the partial derivative of the variance-covariance matrix for the state variables with respect to these state variables is nonsingular. They also show that this analysis applies whether or not there is a distinct payoff at the terminal time as in Anderson and Raimondo (2008). The applied examples considered here satisfy the necessary conditions for a well-defined solution.
40Schroder and Skiadas (1999, 2002, 2003, 2005, 2008) complete this analysis for more complex circumstances including trading constraints, non-tradeable income, discontinuous information, and generalized preferences.
41Duffie and Epstein (1992b) and Duffie and Skiadas (1994) derive this relation from the Hamilton-Jacobi-Bellman equation and optimal decisions of the representative investor in the general case with multiple assets, as in Section 4. In this case the one share of stock is replaced by the market portfolio for all stocks available to the investor.
42Ai (2010) provides a recent example of such a model in which the state variable is the expected growth rate of technology for the economy.
43Knowledge of the solution to the IVP would also be useful for dynamic general equilibrium models in continuous time, since this solution also determines the aggregate consumption in the economy following (113).
44This discussion presumes a stochastic process for the state variable which has the same form as the expected return on stocks, (109). Hugonnier et al. (2012) provide the known properties of the solution to such stochastic processes in multiple dimensions.
45Since the expected return on assets from the asset pricing model is a ![]() function of the state variable
function of the state variable ![]() , one can derive the stochastic process for the expected return using Ito’s Lemma (96). Such a stochastic process would be dependent on the first three derivatives of the solution to the IVP (114).
, one can derive the stochastic process for the expected return using Ito’s Lemma (96). Such a stochastic process would be dependent on the first three derivatives of the solution to the IVP (114).
46Cochrane (2005) organizes his discussion of asset pricing around this pricing relation.
47The superscript for the surplus consumption ratio, ![]() , has been deleted for notational convenience.
, has been deleted for notational convenience.
48The program is written in Maple and run on a standard PC.
49They use ![]() for the case of
for the case of ![]() and
and ![]() , and use
, and use ![]() for the case of
for the case of ![]() and
and ![]() .
.
50If one accounts for the global properties of the solution as in the stochastic differential utility model considered below, then these extreme values would play a role.
51See Cochrane (2005, Chapters 24 and 25) for the detailed discussion of these properties.
52In Wachter (2006) the second state variable is inflation.
53The expressions for the parameters in the ODE are different from (114) and are given in Chen et al. (2013).
54The expected return in Figure 5 is higher than in Figure 7, since the former dealt with stock returns and the latter deals with the return on wealth.
55See Shreve (2004, pp. 158–159 and Exercise 4.9).
56In the other cases the boundary condition (147) would be modified to assure the growth condition on the solution is satisfied. This would assure that the bound in (119) would be satisfied.