Analyzing Fiscal Policies in a Heterogeneous-Agent Overlapping-Generations Economy
Shinichi Nishiyamaa and Kent Smettersb, aMacroeconomic Analysis Division, Congressional Budget Office, USA, bWharton School of Business, University of Pennsylvania, USA, [email protected], [email protected]
Abstract
The overlapping generations (OLG) life-cycle model with heterogeneous agents has become the main workhorse for evaluating the welfare and macroeconomic effects of major fiscal policy changes, including reforms to tax and social insurance systems. This chapter shows how to construct and solve a OLG model with idiosyncratic shocks, which allows for analyzing the inter- and intra-generational welfare and macroeconomic impact of policy changes.
Keywords
Life cycle; Overlapping generations; Dynamic programming; Fiscal policy; Welfare
JEL Classification Codes
D91; E62; H31
1 Introduction
The heterogeneous-agent overlapping-generations (OLG) model is the most persuasive framework for analyzing fiscal policy changes. Unlike the representative-agent infinite-horizon model, the heterogeneous-agent OLG model (1) accommodates the life-cycle properties that are important for determining labor supply and savings choices, (2) allows for intra-generational heterogeneity in households, which is necessary for analyzing the impact of policy changes on the income and wealth distributions, and (3) incorporates the foundation for the relevancy of the inter-generational distribution of wealth, which is important for analyzing fiscal policies that change the timing of taxes.
Solving a heterogeneous-agent OLG model that is rich enough to analyze a realistic fiscal policy change, however, can be computationally challenging. There are technically infinitely many heterogeneous agents in the model economy, and we need to solve their optimization problems for many periods. The wealth distribution must also be tracked over time. Only the simplest varieties of OLG models can be solved using “black box” large-scale constrained optimizers. Heterogeneous-agent models, such as that considered herein, must be tackled using the explicit formulation of dynamic programming that is embedded within a general optimization routine to close the system in general equilibrium.
This chapter shows how to solve a heterogeneous-agent OLG model that includes elastic labor supply as well as a progressive individual income tax and a Social Security system that are similar to those in the US economy. We solve for the Kuhn-Tucker conditions for each agent in each period by using a Newton-type nonlinear equation solver. The decision rules of a heterogeneous agent is then embedded within a Gauss-Jacobi iteration of factor prices and government policy variables in order to produce rational expectations of those in the steady-state equilibrium and the equilibrium transition path. This approach is straightforward and fairly “general purpose” in nature, thereby allowing it to be easily extended to accommodate additional complexity.
The rest of the chapter is organized as follows: Section 2 provides a brief overview of the existing literature and applications of the OLG model. Section 3 describes the stylized heterogeneous-agent OLG model with a progressive income tax and a realistic Social Security system. Section 4 explains the computational algorithms to solve the optimization problem of heterogeneous agents and to solve the overall model economy for an equilibrium, Section 5 shows the calibration of the baseline economy to the US economy, Section 6 demonstrates the features of the heterogeneous-agent OLG model numerically by using a simple consumption tax reform and Social Security privatization as examples, and Section 7 concludes the chapter.
2 Existing Literature
The literature using OLG models to analyze fiscal policy issues is now quite vast. The theoretical foundations for the life-cycle model can be traced to the pioneering work by Samuelson (1958) and Diamond (1965). Analyzing fiscal policies computationally, however, began with the influential works of Shoven and Whalley (1973) and Auerbach and Kotlikoff (1987).
Deterministic Economy with No Lifetime Heterogeneity
While not technically a modern life-cycle model, Shoven and Whalley showed how Scarf’s (1967) algorithm could be generalized to compute a competitive equilibrium in the presence of taxes; they also proved the existence of such an equilibrium. Auerbach and Kotlikoff were first to solve a general-equilibrium fiscal policy model with life-cycle consumers and overlapping generations. Their model included transaction costs as well as a way to measure pure (first-best) Hicksian efficiency gains in general equilibrium. They were also aware that making comparisons across steady states could be misleading, especially for analyzing reforms to Social Security and taxes. So, their model included transitional dynamics that could last up to 150 years. Laitner (1990) proved the existence and uniqueness of competitive equilibrium in a simplified version of the Auerbach and Kotlikoff model.
The original version of the Auerbach and Kotlikoff model had no uncertainty or non-convexities, which allowed them to solve their model using Euler-based methods instead of with dynamic programming. The household side of the economy was solved by integrating the standard intertemporal Euler equation across the finite lifetime to obtain a functional relationship between the “initial age” of consumption and consumption at each future age. The “initial age” was either the first year of consumption as an independent economic actor (usually age 21) or the current age of a mature economic actor immediately after a policy change that would alter current consumption. This functional relationship, along with the first-order condition between consumption and leisure, was then inserted into the household’s intertemporal budget constraint to derive a value of consumption at the initial age that was only a function of current and future household productivity levels, factor prices, and fiscal policy variables. Future consumption levels were then easily computed using the Euler equation (the leisure choice was determined by its relationship with consumption using its own first-order condition). The resulting solution was very accurate because they didn’t require any sort of interpolation of the form that is required with modern dynamic programming.
This household problem itself, however, was only partial equilibrium in nature since it was calculated using a conjectured path for factor prices. The Auerbach and Kotlikoff model, therefore, also included an “outer loop” that helped solve for the general-equilibrium solution. Specifically, the household levels of capital and labor supplies were summed up across the measure of households at each age, their corresponding values were inserted into a neoclassical production function and a new set of factor prices were then generated. The household problem was then recomputed with these new factor prices, and the process was repeated until the difference in factor prices between iterations became sufficiently small. While more modern models no longer integrate the Euler equation to solve the household problem, they continue to use the essence of the Auerbach and Kotlikoff “outer loop” mechanism to solve for general equilibrium.
Deterministic Economy with Heterogeneity
In the original Auerbach and Kotlikoff model, the only heterogeneity that existed was by age. An overlapping young household and an older household had the same lifetime resources and so their consumption and leisure choices only differed because they were at different points in their life cycle.
Hence, the next generation of models allowed for heterogeneity by lifetime income groups. Like the Auerbach and Kotlikoff model, these models were deterministic and solved using Euler-based methods described above, but for multiple types of households. In effect, the household’s partial equilibrium problem was solved a dozen or so times, once per lifetime income group, before aggregating the results in the outer loop (although some models did not compute general-equilibrium solutions). The related works include Fullerton and Rogers (1993), Kotlikoff et al. (1998, 1999, 2007), Altig and Carlstrom (1999), and Altig et al. (2001).
Idiosyncratic Shocks, Heterogeneity, and Deterministic Aggregate Variables
The next generation of models introduced uncertainty where households face idiosyncratic risks. However, the aggregate economy—and, hence, factor prices—remained deterministic. Still, these models incorporate a richer source of heterogeneity and allow households to save precautiously against uninsurable risks. This uncertainty typically takes the form of stochastic wages, although sometimes longevity uncertainty is considered if private annuities are assumed to be unavailable. The related works include Bewley (1986), Laitner (1992), Huggett (1993, 1996), Aiyagari (1994), Ríos-Rull (1999), İmrohoroğlu et al. (1995), Hubbard et al. (1995), Carroll (1997), Conesa and Krueger (1999, 2006), Storesletten et al. (2001, 2004), Domeij and Heathcote (2004), Nishiyama and Smetters (2005, 2007), Conesa et al. (2009). Some of those models focused on steady states, allowing them to analyze changes to macroeconomic variables over the long run. Some of the models also computed the transitional effects of policy changes from one steady state to the next. Including the transition dynamics then allows the models to also be used to analyze the welfare impact of fiscal policy reforms that, for example, might benefit future steady-state generations at the cost to transitional generations. Our current chapter is in the tradition of these models and so we won’t spend more time here discussing their solution techniques. Heathcote et al. (2009) also provide an excellent survey of these types of models.
Heterogeneity and Stochastic Aggregate Variables
The next frontier of OLG models is still evolving and they seek to incorporate shocks to macroeconomic variables that also allow for factor prices to be uncertain. These types of models can be used to study the value of reducing the effects of business cycles, the term structure of debt, and optimal risk sharing across generations. The computational challenges, however, are significant because the underlying size of the state space is much too large for standard dynamic programming techniques. Attempts to break this so-called curse of dimensionality have employed various techniques: randomization (Rust, 1997); modeling the wealth distribution using a simple two-parameter distribution family (Krusell and Smith, 1998); restricting computations to key points in the state space (Krueger and Kubler, 2004, 2006); and, most recently, combining simulation and projection approaches (Judd et al., 2012). Using the last technique, Hasanhodzic and Kotlikoff (2012) solved an 80-period OLG model with aggregate risk. Thus far, however, there has not been a many-period OLG model that combines aggregate uncertainty with idiosyncratic risk.
3 Stylized Model Economy
The economy consists of a large number of overlapping-generation households, a perfectly competitive representative firm with constant-returns-to-scale technology, and a government with a commitment technology. The households are heterogeneous and face uninsurable income risks in the tradition of Bewley (1986), Huggett (1993), Aiyagari (1994), Carroll (1997), and many others. The time is discrete and one model period is a year, which is denoted by ![]() . In a steady-state (stationary) equilibrium, the model economy is assumed to be on a balanced-growth path with a labor-augmenting productivity growth rate
. In a steady-state (stationary) equilibrium, the model economy is assumed to be on a balanced-growth path with a labor-augmenting productivity growth rate ![]() and a population growth rate
and a population growth rate ![]() . In the following model description, individual variables other than working hours are thus growth-adjusted by
. In the following model description, individual variables other than working hours are thus growth-adjusted by ![]() and aggregate variables are adjusted by
and aggregate variables are adjusted by ![]() .
.
3.1 The Households
Households are heterogeneous with respect to their age, ![]() , beginning-of-period wealth,
, beginning-of-period wealth, ![]() , average historical earnings,
, average historical earnings, ![]() , and working ability,
, and working ability, ![]() . The households enter the economy and start working at age
. The households enter the economy and start working at age ![]() , which corresponds to real age 21. They retire at age
, which corresponds to real age 21. They retire at age ![]() and live at most up to age
and live at most up to age ![]() . The average historical earnings are used to approximate the average indexed monthly earnings (AIME) to determine individual Social Security benefits. The individual working ability is equivalent to an hourly wage, and it follows the first-order Markov process. In every period,
. The average historical earnings are used to approximate the average indexed monthly earnings (AIME) to determine individual Social Security benefits. The individual working ability is equivalent to an hourly wage, and it follows the first-order Markov process. In every period, ![]() , heterogeneous households each receive an idiosyncratic working ability shock,
, heterogeneous households each receive an idiosyncratic working ability shock, ![]() , and they choose consumption,
, and they choose consumption, ![]() , working hours,
, working hours, ![]() , and wealth at the beginning of next period,
, and wealth at the beginning of next period, ![]() , to maximize their expected (remaining) lifetime utility.
, to maximize their expected (remaining) lifetime utility.
3.1.1 The State Variables and the Government Policy
Let ![]() and
and ![]() denote the individual state of a household and the aggregate state of the economy in period
denote the individual state of a household and the aggregate state of the economy in period ![]() , respectively,
, respectively,
![]()
where ![]() is the population density function of households, and
is the population density function of households, and ![]() is the government’s net worth at the beginning of period
is the government’s net worth at the beginning of period ![]() . Let
. Let ![]() be the government policy schedule at the beginning of period
be the government policy schedule at the beginning of period ![]() ,
,
![]()
where ![]() is government consumption,
is government consumption, ![]() is a lump-sum transfer per household,
is a lump-sum transfer per household, ![]() is a progressive income tax function,
is a progressive income tax function, ![]() is a flat consumption tax rate,
is a flat consumption tax rate, ![]() is a Social Security payroll tax function,
is a Social Security payroll tax function, ![]() is a Social Security benefit function,
is a Social Security benefit function, ![]() is a uniform transfer per working-age household from accidental bequests, and
is a uniform transfer per working-age household from accidental bequests, and ![]() is the government’s net worth at the beginning of the next period.
is the government’s net worth at the beginning of the next period.
3.1.2 The Household’s Optimization Problem
Let ![]() be the value function of the household at the beginning of period
be the value function of the household at the beginning of period ![]() . Then, their optimization problem is
. Then, their optimization problem is
![]() (1)
(1)
subject to the constraints for the decision variables,
![]() (2)
(2)
and the law of motion of the individual state,
![]() (3)
(3)
 (4)
(4)
![]() (5)
(5)
where ![]() is a period utility function,
is a period utility function, ![]() is a growth-adjusted discount factor explained in more detail below,
is a growth-adjusted discount factor explained in more detail below, ![]() is a conditional survival probability at the end of age
is a conditional survival probability at the end of age ![]() if the household is alive at the beginning of age
if the household is alive at the beginning of age ![]() , and
, and ![]() is an expected value operator. The variable
is an expected value operator. The variable ![]() is an interest rate,
is an interest rate, ![]() is a wage rate per efficiency unit of labor,
is a wage rate per efficiency unit of labor, ![]() is an indicator function that returns 1 if the condition in
is an indicator function that returns 1 if the condition in ![]() holds and 0 otherwise,
holds and 0 otherwise, ![]() is an exogenous retirement age, and
is an exogenous retirement age, and ![]() is the maximum taxable earnings for the OASI program. Wealth at the beginning of next period,
is the maximum taxable earnings for the OASI program. Wealth at the beginning of next period, ![]() , is adjusted by the productivity growth rate,
, is adjusted by the productivity growth rate, ![]() . The average historical earnings,
. The average historical earnings, ![]() , are wage-indexed and, thus, need not be growth-adjusted. The price indexation of AIME after age 60 is reflected in the Social Security benefit function.
, are wage-indexed and, thus, need not be growth-adjusted. The price indexation of AIME after age 60 is reflected in the Social Security benefit function.
3.1.3 Perfect Annuity Markets [Optional]
When perfect annuity markets are available in the model economy, the household’s budget constraint, (4), is modified to
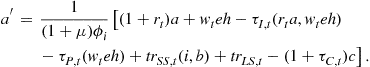
In the absence of an intentional bequest motive, household wealth is fully annuitized. Thus ![]() , and the actuarially fair price of annuity is
, and the actuarially fair price of annuity is ![]() .
.
3.1.4 Natural Borrowing Constraint [Optional]
We can relax the borrowing constraint, ![]() , by introducing the natural borrowing constraint,
, by introducing the natural borrowing constraint, ![]() , such that
, such that
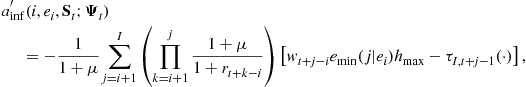
where ![]() is the lowest possible working ability at age
is the lowest possible working ability at age ![]() given that the current working ability is
given that the current working ability is ![]() , and
, and ![]() is the maximum number of working hours. When factor prices and working hours are endogenous and the income tax is progressive, however, setting a precise natural borrowing constraint is not practical. The reason is that a small change in factor prices or tax rates during an iteration or due to a policy change makes the household’s problem hard to solve. A simpler way to relax the borrowing constraint is to set the age-specific but fixed minimum wealth levels,
is the maximum number of working hours. When factor prices and working hours are endogenous and the income tax is progressive, however, setting a precise natural borrowing constraint is not practical. The reason is that a small change in factor prices or tax rates during an iteration or due to a policy change makes the household’s problem hard to solve. A simpler way to relax the borrowing constraint is to set the age-specific but fixed minimum wealth levels, ![]() , as follows:
, as follows:
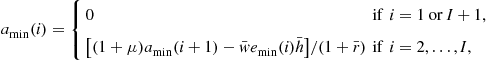
where ![]() is the lowest working ability for age
is the lowest working ability for age ![]() , and
, and ![]() , and
, and ![]() are the interest rate, the wage rate, and the average working hours, respectively, in the baseline economy.1
are the interest rate, the wage rate, and the average working hours, respectively, in the baseline economy.1
3.1.5 The Household’s Preference
The household’s period utility function is a combination of Cobb-Douglas and constant relative risk aversion (CRRA) preferences,
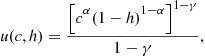 (6)
(6)
which is consistent with a growth economy. With this preference, the growth-adjusted discount factor is ![]() , where
, where ![]() is the original discount factor. While the solution approach discussed later works for other utility functions as well, it is important that any utility function satisfies the requirements of balanced-growth path as derived in King et al. (1988).
is the original discount factor. While the solution approach discussed later works for other utility functions as well, it is important that any utility function satisfies the requirements of balanced-growth path as derived in King et al. (1988).
3.1.6 The Income Tax Function
The individual income tax function is one of Gouveia and Strauss (1994),
![]()
where ![]() is the household’s taxable income with constant deductions and exemptions
is the household’s taxable income with constant deductions and exemptions ![]() . While a smooth tax function is not strictly required, it does tend to speed up the rate of convergence to a fixed point without giving up much precision. We can optionally consider a tax on Social Security benefits. In that case, the income tax function is modified to
. While a smooth tax function is not strictly required, it does tend to speed up the rate of convergence to a fixed point without giving up much precision. We can optionally consider a tax on Social Security benefits. In that case, the income tax function is modified to
![]()
where ![]() , and
, and ![]() calculates the taxable portion of Social Security benefits.2
calculates the taxable portion of Social Security benefits.2
3.1.7 The Social Security System
The Social Security payroll tax function is
![]()
where ![]() is the flat Old-Age and Survivors Insurance (OASI) tax rate that includes the employer’s portion. The payroll tax ceiling is captured by
is the flat Old-Age and Survivors Insurance (OASI) tax rate that includes the employer’s portion. The payroll tax ceiling is captured by ![]() and produces a non-convexity in the household’s optimization problem. The Social Security benefit function is kinked and equal to
and produces a non-convexity in the household’s optimization problem. The Social Security benefit function is kinked and equal to

where ![]() and
and ![]() are the thresholds for the three replacement rate brackets, 90%, 32%, and 15%, that calculate the Social Security benefit from the average historical earnings, and
are the thresholds for the three replacement rate brackets, 90%, 32%, and 15%, that calculate the Social Security benefit from the average historical earnings, and ![]() is the benefit adjustment factor to balance the budget.
is the benefit adjustment factor to balance the budget.
3.1.8 The Household’s Decision Rules
Solving the household’s optimization problem for ![]() , and
, and ![]() for all possible states, we obtain the household’s decision rules and the average historical earnings at the beginning of next period as
for all possible states, we obtain the household’s decision rules and the average historical earnings at the beginning of next period as ![]() , and
, and

3.1.9 The Distribution of Households
Let ![]() be the population density function of households in period
be the population density function of households in period ![]() , and let
, and let ![]() be the corresponding cumulative distribution function. We assume that households enter the economy with no assets and earning histories,
be the corresponding cumulative distribution function. We assume that households enter the economy with no assets and earning histories, ![]() , and that the growth-adjusted population of the age
, and that the growth-adjusted population of the age ![]() household is normalized to unity,
household is normalized to unity,
![]()
The law of motion of the growth-adjusted population distribution is, for ![]() ,
,
![]()
where ![]() is the population growth rate, and
is the population growth rate, and ![]() is the transition probability density function of working ability from age
is the transition probability density function of working ability from age ![]() to
to ![]() .
.
3.1.10 The Supply of Capital and Labor
Total private wealth, ![]() , national wealth,
, national wealth, ![]() , which is equal to capital stock in a closed economy, and labor supply in efficiency units,
, which is equal to capital stock in a closed economy, and labor supply in efficiency units, ![]() , are
, are
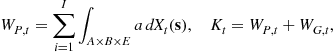 (7)
(7)
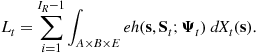 (8)
(8)
3.2 The Representative Firm
In each period, the representative firm chooses the capital input, ![]() , and the labor input,
, and the labor input, ![]() , to maximize its period profit, taking factor prices,
, to maximize its period profit, taking factor prices, ![]() and
and ![]() , as given,
, as given,
![]() (9)
(9)
![]() is a constant-returns-to-scale production function,
is a constant-returns-to-scale production function,
![]() (10)
(10)
where ![]() is the total factor productivity and
is the total factor productivity and ![]() is the depreciation rate of capital. The firm’s profit maximizing conditions are
is the depreciation rate of capital. The firm’s profit maximizing conditions are
![]() (11)
(11)
3.2.1 A Closed Economy
In a closed economy, the factor markets clear when
![]() (12)
(12)
Therefore, gross domestic product, which is identical to gross national product, ![]() , is determined by
, is determined by
![]() (13)
(13)
In this chapter, for simplicity, we assume that the government’s fixed capital is as productive as private fixed capital. In the National Income and Product Account (NIPA), however, imputed capital income from the government’s fixed capital is assumed to be zero, and only depreciation, ![]() , is included in gross domestic product as consumption of fixed capital. That is, when the capital stock is divided into private fixed capital,
, is included in gross domestic product as consumption of fixed capital. That is, when the capital stock is divided into private fixed capital, ![]() , and the government’s fixed capital,
, and the government’s fixed capital, ![]() , the gross domestic (national) product is
, the gross domestic (national) product is
![]()
3.2.2 A Small Open Economy [Optional]
In a small open economy, factor prices, ![]() and
and ![]() , are fixed at baseline (international) levels, as international capital flows ensure that the capital-labor ratio is determined by the world interest rate that is attained in the economy. In an equilibrium, the domestic capital stock,
, are fixed at baseline (international) levels, as international capital flows ensure that the capital-labor ratio is determined by the world interest rate that is attained in the economy. In an equilibrium, the domestic capital stock, ![]() , and labor supply,
, and labor supply, ![]() , therefore, are determined to satisfy the firm’s profit maximizing conditions,
, therefore, are determined to satisfy the firm’s profit maximizing conditions,
![]()
Gross domestic product, ![]() , and gross national product,
, and gross national product, ![]() , are determined by
, are determined by
![]()
respectively, and the debt held by foreign countries (foreign wealth), ![]() , is
, is
![]()
3.3 The Government
The government’s income tax revenue, ![]() , is
, is
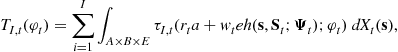 (14)
(14)
while the consumption tax revenue, ![]() , is
, is
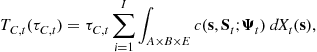 (15)
(15)
and the lump-sum transfer spending, ![]() , is
, is
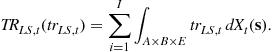 (16)
(16)
The Social Security (OASI) payroll tax revenue, ![]() , is
, is
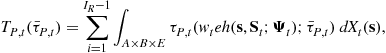 (17)
(17)
and the Social Security benefit expenditure, ![]() , is
, is
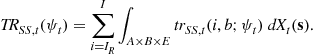 (18)
(18)
The law of motion of the government’s net worth, ![]() , is
, is
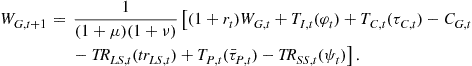 (19)
(19)
3.3.1 Accidental Bequests
For simplicity, we assume that the government collects remaining wealth held by deceased households at the end of period ![]() and distributes it to working-age households in a lump-sum manner in the same period.3 Since there are no aggregate shocks in the model economy, the government can perfectly predict the sum of accidental bequests during each period. The government revenue from these accidental bequests,
and distributes it to working-age households in a lump-sum manner in the same period.3 Since there are no aggregate shocks in the model economy, the government can perfectly predict the sum of accidental bequests during each period. The government revenue from these accidental bequests, ![]() , is
, is
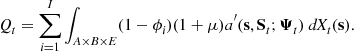 (20)
(20)
The uniform bequest that each working-age household receives, ![]() , is
, is
 (21)
(21)
3.4 Recursive Competitive Equilibrium
The recursive competitive equilibrium of this model economy is defined as follows.
3.4.1 DEFINITION Recursive Competitive Equilibrium
Let ![]() be the individual state of households, let
be the individual state of households, let ![]() be the aggregate state of the economy, and let
be the aggregate state of the economy, and let ![]() be the government policy schedule committed at the beginning of period
be the government policy schedule committed at the beginning of period ![]() ,
,
![]()
A time series of factor prices and the government policy variables,
![]()
the value functions of households, ![]() , the decision rules of households,
, the decision rules of households,
![]()
and the distribution of households, ![]() , are in a recursive competitive equilibrium if, for all
, are in a recursive competitive equilibrium if, for all ![]() , each household solves the optimization problem, (1)–(5) , taking
, each household solves the optimization problem, (1)–(5) , taking ![]() and
and ![]() as given; the firm solves its profit maximization problem, (9)–(11) ; the government policy schedule satisfies conditions (14)–(19) ; and the factor markets are cleared as shown in Eqs. (7), (8), and (12). The economy is in a steady-state equilibrium, and thus on the balanced-growth path, if, in addition,
as given; the firm solves its profit maximization problem, (9)–(11) ; the government policy schedule satisfies conditions (14)–(19) ; and the factor markets are cleared as shown in Eqs. (7), (8), and (12). The economy is in a steady-state equilibrium, and thus on the balanced-growth path, if, in addition, ![]() and
and ![]() for all
for all ![]() .
.
In the above competitive equilibrium, the resource (feasibility) constraint is satisfied—the goods market clears—in each period by Walras’ law, that is,
![]()
in a closed economy, or
![]()
in a small open economy.
3.5 Social Welfare Measures
Suppose that the economy is in the initial equilibrium in period ![]() and that the government introduces a new policy at the beginning of period 1. Then, the (remaining) lifetime value of a household of state
and that the government introduces a new policy at the beginning of period 1. Then, the (remaining) lifetime value of a household of state ![]() is denoted by
is denoted by ![]() before the policy change and
before the policy change and ![]() for
for ![]() after the policy change.
after the policy change.
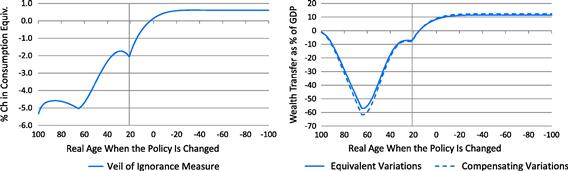
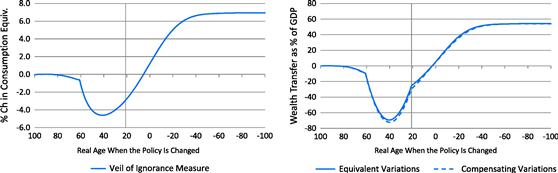
3.5.1 The Veil of Ignorance
Under the veil of ignorance welfare measure, the welfare gains or losses of newborn (age ![]() ) households at the beginning of period
) households at the beginning of period ![]() are calculated by the uniform percent changes,
are calculated by the uniform percent changes, ![]() , in the baseline consumption path that would make their unconditional (ex ante) expected lifetime utility equivalent with the expected lifetime utility after the policy change, that is,
, in the baseline consumption path that would make their unconditional (ex ante) expected lifetime utility equivalent with the expected lifetime utility after the policy change, that is,
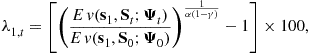
where ![]() ,4 and
,4 and
![]()
Similarly, the average welfare changes of households of age ![]() at the time of policy change
at the time of policy change ![]() are calculated by the uniform percent changes,
are calculated by the uniform percent changes, ![]() , required in the baseline consumption path so that the expected remaining lifetime value would be equal to the expected remaining lifetime value after the policy change, that is,
, required in the baseline consumption path so that the expected remaining lifetime value would be equal to the expected remaining lifetime value after the policy change, that is,
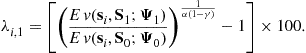
Note that ![]() for
for ![]() shows the cohort-average welfare changes of all current households alive at the time of policy change, and
shows the cohort-average welfare changes of all current households alive at the time of policy change, and ![]() for
for ![]() shows the cohort-average welfare changes of all future households.
shows the cohort-average welfare changes of all future households.
3.5.2 Equivalent Variations
The equivalent variation of a household of state ![]() is the one-time wealth transfer that generates as much welfare gain in the baseline economy as the policy change. The equivalent variations of newborn (age
is the one-time wealth transfer that generates as much welfare gain in the baseline economy as the policy change. The equivalent variations of newborn (age ![]() ) households at the beginning of period
) households at the beginning of period ![]() are calculated as
are calculated as ![]() such that
such that
![]()
and the equivalent variations of age ![]() at the time of policy change
at the time of policy change ![]() are calculated as
are calculated as ![]() such that
such that
![]()
The average (growth adjusted) equivalent variations by age cohort are calculated as

for ![]() and
and ![]() , where
, where ![]() is the growth-adjusted population of age
is the growth-adjusted population of age ![]() , which is time-invariant,
, which is time-invariant,
![]()
3.5.3 Compensating Variations
The compensating variation of a household of state ![]() is the one-time negative wealth transfer that restores the baseline welfare level in the alternative economy after the policy change. The compensating variations of newborn (age
is the one-time negative wealth transfer that restores the baseline welfare level in the alternative economy after the policy change. The compensating variations of newborn (age ![]() ) households at the beginning of period
) households at the beginning of period ![]() are calculated as
are calculated as ![]() such that
such that
![]()
and the compensating variations of age ![]() at the time of policy change
at the time of policy change ![]() are calculated as
are calculated as ![]() such that
such that
![]()
The average (growth adjusted) compensating variations by age cohort are calculated as
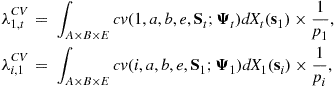
for ![]() and
and ![]() .
.
We could technically calculate the present discount sum of compensating variations of all current and future households. However, a positive present discount sum does not, in general, imply a Hicksian increase in efficiency from the policy change. The reason is that, once wealth is actually transferred from winners to losers, the household’s optimal saving and labor supply will change, due to the wealth effect, and the factor prices and the government policy variables will also change. Nishiyama and Smetters (2005, 2007) examine how to calculate efficiency gains in general equilibrium.
4 Computational Algorithm
We solve the household’s optimization problem, (1)–(5) , recursively from age ![]() to age 1 by discretizing the state variables as follows: the asset space,
to age 1 by discretizing the state variables as follows: the asset space, ![]() , into
, into ![]() nodes,
nodes, ![]() ; the average historical earning space,
; the average historical earning space, ![]() , into
, into ![]() nodes,
nodes, ![]() ; and, the working ability space,
; and, the working ability space, ![]() , into
, into ![]() nodes for each age,
nodes for each age, ![]() .5 Since the working ability of a retired household is assumed to be
.5 Since the working ability of a retired household is assumed to be ![]() , the total number of nodes for which we solve the household’s optimization problem in each period
, the total number of nodes for which we solve the household’s optimization problem in each period ![]() is
is ![]() .6
.6
Let ![]() be a time series of vectors of factor prices and government policy variables that describes a future path of the aggregate economy,
be a time series of vectors of factor prices and government policy variables that describes a future path of the aggregate economy,
![]()
The household’s value function is shown as ![]() , and the factor prices and endogenous government policy variables are shown as
, and the factor prices and endogenous government policy variables are shown as ![]() , and so on, for
, and so on, for ![]() . It is impossible to solve the model of this form because the dimension of
. It is impossible to solve the model of this form because the dimension of ![]() is infinite. In the absence of aggregate productivity or policy shocks, however, we can avoid this “curse of dimensionality” by replacing
is infinite. In the absence of aggregate productivity or policy shocks, however, we can avoid this “curse of dimensionality” by replacing ![]() with
with ![]() . Since the time series
. Since the time series ![]() is deterministic and perfectly foreseeable, it suffices to find the fixed point of
is deterministic and perfectly foreseeable, it suffices to find the fixed point of ![]() to solve the model economy for an equilibrium transition path.
to solve the model economy for an equilibrium transition path.
In this section, we first explain the algorithm to solve the household’s optimization problem for each individual state node,
![]()
taking ![]() as given. Then, we explain how to solve the model for a steady-state equilibrium (balanced-growth path) and an equilibrium transition path.
as given. Then, we explain how to solve the model for a steady-state equilibrium (balanced-growth path) and an equilibrium transition path.
4.1 Solving the Household’s Problem
We solve the household’s optimization problem backward from age ![]() to age 1 by assuming the terminal value to be zero,
to age 1 by assuming the terminal value to be zero,
![]()
where ![]() is the individual state vector of the household at age
is the individual state vector of the household at age ![]() . The following computational algorithm is a simpler version of those in Nishiyama (2010, 2011).7
. The following computational algorithm is a simpler version of those in Nishiyama (2010, 2011).7
4.1.1 The Household’s Optimization Problem
The optimization problem of the household at age ![]() in period
in period ![]() , (1)–(5) , is modified to
, (1)–(5) , is modified to
![]()
subject to the constraints for the decision variables,

and the law of motion of the state variables,
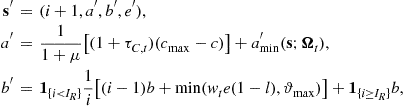
where ![]() is the lowest possible wealth at the beginning of next period, which is equal to 0 in our default assumption, but it could also be allowed to be negative.
is the lowest possible wealth at the beginning of next period, which is equal to 0 in our default assumption, but it could also be allowed to be negative.
4.1.2 The Complementarity Problem
The objective function of the household’s problem is
![]()
Then, combining with the law of motion of the state variables, the first-order conditions for an interior solution are
![]() (22)
(22)
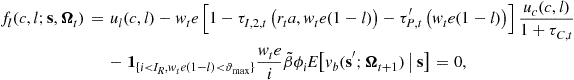 (23)
(23)
where ![]() is the marginal labor income tax rate, and
is the marginal labor income tax rate, and ![]() is the marginal payroll tax rate. Equation (22) is the Euler equation, and Eq. (23) is the marginal rate of substitution condition of consumption for leisure.8 With the inequality constraints for the decision variables, the Kuhn-Tucker conditions of the household’s problem are shown as the following nonlinear complementarity problem,
is the marginal payroll tax rate. Equation (22) is the Euler equation, and Eq. (23) is the marginal rate of substitution condition of consumption for leisure.8 With the inequality constraints for the decision variables, the Kuhn-Tucker conditions of the household’s problem are shown as the following nonlinear complementarity problem,
![]()
As explained in Billups (2000, 2002) and Miranda and Fackler (2002), the above complementarity problem is expressed compactly as the nonlinear system of equations,
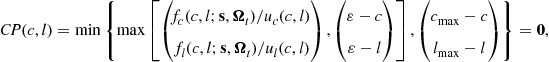 (24)
(24)
where ![]() is a small positive number.9
is a small positive number.9
The marginal utilities and marginal values in (22) and (23) could be very large or very small, depending on the state of the household. Therefore, in (24), we divide ![]() by
by ![]() and
and ![]() by
by ![]() . This scale adjustment helps reducing numerical errors when we use a nonlinear equation solver. Following Billups and Miranda et al. we also replace the
. This scale adjustment helps reducing numerical errors when we use a nonlinear equation solver. Following Billups and Miranda et al. we also replace the ![]() and
and ![]() operators with the Fischer-Burmeister function and its variation,
operators with the Fischer-Burmeister function and its variation,
![]()
respectively, to make the above system of equations differentiable without altering the solutions.10 We solve the above complementarity problem, (24), for ![]() and
and ![]() by using a Newton-type nonlinear equation solver, NEQNF, of the IMSL Fortran Numerical Library. This library subroutine uses a modified Powell hybrid algorithm and a finite-difference approximation to the Jacobian. We evaluate the marginal values,
by using a Newton-type nonlinear equation solver, NEQNF, of the IMSL Fortran Numerical Library. This library subroutine uses a modified Powell hybrid algorithm and a finite-difference approximation to the Jacobian. We evaluate the marginal values, ![]() and
and ![]() , between nodes in (22) and (23) by using either bilinear interpolation or 2-dimensional quadratic interpolation, QD2VL, of corresponding marginal value functions, (26) and (27), explained below.
, between nodes in (22) and (23) by using either bilinear interpolation or 2-dimensional quadratic interpolation, QD2VL, of corresponding marginal value functions, (26) and (27), explained below.
4.1.3 Value and Marginal Value Functions
Once we obtain the optimal decision, we next calculate the value of the household with the current state ![]() in period
in period ![]() as
as
![]() (25)
(25)
and the corresponding marginal values as
![]() (26)
(26)
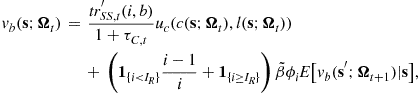 (27)
(27)
where ![]() is the marginal capital income tax rate, and
is the marginal capital income tax rate, and ![]() is the marginal OASI benefits with respect to
is the marginal OASI benefits with respect to ![]() ,
,
![]()
Equation (26) is the well-known formula of the marginal value with respect to wealth, which we can derive using the envelope theorem.
4.2 Finding the Distribution of Households
Let ![]() be the discrete population distribution function of households in period
be the discrete population distribution function of households in period ![]() , where the population of age
, where the population of age ![]() households is normalized to unity,
households is normalized to unity,
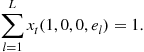
Then, the law of motion of growth-adjusted population distribution is, for ![]() ,
,
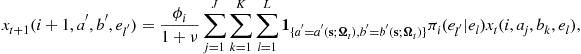
where ![]() . Since
. Since ![]() and
and ![]() are typically not on a node in
are typically not on a node in ![]() , the population in the next period is distributed into four adjacent nodes,
, the population in the next period is distributed into four adjacent nodes, ![]() ,
, ![]() , where
, where ![]() and
and ![]() .
.
The algorithm to calculate ![]() from
from ![]() is as follows: First, set
is as follows: First, set ![]() for all
for all ![]() and set
and set ![]() for
for ![]() , where
, where ![]() is the working ability distribution of age
is the working ability distribution of age ![]() households. Then, for
households. Then, for ![]() , and
, and ![]() , do the following:
, do the following:
1. Find the indexes ![]() and
and ![]() that satisfy
that satisfy
![]()
If ![]() , set the index as
, set the index as ![]() for extrapolation.
for extrapolation.
2. Calculate the interpolation (extrapolation) weights,
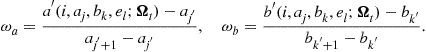
3. For ![]() , update the next period distribution as
, update the next period distribution as

where ![]() is a
is a ![]() matrix.
matrix.
We can find the steady-state distribution of households by replacing ![]() with
with ![]() in Step 3 and calculate
in Step 3 and calculate ![]() recursively from age
recursively from age ![]() to
to ![]() .11
.11
4.3 Solving the Model for an Equilibrium
The following computational algorithm is a modified version of that in Nishiyama and Smetters (2003, 2005, 2007). The procedure to find an equilibrium transition path is shown in Conesa and Krueger (1999), Domeij and Heathcote (2004), and others.
4.3.1 A Steady-State Equilibrium
The steady-state equilibrium with a time-invariant government policy schedule, ![]() , is obtained as follows:
, is obtained as follows:
1. Set the initial values of factor prices and government policy variables, ![]() .
.
2. Given ![]() , find the decision rules,
, find the decision rules, ![]() , the value function,
, the value function, ![]() , and the marginal value functions,
, and the marginal value functions, ![]() and
and ![]() , of the households recursively from age
, of the households recursively from age ![]() to age 1, starting with
to age 1, starting with ![]() .12
.12
3. Find the steady-state population distribution of households, ![]() recursively from age
recursively from age ![]() to age
to age ![]() by using the obtained decision rules,
by using the obtained decision rules, ![]() and
and ![]() , as well as the Markov transition matrix of the working ability shock.
, as well as the Markov transition matrix of the working ability shock.
4. Using the decision rules and the population distribution function, compute the aggregate variables, ![]() , and others, the new factor prices,
, and others, the new factor prices, ![]() , and the new government policy variables,
, and the new government policy variables, ![]() , that satisfy the policy schedule,
, that satisfy the policy schedule, ![]() .
.
5. If the difference between ![]() and
and ![]() is small enough, then stop. Otherwise, update
is small enough, then stop. Otherwise, update ![]() by using
by using ![]() and return to Step 2.13
and return to Step 2.13
In many cases, only one or two government policy variables are endogenous and the others are exogenous. In Step 5, it is easier to check the convergence of ![]() instead of
instead of ![]() , but we usually need to dampen the iteration process of
, but we usually need to dampen the iteration process of ![]() as
as
![]()
Most of the time, ![]() or
or ![]() works well for a heterogeneous-agent model similar to the one calibrated in Section 5. However, if households are less heterogeneous, idiosyncratic shocks are smaller, or labor supply is very elastic, we probably have to reduce
works well for a heterogeneous-agent model similar to the one calibrated in Section 5. However, if households are less heterogeneous, idiosyncratic shocks are smaller, or labor supply is very elastic, we probably have to reduce ![]() to 0.5 or lower.
to 0.5 or lower.
Solving the model for a steady-state equilibrium involves finding the fixed point in the space spanned by vector ![]() . To stop the Gauss-Jacobi iteration process of
. To stop the Gauss-Jacobi iteration process of ![]() , we usually use the supremum norm of the relative difference,
, we usually use the supremum norm of the relative difference, ![]() , where
, where ![]() , for example.
, for example.
4.3.2 An Equilibrium Transition Path
Let’s assume that the economy is in the initial steady-state equilibrium with a government policy schedule ![]() in period
in period ![]() and that the government announces a new policy schedule
and that the government announces a new policy schedule ![]() at the beginning of period
at the beginning of period ![]() . The equilibrium transition path from the initial steady state to a new final steady state is computed as follows:
. The equilibrium transition path from the initial steady state to a new final steady state is computed as follows:
1. Choose a large number ![]() so that the economy will reasonably reach the new steady-state equilibrium within
so that the economy will reasonably reach the new steady-state equilibrium within ![]() periods. Then, set the initial values of factor prices and government policy variables,
periods. Then, set the initial values of factor prices and government policy variables, ![]() , that are consistent with the new policy
, that are consistent with the new policy ![]() .
.
2. Given ![]() , compute the final steady-state equilibrium in period
, compute the final steady-state equilibrium in period ![]() , that is, find the decision rules,
, that is, find the decision rules, ![]() , value function,
, value function, ![]() , and marginal value functions,
, and marginal value functions, ![]() and
and ![]() , of the households from age
, of the households from age ![]() to age 1, as explained above.
to age 1, as explained above.
3. Given ![]() , find the decision rules,
, find the decision rules, ![]() , value function,
, value function, ![]() , and marginal value functions,
, and marginal value functions, ![]() and
and ![]() , of the households (from age
, of the households (from age ![]() to age 1 for each period) from period
to age 1 for each period) from period ![]() to period
to period ![]() , using
, using ![]() ,
, ![]() , and
, and ![]() recursively.14
recursively.14
4. Set ![]() and
and ![]() , since the economy is still in the initial steady-state equilibrium at the beginning of period
, since the economy is still in the initial steady-state equilibrium at the beginning of period ![]() .
.
5. Using the decision rules, ![]() , and the initial population distribution,
, and the initial population distribution, ![]() , compute the aggregate variables,
, compute the aggregate variables, ![]() , and others, the new factor prices
, and others, the new factor prices ![]() , the new government policy variables,
, the new government policy variables, ![]() , and the distribution of households,
, and the distribution of households, ![]() , recursively from period
, recursively from period ![]() to period
to period ![]() .15
.15
6. If the difference between ![]() and
and ![]() is small enough, then stop. Otherwise, update
is small enough, then stop. Otherwise, update ![]() by using
by using ![]() and return to Step 2. If there is no change in
and return to Step 2. If there is no change in ![]() , then, return to Step 3.
, then, return to Step 3.
If the policy change is deficit financing for the first several years before the government’s net worth, ![]() , is stabilized, then, we need to calculate the final steady state in Step 2 repeatedly until
, is stabilized, then, we need to calculate the final steady state in Step 2 repeatedly until ![]() is converged. In Step 6, we can check the convergence of
is converged. In Step 6, we can check the convergence of ![]() instead of
instead of ![]() , but we usually need to dampen its iteration process as
, but we usually need to dampen its iteration process as
![]()
Similar to a steady-state equilibrium, solving the model for an equilibrium transition path involves finding the fixed point in the space of large matrix ![]() . To stop the iteration process, we similarly use the supremum norm of the relative difference,
. To stop the iteration process, we similarly use the supremum norm of the relative difference, ![]() , where
, where ![]() , for example. In addition, to see if
, for example. In addition, to see if ![]() is large enough for the model economy to reach the final steady state in period
is large enough for the model economy to reach the final steady state in period ![]() , we can check if the relative difference between
, we can check if the relative difference between ![]() and
and ![]() is small,
is small, ![]()
![]() , where
, where ![]() .
.
5 Calibration to the US Economy
We assume that the baseline economy is in a steady-state equilibrium, so that the economy is on a balanced-growth path with the current-law tax and Social Security systems. Table 1 shows the main parameter values and baseline government policy values of the model economy.
Table 1
Main parameter values and baseline government policy values.

One unit of income in the model economy is equal to $142,582 in 2011 dollars.
5.1 Demographics, Preference, and Technology Parameters
The households are assumed to enter the economy at the beginning of age ![]() (real life age 21). The maximum possible age,
(real life age 21). The maximum possible age, ![]() , in the model economy is
, in the model economy is ![]() (real life age 100). The retirement age,
(real life age 100). The retirement age, ![]() , is fixed to be
, is fixed to be ![]() (real life age 65). The labor-augmenting productivity growth rate,
(real life age 65). The labor-augmenting productivity growth rate, ![]() , is set at 1.8%, which is close to the average growth rate, 1.82%, of real GDP per capita from the year 1971 through 2011. The population growth rate,
, is set at 1.8%, which is close to the average growth rate, 1.82%, of real GDP per capita from the year 1971 through 2011. The population growth rate,![]() , is set at 1.0%, which is also close to the average population growth rate, 0.96%, from 1971 through 2011. The conditional survival rate,
, is set at 1.0%, which is also close to the average population growth rate, 0.96%, from 1971 through 2011. The conditional survival rate, ![]() , at the end of age
, at the end of age ![]() , given that the households are alive at the beginning of age
, given that the households are alive at the beginning of age ![]() , is calculated from Table 4.C6 “2007 Period Life Table” in Social Security Administration (2013). We use the survival rates of women to approximate the survival rates of households. The survival rate at the end of age
, is calculated from Table 4.C6 “2007 Period Life Table” in Social Security Administration (2013). We use the survival rates of women to approximate the survival rates of households. The survival rate at the end of age ![]() is replaced by zero. When the population (the number of households) of age
is replaced by zero. When the population (the number of households) of age ![]() is normalized to unity, total population is 45.26 and working-age population is 34.88.
is normalized to unity, total population is 45.26 and working-age population is 34.88.
The share parameter of consumption, ![]() , in the Cobb-Douglas-CRRA utility function, (6), is set at 0.36, following the real business cycle literature (for example, Cooley and Prescott, 1995). The coefficient of relative risk aversion,
, in the Cobb-Douglas-CRRA utility function, (6), is set at 0.36, following the real business cycle literature (for example, Cooley and Prescott, 1995). The coefficient of relative risk aversion, ![]() , is set at 3.0, which is roughly in the middle of those in the macro public finance literature. For example, Domeij and Heathcote (2004) use 1.0, İmrohoroğlu et al. (1995) use 2.0, and Auerbach and Kotlikoff (1987) and Conesa et al. (2009) both use 4.0. When
, is set at 3.0, which is roughly in the middle of those in the macro public finance literature. For example, Domeij and Heathcote (2004) use 1.0, İmrohoroğlu et al. (1995) use 2.0, and Auerbach and Kotlikoff (1987) and Conesa et al. (2009) both use 4.0. When ![]() , and the average working hours,
, and the average working hours, ![]() , equals 0.3324, which are the values in our baseline economy, the Frisch elasticity of working hours for the average household then is calculated as
, equals 0.3324, which are the values in our baseline economy, the Frisch elasticity of working hours for the average household then is calculated as
![]()
We can adjust the elasticity by changing either ![]() , or the value of maximum working hours, which is currently set to 1.0. The discount factor,
, or the value of maximum working hours, which is currently set to 1.0. The discount factor, ![]() , is set at 0.9964 so that the baseline capital-GDP ratio,
, is set at 0.9964 so that the baseline capital-GDP ratio, ![]() , is 3.0, which is close to the average ratio of fixed capital stock to GDP, which was 3.06 in 2007–2011 and 3.02 in 2010–2011, in the National Income and Product Account (NIPA) data. When
, is 3.0, which is close to the average ratio of fixed capital stock to GDP, which was 3.06 in 2007–2011 and 3.02 in 2010–2011, in the National Income and Product Account (NIPA) data. When ![]() and
and ![]() , the growth-adjusted discount factor is
, the growth-adjusted discount factor is
![]()
The share parameter of capital stock, ![]() , in the Cobb-Douglas production function, shown in Eq. (10), is set equal to 0.384, so that the share of labor income in GDP is 0.616, which is the historical average during the period 2007–2011 in the NIPA. The average share of capital income in GDP in these same years is close to 0.162. When the capital-GDP ratio is 3.0, the interest rate,
, in the Cobb-Douglas production function, shown in Eq. (10), is set equal to 0.384, so that the share of labor income in GDP is 0.616, which is the historical average during the period 2007–2011 in the NIPA. The average share of capital income in GDP in these same years is close to 0.162. When the capital-GDP ratio is 3.0, the interest rate, ![]() , is
, is ![]() , and the depreciation rate of capital stock,
, and the depreciation rate of capital stock, ![]() , is set to
, is set to ![]() . Total factor productivity,
. Total factor productivity, ![]() , in the production function is set at 0.8839 so that the average wage rate,
, in the production function is set at 0.8839 so that the average wage rate, ![]() , is normalized to unity in the baseline economy. The average labor income of households between the ages 21 and 64 is $64,162 in the 2010 Survey of Consumer Finances. With the growth rate of labor income, 3.3%, in the 2011 NIPA, the average household labor income is about $66,279 in 2011. The average labor income is calculated as 0.4648 in the baseline economy. Thus, one unit in the model economy corresponds to $142,582 in 2011. We use this number to set the parameters of income tax and Social Security functions.
, is normalized to unity in the baseline economy. The average labor income of households between the ages 21 and 64 is $64,162 in the 2010 Survey of Consumer Finances. With the growth rate of labor income, 3.3%, in the 2011 NIPA, the average household labor income is about $66,279 in 2011. The average labor income is calculated as 0.4648 in the baseline economy. Thus, one unit in the model economy corresponds to $142,582 in 2011. We use this number to set the parameters of income tax and Social Security functions.
5.2 Market Wage Processes
The working ability, ![]() , of an age
, of an age ![]() household in the model economy is assumed to satisfy
household in the model economy is assumed to satisfy
![]()
where ![]() is the median wage rate at age
is the median wage rate at age ![]() , and
, and ![]() is the persistent shock. The persistent shock follows an AR(1) process,
is the persistent shock. The persistent shock follows an AR(1) process,
![]()
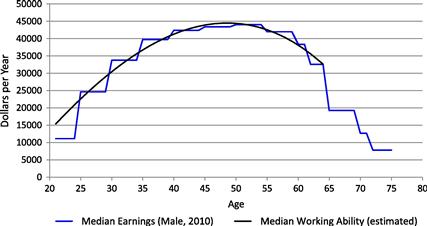
The median working ability, ![]() , for ages 21–64 is constructed with the 2010 male-worker earnings from Table 4.B6 “Median Earnings of Workers by Age” in Social Security Administration (2013). The median labor income of all workers probably somewhat understates the working ability, because some workers, especially female workers and young workers, choose not to work full time. The working ability profile by age is approximated by a cubic function of age, and it is estimated by OLS regression over the median earnings of individuals between ages 25 and 61, excluding those of individuals of ages 21–24 and 62–64 who may be in schooling or enjoying early retirement. Figure 1 shows the median earnings in the data and the estimated median working ability profile. In the model economy, the average of the median working ability,
, for ages 21–64 is constructed with the 2010 male-worker earnings from Table 4.B6 “Median Earnings of Workers by Age” in Social Security Administration (2013). The median labor income of all workers probably somewhat understates the working ability, because some workers, especially female workers and young workers, choose not to work full time. The working ability profile by age is approximated by a cubic function of age, and it is estimated by OLS regression over the median earnings of individuals between ages 25 and 61, excluding those of individuals of ages 21–24 and 62–64 who may be in schooling or enjoying early retirement. Figure 1 shows the median earnings in the data and the estimated median working ability profile. In the model economy, the average of the median working ability, ![]() , for ages 21–64 is normalized to unity.
, for ages 21–64 is normalized to unity.
The autocorrelation parameter, ![]() , of the log persistent shock is set at 0.95, which is, again, roughly in the middle of those in the previous literature. For example, Domeij and Heathcote (2004) use 0.90, Huggett (1996) uses 0.96, and Conesa et al. (2009) use 0.98. The standard deviation,
, of the log persistent shock is set at 0.95, which is, again, roughly in the middle of those in the previous literature. For example, Domeij and Heathcote (2004) use 0.90, Huggett (1996) uses 0.96, and Conesa et al. (2009) use 0.98. The standard deviation, ![]() , of the transitory shock,
, of the transitory shock, ![]() , is set at 0.220, and the variance of
, is set at 0.220, and the variance of ![]() is set at
is set at
![]()
Then, the variance of ![]() is calculated recursively as
is calculated recursively as
![]()
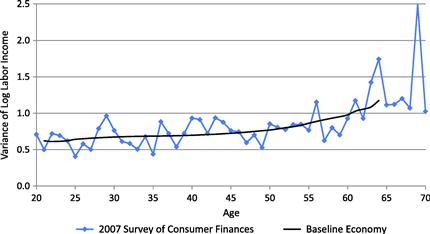
Figure 2 shows that the variances of log labor income calculated using the 2007 Survey of Consumer Finances data and those in the baseline economy are quite similar.
The log persistent shock, ![]() , is first discretized into 11 levels for each age using Gauss-Hermite quadrature nodes. Then, five levels of
, is first discretized into 11 levels for each age using Gauss-Hermite quadrature nodes. Then, five levels of ![]() are generated by combining four nodes in each tail distribution into one node. The unconditional probability distribution of these five nodes is
are generated by combining four nodes in each tail distribution into one node. The unconditional probability distribution of these five nodes is ![]() for
for ![]() . The Markov transition matrix of an age
. The Markov transition matrix of an age ![]() household,
household, ![]() , that corresponds to
, that corresponds to ![]() is calculated by using the bivariate normal distribution function as
is calculated by using the bivariate normal distribution function as

for ![]() , and
, and
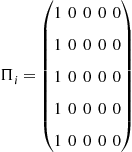
5.3 The Government’s Policy Functions
The individual income tax function follows Gouveia and Strauss (1994). The parameters of the progressive tax function are estimated using OLS regression across the statutory marginal tax rates in 2011. One of the parameters, ![]() , is the limit of the marginal tax rate as taxable income goes to infinity. It is computed as follows. First,
, is the limit of the marginal tax rate as taxable income goes to infinity. It is computed as follows. First, ![]() is set at 0.35, the highest marginal tax rate in 2011. The other two parameters,
is set at 0.35, the highest marginal tax rate in 2011. The other two parameters, ![]() and
and ![]() , are then estimated by OLS (equally weighted for taxable income between $0 and $500,000), assuming 60% of the households are married and 40% are single.16 Then,
, are then estimated by OLS (equally weighted for taxable income between $0 and $500,000), assuming 60% of the households are married and 40% are single.16 Then, ![]() is reduced to 0.2957 from 0.35 so that the ratio of the income tax revenue to GDP,
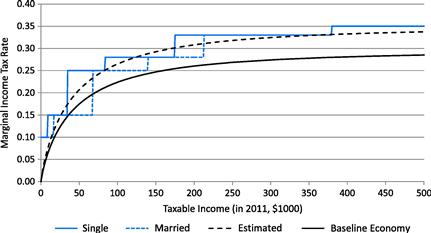
is reduced to 0.2957 from 0.35 so that the ratio of the income tax revenue to GDP, ![]() , is 10% in the baseline economy. Figure 3 shows the statutory, estimated, and effective marginal income tax rates.
, is 10% in the baseline economy. Figure 3 shows the statutory, estimated, and effective marginal income tax rates.
As explained above, one unit in the model economy corresponds to $142,582 in 2011. (Recall that average household labor income is 0.4648 units.) In the same year, the standard deductions of a single household and a married household are $5800 and $11,600, respectively, and the exemption is $3700 per person. 60% of the households are assumed to be married and 40% are single. So, the average deduction and exemption per household is $15,200, and ![]() is set at 0.1066 in the model economy. For simplicity, exemptions for dependent children are not considered in this calibration.
is set at 0.1066 in the model economy. For simplicity, exemptions for dependent children are not considered in this calibration.
The OASI payroll tax rate is 5.3% for an employee and 5.3% for an employer. The payroll tax rate, ![]() , for earnings below the maximum taxable earnings is set at 0.10, which is approximately equal to
, for earnings below the maximum taxable earnings is set at 0.10, which is approximately equal to ![]() . The maximum taxable earnings of the OASI payroll tax are $106,800 in 2011. When
. The maximum taxable earnings of the OASI payroll tax are $106,800 in 2011. When ![]() of married households are two-earner households, hence, 40% of all households are two-earner households, the average maximum taxable earnings are $149,520 and
of married households are two-earner households, hence, 40% of all households are two-earner households, the average maximum taxable earnings are $149,520 and ![]() is set at 1.0487. In the current US Social Security system, the thresholds to calculate primary insurance amounts (PIAs) are set for each age cohort when they reach age 62. In the model economy, the growth-adjusted thresholds are assumed to be fixed for all age cohorts, and the PIAs are adjusted later by using the long-term productivity growth rate and years from age 60. Thus, the model simply uses the thresholds for the age 62 cohort in 2011 after scale adjustment. Again, since 40% of all households are assumed to be two-earner households, the two thresholds are, on average, $12,583 and $75,886, respectively, and the parameters are set at
is set at 1.0487. In the current US Social Security system, the thresholds to calculate primary insurance amounts (PIAs) are set for each age cohort when they reach age 62. In the model economy, the growth-adjusted thresholds are assumed to be fixed for all age cohorts, and the PIAs are adjusted later by using the long-term productivity growth rate and years from age 60. Thus, the model simply uses the thresholds for the age 62 cohort in 2011 after scale adjustment. Again, since 40% of all households are assumed to be two-earner households, the two thresholds are, on average, $12,583 and $75,886, respectively, and the parameters are set at ![]() and
and ![]() . The OASDI benefit adjustment factor,
. The OASDI benefit adjustment factor, ![]() , is set at 1.0153 in the baseline economy so that the OASI budget is balanced.
, is set at 1.0153 in the baseline economy so that the OASI budget is balanced.
For simplicity, non-Social Security government spending is assumed to be government consumption. So, government consumption, ![]() , is equal to tax revenue,
, is equal to tax revenue, ![]() . The lump-sum transfer,
. The lump-sum transfer, ![]() , and the government’s net worth,
, and the government’s net worth, ![]() , are both set at 0 in the baseline economy. Accidental bequests per working-age household are calculated as 0.0244 in the baseline economy.
, are both set at 0 in the baseline economy. Accidental bequests per working-age household are calculated as 0.0244 in the baseline economy.
6 Policy Experiments
This section explains two examples of policy experiments. The economy is assumed to be in a steady-state equilibrium, or equivalently, on the balanced-growth path in year 0. At the beginning of year 1, the government announces and introduces a permanent (possibly phased-in) fiscal policy change.17 The government policy is assumed to be credible and so persistent. After the policy change, or its announcement, the economy responds and eventually approaches a new steady-state equilibrium.
In the first experiment, the government cuts the marginal income tax rates proportionally by 50% and finances the revenue reduction by increasing the consumption tax rate so that the government budget is balanced each year throughout the transition path. This experiment is similar to that in Nishiyama and Smetters (2005). In the second experiment, the government introduces a “partial privatization” of the Social Security pension. The government cuts the OASI benefits by 50% in a phased-in manner, cohort by cohort, for the first 40 years and reduces the payroll tax rate to balance the Social Security budget each year. The second experiment is similar to that in Nishiyama and Smetters (2007).
6.1 Consumption Tax Reform
We assume that the government reduces the marginal income tax rates proportionally by 50% at the beginning of year 1 and keeps the tax rates at the same levels throughout. Then, the government increases and adjusts the consumption tax rate to balance the non-Social-Security budget each year. Because the policy change also alters the size of the Social Security payroll tax revenue by changing labor supply, the government also adjusts the pay-as-you-go benefits proportionally to balance the Social Security budget each year.
6.1.1 The Computational Procedure
In the model economy, we reduce one of the marginal income tax rate parameters, ![]() , from 0.2957 to 0.1479 in years
, from 0.2957 to 0.1479 in years ![]() . We also increase the flat consumption tax rate,
. We also increase the flat consumption tax rate, ![]() , and change the OASI benefit adjustment factor,
, and change the OASI benefit adjustment factor, ![]() , to balance the government budget in years
, to balance the government budget in years ![]() ; more specifically, we find
; more specifically, we find ![]() and
and ![]() such that
such that
![]()
given the balanced-budget condition, ![]() , for all
, for all ![]() .
.
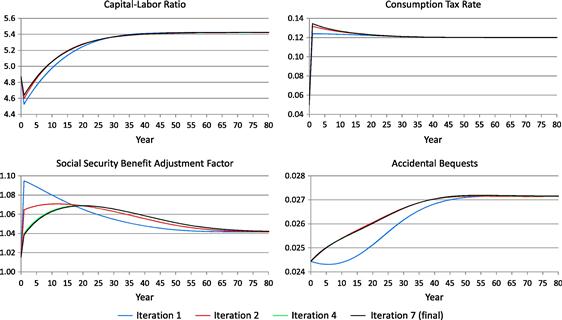
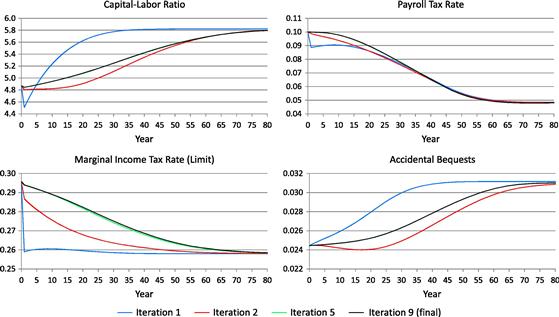
Figure 4 shows the iteration process of the capital-labor ratio and the endogenous government policy variables. The model is solved for T = 150 years, and the economy in year ![]() is assumed to be in its final steady-state equilibrium. The initial values of these iteration variables in years
is assumed to be in its final steady-state equilibrium. The initial values of these iteration variables in years ![]() are set equal to their corresponding values in the final steady state. In this policy experiment, it takes only seven iterations to reach the equilibrium transition path.18 Although the capital-labor ratio and the endogenous policy variables in the first and second iterations are noticeably different from those in the 7th iteration, the values from the 4th and 7th iterations are not distinguishable from the graph.19
are set equal to their corresponding values in the final steady state. In this policy experiment, it takes only seven iterations to reach the equilibrium transition path.18 Although the capital-labor ratio and the endogenous policy variables in the first and second iterations are noticeably different from those in the 7th iteration, the values from the 4th and 7th iterations are not distinguishable from the graph.19
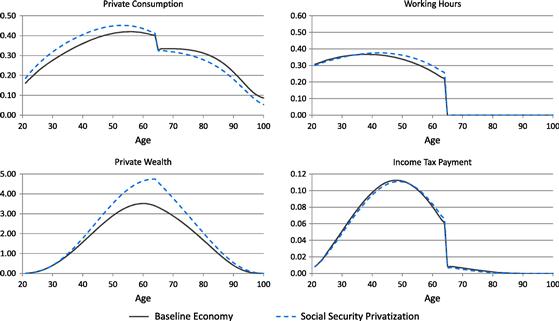
6.1.2 The Long-Run Effect
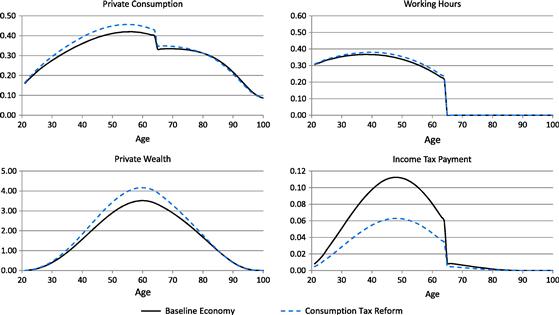
Figure 5 shows the long-run effects of the consumption tax reform over the life cycle of the households. In this reform, the tax burden shifts from an income tax, which is largely borne by the working-age households, to a consumption tax, which is borne more uniformly. Because the marginal tax rates on capital income are lower, and total tax payments are larger after the retirement, households increase their life-cycle savings while they are working. Because the marginal tax rates on labor income are lower, and the labor income tax becomes less progressive, households also increase their working hours, especially during their 40s and 50s when their labor income and marginal income tax rates are relatively high. The increase in private wealth is larger than the increase in labor supply. Thus, the wage rate rises and the interest rate falls. Private consumption (before consumption tax) increases when the households are younger than age 80 and decreases when they are age 80 or older.
6.1.3 The Transition Effect
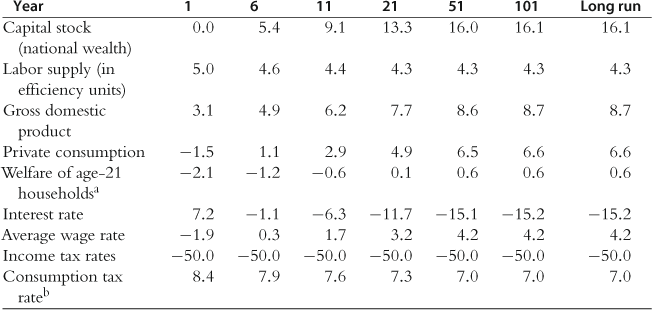
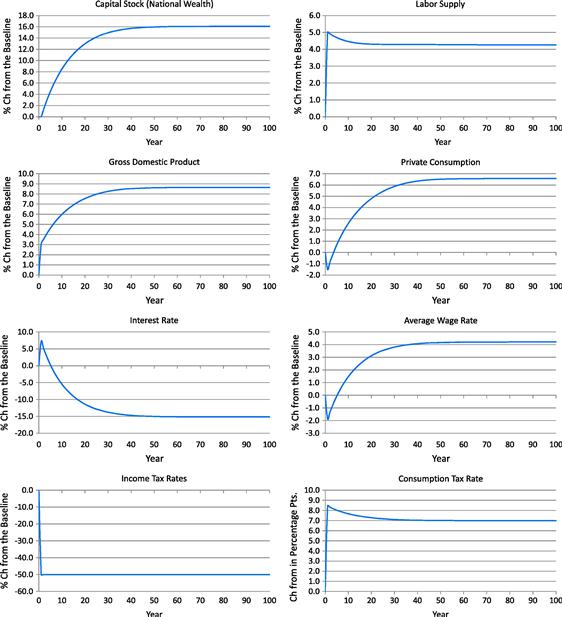
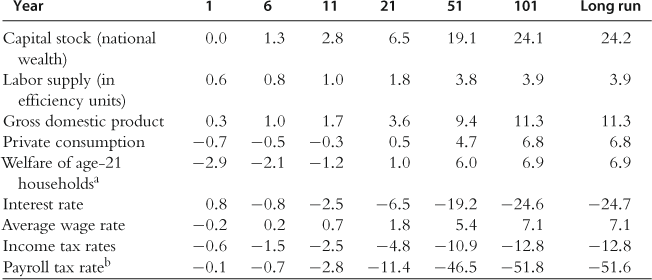
Table 2 and Figure 6 show the transition effect of the consumption tax reform on macroeconomic variables. When the marginal income tax rates are proportionally reduced by 50%, the consumption tax must be increased by 8.4 percentage points, from 5.0% to 13.4%, in year 1 and by 7.0 percentage points in the long run. In the short run, the implicit “lump-sum levy” from the new consumption tax hurts older households who are alive at the time of the policy change. This negative wealth effect causes labor supply to increase more in the short run than in the long run, and the welfare loss of current households is much larger than that of future households. Capital stock (national wealth) increases by 9.1% in year 11 and by 16.1% in the long run, relative to the baseline (initial steady-state) economy. Labor supply (in efficiency units) increases by 5.0% in year 1 and by 4.3% in the long run. Accordingly, gross domestic product increases by 3.1% in year 1 and by 8.7% in the long run. Private consumption (before the consumption tax) decreases by 1.5% in year 1 but increases by 6.6% in the long run. The interest rate falls by 15.2%, from 5.4% to 4.6%, in the long run, because the increase in capital stock is larger than the increase in labor supply. The average wage rate rises by 4.2% in the long run.
6.1.4 The Welfare Effect
Although the changes in gross domestic product from the baseline economy are positive throughout the transition path, the average welfare of age 21 (newborn) households is reduced in the short run. In the veil of ignorance measure in consumption equivalence, age-21 households in year 1 are worse off, on average, by 2.1% of their own consumption in the baseline economy, although newborn households are better off by 0.6% in the long run. Younger households, both in the short run and long run, tend to benefit from the implicit “lump-sum levy” on existing life-cycle wealth that was accumulated by older households at the time of reform. They also benefit from the reduced distortions to savings, which lowers the relative price of future consumption. However, there are two competing economic effects: the consumption base is smaller than the income tax base; it is also less progressive. The smaller size of the tax base requires larger distorting tax rates on labor supply; the reduction in progressivity also removes some of the tacit insurance against negative wage shocks which are otherwise uninsurable. Indeed, increasing the coefficient of relative risk aversion tends to reduce any welfare gain.
Figure 7 shows the welfare changes of the consumption tax reform by age cohort. The first panel shows the veil of ignorance welfare measure in consumption equivalence. The horizontal axis shows the real age of households (the age cohort) when the policy is changed (year 1). The households on or to the left of the vertical line (age 21) are the current households at the time of policy reform, and the households to the right of the vertical line are the future households. As shown in the above, age-21 households in year 1 are worse off by 2.1% as a percentage of their own baseline consumption. Age-65 households in year 1, who have just retired, are worse off by 5.0% in consumption. The welfare loss of elderly households is larger, because these households face the higher consumption tax rate without being benefited from the lower marginal income tax rates. Future households who enter the economy in year 20 or later are better off, because they can work at higher wages and inherit larger bequests. In the long run, age-21 households are better off by 0.6%.
The second panel of Figure 7 shows the equivalent variations and the compensating variations as a percentage of the baseline GDP per household. In theory, the equivalent variation measure is better than the compensating variation measure when there are wealth effects on consumption and leisure. The figure shows, however, the two variation measures are very similar to each other and mainly differ due to minor numerical residuals in interpolation. The equivalent and compensating variation results are also similar to the veil of ignorance measure. In the equivalent (compensating) variation measure, age-21 households in year 1 are worse off by 7.1% (8.0%) in wealth stated as a percentage of the baseline GDP per household, and age-65 households in year 1 are worse off by 56.6% (61.4%). The future households who enter the economy in year 8 or later are better off, and age-21 households are better off by 11.5% (12.3%) in wealth in the long run.
Table 3 shows the welfare changes of the consumption tax reform by age and working ability cohort. In the table, ![]() shows the lowest temporary working ability and the
shows the lowest temporary working ability and the ![]() shows the highest temporary working ability of each age cohort. The first panel of the table shows the veil of ignorance in consumption equivalence, which indicates that low income households are worse off and high income households are relatively better off as a result of the policy reform. The second panel shows the equivalent variations as a percentage of the baseline GDP per household. Age-21 households in year 1 with the lowest working ability are worse off by 5.3% of their own consumption in the baseline economy, but the households in the same age cohort with the median working ability are worse off by 12.6%, an even larger amount. The reason is that the median household has a relatively lower marginal value of wealth. Age-61 households in year 1 with the highest working ability are worse off by 80.2%. This loss is very large because these households have only 4 years remaining to work, and they have accumulated a larger amount of wealth to consume for the rest of their lives.
shows the highest temporary working ability of each age cohort. The first panel of the table shows the veil of ignorance in consumption equivalence, which indicates that low income households are worse off and high income households are relatively better off as a result of the policy reform. The second panel shows the equivalent variations as a percentage of the baseline GDP per household. Age-21 households in year 1 with the lowest working ability are worse off by 5.3% of their own consumption in the baseline economy, but the households in the same age cohort with the median working ability are worse off by 12.6%, an even larger amount. The reason is that the median household has a relatively lower marginal value of wealth. Age-61 households in year 1 with the highest working ability are worse off by 80.2%. This loss is very large because these households have only 4 years remaining to work, and they have accumulated a larger amount of wealth to consume for the rest of their lives.
Table 3
The welfare change, by age and working ability cohort, of consumption tax reform.
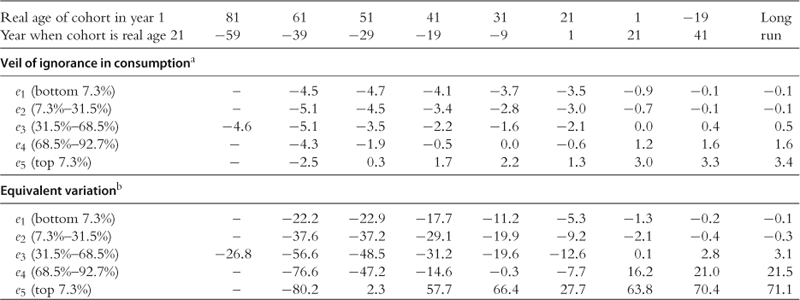
aThe percent changes in annual consumption that are equivalent with the cohort-average welfare changes.
bThe cohort-averages of one-time wealth transfers, as a percentage of baseline GDP per household, that are equivalent with the individual welfare changes.
6.2 Social Security Privatization
In our next policy experiment, we now instead assume that the government reduces the OASI benefits by 50%, phased in linearly over the next 40 years. Then, the government reduces the OASI payroll tax rate to balance the Social Security budget each year. Because the policy changes a household’s labor supply and saving, the government also must adjust the marginal income tax rates proportionally to balance the non-Social-Security budget each year.
6.2.1 The Computational Procedure
In the model economy, we change the OASI benefit adjustment factor, ![]() , as follows. For households aged 61
, as follows. For households aged 61 ![]() or older in period 1, their benefit adjustment factor remains unchanged,
or older in period 1, their benefit adjustment factor remains unchanged,
![]()
For households aged 21 ![]() or younger in period 1, their benefit adjustment factor is reduced by 50%,
or younger in period 1, their benefit adjustment factor is reduced by 50%,
![]()
Finally, for households aged between 22 ![]() and 60
and 60 ![]() , their benefit adjustment factor is the weighted average of the above two parameter values, that is,
, their benefit adjustment factor is the weighted average of the above two parameter values, that is,
![]()
Then, we also reduce the OASI payroll tax rate, ![]() , to balance the Social Security budget and change the marginal income tax rate parameter,
, to balance the Social Security budget and change the marginal income tax rate parameter, ![]() , to balance the rest of the government budget in years
, to balance the rest of the government budget in years ![]() ; more specifically, we find the values of
; more specifically, we find the values of ![]() and
and ![]() such that
such that
![]()
given the balanced-budget condition, ![]() , for all
, for all ![]() .
.
Figure 8 shows the iteration process of the capital-labor ratio and the endogenous government policy variables. In this policy experiment, it takes nine iterations to solve the model for the equilibrium transition path. Similar to the previous experiment, the initial values of these policy variables in years ![]() are set to be equal to the values in the final steady state. Although the capital-labor ratio and the endogenous policy variables in the first iteration are significantly different from those in the 9th iteration, the values in iterations five and nine are not distinguishable from the graph.20
are set to be equal to the values in the final steady state. Although the capital-labor ratio and the endogenous policy variables in the first iteration are significantly different from those in the 9th iteration, the values in iterations five and nine are not distinguishable from the graph.20
6.2.2 The Long-Run Effect
Figure 9 shows the long-run effects of the Social Security privatization over the life cycle of the households. In this experiment, the OASI benefits are reduced by 50%, given the household’s PIA based on its average historical earnings. In response, the working-age households save more wealth in order to replace the Social Security benefits. Since the increase in capital stock (national wealth) is larger than the increase in labor supply, the interest rate falls and the wage rate rises in the long run. The payroll tax rate reduction reduces the marginal tax rates on labor income. Thus, the households also increase their working hours when they are age 35 or older. Households decrease their working hours when they are young because the interest rate is lower and they shift part of their leisure to earlier years. Private consumption increases before the retirement and decreases after the retirement for two reasons. First, the working-age households are less liquidity constrained when the payroll tax rate is reduced, and so they can afford more consumption. Second, since the interest rate is lower, households shift their consumption from their retirement period to the working period.
6.2.3 The Transition Effect
Table 4 and Figure 10 show the transition effect of the Social Security privatization on aggregate and policy variables. Because the policy experiment is phased in over 40 years, it takes much longer to reach the new steady-state economy relative to the consumption tax reform experiment considered earlier. Life-cycle saving for retirement increases, raising the capital stock by 2.8% in year 11, by 19.1% in year 51, and by 24.2% in the long run. The payroll tax rate falls by only 2.8% in year 11 but by 51.6% in the long run. Labor supply increases by 1.0% in year 11 and by 3.9% in the long run. Gross domestic output also increases by 1.7% in year 11 and 11.3% in the long run. Private consumption decreases by 0.7% in year 1 but increases by 6.8% in the long run. The interest rate falls by 24.7%, from 5.4% to 4.1%, in the long run, and the average wage rate rises by 7.1% in the long run.
6.2.4 The Welfare Effect
Although the changes in gross domestic product are positive throughout the transition path similar to the previous policy experiment, the average welfare of age-21 households has been reduced in the short run. In the veil of ignorance measure in consumption equivalence, age-21 households in year 1 are worse off on average by 2.9% because they help pay for the policy transition path during their working years but collect a substantially reduced benefit upon retirement.21 However, age-21 households born in the long run are better off by 6.9% because they are born into a world with a smaller Social Security system. While they receive a smaller Social Security benefit, they also pay fewer taxes, which they prefer when the economy is dynamically efficient (that is, the interest rate exceeds the growth rate of the payroll tax base).
Figure 11 shows the welfare changes of Social Security privatization by age cohort. The first panel shows the veil of ignorance welfare measure in consumption equivalence. Age-21 households in year 1 are worse off by 2.9% as a percentage of their own baseline consumption. Age-65 households in year 1, who have just retired, are worse off by 0.5% of consumption. Households aged 61 or older at the time of the policy change are protected, by construction, from any reduction in benefits. But these households are slightly worse off due to the reduction in capital income from a falling interest rate. Households aged 60 or younger at the time of the reform are significantly worse off because they help pay for the policy transition path but receive lower future benefits when they retire. Households born in the long run are obviously better off. Age-21 households who enter the economy in year 17 or later are better off. The second panel of Figure 11 shows the equivalent variations and the compensating variations as a percentage of the baseline GDP per household. In equivalent (compensating) variation measure, age-21 households in year 1 are worse off by 25.3% (29.4%) in wealth as a percentage of the baseline GDP per household, and age-65 households in year 1 are worse off by 6.6% (7.1%). Future households who enter the economy in year 20 or later are better off, and age-21 households are better off by 54.1% (54.1%) in wealth in the long run.
Table 5 shows the welfare changes of the Social Security privatization by age and working ability cohort. The first panel of the table shows the veil of ignorance measure in consumption equivalence. Age-21 households in year 1 are all worse off by the policy reform, because they help pay for the transition while receiving fewer benefits. Age-51 households in year 1 are also worse off but the welfare losses are smaller for high income households. In the long run, future households are better off and the welfare gains are larger for low income households. The second panel shows the equivalent variations as a percentage of the baseline GDP per household. Current households are worse off by the policy reform, and the welfare losses are larger for high income households. Future households are better off, especially in the long run, and the welfare gains are larger for high income households. The reason is that high income households tend to have larger wealth and so their marginal value of wealth is lower.
Table 5
The welfare change, by age and working ability cohort, of Social Security privatization.
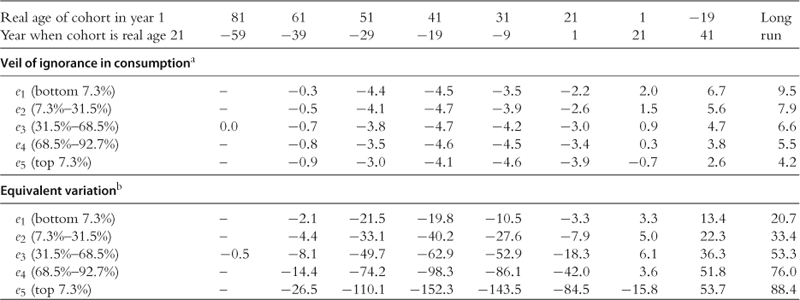
aThe percent changes in annual consumption that are equivalent with the cohort-average welfare changes.
bThe cohort-averages of one-time wealth transfers, as a percentage of baseline GDP per household, that are equivalent with the individual welfare changes.
7 Concluding Remarks
The heterogeneous-agent overlapping-generations framework is the main workhorse for analyzing fiscal policy changes with possible intra-generational and inter-generational wealth redistribution. The pioneering early work of Auerbach and Kotlikoff (1987) showed how to solve a deterministic OLG model with limited heterogeneity by using standard Euler-equation methods. However, the OLG model is computationally challenging to solve in the presence of the wide range of heterogeneity and uncertainty. This chapter explains how to solve the heterogeneous-agent OLG model with idiosyncratic uncertainty by deploying recursive methods. Adding idiosyncratic uncertainty allows us to recognize the impact that policy changes might have on the pooling of idiosyncratic risks that are typically hard to ensure in the private market. This specific channel often has first-order effects.
The computational algorithms explained in this chapter are quite straightforward. We discretize the state space of a heterogeneous household. For each node and each period, we solve the household problem by using a standard Newton-type nonlinear equation solver and a linear or quadratic interpolation. Using the household’s decision rules, then, we obtain the time series of factor prices and government policy variables (parameters) by Gauss-Jacobi type iterations.
Although there are not any surprising tricks in the procedure, the computation is fairly efficient. When the number of ages is ![]() , the number of asset nodes is
, the number of asset nodes is ![]() , the number of average historical earnings nodes is
, the number of average historical earnings nodes is ![]() , the number of working ability nodes is
, the number of working ability nodes is ![]() , and the number of years is
, and the number of years is ![]() . In our policy experiments in Section 6, it took just 368 s per iteration on a desktop PC with Intel Xeon W3670 (3.20 GHz) without parallelization. Because most policy experiments take only 6 to 9 iterations of factor prices and policy variables to converge, we can solve the model for an equilibrium transition path of 150 periods within an hour.
. In our policy experiments in Section 6, it took just 368 s per iteration on a desktop PC with Intel Xeon W3670 (3.20 GHz) without parallelization. Because most policy experiments take only 6 to 9 iterations of factor prices and policy variables to converge, we can solve the model for an equilibrium transition path of 150 periods within an hour.
It follows that it does not cause a serious problem to add more decision variables. Since we use a Newton-type iteration to solve the individual household’s problem, the computational cost will increase only quadratically. However, the computation would be much more costly if we add a state variable. If the new state variable is discretized into 20 nodes, it will generally take 20 times longer to solve the model, and it will require much more memory. We need to consider using a better interpolation method to reduce the total number of nodes in the state space.22 Moreover, using parallel processing becomes a necessity with many state variables.
The much bigger challenge, however, is adding aggregate uncertainty to the heterogeneous-agent OLG framework herein, thereby allowing for stochastic factor prices and policy variables. Unfortunately, the “curse of dimensionality” quickly takes over since the distribution of heterogeneous households must be indexed across many aggregate states. While various techniques discussed in Section 2 might someday be recruited to help solve models with aggregate uncertainty, that frontier still appears to be far away, although considerable progress is being made.
References
1. Aiyagari SR. Uninsured idiosyncratic risk and aggregate saving. Quarterly Journal of Economics. 1994;109:659–684.
2. Altig D, Carlstrom CT. Marginal tax rates and income inequality in a life-cycle model. American Economic Review. 1999;89:1197–1215.
3. Altig D, Auerbach A, Kotlikoff L, Smetters K, Walliser J. Simulating fundamental tax reform in the United States. American Economic Review. 2001;91:574–595.
4. Auerbach AJ, Kotlikoff LJ. Dynamic Fiscal Policy. Cambridge, UK: Cambridge University Press; 1987.
5. Bewley T. Stationary monetary equilibrium with a continuum of independently fluctuating consumers. In: Hildenbrand W, Mas-Colell A, eds. Contributions to Mathematical Economics in Honor of Gerard Debreu. New York, NY: North-Holland; 1986.
6. Billups SC. Improving the robustness of descent-based methods for semismooth equations using proximal perturbations. Mathematical Programming, Series A. 2000;87:153–175.
7. Billups SC. A homotopy-based algorithm for mixed complementarity problems. SIAM Journal on Optimization. 2002;12:583–605.
8. Carroll CD. Buffer-stock saving and the life cycle/permanent income hypothesis. Quarterly Journal of Economics. 1997;112:1–55.
9. Conesa JC, Krueger D. Social Security reform with heterogeneous agents. Review of Economic Dynamics. 1999;2:757–795.
10. Conesa JC, Krueger D. On the optimal progressivity of the income tax code. Journal of Monetary Economics. 2006;53:1425–1450.
11. Conesa JC, Kitao S, Krueger D. Taxing capital? Not a bad idea after all!. American Economic Review. 2009;99:25–48.
12. Cooley TF, Prescott EC. Economic growth and business cycle. In: Cooley TF, ed. Frontiers of Business Cycle Research. Princeton, NJ: Princeton University Press; 1995.
13. Diamond P. National debt in a neoclassical growth model. American Economic Review. 1965;55:1126–1150.
14. Domeij D, Heathcote J. On the distributional effects of reducing capital taxes. International Economic Review. 2004;45:523–554.
15. Fullerton D, Rogers DL. Who Bears the Lifetime Tax Burden? Washington, DC: Brookings Institution; 1993.
16. Gouveia M, Strauss RP. Effective federal individual income tax functions: an exploratory empirical analysis. National Tax Journal. 1994;47:317–339.
17. Hasanhodzic J, Kotlikoff L. Is generational risk a big deal and can it be mitigated? Mimeo: Boston University; 2012.
18. Heathcote J, Storesletten K, Violante G. Quantitative macroeconomics with heterogenous households. Annual Review of Economics. 2009;1:319–354.
19. Hubbard RG, Skinner J, Zeldes SP. Precautionary saving and social insurance. Journal of Political Economy. 1995;103:360–399.
20. Huggett M. The risk-free rate in heterogeneous-agent incomplete-insurance economies. Journal of Economic Dynamics and Control. 1993;17:953–969.
21. Huggett M. Wealth distribution in life-cycle economies. Journal of Monetary Economics. 1996;38:469–494.
22. İmrohoroğlu A, İmrohoroğlu S, Joines DH. A life cycle analysis of Social Security. Economic Theory. 1995;6:83–114.
23. Judd, K.L., Maliar, L., Maliar, S. 2012. Merging simulation and projection approaches to solve high-dimensional problems. NBER Working Paper No. 18501.
24. King RG, Plosser CI, Rebelo ST. Production, growth and business cycles: I The basic neoclassical model. Journal of Monetary Economics. 1988;21:195–232.
25. Kotlikoff LJ, Smetters KA, Walliser J. Social security: privatization and progressivity. American Economic Review. 1998;88:137–141.
26. Kotlikoff LJ, Smetters K, Walliser J. Privatizing Social Security in the United States–comparing the options. Review of Economic Dynamics. 1999;2:532–574.
27. Kotlikoff LJ, Smetters K, Walliser J. Mitigating America’s demographic dilemma by pre-funding Social Security. Journal of Monetary Economics. 2007;54:247–266.
28. Krueger D, Kubler F. Computing equilibrium in OLG models with stochastic production. Journal of Economic Dynamics and Control. 2004;28:1411–1436.
29. Krueger D, Kubler F. Pareto-improving Social Security reform when financial markets are incomplete!? American Economic Review. 2006;96:737–755.
30. Krusell P, Smith Jr AA. Income and wealth heterogeneity in the macroeconomy. Journal of Political Economy. 1998;106:867–896.
31. Laitner J. Tax changes and phase diagrams for an overlapping generations model. Journal of Political Economy. 1990;98:193–220.
32. Laitner J. Random earnings differences, lifetime liquidity constraints, and altruistic intergenerational transfers. Journal of Economic Theory. 1992;58:135–170.
33. Miranda MJ, Fackler PL. Applied Computational Economics and Finance. Cambridge, MA: MIT Press; 2002.
34. Nishiyama, S. 2010. The joint labor supply decision of married couples and the Social Security pension system. Michigan Retirement Research Center Working Paper WP2010-229.
35. Nishiyama S. The budgetary and welfare effects of tax-deferred retirement saving accounts. Journal of Public Economics. 2011;95:1561–1578.
36. Nishiyama, S., Smetters, K. 2003. Consumption taxes and economic efficiency in a stochastic OLG economy. NBER Working Paper No. 9492.
37. Nishiyama S, Smetters K. Consumption taxes and economic efficiency with idiosyncratic wage shocks. Journal of Political Economy. 2005;113:1088–1115.
38. Nishiyama S, Smetters K. Does Social Security privatization produce efficiency gains? Quarterly Journal of Economics. 2007;122:1677–1719.
39. Ríos-Rull JV. Computation of equilibria in heterogeneous-agent models. In: Marimon R, Scott A, eds. Computational Methods for the Study of Dynamic Economies. Oxford, UK: Oxford University Press; 1999.
40. Rust J. Using randomization to break the curse of dimensionality. Econometrica. 1997;65:487–516.
41. Samuelson PA. An exact consumption-loan model of interest with or without the social contrivance of money. Journal of Political Economy. 1958;66:467–482.
42. Scarf HE. On the computation of equilibrium prices. In: Fellner W, ed. Ten Economic Studies in the Tradition of Irving Fisher. New York, NY: John Wiley and Sons Inc; 1967.
43. Shoven JB, Whalley J. General equilibrium with taxes: A computational procedure and an existence proof. Review of Economic Studies. 1973;40:475–489.
44. Social Security Administration. Annual statistical supplement to the Social Security bulletin 2012. SSA, Publication 2013:13–11700.
45. Storesletten K, Telmer CI, Yaron A. The welfare cost of business cycles revisited: finite lives and cyclical variation in idiosyncratic risk. European Economic Review. 2001;45:1311–1339.
46. Storesletten K, Telmer CI, Yaron A. Consumption and risk sharing over the life cycle. Journal of Monetary Economics. 2004;51:609–633.
1Although the households in the model economy are committed to repay their debt, some of those possibly die with negative net worth. To deal with this (default) risk, we can also assume that the lenders force the borrowers to purchase life insurance. However, the macroeconomic effect of this additional assumption is small because the mortality rates of working-age households are low.
2For the taxation on Social Security benefits, see Tables 2.A.31–32 in Social Security Administration (2013).
3Nishiyama and Smetters (2007) have considered a little more realistic distribution methods that better preserve the distribution of wealth.
4The calculation of ![]() depends on the period utility function. With the utility function, (6), when consumption proportionally increases by
depends on the period utility function. With the utility function, (6), when consumption proportionally increases by ![]() , the household value increases by
, the household value increases by ![]() .
.
5In the model economy described in Section 3, there are many heterogeneous households, some of those are liquidity constrained, and the government fiscal policy includes a progressive income tax and a progressive Social Security system. Therefore, we cannot use the linear-quadratic approximation of decision rules and value functions to solve the model.
6In Sections 5 and 6, we set ![]() , and
, and ![]() . The total number of nodes is 332,800 in each period and 49,920,000 over a transition path. It usually takes 6–10 iterations to solve the model for an equilibrium. So, we need to solve the household’s problem 300–500 million times to find an equilibrium transition path.
. The total number of nodes is 332,800 in each period and 49,920,000 over a transition path. It usually takes 6–10 iterations to solve the model for an equilibrium. So, we need to solve the household’s problem 300–500 million times to find an equilibrium transition path.
7Auerbach and Kotlikoff (1987) solve their household’s optimization problem cohort by cohort. In the presence of idiosyncratic wage shocks, however, it is more efficient to solve the problem period by period.
8The deviation from the usual first-order conditions is the third term in (23), which considers the marginal effect of an additional working hour on the future Social Security benefits.
9The value of ![]() should be small enough that the constraints,
should be small enough that the constraints, ![]() and
and ![]() , will never be binding. We can alternatively deal with these strict positivity conditions by log transformation, defining
, will never be binding. We can alternatively deal with these strict positivity conditions by log transformation, defining ![]() as a function of
as a function of ![]() and
and ![]() .
.
10This is because ![]() . Similarly,
. Similarly, ![]() .
.
11To preserve the measure of households, the distribution of households in the next period must be calculated with linear or bilinear interpolation. Yet, this procedure is much more efficient than finding the distribution by simulation.
12Within a given age ![]() , the households’ problem at any state can be solved independently of the other states, thereby creating a large opportunity for parallelizing the computations, which is especially useful if more state variables are added.
, the households’ problem at any state can be solved independently of the other states, thereby creating a large opportunity for parallelizing the computations, which is especially useful if more state variables are added.
13A simple Gauss-Jacobi–type iteration of factor prices and government policy variables, ![]() , is more efficient than a Newton-type iteration, because the household decision rules are sensitive to the changes in
, is more efficient than a Newton-type iteration, because the household decision rules are sensitive to the changes in ![]() .
.
14In Step 3, we obtain all of the decision rules and value functions in the transition path without updating a set of factor prices and government policy variables, ![]() . Thus, the procedure adopted here is Gauss-Jacobi iteration. Ríos-Rull (1999) explains a different solution algorithm that uses Gauss-Seidel iteration.
. Thus, the procedure adopted here is Gauss-Jacobi iteration. Ríos-Rull (1999) explains a different solution algorithm that uses Gauss-Seidel iteration.
15The size of the decision rules, ![]() , obtained in Step 2 and used in Step 5 is
, obtained in Step 2 and used in Step 5 is ![]() bytes in single precision. In many cases, therefore, we need to store the decision rules on the hard disk rather than in the memory space.
bytes in single precision. In many cases, therefore, we need to store the decision rules on the hard disk rather than in the memory space.
16In the 2007 Survey of Consumer Finances, 62% of age 21–64 households are married and 59% of age 21–95 (all) households are married.
17We can also calculate the announcement effect if the policy change is announced in year 1 and actually introduced in year ![]() . The procedure to solve the model for the equilibrium transition path is exactly the same.
. The procedure to solve the model for the equilibrium transition path is exactly the same.
18If we set the initial guess of ![]() for
for ![]() by using the values of
by using the values of ![]() , we then don’t have to solve the household’s problem to obtain the decision rules in the first iteration, since
, we then don’t have to solve the household’s problem to obtain the decision rules in the first iteration, since ![]() for all
for all ![]() . Therefore, the cost of this policy experiment is effectively just six iterations.
. Therefore, the cost of this policy experiment is effectively just six iterations.
19In this policy experiment, it took 2203 s to solve the model for the equilibrium transition path on a desktop PC with Intel Xeon W3670 (3.20 GHz) without parallelization. The computation cost is ![]() or 6 min per iteration.
or 6 min per iteration.
20In this policy experiment, it took 2942 s to solve the model for the equilibrium transition path on a desktop PC with Intel Xeon W3670 (3.20 GHz). The computation cost is ![]() .
.
21The welfare loss in the short run is partially exacerbated by the reduced redistribution from the OASI system. The short-run welfare loss is smaller if the income tax rates are instead changed in a progressive manner in order to finance the transition cost.
22The linear-quadratic approximation is another possible solution when the state space is high dimensional. However, we cannot use this approximation in a heterogeneous-agent economy.
*The authors would like to thank an anonymous referee for this chapter, Zhigang Feng, the participants of the Initiative for Computational Economics Conference, and Ph.D. students at Georgia State University for their comments and suggestions.