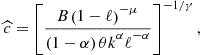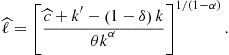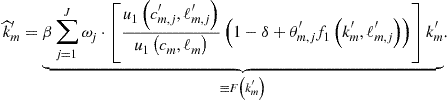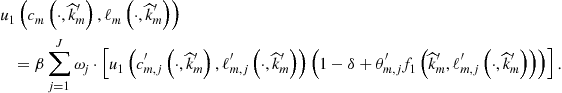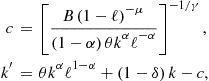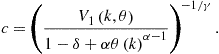Numerical Methods for Large-Scale Dynamic Economic Models
Lilia Maliar and Serguei Maliar, T24, Hoover Institution, Stanford, CA, USA, [email protected]
Abstract
We survey numerical methods that are tractable in dynamic economic models with a finite, large number of continuous state variables. (Examples of such models are new Keynesian models, life-cycle models, heterogeneous-agents models, asset-pricing models, multisector models, multicountry models, and climate change models.) First, we describe the ingredients that help us to reduce the cost of global solution methods. These are efficient nonproduct techniques for interpolating and approximating functions (Smolyak, stochastic simulation, and ![]() -distinguishable set grids), accurate low-cost monomial integration formulas, derivative-free solvers, and numerically stable regression methods. Second, we discuss endogenous grid and envelope condition methods that reduce the cost and increase accuracy of value function iteration. Third, we show precomputation techniques that construct solution manifolds for some models’ variables outside the main iterative cycle. Fourth, we review techniques that increase the accuracy of perturbation methods: a change of variables and a hybrid of local and global solutions. Finally, we show examples of parallel computation using multiple CPUs and GPUs including applications on a supercomputer. We illustrate the performance of the surveyed methods using a multiagent model. Many codes are publicly available.
-distinguishable set grids), accurate low-cost monomial integration formulas, derivative-free solvers, and numerically stable regression methods. Second, we discuss endogenous grid and envelope condition methods that reduce the cost and increase accuracy of value function iteration. Third, we show precomputation techniques that construct solution manifolds for some models’ variables outside the main iterative cycle. Fourth, we review techniques that increase the accuracy of perturbation methods: a change of variables and a hybrid of local and global solutions. Finally, we show examples of parallel computation using multiple CPUs and GPUs including applications on a supercomputer. We illustrate the performance of the surveyed methods using a multiagent model. Many codes are publicly available.
Keywords
High dimensions; Large scale; Projection; Perturbation; Stochastic simulation; Value function iteration; Endogenous grid; Envelope condition; Smolyak; ![]() -distinguishable set; Curse of dimensionality; Precomputation; Manifold; Parallel computation; Supercomputers
-distinguishable set; Curse of dimensionality; Precomputation; Manifold; Parallel computation; Supercomputers
JEL Classification Codes
C63; C68
1 Introduction
The economic literature is moving to richer and more complex dynamic models. Heterogeneous-agents models may have a large number of agents that differ in one or several dimensions, and models of firm behavior may have a large number of heterogeneous firms and different production sectors.1 Asset-pricing models may have a large number of assets; life-cycle models have at least as many state variables as the number of periods (years); and international trade models may have state variables of both domestic and foreign countries.2 New Keynesian models may have a large number of state variables and kinks in decision functions due to a zero lower bound on nominal interest rates.3 Introducing new features into economic models increases their complexity and dimensionality even further.4 Moreover, in some applications, dynamic economic models must be solved a large number of times under different parameters vectors.5
Dynamic economic models do not typically admit closed-form solutions. Moreover, conventional numerical solution methods—perturbation, projection, and stochastic simulation—become intractable (i.e., either infeasible or inaccurate) if the number of state variables is large. First, projection methods build on tensor-product rules; they are accurate and fast in models with few state variables but their cost grows rapidly as the number of state variables increases; see, e.g., a projection method of Judd (1992). Second, stochastic simulation methods rely on Monte Carlo integration and least-squares learning; they are feasible in high-dimensional problems but their accuracy is severely limited by the low accuracy of Monte Carlo integration; also, least-squares learning is often numerically unstable, see, e.g., a parameterized expectation algorithm of Marcet (1988). Finally, perturbation methods solve models in a steady state using Taylor expansions of the models’ equations. They are also practical for solving large-scale models but the range of their accuracy is uncertain, particularly in the presence of strong nonlinearities and kinks in decision functions; see, e.g., a perturbation method of Judd and Guu (1993).
In this chapter, we show how to re-design conventional projection, stochastic simulation, and perturbation methods to make them tractable (i.e., both feasible and accurate) in broad and empirically relevant classes of dynamic economic models with finite large numbers of continuous state variables.6
Let us highlight four key ideas. First, to reduce the cost of projection methods, Krueger and Kubler (2004) replace an expensive tensor-product grid with a low-cost, nonproduct Smolyak sparse grid. Second, Judd et al. (2011b) introduce a generalized stochastic simulation algorithm in which inaccurate Monte Carlo integration is replaced with accurate deterministic integration and in which unstable least-squares learning is replaced with numerically stable regression methods. Third, Judd et al. (2012) propose a ![]() -distinguishable set method that merges stochastic simulation and projection: it uses stochastic simulation to identify a high-probability area of the state space and it uses projection-style analysis to accurately solve the model in this area. Fourth, to increase the accuracy of perturbation methods, we describe two techniques. One is a change of variables of Judd (2003): it constructs many locally equivalent Taylor expansions and chooses the one that is most accurate globally. The other is a hybrid of local and global solutions by Maliar et al. (2013) that combines local solutions produced by a perturbation method with global solutions constructed to satisfy the model’s equation exactly.
-distinguishable set method that merges stochastic simulation and projection: it uses stochastic simulation to identify a high-probability area of the state space and it uses projection-style analysis to accurately solve the model in this area. Fourth, to increase the accuracy of perturbation methods, we describe two techniques. One is a change of variables of Judd (2003): it constructs many locally equivalent Taylor expansions and chooses the one that is most accurate globally. The other is a hybrid of local and global solutions by Maliar et al. (2013) that combines local solutions produced by a perturbation method with global solutions constructed to satisfy the model’s equation exactly.
Other ingredients that help us to reduce the cost of solution methods in high-dimensional problems are efficient nonproduct techniques for representing, interpolating, and approximating functions; accurate, low-cost monomial integration formulas; and derivative-free solvers. Also, we describe an endogenous grid method of Carroll (2005) and an envelope condition method of Maliar and Maliar (2013) that simplify rootfinding in the Bellman equation, thus reducing dramatically the cost of value function iteration. Furthermore, we show precomputation techniques that save on cost by constructing solution manifolds outside the main iterative cycle, namely, precomputation of intratemporal choice by Maliar and Maliar (2005a), precomputation of integrals by Judd et al. (2011d), and imperfect aggregation by Maliar and Maliar (2001).
Finally, we argue that parallel computation can bring us a further considerable reduction in computational expense. Parallel computation arises naturally on recent computers, which are equipped with multiple central processing units (CPUs) and graphics processing units (GPUs). It is reasonable to expect capacities for parallel computation will continue to grow in the future. Therefore, we complement our survey of numerical methods with a discussion of parallel computation tools that may reduce the cost of solving large-scale dynamic economic models. First, we revisit the surveyed numerical methods and we distinguish those methods that are suitable for parallelizing. Second, we review MATLAB tools that are useful for parallel computation, including parallel computing toolboxes for multiple CPUs and GPUs, a deployment tool for creating executable files and a mex tool for incorporating routines from other programming languages such as C or Fortran. Finally, we discuss how to solve large-scale applications using supercomputers; in particular, we provide illustrative examples on Blacklight supercomputer from the Pittsburgh Supercomputing Center.
The numerical techniques surveyed in this chapter proved to be remarkably successful in applications. Krueger and Kubler (2004) solve life-cycle models with 20–30 periods using a Smolyak method. Judd et al. (2011b) compute accurate quadratic solutions to a multiagent optimal growth model with up to 40 state variables using GSSA. Hasanhodzic and Kotlikoff (2013) used GSSA to solve life-cycle models with up to 80 periods. Kollmann et al. (2011b) compare the performance of six state-of-the-art methods in the context of real business cycle models of international trade with up to 20 state variables. Maliar et al. (2013) show hybrids of perturbation and global solutions that take just a few seconds to construct but that are nearly as accurate as the most sophisticated global solutions. Furthermore, the techniques described in the chapter can solve problems with kinks and strong nonlinearities; in particular, a few recent papers solve moderately large new Keynesian models with a zero lower bound on nominal interest rates: see Judd et al. (2011d, 2012), Fernández-Villaverde et al. (2012), and Aruoba and Schorfheide (2012). Also, the surveyed techniques can be used in the context of large-scale dynamic programming problems: see Maliar and Maliar (2012a,b). Finally, Aldrich et al. (2011), Valero et al. (2012), Maliar (2013), and Cai et al. (2013a,b) demonstrate that a significant reduction in cost can be achieved using parallel computation techniques and more powerful hardware and software.7
An important question is how to evaluate the quality of numerical approximations. In the context of complex large-scale models, it is typically hard to prove convergence theorems and to derive error bounds analytically. As an alternative, we control the quality of approximations numerically using a two-stage procedure outlined in Judd et al. (2011b). In Stage 1, we attempt to compute a candidate solution. If the convergence is achieved, we proceed to Stage 2, in which we subject a candidate solution to a tight accuracy check. Specifically, we construct a new set of points on which we want a numerical solution to be accurate (typically, we use a set of points produced by stochastic simulation) and we compute unit-free residuals in the model’s equations in all such points. If the economic significance of the approximation errors is small, we accept a candidate solution. Otherwise, we tighten up Stage 1; for example, we use a larger number of grid points, a more flexible approximating function, a more demanding convergence criterion, etc.
We assess the performance of the surveyed numerical solution methods in the context of a canonical optimal growth model with heterogeneous agents studied in Kollmann et al. (2011b). We implement six solution methods: three global Euler equation methods (a version of the Smolyak method in line with Judd et al. (2013), a generalized stochastic simulation algorithm of Judd et al. (2011b), and an ![]() -distinguishable set algorithm of Judd et al. (2012)); two global dynamic programming methods (specifically, two versions of the envelope condition method of Maliar and Maliar (2012b, 2013), one that solves for value function and the other that solves for derivatives of value function); and a hybrid of the perturbation and global solutions methods of Maliar et al. (2013). In our examples, we compute polynomial approximations of degrees up to 3, while the solution methods studied in Kollmann et al. (2011b) are limited to polynomials of degrees 2.
-distinguishable set algorithm of Judd et al. (2012)); two global dynamic programming methods (specifically, two versions of the envelope condition method of Maliar and Maliar (2012b, 2013), one that solves for value function and the other that solves for derivatives of value function); and a hybrid of the perturbation and global solutions methods of Maliar et al. (2013). In our examples, we compute polynomial approximations of degrees up to 3, while the solution methods studied in Kollmann et al. (2011b) are limited to polynomials of degrees 2.
The surveyed methods proved to be tractable, accurate, and reliable. In our experiments, unit-free residuals in the model’s equation are less than 0.001% on a stochastic simulation of 10,000 observations for most accurate methods. Our main message is that all three classes of methods considered can produce highly accurate solutions if properly implemented. Stochastic simulation methods become as accurate as projection methods if they build on accurate deterministic integration methods and numerically stable regression methods. Perturbation methods can deliver high accuracy levels if their local solutions are combined with global solutions using a hybrid style of analysis. Finally, dynamic programming methods are as accurate as Euler equation methods if they approximate the derivatives of value function instead of, or in addition to, value function itself.
In our numerical analysis, we explore a variety of interpolation, integration, optimization, fitting, and other computational techniques, and we evaluate the role of these techniques in accuracy and cost of the numerical solutions methods. At the end of this numerical exploration, we provide a detailed list of practical recommendations and tips on how computational techniques can be combined, coordinated, and implemented more efficiently in the context of large-scale applications.
The rest of the paper is organized as follows: in Section 2, we discuss the related literature. In Section 3, we provide a roadmap of the chapter. Through Sections 4–9, we introduce computational techniques that are tractable in problems with high dimensionality. In Section 10, we focus on parallel computation techniques. In Sections 11 and 12, we assess the performance of the surveyed numerical solution methods in the context of multiagent models. Finally, in Section 13, we conclude.
2 Literature Review
There is a variety of numerical methods in the literature for solving dynamic economic models; for reviews, see Taylor and Uhlig (1990), Rust (1996), Gaspar and Judd (1997), Judd (1998), Marimon and Scott (1999), Santos (1999), Christiano and Fisher (2000), Miranda and Fackler (2002), Adda and Cooper (2003), Aruoba et al. (2006), Kendrik et al. (2006), Heer and Maußner (2008, 2010), Lim and McNelis (2008), Stachursky (2009), Canova (2007), Den Haan (2010), Kollmann et al. (2011b). However, many of the existing methods are subject to the “curse of dimensionality”—that is, their computational expense grows exponentially with the dimensionality of state space.8
High-dimensional dynamic economic models represent three main challenges to numerical methods. First, the number of arguments in decision functions increases with the dimensionality of the problem and such functions become increasingly costly to approximate numerically (also, we may have more functions to approximate). Second, the cost of integration increases as the number of exogenous random variables increases (also, we may have more integrals to approximate). Finally, larger models are normally characterized by larger and more complex systems of equations, which are more expensive to solve numerically.
Three classes of numerical solution methods in the literature are projection, perturbation, and stochastic simulation. Projection methods are used in, e.g., Judd (1992), Gaspar and Judd (1997), Christiano and Fisher (2000), Aruoba et al. (2006), and Anderson et al. (2010). Conventional projection methods are accurate and fast in models with few state variables; however, they become intractable even in medium-scale models. This is because, first, they use expensive tensor-product rules both for interpolating decision functions and for approximating integrals and, second, because they use expensive Newton’s methods for solving nonlinear systems of equations.
Perturbation methods are introduced to economics in Judd and Guu (1993) and become a popular tool in the literature. For examples of applications of perturbation methods, see Gaspar and Judd (1997), Judd (1998), Collard and Juillard (2001, 2011), Jin and Judd (2002), Judd (2003), Schmitt-Grohé and Uribe (2004), Fernández-Villaverde and Rubio-Ramírez (2007), Aruoba et al. (2006), Swanson et al. (2006), Kim et al. (2008), Chen and Zadrozny (2009), Reiter (2009), Lombardo (2010), Adjemian et al. (2011), Gomme and Klein (2011), Maliar and Maliar (2011), Maliar et al. (2013), Den Haan and De Wind (2012), Mertens and Judd (2013), and Guerrieri and Iacoviello (2013) among others. Perturbation methods are practical for problems with very high dimensionality; however, the accuracy of local solutions may deteriorate dramatically away from the steady-state point in which such solutions are computed, especially in the presence of strong nonlinearities and kinks in decision functions.
Finally, simulation-based solution methods are introduced to the literature by Fair and Taylor (1983) and Marcet (1988). The former paper presents an extended path method for solving deterministic models while the latter paper proposes a parameterized expectation algorithm (PEA) for solving economic models with uncertainty. Simulation techniques are used in the context of many other solution methods, e.g., Smith (1991, 1993), Aiyagari (1994), Rust (1997), Krusell and Smith (1998), and Maliar and Maliar (2005a), as well as in the context of learning methods: see, e.g., Marcet and Sargent (1989), Tsitsiklis (1994), Bertsekas and Tsitsiklis (1996), Pakes and McGuire (2001), Evans and Honkapohja (2001), Weintraub et al. (2008), Powell (2011), Jirnyi and Lepetyuk (2011); see Birge and Louveaux (1997) for a review of stochastic programming methods and see also Fudenberg and Levine (1993) and Cho and Sargent (2008) for a related concept of self-conforming equilibria. Simulation and learning methods are feasible in problems with high dimensionality. However, Monte Carlo integration has a low rate of convergence—a square root of the number of observations—which considerably limits the accuracy of such methods since an infeasibly long simulation is needed to attain high accuracy levels. Moreover, least-squares learning is numerically unstable in the context of stochastic simulation.9
The above discussion raises three questions: first, how can one reduce the cost of conventional projection methods in high-dimensional problems (while maintaining their high accuracy levels)? Second, how can one increase the accuracy of perturbation methods (while maintaining their low computational expense)? Finally, how can one enhance their numerical stability of stochastic simulation methods and increase the accuracy (while maintaining a feasible simulation length)? These questions were addressed in the literature, and we survey the findings of this literature below.
To make projection methods tractable in large-scale problems, Krueger and Kubler (2004) introduce to the economic literature a Smolyak sparse grid technique; see also Malin et al. (2011). The sparse grid technique, introduced to the literature by Smolyak (1963), selects only a small subset of tensor-product grid elements that are most important for the quality of approximation. The Smolyak grid reduces the cost of projection methods dramatically without a significant accuracy loss. Winschel and Krätzig (2010) apply the Smolyak method for developing state-space filters that are tractable in problems with high dimensionality. Fernández-Villaverde et al. (2012) use the Smolyak method to solve a new Keynesian model. Finally, Judd et al. (2013) modify and generalize the Smolyak method in various dimensions to improve its performance in economic applications.
To increase the accuracy of stochastic simulation methods, Judd et al. (2011b) introduce a generalized stochastic simulation algorithm (GSSA) which uses stochastic simulation as a way to obtain grid points for computing solutions but replaces an inaccurate Monte Carlo integration method with highly accurate deterministic (quadrature and monomial) methods. Furthermore, GSSA replaces the least-squares learning method with regression methods that are robust to ill-conditioned problems, including least-squares methods that use singular value decomposition, Tikhonov regularization, least-absolute deviations methods, and the principal component regression method. The key advantage of stochastic simulation and learning methods is that they solve models only in the area of the state space where the solution “lives.” Thus, they avoid the cost of finding a solution in those areas that are unlikely to happen in equilibrium. GSSA preserves this useful feature but corrects the shortcomings of the earlier stochastic simulation approaches. It delivers accuracy levels that are comparable to the best accuracy attained in the related literature.
Furthermore, Judd et al. (2010, 2012) introduce two solution methods that merge stochastic simulation and projection techniques, a cluster grid algorithm (CGA) and ![]() -distinguishable set method (EDS). Both methods use stochastic simulation to identify a high-probability area of the state space, cover this area with a relatively small set of representative points, and use projection-style techniques to solve a model on the constructed set (grid) of points. The two methods differ in the way in which they construct representative points: CGA partitions the simulated data into clusters and uses the centers of the clusters as grid points while EDS selects a roughly evenly spaced subset of simulated points. These two approaches are used to solve moderately large new Keynesian models, namely, Judd et al. (2011b) and Aruoba and Schorfheide (2012) use clustering techniques while Judd et al. (2012) use the EDS construction.
-distinguishable set method (EDS). Both methods use stochastic simulation to identify a high-probability area of the state space, cover this area with a relatively small set of representative points, and use projection-style techniques to solve a model on the constructed set (grid) of points. The two methods differ in the way in which they construct representative points: CGA partitions the simulated data into clusters and uses the centers of the clusters as grid points while EDS selects a roughly evenly spaced subset of simulated points. These two approaches are used to solve moderately large new Keynesian models, namely, Judd et al. (2011b) and Aruoba and Schorfheide (2012) use clustering techniques while Judd et al. (2012) use the EDS construction.
As far as integration is concerned, there is a variety of methods that are tractable in high-dimensional problems, e.g., Monte Carlo methods, quasi-Monte Carlo methods, and nonparametric methods; see Niederreiter (1992), Geweke (1996), Rust (1997), Judd (1998), Pagan and Ullah (1999), Scott and Sain (2005) for reviews. However, the quality of approximations of integrals differs considerably across methods. For models with smooth decision functions, deterministic Gaussian quadrature integration methods with just a few nodes are far more accurate than Monte Carlo methods with thousands of random draws; see Judd et al. (2011a,b) for numerical examples. However, the cost of Gaussian product rules is prohibitive in problems with high dimensionality; see Gaspar and Judd (1997). To ameliorate the curse of dimensionality, Judd (1998) introduces to the economic literature nonproduct monomial integration formulas. Monomial formulas turn out to be a key piece for constructing global solution methods that are tractable in high-dimensional applications. Such formulas combine a low cost with high accuracy and can be generalized to the case of correlated exogenous shocks using a Cholesky decomposition; see Judd et al. (2011b) for a detailed description of monomial formulas, as well as for a numerical assessment of the accuracy and cost of such formulas in the context of economically relevant examples.
Finally, we focus on numerical methods that can solve large systems of nonlinear equations. In the context of Euler equation approaches, Maliar et al. (2011) argue that the cost of finding a solution to a system of equilibrium conditions can be reduced by dividing the whole system into two parts: intratemporal choice conditions (those that contain variables known at time ![]() ) and intertemporal choice conditions (those that contain some variables unknown at time
) and intertemporal choice conditions (those that contain some variables unknown at time ![]() ). Maliar and Maliar (2013) suggest a similar construction in the context of dynamic programming methods; specifically, they separate all optimality conditions into a system of the usual equations that identifies the optimal quantities and a system of functional equations that identifies a value function.
). Maliar and Maliar (2013) suggest a similar construction in the context of dynamic programming methods; specifically, they separate all optimality conditions into a system of the usual equations that identifies the optimal quantities and a system of functional equations that identifies a value function.
The system of intertemporal choice conditions (functional equations) must be solved with respect to the parameters of the approximating functions. In a high-dimensional model this system is large, and solving it with Newton-style methods may be expensive. In turn, the system of intratemporal choice conditions is much smaller in size; however, Newton’s methods can still be expensive because such a system must be solved a large number of times (in each grid point, time period, and future integration node). As an alternative to Newton’s methods, we advocate the use of a simple derivative-free fixed-point iteration method in line with the Gauss-Jacobi and Gauss-Siedel schemes. In particular, Maliar et al. (2011) propose a simple iteration-on-allocation solver that can find the intratemporal choice in many points simultaneously and that produces essentially zero approximation errors in all intratemporal choice conditions. See Wright and Williams (1984), Miranda and Helmberger (1988), and Marcet (1988) for early applications of fixed-point iteration to economic problems; see Judd (1998) for a review of various fixed-point iteration schemes. Also, see Eaves and Schmedders (1999) and Judd et al. (2012b), respectively, for applications of homotopy methods and efficient Newton’s methods to economic problems.
A February 2011 special issue of the Journal of Economic Dynamics and Control (henceforth, the JEDC project) studied the performance of six state-of-the-art solution methods in the context of an optimal growth model with heterogeneous agents (interpreted as countries). The model includes up to 10 countries (20 state variables) and features heterogeneity in preferences and technology, complete markets, capital adjustment cost, and elastic labor supply. The objectives of this project are outlined in Den Haan et al. (2011). The participating methods are a perturbation method of Kollmann et al. (2011a), a stochastic simulation and cluster grid algorithms of Maliar et al. (2011), a monomial rule Galerkin method of Pichler (2011), and a Smolyak’s collocation method of Malin et al. (2011). The methodology of the numerical analysis is described in Juillard and Villemot (2011). In particular, they develop a test suite that evaluates the accuracy of solutions by computing unit-free residuals in the model’s equations. The residuals are computed both on sets of points produced by stochastic simulation and on sets of points situated on a hypersphere. These two kinds of accuracy checks are introduced in Jin and Judd (2002) and Judd (1992), respectively; see also Den Haan and Marcet (1994) and Santos (2000) for other techniques for accuracy evaluation.
The results of the JEDC comparison are summarized in Kollmann et al. (2011b). The main findings are as follows: First, an increase in the degree of an approximating polynomial function by 1 increases the accuracy levels roughly by an order of magnitude (provided that other computational techniques, such as integration, fitting, intratemporal choice, etc., are sufficiently accurate). Second, methods that operate on simulation-based grids are very accurate in the high-probability area of the state space, while methods that operate on exogenous hypercube domains are less accurate in that area—although their accuracy is more uniformly distributed on a large multidimensional hypercube. Third, Monte Carlo integration is very inaccurate and restricts the overall accuracy of solutions. In contrast, monomial integration formulas are very accurate and reliable. Finally, approximating accurately the intratemporal choice is critical for the overall accuracy of solutions.
The importance of solving for intratemporal choice with a high degree of accuracy is emphasized by Maliar et al. (2011), who define the intertemporal choice (capital functions) parametrically; however, they define the intratemporal choice (consumption and leisure) nonparametrically as quantities that satisfy the intratemporal choice conditions given the future intertemporal choice. Under this construction, stochastic simulation and cluster grid algorithms of Maliar et al. (2011) solve for the intratemporal choice with essentially zero approximation errors (using an iteration-on-allocation solver). In contrast, the other methods participating in the JEDC comparison solve for some of the intertemporal choice variables parametrically and face such large errors in the intratemporal choice conditions that they dominate the overall accuracy of their solutions.
All six methods that participated in the JEDC comparison analysis work with Euler equations. In addition to the Euler equation approach, we are interested in constructing Bellman equation approaches that are tractable in high-dimensional applications. In general, there is no simple one-to-one relation between the Bellman and Euler equation approaches. For some problems, the value function is not differentiable, and we do not have Euler equations. On the contrary, for other problems (e.g., problems with distortionary taxation, externalities, etc.), we are able to derive the Euler equation even though such problems do not admit dynamic programming representations; for a general discussion of dynamic programming methods and their applications to economic problems, see Bertsekas and Tsitsiklis (1996), Rust (1996, 1997, 2008), Judd (1998), Santos (1999), Judd et al. (2003), Aruoba et al. (2006), Powell (2011), Fukushima and Waki (2011), Cai and Judd (2010, 2012), among others.
The Bellman and Euler equation approaches are affected by the curse of dimensionality in a similar way. Hence, the same kinds of remedies can be used to enhance their performance in large-scale applications, including nonproduct grid construction, monomial integration, and derivative-free solvers. However, there is an additional important computational issue that is specific to the dynamic programming methods: expensive rootfinding. To find a solution to the Bellman equation in a single grid point, conventional value function iteration (VFI) explores many different candidate points and, in each such point, it interpolates value function in many integration nodes to approximate expectations. Conventional VFI is costly even in low-dimensional problems; see Aruoba et al. (2006) for an assessment of its cost.
Two alternatives to conventional VFI are proposed in the literature. First, Carroll (2005) shows an endogenous grid method (EGM) that can significantly reduce the cost of conventional VFI by using future endogenous state variables for constructing grid points instead of the current ones; see also Barillas and Fernández-Villaverde (2007) and Villemot (2012) for applications of EGM to models with elastic labor supply and sovereign debt, respectively. Second, Maliar and Maliar (2013) show an envelope condition method (ECM) that replaces conventional expensive backward-looking iteration on value function with a cheaper, forward-looking iteration. Also, Maliar and Maliar (2013) develop versions of EGM and ECM that approximate derivatives of the value function and deliver much higher accuracy levels than similar methods approximating the value function itself. Finally, Maliar and Maliar (2012a,b) use a version of ECM to solve a multicountry model studied in Kollmann et al. (2011b) and show that value function iteration methods can successfully compete with most efficient Euler equation methods in high-dimensional applications.
Precomputation—computation of a solution to some model’s equations outside the main iterative cycle—is a technique that can reduce the cost of global solution methods even further. We review three examples. First, Maliar and Maliar (2005a) introduce a technique of precomputing of intratemporal choice. It constructs the intratemporal choice manifolds outside the main iterative cycle and uses the constructed manifolds inside the cycle as if a closed-form solution were available; see Maliar et al. (2011) for a further development of this technique. Second, Judd et al. (2011d) propose a technique of precomputation of integrals. This technique makes it possible to construct conditional expectation functions in the stage of initialization of a solution algorithm and, in effect, converts a stochastic problem into a deterministic one. Finally, Maliar and Maliar (2001, 2003a) introduce an analytical technique of imperfect aggregation, which allows us to characterize the aggregate behavior of a multiagent economy in terms of a one-agent model.
There are many other numerical techniques that are useful in the context of global solution methods. In particular, Tauchen (1986) and Tauchen and Hussey (1991) propose a discretization method that approximates a Markov process with a finite-state Markov chain. Such a discretization can be performed using nonproduct rules, combined with other computational techniques that are tractable in large-scale applications. For example, Maliar et al. (2010) and Young (2010) develop variants of Krusell and Smith’s (1998) method that replaces stochastic simulation with iteration on discretized ergodic distribution; the former method iterates backward as in Rios-Rull (1997) while the latter method introduces a forward iteration; see also Horvath (2012) for an extension. These two methods deliver the most accurate approximations to the aggregate law of motion in the context of Krusell and Smith’s (1998) model studied in the comparison analysis of Den Haan (2010). Of special interest are techniques that are designed for dealing with multiplicity of equilibria, such as simulation-based methods of Peralta-Alva and Santos (2005), a global solution method of Feng et al. (2009), and Gröbner bases introduced to economics by Kubler and Schmedders (2010). Finally, an interaction of a large number of heterogeneous agents is studied by agent-based computational economics. In this literature, behavioral rules of agents are not necessarily derived from optimization and that the interaction of the agents does not necessarily lead to an equilibrium; see Tesfatsion and Judd (2006) for a review.
We next focus on the perturbation class of solution methods. Specifically, we survey two techniques that increase the accuracy of local solutions produced by perturbation methods. The first technique—a change of variables—is introduced by Judd (2003), who pointed out that an ordinary Taylor expansion can be dominated in accuracy by other expansions implied by changes of variables (e.g., an expansion in levels may lead to more accurate solutions than that in logarithms or vice versa). All the expansions are equivalent in the steady state but differ globally. The goal is to choose an expansion that performs best in terms of accuracy on the relevant domain. In the context of a simple optimal growth model, Judd (2003) finds that a change of variables can increase the accuracy of the conventional perturbation method by two orders of magnitude. Fernández-Villaverde and Rubio-Ramírez (2006) show how to apply the method of change of variables to a model with uncertainty and an elastic labor supply.
The second technique—a hybrid of local and global solutions—is developed by Maliar et al. (2013). Their general presentation of the hybrid method encompasses some previous examples in the literature obtained using linear and loglinear solution methods; see Dotsey and Mao (1992) and Maliar et al. (2010, 2011). This perturbation-based method computes a standard perturbation solution, fixes some perturbation decision functions, and finds the remaining decision functions to exactly satisfy certain models’ equations. The construction of the latter part of the hybrid solution mimics global solution methods: for each point of the state space considered, nonlinear equations are solved either analytically (when closed-form solutions are available) or with a numerical solver. In numerical examples studied in Maliar et al. (2013), some hybrid solutions are orders of magnitude more accurate than the original perturbation solutions and are comparable in accuracy to solutions produced by global solution methods.
Finally, there is another technique that can help us to increase the accuracy of perturbation methods. Namely, it is possible to compute Taylor expansion around stochastic steady state instead of deterministic steady state. Such a steady state is computed by taking into account the attitude of agents toward risk. This idea is developed in Juillard (2011) and Maliar and Maliar (2011): the former article computes a stochastic steady state numerically, whereas the latter article uses analytical techniques of precomputation of integrals introduced in Judd et al. (2011d).
We complement our survey of efficient numerical methods with a discussion of recent developments in hardware and software that can help to reduce the cost of large-scale problems. Parallel computation is the main tool for dealing with computationally intensive tasks in recent computer science literature. A large number of central processing units (CPUs) or graphics processing units (GPUs) are connected with a fast network and are coordinated to perform a single job. Early applications of parallel computation to economic problems are dated back to Amman (1986, 1990), Chong and Hendry (1986), Coleman (1992), Nagurney and Zhang (1998); also, see Nagurney (1996) for a survey. But after the early contributions, parallel computation received little attention in the economic literature. Recently, the situation has begun to change. In particular, Doornik et al. (2006) review applications of parallel computation in econometrics; Creel (2005, 2008) and Creel and Goffe (2008) illustrate the benefits of parallel computation in the context of several economically relevant examples; Sims et al. (2008) employ parallel computation in the context of large-scale Markov switching models; Aldrich et al. (2011), Morozov and Mathur (2012) apply GPU computation to solve dynamic economic models; Durham and Geweke (2012) use GPUs to produce sequential posterior simulators for applied Bayesian inference; Cai et al. (2012) apply high-throughput computing (Condor network) to implement value function iteration; Valero et al. (2013) review parallel computing tools available in MATLAB and illustrate their application by way of examples; and, finally, Maliar (2013) assesses efficiency of parallelization using message passing interface (MPI) and open memory programming (OpenMP) in the context of high-performance computing (a Blacklight supercomputer).
In particular, Maliar (2013) finds that information transfers on supercomputers are far more expensive than on desktops. Hence, the problem must be sufficiently large to ensure gains from parallelization. The task assigned to each core must be at least few seconds if several cores are used, and it must be a minute or more if a large number (thousands) of cores are used. Maliar (2013) also finds that for small problems, OpenMP leads to a higher efficiency of parallelization than MPI. Furthermore, Valero et al. (2013) explore options for reducing the cost of a Smolyak solution method in the context of large-scale models studied in the JEDC project. Parallelizing the Smolyak method effectively is a nontrivial task because there are large information transfers between the outer and inner loops and because certain steps should be implemented in a serial manner. Nonetheless, considerable gains from parallelization are possible even on a desktop computer. Specifically, in a model with 16 state variables, Valero et al. (2013) attain the efficiency of parallelization of nearly 90% on a four-core machine via a parfor tool. Furthermore, translating expensive parts of the MATLAB code into C++ via a mex tool also leads to a considerable reduction in computational expense in some examples. However, transferring expensive computations to GPUs does not reduce the computational expense: a high cost of transfers between CPUs and GPUs outweighs the gains from parallelization.
3 The Chapter at a Glance
In this section, we provide a roadmap of the chapter and highlight the key ideas using a collection of simple examples.
A Neoclassical Stochastic Growth Model
The techniques surveyed in the chapter are designed for dealing with high-dimensional problems. However, to explain these techniques, we use the simplest possible framework, the standard one-sector neoclassical growth model. Later, in Sections 11 and 12, we show how such techniques can be applied for solving large-scale heterogeneous-agents models.
We consider a model with elastic labor supply. The agent solves:
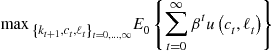 (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
where ![]() is given;
is given; ![]() is the expectation operator conditional on information at time
is the expectation operator conditional on information at time ![]() , and
, and ![]() are consumption, labor, end-of-period capital, and productivity level, respectively;
are consumption, labor, end-of-period capital, and productivity level, respectively; ![]() and
and ![]() are the utility and production functions, respectively, both of which are strictly increasing, continuously differentiable, and concave.
are the utility and production functions, respectively, both of which are strictly increasing, continuously differentiable, and concave.
Our goal is to solve for a recursive Markov equilibrium in which the decisions on next-period capital, consumption, and labor are made according to some time-invariant state contingent functions ![]() , and
, and ![]() .
.
A version of model (1)–(3) in which the agent does not value leisure and supplies to the market all her time endowment is referred to as a model with inelastic labor supply. Formally, such a model is obtained by replacing ![]() and
and ![]() with
with ![]() and
and ![]() in (1) and (2), respectively.
in (1) and (2), respectively.
First-Order Conditions
We assume that a solution to model (1)–(3) is interior and satisfies the first-order conditions (FOCs)
![]() (4)
(4)
![]() (5)
(5)
and budget constraint (2). Here, and further on, notation of type ![]() stands for the first-order partial derivative of a function
stands for the first-order partial derivative of a function ![]() with respect to a variable
with respect to a variable ![]() . Condition (4) is called the Euler equation.
. Condition (4) is called the Euler equation.
An Example of a Global Projection-Style Euler Equation Method
We approximate functions ![]() , and
, and ![]() numerically. As a starting point, we consider a projection-style method in line with Judd (1992) that approximates these functions to satisfy (2)–(5) on a grid of points.
numerically. As a starting point, we consider a projection-style method in line with Judd (1992) that approximates these functions to satisfy (2)–(5) on a grid of points.

We use the assumed decision functions to determine the choices in the current period ![]() , as well as to determine these choices in
, as well as to determine these choices in ![]() possible future states
possible future states ![]() , and
, and ![]() .
.
Unidimensional Grid Points and Basis Functions
To solve the model, we discretize the state space into a finite set of grid points ![]() . Our construction of a multidimensional grid begins with unidimensional grid points and basis functions. The simplest possible choice is a family of ordinary polynomials and a grid of uniformly spaced points but many other choices are possible. In particular, a useful alternative is a family of Chebyshev polynomials and a grid composed of extrema of Chebyshev polynomials. Such polynomials are defined in an interval
. Our construction of a multidimensional grid begins with unidimensional grid points and basis functions. The simplest possible choice is a family of ordinary polynomials and a grid of uniformly spaced points but many other choices are possible. In particular, a useful alternative is a family of Chebyshev polynomials and a grid composed of extrema of Chebyshev polynomials. Such polynomials are defined in an interval ![]() , and thus, the model’s variables such as
, and thus, the model’s variables such as ![]() and
and ![]() must be rescaled to be inside this interval prior to any computation. In Table 1, we compare two choices discussed above: one is ordinary polynomials and a grid of uniformly spaced points and the other is Chebyshev polynomials and a grid of their extrema.
must be rescaled to be inside this interval prior to any computation. In Table 1, we compare two choices discussed above: one is ordinary polynomials and a grid of uniformly spaced points and the other is Chebyshev polynomials and a grid of their extrema.
Table 1
Ordinary and Chebyshev unidimensional polynomials.

Notes: Ordinary polynomial of degree ![]() is given by
is given by ![]() ; Chebyshev polynomial of degree
; Chebyshev polynomial of degree ![]() is given by
is given by ![]() ; and finally,
; and finally, ![]() extrema of Chebyshev polynomials of degree
extrema of Chebyshev polynomials of degree ![]() are given by
are given by ![]() .
.
As we see, Chebyshev polynomials are just linear combinations of ordinary polynomials. If we had an infinite arithmetic precision on a computer, it would not matter which family of polynomials we use. But with a finite number of floating points, Chebyshev polynomials have an advantage over ordinary polynomials. To see the point, in Figure 1 we plot ordinary and Chebyshev polynomials of degrees from 1 to 5.
For the ordinary polynomial family, the basis functions look very similar on ![]() . Approximation methods using ordinary polynomials may fail because they cannot distinguish between similarly shaped polynomial terms such as
. Approximation methods using ordinary polynomials may fail because they cannot distinguish between similarly shaped polynomial terms such as ![]() and
and ![]() . In contrast, for the Chebyshev polynomial family, basis functions have very different shapes and are easy to distinguish.
. In contrast, for the Chebyshev polynomial family, basis functions have very different shapes and are easy to distinguish.
We now illustrate the use of Chebyshev polynomials for approximation by way of example.
It is possible to use Chebyshev polynomials with other grids, but the grid of extrema of Chebyshev polynomials is a perfect match. (The extrema listed in Table 1 are also seen in Figure 1.) First, the resulting approximations are uniformly accurate, and the error bounds can be constructed. Second, there is a unique set of coefficients such that a Chebyshev polynomial function of degree ![]() matches exactly
matches exactly ![]() given values, and this property carries over to multidimensional approximations that build on unidimensional Chebyshev polynomials. Finally, the coefficients that we compute in our example using an inverse problem can be derived in a closed form using the property of orthogonality of Chebyshev polynomials. The advantages of Chebyshev polynomials for approximation are emphasized by Judd (1992) in the context of projection methods for solving dynamic economic models; see Judd (1998) for a further discussion of Chebyshev as well as other orthogonal polynomials (Hermite, Legendre, etc.).
given values, and this property carries over to multidimensional approximations that build on unidimensional Chebyshev polynomials. Finally, the coefficients that we compute in our example using an inverse problem can be derived in a closed form using the property of orthogonality of Chebyshev polynomials. The advantages of Chebyshev polynomials for approximation are emphasized by Judd (1992) in the context of projection methods for solving dynamic economic models; see Judd (1998) for a further discussion of Chebyshev as well as other orthogonal polynomials (Hermite, Legendre, etc.).
Multidimensional Grid Points and Basis Functions
In Step 1 of the Euler equation algorithm, we must specify a method for approximating, representing, and interpolating two-dimensional functions. A tensor-product method constructs multidimensional grid points and basis functions using all possible combinations of unidimensional grid points and basis functions. As an example, let us approximate the capital decision function ![]() . First, we take two grid points for each state variable, namely,
. First, we take two grid points for each state variable, namely, ![]() and
and ![]() , and we combine them to construct two-dimensional grid points,
, and we combine them to construct two-dimensional grid points, ![]()
![]() . Second, we take two basis functions for each state variable, namely,
. Second, we take two basis functions for each state variable, namely, ![]() and
and ![]() , and we combine them to construct two-dimensional basis functions
, and we combine them to construct two-dimensional basis functions ![]() . Third, we construct a flexible functional form for approximating
. Third, we construct a flexible functional form for approximating ![]() ,
,
![]() (6)
(6)
Finally, we identify the four unknown coefficients ![]() such that
such that ![]() and
and ![]() coincide exactly in the four grid points constructed. That is, we write
coincide exactly in the four grid points constructed. That is, we write ![]() , where
, where
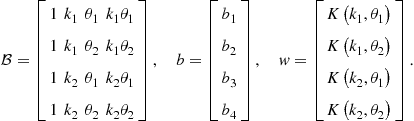 (7)
(7)
If ![]() has full rank, then coefficient vector
has full rank, then coefficient vector ![]() is uniquely determined by
is uniquely determined by ![]() . The obtained approximation (6) can be used to interpolate the capital decision function in each point off the grid.
. The obtained approximation (6) can be used to interpolate the capital decision function in each point off the grid.
Tensor-product constructions are successfully used in the literature to solve economic models with few state variables; see, e.g., Judd (1992). However, the number of grid points and basis functions grows exponentially (i.e., as ![]() ) with the number of state variables
) with the number of state variables ![]() . For problems with high dimensionality, we need nonproduct techniques for constructing multidimensional grid points and basis functions.
. For problems with high dimensionality, we need nonproduct techniques for constructing multidimensional grid points and basis functions.
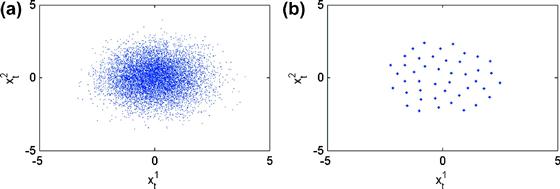
Nonproduct techniques for constructing multidimensional grids are the first essential ingredient of solution methods for high-dimensional problems. We survey several such techniques, including Smolyak (sparse), stochastic simulation, ![]() -distinguishable set, and cluster grids. The above techniques attack the curse of dimensionality in two different ways: one is to reduce the number of points within a fixed solution domain and the other is to reduce the size of the domain itself. To be specific, the Smolyak method uses a fixed geometry, a multidimensional hypercube, but chooses a small set of points within the hypercube. In turn, a stochastic simulation method uses an adaptive geometry: it places grid points exclusively in the area of the state space in which the solution “lives” and thus avoids the cost of computing a solution in those areas that are unlikely to happen in equilibrium. Finally, an
-distinguishable set, and cluster grids. The above techniques attack the curse of dimensionality in two different ways: one is to reduce the number of points within a fixed solution domain and the other is to reduce the size of the domain itself. To be specific, the Smolyak method uses a fixed geometry, a multidimensional hypercube, but chooses a small set of points within the hypercube. In turn, a stochastic simulation method uses an adaptive geometry: it places grid points exclusively in the area of the state space in which the solution “lives” and thus avoids the cost of computing a solution in those areas that are unlikely to happen in equilibrium. Finally, an ![]() -distinguishable set and cluster grid methods combine an adaptive geometry with an efficient discretization: they distinguish a high-probability area of the state space and cover such an area with a relatively small set of points. We survey these techniques in Section 4.
-distinguishable set and cluster grid methods combine an adaptive geometry with an efficient discretization: they distinguish a high-probability area of the state space and cover such an area with a relatively small set of points. We survey these techniques in Section 4.
Numerical Integration
In Step 2 of the Euler equation algorithm, we need to specify a method for approximating integrals. As a starting point, we consider a simple two-node Gauss-Hermite quadrature method that approximates an integral of a function of a normally distributed variable ![]() with a weighted average of just two values
with a weighted average of just two values ![]() and
and ![]() that happen with probability
that happen with probability ![]() , i.e.,
, i.e.,
![]()
where ![]() is a bounded continuous function, and
is a bounded continuous function, and ![]() is a density function of a normal distribution. Alternatively, we can use a three-node Gauss-Hermite quadrature method, which uses nodes
is a density function of a normal distribution. Alternatively, we can use a three-node Gauss-Hermite quadrature method, which uses nodes ![]() and weights
and weights ![]() and
and ![]() or even a one-node Gauss-Hermite quadrature method, which uses
or even a one-node Gauss-Hermite quadrature method, which uses ![]() and
and ![]() .
.
Another possibility is to approximate integrals using Monte Carlo integration. We can make ![]() random draws and approximate an integral with a simple average of the draws,
random draws and approximate an integral with a simple average of the draws,
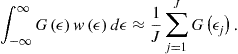
Let us compare the above integration methods using an example.
Note that the quadrature method with two nodes delivers the exact value of the integral. Even with just one node, the quadrature method can deliver an accurate integral if ![]() is close to linear (which is often the case in real business cycle models), i.e.,
is close to linear (which is often the case in real business cycle models), i.e., ![]() . To evaluate the accuracy of Monte Carlo integration, let us use
. To evaluate the accuracy of Monte Carlo integration, let us use ![]() , which is consistent with the magnitude of fluctuations in real business cycle models. Let us concentrate just on the term
, which is consistent with the magnitude of fluctuations in real business cycle models. Let us concentrate just on the term ![]() for which the expected value and standard deviation are
for which the expected value and standard deviation are ![]() and
and ![]() , respectively. The standard deviation depends on the number of random draws: with one random draw, it is
, respectively. The standard deviation depends on the number of random draws: with one random draw, it is ![]() and with 1,000,000 draws, it is
and with 1,000,000 draws, it is ![]() . The last number represents an (expected) error in approximating the integral and places a restriction on the overall accuracy of solutions that can be attained by a solution algorithm using Monte Carlo integration. An infeasibly long simulation is needed for a Monte Carlo method to deliver the same accuracy level as that of Gauss-Hermite quadrature in our example.
. The last number represents an (expected) error in approximating the integral and places a restriction on the overall accuracy of solutions that can be attained by a solution algorithm using Monte Carlo integration. An infeasibly long simulation is needed for a Monte Carlo method to deliver the same accuracy level as that of Gauss-Hermite quadrature in our example.
Why is Monte Carlo integration inefficient in the context of numerical methods for solving dynamic economic models? This is because we compute expectations as do econometricians, who do not know the true density function of the data-generating process and have no choice but to estimate such a function from noisy data using a regression. However, when solving an economic model, we do know the process for shocks. Hence, we can construct the “true” density function and we can use such a function to compute integrals very accurately, which is done by the Gauss-Hermite quadrature method.
In principle, the Gauss-Hermite quadrature method can be extended to an arbitrary dimension using a tensor-product rule; see, e.g., Gaspar and Judd (1997). However, the number of integration nodes grows exponentially with the number of shocks in the model. To ameliorate the curse of dimensionality, we again need to avoid product rules. Monomial formulas are a nonproduct integration method that combines high accuracy and low cost; this class of integration methods is introduced to the economic literature in Judd (1998). Integration methods that are tractable in problems with a large number of shocks are surveyed in Section 5.
Optimization Methods
In Step 3 of the algorithm, we need to solve a system of nonlinear equations with respect to the unknown parameters vectors ![]() . In principle, this can be done with Newton-style optimization methods; see, e.g., Judd (1992). Such methods compute first and second derivatives of an objective function with respect to the unknowns and move in the direction of gradient descent until a solution is found. Newton methods are fast and efficient in small problems but become increasingly expensive when the number of unknowns increases. In high-dimensional applications, we may have thousands of parameters in approximating functions, and the cost of computing derivatives may be prohibitive. In such applications, derivative-free optimization methods are an effective alternative. In particular, a useful choice is a fixed-point iteration method that finds a root to an equation
. In principle, this can be done with Newton-style optimization methods; see, e.g., Judd (1992). Such methods compute first and second derivatives of an objective function with respect to the unknowns and move in the direction of gradient descent until a solution is found. Newton methods are fast and efficient in small problems but become increasingly expensive when the number of unknowns increases. In high-dimensional applications, we may have thousands of parameters in approximating functions, and the cost of computing derivatives may be prohibitive. In such applications, derivative-free optimization methods are an effective alternative. In particular, a useful choice is a fixed-point iteration method that finds a root to an equation ![]() by constructing a sequence
by constructing a sequence ![]() . We illustrate this method using an example.
. We illustrate this method using an example.
The advantage of fixed-point iteration is that it can iterate in this simple manner on objects of any dimensionality, for example, on a vector of the polynomial coefficients. The cost of this procedure does not grow considerably with the number of polynomial coefficients. The shortcoming is that it does not always converge. For example, if we wrote the above equation as ![]() and implemented fixed-point iteration
and implemented fixed-point iteration ![]() , we would obtain a sequence that diverges to
, we would obtain a sequence that diverges to ![]() starting from
starting from ![]() .
.
We survey derivative-free optimization methods in Section 6, and we show how to enhance their convergence properties by using damping. We apply fixed-point iteration in two different contexts. One is to solve for parameters vectors in approximating functions and the other is to solve for quantities satisfying a system of equilibrium conditions. The latter version of fixed-point iteration is advocated in Maliar et al. (2011) and is called iteration-on-allocation.
An Example of a Global Projection-Style Dynamic Programming Algorithm
We can also use a projection-style algorithm to solve for a value function ![]() .
.

Observe that this dynamic programming method also requires us to approximate multidimensional functions and integrals. Hence, our discussion about the curse of dimensionality and the need of nonproduct grids and nonproduct integration methods applies to dynamic programming algorithms as well. Furthermore, if a solution to the Bellman equation is interior, derivative-free optimization methods are also a suitable choice.
There are issues that are specific to dynamic programming problems, in addition to those issues that are common for dynamic programming and Euler equation methods. The first issue is that conventional value function iteration leads to systems of optimality conditions that are expensive to solve numerically. As an example, let us consider a version of model (8)–(10) with inelastic labor supply. We combine FOC ![]() with budget constraint (10) to obtain
with budget constraint (10) to obtain
![]() (11)
(11)
We parameterize ![]() with the simplest possible first-degree polynomial
with the simplest possible first-degree polynomial ![]() . Then, (11) is
. Then, (11) is
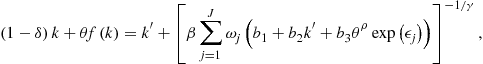 (12)
(12)
where we assume ![]() (and hence,
(and hence, ![]() ) for expository convenience. Solving (12) with respect to
) for expository convenience. Solving (12) with respect to ![]() is expensive even in this simple case. We need to find a root numerically by computing
is expensive even in this simple case. We need to find a root numerically by computing ![]() in a large number of candidate points
in a large number of candidate points ![]() , as well as by approximating expectations for each value of
, as well as by approximating expectations for each value of ![]() considered. For high-dimensional problems, the cost of conventional value function iteration is prohibitive.
considered. For high-dimensional problems, the cost of conventional value function iteration is prohibitive.
Two methods are proposed to simplify rootfinding to (12), one is an endogenous grid method of Carroll (2005) and the other is an envelope condition method of Maliar and Maliar (2013). The essence of Carroll’s (2005) method is the following simple observation: it is easier to solve (12) with respect to ![]() given
given ![]() than to solve it with respect to
than to solve it with respect to ![]() given
given ![]() . Hence, Carroll (2005) fixes future endogenous state variable
. Hence, Carroll (2005) fixes future endogenous state variable ![]() as grid points and treats current endogenous state variable
as grid points and treats current endogenous state variable ![]() as an unknown.
as an unknown.
The envelope condition method of Maliar and Maliar (2012a,b) builds on a different idea. Namely, it replaces backward-looking iteration based on a FOC by forward-looking iteration based on an envelope condition. For a version of (8)–(10) with inelastic labor supply, the envelope condition is ![]() , which leads to an explicit formula for consumption
, which leads to an explicit formula for consumption
![]() (13)
(13)
where we again assume ![]() . Since
. Since ![]() follows directly from the envelope condition, and since
follows directly from the envelope condition, and since ![]() follows directly from budget constraint (9), no rootfinding is needed at all in this example.
follows directly from budget constraint (9), no rootfinding is needed at all in this example.
Our second issue is that the accuracy of Bellman equation approaches is typically lower than that of similar Euler equation approaches. This is because the object that is relevant for accuracy is the derivative of value function ![]() and not
and not ![]() itself (namely,
itself (namely, ![]() enters optimality conditions (11) and (13) and determines the optimal quantities and not
enters optimality conditions (11) and (13) and determines the optimal quantities and not ![]() ). If we approximate
). If we approximate ![]() with a polynomial of degree
with a polynomial of degree ![]() , we effectively approximate
, we effectively approximate ![]() with a polynomial of degree
with a polynomial of degree ![]() , i.e., we effectively “lose” one polynomial degree after differentiation with the corresponding accuracy loss. To avoid this accuracy loss, Maliar and Maliar (2013) introduce variants of the endogenous grid and envelope condition methods that solve for derivatives of value function instead of or in addition to the value function itself. These variants produce highly accurate solutions.
, i.e., we effectively “lose” one polynomial degree after differentiation with the corresponding accuracy loss. To avoid this accuracy loss, Maliar and Maliar (2013) introduce variants of the endogenous grid and envelope condition methods that solve for derivatives of value function instead of or in addition to the value function itself. These variants produce highly accurate solutions.
Precomputation
Steps inside the main iterative cycle are repeated a large number of times. Computational expense can be reduced if some expensive steps are taken outside the main iterative cycle, i.e., precomputed.
As an example, consider a method of precomputation of integrals introduced in Judd et al. (2011d). Let us parameterize ![]() by
by ![]() . The key here is to observe that we can compute the expectation of
. The key here is to observe that we can compute the expectation of ![]() up-front, without solving the model,
up-front, without solving the model,
![]()
where under assumption (10), we have ![]() . With this result, we rewrite Bellman equation (8) as
. With this result, we rewrite Bellman equation (8) as
![]()
Effectively, this converts a stochastic Bellman equation into a deterministic one. The effect of uncertainty is fully captured by a precomputed value ![]() . Judd et al. (2011d) also develop precomputation of integrals in the context of Euler equation methods.
. Judd et al. (2011d) also develop precomputation of integrals in the context of Euler equation methods.
Maliar and Maliar (2005b) and Maliar et al. (2011) introduce another kind of precomputation, one that constructs the solution manifolds outside the main iterative cycle. For example, consider (2) and (5),
![]()
If ![]() is fixed, we have a system of two equations with two unknowns,
is fixed, we have a system of two equations with two unknowns, ![]() and
and ![]() . Solving this system once is not costly but solving it repeatedly in each grid point and integration node inside the main iterative cycle may have a considerable cost even in our simple example. We precompute the choice of
. Solving this system once is not costly but solving it repeatedly in each grid point and integration node inside the main iterative cycle may have a considerable cost even in our simple example. We precompute the choice of ![]() and
and ![]() to reduce this cost. Specifically, outside the main iterative cycle, we specify a grid of points for
to reduce this cost. Specifically, outside the main iterative cycle, we specify a grid of points for ![]() , and we find a solution for
, and we find a solution for ![]() and
and ![]() in each grid point. The resulting solution manifolds
in each grid point. The resulting solution manifolds ![]() and
and ![]() give us
give us ![]() and
and ![]() for each given triple
for each given triple ![]() . Inside the main iterative cycle, we use the precomputed manifolds to infer consumption and labor choices as if their closed-form solutions in terms of
. Inside the main iterative cycle, we use the precomputed manifolds to infer consumption and labor choices as if their closed-form solutions in terms of ![]() were available.
were available.
Finally, Maliar and Maliar (2001, 2003a) introduce a technique of imperfect aggregation that makes it possible to precompute aggregate decision rules in certain classes of heterogeneous-agent economies. The precomputation methods are surveyed in Section 8.
Perturbation Methods
Perturbation methods approximate a solution in just one point—a deterministic steady state—using Taylor expansions of the optimality conditions. The costs of perturbation methods do not increase rapidly with the dimensionality of the problem. However, the accuracy of a perturbation solution may deteriorate dramatically away from the steady state in which such a solution is computed.
One technique that can increase the accuracy of perturbation methods is a change of variables proposed by Judd (2003). Among many different Taylor expansions that are locally equivalent, we must choose the one that is most accurate globally. For example, consider two approximations for the capital decision function,
![]()
Let ![]() be a steady state. If we set
be a steady state. If we set ![]() and
and ![]() , then
, then ![]() and
and ![]() are locally equivalent in a sense that they have the same values and the same derivatives in the steady state. Hence, we can compare their accuracy away from the steady state and choose the one that has a higher overall accuracy.
are locally equivalent in a sense that they have the same values and the same derivatives in the steady state. Hence, we can compare their accuracy away from the steady state and choose the one that has a higher overall accuracy.
The other technique for increasing the accuracy of perturbation methods is a hybrid of local and global solutions developed in Maliar et al. (2013). The idea is to combine local solutions produced by a perturbation method with global solutions that are constructed to satisfy the model’s equations exactly. For example, assume that a first-order perturbation method delivers us a solution ![]() and
and ![]() in a model with inelastic labor supply. We keep the perturbation solution for
in a model with inelastic labor supply. We keep the perturbation solution for ![]() but replace
but replace ![]() with a new function for consumption
with a new function for consumption ![]() that is constructed to satisfy (9) exactly
that is constructed to satisfy (9) exactly
![]()
The obtained ![]() are an example of a hybrid solution. This particular hybrid solution produces a zero residual in the budget constraint unlike the original perturbation solution that produces nonzero residuals in all the model’s equations. The techniques for increasing the accuracy of perturbation methods are surveyed in Section 9.
are an example of a hybrid solution. This particular hybrid solution produces a zero residual in the budget constraint unlike the original perturbation solution that produces nonzero residuals in all the model’s equations. The techniques for increasing the accuracy of perturbation methods are surveyed in Section 9.
Parallel Computing
In the past decades, the speed of computers was steadily growing. However, this process has a natural limit (because the speed of electricity along the conducting material is limited and because the thickness and length of the conducting material are limited). The recent progress in solving computationally intense problems is related to parallel computation. We split a large problem into smaller subproblems, allocate the subproblems among many workers (computers), and solve them simultaneously. Each worker does not have much power but all together they can form a supercomputer. However, to benefit from this new computation technology, we need to design solution methods in a manner that is suitable for parallelizing. We also need hardware and software that support parallel computation. These issues are discussed in Section 10.
Methodology of the Numerical Analysis and Computational Details
Our solution procedure has two stages. In Stage 1, a method attempts to compute a numerical solution to a model. Provided that it succeeds, we proceed to Stage 2, in which we subject a candidate solution to a tight accuracy check. We specifically construct a set of points ![]() that covers an area in which we want the solution to be accurate, and we compute unit-free residuals in the model’s equations:
that covers an area in which we want the solution to be accurate, and we compute unit-free residuals in the model’s equations:
![]() (14)
(14)
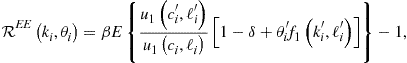 (15)
(15)
![]() (16)
(16)
where ![]() , and
, and ![]() are the residuals in budget constraint (9), Euler equation (4), and FOC for the marginal utility of leisure (5). In the exact solution, such residuals are zero, so we can judge the quality of approximation by how far these residuals are away from zero.
are the residuals in budget constraint (9), Euler equation (4), and FOC for the marginal utility of leisure (5). In the exact solution, such residuals are zero, so we can judge the quality of approximation by how far these residuals are away from zero.
In most experiments, we evaluate residuals on stochastic simulation (we use 10,200 observations and we discard the first 200 observations to eliminate the effect of initial conditions). This style of accuracy checks is introduced in Jin and Judd (2002). In some experiments, we evaluate accuracy on deterministic sets of points that cover a given area in the state space such as a hypersphere or hypercube; this kind of accuracy check is proposed by Judd (1992). We must emphasize that we never evaluate residuals on points used for computing a solution in Stage 1 (in particular, for some methods the residuals in the grid points are zeros by construction) but we do so on a new set of points constructed for Stage 2.
If either a solution method fails to converge in Stage 1 or the quality of a candidate solution in Stage 2 is economically inacceptable, we modify the algorithm’s design (i.e., the number and placement of grid points, approximating functions, integration method, fitting method, etc.) and we repeat the computations until a satisfactory solution is produced.
Parameterizations of the Model
In Sections (4)–(10), we report the results of numerical experiments. In those experiments, we parameterize model (1)–(3) with elastic labor supply by
![]() (17)
(17)
where parameters ![]() . We use
. We use ![]() , and we use
, and we use ![]() and
and ![]() to parameterize the stochastic process (3). For the utility parameters, our benchmark choice is
to parameterize the stochastic process (3). For the utility parameters, our benchmark choice is ![]() and
and ![]() but we also explore other values of
but we also explore other values of ![]() and
and ![]() .
.
In the model with inelastic labor supply, we assume ![]() and
and ![]() , i.e.,
, i.e.,
![]() (18)
(18)
Finally, we also study the latter model under the assumptions of full depreciation of capital, ![]() , and the logarithmic utility function,
, and the logarithmic utility function, ![]() ; this version of the model has a closed-form solution:
; this version of the model has a closed-form solution: ![]() and
and ![]() .
.
Reported Numerical Results
For each computational experiment, we report two accuracy measures, namely, the average and maximum absolute residuals across both the optimality conditions and ![]() test points. The residuals are represented in
test points. The residuals are represented in ![]() units, for example,
units, for example, ![]() means that a residual in the budget constraint is
means that a residual in the budget constraint is ![]() , and
, and ![]() means such a residual is
means such a residual is ![]() .
.
As a measure of computational expense, we report the running time. Unless specified separately, we use MATLAB, version 7.6.0.324 (R2008a) and a desktop computer with a Quad processor Intel® CoreTM i7 CPU920 @2.67 GHz, RAM 6,00 GB, and Windows Vista 64 bit.
Acronyms Used
We summarize all the acronyms used in the chapter in Table 2.
4 Nonproduct Approaches to Representing, Approximating, and Interpolating Functions
We survey nonproduct approaches to representing, approximating, and interpolating functions that can mitigate the curse of dimensionality. Let us consider a canonical approximation problem. Let ![]() be a smooth function, and let
be a smooth function, and let ![]() be a parametric function of the form
be a parametric function of the form
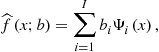 (19)
(19)
where ![]() is a basis function, and
is a basis function, and ![]() is a parameters vector. We aim to find
is a parameters vector. We aim to find ![]() such that
such that ![]() within a given area of
within a given area of ![]() .
.
We construct a grid of ![]() points
points ![]() within a given area of
within a given area of ![]() and compute the residuals,
and compute the residuals, ![]() , defined as a difference between the true function,
, defined as a difference between the true function, ![]() , and its approximation,
, and its approximation, ![]() ,
,
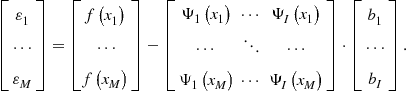 (20)
(20)
Our objective is to find ![]() to minimize the residuals according to some norm.
to minimize the residuals according to some norm.
An approximation method includes the following three steps:
(i) Construction of basis functions ![]() for (19).
for (19).
(ii) Selection of grid points ![]() for (20).
for (20).
(iii) Identification of parameters vector ![]() that ensures that
that ensures that ![]() within a given area of
within a given area of ![]() .
.
We consider two types of approximation methods, a collocation method and a weighted residuals method. Collocation is the case when ![]() , i.e., the number of grid points is the same as the number of basis functions. If the matrix of basis functions in the right side of (20) has full rank, we can find
, i.e., the number of grid points is the same as the number of basis functions. If the matrix of basis functions in the right side of (20) has full rank, we can find ![]() that makes the residuals be equal to zero in all grid points (we have a system of
that makes the residuals be equal to zero in all grid points (we have a system of ![]() linear equations with
linear equations with ![]() unknowns that admits a unique solution for
unknowns that admits a unique solution for ![]() ). Approximation
). Approximation ![]() coincides with true function
coincides with true function ![]() in all grid points, i.e.,
in all grid points, i.e., ![]() for all
for all ![]() . In this case,
. In this case, ![]() interpolates
interpolates ![]() off the grid.
off the grid.
A weighted residuals method is the case when ![]() . Since there are more equations than unknowns, parameters vector
. Since there are more equations than unknowns, parameters vector ![]() is overdetermined, and the system of equation (20) has no solution in a sense that we cannot make all the residuals be zeros in all grid points. The best we can do is to find
is overdetermined, and the system of equation (20) has no solution in a sense that we cannot make all the residuals be zeros in all grid points. The best we can do is to find ![]() that minimizes the residuals according to some norm, e.g., a least-squares norm in which all the residuals have equal weights, i.e.,
that minimizes the residuals according to some norm, e.g., a least-squares norm in which all the residuals have equal weights, i.e., ![]() . This is like the usual least-squares regression in which we have many data points for identifying relatively few regression coefficients. Since approximation
. This is like the usual least-squares regression in which we have many data points for identifying relatively few regression coefficients. Since approximation ![]() does not coincide with true function
does not coincide with true function ![]() in all grid points, we say that
in all grid points, we say that ![]() approximates
approximates ![]() off the grid (instead of saying “interpolates”).
off the grid (instead of saying “interpolates”).
In the remainder of the section, we consider three methods that construct the approximation of type (19) in a way which is tractable for high-dimensional problems. These are a Smolyak method, a generalized stochastic simulation method, and an ![]() -distinguishable set method. The first one is a collocation method, while the latter two are weighted residuals methods.
-distinguishable set method. The first one is a collocation method, while the latter two are weighted residuals methods.
4.1 Smolyak’s (1963) Sparse Grid Method
In a seminal work, Smolyak (1963) introduces a numerical technique for integrating, representing, and interpolating smooth functions on multidimensional hypercubes. The Smolyak method constructs multidimensional grid points and basis functions using nonproduct rules. The complexity of the Smolyak method grows polynomially with the dimensionality of the hypercube, i.e., the method is not subject to the curse of dimensionality (at least in a space of smooth functions).
The Smolyak grid was incorporated into numerical methods for solving dynamic economic models by Krueger and Kubler (2004); see also Malin et al. (2011). Furthermore, Winschel and Krätzig (2010) apply the Smolyak method for developing state-space filters that are tractable in problems with large dimensionality. Fernández-Villaverde et al. (2012) use the Smolyak method to solve a new Keynesian model. Finally, Judd et al. (2013) generalize the Smolyak method in various dimensions to improve its performance in economic applications.
We present the Smolyak method in two different ways. In Section 4.1.1, we derive the Smolyak interpolation formula using intuitive arguments which allows us to illustrate how the method works. In particular, we do not rely on the conventional interpolation formula but construct Smolyak polynomials using a Smolyak rule; also, we do not rely on the conventional formula for the Smolyak coefficients but obtain such coefficients from an inverse problem; in this presentation, we follow Judd et al. (2013). Then, in Section 4.1.2, we give a more conventional exposition of the Smolyak method in line with the analysis of Barthelmann et al. (2000), Krueger and Kubler (2004), and Malin et al. (2011). Finally, in Section 4.1.3, we discuss the relation between the analysis in Judd et al. (2013) and the conventional Smolyak interpolation in the literature.
4.1.1 How Does the Smolyak Method Work?
We introduce the Smolyak method in the context of a simple two-dimensional example. We show how the Smolyak method implements the three steps discussed in the beginning of the section, i.e., how it (i) constructs grid points, (ii) constructs a polynomial function, and (iii) identifies the polynomial coefficients for interpolation.
Smolyak Grid
The idea of the Smolyak method is appealing. Among all elements produced by a tensor-product rule, some elements are more important for the quality of approximation than the others. The Smolyak method orders all the tensor-product elements by their potential importance for the quality of approximation and selects the most important ones. A parameter, called approximation level, controls how many tensor-product elements are included in a specific Smolyak approximation. By increasing the approximation level, we add new elements and improve the quality of approximation.
Consider the following five unidimensional grid points ![]() .10 If we use a tensor-product rule to construct two-dimensional grid points, we obtain 25 such grid points
.10 If we use a tensor-product rule to construct two-dimensional grid points, we obtain 25 such grid points ![]() .
.
The Smolyak method constructs grid points in a different manner. First, we use the unidimensional grid points to construct the following sequence of sets:
The sets are nested: each subsequent set contains all the elements of the previous set.
Second, we construct all possible two-dimensional tensor products using elements from the nested sets. These products are shown in Table 3 for ![]() .
.
Finally, we select elements from those cells in Table 3 that satisfy a Smolyak rule: the index of a column ![]() plus the index of a row
plus the index of a row ![]() is smaller than or equal to
is smaller than or equal to ![]() , i.e.,
, i.e.,
![]() (21)
(21)
where ![]() is the approximation level parameter and
is the approximation level parameter and ![]() is the dimensionality of the problem (in our case,
is the dimensionality of the problem (in our case, ![]() ).
).
Let ![]() denote the Smolyak grid for a problem with dimensionality
denote the Smolyak grid for a problem with dimensionality ![]() and approximation level
and approximation level ![]() . We use the Smolyak rule (21) to construct two-dimensional grid points for our example.
. We use the Smolyak rule (21) to construct two-dimensional grid points for our example.
• If ![]() , then (21) implies
, then (21) implies ![]() . The only case that satisfies this restriction is when
. The only case that satisfies this restriction is when ![]() and
and ![]() , so that the Smolyak grid is a single point
, so that the Smolyak grid is a single point
![]() (22)
(22)
• If ![]() , then
, then ![]() . The three cases that satisfy this restriction are (a)
. The three cases that satisfy this restriction are (a) ![]() ; (b)
; (b) ![]() ; (c)
; (c) ![]() . The nonrepeating five Smolyak points are
. The nonrepeating five Smolyak points are
![]() (23)
(23)
• If ![]() , then
, then ![]() . The six cases satisfying this restriction are (a)
. The six cases satisfying this restriction are (a) ![]() ; (b)
; (b) ![]() ; (c)
; (c) ![]() ; (d)
; (d) ![]() ; (e)
; (e) ![]() ; (f)
; (f) ![]() . The 13 Smolyak points are
. The 13 Smolyak points are
 (24)
(24)
Observe that the elements that satisfy (21) are situated on the diagonals that expand from the upper left corner of the table toward the lower right corner. The Smolyak grid points under ![]() are illustrated in Figure 2; for comparison, we also show a tensor-product grid of
are illustrated in Figure 2; for comparison, we also show a tensor-product grid of ![]() points. The number of points in the Smolyak sparse grid increases polynomially with dimensionality
points. The number of points in the Smolyak sparse grid increases polynomially with dimensionality ![]() . In particular, for
. In particular, for ![]() and
and ![]() , the number of points in the Smolyak grid is
, the number of points in the Smolyak grid is ![]() and
and ![]() , respectively, which means that the size of the Smolyak grid grows, respectively, linearly and quadratically with
, respectively, which means that the size of the Smolyak grid grows, respectively, linearly and quadratically with ![]() ; see Table 4 for a comparison of the number of points in the Smolyak and tensor-product grids. A relatively small number of Smolyak grid points contrasts sharply with a large number of tensor-product grid points which grows exponentially with the dimensionality of the problem (curse of dimensionality).
; see Table 4 for a comparison of the number of points in the Smolyak and tensor-product grids. A relatively small number of Smolyak grid points contrasts sharply with a large number of tensor-product grid points which grows exponentially with the dimensionality of the problem (curse of dimensionality).
Smolyak Polynomials
The construction of Smolyak polynomials is parallel to the construction of the Smolyak grid. We build the Smolyak multidimensional polynomial function using a family of unidimensional Chebyshev basis functions composed of five terms, ![]() .11 Again, we can construct two-dimensional basis functions using a tensor product of the unidimensional basis functions, which would give us 25 of such basis functions.
.11 Again, we can construct two-dimensional basis functions using a tensor product of the unidimensional basis functions, which would give us 25 of such basis functions.
However, under the Smolyak method, we first construct a sequence of nested sets using the given unidimensional basis functions:
Second, we list all possible two-dimensional tensor products of the unidimensional Smolyak sequences (we denote dimensions by ![]() and
and ![]() ); see Table 5.
); see Table 5.
Finally, we select the elements from the table which are implied by the Smolyak rule (21). Let ![]() denote the Smolyak basis functions for a problem with dimensionality
denote the Smolyak basis functions for a problem with dimensionality ![]() and approximation level
and approximation level ![]() . For the two-dimensional case, we have:
. For the two-dimensional case, we have:
• If ![]() , then
, then ![]() . The only case that satisfies this restriction is when
. The only case that satisfies this restriction is when ![]() and
and ![]() , and thus there is just one Smolyak basis function
, and thus there is just one Smolyak basis function
![]() (25)
(25)
• If ![]() , then
, then ![]() . There are three combinations of
. There are three combinations of ![]() and
and ![]() that satisfy this restriction, and the corresponding five Smolyak basis functions are
that satisfy this restriction, and the corresponding five Smolyak basis functions are
![]() (26)
(26)
• If ![]() , then
, then ![]() . There are six combinations of
. There are six combinations of ![]() and
and ![]() that satisfy this restriction, and the 13 Smolyak basis functions are
that satisfy this restriction, and the 13 Smolyak basis functions are
 (27)
(27)
By construction, in this example, the number of basis functions in Smolyak polynomial is equal to the number of points in the Smolyak grid; compare Tables 3 and 5. The same is true for a Smolyak grid ![]() and Smolyak polynomial
and Smolyak polynomial ![]() under any
under any ![]() and
and ![]() .
.
Smolyak Interpolation Under d = 2 and 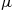 = 1
= 1
We now show Smolyak interpolation. Suppose we must interpolate a two-dimensional function ![]() on a square
on a square ![]() (i.e., we must construct a function
(i.e., we must construct a function ![]() that matches
that matches ![]() exactly in a finite set of points). We consider
exactly in a finite set of points). We consider ![]() , in which case the interpolating function is composed of family
, in which case the interpolating function is composed of family ![]() of five Smolyak basis functions distinguished in (26),
of five Smolyak basis functions distinguished in (26),
![]() (28)
(28)
where ![]() is a vector of five unknown coefficients.
is a vector of five unknown coefficients.
The unknown coefficients must be chosen to match the values of ![]() in five Smolyak grid points
in five Smolyak grid points ![]() distinguished in (23). This yields a system of linear equations
distinguished in (23). This yields a system of linear equations ![]() , where
, where
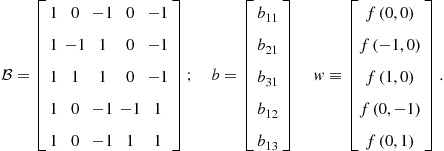 (29)
(29)
The solution to this system is given by ![]() ,
,
 (30)
(30)
Substituting ![]() into the Smolyak polynomial function (28) gives us
into the Smolyak polynomial function (28) gives us ![]() that can be used to interpolate
that can be used to interpolate ![]() in any point of
in any point of ![]() .
.
As we see, Smolyak interpolation works similarly to conventional tensor-product interpolation described in Section 2 and used in, e.g., Judd (1992). The key feature of the Smolyak method is that it uses fewer elements than does a tensor-product method. In our two-dimensional case, the difference is not so large, but in high-dimensional problems, the number of Smolyak elements is just an infinitesimally small fraction of the tensor-product elements, as Table 4 shows.
4.1.2 The Automated Smolyak Method
Our construction of Smolyak interpolation has been done manually. Tables 3 and 5 contain, respectively, repeated grid points and repeated polynomial terms. However, when constructing the interpolation function (28), we list points and basis functions in a way that avoids repetitions.
In applications, the Smolyak construction cannot rely on a visual inspection of the tables and must be automated. Smolyak (1963) does not propose an algorithmic procedure that automates the construction of multidimensional grids and basis functions. He defines these objects mathematically and provides accuracy bounds for some classes of periodic functions.
An algorithm for constructing Smolyak elements was proposed in the subsequent literature. The conventional procedure for automating the Smolyak method is based on an interpolation formula developed in Wasilkowski and Woźniakowski (1999, Lemma 1) and Delvos (1982, Theorem 1). We provide this formula below and illustrate its use by way of example.
A Formula for Smolyak Interpolation
The following formula is used to interpolate ![]() defined on a hypercube
defined on a hypercube ![]() :
:
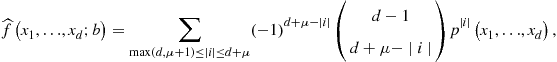 (31)
(31)
where ![]() is the sum of tensor products of unidimensional basis functions
is the sum of tensor products of unidimensional basis functions ![]() whose indices satisfy
whose indices satisfy ![]() and
and
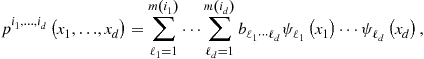 (32)
(32)
where ![]() is the number of elements in unidimensional nested sets
is the number of elements in unidimensional nested sets ![]() , respectively;
, respectively; ![]() are unidimensional basis functions in dimensions
are unidimensional basis functions in dimensions ![]() , respectively;
, respectively; ![]() , and
, and ![]() are the polynomial coefficients given by
are the polynomial coefficients given by
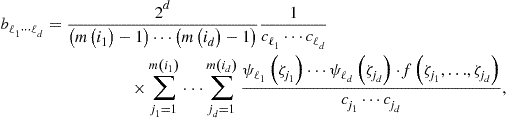 (33)
(33)
where ![]() are grid points in the dimensions
are grid points in the dimensions ![]() , respectively;
, respectively; ![]() for
for ![]() and
and ![]() for
for ![]() . If along any dimension
. If along any dimension ![]() , we have
, we have ![]() , this dimension is dropped from the computation of the coefficient, i.e.,
, this dimension is dropped from the computation of the coefficient, i.e., ![]() is set to 1 and
is set to 1 and ![]() is set to 1.
is set to 1.
Smolyak Interpolation Under d = 2 and 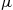 = 1 Revisited
= 1 Revisited
We now illustrate the application of the interpolation formula (31) in the context of an example with ![]() and
and ![]() studied in Section 4.1.1. For the case of
studied in Section 4.1.1. For the case of ![]() , we have
, we have ![]() . This is satisfied in three cases: (a)
. This is satisfied in three cases: (a) ![]() ; (b)
; (b) ![]() ; (c)
; (c) ![]() . From (32), we obtain
. From (32), we obtain
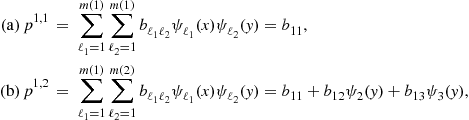 (34)
(34)
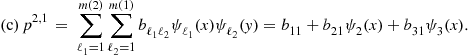 (35)
(35)
Collecting the elements ![]() with the same sum of
with the same sum of ![]() and
and ![]() , i.e.,
, i.e., ![]() , we obtain
, we obtain
![]() (36)
(36)
![]() (37)
(37)
The Smolyak polynomial function (31) for the case ![]() and
and ![]() is given by
is given by
 (38)
(38)
Formula (38) coincides with (28) if instead of ![]() ’s in (38), we substitute the corresponding Chebyshev unidimensional basis functions.
’s in (38), we substitute the corresponding Chebyshev unidimensional basis functions.
Let us now compute the coefficients using (33). Coefficient ![]() appears in
appears in ![]() with
with ![]() and
and ![]() . The Smolyak nested sets of grid points are
. The Smolyak nested sets of grid points are ![]() and
and ![]() , i.e., the first three grid points are
, i.e., the first three grid points are ![]() . Condition (33) implies
. Condition (33) implies
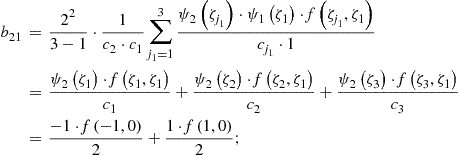
and ![]() is obtained similarly,
is obtained similarly,
![]()
Coefficient ![]() is given by
is given by
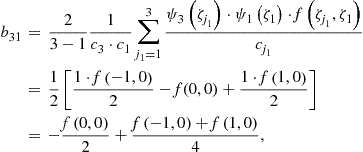
and ![]() is obtained similarly
is obtained similarly
![]()
Conditions defining ![]() , and
, and ![]() are the same as those we had in (30). Formula (33) cannot be used to find
are the same as those we had in (30). Formula (33) cannot be used to find ![]() . We use (38) instead, which implies
. We use (38) instead, which implies
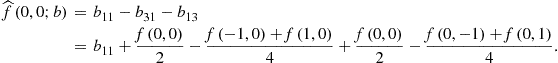
Since under interpolation, we must have ![]() , the last formula implies
, the last formula implies
![]()
which coincides with the condition for ![]() in (30).
in (30).
4.1.3 Conventional Interpolation Formula with Repetitions of Elements Is Inefficient
The conventional interpolation formula (31)–(33) is inefficient. First, it creates a long list with many repeated elements from all tensors that satisfy
![]() (39)
(39)
and then, it assigns weights to each element in the list such that the repeated elements are cancelled out.
The number of repeated elements in the list increases with both the dimensionality of the problem and the approximation level. In particular, for our two-dimensional example, the list involves seven elements under ![]() (i.e., two elements are repeated) and 25 elements under
(i.e., two elements are repeated) and 25 elements under ![]() (i.e., 12 elements are repeated). In high-dimensional applications, the number of repetitions is hideous, which seriously limits the capacities of the Smolyak method.
(i.e., 12 elements are repeated). In high-dimensional applications, the number of repetitions is hideous, which seriously limits the capacities of the Smolyak method.
To summarize, the original Smolyak’s (1963) construction provides us with a set of grid points and basis functions that are an efficient choice for interpolation. However, the formula based on (39) is an inefficient way to arrive to such grid points and basis functions. Judd et al. (2013) show a Smolyak interpolation formula that avoids repetitions of elements and that is an efficient alternative to the conventional interpolation formula based on (39).
4.2 Generalized Stochastic Simulation Algorithm
The idea of finding solutions to economic models using stochastic simulation dates back to Marcet’s (1988) parameterized expectations algorithm (PEA), which was later developed in Den Haan and Marcet (1990); see Marcet and Lorenzoni (1999) for a detailed description of this algorithm. PEA is feasible in high-dimensional problems but its overall accuracy is limited by a low accuracy of Monte Carlo integration. Moreover, PEA builds on least-squares learning which is numerically unstable in the context of stochastic simulation. Judd et al. (2009, 2011b) propose a generalized stochastic simulation algorithm (GSSA), in which inaccurate Monte Carlo integration is replaced with accurate deterministic integration, and in which unstable least-squares learning is replaced with regression methods suitable for dealing with ill-conditioned problems. The resulting GSSA method is numerically stable and delivers accuracy of solutions comparable to the best accuracy attained in the related literature. In particular, Hasanhodzic and Kotlikoff (2013) applied GSSA to solve life-cycle models with up to 80 periods.
Again, for the sake of expositional convenience, we work with a simple two-dimensional example. In Sections 4.2.1, 4.2.2, and 4.2.3, we show how stochastic simulation methods implement the three steps outlined in the beginning of Section 4: (i) constructs a grid of simulated points, (ii) constructs an approximating function using some nonproduct rules, and (iii) identifies the parameters in the approximating function by way of regression. In the remainder of the section, we discuss advantages and shortcomings of stochastic simulation methods, provide a description of PEA and GSSA, and discuss computational techniques that can improve the performance of stochastic simulation methods in problems with high dimensionality.
4.2.1 A Grid of Simulated Points
A stochastic simulation approach solves a dynamic economic model on a grid composed of simulated points. Constructing such a grid is simple. As an example, consider the neoclassical stochastic growth model (1)–(3) described in Section 3. We draw and fix a sequence of productivity shocks ![]() and construct productivity levels
and construct productivity levels ![]() using (3). We guess a parametric function
using (3). We guess a parametric function ![]() that approximates the true capital decision function,
that approximates the true capital decision function, ![]() , choose initial condition
, choose initial condition ![]() , fix the coefficient vector
, fix the coefficient vector ![]() , and simulate the model forward using
, and simulate the model forward using ![]() . The resulting series
. The resulting series ![]() are used as a grid for finding a solution.
are used as a grid for finding a solution.
4.2.2 An Approximating Function
As a set of basis functions for approximation, we can use any family of functions which is sufficiently flexible (to ensure a sufficiently high accuracy), and which does not grow too rapidly with the dimensionality of the problem (to ensure a reasonably low cost). In particular, Judd et al. (2011b) advocate families of complete polynomials that are linear in coefficients ![]() , i.e.,
, i.e.,
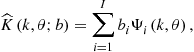 (40)
(40)
where ![]() is a set of basis functions and
is a set of basis functions and ![]() . The basis functions can be ordinary polynomials, e.g.,
. The basis functions can be ordinary polynomials, e.g., ![]() , or some other polynomials; for example, Judd et al. (2011b) and Maliar et al. (2011) combine a grid of points produced by stochastic simulation with Hermite and Smolyak polynomials, respectively. The numbers of terms in a complete polynomial function of degrees one, two, and three are given by
, or some other polynomials; for example, Judd et al. (2011b) and Maliar et al. (2011) combine a grid of points produced by stochastic simulation with Hermite and Smolyak polynomials, respectively. The numbers of terms in a complete polynomial function of degrees one, two, and three are given by ![]() , i.e., they grow linearly, quadratically, and cubically, respectively.
, i.e., they grow linearly, quadratically, and cubically, respectively.
4.2.3 Finding the Polynomial Coefficients by Way of Regression
We estimate the coefficients in (40) by way of regression
![]() (41)
(41)
where ![]() is the model’s variable for which we aim to approximate the decision function, e.g.,
is the model’s variable for which we aim to approximate the decision function, e.g., ![]() is the list of basis functions in (40), e.g.,
is the list of basis functions in (40), e.g., ![]() with
with ![]() being the polynomial degree; and
being the polynomial degree; and ![]() is the residual between the true value of
is the residual between the true value of ![]() and fitted value
and fitted value ![]() . Regression equation (41) is a special case of the general approximation problem (20).
. Regression equation (41) is a special case of the general approximation problem (20).
If simulated points are used as a grid, then basis functions do not have the property of orthogonality. In particular, there is no guarantee that any specific polynomial function composed of ![]() basis functions will pass exactly through
basis functions will pass exactly through ![]() simulated points, unlike they do in the Smolyak collocation method. Therefore, we will not try to fit the approximating function exactly to any of the simulated points; instead, we will proceed as is done in the regression analysis in econometrics. Namely, we will choose a simulation length to be larger than the number of explanatory variables, i.e.,
simulated points, unlike they do in the Smolyak collocation method. Therefore, we will not try to fit the approximating function exactly to any of the simulated points; instead, we will proceed as is done in the regression analysis in econometrics. Namely, we will choose a simulation length to be larger than the number of explanatory variables, i.e., ![]() , and we will identify coefficients
, and we will identify coefficients ![]() by minimizing the residuals in regression equation (41). As we will see, the way in which the regression coefficients are estimated will play an important role in the accuracy and numerical stability of stochastic simulation methods.
by minimizing the residuals in regression equation (41). As we will see, the way in which the regression coefficients are estimated will play an important role in the accuracy and numerical stability of stochastic simulation methods.
4.2.4 Advantages of the Stochastic Simulation Approach
The key advantage of the stochastic simulation approach is that it produces an adaptive grid. Points that are realized in simulation belong to a high-probability set of a given model; we also refer to this set as an essentially ergodic set; see Judd et al. (2012) for a formal definition of an essentially ergodic set. By focusing just on those points, we can save on the cost of computing a solution in those areas that are not visited in equilibrium. How much can one save on cost by focusing on the essentially ergodic set instead of a multidimensional hypercube that encloses such a set? As an illustration, in Figure 3, we plot the simulated series of capital and productivity levels for the one-agent model (1)–(3). The essentially ergodic set takes the form of an oval, and the rectangular area that sits outside of the oval’s boundaries is effectively never visited. In the two-dimensional case, a circle inscribed within a square occupies about ![]() of the area of the square, and an oval inscribed in this way occupies an even smaller area. Thus, the essentially ergodic set is at least
of the area of the square, and an oval inscribed in this way occupies an even smaller area. Thus, the essentially ergodic set is at least ![]() smaller than the hypercube enclosing this set. In general, the ratio of the volume of a
smaller than the hypercube enclosing this set. In general, the ratio of the volume of a ![]() -dimensional hypersphere of diameter
-dimensional hypersphere of diameter ![]() , to the volume of a
, to the volume of a ![]() -dimensional hypercube of width
-dimensional hypercube of width ![]() , is
, is
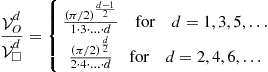 (42)
(42)
The ratio ![]() declines very rapidly with the dimensionality of the state space. For example, for dimensions three, four, five, ten, and thirty, this ratio is
declines very rapidly with the dimensionality of the state space. For example, for dimensions three, four, five, ten, and thirty, this ratio is ![]() , and
, and ![]() , respectively.
, respectively.
This example suggests that focusing on the right geometry can be critical for accuracy and cost in high-dimensional applications. Potential benefits are twofold: first, when computing a solution on an essentially ergodic set, we face just a fraction of the cost we would have faced on a hypercube grid, used in conventional projection methods. The higher the dimensionality of a problem, the larger the reduction in cost is likely to be. Second, when fitting a polynomial on an essentially ergodic set, stochastic simulation methods focus on a relevant solution domain and can get a better fit inside this domain than methods that operate on a hypercube and that face a trade-off between the fit inside and outside the relevant domain.
4.2.5 Marcet’s (1988) Parameterized Expectations Algorithm
Marcet’s (1988) parameterized expectations algorithm (PEA) approximates the expectation function in the right side of the Euler equation by an exponentiated polynomial of logarithm of the state variables,
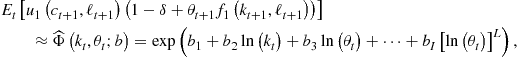 (43)
(43)
where ![]() is a degree of approximating polynomial. This also identifies the left side of the Euler equation as
is a degree of approximating polynomial. This also identifies the left side of the Euler equation as ![]() .12 Using the assumed
.12 Using the assumed ![]() , PEA simulates the model forward to construct the series
, PEA simulates the model forward to construct the series ![]() . Next, it approximates the conditional expectation function by the realized value of the integrand for each
. Next, it approximates the conditional expectation function by the realized value of the integrand for each ![]() ,
,
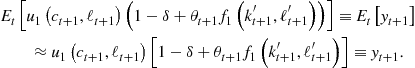 (44)
(44)
Finally, PEA fits values of ![]() to
to ![]() using a nonlinear least-squares (NLLS) regression to compute
using a nonlinear least-squares (NLLS) regression to compute ![]() ; it iterates on
; it iterates on ![]() until convergence.
until convergence.
Marcet’s (1988) implementation of a stochastic simulation algorithm has important shortcomings that limit both accuracy and numerical stability. First, the PEA uses stochastic simulation not only to construct a grid of points for approximating the solution but also as a set of nodes for integration. However, the one-node Monte Carlo method used has low accuracy (unless the simulation length is impractically long). This is not surprising given that PEA replaces an expectation of a random variable ![]() with just one realization of this variable
with just one realization of this variable ![]() ; see Section 5.3 for a discussion of the accuracy of this integration method.
; see Section 5.3 for a discussion of the accuracy of this integration method.
Second, PEA relies on standard least-squares (LS) learning methods for fitting the approximating functions to simulated data, and such LS methods are numerically unstable in the given context (beyond the first-degree polynomials). This is because monomial terms constructed on simulated series are highly correlated in the studied class of economic models. The multicollinearity problem is severe even under low-degree polynomials. In particular, Den Haan and Marcet (1990) report that in a second-degree PEA solution, the cross term ![]() in (43) is highly correlated with the other terms and must be removed from the regression.
in (43) is highly correlated with the other terms and must be removed from the regression.
Finally, PEA builds on a nonlinear approximating function, which is an additional source of numerical instability and computational expense. The resulting nonlinear regression model must be estimated with NLLS methods. Such methods need a good initial guess, may deliver multiple minima, and on many occasions fail to converge; moreover, nonlinear optimization is costly because it requires computing Jacobian and Hessian matrices; see Christiano and Fisher (2000) for a discussion.
4.2.6 Generalized Stochastic Simulation Algorithm by Judd et al. (2011b)
Judd et al. (2011b) propose a generalized stochastic simulation algorithm (GSSA) that does not suffer from the above shortcomings. First, GSSA uses stochastic simulation only for constructing a grid on which a solution is approximated; however, it computes integrals using accurate quadrature and monomial integration formulas described in Sections 5.1 and 5.2, respectively. Second, GSSA stabilizes stochastic simulation by using regression methods that are suitable for ill-conditioned problems. Finally, GSSA uses families of basis functions of type (40) that are linear in coefficients ![]() , and it builds the fitting step on a linear regression model that can be estimated with simple and reliable linear approximation methods. As a result, GSSA can deliver high-degree polynomial approximations and attain accuracy of solutions comparable to the best accuracy in the related literature. Below, we show regression methods and other techniques that GSSA uses to stabilize stochastic simulation.
, and it builds the fitting step on a linear regression model that can be estimated with simple and reliable linear approximation methods. As a result, GSSA can deliver high-degree polynomial approximations and attain accuracy of solutions comparable to the best accuracy in the related literature. Below, we show regression methods and other techniques that GSSA uses to stabilize stochastic simulation.
Ill-Conditioned LS Problem
We now explain when the multicollinearity arises and show how it affects the regression outcomes. We consider the simplest possible approximating family, the one composed of ordinary polynomials. The objective is to fit simulated series for a variable ![]() on an ordinary polynomial function of the current state variables
on an ordinary polynomial function of the current state variables ![]() as shown in (41).
as shown in (41).
Consider the standard LS approach to regression equation (41):
![]() (45)
(45)
where ![]() denotes the
denotes the ![]() vector norm;
vector norm; ![]() and
and ![]()
![]() .
.
The solution to (45) is
![]() (46)
(46)
LS problem (45) is often ill-conditioned when ![]() is generated by stochastic simulation. To measure the degree of ill-conditioning, we use the condition number of matrix
is generated by stochastic simulation. To measure the degree of ill-conditioning, we use the condition number of matrix ![]() , denoted by
, denoted by ![]() and defined as follows: We order the eigenvalues,
and defined as follows: We order the eigenvalues, ![]() , of
, of ![]() by their magnitude,
by their magnitude, ![]() , and find a ratio of the largest eigenvalue,
, and find a ratio of the largest eigenvalue, ![]() , of
, of ![]() to its smallest eigenvalue,
to its smallest eigenvalue, ![]() , i.e.,
, i.e., ![]() . The eigenvalues of
. The eigenvalues of ![]() are defined by the standard eigenvalue decomposition
are defined by the standard eigenvalue decomposition ![]() , where
, where ![]() is a diagonal matrix of eigenvalues of
is a diagonal matrix of eigenvalues of ![]() , and
, and ![]() is an orthogonal matrix of eigenvectors of
is an orthogonal matrix of eigenvectors of ![]() . A large condition number implies that
. A large condition number implies that ![]() is close to being singular and not invertible and tells us that any linear operation, such as (46), is very sensitive to perturbation and numerical errors (such as round-off errors).
is close to being singular and not invertible and tells us that any linear operation, such as (46), is very sensitive to perturbation and numerical errors (such as round-off errors).
Two causes of ill-conditioning are multicollinearity and poor scaling of the variables constituting ![]() . Multicollinearity occurs when the variables forming
. Multicollinearity occurs when the variables forming ![]() are significantly correlated. The following example illustrates the effects of multicollinearity on the LS solution (we analyze the sensitivity to changes in
are significantly correlated. The following example illustrates the effects of multicollinearity on the LS solution (we analyze the sensitivity to changes in ![]() but the results are similar for the sensitivity to changes in
but the results are similar for the sensitivity to changes in ![]() ).
).
The scaling problem arises when the columns of ![]() have significantly different means and variances (due to differential scaling among either the state variables,
have significantly different means and variances (due to differential scaling among either the state variables, ![]() and
and ![]() , or their functions, e.g.,
, or their functions, e.g., ![]() and
and ![]() ). A column with only very small entries will be treated as if it were a column of zeros. The next example illustrates the effect of the scaling problem.
). A column with only very small entries will be treated as if it were a column of zeros. The next example illustrates the effect of the scaling problem.
A comparison of Examples 1 and 2 shows that multicollinearity and poor scaling magnify the impact of perturbations on the OLS solution. Each iteration of a stochastic simulation algorithm produces changes in simulated data (perturbations). In the presence of ill-conditioning, these changes, together with numerical errors, may induce large, erratic jumps in the regression coefficients and failures to converge.
Data Normalization
Data normalization addresses the scaling issues highlighted in Example 2. We center and scale both the response variable ![]() and the explanatory variables of
and the explanatory variables of ![]() to have a zero mean and unit standard deviation. We then estimate a regression model without an intercept to obtain the vector of coefficients
to have a zero mean and unit standard deviation. We then estimate a regression model without an intercept to obtain the vector of coefficients ![]() . We finally restore the coefficients
. We finally restore the coefficients ![]() and the intercept
and the intercept ![]() in the original (unnormalized) regression model according to
in the original (unnormalized) regression model according to ![]() , and
, and ![]() , where
, where ![]() and
and ![]() are the sample means, and
are the sample means, and ![]() and
and ![]() are the sample standard deviations of the original unnormalized variables
are the sample standard deviations of the original unnormalized variables ![]() and
and ![]() , respectively.
, respectively.
Choosing a Family of Basis Functions
An obvious example of a family of type (40) is an ordinary polynomial family, ![]() . However, as we argued in Section 3, the basis functions of this family look very similar (e.g.,
. However, as we argued in Section 3, the basis functions of this family look very similar (e.g., ![]() looks similar to
looks similar to ![]() , and
, and ![]() looks similar to
looks similar to ![]() ). As a result, the explanatory variables in the regression equation are likely to be strongly correlated (i.e., the LS problem is ill-conditioned) and estimation methods (e.g., OLS) may fail because they cannot distinguish between similarly shaped polynomial terms.
). As a result, the explanatory variables in the regression equation are likely to be strongly correlated (i.e., the LS problem is ill-conditioned) and estimation methods (e.g., OLS) may fail because they cannot distinguish between similarly shaped polynomial terms.
In contrast, for families of orthogonal polynomials (e.g., Hermite, Chebyshev, Legendre), basis functions have very different shapes and, hence, the multicollinearity problem is likely to manifest to a smaller degree, if at all. In the context of GSSA, we consider the family of Hermite polynomials. Such polynomials can be defined with a simple recursive formula: ![]() , and
, and ![]() , which yields
, which yields ![]() , and
, and ![]() .
.
Two points are in order. First, while Hermite polynomials are orthogonal under the Gaussian density function, they are not orthogonal under the ergodic measure derived from stochastic simulation. Still, Hermite polynomials are far less correlated than ordinary polynomials which suffice to avoid ill-conditioning. Second, even though using Hermite polynomials helps us avoid ill-conditioning in one variable, they may not suffice to deal with multicollinearity across variables. For example, if ![]() and
and ![]() are perfectly correlated, certain Hermite polynomial terms for
are perfectly correlated, certain Hermite polynomial terms for ![]() and
and ![]() , such as
, such as ![]() and
and ![]() , are also perfectly correlated and, hence,
, are also perfectly correlated and, hence, ![]() is singular. Thus, we may still need to complement Hermite polynomials with regression methods that suit ill-conditioned problems.13
is singular. Thus, we may still need to complement Hermite polynomials with regression methods that suit ill-conditioned problems.13
Approximation Methods Suitable for Dealing with Multicollinearity
We now review fitting (regression) techniques that are suitable for dealing with ill-conditioned problems. We also discuss the choice of a family of approximating functions; see Judd et al. (2011b) for more details.
Ls-SVD
We now present two LS methods that are more robust to ill-conditioning than the standard OLS method. The first approach, called LS using SVD (LS-SVD), relies on a singular value decomposition (SVD) of ![]() . We use the SVD of
. We use the SVD of ![]() to rewrite OLS solution (46) in a way that does not require an explicit computation of
to rewrite OLS solution (46) in a way that does not require an explicit computation of ![]() . For a matrix
. For a matrix ![]() with
with ![]() , an SVD decomposition is
, an SVD decomposition is
![]() (49)
(49)
where ![]() and
and ![]() are orthogonal matrices and
are orthogonal matrices and ![]() is a diagonal matrix with diagonal entries
is a diagonal matrix with diagonal entries ![]() , known as singular values of
, known as singular values of ![]() .14 The condition number of
.14 The condition number of ![]() is its largest singular value divided by its smallest singular value,
is its largest singular value divided by its smallest singular value, ![]() . The singular values of
. The singular values of ![]() are related to the eigenvalues of
are related to the eigenvalues of ![]() by
by ![]() . This implies that
. This implies that ![]() . The OLS estimator
. The OLS estimator ![]() in terms of SVD (49) is
in terms of SVD (49) is
![]() (50)
(50)
With an infinite-precision computer, OLS formula (46) and LS-SVD formula (50) give us identical estimates of ![]() . With a finite-precision computer, the standard OLS estimator cannot be computed reliably if
. With a finite-precision computer, the standard OLS estimator cannot be computed reliably if ![]() is ill-conditioned. However, it is still possible that
is ill-conditioned. However, it is still possible that ![]() is sufficiently well-conditioned so that the LS-SVD estimator can be computed successfully.15
is sufficiently well-conditioned so that the LS-SVD estimator can be computed successfully.15
RLS-Tikhonov
The second approach, called regularized LS using Tikhonov regularization (RLS-Tikhonov), imposes penalties based on the size of the regression coefficients. In essence, a regularization method replaces an ill-conditioned problem with a well-conditioned problem that gives a similar answer. In statistics, Tikhonov regularization is known as ridge regression and is classified as a shrinkage method because it shrinks the norm of estimated coefficient vector relative to the nonregularized solution. Formally, Tikhonov regularization imposes an ![]() penalty on the magnitude of the regression-coefficient vector; i.e., for a regularization parameter
penalty on the magnitude of the regression-coefficient vector; i.e., for a regularization parameter ![]() , the vector
, the vector ![]() solves
solves
![]() (51)
(51)
where ![]() and
and ![]() are centered and scaled, and
are centered and scaled, and ![]() . The parameter
. The parameter ![]() controls the amount by which the regression coefficients are shrunk, with larger values of
controls the amount by which the regression coefficients are shrunk, with larger values of ![]() leading to greater shrinkage.
leading to greater shrinkage.
Finding an FOC of (51) with respect to ![]() gives us the following estimator
gives us the following estimator
![]() (52)
(52)
where ![]() is an identity matrix of order
is an identity matrix of order ![]() . Note that Tikhonov regularization adds a positive constant multiple of the identity matrix to
. Note that Tikhonov regularization adds a positive constant multiple of the identity matrix to ![]() prior to inversion. Thus, if
prior to inversion. Thus, if ![]() is nearly singular, the matrix
is nearly singular, the matrix ![]() is less singular, reducing problems in computing
is less singular, reducing problems in computing ![]() .
.
LAD Approaches
LAD, or ![]() , regression methods use linear programming to minimize the sum of absolute deviations. LAD methods do not construct
, regression methods use linear programming to minimize the sum of absolute deviations. LAD methods do not construct ![]() and avoid the ill-conditioning. The basic LAD method solves the optimization problem
and avoid the ill-conditioning. The basic LAD method solves the optimization problem
![]() (53)
(53)
where ![]() denotes the
denotes the ![]() vector norm, and
vector norm, and ![]() denotes the absolute value. Without a loss of generality, we assume that
denotes the absolute value. Without a loss of generality, we assume that ![]() and
and ![]() are centered and scaled.
are centered and scaled.
There is no explicit solution to LAD problem (53), but the LAD problem (53) is equivalent to the linear programming problem:
![]() (54)
(54)
![]() (55)
(55)
where ![]() . The problem has
. The problem has ![]() unknowns. Although this formulation of the LAD problem is intuitive, it is not the most suitable for a numerical analysis. Judd et al. (2011b) show primal and dual implementations of the LAD problems that are more convenient for numerical treatment.
unknowns. Although this formulation of the LAD problem is intuitive, it is not the most suitable for a numerical analysis. Judd et al. (2011b) show primal and dual implementations of the LAD problems that are more convenient for numerical treatment.
Regularized LAD Approaches
Similar to the LS case, we can modify the original LAD problem (53) to incorporate an ![]() penalty on the coefficient vector
penalty on the coefficient vector ![]() . We refer to the resulting problem as a regularized LAD (RLAD). Like Tikhonov regularization, the RLAD problem shrinks the values of the coefficients toward zero. Introducing an
. We refer to the resulting problem as a regularized LAD (RLAD). Like Tikhonov regularization, the RLAD problem shrinks the values of the coefficients toward zero. Introducing an ![]() penalty in place of the
penalty in place of the ![]() penalty used in Tikhonov regularization allows us to have the same benefits of shrinking the coefficients but in the context of a linear programming approach. Formally, for a given regularization parameter
penalty used in Tikhonov regularization allows us to have the same benefits of shrinking the coefficients but in the context of a linear programming approach. Formally, for a given regularization parameter ![]() , the RLAD problem finds a vector
, the RLAD problem finds a vector ![]() that solves
that solves
![]() (56)
(56)
where ![]() and
and ![]() are centered and scaled, and
are centered and scaled, and ![]() . See Judd et al. (2011b) for a detailed description of the primal and dual formulations of the regularized LAD problems.
. See Judd et al. (2011b) for a detailed description of the primal and dual formulations of the regularized LAD problems.
Principal Component Method
A principal component method reduces the multicollinearity in the data to a given target level. Let ![]() be a matrix of centered and scaled explanatory variables and consider the SVD of
be a matrix of centered and scaled explanatory variables and consider the SVD of ![]() defined in (49). Let us make a linear transformation of
defined in (49). Let us make a linear transformation of ![]() using
using ![]() , where
, where ![]() and
and ![]() is the matrix of singular vectors of
is the matrix of singular vectors of ![]() defined by (49). Vectors
defined by (49). Vectors ![]() are called principal components of
are called principal components of ![]() . They are orthogonal,
. They are orthogonal, ![]() for any
for any ![]() , and their norms are related to singular values
, and their norms are related to singular values ![]() by
by ![]() . Principal components have two noteworthy properties. First, the sample mean of each principal component
. Principal components have two noteworthy properties. First, the sample mean of each principal component ![]() is equal to zero, since it is given by a linear combination of centered variables
is equal to zero, since it is given by a linear combination of centered variables ![]() , each of which has a zero mean; second, the variance of each principal component is equal to
, each of which has a zero mean; second, the variance of each principal component is equal to ![]() , because we have
, because we have ![]() .
.
By construction of the SVD, if ![]() has a zero variance (equivalently, a zero singular value,
has a zero variance (equivalently, a zero singular value, ![]() ), then all entries of
), then all entries of ![]() are equal to zero,
are equal to zero, ![]() , which implies that variables
, which implies that variables ![]() constituting this particular principal component are linearly dependent. Therefore, we can reduce the degrees of ill-conditioning of
constituting this particular principal component are linearly dependent. Therefore, we can reduce the degrees of ill-conditioning of ![]() to some target level by excluding low-variance principal components corresponding to small singular values.
to some target level by excluding low-variance principal components corresponding to small singular values.
Let ![]() represent the largest condition number of
represent the largest condition number of ![]() that we are willing to tolerate. Let us compute the ratios of the largest singular value to all other singular values,
that we are willing to tolerate. Let us compute the ratios of the largest singular value to all other singular values, ![]() . (Recall that the last ratio is the actual condition number of matrix
. (Recall that the last ratio is the actual condition number of matrix ![]() ). Let
). Let ![]() be the first
be the first ![]() principal components for which
principal components for which ![]() , and let us remove the last
, and let us remove the last ![]() principal components for which
principal components for which ![]() . By construction,
. By construction, ![]() has a condition number which is smaller than or equal to
has a condition number which is smaller than or equal to ![]() .
.
Let us consider regression equation (41) and let us approximate ![]() using
using ![]() such that
such that ![]() , where
, where ![]() contains the first
contains the first ![]() right singular vectors of
right singular vectors of ![]() and
and ![]() . The resulting regression equation is
. The resulting regression equation is
![]() (57)
(57)
where ![]() is centered and scaled. The coefficients
is centered and scaled. The coefficients ![]() can be estimated by any of the methods described in this section. For example, we can compute OLS estimator (46). Once we compute
can be estimated by any of the methods described in this section. For example, we can compute OLS estimator (46). Once we compute ![]() , we can recover the coefficients as
, we can recover the coefficients as ![]() . Instead of the principal component methods, we can use a truncated SVD method; see Judd et al. (2011b) for a description of this method.
. Instead of the principal component methods, we can use a truncated SVD method; see Judd et al. (2011b) for a description of this method.
4.2.7 Numerical Illustration of the Importance of the Approximating Function and Fitting Method
As an illustration, we consider the one-agent model with inelastic labor supply under parameterization (18) that allows for a closed-form solution. Judd et al. (2011b) use the GSSA method to solve this model under a simulation length ![]() ; see Judd et al. (2011b) for details. In Table 6, we provide the results that illustrate the importance of a choice of the approximating function. When the OLS method is used with unnormalized data and ordinary polynomials, we cannot go beyond the second-degree polynomial approximations. The data normalization improves the performance of the OLS method; however, we still cannot calculate more than a third-degree polynomial approximation. The introduction of Hermite polynomials completely resolves the ill-conditioning of the LS problem: OLS can compute all five degrees of the polynomial approximations, and the accuracy of these approximations improves systematically as we move from the first- to the fifth-degree polynomials, e.g., the average Euler equation residuals decrease from
; see Judd et al. (2011b) for details. In Table 6, we provide the results that illustrate the importance of a choice of the approximating function. When the OLS method is used with unnormalized data and ordinary polynomials, we cannot go beyond the second-degree polynomial approximations. The data normalization improves the performance of the OLS method; however, we still cannot calculate more than a third-degree polynomial approximation. The introduction of Hermite polynomials completely resolves the ill-conditioning of the LS problem: OLS can compute all five degrees of the polynomial approximations, and the accuracy of these approximations improves systematically as we move from the first- to the fifth-degree polynomials, e.g., the average Euler equation residuals decrease from ![]() to
to ![]() .
.
Table 6
Conventional OLS in the one-agent model with a closed-form solution: ordinary polynomial with unnormalized and normalized data and Hermite polynomials.a
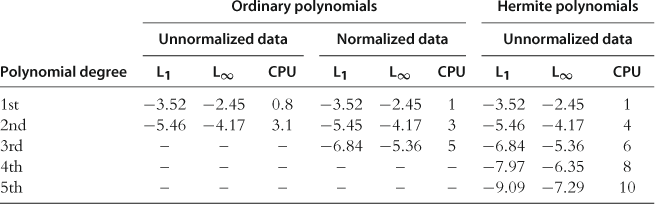
aNotes: ![]() and
and ![]() are, respectively, the average and maximum of absolute residuals across optimality conditions and test points (in log10 units). CPU is the time necessary for computing a solution (in seconds). These results are reproduced from Judd et al. (2011b), Table 1.
are, respectively, the average and maximum of absolute residuals across optimality conditions and test points (in log10 units). CPU is the time necessary for computing a solution (in seconds). These results are reproduced from Judd et al. (2011b), Table 1.
In Table 7, we illustrate the importance of the fitting methods. The RLS-Tikhonov method leads to visibly less accurate solutions than the LS-SVD method. This happens because RLS-Tikhonov and LS-SVD work with different objects: the former works with a very ill-conditioned matrix ![]() , while the latter works with a better conditioned matrix
, while the latter works with a better conditioned matrix ![]() . Under RLAD-DP and LS-SVD, the solutions are very accurate: the average Euler equation residuals decrease from
. Under RLAD-DP and LS-SVD, the solutions are very accurate: the average Euler equation residuals decrease from ![]() to
to ![]() when the polynomial degree increases from one to five.
when the polynomial degree increases from one to five.
Table 7
Other fitting methods in the one-agent model with a closed-form solution: RLS-Tikhonov, RLAD-DP and LS-SVD.a
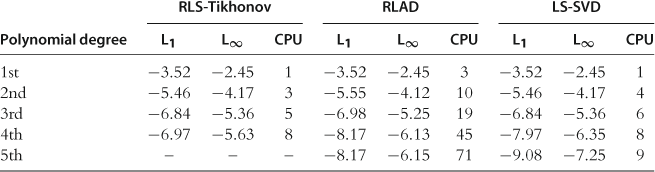
aNotes: ![]() and
and ![]() are, respectively, the average and maximum of absolute residuals across optimality conditions and test points (in log10 units). CPU is the time necessary for computing a solution (in seconds). RLS-Tikhonov uses ordinary polynomials and
are, respectively, the average and maximum of absolute residuals across optimality conditions and test points (in log10 units). CPU is the time necessary for computing a solution (in seconds). RLS-Tikhonov uses ordinary polynomials and ![]() . RLAD uses ordinary polynomials and
. RLAD uses ordinary polynomials and ![]() . LS-SVD uses Hermite polynomials. These results are reproduced from Judd et al. (2011b), Table 1. RLAD corresponds to RLAD-DP in Judd et al. (2011b), where DP stands for a dual problem.
. LS-SVD uses Hermite polynomials. These results are reproduced from Judd et al. (2011b), Table 1. RLAD corresponds to RLAD-DP in Judd et al. (2011b), where DP stands for a dual problem.
4.3  -Distinguishable Set and Cluster Grid Algorithms
-Distinguishable Set and Cluster Grid Algorithms
The Smolyak method provides an efficient nonproduct discretization of a hypercube; however, the hypercube itself is not an efficient choice for a solution domain. In order to capture all points that are visited in equilibrium, the hypercube must typically contain large areas that are unlikely to happen in equilibrium. In turn, simulated points used by GSSA occupy a much smaller area than the hypercube and allow us to focus on a relevant solution domain. However, a set of simulated points itself is not an efficient discretization of such a domain because a grid of simulated points is unevenly spaced; has many closely located, redundant points; and contains some points in low-density regions.
Judd et al. (2012) introduce an ![]() -distinguishable set (EDS) technique that selects a subset of points situated at the distance of at least
-distinguishable set (EDS) technique that selects a subset of points situated at the distance of at least ![]() from one another. This construction combines the best features of stochastic simulation and hypercube grids; namely, it combines an adaptive geometry with efficient discretization. In Figure 4a and b, we shows an example of such a grid for the one-agent model.
from one another. This construction combines the best features of stochastic simulation and hypercube grids; namely, it combines an adaptive geometry with efficient discretization. In Figure 4a and b, we shows an example of such a grid for the one-agent model.
As is seen in the figure, the resulting EDS covers the high-probability area of the state space roughly uniformly. The EDS grid can be combined with any family of approximating functions, in particular with those of type (40). As in the case of stochastic simulation methods, we use more EDS grid points than the parameters in the approximating function, and we identify the parameters of such a function using regression methods that are robust to ill-conditioned problems. Therefore, we just focus on explaining how the EDS grid is constructed.
4.3.1 Eliminating Simulated Points Outside the High-Probability Set
Let us assume some equilibrium law of motion ![]() for state variables
for state variables
![]() (58)
(58)
where ![]() is a vector of
is a vector of ![]() (exogenous and endogenous) state variables. We first select a subset of simulated points which belong to an essentially ergodic set
(exogenous and endogenous) state variables. We first select a subset of simulated points which belong to an essentially ergodic set ![]() using the following algorithm.
using the following algorithm.

In Step 2, we include only each ![]() th observation in the sample
th observation in the sample ![]() to make random draws (approximately) independent. As far as Step 3 is concerned, there are various methods in statistics that can be used to estimate the density function from a given set of data; see Scott and Sain (2005) for a review. We use one such method, namely, a multivariate kernel algorithm with a normal kernel which estimates the density function in a point
to make random draws (approximately) independent. As far as Step 3 is concerned, there are various methods in statistics that can be used to estimate the density function from a given set of data; see Scott and Sain (2005) for a review. We use one such method, namely, a multivariate kernel algorithm with a normal kernel which estimates the density function in a point ![]() as
as
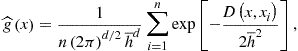 (59)
(59)
where ![]() is the bandwidth parameter and
is the bandwidth parameter and ![]() is the distance between
is the distance between ![]() and
and ![]() . The complexity of Algorithm
. The complexity of Algorithm ![]() is
is ![]() because it requires us to compute pairwise distances between all sample points. Finally, in Step 3, we do not choose the density cutoff
because it requires us to compute pairwise distances between all sample points. Finally, in Step 3, we do not choose the density cutoff ![]() but a fraction of the sample to be removed,
but a fraction of the sample to be removed, ![]() , which is related to
, which is related to ![]() by
by ![]() . For example,
. For example, ![]() means that we remove the
means that we remove the ![]() of the sample which has the lowest density.
of the sample which has the lowest density.
4.3.2 Constructing an  -Distinguishable Set of Points
-Distinguishable Set of Points
Formally, we define an EDS as follows. Let ![]() be a bounded metric space. A set
be a bounded metric space. A set ![]() consisting of points
consisting of points ![]() is called
is called ![]() -distinguishable if
-distinguishable if ![]() for all
for all ![]() , where
, where ![]() is a parameter. EDSs are used in mathematical literature that studies entropy; see Temlyakov (2011) for a review. This literature focuses on a problem of constructing an EDS that covers a given subset of
is a parameter. EDSs are used in mathematical literature that studies entropy; see Temlyakov (2011) for a review. This literature focuses on a problem of constructing an EDS that covers a given subset of ![]() (such as a multidimensional hypercube). Judd et al. (2012) study a different problem: they construct an EDS for a given discrete set of points. To this purpose, they introduce the following algorithm.
(such as a multidimensional hypercube). Judd et al. (2012) study a different problem: they construct an EDS for a given discrete set of points. To this purpose, they introduce the following algorithm.

The complexity of Algorithm ![]() is of the order
is of the order ![]() . When no points are eliminated from
. When no points are eliminated from ![]() , i.e.,
, i.e., ![]() , the complexity is quadratic,
, the complexity is quadratic, ![]() , which is the upper bound on cost. However, the number of points
, which is the upper bound on cost. However, the number of points ![]() in an EDS is bounded from above if
in an EDS is bounded from above if ![]() is bounded. This means that asymptotically, when
is bounded. This means that asymptotically, when ![]() , the complexity of Algorithm
, the complexity of Algorithm ![]() is linear,
is linear, ![]() .
.
The distance between simulated points depends on measurement units of and correlation between variables (this affects the resulting EDS). Therefore, prior to using Algorithms ![]() and
and ![]() , we normalize and orthogonalize the simulated data using the principal component (PC) transformation. As a measure of distance between two observations
, we normalize and orthogonalize the simulated data using the principal component (PC) transformation. As a measure of distance between two observations ![]() and
and ![]() , we use the Euclidean distance between their PCs, namely,
, we use the Euclidean distance between their PCs, namely, ![]() , where all principal components
, where all principal components ![]() are normalized to have unit variance.
are normalized to have unit variance.
In Figure 5, we illustrate the described two-step procedure by way of an example of the one-agent model.
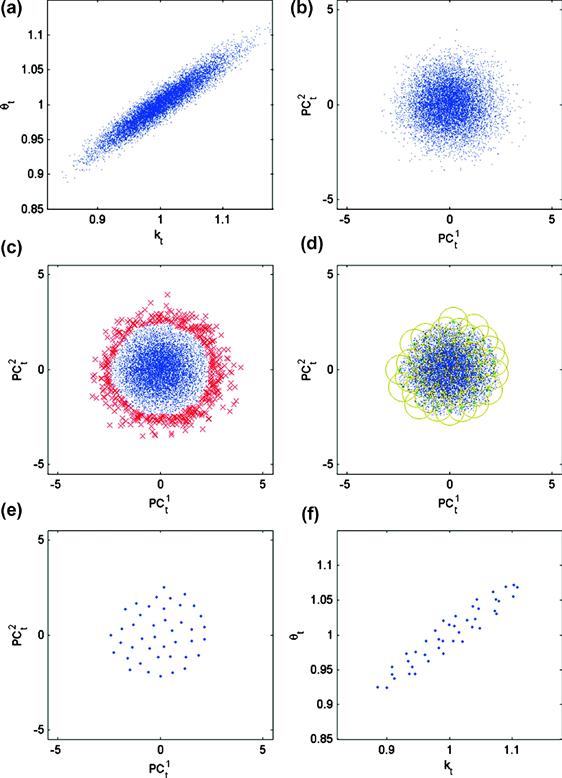
Figure 5 (a) Simulated points. (b) Principal components (PCs). (c) Density levels on PCs. (d) Constructing EDS. (e) EDS on PCs. (f) EDS on original data.
We simulate time series for capital and productivity level of ![]() periods, and we select a sample of
periods, and we select a sample of ![]() observations by taking each
observations by taking each ![]() th point (to make the draws independent); see Figure 5a. We orthogonalize the data using PC transformation and we normalize the PCs to a unit variance; see Figure 5b. We estimate the density function using the multivariate kernel algorithm with the standard bandwidth of
th point (to make the draws independent); see Figure 5a. We orthogonalize the data using PC transformation and we normalize the PCs to a unit variance; see Figure 5b. We estimate the density function using the multivariate kernel algorithm with the standard bandwidth of ![]() , and we remove from the sample
, and we remove from the sample ![]() of simulated points in which the density was lowest; see Figure 5c. We construct an EDS; see Figure 5d. We plot such a set in the PC and original coordinates in Figure 5e and f, respectively. The constructed EDS appears to be evenly spaced.
of simulated points in which the density was lowest; see Figure 5c. We construct an EDS; see Figure 5d. We plot such a set in the PC and original coordinates in Figure 5e and f, respectively. The constructed EDS appears to be evenly spaced.
More details about the EDS sets and their applications for solving dynamic economic models are given in Judd et al. (2012); in particular, this paper establishes the dispersion, cardinality, and degree of uniformity of the EDS grid. Also, Judd et al. (2012) perform the worst-case analysis and relate the results to recent mathematical literature on covering problems (see Temlyakov, 2011) and random sequential packing problems (see Baryshnikov et al., 2008). Judd et al. (2012) use the EDS algorithm to compute accurate quadratic solutions to a multicountry neoclassical growth model with up to 80 state variables, as well as to solve a large-scale new Keynesian model with a zero lower bound on nominal interest rates.
4.3.3 Other Grids on the Ergodic Set
We have described just one specific procedure for forming a discrete approximation to the essentially ergodic set of an economic model. Below, we outline other techniques that can be used for this purpose.
First, the two-step procedure outlined above has a complexity of order ![]() because the kernel algorithm computes pairwise distances between all observations in the sample. This is not a problem for the size of applications we study in this chapter; however, it is expensive for large samples. Judd et al. (2012) describe an alternative procedure that has a lower complexity of
because the kernel algorithm computes pairwise distances between all observations in the sample. This is not a problem for the size of applications we study in this chapter; however, it is expensive for large samples. Judd et al. (2012) describe an alternative procedure that has a lower complexity of ![]() . The complexity is reduced by inverting the steps in the two-step procedure: first an EDS is constructed on all simulated points, and then the points in which the density is low are removed.
. The complexity is reduced by inverting the steps in the two-step procedure: first an EDS is constructed on all simulated points, and then the points in which the density is low are removed.
Second, one can use methods from cluster analysis to select a set of representative points from a given set of simulated points (instead of constructing an EDS set). We partition the simulated data into clusters (groups of closely located points) and we replace each cluster with one representative point. Examples of cluster grids are shown in Figure 6. The clustering techniques are demonstrated in Judd et al. (2012a) using two clustering methods: an agglomerative hierarchical and a K-means method. Such techniques were used to produce all the results in Judd et al. (2010, 2011d) and were found to lead to highly accurate solutions. However, the cost of constructing cluster grids is higher than that of EDS grids. Judd et al. (2011d) and Aruoba and Schorfheide (2012) use clustering techniques to solve a new Keynesian model with a zero lower bound on nominal interest rates.
4.3.4 Numerical Illustration of the Accuracy of the Smolyak Method
Judd et al. (2012) compare the accuracy of solutions under the conventional Smolyak grid and EDS grids in the one-agent model with inelastic labor supply parameterized by (18). To make the results comparable, Judd et al. (2012) construct an EDS grid with the same target number of points (namely, 13) as in the Smolyak grid and use ordinary polynomials up to degree three under both the Smolyak and EDS grids. The accuracy is evaluated on two sets of points: one is a stochastic simulation of 10,000 points and the other is a set of ![]() points that are uniformly spaced on the same solution domain as the one used by the Smolyak method. The results are shown in Table 8.
points that are uniformly spaced on the same solution domain as the one used by the Smolyak method. The results are shown in Table 8.
Table 8
Smolyak grid versus EDS grid in the one-agent model.a
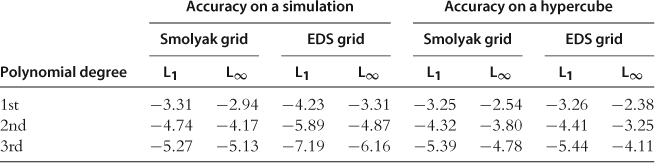
aNotes: ![]() and
and ![]() are, respectively, the average and maximum of absolute residuals across optimality condition and test points (in log10 units) on a stochastic simulation of 10,000 observations. The results are reproduced from Judd et al. (2012a), Table 2.
are, respectively, the average and maximum of absolute residuals across optimality condition and test points (in log10 units) on a stochastic simulation of 10,000 observations. The results are reproduced from Judd et al. (2012a), Table 2.
The accuracy ranking depends critically on the choice of points in which the accuracy is evaluated. The EDS method is significantly more accurate than the Smolyak method when the accuracy is evaluated on a stochastic simulation. This is because under an adaptive domain, we fit a polynomial function directly in an essentially ergodic set; while under the conventional hypercube grid, we fit a polynomial function in a larger hypercube domain and face a trade-off between the fit inside and outside the essentially ergodic set.
Nevertheless, the Smolyak method produces smaller maximum residuals than the EDS method when the accuracy is evaluated on a deterministic hypercube domain. This is because the EDS method is designed to be accurate in the ergodic set (simulated points), and its accuracy decreases away from the ergodic set while the conventional Smolyak (1963) method produces solutions that are uniformly accurate on a larger hypercube domain.
5 Approximation of Integrals
We study a class of methods that approximates multidimensional integrals by a weighted sum of integrands, i.e.,
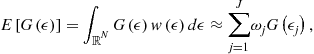 (60)
(60)
where ![]() is a vector of uncorrelated variables;
is a vector of uncorrelated variables; ![]() is a continuous bounded function;
is a continuous bounded function; ![]() is a density function normalized by
is a density function normalized by ![]() is a set of nodes; and
is a set of nodes; and ![]() is a set of weights normalized by
is a set of weights normalized by ![]() .
.
We restrict attention to the case of random variables that are normally distributed with zero mean and unit standard deviation, i.e., ![]() , where
, where ![]() is a vector of zeros and
is a vector of zeros and ![]() is an identity matrix; and
is an identity matrix; and ![]() is a density function of a multivariate normal distribution. However, our analysis is easy to extend to other random processes.
is a density function of a multivariate normal distribution. However, our analysis is easy to extend to other random processes.
Typically, there is a trade-off between accuracy and cost of integration methods: having more nodes leads to a more accurate approximation of integrals but is also more expensive. Hence, we describe several alternative integration methods that differ in accuracy and cost. While we describe the integration rules for the case of uncorrelated variables, at the end of the section we show how all the results can be generalized for the case of correlated variables using a Cholesky decomposition.
5.1 Gauss-Hermite Product Quadrature Rules
The Gauss-Hermite quadrature method provides a set of integration nodes ![]() and weights
and weights ![]() for approximation of a unidimensional version of integral (60),
for approximation of a unidimensional version of integral (60),
 (61)
(61)
In Section 3, we show nodes and weights for one-, two-, and three-node Gauss-Hermite quadrature methods.
We can extend the unidimensional Gauss-Hermite quadrature rule to the multidimensional quadrature rule by way of a tensor-product rule:
 (62)
(62)
where ![]() and
and ![]() are, respectively, weights and nodes in a dimension
are, respectively, weights and nodes in a dimension ![]() derived from the unidimensional Gauss-Hermite quadrature rule (note that, in general, the number of nodes in one dimension,
derived from the unidimensional Gauss-Hermite quadrature rule (note that, in general, the number of nodes in one dimension, ![]() , can differ across dimensions). The total number of nodes is given by the product
, can differ across dimensions). The total number of nodes is given by the product ![]() . The total number of nodes grows exponentially with the dimensionality
. The total number of nodes grows exponentially with the dimensionality ![]() ; under the assumption that
; under the assumption that ![]() for all dimensions, the total number of nodes is
for all dimensions, the total number of nodes is ![]() .
.
Consider a two-node Gauss-Hermite quadrature rule for a model with two shocks; then we have ![]() ; see Figure 7a.
; see Figure 7a.
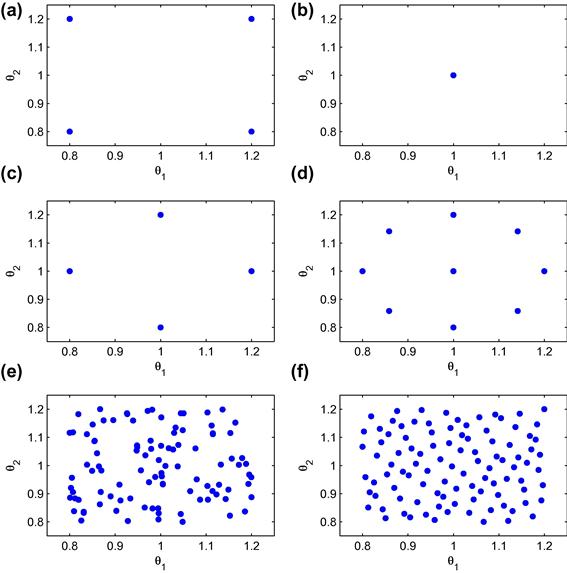
Figure 7 (a) Quadrature rule Q(2). (b) Quadrature rule Q(1). (c) Monomial rule M1. (d) Monomial rule M2. (e) Monte Carlo draws. (f) Sobol grid.
Under a ![]() -node Gauss-Hermite product rule, the number of nodes grows rapidly with the number of exogenous random variables,
-node Gauss-Hermite product rule, the number of nodes grows rapidly with the number of exogenous random variables, ![]() . Even if there are just two nodes for each random variable, the total number of nodes is prohibitively large for large
. Even if there are just two nodes for each random variable, the total number of nodes is prohibitively large for large ![]() ; for example, if
; for example, if ![]() , we have
, we have ![]() nodes. This makes product rules impractical for high-dimensional applications.
nodes. This makes product rules impractical for high-dimensional applications.
There is a specific case of Gauss-Hermite quadrature rule, a one-node quadrature rule ![]() , which is the cheapest possible deterministic integration method; see Figure 7b.
, which is the cheapest possible deterministic integration method; see Figure 7b.
This rule has just one node independently of the number of shocks ![]() . In the context of one- and multicountry growth models, Maliar et al. (2011) find that this simple rule leads to just a slightly lower accuracy of solutions than the most accurate deterministic methods.
. In the context of one- and multicountry growth models, Maliar et al. (2011) find that this simple rule leads to just a slightly lower accuracy of solutions than the most accurate deterministic methods.
5.2 Monomial Rules
Monomial integration rules are nonproduct: they construct a relatively small set of nodes distributed in some way within a multidimensional hypercube. The computational expense of monomial rules grows only polynomially with the dimensionality of the problem, which makes them feasible for problems with large dimensionality. Monomial rules are introduced to economic literature in Judd (1998). Monomial formulas are used for approximating integrals by all global methods focusing on large-scale applications, e.g., Judd et al. (2010, 2011a,b, 2012), Malin et al. (2011), Maliar et al. (2011), and Pichler (2011). The last paper also uses monomial rules for constructing a grid of points for finding a solution. Finally, Juillard and Villemot (2011) use monomial formulas for implementing the accuracy checks.
5.2.1 Monomial Rule 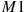 with
with 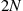 Nodes
Nodes
Consider the following simple example of the monomial rule with ![]() nodes which we denote
nodes which we denote ![]() :
:
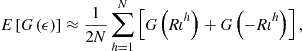 (63)
(63)
where ![]() and
and ![]() , and
, and ![]() is a vector whose
is a vector whose ![]() th element is equal to one and the remaining elements are equal to zero, i.e.,
th element is equal to one and the remaining elements are equal to zero, i.e., ![]() .
.
![]() constructs nodes by considering deviations of each random variable holding the other random variables fixed to their expected values. Let us illustrate this rule with a two-dimensional example.
constructs nodes by considering deviations of each random variable holding the other random variables fixed to their expected values. Let us illustrate this rule with a two-dimensional example.
The integration nodes produced by this monomial rule are shown in Figure 7c. Since the cost of ![]() increases with
increases with ![]() only linearly, this rule is feasible for the approximation of integrals with very large dimensionality. For example, with
only linearly, this rule is feasible for the approximation of integrals with very large dimensionality. For example, with ![]() , the total number of nodes is just
, the total number of nodes is just ![]() .
.
5.2.2 Monomial Rule 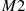 with
with 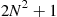 Nodes
Nodes
Many other monomial rules are available in the mathematical literature; see Stroud (1971), pp. 315–329, and Judd (1998), p. 275, for a discussion. Below, we show a monomial rule with ![]() nodes, denoted by
nodes, denoted by ![]() ,
,
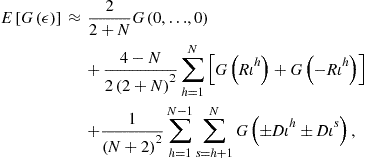 (64)
(64)
where ![]() and
and ![]() . A two-dimensional example of this rule is illustrated in the example below.
. A two-dimensional example of this rule is illustrated in the example below.
The cost of ![]() grows quadratically with
grows quadratically with ![]() but it is still feasible with high dimension. For example, with
but it is still feasible with high dimension. For example, with ![]() , the total number of nodes is just
, the total number of nodes is just ![]() , which is still manageable.
, which is still manageable.
5.3 Monte Carlo Integration Method
A ![]() -node Monte Carlo integration method, denoted by
-node Monte Carlo integration method, denoted by ![]() , draws
, draws ![]() shocks,
shocks, ![]() and approximates the integral by the average of the integrand’s values across the shocks
and approximates the integral by the average of the integrand’s values across the shocks
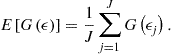 (65)
(65)
See Figure 7e for a Monte Carlo method with 100 realizations. A one-node version of the Monte Carlo integration method is used in Marcet’s (1988) PEA (namely, the future expectation of a random variable is approximated by one realization of the variable). As we argued in Section 3, this method is inaccurate and limits the overall accuracy of solutions produced by numerical solution methods.
5.4 Quasi-Monte Carlo Integration Methods
Quasi-Monte Carlo methods construct a set of nodes that are uniformly spaced in a given area of the state space. Normally, the nodes are constructed in a multidimensional hypercube. It is possible to construct a uniformly spaced set of nodes in a hypercube using a tensor-product grid of unidimensional uniformly spaced nodes, but this technique is subject to the curse of dimensionality. Quasi-Monte Carlo methods construct a uniformly spaced grid of nodes using nonproduct techniques. The number of grid points is controlled by a researcher. The accuracy of quasi-Monte Carlo methods is generally higher than that of Monte Carlo methods. Applications of quasi-Monte Carlo sequences to solving dynamic economic models are studied in Rust (1997); see also Geweke (1996) for a discussion.
Our presentation relies on the standard notion of uniformity in the literature, which is the discrepancy of a given set of points from the uniformly distributed set of points; see Niederreiter (1992), p. 14. Let ![]() be a set consisting of points
be a set consisting of points ![]() , and let
, and let ![]() be a family of Lebesgue-measurable subsets of
be a family of Lebesgue-measurable subsets of ![]() . The discrepancy of
. The discrepancy of ![]() under
under ![]() is given by
is given by ![]() , where
, where ![]() counts the number of points from
counts the number of points from ![]() in
in ![]() , and
, and ![]() is a Lebesgue measure of
is a Lebesgue measure of ![]() . Thus,
. Thus, ![]() measures the discrepancy between the fraction of points
measures the discrepancy between the fraction of points ![]() contained in
contained in ![]() and the fraction of space
and the fraction of space ![]() occupied by
occupied by ![]() . If the discrepancy is low,
. If the discrepancy is low, ![]() , the distribution of points in
, the distribution of points in ![]() is close to uniform.
is close to uniform.
The measure of discrepancy commonly used in the literature is the star discrepancy. The star discrepancy ![]() is defined as the discrepancy of
is defined as the discrepancy of ![]() over the family
over the family ![]() generated by the intersection of all subintervals of
generated by the intersection of all subintervals of ![]() of the form
of the form ![]() , where
, where ![]() . Let
. Let ![]() be a sequence of elements on
be a sequence of elements on ![]() , and let
, and let ![]() be the first
be the first ![]() terms of
terms of ![]() . Niederreiter (1992), p. 32, suggests calling a sequence
. Niederreiter (1992), p. 32, suggests calling a sequence ![]() low discrepancy if
low discrepancy if ![]() , i.e., if the star discrepancy converges to zero asymptotically at a rate at least of order
, i.e., if the star discrepancy converges to zero asymptotically at a rate at least of order ![]() .
.
The star discrepancy of points which are randomly drawn from a uniform distribution ![]() also converges to zero asymptotically,
also converges to zero asymptotically, ![]() , a.e. but its rate of convergence
, a.e. but its rate of convergence ![]() is far lower than that of low-discrepancy sequences. This rate of convergence follows directly from the law of iterated logarithm by Kiefer (1961); see Niederreiter (1992), pp. 166–168, for a general discussion on how to use Kiefer’s (1961) results for assessing the discrepancy of random sequences.
is far lower than that of low-discrepancy sequences. This rate of convergence follows directly from the law of iterated logarithm by Kiefer (1961); see Niederreiter (1992), pp. 166–168, for a general discussion on how to use Kiefer’s (1961) results for assessing the discrepancy of random sequences.
The simplest example of a sequence, equidistributed on ![]() , is a Weyl sequence
, is a Weyl sequence ![]() , where
, where ![]() is irrational and
is irrational and ![]() is a fractional part of
is a fractional part of ![]() . For example, let
. For example, let ![]() . Then, we have
. Then, we have ![]() , etc. This sequence can be generalized to a
, etc. This sequence can be generalized to a ![]() -dimensional case using
-dimensional case using ![]() distinct and linearly independent irrational numbers
distinct and linearly independent irrational numbers ![]() ; this yields a sequence
; this yields a sequence ![]() whose points are equidistributed over the
whose points are equidistributed over the ![]() . There is a variety of other low-discrepancy sequences in the literature including Haber, Baker, Niederreiter, and Sobol sequences; see Niederreiter (1992) for a review. As an example, we draw a two-dimensional Sobol sequence with 100 points; see Figure 7f. Thus, to perform integration, we use a low-discrepancy sequence in the same way as we use a number of Monte Carlo random draws.
. There is a variety of other low-discrepancy sequences in the literature including Haber, Baker, Niederreiter, and Sobol sequences; see Niederreiter (1992) for a review. As an example, we draw a two-dimensional Sobol sequence with 100 points; see Figure 7f. Thus, to perform integration, we use a low-discrepancy sequence in the same way as we use a number of Monte Carlo random draws.
5.5 Nonparametric Kernel-Density Methods
Suppose we observe a set of data ![]() , and we must compute the conditional expectation function
, and we must compute the conditional expectation function ![]() , for some
, for some ![]() . A general class of nonparametric estimators can be written as
. A general class of nonparametric estimators can be written as
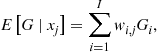 (66)
(66)
where ![]() is a weight function that satisfies
is a weight function that satisfies ![]() and
and ![]() , with
, with ![]() being a distance between points
being a distance between points ![]() and
and ![]() . In other words, expectation
. In other words, expectation ![]() is given by a weighted sum of all observations in the sample, and a weight
is given by a weighted sum of all observations in the sample, and a weight ![]() placed on each observation
placed on each observation ![]() depends on how far this particular observation is from observation
depends on how far this particular observation is from observation ![]() in which the expectation is evaluated. Nadaraya (1964) and Watson (1964) propose to construct the weights using the multivariate normal kernel
in which the expectation is evaluated. Nadaraya (1964) and Watson (1964) propose to construct the weights using the multivariate normal kernel
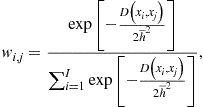 (67)
(67)
where ![]() is a parameter which effectively represents the width of the interval in which the expectation is estimated. There are many other alternatives for the weight function in the literature on nonparametric estimation; see Pagan and Ullah (1999). The difficult problem in statistics is to choose the width parameter
is a parameter which effectively represents the width of the interval in which the expectation is estimated. There are many other alternatives for the weight function in the literature on nonparametric estimation; see Pagan and Ullah (1999). The difficult problem in statistics is to choose the width parameter ![]() . There are two procedures in the literature for identifying this parameter, namely, cross-validation and plug-in. Typically, an iterative procedure is used: assume some
. There are two procedures in the literature for identifying this parameter, namely, cross-validation and plug-in. Typically, an iterative procedure is used: assume some ![]() , compute the expectation function, and check
, compute the expectation function, and check ![]() by using some criterion; and iterate until a fixed point
by using some criterion; and iterate until a fixed point ![]() is obtained. A recent example of application of nonparametric methods for solving dynamic economic models is Jirnyi and Lepetyuk (2011).
is obtained. A recent example of application of nonparametric methods for solving dynamic economic models is Jirnyi and Lepetyuk (2011).
5.6 Approximating a Markov Process Using a Markov Chain
There are other combinations of techniques of potential interest that are not described above. For example, Tauchen (1986) shows how to accurately approximate unidimensional integrals by discretizing an autoregressive process into a finite-state Markov chain; and Tauchen and Hussey (1991) generalize their analysis to multidimensional cases. Such a discretization can be performed using nonproduct rules that are tractable in high-dimensional applications. This discretization method can be combined with other computational techniques surveyed in the present chapter to construct numerical solution methods that are tractable in high-dimensional applications.
5.7 Correlated Shocks and Cholesky Decomposition
We finally show how to extend the described integration methods to the case when the shocks are correlated. To be specific, we evaluate a multidimensional integral of the form
![]() (68)
(68)
where ![]() follows a multivariate normal distribution,
follows a multivariate normal distribution, ![]() , with
, with ![]() being a vector of means and
being a vector of means and ![]() being a variance-covariance matrix, and
being a variance-covariance matrix, and ![]() is a density function of the multivariate Normal distribution,
is a density function of the multivariate Normal distribution,
![]() (69)
(69)
with ![]() denoting the determinant of
denoting the determinant of ![]() .
.
If random variables ![]() are correlated, we must rewrite the integral in terms of uncorrelated variables prior to numerical integration. Given that
are correlated, we must rewrite the integral in terms of uncorrelated variables prior to numerical integration. Given that ![]() is symmetric and positive-definite, it has a Cholesky decomposition,
is symmetric and positive-definite, it has a Cholesky decomposition, ![]() , where
, where ![]() is a lower triangular matrix with strictly positive diagonal entries. The Cholesky decomposition of
is a lower triangular matrix with strictly positive diagonal entries. The Cholesky decomposition of ![]() allows us to transform correlated variables
allows us to transform correlated variables ![]() into uncorrelated
into uncorrelated ![]() with the following linear change of variables:
with the following linear change of variables:
![]() (70)
(70)
Note that ![]() . Using (70) and taking into account that
. Using (70) and taking into account that ![]() and that
and that ![]() , we obtain
, we obtain
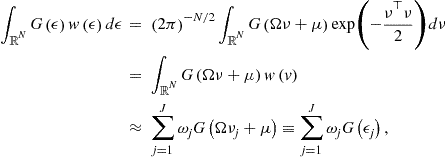 (71)
(71)
where ![]() , with
, with ![]() . Comparing (60) and (71) shows that with correlated shocks, we can use the same formula as with uncorrelated normalized shocks with the only modification that instead of a node implied by a given integration rule we use a transformed node
. Comparing (60) and (71) shows that with correlated shocks, we can use the same formula as with uncorrelated normalized shocks with the only modification that instead of a node implied by a given integration rule we use a transformed node ![]() , where
, where ![]() is a node for uncorrelated shocks.
is a node for uncorrelated shocks.
5.8 Numerical Illustration of the Importance of the Integration Method
We compare the simulation-based and nonparametric methods with the parametric ones. As we will see, the performance of simulation-based integration is poor, and the performance of the nonparametric integration methods is even poorer. The reason is that we disregard information about the true density function by replacing it with the estimated (noisy) density function. Econometricians use the estimated density function because the true one is not available. However, in economic models we define the process for shocks and we do know density functions. We can do much better by using deterministic (quadrature and monomial) rules rather than simulation-based methods. We provide an illustration below.
5.8.1 Monte Carlo Integration
The Monte Carlo integration method is feasible in high-dimensional applications (because we control the number of draws) but its accuracy is generally far lower than that of the deterministic integration methods. Judd et al. (2011b) study a version of the one-agent model with inelastic labor supply under assumption (18). They assess the performance of GSSA based on the Monte Carlo method, ![]() , with
, with ![]() and
and ![]() random nodes in each simulated point and, the Gauss-Hermite quadrature method,
random nodes in each simulated point and, the Gauss-Hermite quadrature method, ![]() , with
, with ![]() and
and ![]() deterministic nodes. The results are provided in Table 9. Under Monte Carlo integration, high-degree polynomials do not necessarily lead to more accurate solutions than low-degree polynomials because the overall accuracy is dominated by errors produced by an integration method. Surprisingly, a one-node Gauss-Hermite quadrature method,
deterministic nodes. The results are provided in Table 9. Under Monte Carlo integration, high-degree polynomials do not necessarily lead to more accurate solutions than low-degree polynomials because the overall accuracy is dominated by errors produced by an integration method. Surprisingly, a one-node Gauss-Hermite quadrature method, ![]() , leads to more accurate solutions than a 2,000-node Monte Carlo method
, leads to more accurate solutions than a 2,000-node Monte Carlo method ![]() . A two-node Gauss-Hermite quadrature method,
. A two-node Gauss-Hermite quadrature method, ![]() , produces very accurate solutions with the residuals of order
, produces very accurate solutions with the residuals of order ![]() . Increasing the number of quadrature nodes does not visibly improve the accuracy. Monomial integration rules deliver the same (high) accuracy levels as the quadrature rules; see Judd et al. (2011b) for more details.
. Increasing the number of quadrature nodes does not visibly improve the accuracy. Monomial integration rules deliver the same (high) accuracy levels as the quadrature rules; see Judd et al. (2011b) for more details.
Table 9
Monte Carlo integration and quadrature integration in the one-agent model.a
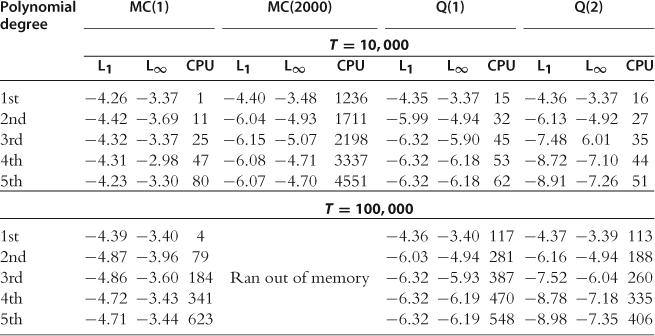
aNotes: ![]() and
and ![]() are, respectively, the average and maximum of absolute residuals across optimality conditions and test points (in log10 units). CPU is the time necessary for computing a solution (in seconds). T is the simulation length.
are, respectively, the average and maximum of absolute residuals across optimality conditions and test points (in log10 units). CPU is the time necessary for computing a solution (in seconds). T is the simulation length. ![]() and
and ![]() denote a
denote a ![]() -node Monte Carlo and quadrature integration methods, respectively. These results are reproduced from Judd et al. (2011b), Table 2.
-node Monte Carlo and quadrature integration methods, respectively. These results are reproduced from Judd et al. (2011b), Table 2.
The above results illustrate a slow ![]() rate of convergence of the Monte Carlo method. To achieve high accuracy of solutions under the Monte Carlo method, we must increase the sample size by many orders of magnitude, which is infeasible in practice.
rate of convergence of the Monte Carlo method. To achieve high accuracy of solutions under the Monte Carlo method, we must increase the sample size by many orders of magnitude, which is infeasible in practice.
5.8.2 Nonparametric Kernel-Density Integration Method
It might be tempting to solve for decision functions using a fully nonparametric solution method. The advantage of this approach is that we do not need to make any assumptions about a functional form for decision functions. Instead, we just simulate the model, compute the expectation using the simulated data, and let the model itself choose what is the best possible approximation. Unfortunately, such nonparametric methods are not competitive in the studied applications due to their high computational expense and low rate of convergence (equivalently, low accuracy).
As an illustration, we assess the performance of a nonparametric kernel-density method in the context of the model with inelastic labor supply under the assumptions (18). To give the best chance to the nonparametric method, we choose the width parameter, ![]() , optimally, namely, we compute an accurate parametric solution, and we find the value of
, optimally, namely, we compute an accurate parametric solution, and we find the value of ![]() for which conditional expectations delivered by the parametric and nonparametric methods are as close as possible on a set of the simulated points considered (this technique is not feasible in statistics where the true expectation function is unknown). We find the solutions under
for which conditional expectations delivered by the parametric and nonparametric methods are as close as possible on a set of the simulated points considered (this technique is not feasible in statistics where the true expectation function is unknown). We find the solutions under ![]() , and
, and ![]() . The solution procedure is expensive since we have to find an expectation in each simulation point by averaging up all simulated points. Furthermore, there is no natural way to assess the accuracy of nonparametric solutions. We therefore take a time-series solution delivered by the nonparametric method, regress it on an ordinary polynomial function of degrees from one to five, and use the resulting parametric function to run accuracy checks. The results are shown in Table 10. As we see, the performance of the nonparametric integration method is poor. The running time is large and increases rapidly with the simulation length. Under
. The solution procedure is expensive since we have to find an expectation in each simulation point by averaging up all simulated points. Furthermore, there is no natural way to assess the accuracy of nonparametric solutions. We therefore take a time-series solution delivered by the nonparametric method, regress it on an ordinary polynomial function of degrees from one to five, and use the resulting parametric function to run accuracy checks. The results are shown in Table 10. As we see, the performance of the nonparametric integration method is poor. The running time is large and increases rapidly with the simulation length. Under ![]() and
and ![]() , the accuracy is so low that the solution is numerically unstable in simulation. Under
, the accuracy is so low that the solution is numerically unstable in simulation. Under ![]() , the numerical stability is achieved but the accuracy is still very low compared to parametric solutions reported in Table 9.
, the numerical stability is achieved but the accuracy is still very low compared to parametric solutions reported in Table 9.
Table 10
Nonparametric kernel-density integration method.a
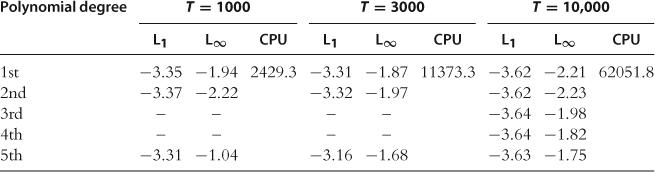
aNotes: ![]() and
and ![]() are, respectively, the average and maximum of absolute approximation errors across optimality conditions and test points (in log10 units). CPU is the time necessary for computing a solution (in seconds). T is the sample size.
are, respectively, the average and maximum of absolute approximation errors across optimality conditions and test points (in log10 units). CPU is the time necessary for computing a solution (in seconds). T is the sample size.
The rate of convergence of the Nadaraya-Watson method we use is always slower than that of the Monte Carlo method and decreases with the number of random variables with respect to which the expectation is evaluated. When there are ![]() random variables and
random variables and ![]() simulated points, and when we use the same value of width
simulated points, and when we use the same value of width ![]() for all random variables, the convergence rate is of the order
for all random variables, the convergence rate is of the order ![]() ; see Bierens (1994), Theorem 10.2.2. For our example,
; see Bierens (1994), Theorem 10.2.2. For our example, ![]() and hence, the convergence rate is of the order
and hence, the convergence rate is of the order ![]() . There are other nonparametric estimators, e.g., local linear regressions, but their convergence properties are also poor.
. There are other nonparametric estimators, e.g., local linear regressions, but their convergence properties are also poor.
6 Derivative-Free Optimization Methods
In this section, we focus on solving systems of nonlinear equations that arise in the context of the Euler equation methods. Our main tool is a simple derivative-free fixed-point iteration (FPI) method. Assume that we need to solve an equation ![]() (any equation can be represented in this form). We implement the following iterative procedure.
(any equation can be represented in this form). We implement the following iterative procedure.

FPI has two advantages over Newton-style methods. First, FPI does not require us to compute derivatives (such as Jacobian or Hessian); as a result, its cost does not increase considerably with the dimensionality of the problem. Second, FPI can iterate on any object ![]() at once (variable, vector of variables, matrix, time series, vector of coefficients, etc.), while Newton-style methods compute a solution point-by-point and are more difficult to vectorize or parallelize.
at once (variable, vector of variables, matrix, time series, vector of coefficients, etc.), while Newton-style methods compute a solution point-by-point and are more difficult to vectorize or parallelize.
The drawback of the FPI method is that it may fail to converge. However, damping can often help us to achieve the convergence. Instead of a full updating at the end of the iteration ![]() , we use a partial updating
, we use a partial updating ![]() for some
for some ![]() . By varying a damping parameter
. By varying a damping parameter ![]() , we can control how much
, we can control how much ![]() changes from one iteration to another and avoid explosive paths. FPI with damping systematically converged in all our numerical experiments. Note that we need to adjust the convergence criterion
changes from one iteration to another and avoid explosive paths. FPI with damping systematically converged in all our numerical experiments. Note that we need to adjust the convergence criterion ![]() to the damping parameter
to the damping parameter ![]() , for example, by replacing
, for example, by replacing ![]() with
with ![]() ; otherwise, the convergence will critically depend on the value of
; otherwise, the convergence will critically depend on the value of ![]() assumed and can be trivially achieved by using a very small value of
assumed and can be trivially achieved by using a very small value of ![]() . In the remainder of the section, we illustrate the applications of FPI by way of examples.
. In the remainder of the section, we illustrate the applications of FPI by way of examples.
6.1 Separation of Intertemporal and Intratemporal Choices
Equilibrium conditions of dynamic economic models are not symmetric in a sense that some of them contain only current variables (known at ![]() ), while the others contain both current and future variables (unknown at
), while the others contain both current and future variables (unknown at ![]() ); we refer to these two groups of conditions as the intratemporal and intertemporal choice conditions, respectively. Maliar et al. (2011) show how to exploit this asymmetry of the equilibrium conditions to solve for equilibrium more efficiently. Specifically, they find solutions to the intertemporal choice conditions in terms of state contingent functions; however, they find solutions to the intratemporal choice conditions in terms of equilibrium quantities. Below, we show how this construction can be implemented in the context of model (1)–(3).
); we refer to these two groups of conditions as the intratemporal and intertemporal choice conditions, respectively. Maliar et al. (2011) show how to exploit this asymmetry of the equilibrium conditions to solve for equilibrium more efficiently. Specifically, they find solutions to the intertemporal choice conditions in terms of state contingent functions; however, they find solutions to the intratemporal choice conditions in terms of equilibrium quantities. Below, we show how this construction can be implemented in the context of model (1)–(3).
6.1.1 Intratemporal Choice FOCs
Let us collect the intratemporal choice conditions of problem (1)–(3) that contain only the variables known at time ![]() :
:
![]() (72)
(72)
![]() (73)
(73)
The above system contains five variables, namely, ![]() ,
, ![]() . We can solve it with respect to two variables if the remaining three variables are fixed. In the benchmark case, we fix
. We can solve it with respect to two variables if the remaining three variables are fixed. In the benchmark case, we fix ![]() and
and ![]() , and we solve for
, and we solve for ![]() .
.
6.1.2 Intertemporal Choice FOCs
The FOC of problem (1)–(3) with respect to capital contains both current and future variables
![]() (74)
(74)
Note that (74) cannot be treated in the same way as (72), (73). In particular, fixing ![]() is not sufficient for computing
is not sufficient for computing ![]() from (74). We need a method that allows us to infer the values of future variables
from (74). We need a method that allows us to infer the values of future variables ![]() in all possible future economy’s states
in all possible future economy’s states ![]() .
.
To find a solution to the intertemporal choice conditions, we use a Markov structure of the decision functions, namely, we parameterize ![]() with a flexible functional form
with a flexible functional form ![]() , and we solve for a coefficient vector
, and we solve for a coefficient vector ![]() that approximately satisfies (74).
that approximately satisfies (74).
6.1.3 A Global Euler Equation Method with a Separation of Intertemporal and Intratemporal Choices
We now outline a global Euler equation method that finds a solution to (1)–(3) by separating the intertemporal and intratemporal choice conditions.

The inner and outer loops in the algorithm correspond to the intratemporal and intertemporal planner’s choice, respectively. Note that planner has to solve for the intratemporal choice ![]() times, one time at present and
times, one time at present and ![]() times in all possible future states (integration nodes). The problems solved at Step 3a and 3b are identical. We next discuss how to find a solution to the intratemporal and intertemporal choice conditions in more detail.
times in all possible future states (integration nodes). The problems solved at Step 3a and 3b are identical. We next discuss how to find a solution to the intratemporal and intertemporal choice conditions in more detail.
6.2 The Intratemporal Choice Quantities
Consider system (72), (73) under utility and production function parameterizations in (17),
![]() (75)
(75)
![]() (76)
(76)
This system has a small number of equations, and, in principle, Newton solvers can be used to solve for ![]() and
and ![]() in terms of
in terms of ![]() . However, we must solve this system a large number of times, namely, for each value of
. However, we must solve this system a large number of times, namely, for each value of ![]() on the grid, and for
on the grid, and for ![]() future states
future states ![]() corresponding to each grid point, i.e.,
corresponding to each grid point, i.e., ![]() times in total for every iteration on the outer loop. The cost of solving this system repeatedly can be large, especially in high-dimensional problems.
times in total for every iteration on the outer loop. The cost of solving this system repeatedly can be large, especially in high-dimensional problems.
Maliar et al. (2011) develop a derivative-free solver called iteration-on-allocation. This method solves a system of nonlinear equations by performing FPI on the intratemporal choice variables in line with Gauss-Jacobi and Gauss-Siedel iteration schemes; see Judd (1998) for a detailed description of these schemes. Below, we illustrate iteration-on-allocation in the context of system (75), (76).
Therefore, we apply iteration-on-allocation ![]() times to system (77), (78). Namely, we solve for quantities
times to system (77), (78). Namely, we solve for quantities ![]() given
given ![]() in all grid points, and we solve for quantities
in all grid points, and we solve for quantities ![]() given
given ![]() for all
for all ![]() .
.
The iteration-on-allocation method has the following valuable feature: it delivers exact solutions to the intratemporal choice condition both at present and future (up to a given degree of precision). The residuals in the intratemporal choice conditions are all zeros by construction, and the only condition that has nonzero residuals is the Euler equation (74).
The iteration-on-allocation method is used by Maliar et al. (2011) to compute the intratemporal choice in the context of the JEDC comparison analysis. A high accuracy of iteration-on-allocation gives an important advantage in accuracy to the stochastic simulation and cluster grid algorithms of Maliar et al. (2011) over the other methods participating in the JEDC comparison analysis; see Kollmann et al. (2011b). Those other methods approximate some of the intratemporal choice variables in terms of state contingent functions and face large residuals in some intratemporal choice conditions which dominate the overall accuracy of solutions.
Finally, let us mention that many different implementations of the iteration-on-allocation method are possible. First, in Eq. (78), we can use consumption obtained in the previous iteration, ![]() , instead of consumption obtained in the current iteration,
, instead of consumption obtained in the current iteration, ![]() (this is the difference between the Gauss-Jacobi and Gauss-Siedel iterative schemes). Second, we can switch the order of equations, as well as change the way in which we express the variables from the equations. For example, we can express labor from the first equation (75), and we can express consumption from the second equation (76). A specific implementation can affect the numerical stability and speed of convergence of the iteration-on-allocation method.
(this is the difference between the Gauss-Jacobi and Gauss-Siedel iterative schemes). Second, we can switch the order of equations, as well as change the way in which we express the variables from the equations. For example, we can express labor from the first equation (75), and we can express consumption from the second equation (76). A specific implementation can affect the numerical stability and speed of convergence of the iteration-on-allocation method.
6.3 The Intertemporal Choice Functions
Consider Euler equation (74) on a grid of points ![]() ,
,
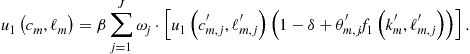 (79)
(79)
In the outer loop, we must find a vector of parameters ![]() such that (79) is satisfied either exactly (collocation methods) or approximately (weighted residuals methods) on a given grid of points. Again, this is possible to do using Newton-style solvers; see, e.g., Judd (1992) and Gaspar and Judd (1997). To be specific, we fix some
such that (79) is satisfied either exactly (collocation methods) or approximately (weighted residuals methods) on a given grid of points. Again, this is possible to do using Newton-style solvers; see, e.g., Judd (1992) and Gaspar and Judd (1997). To be specific, we fix some ![]() , compute
, compute ![]() and
and ![]() , solve for
, solve for ![]() and
and ![]() from the intratemporal choice conditions, and substitute the results in the Euler equation (79) to evaluate the residuals. We subsequently perform iterations on
from the intratemporal choice conditions, and substitute the results in the Euler equation (79) to evaluate the residuals. We subsequently perform iterations on ![]() until the residuals are minimized. However, this procedure is expensive when the number of coefficients in
until the residuals are minimized. However, this procedure is expensive when the number of coefficients in ![]() is large. For problems with high dimensionality, our preferred method is again FPI.
is large. For problems with high dimensionality, our preferred method is again FPI.
In the true solution, we have a fixed-point property ![]() , and these two variables cancel out, making equations (79) and (80) to be equivalent. However, in the iterative process, we have
, and these two variables cancel out, making equations (79) and (80) to be equivalent. However, in the iterative process, we have ![]() , and the difference between those quantities guides us in the process of convergence to the true solution.
, and the difference between those quantities guides us in the process of convergence to the true solution.
We can use different FPI representations of the Euler equation to parameterize decision functions of other variables; for example, we can parameterize the consumption decision function by premultiplying the left and right sides of Euler equation (74) by ![]() and
and ![]() , respectively; see Den Haan (1990) and Marcet and Lorenzoni (1999) for related examples.
, respectively; see Den Haan (1990) and Marcet and Lorenzoni (1999) for related examples.
Among many possible variants of FPI for finding ![]() , we distinguish one special case, which is known as time iteration and is used in, e.g., the Smolyak method of Malin et al. (2011). In the context of our example, we fix
, we distinguish one special case, which is known as time iteration and is used in, e.g., the Smolyak method of Malin et al. (2011). In the context of our example, we fix ![]() and represent all choice variables as functions of
and represent all choice variables as functions of ![]() , namely, we first identify
, namely, we first identify ![]() and we then identify
and we then identify ![]() and
and ![]() to satisfy the intratemporal choice conditions under given
to satisfy the intratemporal choice conditions under given ![]() and
and ![]() . With this representation, we can implement the following iterative process.
. With this representation, we can implement the following iterative process.
The name time iteration emphasizes the similarity of this iterative process to value function iteration. Namely, we restrict future end-of-period capital ![]() , and we solve for current end-of-period capital
, and we solve for current end-of-period capital ![]() , in the same way as in the case of dynamic programming methods, we fix the future value function,
, in the same way as in the case of dynamic programming methods, we fix the future value function, ![]() , in the right side of the Bellman equation, and we solve for the present value function,
, in the right side of the Bellman equation, and we solve for the present value function, ![]() , in the left side of the Bellman equation; see Section 7 for more details. Some theoretical arguments suggest that time iteration is more stable numerically than other versions of FPI (because for some simple equilibrium problem, time iteration possesses the property of contraction mapping as does value function iteration; see Judd (1998) for a discussion). However, the contraction mapping is not preserved in more complex equilibrium problems so it is not clear which of many possible versions of FPI will perform best in terms of convergence.
, in the left side of the Bellman equation; see Section 7 for more details. Some theoretical arguments suggest that time iteration is more stable numerically than other versions of FPI (because for some simple equilibrium problem, time iteration possesses the property of contraction mapping as does value function iteration; see Judd (1998) for a discussion). However, the contraction mapping is not preserved in more complex equilibrium problems so it is not clear which of many possible versions of FPI will perform best in terms of convergence.
Certainly, time iteration is far more expensive than our benchmark simple FPI described in Example 11. Even in the simple growth model, it requires us to find ![]() satisfying (81) using a numerical solver. In more complex high-dimensional problems, time iteration is even more expensive because it requires us to solve a system of several Euler equations with respect to several unknowns. In contrast, FPI of type (80) is trivial to implement in problems with any dimensionality since only straightforward calculations are needed.
satisfying (81) using a numerical solver. In more complex high-dimensional problems, time iteration is even more expensive because it requires us to solve a system of several Euler equations with respect to several unknowns. In contrast, FPI of type (80) is trivial to implement in problems with any dimensionality since only straightforward calculations are needed.
6.4 Coordination Between the Intratemporal and Intertemporal Choices
A specific way in which we define and coordinate the intertemporal and intratemporal choices can significantly affect the accuracy and speed of a solution method.
First, under some parameterizations, the system of intratemporal choice conditions can be easier to solve than under others. For example, Maliar and Maliar (2005b) use the labor decision function ![]() as an intertemporal choice instead of the capital decision function
as an intertemporal choice instead of the capital decision function ![]() . In this case, we fix
. In this case, we fix ![]() and solve (72), (73) with respect to
and solve (72), (73) with respect to ![]() . Under parameterization (17), the solution to the resulting intratemporal choice conditions can be characterized analytically.
. Under parameterization (17), the solution to the resulting intratemporal choice conditions can be characterized analytically.
Second, we must compute the intertemporal and intratemporal choices in a way that delivers similar accuracy levels in all models’ equations. If some decision functions are computed less accurately than the others, the overall accuracy of solutions will be determined by the least accurate decision function; see Maliar et al. (2011) for related examples and further discussion.
Finally, solving for the intratemporal choice with a high degree of accuracy may be unnecessary in every outer-loop iteration. For example, consider Example 10. Instead of solving for the intratemporal choice accurately in initial outer-loop iterations, we perform a fixed number of iterations in the inner loop, let us say 10. (Each time, we start the inner loop iterations from quantities ![]() that were obtained at the end of the previous outer-loop iteration). As the capital decision function
that were obtained at the end of the previous outer-loop iteration). As the capital decision function ![]() refines along the outer-loop iterations, so does the intertemporal choice; this technique is used by Maliar et al. (2011) to reduce the computational expense of finding the intratemporal choice in problems with high dimensionality. A possible shortcoming of this technique is that too inaccurate calculations of the intratemporal choice may reduce the numerical stability and may slow down the convergence of
refines along the outer-loop iterations, so does the intertemporal choice; this technique is used by Maliar et al. (2011) to reduce the computational expense of finding the intratemporal choice in problems with high dimensionality. A possible shortcoming of this technique is that too inaccurate calculations of the intratemporal choice may reduce the numerical stability and may slow down the convergence of ![]() in the outer loop; to deal with this shortcoming, one must choose the damping parameter appropriately.
in the outer loop; to deal with this shortcoming, one must choose the damping parameter appropriately.
6.5 Numerical Illustration of the Importance of Coordination
Maliar et al. (2011) illustrate the importance of coordination between different computational techniques by showing an example in which the total accuracy is dominated by the least accurate decision function. Specifically, they consider two alternatives in the context of a two-agent version of model (1)–(3) with inelastic labor supply:
Alternative 1. Approximate consumption of the first agent, ![]() , with a second-degree polynomial (the capital decision function is also approximated with a second-degree polynomial), and compute consumption of the second agent,
, with a second-degree polynomial (the capital decision function is also approximated with a second-degree polynomial), and compute consumption of the second agent, ![]() , to satisfy an FOC with respect to consumption.
, to satisfy an FOC with respect to consumption.
Alternative 2. Solve for ![]() and
and ![]() to satisfy exactly the budget constraint and an FOC with respect to consumption using iteration-on-allocation.
to satisfy exactly the budget constraint and an FOC with respect to consumption using iteration-on-allocation.
Thus, under alternative 1, ![]() is approximated with error and this error is transmitted to
is approximated with error and this error is transmitted to ![]() , while under alternative 2,
, while under alternative 2, ![]() and
and ![]() are calculated exactly. Table 11 shows the results. As we can see, a parametric polynomial approximation of the intratemporal choice (i.e., alternative 1) reduces the overall accuracy of solutions by about an order of magnitude compared to the case when all the intratemporal choice variables are computed accurately using iteration-on-allocation (i.e., alternative 2). In this particular example, to have a comparable accuracy in the capital and consumption choices under alternative 1, one needs to approximate the consumption decision function with a polynomial of a degree higher than that used for parametric approximations of the capital decision function.
are calculated exactly. Table 11 shows the results. As we can see, a parametric polynomial approximation of the intratemporal choice (i.e., alternative 1) reduces the overall accuracy of solutions by about an order of magnitude compared to the case when all the intratemporal choice variables are computed accurately using iteration-on-allocation (i.e., alternative 2). In this particular example, to have a comparable accuracy in the capital and consumption choices under alternative 1, one needs to approximate the consumption decision function with a polynomial of a degree higher than that used for parametric approximations of the capital decision function.
Table 11
Intertemporal choice in the two-agent model: one policy function versus iteration-on-allocation (in both the solution and simulation procedures).a

aNotes: ![]() and
and ![]() are, respectively, the average and maximum of absolute residuals across test points (in log10 units). An entry “–” is used if accuracy measure is below −10 (such residuals are viewed as negligible). The results are reproduced from Maliar et al. (2011), Table 1.
are, respectively, the average and maximum of absolute residuals across test points (in log10 units). An entry “–” is used if accuracy measure is below −10 (such residuals are viewed as negligible). The results are reproduced from Maliar et al. (2011), Table 1.
7 Dynamic Programming Methods for High-Dimensional Problems
The efficient techniques for interpolation, integration, and optimization described in Sections 4,5 and 6, respectively, apply to dynamic programming (DP) methods in the same way as they do to the Euler equation methods. DP methods which are analogs to the previously described Euler equation methods are developed and tested. In particular, Maliar and Maliar (2005a) introduce a solution method that approximates the value function by simulation and use this method to solve a multisector model with six state variables. Judd et al. (2011d) apply a value function iteration version of the GSSA method to solve a multicountry model with up to 20 countries (40 state variables). Judd et al. (2012) implement a value function iteration method operating on the EDS grid. Finally, Maliar and Maliar (2012a,b) use a version of ECM to solve a multicountry model studied in Kollmann et al. (2011b).
We therefore concentrate on two questions that are specific to DP methods. First, conventional value function iteration (VFI) leads to systems of equations that are expensive to solve, especially in high-dimensional applications. We describe two approaches that reduce the cost of conventional VFI: an endogenous grid method (EGM) of Carroll (2005) and an envelope condition method (ECM) of Maliar and Maliar (2013). Second, value function iteration produces less accurate solutions than Euler equation methods. We describe versions of EGM and ECM methods developed in Maliar and Maliar (2013) that approximate derivatives of the value function instead of, or in addition to, the value function itself and that deliver high accuracy levels comparable to those produced by Euler equation methods. We illustrate the above methods in the context of the one-agent model. In Section 12, we use a version of ECM to solve large-scale DP problems.
7.1 Conventional Value Function Iteration
As a starting point, we describe conventional VFI. To simplify the exposition, we consider a version of model (1)–(3) with inelastic labor supply. In the DP form, this model can be written as
![]() (82)
(82)
![]() (83)
(83)
![]() (84)
(84)
If a solution to Bellman (82)–(84) is interior, the optimality quantities satisfy the FOC,
![]() (85)
(85)
Conventional VFI goes backward: it guesses a value function in period ![]() , and it solves for a value function in period
, and it solves for a value function in period ![]() using the Bellman equation; this procedure is referred to as time iteration in the literature.
using the Bellman equation; this procedure is referred to as time iteration in the literature.

Here, we approximate ![]() parametrically, namely, we parameterize
parametrically, namely, we parameterize ![]() with a flexible functional form
with a flexible functional form ![]() , and we solve for a coefficient vector
, and we solve for a coefficient vector ![]() that approximately satisfies (82). In turn, the policy functions satisfying (83), (85) are computed in terms of quantities, i.e., nonparametrically. Conditions (83), (85) can be viewed as intratemporal choice conditions, and condition (82) can be viewed as an intertemporal choice condition. This separation is parallel to the one introduced in Maliar et al. (2011) for the Euler equation methods and is discussed in Section 6.
that approximately satisfies (82). In turn, the policy functions satisfying (83), (85) are computed in terms of quantities, i.e., nonparametrically. Conditions (83), (85) can be viewed as intratemporal choice conditions, and condition (82) can be viewed as an intertemporal choice condition. This separation is parallel to the one introduced in Maliar et al. (2011) for the Euler equation methods and is discussed in Section 6.
The main shortcoming of conventional VFI is that the system of equations in the inner loop is expensive to solve numerically. Indeed, consider (83) and (85) under our benchmark parameterization.
To find a root to (86), we must explore many different candidate points ![]() . For each candidate point, we must interpolate
. For each candidate point, we must interpolate ![]() to
to ![]() new values
new values ![]() , as well as to approximate conditional expectation
, as well as to approximate conditional expectation ![]() . The cost of this procedure is high even in models with few state variables; see Aruoba et al. (2006) for examples assessing the cost of VFI.
. The cost of this procedure is high even in models with few state variables; see Aruoba et al. (2006) for examples assessing the cost of VFI.
7.2 Reducing the Cost of Dynamic Programming Methods
We now describe two methods that reduce the cost of conventional VFI: an endogenous grid method of Carroll (2005) and an envelope condition method of Maliar and Maliar (2013).
7.2.1 Endogenous Grid Method
Carroll (2005) introduces an endogenous grid method (EGM) that simplifies rootfinding under VFI. The key idea of EGM is to construct a grid on future endogenous state variables instead of current endogenous state variables. EGM dominates conventional VFI because in a typical economic model, it is easier to solve for ![]() given
given ![]() than to solve for
than to solve for ![]() given
given ![]() . Below, we outline EGM for our example (the steps that coincide under conventional VFI and EGM are omitted).
. Below, we outline EGM for our example (the steps that coincide under conventional VFI and EGM are omitted).

Since the values of ![]() are fixed (they are grid points), it is possible to up-front compute
are fixed (they are grid points), it is possible to up-front compute ![]() and
and ![]() . Now, system (83) and (85) can be written as follows:
. Now, system (83) and (85) can be written as follows:
Equation (87) is easier to solve numerically than (86) because it does not involve either interpolation or approximation of a conditional expectation. Furthermore, Carroll (2005) finds a clever change of variables that simplifies rootfinding even further and effectively allows us to solve (87) in a closed form. He introduces a new variable ![]() , which allows us to rewrite Bellman equation (82)–(84) as
, which allows us to rewrite Bellman equation (82)–(84) as
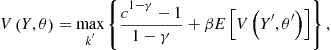 (88)
(88)
![]() (89)
(89)
![]() (90)
(90)
where ![]() . The FOC of (88)–(90) is
. The FOC of (88)–(90) is
![]() (91)
(91)
FOC (91) allows us to compute ![]() directly since
directly since ![]() follows directly from the (endogenous) grid points and so does the conditional expectation in the right side of (91). Given
follows directly from the (endogenous) grid points and so does the conditional expectation in the right side of (91). Given ![]() , we find
, we find ![]() and, subsequently, we find
and, subsequently, we find ![]() in the left side of (88). This provides a basis for iterating on the Bellman equation (88) without using a numerical solver. Once the convergence is achieved, we find
in the left side of (88). This provides a basis for iterating on the Bellman equation (88) without using a numerical solver. Once the convergence is achieved, we find ![]() that corresponds to the constructed endogenous grid by solving
that corresponds to the constructed endogenous grid by solving ![]() with respect to
with respect to ![]() for each value
for each value ![]() . This step does require us to use a numerical solver, but just once, at the very end of the iteration procedure.
. This step does require us to use a numerical solver, but just once, at the very end of the iteration procedure.
7.2.2 Envelope Condition Method
The envelope condition method (ECM) of Maliar and Maliar (2013) simplifies rootfinding using a different mechanism. First, ECM does not perform conventional backward iteration on the Bellman equation but iterates forward. Second, to construct policy functions, ECM uses the envelope condition instead of the FOCs used by conventional VFI and EGM. The systems of equations produced by ECM are typically easier to solve than those produced by conventional VFI. In this sense, ECM is similar to EGM.
For problem (82)–(84), the envelope condition is given by
![]() (92)
(92)
Typically, the envelope condition used to derive the Euler equation ((92) is updated to get ![]() and the result is substituted into (85) to eliminate the unknown derivative of the value function). In ECM, the envelope condition is used to solve for the intratemporal choice by combining (92) and (85).
and the result is substituted into (85) to eliminate the unknown derivative of the value function). In ECM, the envelope condition is used to solve for the intratemporal choice by combining (92) and (85).
ECM proceeds as follows (the steps that coincide under VFI and ECM are omitted):

Consider again our benchmark example under parameterization (18).
In this example, ECM is simpler than Carroll’s (2005) EGM since all the policy functions can be constructed analytically and a solver need not be used at all (not even once).

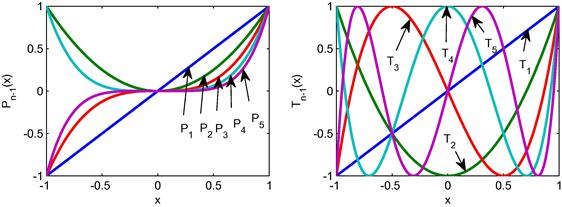
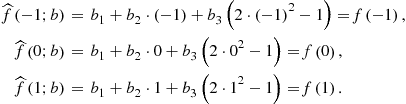
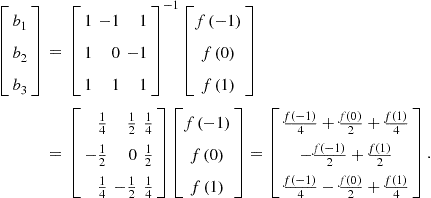
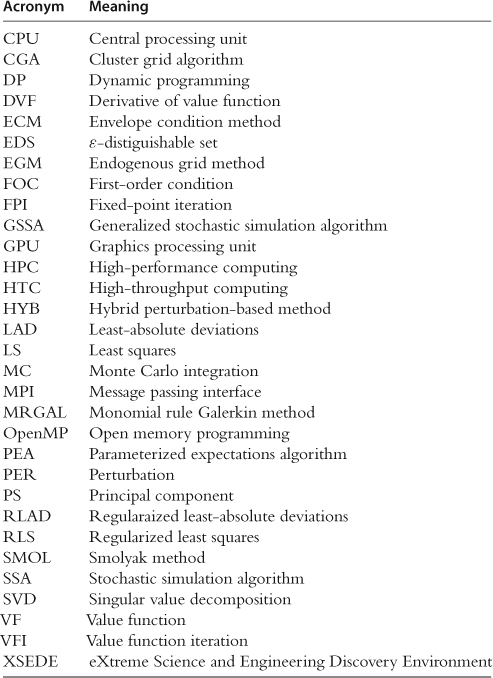

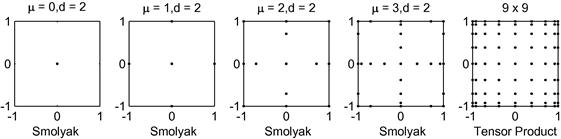
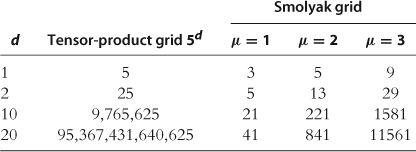
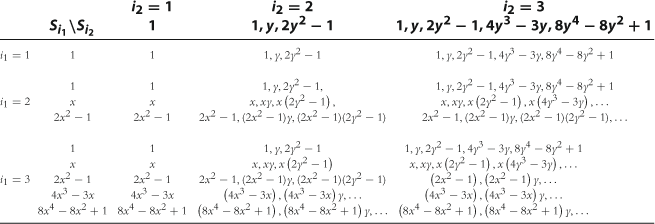
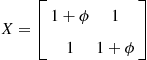 with
with 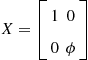 with
with