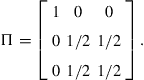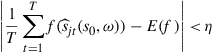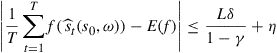Analysis of Numerical Errors
Adrian Peralta-Alvaa and Manuel S. Santosb, aResearch Division, Federal Reserve Bank of Saint Louis, St Louis, MO, USA, bDepartment of Economics, University of Miami, Coral Gables, FL, USA
Abstract
This paper provides a general framework for the quantitative analysis of stochastic dynamic models. We review the convergence properties of some numerical algorithms and available methods to bound approximation errors. We then address the convergence and accuracy properties of the simulated moments. We study both optimal and non-optimal economies. Optimal economies generate smooth laws of motion defining Markov equilibria, and can be approximated by recursive methods with contractive properties. Non-optimal economies, however, lack existence of continuous Markov equilibria, and need to be simulated by numerical methods with weaker approximation properties.
Keywords
Dynamic stochastic economy; Markov equilibrium; Numerical solution; Approximation error; Accuracy; Simulation-based estimation; Consistency
JEL Classification Codes
C63; E60
1 Introduction
Numerical methods are essential to assess the predictions of non-linear economic models. Indeed, a vast majority of economic models lack analytical solutions, and hence researchers must rely on numerical algorithms—which contain approximation errors. At the heart of modern quantitative analysis is the presumption that the numerical method mimics well the original model statistics. In practice, however, matters are not so simple and there are many situations in which researchers are unable to control for undesirable propagating effects of numerical errors.
In static economies it is usually easy to bound the size of the error. But in infinite-horizon models we have to realize that numerical errors may cumulate in unexpected ways. Cumulative errors can be bounded in models where equilibria may be approximated by contraction operators. But if the contraction property is missing then the most that one can hope for is to establish asymptotic properties of the numerical solution as we refine the approximation.
Model simulations are mechanically performed in macroeconomics and other disciplines, but there is much to be learned about laws of large numbers that can justify the convergence of the simulated moments, and the propagating effects of numerical errors in these simulations. Numerical errors may bias stationary solutions and parameter estimates from simulation-based estimation.
Hence, simulation-based estimation must cope with changes in parameter values affecting the dynamics of the system. Indeed, the estimation process encompasses a continuum of invariant distributions indexed by a vector of parameters. Therefore, simulation-based estimation needs fast and accurate algorithms that can sample the parameter space. Asymptotic properties of these estimators such as consistency and normality are much harder to establish than in traditional data-based estimation in which there is a unique stochastic distribution given by the data-generating process.
This chapter is intended to survey theoretical work on the convergence properties of numerical algorithms and the accuracy of simulations. More specifically, we shall review the established literature with an eye toward a better understanding of the following issues: (i) convergence properties of numerical algorithms and accuracy tests that can bound the size of approximation errors, (ii) accuracy properties of the simulated moments from numerical algorithms and laws of large numbers that can justify model simulation, and (iii) calibration and simulation-based estimation.
We study these issues along with a few illustrative examples. We focus on a large class of dynamic general equilibrium models of wide application in economics and finance. We break the analysis into optimal and non-optimal economies. Optimal economies satisfy the welfare theorems. Hence, equilibria can be computed by associated optimization problems, and under regular conditions these equilibria admit Markovian representations defined by continuous (or differentiable) policy functions. Non-optimal economies may lack the existence of Markov equilibria over the natural state space—or such equilibria may not be continuous. One could certainly restore the Markovian property by expanding the state space, but the non-continuity of the equilibrium remains. These technical problems limit the application of standard algorithms which assume continuous or differentiable approximation rules. (Differentiability properties of the solution are instrumental to characterize the dynamics of the system and to establish error bounds.)
We here put together several results for the computation and simulation of upper semicontinuous correspondences. The idea is to build reliable algorithms and laws of large numbers that can be applied to economies with market frictions and heterogeneous agents as commonly observed in many macroeconomic models.
Section 2 lays out an analytical setting conformed by several equilibrium conditions that include feasibility constraints and first-order conditions. This simplified framework is appropriate for computation. We then consider three illustrative examples: a growth model with taxes, a consumption-based asset-pricing model, and an overlapping generations economy. We show how these economies can readily be mapped into our general framework of analysis.
Our main theoretical results are presented in Sections 3 and 4. Each section starts with a review of some numerical solution methods, and then goes into the analysis of associated computational errors and convergence of the simulated statistics. Section 3 deals with models with continuous Markov equilibria. There is a vast literature on the computation of these equilibria, and here we only deal with the bare essentials. We nevertheless provide a more comprehensive study of the associated error from numerical approximations. Some regularity conditions, such as differentiability or contraction properties, may become instrumental to validate error bounds. These conditions are also needed to establish accuracy and consistency properties of simulation-based estimators.
Section 4 is devoted to non-optimal economies. For this family of models, Markov equilibria on the natural state space may fail to exist, and standard computational methods—which iterate over continuous functions—may produce inaccurate solutions. We present a reliable algorithm based on the iteration over candidate equilibrium correspondences. The algorithm has good convergence and approximation properties, and its fixed point contains a Markovian correspondence that generates all competitive equilibria. Hence, competitive equilibria still admit a recursive representation. But this representation may only be obtained in an enlarged state space (which includes the shadow values of asset holdings), and may not be continuous. The non-continuity of the equilibrium solution precludes application of standard laws of large numbers. This is problematic because we need an asymptotic theory to justify the simulation and estimation of economies with frictions. We discuss some important accuracy results as well as an extended version of the law of large numbers which entails that the sample moments from numerical approximations must approach those of some invariant distribution of the model as the error in the approximated equilibrium correspondence vanishes.
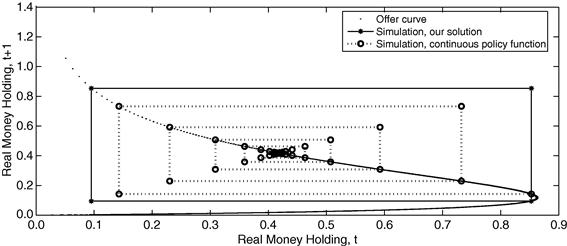
Section 5 presents several numerical experiments. We first study a standard business cycle model. This optimal planning problem becomes handy to assess the accuracy of the computed solutions using the Euler equation residuals. We then introduce some non-optimal economies in which simple Markov equilibria may fail to exist: an overlapping generations economy and an asset-pricing model with endogenous constraints. These examples make clear that standard solution methods would result in substantial computational errors that may drastically change the ergodic sets and corresponding equilibrium dynamics. The equilibrium solutions are then computed by a reliable algorithm introduced in Section 4. This algorithm can also be applied to some other models of interest with heterogeneous agents such as a production economy with taxes and individual rationality constraints, and a consumption-based asset-pricing model with collateral requirements. There are cases in which the solution of this robust algorithm approaches a continuous policy function, and hence we have numerical evidence of existence of a unique equilibrium. Uniqueness of equilibrium guarantees the existence and continuity of a simple Markov equilibrium—which simplifies the computation and simulation of the model. Uniqueness of equilibrium is hard to check using standard numerical methods.
We conclude in Section 6 with further comments and suggestions.
2 Dynamic Stochastic Economies
Our objective is to study quantitative properties of stochastic sequences ![]() that emerge as equilibria of our model economies. These equilibrium sequences arise from the solution of non-linear equation systems, the intertemporal optimization behavior of individual agents, as well as the economy’s aggregate constraints, and the exogenously given sequence of shocks
that emerge as equilibria of our model economies. These equilibrium sequences arise from the solution of non-linear equation systems, the intertemporal optimization behavior of individual agents, as well as the economy’s aggregate constraints, and the exogenously given sequence of shocks ![]() . Our framework of analysis encompasses both competitive and non-competitive economies, with or without a government sector, and incomplete financial markets.
. Our framework of analysis encompasses both competitive and non-competitive economies, with or without a government sector, and incomplete financial markets.
Time is discrete, ![]() , and
, and ![]() is a history of shocks up to period
is a history of shocks up to period ![]() , which is governed by a time-invariant Markov process. For convenience, let us decompose the economic variables of interest as
, which is governed by a time-invariant Markov process. For convenience, let us decompose the economic variables of interest as ![]() . Vector
. Vector ![]() represents predetermined variables, such as capital stocks and portfolio holdings. Future values of these variables will be determined endogenously by current and future actions. Vector
represents predetermined variables, such as capital stocks and portfolio holdings. Future values of these variables will be determined endogenously by current and future actions. Vector ![]() denotes all other current endogenous variables such as consumption, investment, asset prices, interest rates, and so on. Further more, sometimes vector
denotes all other current endogenous variables such as consumption, investment, asset prices, interest rates, and so on. Further more, sometimes vector ![]() may include the shock
may include the shock ![]() .
.
The dynamics of state vector ![]() will be captured by a system of non-linear equations:
will be captured by a system of non-linear equations:
![]() (1)
(1)
Function ![]() may incorporate technological constraints and individual budget constraints. Likewise, present and future values of vector
may incorporate technological constraints and individual budget constraints. Likewise, present and future values of vector ![]() are linked by the non-linear system:
are linked by the non-linear system:
![]() (2)
(2)
where ![]() is the expectations operator conditioning on information at time
is the expectations operator conditioning on information at time ![]() . Conditions describing function
. Conditions describing function ![]() may correspond to individual optimality conditions (such as Euler equations), short-sales and liquidity requirements, endogenous borrowing constraints, individual rationality constraints, and market clearing conditions.
may correspond to individual optimality conditions (such as Euler equations), short-sales and liquidity requirements, endogenous borrowing constraints, individual rationality constraints, and market clearing conditions.
We now present three different examples to illustrate that standard macro models can readily be mapped into this framework.
2.1 A Growth Model with Taxes
The economy is made up of a representative household and a single firm. The exogenously given stochastic process ![]() is an index of total factor productivity. For given sequences of rental rates,
is an index of total factor productivity. For given sequences of rental rates, ![]() , wages,
, wages, ![]() , profits redistributed by the firm,
, profits redistributed by the firm, ![]() , government lump-sum transfers,
, government lump-sum transfers, ![]() , and tax functions,
, and tax functions, ![]() , the household solves the following optimization problem:
, the household solves the following optimization problem:
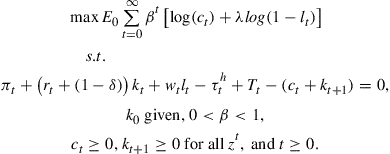 (3)
(3)
Here, ![]() denotes consumption,
denotes consumption, ![]() denotes the amount of labor supplied, and
denotes the amount of labor supplied, and ![]() denotes holdings of physical capital. Parameter
denotes holdings of physical capital. Parameter ![]() is the discount factor and
is the discount factor and ![]() is the capital depreciation rate. Taxes
is the capital depreciation rate. Taxes ![]() may be non-linear functions of income variables (such as capital or labor income) and of the aggregate capital stock
may be non-linear functions of income variables (such as capital or labor income) and of the aggregate capital stock ![]() . Households take the sequences of tax functions as given—contingent upon the history of realizations
. Households take the sequences of tax functions as given—contingent upon the history of realizations ![]() .
.
For a given sequence of technology shocks ![]() , factor prices, and output taxes
, factor prices, and output taxes ![]() , the representative firm seeks to maximize one-period profits by selecting the optimal amount of capital and labor
, the representative firm seeks to maximize one-period profits by selecting the optimal amount of capital and labor
![]()
All tax revenues are rebated back to the representative household as lump-sum transfers ![]() .
.
For a given sequence of tax functions ![]() and transfers
and transfers ![]() , a competitive equilibrium for this economy is conformed by stochastic sequences of factor prices and profits
, a competitive equilibrium for this economy is conformed by stochastic sequences of factor prices and profits ![]() , and sequences of consumption, capital and labor allocations
, and sequences of consumption, capital and labor allocations ![]() , such that: (i)
, such that: (i) ![]() solve the above optimization problem of the household; and
solve the above optimization problem of the household; and ![]() maximizes one-period profits for the firm; (ii) the supplies of capital and labor are equal to the quantities demanded:
maximizes one-period profits for the firm; (ii) the supplies of capital and labor are equal to the quantities demanded: ![]() , and
, and ![]() ; and (iii) consumption and investment allocations are feasible
; and (iii) consumption and investment allocations are feasible
![]() (4)
(4)
Getting back to our general framework, we observe that capital is the only predetermined endogenous variable: ![]() , while consumption and hours worked are the endogenous variables
, while consumption and hours worked are the endogenous variables ![]() . Function
. Function ![]() is thus given by (4). We also have the intertemporal equilibrium conditions:
is thus given by (4). We also have the intertemporal equilibrium conditions:
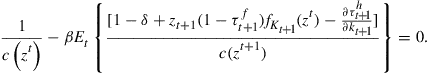 (5)
(5)
![]() (6)
(6)
It follows that ![]() is defined by equation systems (5) and (6) over constraint (3).
is defined by equation systems (5) and (6) over constraint (3).
2.2 An Asset-Pricing Model with Financial Frictions
The economy is populated by a finite number of agents, ![]() . At each node
. At each node ![]() , there exist spot markets for the consumption good and a fixed set
, there exist spot markets for the consumption good and a fixed set ![]() of securities. For convenience we assume that the supply of each security is equal to unity. Among these securities, we may include a one-period real bond which is a promise to one unit of the consumption good at all successor nodes
of securities. For convenience we assume that the supply of each security is equal to unity. Among these securities, we may include a one-period real bond which is a promise to one unit of the consumption good at all successor nodes ![]() . Our general stylized framework above can embed several financial frictions such as incomplete markets, collateral requirements, and short-sale constraints.
. Our general stylized framework above can embed several financial frictions such as incomplete markets, collateral requirements, and short-sale constraints.
Each agent ![]() maximizes the intertemporal objective
maximizes the intertemporal objective
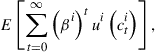 (7)
(7)
where ![]() , and
, and ![]() is strictly increasing, strictly concave, and continuously differentiable with derivative
is strictly increasing, strictly concave, and continuously differentiable with derivative ![]() . At each node
. At each node ![]() the agent receives
the agent receives ![]() units of the consumption good contingent on the present realization
units of the consumption good contingent on the present realization ![]() . Securities are specified by the current vector of prices,
. Securities are specified by the current vector of prices, ![]() , and the vectors of dividends
, and the vectors of dividends ![]() promised to deliver at future information sets
promised to deliver at future information sets ![]() for
for ![]() . The vector of security prices
. The vector of security prices ![]() is non-negative, and the vector of dividends
is non-negative, and the vector of dividends ![]() is positive and depends only on the current realization of the vector of shocks
is positive and depends only on the current realization of the vector of shocks ![]() .
.
For a given price process ![]() , each agent
, each agent ![]() can choose desired quantities of consumption and security holdings
can choose desired quantities of consumption and security holdings ![]() subject to the following sequence of budget constraints
subject to the following sequence of budget constraints
![]() (8)
(8)
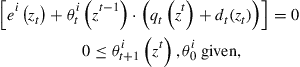 (9)
(9)
for all ![]() . Note that (9) imposes non-negative holdings of all securities. Let
. Note that (9) imposes non-negative holdings of all securities. Let ![]() be the associated vector of multipliers to this non-negativity constraint.
be the associated vector of multipliers to this non-negativity constraint.
A competitive equilibrium for this economy is a collection of vectors ![]() such that: (i) each agent
such that: (i) each agent ![]() maximizes the objective (7) subject to constraints (8) and (9); and (ii) markets clear:
maximizes the objective (7) subject to constraints (8) and (9); and (ii) markets clear:
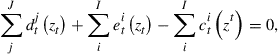 (10)
(10)
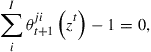 (11)
(11)
for ![]() , all
, all ![]() .
.
It is not hard to see that this model can be mapped into our analytical framework. Again, the vector of exogenous shocks ![]() defines sequences of endowments and dividends,
defines sequences of endowments and dividends, ![]() . Without loss of generality, we have assumed that the space of asset holdings is given by
. Without loss of generality, we have assumed that the space of asset holdings is given by ![]() . Asset holdings
. Asset holdings ![]() are the predetermined variables corresponding to vector
are the predetermined variables corresponding to vector ![]() , whereas consumption
, whereas consumption ![]() and asset prices
and asset prices ![]() are the current endogenous variables corresponding to vector
are the current endogenous variables corresponding to vector ![]() .
.
Function ![]() is simply given by the vector of individual budget constraints (8) and (9). Function
is simply given by the vector of individual budget constraints (8) and (9). Function ![]() is defined by the first-order conditions for intertemporal utility maximization over the equilibrium conditions for the aggregate good and financial markets (10) and (11). Observe that all constraints hold with equality as we introduce the associated vectors of multipliers
is defined by the first-order conditions for intertemporal utility maximization over the equilibrium conditions for the aggregate good and financial markets (10) and (11). Observe that all constraints hold with equality as we introduce the associated vectors of multipliers ![]() for the non-negativity constraints.
for the non-negativity constraints.
2.3 An Overlapping Generations Economy
We study a version of the economy analyzed by Kubler and Polemarchakis (2004). The economy is subject to an exogenously given sequence of shocks ![]() , with
, with ![]() for all
for all ![]() . At each date,
. At each date, ![]() new individuals appear in the economy and stay present for
new individuals appear in the economy and stay present for ![]() periods. Thus, agents are defined by their individual type
periods. Thus, agents are defined by their individual type ![]() , and the specific date-event in which they initiate their life span
, and the specific date-event in which they initiate their life span ![]() . There are
. There are ![]() goods, and each individual receives a positive stochastic endowment
goods, and each individual receives a positive stochastic endowment ![]() at every node
at every node ![]() while present in the economy. Endowments are assumed to be Markovian—defined by the type of the agent,
while present in the economy. Endowments are assumed to be Markovian—defined by the type of the agent, ![]() , age,
, age, ![]() , and the current realization of the shock,
, and the current realization of the shock, ![]() . Preferences over stochastic consumption streams
. Preferences over stochastic consumption streams ![]() are represented by an expected utility function
are represented by an expected utility function
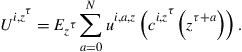 (12)
(12)
Again, we impose a Markovian structure on preferences—assumed to depend on ![]() , and the current realized value
, and the current realized value ![]() .
.
At each date-event ![]() agents can trade one-period bonds that pay one unit of numeraire good
agents can trade one-period bonds that pay one unit of numeraire good ![]() regardless of the state of the world next period. These bonds are always in zero net supply, and
regardless of the state of the world next period. These bonds are always in zero net supply, and ![]() is the price of a bond that trades at date-event
is the price of a bond that trades at date-event ![]() . An infinitely lived Lucas tree may also be available from time zero. The tree produces a random stream of dividends
. An infinitely lived Lucas tree may also be available from time zero. The tree produces a random stream of dividends ![]() of consumption good 1. Then,
of consumption good 1. Then, ![]() is the market value of the tree, and
is the market value of the tree, and ![]() the holdings of bonds and shares of the tree for agent
the holdings of bonds and shares of the tree for agent ![]() . Shares cannot be sold short.
. Shares cannot be sold short.
Each individual consumer ![]() faces the following budget constraints for periods
faces the following budget constraints for periods ![]() ,
,
![]()
![]() (13)
(13)
![]() (14)
(14)
![]() (15)
(15)
Note that (14) insures that stock holdings must be non-negative, whereas (15) insures that debts must be honored in the terminal period.
As before, a competitive equilibrium for this economy is conformed by sequences of prices, ![]() , consumption allocations,
, consumption allocations, ![]() , and asset holdings
, and asset holdings ![]() for all agents over their corresponding ages, such that: (i) each agent maximizes her expected utility subject to individual budget constraints, (ii) the goods markets clear: consumption allocations add up to the aggregate endowment at all possible date-events, and (iii) financial markets clear: bond holdings add up to zero and share holdings add up to one.
for all agents over their corresponding ages, such that: (i) each agent maximizes her expected utility subject to individual budget constraints, (ii) the goods markets clear: consumption allocations add up to the aggregate endowment at all possible date-events, and (iii) financial markets clear: bond holdings add up to zero and share holdings add up to one.
Now, our purpose is to clarify how to map this model into the analytical framework developed before. The vector of exogenous shocks is ![]() , which defines the endowment and dividend processes
, which defines the endowment and dividend processes ![]() . As predetermined variables we have
. As predetermined variables we have ![]() ; that is, the portfolio holdings for all agents
; that is, the portfolio holdings for all agents ![]() alive at every date-event
alive at every date-event ![]() . And as current endogenous variables we have
. And as current endogenous variables we have ![]() the consumption allocations and the prices of both the bond and the Lucas tree for every date-event
the consumption allocations and the prices of both the bond and the Lucas tree for every date-event ![]() .
.
For the sake of the presentation, let’s consider a version of the model with one consumption good and two agents that live for two periods. Function ![]() is simply given by the vector of individual budget constraints (13). Function
is simply given by the vector of individual budget constraints (13). Function ![]() is defined by: (i) the individual optimality conditions for bonds
is defined by: (i) the individual optimality conditions for bonds
![]() (16)
(16)
(ii) if the Lucas tree is available, the Euler equation
![]() (17)
(17)
where ![]() is the multiplier on the short-sales constraints (14); and (iii) market clearing conditions. It is evident that many other constraints may be brought up into the analysis, such as a collateral restriction along the lines of Kubler and Schmedders (2003) that set up a limit for negative holdings of the bond based on the value of the holdings of the tree.
is the multiplier on the short-sales constraints (14); and (iii) market clearing conditions. It is evident that many other constraints may be brought up into the analysis, such as a collateral restriction along the lines of Kubler and Schmedders (2003) that set up a limit for negative holdings of the bond based on the value of the holdings of the tree.
3 Numerical Solution of Simple Markov Equilibria
For the above models, fairly general conditions guarantee the existence of stochastic equilibrium sequences. But even if the economy has a Markovian structure (i.e., the stochastic process driving the exogenous shocks and conditions (1) and (2) over the constraints is Markovian), equilibrium sequences may depend on some history of shocks. Equilibria with this type of path dependence are not amenable to numerical or statistical methods.
Hence, most quantitative research has focused on models where one can find continuous functions ![]() such that the sequences
such that the sequences
![]() (18)
(18)
generate a competitive equilibrium. Following Krueger and Kubler (2008), a competitive equilibrium that can be generated by equilibrium functions of the form (18) will be called a simple Markov equilibrium.
For frictionless economies the second welfare theorem applies—equilibrium allocations can be characterized as solutions to a planner’s problem. Using dynamic programming arguments, well-established conditions on primitives insure the existence of a simple Markov equilibrium (cf., Stokey et al., 1989). Matters are more complicated in models with real distortions such as taxes, or with financial frictions such as incomplete markets and collateral constraints. Section 4 details the issues involved. In this section we will review some results on the accuracy of numerical methods for simple Markov equilibria. First, we discuss some of the algorithms available to approximate equilibrium function ![]() . Then, we study methods to determine the accuracy of such approximations. Finally, we discuss how the approximation error in the policy function may propagate over the simulated moments affecting the estimation of parameter values.
. Then, we study methods to determine the accuracy of such approximations. Finally, we discuss how the approximation error in the policy function may propagate over the simulated moments affecting the estimation of parameter values.
3.1 Numerical Approximations of Equilibrium Functions
We can think of two major families of algorithms approximating simple Markov equilibria. The first group approximates directly the equilibrium functions (1) and (2) using the Euler equations and constraints (a variation of this method is Marcet’s original parameterized expectations algorithm that indirectly gets the equilibrium function via an approximation of the expectations function below, e.g., see Christiano and Fisher (2000)). These numerical algorithms may use local approximation techniques (perturbation methods), or global approximation techniques (projection methods). Projection methods require finding the fixed point of an equations system which may be highly non-linear. Hence, projection methods offer no guarantee of global convergence and uniqueness of the solution.
Another family of algorithms is based on dynamic programming (DP). The DP algorithms are reliable and have desirable convergence properties. However, their computational complexity increases quite rapidly with the dimension of the state space, especially because maximizations must be performed at each iteration. In addition, DP methods cannot be extended to models with distortions where the welfare theorems do not apply. For instance, in the above examples in Section 2, for most formulations, the growth model with taxes, the asset-pricing model with various added frictions, and the overlapping generations economy cannot be solved directly by DP methods. In all these economies, an equilibrium solution cannot be characterized by a social planning problem.
3.1.1 Methods Based on the Euler Equations
Simple Markov equilibria are characterized by continuous functions ![]() that satisfy
that satisfy
![]() (19)
(19)
![]() (20)
(20)
for all ![]() . Of course, in the absence of an analytical solution the system must be solved by numerical approximations.
. Of course, in the absence of an analytical solution the system must be solved by numerical approximations.
As mentioned above, two basic approaches are typically used to obtain approximate functions ![]() . Perturbation methods—pioneered by Judd and Guu (1997)—take a Taylor approximation around a point with known solution or quite close to the exact solution. This point typically corresponds to the deterministic steady state of the model, that is, an equilibrium where
. Perturbation methods—pioneered by Judd and Guu (1997)—take a Taylor approximation around a point with known solution or quite close to the exact solution. This point typically corresponds to the deterministic steady state of the model, that is, an equilibrium where ![]() for all
for all ![]() . Projection methods—developed by Judd (1992)—aim instead at more global approximations. First, a finite-dimensional space of functions is chosen that can approximate arbitrarily well continuous mappings. Common finite-dimensional spaces include finite elements (tent maps, splines, polynomials defined in small neighborhoods), or global bases such as polynomials or other functions defined over the whole domain
. Projection methods—developed by Judd (1992)—aim instead at more global approximations. First, a finite-dimensional space of functions is chosen that can approximate arbitrarily well continuous mappings. Common finite-dimensional spaces include finite elements (tent maps, splines, polynomials defined in small neighborhoods), or global bases such as polynomials or other functions defined over the whole domain ![]() . Second, let
. Second, let ![]() be elements of this finite-dimensional space evaluated at the nodal points
be elements of this finite-dimensional space evaluated at the nodal points ![]() defining these functions. Then, nodal values
defining these functions. Then, nodal values ![]() are obtained as solutions of non-linear systems conformed by equations (19) and (20) evaluated at some pre determined points of the state space
are obtained as solutions of non-linear systems conformed by equations (19) and (20) evaluated at some pre determined points of the state space ![]() . It is assumed that this non-linear system has a well-defined solution—albeit in most cases the existence of the solution is hard to show. And third, rules for the optimal placement of such pre determined points exist for some functional basis; e.g., Chebyshev polynomials that have some regular orthogonality properties could be evaluated at the Chebyshev nodes in the hope of minimizing oscillations.
. It is assumed that this non-linear system has a well-defined solution—albeit in most cases the existence of the solution is hard to show. And third, rules for the optimal placement of such pre determined points exist for some functional basis; e.g., Chebyshev polynomials that have some regular orthogonality properties could be evaluated at the Chebyshev nodes in the hope of minimizing oscillations.
3.1.2 Dynamic Programming
For economies satisfying the conditions of the second welfare theorem, equilibria can be computed by an optimization problem over a social welfare function subject to aggregate feasibility constraints. Then, one can find prices that support the planner’s allocation as a competitive equilibrium with transfer payments. A competitive equilibrium is attained when these transfers are equal to zero. Therefore, we need to search for the appropriate individual weights in the social welfare function in order to make these transfers equal to zero.
Matters are simplified by the principle of optimality: the planner’s intertemporal optimization problem can be summarized by a value function ![]() satisfying Bellman’s functional equation
satisfying Bellman’s functional equation
![]() (21)
(21)
![]()
Here, ![]() is the intertemporal discount factor,
is the intertemporal discount factor, ![]() is the one-period return function, and
is the one-period return function, and ![]() is a correspondence that captures the feasibility constraints of the economy. Note that our vectors
is a correspondence that captures the feasibility constraints of the economy. Note that our vectors ![]() and
and ![]() now refer to allocations only, while in previous decentralized models these vectors may include prices, taxes, or other variables outside the planning problem.
now refer to allocations only, while in previous decentralized models these vectors may include prices, taxes, or other variables outside the planning problem.
Value function ![]() is therefore a fixed point of Bellman’s equation (21). Under mild regularity conditions (cf., Stokey et al., 1989) it is easy to show that this fixed point can be approximated by the following DP operator. Let
is therefore a fixed point of Bellman’s equation (21). Under mild regularity conditions (cf., Stokey et al., 1989) it is easy to show that this fixed point can be approximated by the following DP operator. Let ![]() be the space of bounded functions. Then, operator
be the space of bounded functions. Then, operator ![]() is defined as
is defined as
![]() (22)
(22)
![]()
Operator ![]() is actually a contraction mapping with modulus
is actually a contraction mapping with modulus ![]() . It follows that
. It follows that ![]() is a unique solution of the functional equation (21), and can be found as the limit of the sequence recursively defined by
is a unique solution of the functional equation (21), and can be found as the limit of the sequence recursively defined by ![]() for an arbitrarily given initial function
for an arbitrarily given initial function ![]() . This iterating procedure is called the method of successive approximations, and operator
. This iterating procedure is called the method of successive approximations, and operator ![]() is called the DP operator.
is called the DP operator.
By the contraction property of the DP operator, it is possible to construct reliable numerical algorithms discretizing (22). For instance, Santos and Vigo-Aguiar (1998) establish error bounds for a numerical DP algorithm preserving the contraction property. The analysis starts with a set of piecewise-linear functions defined over state space X on a discrete set of nodal points with grid size ![]() . Then, a discretized version
. Then, a discretized version ![]() of operator
of operator ![]() is obtained by solving the optimization problem (22) at each nodal point. For piecewise-linear interpolation, operator
is obtained by solving the optimization problem (22) at each nodal point. For piecewise-linear interpolation, operator ![]() is also a contraction mapping. Hence, given any grid size
is also a contraction mapping. Hence, given any grid size ![]() , and any initial value function
, and any initial value function ![]() the sequence of functions
the sequence of functions ![]() converges to a unique solution
converges to a unique solution ![]() . Moreover, the contraction property of operator
. Moreover, the contraction property of operator ![]() can help bound the distance between such limit
can help bound the distance between such limit ![]() , and the
, and the ![]() application of this operator,
application of this operator, ![]() . Finally, it is important to remark that this approximation scheme will converge to the true solution of the model as the grid size
. Finally, it is important to remark that this approximation scheme will converge to the true solution of the model as the grid size ![]() goes to zero; that is,
goes to zero; that is, ![]() will be sufficiently close to the original value function
will be sufficiently close to the original value function ![]() for some small
for some small ![]() —as a matter of fact, convergence is of order
—as a matter of fact, convergence is of order ![]() . Of course, once a numerical value function
. Of course, once a numerical value function ![]() has been secured it is easy to obtain good approximations for our equilibrium functions
has been secured it is easy to obtain good approximations for our equilibrium functions ![]() from operator
from operator ![]() .
.
What slows down the DP algorithm is the maximization process at each iteration. Hence, functional interpolation—as opposed to discrete functions just defined over a set of nodal points—facilitates the use of some fast maximization routines. Splines and high-order polynomials may also be operative but these approximations may damage the concavity of the computed functions; moreover, for some interpolations there is no guarantee that the discretized operator is a contraction. There are other procedures to speed up the maximization process. Santos and Vigo-Aguiar (1998) use a multigrid method which can be efficiently implemented by an analysis of the approximation errors. Another popular method is policy iteration—contrary to popular belief this latter algorithm turns out to be quite slow for very fine grids (Santos and Rust, 2004).
3.2 Accuracy
As already pointed out, the quantitative analysis of non-linear models primarily relies on numerical approximations ![]() . Then, care must be exercised so that numerical equilibrium function
. Then, care must be exercised so that numerical equilibrium function ![]() is close enough to the actual decision rule
is close enough to the actual decision rule ![]() ; more precisely, we need to insure that
; more precisely, we need to insure that ![]() , where
, where ![]() is a norm relevant for the problem at hand, and
is a norm relevant for the problem at hand, and ![]() is a tolerance estimate.
is a tolerance estimate.
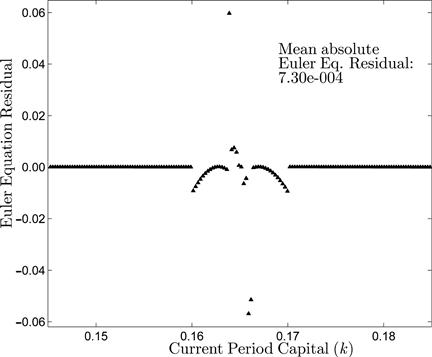
We now present various results for bounding the error in numerical approximations. Error bounds for optimal decision rules are available for some computational algorithms such as the above DP algorithm. It should be noted that these error bounds are not good enough for most quantitative exercises in which the object of interest is the time series properties of the simulated moments. Error bounds for optimal decision rules quantify the period-by-period bias introduced by a numerical approximation. This error, however, may grow in long simulations. A simple example below illustrates this point where the error of the simulated statistics gets large even when the error of the decision rule can be made arbitrarily small. Hence, the last part of this section considers some of the regularity conditions required for desirable asymptotic properties of the statistics from numerical simulations.
3.2.1 Accuracy of Equilibrium Functions
Suppose that we come up with a pair of numerical approximations ![]() . Is there a way of assessing the magnitude of the approximation error without actual knowledge of the solution of the model:
. Is there a way of assessing the magnitude of the approximation error without actual knowledge of the solution of the model: ![]() ?
?
To develop intuition on key ideas behind existing accuracy tests, let us define the Euler equation residuals for functions ![]() as
as
![]() (23)
(23)
![]() (24)
(24)
Note that an exact solution of the model will have Euler equation residuals equal to zero at all possible values of the state ![]() . Hence, “small” Euler equation residuals should indicate that the approximation error is also “small.” The relevant question, of course, is what we mean by “small.” Furthermore, we are circumventing other technical issues since first-order conditions may not be enough to characterize optimal solutions.
. Hence, “small” Euler equation residuals should indicate that the approximation error is also “small.” The relevant question, of course, is what we mean by “small.” Furthermore, we are circumventing other technical issues since first-order conditions may not be enough to characterize optimal solutions.
Den Haan and Marcet (1994) appeal to statistical techniques and propose testing for orthogonality of the Euler equation residuals over current and past information as a measure of accuracy. Since orthogonal Euler equation residuals may occur in spite of large deviations from the optimal policy, Judd (1992) suggests to evaluate the size of the Euler equation residuals over the whole state space as a test for accuracy. Moreover, for strongly concave infinite-horizon optimization problems Santos (2000) demonstrates that the approximation error of the policy function is of the same order of magnitude as the size of the Euler equation residuals, and the constants involved in these error bounds can be related to model primitives.
These theoretical error bounds are based on worse-case scenarios and hence they are usually not optimal for applied work. In some cases, researchers may want to assess numerically the approximation errors in the hope of getting more operative estimates (cf. Santos, 2000). Besides, for some algorithms it is possible to derive error bounds from their approximation procedures. This is the case of the DP algorithm (Santos and Vigo-Aguiar, 1998) and in some models with quadratic-linear approximations (Schmitt-Grohe and Uribe, 2004).
The logic underlying numerical estimation of error bounds from the Euler equation residuals goes as follows (Santos, 2000). We start with a model under a fixed set of parameter values. Then, Euler equation residuals are computed for several numerical equilibrium functions. We need sufficient variability in these approximations in order to obtain good and robust estimates. This variability is obtained by considering various approximation spaces or by changing the grid size. Let ![]() be the approximation with the lowest Euler equation residuals, which would be our best candidate for the true policy function. Then, for each available numerical approximation
be the approximation with the lowest Euler equation residuals, which would be our best candidate for the true policy function. Then, for each available numerical approximation ![]() we compute the approximation constant
we compute the approximation constant
![]() (25)
(25)
Here, ![]() is the max norm in the space of functions. From the available theory (cf. Santos, 2000), the approximation error of the policy function is of the same order of magnitude as that of the Euler equation residuals. Then, the values of
is the max norm in the space of functions. From the available theory (cf. Santos, 2000), the approximation error of the policy function is of the same order of magnitude as that of the Euler equation residuals. Then, the values of ![]() should have bounded variability (unless the approximation
should have bounded variability (unless the approximation ![]() is very close to
is very close to ![]() ). Indeed in many cases
). Indeed in many cases ![]() hovers around certain values. Hence, any upper bound
hovers around certain values. Hence, any upper bound ![]() for these values would be a conservative estimate for the constant involved in these error estimates. It follows that the resulting assessed value,
for these values would be a conservative estimate for the constant involved in these error estimates. It follows that the resulting assessed value, ![]() , can be used to estimate an error bound for our candidate solution:
, can be used to estimate an error bound for our candidate solution:
![]() (26)
(26)
Note that in this last equation we contemplate the error between our best policy function ![]() and the true policy function
and the true policy function ![]() .
.
Therefore, worst-case error bounds are directly obtained from constants given by the theoretical analysis. These bounds are usually very conservative. Numerical estimation of these bounds should be viewed as a heuristic procedure to assess the actual value of the bounding constant. From the available theory we know that the error of the equilibrium function is of the same order of magnitude as the size of the Euler equation residuals. That is, the following error bound holds:
![]() (27)
(27)
We thus obtain an estimate ![]() for constant
for constant ![]() from various comparisons of approximated equilibrium functions.
from various comparisons of approximated equilibrium functions.
3.2.2 Accuracy of the Simulated Moments
Researchers usually focus on long-run properties of equilibrium time series. The common belief is that equilibrium orbits will stabilize and converge to a stationary distribution. Stationary distributions are simply the stochastic counterparts of steady states in deterministic models. Computation of the moments of an invariant distribution for a non-linear model is usually a rather complicated task—even for analytical equilibrium functions. Hence, laws of large numbers are invoked to compute the moments of an invariant distribution from the sample moments.
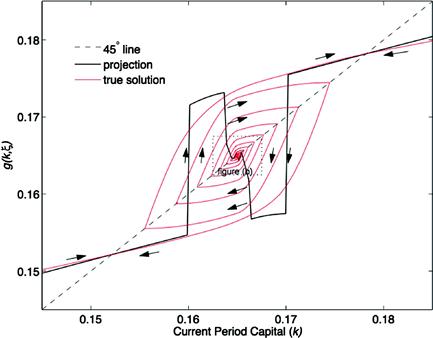
The above one-period approximation error (27) is just a first step to control the cumulative error of numerical simulations. Following Santos and Peralta-Alva (2005), our goal now is to present some regularity conditions so that the error from the simulated statistics converges to zero as the approximated equilibrium function approaches the exact equilibrium function. The following example illustrates that certain convergence properties may not always hold.
Let us now perturb ![]() slightly so that the new stochastic matrix is the following
slightly so that the new stochastic matrix is the following
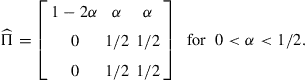
As ![]() , the sequence of stochastic matrices
, the sequence of stochastic matrices ![]() converges to
converges to
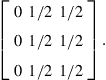
Hence, ![]() is the only possible long-run distribution for the system. Moreover,
is the only possible long-run distribution for the system. Moreover, ![]() is a transient state, and
is a transient state, and ![]() is the only ergodic set. Consequently, a small perturbation on a transition probability
is the only ergodic set. Consequently, a small perturbation on a transition probability ![]() may lead to a pronounced change in its invariant distributions. Indeed, small errors may propagate over time and alter the existing ergodic sets.
may lead to a pronounced change in its invariant distributions. Indeed, small errors may propagate over time and alter the existing ergodic sets.
Santos and Peralta-Alva (2005) show that certain continuity properties of the policy function suffice to establish some generalized laws of large numbers for numerical simulations. To provide a formal statement of their results, we need to lay down some standard concepts and terminology.
For ease of presentation, we restrict attention to exogenous stochastic shocks of the form
![]()
where ![]() is an iid shock. The distribution of this shock
is an iid shock. The distribution of this shock ![]() is denoted by probability measure
is denoted by probability measure ![]() on a measurable space
on a measurable space ![]() . Then, as it is standard in the literature (cf. Stokey et al., 1989) we define a new probability space comprising all infinite sequences
. Then, as it is standard in the literature (cf. Stokey et al., 1989) we define a new probability space comprising all infinite sequences ![]() . Let
. Let ![]() be the countably infinite Cartesian product of copies of E. Let
be the countably infinite Cartesian product of copies of E. Let ![]() be the
be the ![]() -field in
-field in ![]() generated by the collection of all cylinders
generated by the collection of all cylinders ![]() where
where ![]() for
for ![]() . A probability measure
. A probability measure ![]() can be constructed over the finite-dimensional sets as
can be constructed over the finite-dimensional sets as
![]()
Measure ![]() has a unique extension on
has a unique extension on ![]() . Hence, the triple
. Hence, the triple ![]() denotes a probability space. Now, for every initial value
denotes a probability space. Now, for every initial value ![]() and sequence of shocks
and sequence of shocks ![]() , let
, let ![]() be the sample paths generated by the policy functions
be the sample paths generated by the policy functions ![]() , so that
, so that ![]() for all
for all ![]() .
.
Let ![]() be the sample path generated from an approximate policy function
be the sample path generated from an approximate policy function ![]() . Averaging over these sample paths we get sequences of simulated statistics
. Averaging over these sample paths we get sequences of simulated statistics ![]() as defined by some function
as defined by some function ![]() . Let
. Let ![]() be the expected value under an invariant distribution
be the expected value under an invariant distribution ![]() of the original equilibrium function
of the original equilibrium function ![]() . Santos and Peralta-Alva (2005) establish the following result:
. Santos and Peralta-Alva (2005) establish the following result:
Therefore, for a sufficiently good numerical approximation ![]() and for a sufficiently large
and for a sufficiently large ![]() the sequence
the sequence ![]() approaches (almost surely) the expected value
approaches (almost surely) the expected value ![]() of the invariant distribution
of the invariant distribution ![]() of the original equilibrium function
of the original equilibrium function ![]() .
.
Note that this theorem does not require uniqueness of the invariant distribution for each numerical policy function. This requirement would be rather restrictive: numerical approximations may contain multiple steady states. For instance, consider a polynomial approximation of the policy function. As is well understood, the fluctuating behavior of polynomials may give rise to several ergodic sets. But according to the theorem, these multiple distributions from these approximations will eventually be close to the unique invariant distribution of the model. Moreover, if the model has multiple invariant distributions, then there is an extension of Theorem 1 in which the simulated statics of computed policy functions ![]() become close to those of some invariant distribution of the model for
become close to those of some invariant distribution of the model for ![]() large enough [see
large enough [see ![]() .
. ![]() .].
.].
The existence of an invariant distribution is guaranteed under the so-called Feller property (cf. Stokey et al., 1989). The Feller property is satisfied if equilibrium function ![]() is a continuous mapping on a compact domain or if the domain is made up of a finite number of points. (These latter stochastic processes are called Markov chains.) There are several extensions of these results to non-continuous mappings and non-compact domains (cf. Futia, 1982; Hopenhayn and Prescott, 1992; Stenflo, 2001). These papers also establish conditions for uniqueness of the invariant distribution under mixing or contractive conditions. The following contraction property is taken from Stenflo (2001): CONDITION C: There exists a constant
is a continuous mapping on a compact domain or if the domain is made up of a finite number of points. (These latter stochastic processes are called Markov chains.) There are several extensions of these results to non-continuous mappings and non-compact domains (cf. Futia, 1982; Hopenhayn and Prescott, 1992; Stenflo, 2001). These papers also establish conditions for uniqueness of the invariant distribution under mixing or contractive conditions. The following contraction property is taken from Stenflo (2001): CONDITION C: There exists a constant ![]() such that
such that ![]() for all pairs
for all pairs ![]() .
.
Condition C may arise naturally in growth models [Schenk-Hoppe and Schmalfuss (2001)], in learning models (Ellison and Fudenberg, 1993), and in certain types of stochastic games (Sanghvi and Sobel, 1976).
Using Condition C, the following bounds for the approximation error of the simulated moments are established in Santos and Peralta-Alva (2005). A real-valued function ![]() on
on ![]() is called Lipschitz with constant
is called Lipschitz with constant ![]() if
if ![]() for all pairs
for all pairs ![]() and
and ![]() .
.
Again, this is another application of the contraction property, which becomes instrumental to substantiate error bounds. Stachurski and Martin (2008) study a Monte Carlo algorithm for computing densities of invariant measures and establish global asymptotic convergence as well as error bounds.
3.3 Calibration, Estimation, and Testing
As in other applied sciences, economic theories build upon the analysis of highly stylized models. The estimation and testing of these models can be quite challenging, and the literature is still in a process of early development in which various technical problems need to be overcome. Indeed, there are important classes of models for which we still lack a good sense of the types of conditions under which simulation-based methods may yield estimators that achieve consistency and asymptotic normality. Besides, computation of these estimators may turn out to be a quite complex task.
A basic tenet of simulation-based estimation is that parameters are often specified as the by-product of some simplifying assumptions with no close empirical counterparts. These parameter values will affect the equilibrium dynamics which can be highly non-linear. Hence, as a first step in the process of estimation it seems reasonable to characterize the invariant probability measures or steady-state solutions, which commonly determine the long-run behavior of a model. But because of lack of information about the domain and form of these invariant probabilities, the model must be simulated to compute the moments and other useful statistics of these distributions.
Therefore, the process of estimation may entail the simulation of a parameterized family of models. Relatively fast algorithms are thus needed in order to sample the parameter space. Classical properties of these estimators such as consistency and asymptotic normality will depend on various conditions of the equilibrium functions. The study of these asymptotic properties requires methods of analysis of probability theory in its interface with dynamical systems.
Our purpose here is to discuss some available methods for model estimation and testing. To make further progress in this discussion, let us rewrite (18) in the following form
![]() (29)
(29)
![]() (30)
(30)
where ![]() is a vector of parameters, and
is a vector of parameters, and ![]() . Functions
. Functions ![]() and
and ![]() may represent the exact solution of a dynamic model or some numerical approximation. One should realize that the assumptions underlying these functions may be of a different economic significance, since
may represent the exact solution of a dynamic model or some numerical approximation. One should realize that the assumptions underlying these functions may be of a different economic significance, since ![]() governs the law of motion of the vector of endogenous variables
governs the law of motion of the vector of endogenous variables ![]() , and
, and ![]() represents the evolution of the exogenous process
represents the evolution of the exogenous process ![]() . Observe that the vector of parameters
. Observe that the vector of parameters ![]() characterizing the evolution of the exogenous state variables
characterizing the evolution of the exogenous state variables ![]() may influence the law of motion of the endogenous variables
may influence the law of motion of the endogenous variables ![]() , but this endogenous process may also be influenced by some additional parameters
, but this endogenous process may also be influenced by some additional parameters ![]() which may stem from utility and production functions.
which may stem from utility and production functions.
For a given notion of distance the estimation problem may be defined as follows: Find a parameter vector ![]() such that a selected set of model predictions is closest to those of the data generating process. An estimator is thus a rule that yields a sequence of candidate solutions
such that a selected set of model predictions is closest to those of the data generating process. An estimator is thus a rule that yields a sequence of candidate solutions ![]() from finite samples of model simulations and data. It is generally agreed that a reasonable estimator should possess the following consistency property: as sampling errors vanish the sequence of estimated values
from finite samples of model simulations and data. It is generally agreed that a reasonable estimator should possess the following consistency property: as sampling errors vanish the sequence of estimated values ![]() should converge to the optimal solution
should converge to the optimal solution ![]() . Further, we would like the estimator to satisfy asymptotic normality so that it is possible to derive approximate confidence intervals and address questions of efficiency.
. Further, we would like the estimator to satisfy asymptotic normality so that it is possible to derive approximate confidence intervals and address questions of efficiency.
Data-based estimators are usually quite effective, since they may involve low computational cost. For instance, standard non-linear least squares (e.g., Jennrich, 1969) and other generalized estimators (cf., Newey and McFadden, 1994) may be applied whenever functions ![]() and
and ![]() have analytical representations. Similarly, from functions
have analytical representations. Similarly, from functions ![]() and
and ![]() one can compute the likelihood function that posits a probability law for the process
one can compute the likelihood function that posits a probability law for the process ![]() with explicit dependence on the parameter vector
with explicit dependence on the parameter vector ![]() . In general, data-based estimation methods can be applied for closed-form representations of the dynamic process of state variables and vector of parameters. This is particularly restrictive for the law of motion of the endogenous state variables: only under rather special circumstances one obtains a closed-form representation for the solution of a non-linear dynamic model
. In general, data-based estimation methods can be applied for closed-form representations of the dynamic process of state variables and vector of parameters. This is particularly restrictive for the law of motion of the endogenous state variables: only under rather special circumstances one obtains a closed-form representation for the solution of a non-linear dynamic model ![]() .
.
Since a change in ![]() may feed into the dynamics of the system in rather complex ways, traditional (data-based) estimators may be of limited applicability for non-linear dynamic models. Indeed, these estimators do not take into account the effects of parameter changes in the equilibrium dynamics, and hence they can only be applied to full-fledged, structural dynamic models under fairly specific conditions. In traditional estimation there is only a unique distribution generated by the data process, and such distribution is not influenced by the vector of parameters. For a simulation-based estimator, however, the following major analytical difficulty arises: each vector of parameters is manifested in a different dynamical system. Hence, proofs of consistency of the estimator would have to cope with a continuous family of invariant distributions defined over the parameter space.
may feed into the dynamics of the system in rather complex ways, traditional (data-based) estimators may be of limited applicability for non-linear dynamic models. Indeed, these estimators do not take into account the effects of parameter changes in the equilibrium dynamics, and hence they can only be applied to full-fledged, structural dynamic models under fairly specific conditions. In traditional estimation there is only a unique distribution generated by the data process, and such distribution is not influenced by the vector of parameters. For a simulation-based estimator, however, the following major analytical difficulty arises: each vector of parameters is manifested in a different dynamical system. Hence, proofs of consistency of the estimator would have to cope with a continuous family of invariant distributions defined over the parameter space.
An alternative route to the estimation of non-linear dynamic models is via the Euler equations (e.g., see Hansen and Singleton, 1982) where the vector of parameters is determined by a set of orthogonality conditions conforming the first-order conditions or Euler equations of the optimization problem. A main advantage of this approach is that one does not need to model the shock process or to know the functional dependence of the law of motion of the state variables on the vector of parameters, since the objective is to find the best fit for the Euler equations over available data samples, within the admissible region of parameter values. The estimation of the Euler equations can then be carried out by standard non-linear least squares or by some other generalized estimator (Hansen, 1982). However, model estimation via the Euler equations under traditional statistical methods is not always feasible. These methods are only valid for convex optimization problems with interior solutions in which technically the decision variables outnumber the parameters; moreover, the objective and feasibility constraints of the optimization problem must satisfy certain strict separability conditions along with the process of exogenous shocks. Sometimes the model may feature some latent variables or some private information which is not observed by the econometrician (e.g., shocks to preferences); lack of knowledge about these components of the model may preclude the specification of the Euler equations (e.g., Duffie and Singleton, 1993). An even more fundamental limitation is that the estimation is confined to orthogonality conditions generated by the Euler equations, whereas it may be of more economic relevance to estimate or test a model along some other dimensions such as those including certain moments of the invariant distributions or the process of convergence to such stationary solutions.
3.3.1 Calibration
Faced with these complex analytical problems, the economics literature has come up with many simplifying approaches for model estimation. Starting with the real business cycle literature (e.g., Cooley and Prescott, 1995), parameter values are often determined from independent evidence or from other parts of the theory not related to the basic facts selected for testing. This is loosely referred to as model calibration. Christiano and Eichembaum (1992) is a good example of this approach. They consider a business cycle model, and pin down parameter values from various steady-state conditions. In other words, the model is evaluated according to business cycle predictions, and it is calibrated to replicate empirical properties of balanced growth paths. As a matter of fact, Christiano and Eichembaum (1992) are able to provide standard errors for their estimates, and hence their analysis goes beyond most calibration exercises.
3.3.2 Simulation-Based Estimation
The aforementioned limitations of traditional estimation methods for non-linear systems along with advances in computing have fostered the more recent use of estimation and testing based upon simulations of the model. Estimation by model simulation offers more flexibility to evaluate the behavior of the model by computing statistics of its invariant distributions that can be compared with their data counterparts. But this greater flexibility inherent in simulation-based estimators entails a major computational cost: extensive model simulations may be needed to sample the entire parameter space. Relatively little is known about the family of models in which simulation-based estimators would have good asymptotic properties such as consistency and normality. These properties would seem a minimal requirement for a rigorous application of estimation methods under the rather complex and delicate techniques of numerical simulation in which approximation errors may propagate in unexpected ways.
To fix ideas, we will focus on a simulated moments estimator (SME) put forward by Lee and Ingram (1991). This estimation method allows the researcher to assess the behavior of the model along various dimensions. Indeed, the conditions characterizing the estimation process may involve some moments of the model’s invariant distributions or some other features of the dynamics on which the desired vector of parameters must be selected.
Several elements conform the SME. First, one specifies a target function or function of interest which typically would characterize a selected set of moments of the invariant distribution of the model and those of the data generating process. Second, a notion of distance is defined between the selected statistics of the model and its data counterparts. The minimum distance between these statistics is attained at some vector of parameters ![]() in a space
in a space ![]() . Then, the estimation method yields a sequence of candidate solutions
. Then, the estimation method yields a sequence of candidate solutions ![]() over increasing finite samples of the model simulations
over increasing finite samples of the model simulations ![]() and data
and data ![]() so as to approximate the true value
so as to approximate the true value ![]() .
.
(a) The target function (or function of interest) ![]() is assumed to be continuous. This function may represent
is assumed to be continuous. This function may represent ![]() moments of an invariant distribution
moments of an invariant distribution ![]() under
under ![]() defined as
defined as ![]() for
for ![]() . The expected value of
. The expected value of ![]() over the invariant distribution of the data-generating process will be denoted by
over the invariant distribution of the data-generating process will be denoted by ![]() .
.
(b) The distance function ![]() is assumed to be continuous. The minimum distance is attained at a vector of parameter values
is assumed to be continuous. The minimum distance is attained at a vector of parameter values
![]() (31)
(31)
A typical specification of the distance function ![]() is the following quadratic form:
is the following quadratic form:
![]() (32)
(32)
where ![]() is a positive definite
is a positive definite ![]() matrix. Under certain standard assumptions (cf., Santos and Peralta-Alva, 2005, Theorem 3.2) one can show there exists an optimal solution
matrix. Under certain standard assumptions (cf., Santos and Peralta-Alva, 2005, Theorem 3.2) one can show there exists an optimal solution ![]() . Moreover, for the analysis below there is no restriction of generality to consider that
. Moreover, for the analysis below there is no restriction of generality to consider that ![]() is unique.
is unique.
(c) An estimation rule characterized by a sequence of distance functions ![]() and choices for the horizon
and choices for the horizon ![]() of the model simulations. This rule yields a sequence of estimated values
of the model simulations. This rule yields a sequence of estimated values ![]() from associated optimization problems with finite samples of the model simulations
from associated optimization problems with finite samples of the model simulations ![]() and data
and data ![]() . The estimated value
. The estimated value ![]() is obtained as
is obtained as
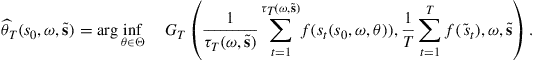 (33)
(33)
We assume that the sequence of continuous functions ![]() converges uniformly to function
converges uniformly to function ![]() for
for ![]() -almost all
-almost all ![]() , and the sequence of functions
, and the sequence of functions ![]() goes to
goes to ![]() for
for ![]() -almost all
-almost all ![]() . Note that both functions
. Note that both functions ![]() and
and ![]() are allowed to depend on the sequence of random shocks
are allowed to depend on the sequence of random shocks ![]() and data
and data ![]() , and
, and ![]() is a measure defined over
is a measure defined over ![]() and
and ![]() . These functions will usually depend on all information available up to time
. These functions will usually depend on all information available up to time ![]() . The rule
. The rule ![]() reflects that the length of model’s simulations may be different from that of data samples.
reflects that the length of model’s simulations may be different from that of data samples.
It should be stressed that problem (31) is defined over population characteristics of the model and of the data-generating process, whereas problem (33) is defined over statistics of finite simulations and data.
By the measurable selection theorem (Crauel, 2002) there exists a sequence of measurable functions ![]() . See Duffie and Singleton (1993) and Santos (2010) for asymptotic properties of this estimator. Sometimes vector
. See Duffie and Singleton (1993) and Santos (2010) for asymptotic properties of this estimator. Sometimes vector ![]() could be estimated independently, and hence we could then try to get an SME estimate of
could be estimated independently, and hence we could then try to get an SME estimate of ![]() . This mixed procedure can still recover consistency and it may save on computational cost. Consistency of the estimator can also be established for numerical approximations: the SME would converge to the true value
. This mixed procedure can still recover consistency and it may save on computational cost. Consistency of the estimator can also be established for numerical approximations: the SME would converge to the true value ![]() as the approximation error goes to zero.
as the approximation error goes to zero.
Another route to estimation is via the likelihood function. The existence of such functions imposes certain regularity conditions on the dynamics of the model which are sometimes hard to check. Fernandez-Villaverde and Rubio-Ramirez (2007) propose computation of the likelihood function by a particle filter. Numerical errors of the computed solution will also affect the likelihood function and the estimated parameter values (see Fernandez-Villaverde et al., 2006). Recent research on dynamic stochastic general equilibrium models has made extensive use of Monte Carlo methods such as the Markov Chain Monte Carlo method and the Metropolis-Hastings algorithm (e.g., Fernandez-Villaverde, 2012).
4 Recursive Methods for Non-optimal Economies
We now get into the more complex issue of numerical simulation of non-optimal economies. In general, these models cannot be computed by associated global optimization problems—ruling out the application of numerical DP algorithms as well as the derivation of error bounds for strongly concave optimization problems. This leaves the field open for algorithms based on approximating the Euler equations such as perturbation and projection methods. These approximation methods, however, search for smooth equilibrium functions; as already pointed out, the existence of continuous Markov equilibria cannot be insured under regularity assumptions. The existence problem is a technical issue which is mostly ignored in the applied literature. See Hellwig (1983) and Kydland and Prescott (1980) for early discussions on the non-existence of simple Markov equilibrium, and Abreu et al. (1990) for a related approach to repeated games.
As it is clear from these early contributions, simple Markov equilibrium may only fail to exist in the presence of multiple equilibria. Then, to insure uniqueness of equilibrium the literature has considered a stronger related condition: monotonicity of equilibrium. This monotonicity condition means that if the values of our predetermined state variables are increased today, then the resulting equilibrium path must always reflect higher values for these variables in the future. Monotonicity is hard to verify in models with heterogeneous agents with constraints that occasionally bind, or in models with incomplete financial markets, or with distorting taxes and externalities.
Indeed, most well-known cases of monotone dynamics have been confined to one-dimensional models. For instance, Coleman (1991), Greenwood and Huffman (1995), and Datta et al. (2002) consider versions of the one-sector neoclassical growth model and establish the existence of a simple Markov equilibrium by an Euler iteration method. This iterative method guarantees uniform convergence, but it does not display the contraction property as the DP algorithm. It is unclear how this approach may be extended to other models, and several examples have been found of non-existence of continuous simple Markov equilibria (cf. Kubler and Schmedders, 2002; Kubler and Polemarchakis, 2004; Santos, 2002).
Therefore, for non-optimal economies a recursive representation of equilibria may only be possible when conditioning over an expanded set of state variables. Following Duffie et al. (1994), the existence of a Markov equilibrium in a generalized space of variables is proved in Kubler and Schmedders (2003) for an asset-pricing model with collateral constraints. Feng et al. (2012) extend these existence results to other economies, and define a Markov equilibrium as a solution over an expanded state of variables that include the shadow values of investment. The addition of the shadow values of investment as state variables facilitates computation of the numerical solution. This formulation was originally proposed by Kydland and Prescott (1980), and later used in Marcet and Marimon (1998) for recursive contracts, and in Phelan and Stacchetti (2001) for a competitive economy with a representative agent. The main insight of Feng et al. (2012) is to develop a reliable and computable algorithm with good approximation properties for the numerical simulation of competitive economies with heterogeneous agents and market frictions including endogenous borrowing constraints. Before advancing to the study of the theoretical issues involved, we begin with a few examples to illustrate some of the pitfalls found in the computation of non-optimal economies.
4.1 Problems in the Simulation of Non-Optimal Economies
The following examples make clear that a continuous Markov equilibrium on the minimal state space may fail to exist. Hence, the application of standard numerical algorithms may actually result in serious quantitative biases. As we will see, other families of algorithms are needed for the numerical approximation of non-optimal economies.
4.1.1 A Growth Model with Taxes
Consider the following parameterization for the growth model with taxes of Section 2:
![]()
Assume that income taxes are only imposed on households’ capital income. More specifically, this form of taxation is determined by the following piecewise-linear schedule:
Santos (2002, Prop. 3.4) shows that a continuous Markov equilibrium fails to exist. For this specification of the model, there are three steady states: the middle steady state is unstable and has two complex eigenvalues while the other two steady states are saddle-path stable; see Figure 1. Standard algorithms approximating the Euler equation would solve for a continuous policy function of the form
![]()
where ![]() belongs to a finite-dimensional space of continuous functions as defined by a vector of parameters
belongs to a finite-dimensional space of continuous functions as defined by a vector of parameters ![]() . We obtain an estimate for
. We obtain an estimate for ![]() by forming a discrete system of Euler equations over as many grid points
by forming a discrete system of Euler equations over as many grid points ![]() as the dimensionality of the parameter space:
as the dimensionality of the parameter space:
![]()
We assume that ![]() belongs to the class of piecewise-linear functions, and employ a uniform grid of 5000 points over the domain
belongs to the class of piecewise-linear functions, and employ a uniform grid of 5000 points over the domain ![]() . The resulting approximation, together with a highly accurate solution (in this case the shooting algorithm can be implemented), is illustrated in Figure 1.
. The resulting approximation, together with a highly accurate solution (in this case the shooting algorithm can be implemented), is illustrated in Figure 1.
This approximation of the Euler equation over piecewise-continuous functions converged up to computer precision in only three iterations. This fast convergence is actually deceptive because as pointed out above no continuous policy function does exist. Indeed, the dynamic behavior implied by the continuous function approximation is quite different from the true one. As a matter of fact, the numerical approximation displays four more steady states, and changes substantially the basins of attraction of the original steady states (see Figure 1).
A further test of the fixed-point solution of this algorithm based on the Euler equation residuals produced mixed results (see Figure 2). First, the average Euler equation residual over the domain of feasible capitals is fairly small, i.e., it is equal to 0.0073. Second, the maximum Euler equation residual is slightly more pronounced in a small area near the unstable steady state. But even in that area, the error is not extremely large: in three tiny intervals the Euler equation residuals are just around 0.06. Therefore, from these computational tests a researcher may be led to conclude that the putative continuous solution should mimic well the true equilibrium dynamics.
4.1.2 An Overlapping Generations Economy
Consider the following specification for the overlapping generations economy presented in Section 2. There are two perishable commodities, and two types of agents that live for two periods. There is no Lucas tree. In the first period of life of each agent, endowments are stochastic and depend only on the current state ![]() , while in the second period they are deterministic. In particular,
, while in the second period they are deterministic. In particular, ![]() ,
, ![]() if
if ![]() , and
, and ![]() ,
, ![]() if
if ![]() , while
, while ![]() and
and ![]() .
.
The utility function of an agent of type 1 is given by
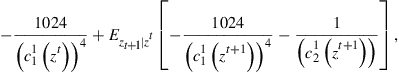
while that of agent of type 2 is given by
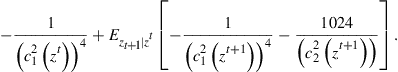
For this model, it is easy to show that a competitive equilibrium exists. Practitioners are, however, interested in competitive equilibria that have a recursive structure on the space of shocks and wealth distributions. Specifically, standard computational methods search for a Markovian equilibrium on the natural state space. Hence, let us consider that there exists a continuous function ![]() such that equilibrium allocations can be characterized by:
such that equilibrium allocations can be characterized by:
![]()
Kubler and Polemarchakis (2004) show that such a representation does not exist for this economy. Specifically, the unique equilibrium of this economy is described by:
2. Given node ![]() with
with ![]() , we have that for all successors of
, we have that for all successors of ![]() , namely,
, namely, ![]() and
and ![]() ,
, ![]() , and
, and ![]() .
.
3. Given node ![]() with
with ![]() , we have that for all successors of
, we have that for all successors of ![]() , namely,
, namely, ![]() and
and ![]() ,
, ![]() , and
, and ![]() .
.
Observe that knowledge of the current shock and wealth distribution is not enough to characterize consumption of the old.
As in our previous example, and in spite of realizing that a recursive equilibrium on the natural state space does not exist, we applied the projection method to obtain a numerical approximation to function ![]() . We employed a grid of 100 equally spaced points under piecewise-linear interpolation, and assumed
. We employed a grid of 100 equally spaced points under piecewise-linear interpolation, and assumed ![]() . Based on this approach, we ended up with an approximated policy function with Euler equation residuals of order
. Based on this approach, we ended up with an approximated policy function with Euler equation residuals of order ![]() (on average). We again find that the time series properties of the approximated policy may be substantially different from the equilibrium dynamics. As a simple illustration, consider Figures 3 and 4. These figures summarize portfolio holdings and the relative price of good two, respectively. In equilibrium bond holdings should equal zero, while the approximate policy yields positive values. Similarly, the relative price of good 2 should equal either 1 or 7.9, depending on the shock, while it takes a continuum of values ranging from 6.5 to 9 in the approximate policy. To further illustrate the differences between approximate and exact solutions, Table 1 reports a simulated sample for the exact and approximate solutions over the same sequence of shocks in a sample path of 10,000 periods.
(on average). We again find that the time series properties of the approximated policy may be substantially different from the equilibrium dynamics. As a simple illustration, consider Figures 3 and 4. These figures summarize portfolio holdings and the relative price of good two, respectively. In equilibrium bond holdings should equal zero, while the approximate policy yields positive values. Similarly, the relative price of good 2 should equal either 1 or 7.9, depending on the shock, while it takes a continuum of values ranging from 6.5 to 9 in the approximate policy. To further illustrate the differences between approximate and exact solutions, Table 1 reports a simulated sample for the exact and approximate solutions over the same sequence of shocks in a sample path of 10,000 periods.
In summary, for non-optimal economies standard solution methods may introduce substantial biases into our quantitative predictions.
4.2 Numerical Solution of Non-Optimal Economies
Feng et al. (2012) develop a numerical algorithm for approximating equilibrium solutions of non-optimal economies. A recursive representation for equilibria is established on a state space conformed by the standard variables, ![]() , and the vector of shadow values of the marginal return to investment for all assets and all agents,
, and the vector of shadow values of the marginal return to investment for all assets and all agents, ![]() . This algorithm is guaranteed to converge and has desirable asymptotic properties.
. This algorithm is guaranteed to converge and has desirable asymptotic properties.
4.2.1 The Theoretical Algorithm
A fundamental element of this approach is operator ![]() . An iterative procedure based on this operator converges to the equilibrium correspondence
. An iterative procedure based on this operator converges to the equilibrium correspondence ![]() . This equilibrium correspondence is defined as the set of possible equilibrium values for
. This equilibrium correspondence is defined as the set of possible equilibrium values for ![]() , given
, given ![]() . As illustrated presently, once the equilibrium correspondence has been secured, we can provide a recursive representation of equilibria on the enlarged state
. As illustrated presently, once the equilibrium correspondence has been secured, we can provide a recursive representation of equilibria on the enlarged state ![]() .
.
Let ![]() be any initial node, and
be any initial node, and ![]() be the set of immediate successor states. For convenience of computation, this set is assumed to be finite. Pick any correspondence
be the set of immediate successor states. For convenience of computation, this set is assumed to be finite. Pick any correspondence ![]() , where
, where ![]() is the set of possible shadow values of investment. Then, for each
is the set of possible shadow values of investment. Then, for each ![]() , we define operator
, we define operator ![]() as the set of all values
as the set of all values ![]() with the property that there are current endogenous variables
with the property that there are current endogenous variables ![]() , and vectors
, and vectors ![]() and
and ![]() for each of the successors of
for each of the successors of ![]() , denoted by
, denoted by ![]() , that satisfy the temporary equilibrium conditions
, that satisfy the temporary equilibrium conditions
![]()
The following result is proved in Feng et al. (2012):
Theorem 3 provides the theoretical foundations for computing equilibria for non-optimal economies. Specifically, this result states that operator ![]() can be applied to any initial guess (correspondence) of possible values
can be applied to any initial guess (correspondence) of possible values ![]() and iterate until a desirable level of convergence to
and iterate until a desirable level of convergence to ![]() is attained. From operator
is attained. From operator ![]() we can select a measurable policy function
we can select a measurable policy function ![]() , and a transition function
, and a transition function ![]() , for all
, for all ![]() . These functions may not be continuous but the state space has been adequately chosen so that they yield a Markovian characterization of a dynamic equilibrium in the enlarged state space
. These functions may not be continuous but the state space has been adequately chosen so that they yield a Markovian characterization of a dynamic equilibrium in the enlarged state space ![]() . An important advantage of this approach is that if multiple equilibria exist then all of them can be computed. If the equilibrium is always unique, then
. An important advantage of this approach is that if multiple equilibria exist then all of them can be computed. If the equilibrium is always unique, then ![]() defines a continuous law of motion or Markovian equilibrium over state variables
defines a continuous law of motion or Markovian equilibrium over state variables ![]() .
.
4.2.2 Numerical Implementation
We first partition the state space into a finite set of simplices ![]() with non-empty interior and maximum diameter
with non-empty interior and maximum diameter ![]() . Over this partition define a family of step correspondences (defined as correspondences that take constant set values over each
. Over this partition define a family of step correspondences (defined as correspondences that take constant set values over each ![]() ). To obtain a computer representation of a step correspondence, the image must be discretized. We can employ an outer approximation in which each set value is defined by
). To obtain a computer representation of a step correspondence, the image must be discretized. We can employ an outer approximation in which each set value is defined by ![]() elements. Using these two discretizations we obtain a computable approximation of operator
elements. Using these two discretizations we obtain a computable approximation of operator ![]() , which we denote by
, which we denote by ![]() . By a suitable selection of an initial condition
. By a suitable selection of an initial condition ![]() and of these outer approximations, the sequence
and of these outer approximations, the sequence ![]() defined recursively as
defined recursively as ![]() converges to a limit point
converges to a limit point ![]() , which must contain the equilibrium correspondence
, which must contain the equilibrium correspondence ![]() . Again, if the equilibrium is always unique then these approximate solutions would converge uniformly to the continuous Markovian equilibrium law of motion. The following result is proved in Feng et al. (2012):
. Again, if the equilibrium is always unique then these approximate solutions would converge uniformly to the continuous Markovian equilibrium law of motion. The following result is proved in Feng et al. (2012):
It should be stressed that we lack a theory of error bounds for non-optimal economies. Nevertheless, Theorem 4 establishes a strong form of uniform convergence. Moreover, under certain regularity conditions the analysis of Kubler and Schmedders (2005) implies that for an approximate equilibrium one can construct some nearby economy so that this equilibrium becomes exact. Kubler (2011) introduces some analytical conditions under which an ![]() -equilibrium is close to an exact equilibrium.
-equilibrium is close to an exact equilibrium.
4.3 Simulated Statistics
To assess model predictions, analysts usually calculate moments of the simulated paths from a numerical approximation. The idea is that the simulated moments should approach those obtained from the original model. As discussed in Section 3, if the optimal policy is a continuous function, or if certain monotonicity conditions hold, it is possible to establish desirable convergence properties of the simulated moments. For non-optimal economies, continuity and monotonicity of Markov equilibria do not come out so naturally. In those models the equilibrium law of motion is described by an expectations correspondence conformed by feasibility and ![]() -
-![]() equilibrium conditions. Hence, for an initial vector of state variables there could be multiple continuation equilibrium paths, and coordination over these multiple equilibria may be required.
equilibrium conditions. Hence, for an initial vector of state variables there could be multiple continuation equilibrium paths, and coordination over these multiple equilibria may be required.
More precisely, for non-optimal models the equilibrium dynamics may take the following form:
![]()
where ![]() is an upper semicontinuous correspondence (instead of a continuous function as in the previous section) over a compact domain
is an upper semicontinuous correspondence (instead of a continuous function as in the previous section) over a compact domain ![]() . By the measurable selection theorem (e.g., Crauel, 2002; Hildenbrand, 1974) there exists a sequence of measurable mappings
. By the measurable selection theorem (e.g., Crauel, 2002; Hildenbrand, 1974) there exists a sequence of measurable mappings ![]() , such that
, such that ![]() for all
for all ![]() and all
and all ![]() (
(![]() denoting closure). Let us pick a measurable selection
denoting closure). Let us pick a measurable selection ![]() . Let
. Let ![]() be the Borel
be the Borel ![]() -algebra of
-algebra of ![]() . Then, we can define a transition probability
. Then, we can define a transition probability ![]() by
by
![]() (34)
(34)
Note that ![]() is a probability measure for each
is a probability measure for each ![]() , and
, and ![]() is a measurable function for each
is a measurable function for each ![]() in
in ![]() .
.
Finally, given an initial probability ![]() on
on ![]() , the evolution of future probabilities,
, the evolution of future probabilities, ![]() , can be specified by the following operator
, can be specified by the following operator ![]() that takes the space of probabilities on
that takes the space of probabilities on ![]() into itself
into itself
![]()
for all ![]() in
in ![]() and
and ![]() . An invariant probability measure or invariant distribution
. An invariant probability measure or invariant distribution ![]() is a fixed point of operator
is a fixed point of operator ![]() , i.e.,
, i.e., ![]() . Measure
. Measure ![]() is called ergodic if
is called ergodic if ![]() or
or ![]() for every invariant set
for every invariant set ![]() under transition probability
under transition probability ![]() .
.
To guarantee the existence of an ergodic measure some researchers have resorted to a discretization of the state space (Ericson and Pakes, 1995). Discrete state spaces are quite convenient to compute the set of invariant measures, but these spaces become awkward for the characterization of optimal solutions and the calibration and estimation of the model. If the state takes a continuum of values then there are two basic ways to establish the existence of an invariant measure (e.g., Crauel, 2002): (i) via the Markov-Kakutani fixed-point theorem: an upper semicontinuous convex-valued correspondence in a compact set has a fixed point and (ii) via a Krylov-Bogoliouboff type argument: the invariant measure is constructed by an iterative process as limit of a sequence of empirical probability measures or time means. Blume (1982) and Duffie et al. (1994) follow (i), and are required to randomize over the existing equilibria to build a convex-valued correspondence. Randomizing over the equilibrium correspondence may result in an undesirable expansion of the equilibrium set.
Recent work by Santos and Peralta-Alva (2012) follows (ii) and dispenses with randomizations. They also validate a generalized law of large numbers that guarantees the convergence of the simulated moments to the population moments of some stationary equilibrium. These results apply naturally to approximate solutions. Hence, the simulated moments from a numerical solution approach asymptotically some invariant distribution of the numerical approximation. Finally, combining these arguments with some convergence results, they establish some accuracy properties for the simulated moments as the approximation error goes to zero. We summarize these results as follows:
(i) ![]() : Transition correspondence
: Transition correspondence ![]() has an invariant probability
has an invariant probability ![]() ; this invariant distribution is constructed as a limit of a sequence of empirical measures using a Krylov-Bogoliouboff type argument. This iterative process is extended to stochastic dynamical systems described by correspondences, and it works when the space of measures is compact and the equilibrium correspondence is upper semicontinuous.
; this invariant distribution is constructed as a limit of a sequence of empirical measures using a Krylov-Bogoliouboff type argument. This iterative process is extended to stochastic dynamical systems described by correspondences, and it works when the space of measures is compact and the equilibrium correspondence is upper semicontinuous.
(ii) ![]() . These laws of motion are obtained under operator
. These laws of motion are obtained under operator ![]() . There are tight upper
. There are tight upper ![]() and lower
and lower ![]() bounds such that with probability one the corresponding moments from simulated paths
bounds such that with probability one the corresponding moments from simulated paths ![]() of these approximate functions stay within the prescribed bounds. More precisely, let
of these approximate functions stay within the prescribed bounds. More precisely, let ![]() and
and ![]() be a function of interest. Let
be a function of interest. Let ![]() represent a simulated moment or some other statistic. Then, with probability one, every limit point of
represent a simulated moment or some other statistic. Then, with probability one, every limit point of ![]() must be within the corresponding bounds
must be within the corresponding bounds ![]() and
and ![]() .
.
(iii) ![]() : For every
: For every ![]() we can consider a sufficiently good discretized operator
we can consider a sufficiently good discretized operator ![]() and equilibrium correspondence
and equilibrium correspondence ![]() such that for every simulated path
such that for every simulated path ![]() there are equilibrium invariant distributions
there are equilibrium invariant distributions ![]() satisfying
satisfying ![]() almost surely. Of course, the model has a unique invariant distribution
almost surely. Of course, the model has a unique invariant distribution ![]() then
then ![]() and the above expression reads as
and the above expression reads as ![]() .
.
In these results, the primitive elements in (i–iii) are Markovian equilibrium selections over the original equilibrium correspondences without performing arbitrary randomizations.
5 Numerical Experiments
In this section we consider some further examples to illustrate the workings of some algorithms and the accuracy of numerical approximations. There is a vast literature devoted to the construction of algorithms computing simple Markov equilibria. We will show how the approximation error can be estimated from the Euler equation residuals. We also consider certain specifications for our model economies with multiple Markov equilibria—or where a Markov equilibrium is not known to exist. In these latter cases the application of algorithms searching for continuous policy functions may lead to rather unsatisfactory results.
5.1 Accuracy for Models with Simple Markov Equilibria
We now consider a specification for the growth model of Section 2 with no taxation. We allow for a CES Bernoulli utility function:
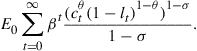
The production technology will be assumed Cobb-Douglas so that total output is thus given by ![]() . In our computations the shock process is set so as to approximate an underlying continuum law of motion
. In our computations the shock process is set so as to approximate an underlying continuum law of motion ![]() , with
, with ![]() .
.
Aruoba et al. (2006) provide a thorough examination of the properties of alternative approximation schemes for the solution of this model. We follow their approach and study the accuracy of approximations employing their basic parameterizations. Let us start with their benchmark case:
![]()
Once we have secured the best possible numerical approximation ![]() , we can provide estimates for the approximation error as described in Section 3. The key element of this approach requires values for
, we can provide estimates for the approximation error as described in Section 3. The key element of this approach requires values for
![]()
where ![]() is any other coarser numerical approximation, and
is any other coarser numerical approximation, and ![]() is the maximum Euler residual under policy
is the maximum Euler residual under policy ![]() .
.
We follow Aruoba et al. (2006) and derive numerical approximations for the model under various approximations, including the policy with the smallest Euler equation residuals ![]() , under the DP approximation, and other faster methods (to obtain alternative
, under the DP approximation, and other faster methods (to obtain alternative ![]() ) such as linear approximations, perturbations (of orders 2 and 5), and projections. We take the highest value for
) such as linear approximations, perturbations (of orders 2 and 5), and projections. We take the highest value for ![]() over all approximations as our estimate
over all approximations as our estimate ![]() for the constant required in the error estimates of Section 3:
for the constant required in the error estimates of Section 3:
![]()
Our accuracy estimates for the baseline specification of the model and for some alternative parameterizations are summarized in Table 2. All errors are estimated for an interval of the deterministic steady state comprising ![]() 30% of the steady-state value.
30% of the steady-state value.
Table 2
Accuracy estimates. Parameterizations are only indicated for deviations from baseline values.
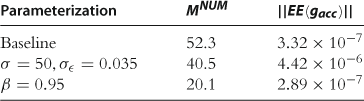
Hence, Aruoba et al. (2006) provide Euler equation residuals of the order of ![]() . Our exercise shows that these residuals translate into approximation errors for the policy function of the order of
. Our exercise shows that these residuals translate into approximation errors for the policy function of the order of ![]() , since the constants
, since the constants ![]() involved in these error estimates are always below 100.
involved in these error estimates are always below 100.
5.2 Simulation of Non-Optimal Economies
5.2.1 An Overlapping Generations Model
We now rewrite the OLG economy of Section 2 along the lines of the classical monetary models of Benhabib and Day (1982) and Grandmont (1985). This version of the model is useful for illustrative purposes because it can be solved with arbitrary accuracy. Hence, we can compare the true solution of the model with alternative numerical approximations. The model is deterministic. There are two agents that live for two periods (except for the initially old agent, who only lives for one period). Each individual receives an endowment ![]() of the perishable good when young and
of the perishable good when young and ![]() when old. There is a single asset, money, that pays zero dividends at each given period. The initial old agent is endowed with the existing money supply
when old. There is a single asset, money, that pays zero dividends at each given period. The initial old agent is endowed with the existing money supply ![]() . Let
. Let ![]() be the price level at time
be the price level at time ![]() . An agent born in period
. An agent born in period ![]() solves:
solves:
![]()
subject to
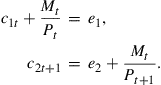
Equilibria can be characterized by the following first-order condition:
![]()
Let ![]() be real money balances at
be real money balances at ![]() . Then,
. Then,
![]()
It follows that all competitive equilibria can be generated by an offer curve in the ![]() space. A simple recursive equilibrium would be described by a function
space. A simple recursive equilibrium would be described by a function ![]() . We focus on the following parameterization:
. We focus on the following parameterization:
![]()
In this case, the offer curve is backward bending (see Figure 5). Hence, the equilibrium correspondence is multivalued. Therefore, standard methods—based on the computation of a continuous equilibrium function ![]() —may portray a partial view of the equilibrium dynamics. There is a unique stationary solution at about
—may portray a partial view of the equilibrium dynamics. There is a unique stationary solution at about ![]() , which is the point of crossing of the offer curve with the 45° line.
, which is the point of crossing of the offer curve with the 45° line.
Comparison with Other Computational Algorithms
A common practice in OLG models is to search for an equilibrium guess function ![]() , and then iterate over the temporary equilibrium conditions. We applied this procedure to our model. Depending on the initial guess, we find that either the upper or the lower arm of the offer curve would emerge as a fixed point. This strong dependence on initial conditions is a rather undesirable feature of this computational method. In particular, if we only consider the lower arm of the actual equilibrium correspondence then all competitive equilibria converge to autarchy. Indeed, the unique absorbing steady state associated with the lower arm of the equilibrium correspondence involves zero monetary holdings. Hence, even in the deterministic version, we need a global approximation of the equilibrium correspondence to analyze the various predictions of the model. As shown in Figure 6, the approximate equilibrium correspondence has a cyclical equilibrium in which real money holdings oscillate between
, and then iterate over the temporary equilibrium conditions. We applied this procedure to our model. Depending on the initial guess, we find that either the upper or the lower arm of the offer curve would emerge as a fixed point. This strong dependence on initial conditions is a rather undesirable feature of this computational method. In particular, if we only consider the lower arm of the actual equilibrium correspondence then all competitive equilibria converge to autarchy. Indeed, the unique absorbing steady state associated with the lower arm of the equilibrium correspondence involves zero monetary holdings. Hence, even in the deterministic version, we need a global approximation of the equilibrium correspondence to analyze the various predictions of the model. As shown in Figure 6, the approximate equilibrium correspondence has a cyclical equilibrium in which real money holdings oscillate between ![]() and
and ![]() . It is also known that the model has a three-period cycle. But if we iterate over the upper arm of the offer curve, we find that money holdings converge monotonically to
. It is also known that the model has a three-period cycle. But if we iterate over the upper arm of the offer curve, we find that money holdings converge monotonically to ![]() (as illustrated by the dashed lines of Figure 6). As a matter of fact, the upper arm is monotonic, and can at most have cycles of period two, whereas the model generates equilibrium cycles of various periodicities.
(as illustrated by the dashed lines of Figure 6). As a matter of fact, the upper arm is monotonic, and can at most have cycles of period two, whereas the model generates equilibrium cycles of various periodicities.
In conclusion, for OLG economies, standard computational methods based on iteration of continuous functions do not guarantee convergence to an equilibrium solution, and may miss some important properties of the equilibrium dynamics. In these economies it seems pertinent to compute the set of ![]() sequential competitive equilibria. It is certainly an easy task to compute this simple model by the algorithm of Section 4 of Feng et al. (2012). We presently illustrate the workings of this reliable algorithm in a stochastic economy with two types of agents.
sequential competitive equilibria. It is certainly an easy task to compute this simple model by the algorithm of Section 4 of Feng et al. (2012). We presently illustrate the workings of this reliable algorithm in a stochastic economy with two types of agents.
5.2.2 Asset-Pricing Models with Market Frictions
An important family of macroeconomic models incorporates financial frictions in the form of sequentially incomplete markets, borrowing constraints, transactions costs, cash-in-advance constraints, and margin and collateral requirements. Fairly general conditions rule out the existence of financial bubbles in these economies; hence, equilibrium asset prices are determined by the expected value of future dividends (Santos and Woodford, 1997). There is, however, no reliable algorithm for the numerical approximation and simulation of these economies. Here, we illustrate the workings of our algorithm in the economy of Kehoe and Levine (2001). These authors provide a characterization of steady-state equilibria for an economy with idiosyncratic risk under exogenous and endogenous borrowing constraints.
The basic economic environment stems from the asset-pricing model of Section 2. There are two possible values for the endowment, high, ![]() , or low,
, or low, ![]() . There is no aggregate risk: one household gets the high endowment while the other one gets the low endowment at every date. There is only one asset, a Lucas tree with a constant dividend,
. There is no aggregate risk: one household gets the high endowment while the other one gets the low endowment at every date. There is only one asset, a Lucas tree with a constant dividend, ![]() . Households maximize expected utility (7) subject to the sequence of budget constraints (8). We now consider an important departure from the basic model of Section 2: endogenous credit limits. More specifically, allocations (and the implied borrowing) must satisfy the participation constraint
. Households maximize expected utility (7) subject to the sequence of budget constraints (8). We now consider an important departure from the basic model of Section 2: endogenous credit limits. More specifically, allocations (and the implied borrowing) must satisfy the participation constraint
![]() (35)
(35)
Here, ![]() denotes the expected discounted value of making consumption equal to the endowment from period
denotes the expected discounted value of making consumption equal to the endowment from period ![]() onwards. This is the payoff of defaulting on credit obligations. The algorithm of Section 4 can be readily modified to accommodate this type of constraint. It simply requires iterating simultaneously on pairs of candidate shadow values of investment and values for participation (the lifetime utility of never defaulting). This operator is monotone (in the set inclusion sense) and thus the approximation results of Section 4 still hold (see Feng et al., 2012).
onwards. This is the payoff of defaulting on credit obligations. The algorithm of Section 4 can be readily modified to accommodate this type of constraint. It simply requires iterating simultaneously on pairs of candidate shadow values of investment and values for participation (the lifetime utility of never defaulting). This operator is monotone (in the set inclusion sense) and thus the approximation results of Section 4 still hold (see Feng et al., 2012).
The Equilibrium Correspondence
Note that market clearing for shares requires ![]() . Hence, in the sequel we let
. Hence, in the sequel we let ![]() be the share holdings of household 1, and
be the share holdings of household 1, and ![]() be the endowment of household 1, for
be the endowment of household 1, for ![]() . Then, the equilibrium correspondence
. Then, the equilibrium correspondence ![]() is a map from the space of possible values for share holdings and endowments for agent 1 into the set of possible equilibrium shadow values of investment for each agent and participation utilities
is a map from the space of possible values for share holdings and endowments for agent 1 into the set of possible equilibrium shadow values of investment for each agent and participation utilities ![]() .
.
The FOCs of the household’s problem are
![]()
Asset holdings and prices are state contingent and thus both ![]() are vectors in
are vectors in ![]() . Observe that
. Observe that ![]() is a ratio of multipliers corresponding to the participation constraints. That is,
is a ratio of multipliers corresponding to the participation constraints. That is, ![]() , where
, where ![]() is a multiplier associated with today’s participation constraint, and
is a multiplier associated with today’s participation constraint, and ![]() is a multiplier associated with tomorrow’s participation constraint at state
is a multiplier associated with tomorrow’s participation constraint at state ![]() . Therefore,
. Therefore, ![]() only if tomorrow’s participation constraint is binding.
only if tomorrow’s participation constraint is binding.
Computational Algorithm
We start with a correspondence ![]() such that
such that ![]() for all
for all ![]() with
with ![]() . It is easy to come up with the initial candidate
. It is easy to come up with the initial candidate ![]() , since the low endowment
, since the low endowment ![]() is a lower bound for consumption, and the marginal utility of consumption can be used to bound asset prices as discounted values of dividends. It is also straightforward to derive bounds for the value of participation that in this case will form part of the enlarged state space.
is a lower bound for consumption, and the marginal utility of consumption can be used to bound asset prices as discounted values of dividends. It is also straightforward to derive bounds for the value of participation that in this case will form part of the enlarged state space.
Iterations of operator ![]() result in new candidate values for the shadow values of investment, and new candidate values for participation. Specifically, given
result in new candidate values for the shadow values of investment, and new candidate values for participation. Specifically, given ![]() , we have that
, we have that ![]() iff we can find portfolio holdings for next period,
iff we can find portfolio holdings for next period, ![]() , a bond price
, a bond price ![]() , multipliers
, multipliers ![]() , continuation shadow values of investment and continuation utilities
, continuation shadow values of investment and continuation utilities ![]() , such that the individual’s intertemporal optimality conditions are satisfied, and are consistent with the definition of promised utilities and with participation constraints
, such that the individual’s intertemporal optimality conditions are satisfied, and are consistent with the definition of promised utilities and with participation constraints
![]()
![]()
Our algorithm can then be used to generate a sequence of approximations to the equilibrium correspondence via the recursion ![]() .
.
Table 3 reports sample statistics for equilibrium time series. In this table, ![]() refers to the price of a state uncontingent share.
refers to the price of a state uncontingent share.
Perfect risk sharing would require constant consumption across states. The endogenous participation constraint prevents perfect risk sharing and so consumption displays some volatility. Since the unique equilibrium is a symmetric stochastic steady state and the agent with the good shock (who is unconstrained) determines the price of the asset, the price of a state uncontingent share is constant. As is well understood, however, the volatility of the pricing kernel of this economy is higher than that of a complete markets economy but we do not report state contingent prices.
6 Concluding Remarks
In this paper we present a systematic approach for the numerical simulation of dynamic economic models. There is a fairly complete theory for the simulation of optimal economies, and a variety of algorithms are available for the computation of these economies. The dynamic programming (DP) algorithm guarantees convergence to the true solution, and the approximation error can be bounded. There are other algorithms for which a numerical solution is not known to exist—or convergence to the numerical solution cannot be guaranteed. These algorithms are usually much faster than the DP algorithm, and easier to implement. We have presented an accuracy test based on the Euler equation residuals which is particularly relevant for non-reliable algorithms. This test can estimate the accuracy of the computed solution from a plot of the residuals without further reference to the particular algorithm computing the solution.
Of course, in dynamic models the one-period error estimated by the Euler equation residuals may cumulate over time. We then develop some approximation properties for the simulated moments and the consistency of the simulation-based estimators. Error bounds and asymptotic normality of these estimators may require further differentiability properties of the invariant distributions of the original model.
For non-optimal economies, a continuous Markov equilibrium may not exist. Hence, algorithms searching for a continuous policy function are usually not adequate. Indeed, we discussed some examples in which standard algorithms produced misleading results. We analyzed a reliable algorithm based on the computation of correspondences rather than functions. We also studied some convergence properties of the numerical solutions. Still, for non-optimal economies there are many open issues such as bounding approximation errors and the estimation of parameter values by simulation-based estimators.
We have focused on the theoretical foundations of numerical simulation rather than on a thorough description of the types of economic models to which this theory can be applied. There are certain models that clearly fall outside the scope of our applications—even though the theoretical results presented here may still offer some useful insights. For instance, see Algan et al. (2010) for algorithms related to the computation of models with a continuum of agents of the type of Krusell and Smith (1998), and Ericson and Pakes (1995) for the computation of a model of an industry.
References
1. Abreu D, Pierce D, Stacchetti E. Toward a theory of repeated games with discounting. Econometrica. 1990;58:1041–1063.
2. Algan, Y., Allais, O., Den Haan, W.J., Rendahl, P., 2010. Solving and simulating models with heterogeneous agents and aggregate uncertainty, manuscript.
3. Aruoba SB, Fernandez-Villaverde J, Rubio-Ramirez J. Comparing solution methods for dynamic equilibrium economies. Journal of Economic Dynamics and Control. 2006;30:2477–2508.
4. Benhabib J, Day RH. A characterization of erratic dynamics in the overlapping generations model. Journal of Economic Dynamics and Control. 1982;4:37–55.
5. Blume LE. New techniques for the study of stochastic equilibrium processes. Journal of Mathematical Economics. 1982;9:61–70.
6. Cooley TF, Prescott EC. Economic growth and business cycles. In: Cooley TF, ed. Frontiers of Business Cycle Research. NJ: Princeton University Press; 1995.
7. Christiano LJ, Eichembaum M. Current business cycle theories and aggregate labor-market fluctuations. American Economic Review. 1992;82:430–450.
8. Christiano LJ, Fisher JDM. Algorithms for solving dynamic models with occasionally binding constraints. Journal of Economic Dynamics and Control. 2000;24:1179–1235.
9. Coleman WJ. Equilibrium in a production economy with an income tax. Econometrica. 1991;59:1091–1104.
10. Crauel H. Random Probability Measures on Polish Spaces Stochastic Monographs. 11 London: Taylor and Francis; 2002.
11. Datta M, Mirman LJ, Reffett KL. Existence and uniqueness of equilibrium in distorted dynamic economies with capital and labor. Journal of Economic Theory. 2002;103:377–410.
12. Den Haan WJ, Marcet A. Accuracy in simulations. Review of Economic Studies. 1994;61:3–17.
13. Duffie D, Geanakoplos J, Mas-Colell A, McLennan A. Stationary Markov equilibria. Econometrica. 1994;62:745–781.
14. Duffie D, Singleton KJ. Simulated moments estimation of Markov models of asset prices. Econometrica. 1993;61:929–952.
15. Ellison G, Fudenberg D. Rules of thumb for social learning. Journal of Political Economy. 1993;101:612–643.
16. Ericson R, Pakes A. Markov-perfect industry dynamics: a framework for empirical work. Review of Economic Studies. 1995;82:53–82.
17. Feng, Z., Miao, J., Peralta-Alva,A., Santos, M.S., 2012. Numerical simulation of nonoptimal dynamic equilibrium models.Working Paper, Federal Reserve Bank of Saint Louis.
18. Fernandez-Villaverde J. Computational Tools and Macroeconomic Applications Lecture Notes University of Pennsylvania 2012.
19. Fernandez-Villaverde J, Rubio-Ramirez JF. Estimating macroeconomic models: A likelihood approach. Review of Economic Studies. 2007;74:1059–1087.
20. Fernandez-Villaverde J, Rubio-Ramirez JF, Santos MS. Convergence properties of the likelihood of computed dynamic models. Econometrica. 2006;74:93–119.
21. Futia C. Invariant distributions and the limiting behavior of Markovian economic models. Econometrica. 1982;50:377–408.
22. Grandmont JM. On endogenous competitive business cycles. Econometrica. 1985;53:995–1045.
23. Greenwood J, Huffman G. On the existence of nonoptimal equilibria in dynamic stochastic economies. Journal of Economic Theory. 1995;65:611–623.
24. Hansen LP. Large sample properties of the generalized method of moments. Econometrica. 1982;50:1029–1054.
25. Hansen LP, Singleton KJ. Generalized instrumental variables estimation of nonlinear rational expectations models. Econometrica. 1982;50:1269–1286.
26. Hellwig M. A note on the implementation of rational expectations equilibria. Economics Letters. 1983;11:1–8.
27. Hildenbrand W. Core and Equilibria of a Large Economy. Princeton, NJ: Princeton University Press; 1974.
28. Hopenhayn H, Prescott EC. Stochastic monotonicity and stationary distributions for dynamic economies. Econometrica. 1992;60:1387–1406.
29. Jennrich RI. Asymptotic properties of non-linear least squares estimators. Annals of Mathematical Statistics. 1969;40:633–643.
30. Judd KL. Projection methods for solving aggregate growth models. Journal of Economic Theory. 1992;58:410–452.
31. Judd KL, Guu SM. Asymptotic methods for aggregate growth models. Journal of Economic Dynamics and Control. 1997;21:1025–1042.
32. Kehoe TJ, Levine DK. Liquidity constrained markets versus debt constrained markets. Econometrica. 2001;69:575–598.
33. Krueger D, Kubler F. Markov equilibria in macroeconomics. In: Durlauf SN, Blume LE, eds. The New Palgrave Dictionary of Economics. second ed. Macmillan 2008.
34. Krusell P, Smith A. Income and wealth heterogeneity in the macroeconomy. Journal of Political Economy. 1998;106:867–896.
35. Kubler F. Verifying competitive equilibria in dynamic economies. Review of Economic Studies. 2011;78:1379–1399.
36. Kubler F, Polemarchakis HM. Stationary Markov equilibria for overlapping generations. Economic Theory. 2004;24:623–643.
37. Kubler F, Schmedders K. Recursive equilibria in economies with incomplete markets. Macroeconomic Dynamics. 2002;6:284–306.
38. Kubler F, Schmedders K. Stationary equilibria in asset-pricing models with incomplete markets and collateral. Econometrica. 2003;71:1767–1795.
39. Kubler F, Schmedders K. Approximate versus exact equilibria in dynamic economies. Econometrica. 2005;73:1205–1235.
40. Kydland FE, Prescott EC. Dynamic optimal taxation, rational expectations and optimal control. Journal of Economic Dynamics and Control. 1980;2:79–91.
41. Lee B-S, Ingram BF. Simulation estimation of time-series models. Journal of Econometrics. 1991;47:197–205.
42. Marcet, A., Marimon, R., 1998. Recursive contracts, Economics Working Papers No. 337, Universitat Pompeu Fabra.
43. Newey WK, McFadden D. Large sample estimation and hypothesis testing. In: Amsterdam: Elsevier, North Holland; 1994;McFadden D, Engle R, eds. Handbook of Econometrics. vol. 4.
44. Phelan C, Stacchetti E. Sequential equilibria in a Ramsey tax model. Econometrica. 2001;69:1491–1518.
45. Sanghvi AP, Sobel MJ. Bayesian games as stochastic processes. International Journal of Game Theory. 1976;5:1–22.
46. Santos MS. Accuracy of numerical solutions using the Euler equation residuals. Econometrica. 2000;68:1337–1402.
47. Santos MS. On non-existence of Markov equilibria for competitive-market economies. Journal of Economic Theory. 2002;105:73–98.
48. Santos MS. Consistency properties of a simulation-based estimator for dynamic processes. Annals of Applied Probability. 2010;20:196–213.
49. Santos MS, Peralta-Alva A. Accuracy of simulations for stochastic dynamic models. Econometrica. 2005;73:1939–1976.
50. Santos, M.S., Peralta-Alva, A. 2012. Ergodic invariant measures for non-optimal economies, manuscript.
51. Santos MS, Rust J. Convergence properties of policy iteration. SIAM Journal on Control and Optimization. 2004;42:2094–2115.
52. Santos MS, Vigo-Aguiar J. Analysis of a numerical dynamic programming algorithm applied to economic models. Econometrica. 1998;66:409–426.
53. Santos MS, Woodford M. Rational asset pricing bubbles. Econometrica. 1997;65:19–58.
54. Schenk-Hoppe KR, Schmalfuss B. Random fixed points in a stochastic Solow growth model. Journal of Mathematical Economics. 2001;36:19–30.
55. Schmitt-Grohe S, Uribe M. Solving dynamic general equilibrium models using a second-order approximation to the policy function. Journal of Economic Dynamics and Control. 2004;28:755–775.
56. Stenflo O. Ergodic theorems for Markov chains represented by iterated function systems. Bulletin of the Polish Academy of Sciences: Mathematics. 2001;49:27–43.
57. Stachurski J, Martin V. Computing the distributions of economic models via simulation. Econometrica. 2008;76:443–450.
58. Stokey NL, Lucas RE, Prescott EC. Recursive Methods in Economic Dynamics. Cambridge, MA: Harvard University Press; 1989.