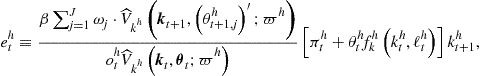• Step 2. Computation of the capital choice.Compute ![]() for
for ![]() .
.
• Step 3. Computation of the intratemporal choice. Compute ![]() satisfying (136), (139), and (140) given
satisfying (136), (139), and (140) given ![]() for
for ![]() .
.
• Step 4. Approximation of conditional expectation.For ![]() ,
,
– ![]() satisfying (136), (139), and (140) given
satisfying (136), (139), and (140) given ![]() for
for ![]() ;
;
(b) evaluate conditional expectation:
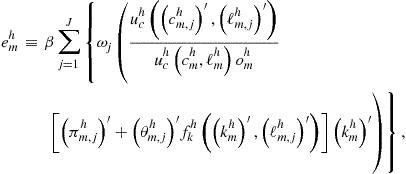
where ![]() and
and ![]() are given by (142) and (143), respectively.
are given by (142) and (143), respectively.
• Step 5. Computation of the intertemporal choice.Find ![]() such that
such that
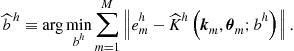
• Step 6. Updating of the coefficient vectors.For each ![]() , compute the coefficient vector for the subsequent iteration
, compute the coefficient vector for the subsequent iteration ![]() using FPI (145).
using FPI (145).
Iterate on Steps 2–6 until convergence of the solution,
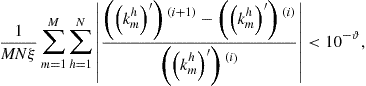
where ![]() and
and ![]() are the
are the ![]() th country’s capital choices on the grid obtained on iterations
th country’s capital choices on the grid obtained on iterations ![]() and
and ![]() , respectively, and
, respectively, and ![]() . Iterate on Steps 1–6 until convergence of the grid.
. Iterate on Steps 1–6 until convergence of the grid.
Computational Details
As in the case of the previous two algorithms, we start simulation from the steady state and assume ![]() as an initial guess for all
as an initial guess for all ![]() . We use complete ordinary polynomial functions of degrees two and three. The simulation length for constructing the EDS grid is
. We use complete ordinary polynomial functions of degrees two and three. The simulation length for constructing the EDS grid is ![]() , and the number of grid points is twice as large as the number of polynomial coefficients to estimate; for example, for the second-degree polynomial case, we have
, and the number of grid points is twice as large as the number of polynomial coefficients to estimate; for example, for the second-degree polynomial case, we have ![]() grid points. In Step 4, to approximate integrals, we use a monomial integration rule
grid points. In Step 4, to approximate integrals, we use a monomial integration rule ![]() with
with ![]() nodes as in (63). In Step 5, we estimate the regression equation by using a least-squares truncated QR factorization method. The damping parameter is
nodes as in (63). In Step 5, we estimate the regression equation by using a least-squares truncated QR factorization method. The damping parameter is ![]() and the tolerance parameter is
and the tolerance parameter is ![]() .
.
11.4 Dynamic Programming Methods
We next implement dynamic programming methods. Specifically, we consider two versions of ECM, one that approximates the value function and the other that approximates derivatives of the value function. As introduced in Maliar and Maliar (2013), the ECM methods rely on a product grid for in two-dimensional examples. In a following-up paper, Maliar and Maliar (2012a,b) implement simulation-based versions of the ECM method that are tractable in high-dimensional applications. These versions of ECM are applied to solve multiagent models studied in the JEDC comparison analysis of Kollmann et al. (2011b). The design of ECM follows the design of GSSA, namely, we combine simulation-based grids with monomial integration rules, numerically stable regression methods, and an FPI method for finding the polynomial coefficients. The results of Maliar and Maliar (2012a,b) are reproduced below. We summarize the implementation of the ECM algorithms in the first two columns of Table 20.
Table 20
Implementation of our Bellman equation algorithms and hybrid algorithm.a
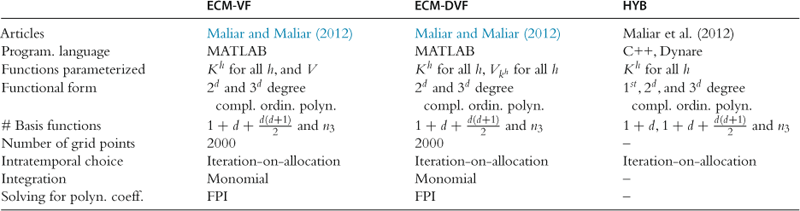
aNotes: ![]() is the model’s dimensionality;
is the model’s dimensionality; ![]() is the number of basis functions in complete ordinary polynomial of degree 3,
is the number of basis functions in complete ordinary polynomial of degree 3, ![]() .
.
11.4.1 Bellman Equation, FOCs, and Envelope Condition
Let us write problem (135)–(137) in the DP form
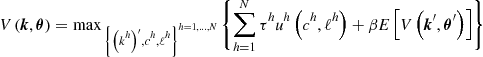 (148)
(148)
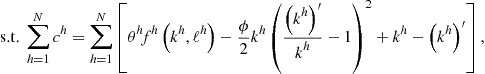 (149)
(149)
![]() (150)
(150)
where ![]() is the optimal value function,
is the optimal value function, ![]() and
and ![]() .
.
Again, we assume that the solution to DP problem (148)–(150) is interior and, hence, satisfies the FOCs and envelope condition, which are, respectively, given by
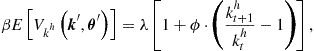 (151)
(151)
![]() (152)
(152)
![]() (153)
(153)
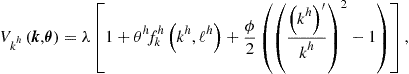 (154)
(154)
where ![]() is the Lagrange multiplier associated with aggregate resource constraint (149).
is the Lagrange multiplier associated with aggregate resource constraint (149).
A solution to dynamic programming problem (148)–(150) is an optimal value function ![]() that satisfies (148)–(154). For our planner’s problem, the Bellman equation implies the Euler equation: by updating envelope condition (154) for the next period and by substituting the resulting condition into (151), we obtain Euler equation (138).
that satisfies (148)–(154). For our planner’s problem, the Bellman equation implies the Euler equation: by updating envelope condition (154) for the next period and by substituting the resulting condition into (151), we obtain Euler equation (138).
11.4.2 Separating the Intertemporal and Intratemporal Choices
The value function iteration aims at approximating a solution to (148)–(154). As in the case of the Euler equation methods, we separate the optimality conditions into the intertemporal and intratemporal choice conditions; see Section 7.
Regarding the intertemporal choice, we combine (152) and (154) to obtain
![]() (155)
(155)
where ![]() and
and ![]() are given by (142) and (143), respectively. We next obtain a condition that relates today’s and tomorrow’s derivatives of the value function by combining FOC (151) and envelope condition (154) to eliminate
are given by (142) and (143), respectively. We next obtain a condition that relates today’s and tomorrow’s derivatives of the value function by combining FOC (151) and envelope condition (154) to eliminate ![]() ,
,
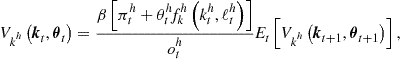 (156)
(156)
where ![]() and
and ![]() are given by (142) and (143), respectively. This condition is parallel to (95) for the one-agent model. We next premultiply (156) from both sides with
are given by (142) and (143), respectively. This condition is parallel to (95) for the one-agent model. We next premultiply (156) from both sides with ![]() , rearrange the terms, and parameterize it with a flexible functional form to obtain
, rearrange the terms, and parameterize it with a flexible functional form to obtain
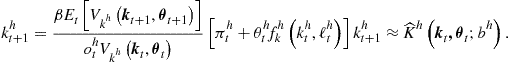 (157)
(157)
The above condition is similar to Euler equation (141) and is written in a way that is convenient for an iterative process.
As far as the intratemporal choice is concerned, conditions (149), (152), and (153) under DP methods are identical to (136), (139), and (140) under the Euler equation methods. As a result, we can use an identical solver for finding the intratemporal choice (we use the iteration-on-allocation procedure described in Section 11.6). We shall recall an important advantage of the DP approaches over the Euler equation approaches. In the former case, we only need to know the intratemporal choice in the current state, while in the latter case, we must also find such a choice in ![]() possible future states (integration nodes). To be more specific, GSSA, EDS, and SMOL-JMMV have to solve for
possible future states (integration nodes). To be more specific, GSSA, EDS, and SMOL-JMMV have to solve for ![]() satisfying (136), (139), and (140), which is expensive. We do not need to solve for those quantities under the DP approach described in this section.
satisfying (136), (139), and (140), which is expensive. We do not need to solve for those quantities under the DP approach described in this section.
11.4.3 Envelope Condition Method Iterating on Value Function
ECM-VF is a variant of the ECM method that iterates on value function.
Steps of ECM-VF
(a) Parameterize ![]() and
and ![]() with flexible functional forms
with flexible functional forms ![]() and
and ![]() , respectively.
, respectively.
(b) Fix simulation length ![]() and initial condition
and initial condition ![]() . Draw and fix for all simulations a sequence of productivity levels
. Draw and fix for all simulations a sequence of productivity levels ![]() using (137).
using (137).
(c) Choose integration nodes, ![]() , and weights,
, and weights, ![]() ,
, ![]() .
.
Iterative cycle. At iteration ![]() , given
, given ![]() , perform the following steps.
, perform the following steps.
• Step 1. Simulation of the solution.Use the assumed capital decision functions ![]() , to recursively calculate a sequence of capital stocks
, to recursively calculate a sequence of capital stocks ![]() corresponding to a given sequence of productivity levels
corresponding to a given sequence of productivity levels ![]() .
.
• Step 2. Computation of the intratemporal choice. Compute ![]() satisfying (136), (139), and (140), given
satisfying (136), (139), and (140), given ![]() for
for ![]() .
.
• Step 3. Approximation of conditional expectation.For ![]() ,
,
(c) use ![]() to find
to find ![]() and to infer
and to infer ![]() for
for ![]() ;
;
(d) evaluate conditional expectation in (157) and compute
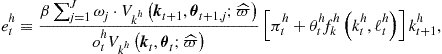
Find ![]() such that
such that
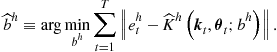
• Step 5. Updating of the coefficient vectors. For each country ![]() , compute the coefficient vector for the subsequent iteration
, compute the coefficient vector for the subsequent iteration ![]() using FPI (145).
using FPI (145).
Iterate on Steps 1–5 until the convergence criterion (147) is satisfied.
Computational Details
To start the iterative process, we use an initial guess: ![]() for all
for all ![]() , and we assume
, and we assume ![]() and
and ![]() for all
for all ![]() . The simulation length is
. The simulation length is ![]() . We use complete ordinary polynomials of degrees two and three. To approximate integrals in Step 3, we use a monomial integration rule
. We use complete ordinary polynomials of degrees two and three. To approximate integrals in Step 3, we use a monomial integration rule ![]() with
with ![]() nodes as in (63). In Step 4, we use a least-squares truncated QR factorization method. The damping parameter is
nodes as in (63). In Step 4, we use a least-squares truncated QR factorization method. The damping parameter is ![]() and the tolerance parameter is
and the tolerance parameter is ![]() .
.
11.4.4 Envelope Condition Method Solving for Derivatives of Value Function
ECM-DVF is a variant of the ECM method that iterates on derivatives of value function. We use (155) to approximate the derivative of value function, ![]() .
.
The Steps of ECM-DVF
The steps that are identical to those in ECM-VF are omitted.
(a) Parameterize ![]() and
and ![]() with flexible functional forms
with flexible functional forms ![]() and
and ![]() , respectively (in both cases, we use ordinary polynomials).
, respectively (in both cases, we use ordinary polynomials).
…
Iterative cycle. At iteration ![]() , given
, given ![]() , perform the following steps.
, perform the following steps.
Computational Details
The computational choice for ECM-DVF is the same as that for ECM-VF.
11.5 Hybrid of Local and Global Solutions
We consider a version of the hybrid perturbation-based method of Maliar et al. (2013) who implement this algorithm for model (135)–(137) studied here; we reproduce the results from that paper. The implementation of the hybrid perturbation-based method is summarized in the last column of Table 20.
As a first step, we compute a solution to model (135)–(137) using the standard perturbation method in levels; to this purpose, we use the Dynare software. We keep the capital policy functions ![]() that are delivered by Dynare and we discard all the other policy functions (i.e., consumption and labor).
that are delivered by Dynare and we discard all the other policy functions (i.e., consumption and labor).
When simulating the solutions and evaluating their accuracy, we proceed as under global Euler equation methods. Namely, we first construct a path for capital, ![]() , and subsequently fill in the corresponding intratemporal allocations
, and subsequently fill in the corresponding intratemporal allocations ![]() by solving (136), (139), and (140) for each given
by solving (136), (139), and (140) for each given ![]() . In this step, we use the iteration-on-allocation solver as described in Section 11.6.
. In this step, we use the iteration-on-allocation solver as described in Section 11.6.
11.6 Solving for Consumption and Labor Using Iteration-on-Allocation
Maliar et al. (2011) emphasize the importance of solving accurately for intratemporal choice for the overall accuracy of solutions; see their Table 1 and see our Table 11 and a related discussion. Also, the comparison results of Kollmann et al. (2011b) lead to the same conclusion: the residuals in the intratemporal choice conditions are larger than the residuals in the intertemporal choice conditions by an order of magnitude and they drive the overall accuracy down for all the methods. An exception is two methods described in Maliar et al. (2011), which solve for all the intratemporal choice variables exactly (up to a given degree of accuracy). Below, we describe the iteration-on-allocation method which is used by the two methods studied in Maliar et al. (2011), as well as by all methods presented in Section 11.
Parameterization of the Model
We solve one of the multicountry models studied in the comparison analysis of Kollmann et al. (2011b), namely, Model II with an asymmetric specification.21 The parameterization of this model is described in Juillard and Villemot (2011). The utility and production functions are given by
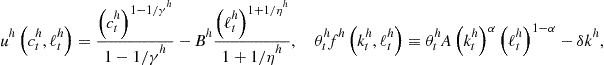 (158)
(158)
where ![]() are the utility-function parameters;
are the utility-function parameters; ![]() is the capital share in production;
is the capital share in production; ![]() is the normalizing constant in output. The country-specific utility-function parameters
is the normalizing constant in output. The country-specific utility-function parameters ![]() and
and ![]() are uniformly distributed in the intervals
are uniformly distributed in the intervals ![]() and
and ![]() across countries
across countries ![]() , respectively. The values of common-for-all-countries parameters are
, respectively. The values of common-for-all-countries parameters are ![]() . The steady-state level of productivity is normalized to one,
. The steady-state level of productivity is normalized to one, ![]() . We also normalize the steady-state levels of capital and labor to one,
. We also normalize the steady-state levels of capital and labor to one, ![]() , which implies
, which implies ![]() and leads to
and leads to ![]() , and
, and ![]() . We chose this parameterization because it represents all challenges posed in the JEDC comparison analysis, namely, a large number of state variables, endogenous labor-leisure choice, heterogeneity in fundamentals, and the absence of closed-form expressions for next-period state and control variables in terms of the current state variables.22
. We chose this parameterization because it represents all challenges posed in the JEDC comparison analysis, namely, a large number of state variables, endogenous labor-leisure choice, heterogeneity in fundamentals, and the absence of closed-form expressions for next-period state and control variables in terms of the current state variables.22
Iteration-on-Allocation
We now show how to solve for the intratemporal choice under assumptions (158) using the iteration-on-allocation solver. Our objective is to solve for ![]() that satisfy (136), (139), and (140)for given
that satisfy (136), (139), and (140)for given ![]() . Under parameterization (158), these conditions can be represented as
. Under parameterization (158), these conditions can be represented as
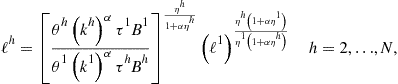 (159)
(159)
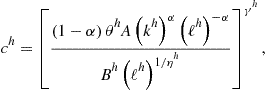 (160)
(160)
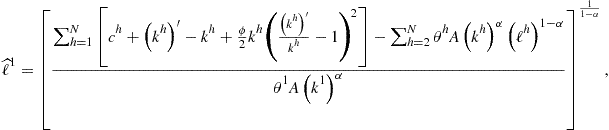 (161)
(161)
where ![]() is a new value of labor of country 1. Condition (159) is obtained by finding a ratio of (139) for two agents, condition (160) follows by combining (139) and (140), and condition (161) follows from (136). For given
is a new value of labor of country 1. Condition (159) is obtained by finding a ratio of (139) for two agents, condition (160) follows by combining (139) and (140), and condition (161) follows from (136). For given ![]() , equations (159)–(161) define a mapping
, equations (159)–(161) define a mapping ![]() . We iterate on labor of the first country,
. We iterate on labor of the first country, ![]() , as follows: assume some initial
, as follows: assume some initial ![]() ; compute
; compute ![]() , from (159); find
, from (159); find ![]() , from (160); obtain
, from (160); obtain ![]() from (161) and stop if
from (161) and stop if ![]() with a given degree of accuracy; compute the next-iteration input as
with a given degree of accuracy; compute the next-iteration input as ![]() and go to the next iteration, where
and go to the next iteration, where ![]() is a damping parameter. Our criterion of convergence is that the average difference of labor choices in two subsequent iterations is smaller than
is a damping parameter. Our criterion of convergence is that the average difference of labor choices in two subsequent iterations is smaller than ![]() .
.
When Iteration-on-Allocation is Used
Iteration-on-allocation allows us to solve for ![]() that satisfy (136), (139), and (140) for any given triple
that satisfy (136), (139), and (140) for any given triple ![]() . For stochastic simulation methods, we use iteration-on-allocations twice: first, we find
. For stochastic simulation methods, we use iteration-on-allocations twice: first, we find ![]() that solve (136), (139), and (140) for all
that solve (136), (139), and (140) for all ![]() that are realized in simulation. Second, we find
that are realized in simulation. Second, we find ![]() that solve the same system (136), (139), and (140) in
that solve the same system (136), (139), and (140) in ![]() integration nodes that correspond to each simulation point, i.e., we find the intratemporal choice for all possible state
integration nodes that correspond to each simulation point, i.e., we find the intratemporal choice for all possible state ![]() that may occur at
that may occur at ![]() given the state
given the state ![]() at
at ![]() . Thus, in the inner loop, we solve for the intratemporal choice
. Thus, in the inner loop, we solve for the intratemporal choice ![]() times: for
times: for ![]() simulated points and for
simulated points and for ![]() possible future states.
possible future states.
Similarly, for projection methods operating on a prespecified grid, we use iteration-on-allocation twice: first, we find ![]() that solve (136), (139), and (140) for all grid points
that solve (136), (139), and (140) for all grid points ![]() , where
, where ![]() is determined by an intertemporal choice function. Second, we find
is determined by an intertemporal choice function. Second, we find ![]() that solve the same system (136), (139), and (140) for
that solve the same system (136), (139), and (140) for ![]() integration nodes that correspond to each grid point, i.e., for all
integration nodes that correspond to each grid point, i.e., for all ![]() where
where ![]() is also known. Thus, in the inner loop, we solve for the intratemporal choice
is also known. Thus, in the inner loop, we solve for the intratemporal choice ![]() times: for
times: for ![]() grid points and for
grid points and for ![]() possible future states.
possible future states.
Finally, we also use iteration-on-allocation when simulating the model and evaluating the accuracy of solutions. Namely, we first construct a path for capital, ![]() , and subsequently fill in the corresponding intratemporal allocations
, and subsequently fill in the corresponding intratemporal allocations ![]() by solving (136), (139), and (140) for each given
by solving (136), (139), and (140) for each given ![]() . This procedure leads to very accurate solutions. However, since the intratemporal choice is defined implicitly, simulating the model is more expensive than under explicitly defined intratemporal choice functions. We use a vectorized version of the iteration-on-allocation method that is very fast in MATLAB.
. This procedure leads to very accurate solutions. However, since the intratemporal choice is defined implicitly, simulating the model is more expensive than under explicitly defined intratemporal choice functions. We use a vectorized version of the iteration-on-allocation method that is very fast in MATLAB.
Initial Guess and Bounds
To start the iteration-on-allocation method, we assume that consumption and labor are equal to their steady-state values. To enhance the numerical stability on initial iterations when the solution is inaccurate, we impose fixed lower and upper bounds (equal to ![]() and
and ![]() of the steady-state level, respectively) on labor. This technique is similar to the moving bounds used in Maliar and Maliar (2003b) to restrict explosive simulated series. With the bounds imposed, the iteration-on-allocation procedure was numerically stable and converged to a fixed point at a good pace in all of our experiments.
of the steady-state level, respectively) on labor. This technique is similar to the moving bounds used in Maliar and Maliar (2003b) to restrict explosive simulated series. With the bounds imposed, the iteration-on-allocation procedure was numerically stable and converged to a fixed point at a good pace in all of our experiments.
Partial Convergence
We shall draw attention to an important aspect of the implementation of iteration-on-allocation in iterative cycles. Finding consumption and labor allocations with a high degree of accuracy on each outer-loop iteration has a high computational cost and is in fact of no use, since on the next iteration we must recompute consumption and labor allocations for a different intratemporal choice. We thus do not target any accuracy criteria in consumption and labor allocations in each iteration of the outer loop, but instead perform 10 subiterations on (159)–(161). We store in memory consumption and labor allocations obtained at the end of the outer loop, and we use these allocations as inputs for the next round of the iteration-on-allocation process. Thus, as the decision functions for capital are refined along the iterations, so do our consumption and labor allocations.
11.7 Accuracy Measures
The measure of accuracy of solutions is the size of residuals in ![]() optimality conditions, namely, optimality conditions (138)–(140) for
optimality conditions, namely, optimality conditions (138)–(140) for ![]() and aggregate resource constraint (136). We represent all the conditions in a unit-free form by
and aggregate resource constraint (136). We represent all the conditions in a unit-free form by
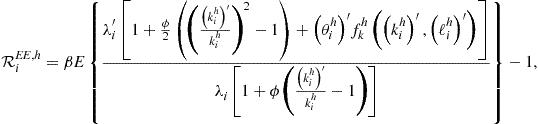 (162)
(162)
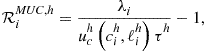 (163)
(163)
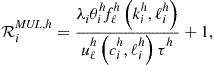 (164)
(164)
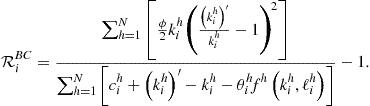 (165)
(165)
We report two accuracy statistics, namely, the average and maximum absolute residuals across ![]() conditions computed in a given set of points.
conditions computed in a given set of points.
Domains on Which Accuracy Is Evaluated
We use two alternatives for a choice of points ![]() in which the residuals are evaluated: one is deterministic and the other is simulated. Our definition of implementation of accuracy checks is the same as the one used in Juillard and Villemot (2011).
in which the residuals are evaluated: one is deterministic and the other is simulated. Our definition of implementation of accuracy checks is the same as the one used in Juillard and Villemot (2011).
Test 1. A deterministic set of points constructed to represent a given area of the state space. We fix a value of ![]() and draw
and draw ![]() points
points ![]() such that the Euclidean distance between each point and the steady state is exactly
such that the Euclidean distance between each point and the steady state is exactly ![]() , i.e.,
, i.e., ![]() , where
, where ![]() represents the steady state, and
represents the steady state, and ![]() is the Euclidean norm. We consider three different values for
is the Euclidean norm. We consider three different values for ![]() . These values allow us to judge how accurate the solution is on a short, medium, and long distance from the steady state.
. These values allow us to judge how accurate the solution is on a short, medium, and long distance from the steady state.
Test 2. A set of simulated points constructed to represent an essentially ergodic set. We draw a sequence of ![]() shocks, calculate
shocks, calculate ![]() using (137), and simulate
using (137), and simulate ![]() using the approximate solution
using the approximate solution ![]() . We start simulation from the steady state
. We start simulation from the steady state ![]() , and we disregard the first 200 points to eliminate the effect of the initial conditions.
, and we disregard the first 200 points to eliminate the effect of the initial conditions.
11.8 Explicit Versus Implicit Solutions
Suppose a numerical algorithm has delivered a solution to model (135)–(137) in the form of the capital decision functions ![]() . Consider two alternative methods for simulating the intratemporal choice:1. Construct a parametric function
. Consider two alternative methods for simulating the intratemporal choice:1. Construct a parametric function ![]() and use this function to find
and use this function to find ![]() for each given
for each given ![]() in simulation (the corresponding
in simulation (the corresponding ![]() can be found from FOC (140)).2. Find
can be found from FOC (140)).2. Find ![]() and
and ![]() that solve system (136), (139), and (140) using a numerical solver (i.e., Newton’s method, iteration-on-allocation, etc.) for each given
that solve system (136), (139), and (140) using a numerical solver (i.e., Newton’s method, iteration-on-allocation, etc.) for each given ![]() .
.
It is clear that there is a trade-off between the accuracy and cost: providing explicit decision functions allows us to simulate a solution more rapidly; however, it may result in lower accuracy compared to the case when the intratemporal choice is characterized implicitly. In the context of the studied model, Maliar et al. (2011) find that alternative 1 reduces accuracy by almost an order of magnitude compared to Alternative 2. The cost of Alternative 2 is moderate if one uses the iteration-on-allocation solver; see Maliar et al. (2011), Table 2.
The same kind of trade-off is observed in the context of DP methods. That is, we can construct explicitly both the value function, ![]() , and some decision rules such as
, and some decision rules such as ![]() , and
, and ![]() , or we can construct explicitly only the value function
, or we can construct explicitly only the value function ![]() and define the decision rules implicitly as a solution to optimality conditions in each point considered.
and define the decision rules implicitly as a solution to optimality conditions in each point considered.
12 Numerical Results for the Multicountry Model
In this section, we assess the performance of the surveyed numerical methods in the context of the multicountry model (135)–(137). We end the section by providing practical recommendations on how to apply numerical solution methods more efficiently in high-dimensional problems.
12.1 Projection Methods
We consider five projection methods; we list them in Table 21. CGA and MRGAL compute a second-degree polynomial approximation; the EDS method computes both second- and third-degree polynomial approximations (we call them EDS2 and EDS3, respectively); and SMOL-JMMV and SMOL-MKK compute an approximation that uses a mixture of the second- and fourth-degree Chebyshev polynomial terms.
Running Times
For each method in Table 22, we report the running times needed to solve the models with ![]() countries. A precise comparison of the computational cost of the studied methods is not possible because different methods are implemented using different hardware and software. Nonetheless, the running times in the table provide us with some idea about the cost of different methods. MRGAL and SMOL-MKK use Newton’s solvers which are fast for small
countries. A precise comparison of the computational cost of the studied methods is not possible because different methods are implemented using different hardware and software. Nonetheless, the running times in the table provide us with some idea about the cost of different methods. MRGAL and SMOL-MKK use Newton’s solvers which are fast for small ![]() (i.e.,
(i.e., ![]() and
and ![]() ) but expensive for large
) but expensive for large ![]() (MRGAL uses a Newton’s method to solve for the coefficients of the approximating polynomials, and SMOL-MKK uses such a method to implement time iteration). In turn, the SMOL-JMMV, EDS, and CGA methods use FPI that avoids the need of numerical solvers. EDS2 becomes fastest for larger
(MRGAL uses a Newton’s method to solve for the coefficients of the approximating polynomials, and SMOL-MKK uses such a method to implement time iteration). In turn, the SMOL-JMMV, EDS, and CGA methods use FPI that avoids the need of numerical solvers. EDS2 becomes fastest for larger ![]() (i.e.,
(i.e., ![]() and
and ![]() ). Overall, the cost of the EDS method grows slowly with
). Overall, the cost of the EDS method grows slowly with ![]() even under third-degree polynomials. The difference between CGA and EDS consists not only in using distinct grid points (cluster grid versus EDS grid) but also in using different integration formulas (EDS uses a cheap monomial formula
even under third-degree polynomials. The difference between CGA and EDS consists not only in using distinct grid points (cluster grid versus EDS grid) but also in using different integration formulas (EDS uses a cheap monomial formula ![]() and CGA implements a two-step procedure, first using
and CGA implements a two-step procedure, first using ![]() and then using
and then using ![]() ); the differing cost of integration accounts for most of the difference in cost between EDS and CGA.
); the differing cost of integration accounts for most of the difference in cost between EDS and CGA.
Table 22
Running times (in seconds) for the projection methods.a

aNotes: The following software and hardware are employed: MATLAB 7 on an Intel(R) Core(TM) 2 CPU, 3 GHz, 4 GB RAM (for MRGAL); Intel Fortran 8.0 on an Intel (R) Xeon (TM) 2.80 GHz CPU, 12 GB RAM (for SMOL-MKK); MATLAB 7 on a Quad Intel(R) Core(TM) i7 CPU920, 2.67 GHz, 6 GB RAM (for EDS and CGA); MATLAB 7 on Intel(R) Core(TM) i7 CPU920 2.67 GHz, 6 GB RAM (for SMOL-JMMV). The results for MRGAL, CGA, and SMOL-MKK are reproduced from Kollmann et al. (2011b), Table 3. The remaining results are our own computations.
Accuracy on a Sphere
In Table 23, we report the absolute size of unit-free residuals on spheres of different radii; see Test 1 in Section 11.7. There are several differences across the methods that critically affect their accuracy. First, the EDS and CGA methods find a solution in a high-probability area of the state space while SMOL-JMMV, MRGAL, and SMOL-MKK operate on hypercubes that are exogenous to the model. Second, SMOL-JMMV, EDS, and CGA solve for the intratemporal choice exactly (using iteration-on-allocation), while MRGAL and SMOL-MKK approximate some of the intratemporal choice variables with state contingent functions. Finally, SMOL-JMMV and SMOL-MKK have more flexible approximating functions than do EDS2, CGA, and MRGAL methods (Smolyak polynomial consists of a mixture of second- and fourth-degree polynomial terms and has four times more terms than a complete second-degree polynomial).
Table 23
Accuracy of the projection methods on a sphere.
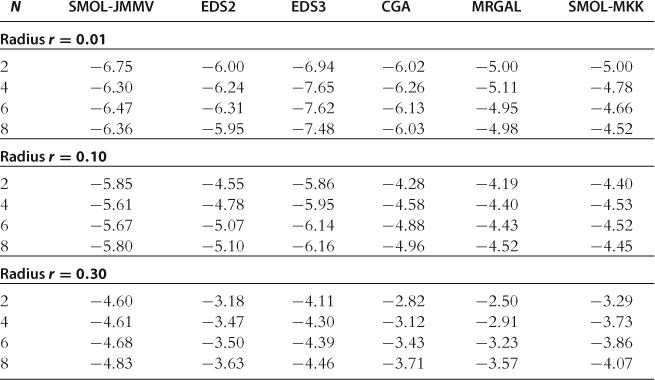
Notes: The numbers reported are maximum absolute residuals (in log10 units) across all equilibrium conditions and 1,000 draws of state variables located on spheres in the state space (centered at steady state) with radii 0.01, 0.10, and 0.30, respectively. The results for MRGAL, CGA, and SMOL-MKK are reproduced from Kollmann et al. (2011b), Table 4. The remaining results are our own computations.
The accuracy ranking of the studied methods is affected by all the above factors. The ergodic set methods (EDS and CGA) fit polynomials in a smaller area than do the SMOL-JMMV, MRGAL, and SMOL-MKK methods that operate on exogenous grids. As a result, the former methods tend to deliver more accurate solutions near the steady state than the latter methods. The SMOL-JMMV, EDS3, and SMOL-MKK have an advantage over the other methods because they use more flexible approximating functions. However, the overall accuracy of the MRGAL and SMOL-MKK methods is dominated by large errors in the intratemporal choice conditions. In particular, Kollmann et al. (2011b) compare the size of residuals across the model’s equations and find that the residuals in the intratemporal choice conditions are larger than those in the intertemporal choice conditions for the MRGAL and SMOL-MKK methods. In contrast, for the SMOL-JMMV, EDS, and CGA methods, such errors are zero by construction. Finally, EDS2 performs somewhat better than CGA, which suggests that a uniform EDS grid leads to more accurate approximations than a grid of clusters, which is less uniform and mimics the density function of the underlying distribution.
Accuracy on a Stochastic Simulation
In Table 24, we report the absolute size of unit-free residuals on a stochastic simulation; see Test 2 in Section 11.7. The tendencies here are similar to those we observed in the test on the spheres. Focusing on the essentially ergodic set, having a more flexible approximating function, and solving for the intratemporal choice accurately are factors that increase the accuracy of solutions. Moreover, since the accuracy is evaluated on a stochastic simulation, the ergodic set methods, EDS and CGA, have the highest chance to be accurate (because the area in which the accuracy is evaluated coincides with the area in which their polynomials are fit) and as a result, overperform the SMOL-JMMV, MRGAL, and SMOL methods which are designed to perform well on exogenous domains.
Table 24
Accuracy of the projection methods on a stochastic simulation.
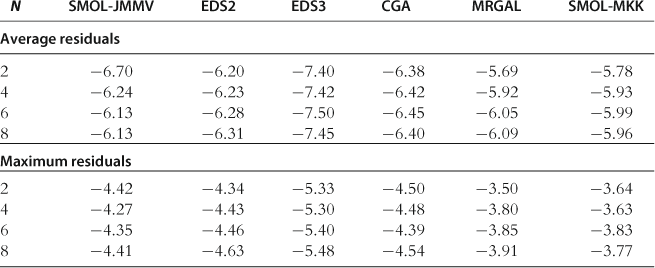
Notes: The numbers reported are average (top panel) and maximum (bottom panel) absolute residuals (log10 units), taken across all equilibrium conditions and all periods for a stochastic simulation of 10,000 periods. The results for MRGAL, CGA, and SMOL-MKK are reproduced from Kollmann et al. (2011b), Table 5. The remaining results are our own computations.
12.2 Generalized Stochastic Simulation Methods
Stochastic simulation methods find solutions by recomputing the series of endogenous state variables on each iteration (the exogenous state variables are held fixed). We consider two stochastic simulation methods, SSA and GSSA. The former is a version of the GSSA algorithm that participated in the comparison analysis of Kollmann et al. (2011b); it computes linear solutions using a one-node Monte Carlo integration rule. The latter version of GSSA is implemented exclusively in this chapter; we compute second- and third-degree polynomial approximations using three alternative integration rules, namely, one-node Monte Carlo, one-node Gauss-Hermite quadrature, and ![]() -node monomial rules described in Sections 5.3, 5.1, and 5.2, respectively. The corresponding methods are referred to as GSSA-MC, GSSA-Q(1), and GSSA-M1, respectively. For SSA studied in Kollmann et al. (2011b), a simulation is of length
-node monomial rules described in Sections 5.3, 5.1, and 5.2, respectively. The corresponding methods are referred to as GSSA-MC, GSSA-Q(1), and GSSA-M1, respectively. For SSA studied in Kollmann et al. (2011b), a simulation is of length ![]() observations. For GSSA-MC, GSSA-Q(1), and GSSA-M1, we use a shorter simulation length,
observations. For GSSA-MC, GSSA-Q(1), and GSSA-M1, we use a shorter simulation length, ![]() .
.
We list the studied methods in Table 25. A detailed description of SSA is provided in Maliar et al. (2011). A general description of GSSA is provided in Section 4.2; in Section 11.3.4, we elaborate a description of this method for the studied multicountry model. More details about GSSA are available in Judd et al. (2011b).
Table 25
Participating stochastic simulation methods.
| Abbreviation | Name |
| SSA | Stochastic simulation algorithm of Maliar et al. (2011) |
| GSSA-MC | Generalized stochastic simulation algorithm of Judd et al. (2011b) using a one-node MC integration |
| GSSA-Q(1) | Generalized stochastic simulation algorithm of Judd et al. (2011b) using a one-node quadrature |
| GSSA-M1 | Generalized stochastic simulation algorithm of Judd et al. (2011b) using a monomial rule |
Running Times
Table 26 reports the running times for the GSSA methods considered. All the results are produced by employing the same software and hardware, so that the comparison of running times across the studied methods is informative. The table shows that having more integration nodes and polynomial terms increases the cost, and the higher is the dimensionality of the problem, the larger is the increase in cost. For example, while under ![]() , the difference in the running time between GSSA2-Q(1) and GSSA3-Q(1) is by a factor less than
, the difference in the running time between GSSA2-Q(1) and GSSA3-Q(1) is by a factor less than ![]() , and under
, and under ![]() , this difference is larger than by a factor
, this difference is larger than by a factor ![]() .
.
Table 26
Running times (in seconds) of the stochastic simulation methods.

Notes: The software and hardware employed are as follows: MATLAB 7 on a Quad Intel(®) Core(TM) i7 CPU920, 2.67GHz, 6 GB RAM. The results for SSA are reproduced from Kollmann et al. (2011b), Table 3 (in terms of notations used for the other methods, SSA means GSSA1-MC). The remaining results are our own computations.
Accuracy on a Sphere
The results for the accuracy test on a sphere are presented in Table 27. The following tendencies are observed: First, the accuracy of solutions increases with both the degree of an approximating polynomial function and the accuracy of integration methods (GSSA3-M1 is the most accurate method in the table). Second, Monte Carlo integration is substantially less accurate than the quadrature and monomial rules, especially for ![]() . Moreover, GSSA3-MC explodes for
. Moreover, GSSA3-MC explodes for ![]() . Among the three methods that use Monte Carlo integration, SSA (that computes linear solutions) is the most accurate, and GSSA3-MC is the least accurate. In this case, large integration errors dominate the accuracy of solutions and a higher degree of polynomials does not lead to more accurate solutions. Furthermore, a simple one-node deterministic rule
. Among the three methods that use Monte Carlo integration, SSA (that computes linear solutions) is the most accurate, and GSSA3-MC is the least accurate. In this case, large integration errors dominate the accuracy of solutions and a higher degree of polynomials does not lead to more accurate solutions. Furthermore, a simple one-node deterministic rule ![]() leads to sufficiently accurate solutions, in particular, for a large radius,
leads to sufficiently accurate solutions, in particular, for a large radius, ![]() . Finally, under accurate monomial integration rule
. Finally, under accurate monomial integration rule ![]() , the accuracy levels produced by stochastic simulation methods are comparable to those produced by the projection methods studied in Section 12.1.
, the accuracy levels produced by stochastic simulation methods are comparable to those produced by the projection methods studied in Section 12.1.
Table 27
Accuracy of the stochastic simulation methods on a sphere.
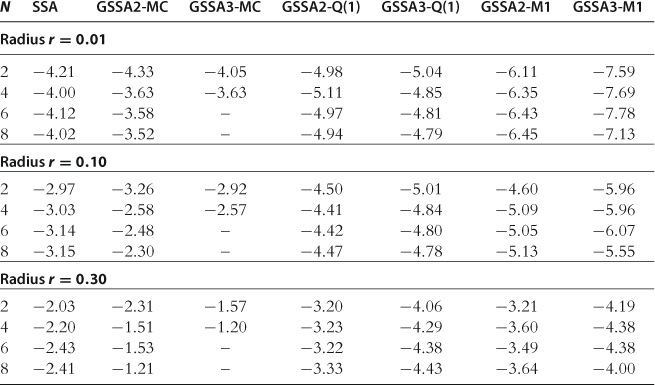
Notes: The numbers reported are maximum absolute residuals (in log10 units) across all equilibrium conditions and 1,000 draws of state variables located on spheres in the state space (centered at steady state) with radii 0.01, 0.10, and 0.30. The results for SSA are reproduced from Kollmann et al. (2011b), Table 4.
Accuracy on a Stochastic Simulation
The results for the accuracy test on a stochastic simulation are presented in Table 28. Again, the tendencies are similar to those we have observed in the test on the spheres. Accurate integration methods and flexible approximating functions are important for accurate solutions. The performance of the Monte Carlo integration method is poor, while a simple ![]() method produces sufficiently accurate solutions in the studied examples.
method produces sufficiently accurate solutions in the studied examples.
Table 28
Accuracy of the stochastic simulation methods on a simulation.
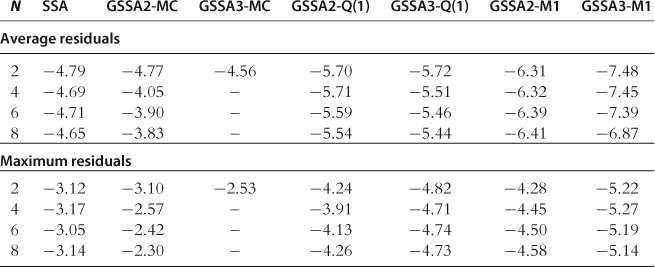
Notes: The numbers reported are averages (top panel) and maximum (bottom panel) absolute residuals (in log10 units), computed across all equilibrium conditions and all periods for a stochastic simulation of 10,000 periods. The results for SSA are reproduced from Kollmann et al. (2011b), Table 5.
12.3 Dynamic Programming Methods
In this section, we study the ECM method. Recall that the ECM method has the advantage over the Euler equation methods that it solves for control variables only at present and does not need to find such variables in all integration nodes. This advantage can be especially important in high-dimensional problems as the number of integration nodes grows with dimensionality. We consider two versions of ECM, one that solves for value function, ECM-VF, and the other that solves for derivatives of value function, ECM-DVF. We use a ![]() -node monomial integration rule and we assume the simulation length of
-node monomial integration rule and we assume the simulation length of ![]() observations. The considered methods are listed in Table 29.
observations. The considered methods are listed in Table 29.
Table 29
Participating Bellman methods.
| Abbreviation | Name and the article |
| ECM-VF | Envelope condition method iterating on value function of Maliar and Maliar (2012a) |
| ECM-DVF | Envelope condition method iterating on derivatives of value function of Maliar and Maliar (2012a) |
A general description of ECM-VF and ECM-DVF methods is provided in Section 7; in Sections 11.4.3 and 11.4.4, we elaborate a description of these methods for the studied multicountry model. More details about these methods are available from Maliar and Maliar (2012a,b, 2013). Both ECM-VF and ECM-DVF compute second- and third-degree polynomial approximations.
Running Times
In Table 30, we provide running times for the ECM methods. We observe that the convergence of ECM-VF is considerably faster than that of ECM-DVF.
Table 30
Running times (in seconds) of the ECM methods.

Notes: The software and hardware employed are as follows: MATLAB 7 on a Quad Intel(®) Core(TM) i7 CPU920, 2.67 GHz, 6 GB RAM. These results are reproduced from Maliar and Maliar (2012a), Table 2.
Accuracy on a Sphere
In Table 31, we report the results for the accuracy test on a sphere. We observe that ECM-VF is considerably less accurate than ECM-DVF given the same degree of approximating the polynomial. This is because if we approximate ![]() with a polynomial of some degree, we effectively approximate
with a polynomial of some degree, we effectively approximate ![]() with a polynomial of one degree less, i.e., we “lose” one polynomial degree.
with a polynomial of one degree less, i.e., we “lose” one polynomial degree.
Table 31
Accuracy of the ECM methods on a sphere.
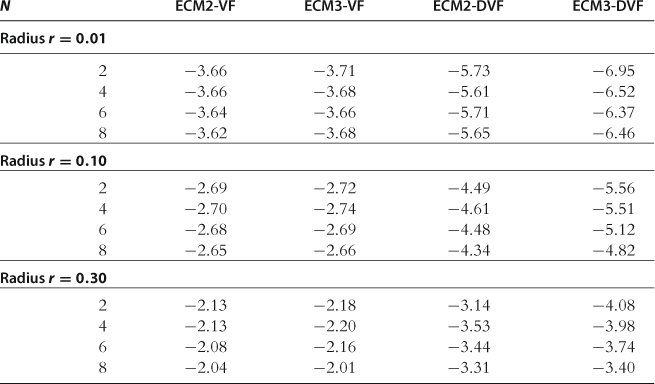
Notes: The numbers reported are maximum absolute residuals (in log10 units) across all equilibrium conditions and 1,000 draws of state variables located on spheres in the state space (centered at steady state) with radii 0.01, 0.10, and 0.30. These results are reproduced from Maliar and Maliar (2012a), Tables 3 and 4, respectively.
Accuracy on a Stochastic Simulation
In Table 32, we provide the results for the accuracy test on a stochastic simulation. Again, ECM-DVF is considerably more accurate than ECM-DVF. The ECM-DVF solutions are comparable in accuracy to the GSSA solutions; for comparison, see GSSA-M1 in Table 28 that uses the same integration method, ![]() , as does ECM-DVF. We conclude that value function iteration methods that approximate derivatives of value function can successfully compete with the Euler equation methods.
, as does ECM-DVF. We conclude that value function iteration methods that approximate derivatives of value function can successfully compete with the Euler equation methods.
Table 32
Accuracy of the ECM methods on a simulation.
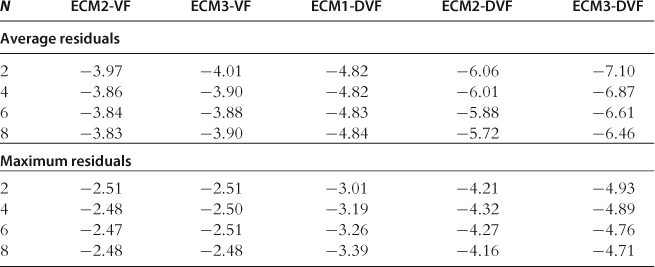
Notes: The numbers reported are averages (top panel) and maximum (bottom panel) absolute residuals (in log10 units), computed across all equilibrium conditions and all periods for a stochastic simulation of 10,000 periods. These results are reproduced from Maliar and Maliar (2012a), Table 2.
12.4 Local Solution Methods
We assess the performance of perturbation methods and show that the accuracy of local solutions can be considerably increased by using the techniques of a change of variables of Judd (2003) and a hybrid of local and global solutions of Maliar et al. (2013). In Table 33, we list the three perturbation-based methods considered. PER-LOG is a perturbation method in logarithms of Kollmann et al. (2011a) which participate in the JEDC comparison analysis. PER-L and HYB-L are the standard and hybrid perturbation methods in levels that are described in Sections 9.1 and 9.4, respectively; see Maliar et al. (2011) for a detailed description of these methods. PER-LOG computes perturbation solutions of orders one and two, while PER-L and HYB-L compute perturbation solutions of orders one, two, and three.
Table 33
Participating perturbation methods.
| Abbreviation | Name |
| PER-LOG | Perturbation method in logs of variables of Kollmann et al. (2011b) |
| PER-L | Perturbation method in levels of variables of Maliar et al. (2012) |
| HYB-L | Perturbation-based hybrid method of Maliar et al. (2012) |
Running Times
The running times for all the perturbation methods are small; see Table 34. For example, the running time for PER1-LOG is one or two milliseconds, and that for PER2-LOG is a few seconds.
Table 34
Running times (in seconds) for the perturbation methods.
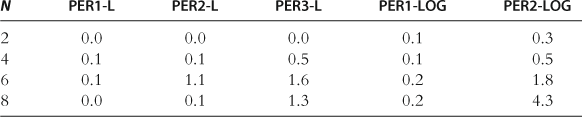
Notes: The following software and hardware are employed: MATLAB 7 on an Intel(®) Pentium(®) 4 CPU, 3.06 GHz, 960 MB RAM (for PER-LOG); Dynare and C++ on workstation with two quad-core Intel® Xeon X5460 processors (clocked at 3.16 GHz), 8 GB of RAM, and running 64 bit Debian GNU/Linux (for PER-L and HPER-L). The results for PER-L and HPER-L are reproduced from Maliar et al. (2012), Tables 1 and 2, and the results for PER-LOG are reproduced from Kollmann et al. (2011b), Table 5.
12.4.1 The Importance of the Change of Variables
The importance of the change of variables can be seen by comparing the results produced by the loglinear perturbation solution methods of Kollmann et al. (2011a) and the linear perturbation solution methods of Maliar et al. (2013).
Accuracy on a Sphere
The results for the accuracy test on a sphere are reported in Table 35. Two tendencies are observed from the table. First, the perturbation method in levels, PER-L, performs very well; it delivers accuracy levels that are comparable to those produced by global projection and stochastic simulation methods (given the same degree of an approximating polynomial function); for a comparison, see Tables 23 and 27, respectively. However, the performance of the perturbation method in logarithms, PER-LOG, is relatively poor. Even for the second-order method PER2-LOG, the maximum residuals can be as large as ![]() , and they can be even larger for the first-order method PER1-LOG. We therefore conjecture that for this specific model, a change of variables from logarithms to levels increases the accuracy of solutions, especially for large deviations from the steady state.
, and they can be even larger for the first-order method PER1-LOG. We therefore conjecture that for this specific model, a change of variables from logarithms to levels increases the accuracy of solutions, especially for large deviations from the steady state.
Table 35
Accuracy of the perturbation methods on a sphere.
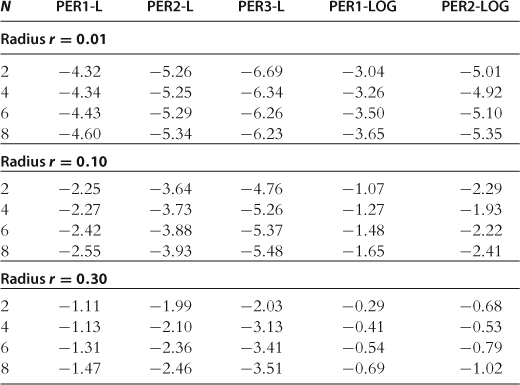
Notes: The numbers reported are maximum absolute residuals (in log10 units) across all equilibrium conditions and 1,000 draws of state variables located on spheres in the state space (centered at steady state) with radii 0.01, 0.10, and 0.30. The results for PER-LOG are reproduced from Kollmann et al. (2011b), Table 4, and those for PER-L are reproduced from Maliar et al. (2012), Tables 1 and 2.
Accuracy on a Stochastic Simulation
The results for the accuracy test on a stochastic simulation are provided in Table 36. Surprisingly, there is not much difference between PER-L and PER-LOG when the accuracy is evaluated on a stochastic simulation: the maximum residuals for the two methods are practically identical.
Table 36
Accuracy of the perturbation methods on a stochastic simulation.
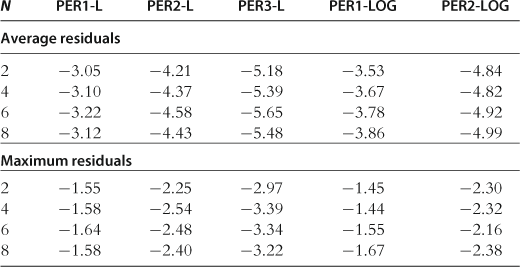
Notes: The numbers reported, in log10 units, are averages (top panel) and maxima (bottom panel) of absolute values of the model’s residuals, where the averages/maxima are taken across all equilibrium conditions and all dates for a stochastic simulation run of 10,000 periods. The results for PER-LOG are reproduced from Kollmann et al. (2011b), Table 5, and those for PER-L are reproduced from Maliar et al. (2012), Tables 1 and 2.
12.4.2 The Benefits of Hybrid Solutions
To implement the hybrid perturbation-based method, we fix the capital decision functions ![]() that are produced by the PER-L method, and we find
that are produced by the PER-L method, and we find ![]() allocations
allocations ![]() satisfying (136), (139), and (140) using the iteration-on-allocation numerical solver as described in Section 11.6. The results are presented in Table 37. We observe that the plain perturbation method, PER-L, produces nonnegligible residuals in all the model’s equations, while the hybrid method, HYB, produces nonnegligible residuals only in the Euler equations (the quantities delivered by the iteration-on-allocation solver, by construction, satisfy the intratemporal conditions exactly). In terms of maximum size of the residuals, the hybrid solutions are sufficiently more accurate than the plain perturbation solutions. The difference in accuracy between PER-L and HYB-L reaches almost two orders of magnitude in the test on a stochastic simulation.
satisfying (136), (139), and (140) using the iteration-on-allocation numerical solver as described in Section 11.6. The results are presented in Table 37. We observe that the plain perturbation method, PER-L, produces nonnegligible residuals in all the model’s equations, while the hybrid method, HYB, produces nonnegligible residuals only in the Euler equations (the quantities delivered by the iteration-on-allocation solver, by construction, satisfy the intratemporal conditions exactly). In terms of maximum size of the residuals, the hybrid solutions are sufficiently more accurate than the plain perturbation solutions. The difference in accuracy between PER-L and HYB-L reaches almost two orders of magnitude in the test on a stochastic simulation.
Table 37
Perturbation versus hybrid perturbation-based methods in the multicountry model with ![]() .
.
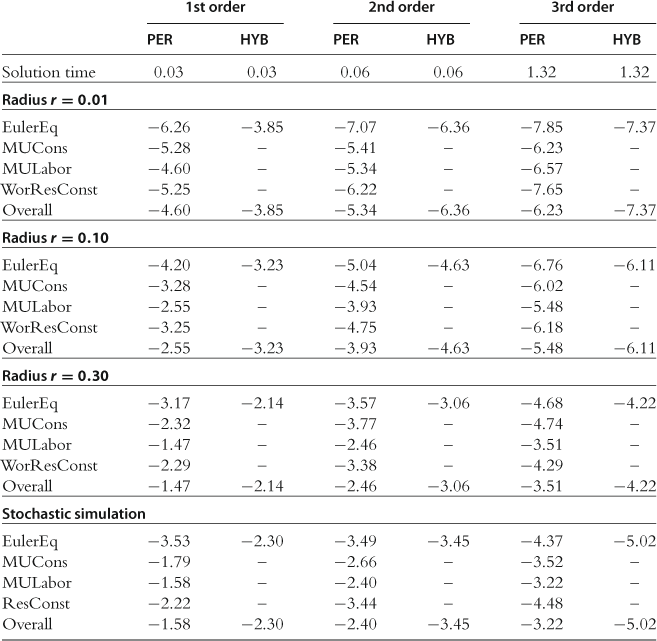
Notes: Both PER and HYB compute solutions in levels. For each model equation (listed in the first column), the table reports maximum absolute errors in log10 units across countries and test points. For panels “Radius ![]() ,” “Radius
,” “Radius ![]() ,” and “Radius
,” and “Radius ![]() ,” the set of test points is 1,000 draws of state variables located on spheres with radii
,” the set of test points is 1,000 draws of state variables located on spheres with radii ![]() , and
, and ![]() , respectively; for panel “stochastic simulation,” the set of test points is a stochastic simulation of 10,000 periods. An entry “–” is used if accuracy measure is below
, respectively; for panel “stochastic simulation,” the set of test points is a stochastic simulation of 10,000 periods. An entry “–” is used if accuracy measure is below ![]() (such errors are viewed as negligible), PER is PER-L, and HYB is HYB-L.
(such errors are viewed as negligible), PER is PER-L, and HYB is HYB-L.
Model equations are as follows: “EulerEq” is Euler equation (74); “MUCons” equates the (scaled) marginal utility of consumption to the Lagrange multiplier, see (72); “MULabor” equates the (scaled) marginal utility of labor to marginal productivity of labor multiplied by the Lagrange multiplier, see (73); “WorResConst” is world resource constraint (136); “Overall” is the maximum error across all the model’s equations; “Solution time” is time for computing a solution. The results for PER and HYB are reproduced from Maliar et al. (2012), Table 2 with kind permission from Springer Science+Business Media B.V.
12.5 Speeding up Computations in MATLAB
In this section, we provide some results on how the cost of numerical methods can be reduced in large-scale applications using MATLAB. Our presentation closely follows Valero et al. (2013), who explore several options for reducing the cost of a Smolyak solution method in the context of model (135)–(137). We focus on three different tools available in MATLAB: parallel computation on multiple CPUs using a “parfor” routine; automated translations of the code to C using a “mex” routine; and parallel computation using multiple GPUs. We refer to the standard MATLAB and these three alternative implementations as “standard,” “parfor,” “mex,” and “GPU,” respectively.
The literature on parallel computing often considers examples in which gains from parallelization are readily obtained. In contrast, the Smolyak method studied in Valero et al. (2013) is a challenging case for parallelization. First, there are large information transfers between the outer and inner loops in the Smolyak method and second, a large fraction of the Smolyak code must be implemented in a serial manner. The running times for our experiments are provided in Table 38 (the solutions delivered are identical in all cases).
Table 38
Running times (in seconds) depending on the implementaion in MATLAB: parfor, mex, GPU.

Notes: The following software and hardware are employed: MATLAB 2012a, Intel(®) Core(TM) i7-2600 CPU @ 3.400 GHz with RAM 12.0 GB and GPU GeFoce GT 545. Also, to compile mex functions, we use Microsoft Windows SDK 7.1 with NET Framework 4.0. These results are reproduced from Valero et al. (2013), Table 2.
Our main finding is that parallel computation using multiple CPUs can speed up the methods for solving dynamic economic models if the dimensionality of the problem is high. To be specific, the parfor implementation does not speed up computations under ![]() ; however, it is almost four times faster under
; however, it is almost four times faster under ![]() . The efficiency of parallelization (132)in the last case is nearly
. The efficiency of parallelization (132)in the last case is nearly ![]() on our four-core machine, namely,
on our four-core machine, namely, ![]() . The mex translation brings speedups in problems with low dimensionality but performs poorly when dimensionality increases. This is because for large problems, nonoptimized C code produced by a mex routine is less efficient than a vectorized MATLAB code. Finally, parallel computation using multiple GPUs does poorly in our case because of standard limitations of GPUs (namely, a high cost of transfers) and because of limitations of the MATLAB language in operating GPUs.
. The mex translation brings speedups in problems with low dimensionality but performs poorly when dimensionality increases. This is because for large problems, nonoptimized C code produced by a mex routine is less efficient than a vectorized MATLAB code. Finally, parallel computation using multiple GPUs does poorly in our case because of standard limitations of GPUs (namely, a high cost of transfers) and because of limitations of the MATLAB language in operating GPUs.
12.6 Practical Recommendations About Solving High-Dimensional Problems: Summary
When designing a solution method, we pursue two main objectives: a high accuracy of solutions and a low computational expense. There is a nontrivial trade-off between these two objectives. We now provide some considerations on how to take into account such a trade-off in order to make solution methods more effective in high-dimensional applications.
(i) Producing accurate solutions is costly in high-dimensional applications. The numbers of grid points, integration nodes, and polynomial terms, as well as the number and complexity of the model’s equations, grow rapidly all together with dimensionality of the state space. Accuracy levels of ![]() that one easily achieves in some model with two state variables are unlikely to be feasible in a similar model with one hundred state variables. Therefore, the first question one must ask is: “How much accuracy do I need in a given application?” The answer depends on the economic significance of the approximation errors. Solutions that are accurate for one purpose may be inaccurate for another purpose. For example, a perturbation method that has large
that one easily achieves in some model with two state variables are unlikely to be feasible in a similar model with one hundred state variables. Therefore, the first question one must ask is: “How much accuracy do I need in a given application?” The answer depends on the economic significance of the approximation errors. Solutions that are accurate for one purpose may be inaccurate for another purpose. For example, a perturbation method that has large ![]() errors in the model’s variables may still be sufficiently accurate for the purpose of evaluating second moments, since a typical sampling error in empirical data is still larger. However, this accuracy level is not sufficient for forecasting; for example, predicting that the US growth rate could be anything within the
errors in the model’s variables may still be sufficiently accurate for the purpose of evaluating second moments, since a typical sampling error in empirical data is still larger. However, this accuracy level is not sufficient for forecasting; for example, predicting that the US growth rate could be anything within the ![]() interval
interval ![]() is too loose to be useful.
is too loose to be useful.
(ii) Given a target accuracy level, the second question one must ask is: “What combination of techniques can attain the given accuracy level at the lowest possible cost?” Here, the cost must be understood as the sum of both running time and programmer’s time. Perturbation methods (incorporated, e.g., in the Dynare platform) are often the cheapest possible alternative in all respects and can deliver accurate solutions to many smooth problems, especially if one uses changes of variables and hybrids of local and global solutions described in this section. Global solution methods are more accurate and flexible but also more costly in terms of both the running time and the programmer’s efforts.
(iii) In the case of global solution methods, coordination in the choice of computational techniques is important for making a solution method cost-efficient. All computational techniques employed must be suitable for high-dimensional applications. For example, if one uses a tensor-product grid, the cost will be prohibitive no matter how efficiently we compute integrals or solve for the intratemporal choice. Moreover, all the techniques used must match each other in terms of attainable accuracy. For example, if one uses Monte Carlo integration, the solutions will be inaccurate no matter how sophisticated is the grid and how flexible is the approximating function.
(iv) Among the global solution methods considered, GSSA delivers a high accuracy of solutions and is very simple to program. It is an especially convenient choice if one needs a solution to be accurate in the high-probability area of the state space (i.e., on a set of points produced by stochastic simulation). The EDS and cluster grid methods require more programming efforts but are also faster. A Smolyak method produces solutions that are uniformly accurate in a hypercube (at the cost of a somewhat lower accuracy in the high-probability area). It is an especially useful choice when the solution must be accurate not only inside but also outside the high-probability area of the state space, for example, when modeling the evolution of a development economy that starts off far below the steady state.
(v) To keep the exposition simple, we limit ourselves to solving stylized one- and multiagent growth models. However, the surveyed techniques can be used to solve a variety of other interesting economic models, such as new Keynesian models, life-cycle models, heterogeneous-agents models, asset-pricing models, multisector models, multicountry models, climate change models, etc. The solution procedures will be similar to those we described in the chapter. Namely, under global solution methods, we parameterize some model’s variables (such as decision functions of heterogeneous agents, firms, countries, etc.) with flexible functional forms, approximate integrals using some discretization method, and solve the resulting systems of the model’s equations with respect to parameters of the approximating functions. Under local solution methods, we produce a perturbation solution and modify this solution to increase its accuracy. Examples of solution procedures for life-cycle models can be found in Krueger and Kubler (2004), and those for new Keynesian models can be found in Judd et al. (2011d, 2012), Fernández-Villaverde et al. (2012), and Aruoba and Schorfheide (2012).
(vi) Orthogonal polynomial families (such as Chebyshev or Hermite) are convenient for numerical work. They prevent us from having ill-conditioned inverse problems, ensure well-defined interpolation, and allow us to derive the interpolation coefficients analytically. However, they are also more costly to construct than the ordinary polynomials and require data transformations. Ordinary polynomials are a possible choice if combined with numerically stable regression methods and if the number of grid points is somewhat larger than the number of polynomial coefficients.
(vii) In the fitting step, we recommend avoiding standard least-squares regression methods (OLS, Gauss-Newton method) and using instead methods that can handle ill-conditioned problems, such as least-squares methods using either QR factorization or SVD or Tikhonov regularization. If the problem is not ill-conditioned, these methods give the same (or almost the same) answer as the standard least-squares method. However, if the problem is ill-conditioned, the standard least-squares methods will fail, while these other methods will succeed.
(viii) For approximating integrals, we recommend using monomial formulas (combined with Cholesky decomposition in the case of serially correlated shocks). The monomial formula with ![]() nodes produces very accurate approximations; the formula with
nodes produces very accurate approximations; the formula with ![]() is even more accurate. We recommend avoiding the use of simulation-based integration methods (such as Monte Carlo, learning, and nonparametric ones) because their convergence rate (accuracy) is low.
is even more accurate. We recommend avoiding the use of simulation-based integration methods (such as Monte Carlo, learning, and nonparametric ones) because their convergence rate (accuracy) is low.
(ix) For solving systems of nonlinear equations, we recommend using a fixed-point iteration method instead of quasi-Newton’s methods, especially if the system of equations is large. Iteration-on-allocation is a simple and effective way to find a solution to a system of the intratemporal choice conditions.
(x) In the case of dynamic programming, conventional VFI based on time iteration is expensive. Using other, cheaper versions of fixed-point iteration for VFI, such as endogenous grid and envelope condition methods, can help us to substantially reduce the cost.
(xi) It is important to accurately solve all the model’s equations, in particular the intratemporal choice ones. If one equation is solved inaccurately, the entire solution is inaccurate. Furthermore, it is important to solve accurately the model’s equations not only when computing solutions but also when simulating the model and evaluating the accuracy of solutions.
(xii) Precomputation can save a lot of time: instead of computing the same thing all over again, we compute it just once, at the beginning of a solution procedure.
(xiii) It is useful to check for codes that are available on the Internet before writing your own software. For example, a MATLAB code accompanying the GSSA method includes generic routines for implementing many numerically stable LS and LAD methods, a routine for generating multidimensional polynomials, and a routine for multidimensional Gauss-Hermite quadrature and monomial integration methods. The code also contains a test suite for evaluating the accuracy of solutions. Not only can this code solve the studied examples but it can be easily adapted to other problems in which the reader may be interested.
(xiv) Parallel computation is a promising tool for many problems but it is not automatically useful in every possible context. Not every method is naturally parallelizable. In some cases, the cost of transfers between the cores can outweigh the gains from parallelization. Also, we must design numerical methods in a way that is suitable for parallelization.
(xv) MATLAB is a useful tool when working on a desktop. It is not well suited for supercomputers, in particular because there is a license limitation. To benefit from supercomputers, one must first make an investment in learning some lower-level programming languages (such as Fortran, C, or Python) as well as learning the Unix operational system and software that supports parallel computation (such as Open MP or MPI).
(xvi) Last but not least, it is always necessary to check the quality of the approximations obtained by, for example, evaluating unit-free residuals on a set of points constructed to represent the domain of interest. The code may have bugs or the accuracy may be insufficient; we are at risk of producing a bunch of random numbers if we do not run accuracy checks.
13 Conclusion
Recent developments in the field of numerical analysis have extended the horizons of what was thought unfeasible just a few years ago. First of all, these are novel solution methods that are tractable, accurate, and reliable in large-scale applications. We build such methods using nonproduct grids, monomial integration methods, derivative-free solvers, and numerically stable regression methods. To simplify rootfinding in the Bellman equation, we employ endogenous grid and envelope conditions methods. To avoid repeating some computations, we use precomputation techniques. Finally, to increase accuracy of perturbation methods, we use changes of variables and construct hybrids of local and global solutions. Taken together, these techniques enable us to accurately solve models with nearly a hundred of state variables using a standard desktop computer and serial MATLAB software.
Parallel computing opens another dimension in numerical analysis of economic models. Gains from parallelization are possible even on desktop computers with few cores. Supercomputers have thousands and thousands of CPUs and GPUs that can be coordinated for computationally intensive tasks. Also, they have large memories to record the results. We hope that these new capacities and possibilities will bring economic research to a qualitatively new level in terms of generality, empirical relevance, and rigor of results.
Acknowledgments
Lilia Maliar and Serguei Maliar acknowledge support from the Hoover Institution and Department of Economics at Stanford University, University of Alicante, Ivie, MCI, and FEDER funds under the Projects SEJ-2007-62656 and ECO2012-36719. We thank the editors Karl Schmedders and Kenneth L. Judd as well as two anonymous referees for many valuable comments. We thank Eric Aldrich, Markus Baldauf, Phillip Blood, Yongyang Cai, Kenneth L. Judd, and Rafael Valero for useful discussions of several issues related to parallel computation. Juan Mora López made useful suggestions about the use of nonparametric statistics in the context of numerical solution methods. We acknowledge XSEDE Grant TG-ASC120048, and we thank Phillip Blood and Rick Costa, scientific specialists from the Pittsburgh Supercomputing Center, for technical support. Much of the material in this chapter builds on our prior joint work with Kenneth L. Judd, Rafael Valero, and Sébastien Villemot. We benefited from the comments of seminar participants at Autonomous University of Barcelona, Birkbeck University of London, Canadian Central Bank, Center for Financial Studies at the European Central Bank, Cornell University, Federal Reserve Bank of San Francisco, Paris School of Economics, Santa Clara University, Stanford University, University of Alicante, University of Bilbao, University of California at Berkeley, University of Chicago, University of Edinburgh, and University of Oxford. We used the material from this chapter in the graduate courses at Stanford University, University of Chicago (ICE 2012), and University of Alicante, and we received a useful feedback from many graduate students, in particular, Monica Bhole, Daniel-Oliver Garcia-Macia, Moritz Lenel, Jessie Li, Davide Malacrino, Erik Madsen, Inna Tsener, and Rafael Valero.
References
1. Acemoglu D, Golosov M, Tsyvinski A, Yared P. A dynamic theory of resource wars. Quarterly Journal of Economics. 2011;127(1):283–331.
2. Adda J, Cooper R. Dynamic Economics: Quantitative Methods and Applications. Cambridge, Massachusetts, London, England: The MIT Press; 2003.
3. Adjemian, S., Bastani, H., Juillard, M., Mihoubi, F., Perendia, G., Ratto, M., Villemot, S., 2011. Dynare: reference manual, version 4. Dynare Working Papers 1, CEPREMAP.
4. Aiyagari R. Uninsured idiosyncratic risk and aggregate saving. Quarterly Journal of Economics. 1994;109:659–684.
5. Aldrich EM, Fernández-Villaverde J, Gallant R, Rubio-Ramírez J. Tapping the supercomputer under your desk: solving dynamic equilibrium models with graphics processors. Journal of Economic Dynamics and Control, Elsevier. 2011;35(3):386–393.
6. Altig D, Christiano L, Eichenbaum M. Firm-specific capital, nominal rigidities and the business cycle. Review of Economic Dynamics. 2004;14(2):225–247.
7. Amador M, Weil P-O. Learning from prices: public communication and welfare. Journal of Political Economy. 2010;118(5):866–907.
8. Amdahl G. The validity of single processor approach to achieving large scale computing capabilities. In: AFIPS procedings. 1967:483–485.
9. Amman H. Are supercomputers useful for optimal control experiments? Journal of Economic Dynamics and Control. 1986;10:127–130.
10. Amman H. Implementing stochastic control software on supercomputing machines. Journal of Economic Dynamics and Control. 1990;14:265–279.
11. Anderson G, Kim J, Yun T. Using a projection method to analyze inflation bias in a micro-founded model. Journal of Economic Dynamics and Control. 2010;34(9):1572–1581.
12. Aruoba, S.B., Schorfheide, F., 2012. Macroeconomic dynamics near the ZLB: a tale of two equilibria. <http://www.ssc.upenn.edu/schorf/papers/AS-ZLB.pdf>.
13. Aruoba SB, Fernández-Villaverde J, Rubio-Ramírez J. Comparing solution methods for dynamic equilibrium economies. Journal of Economic Dynamics and Control. 2006;30:2477–2508.
14. Attanasio O, Pavoni N. Risk sharing in private information models with asset accumulation: explaining the asset smoothness of consumption. Econometrica. 2011;79(4):1027–1068.
15. Bai, Y., Ríos-Rull, J.-V., Storesletten, K., 2012. Demand shocks as productivity shocks. Manuscript.
16. Barillas F, Fernández-Villaverde J. A generalization of the endogenous grid method. Journal of Economic Dynamics and Control, Elsevier. 2007;31:2698–2712.
17. Barthelmann V, Novak E, Ritter K. High dimensional polynomial interpolation on sparse grids. Advances in Computational Mathematics. 2000;12:73–288.
18. Baryshnikov Yu, Eichelbacker P, Schreiber T, Yukich JE. Moderate deviations for some point measures in geometric probability. Annales de l’Institut Henri Poincaré – Probabilités et Statistiques. 2008;44:422–446.
19. Bellman RE. Adaptive Control Processes. Princeton, NJ: Princeton University Press; 1961.
20. Bertsekas D, Tsitsiklis J. Neuro-Dynamic Programming. Athena Scientific, Belmont, Massachusetts: Optimization and Neural computation series; 1996.
21. Bierens HJ. Topics in Advanced Econometrics. Cambridge University Press 1994.
22. Birge JR, Louveaux FV. Introduction to Stochastic Programming. New York: Springer-Verlag; 1997.
23. Blood, P. 2011. Getting started using national computing resources. <http://staff.psc.edu/blood/ICE11/XSEDEICEJuly2011.pdf>.
24. Bloom N. The impact of uncertainty shocks. Econometrica. 2009;77(3):623–685.
25. Borovička, Hansen, L.P., 2012. Examining macroeconomic models through the lens of asset pricing. Federal Reserve Bank of Chicago Working Paper 01.
26. Cai Y, Judd KL. Dynamic programming with shape-preserving rational spline Hermite interpolation. Economics Letters. 2012;117:161–164.
27. Cai, Y., Judd, K.L., Lontzek, T., 2012. DSICE: a dynamic stochastic integrated model of climate and economy. Manuscript.
28. Cai, Y., Judd, K.L., Lontzek, T., 2013a. Continuous-time methods for integrated assessment models. NBER Working Paper 18365.
29. Cai, Y., Judd, K.L., Train, G., Wright, S. 2013b. Solving dynamic programming problems on a computational grid. NBER Working Paper 18714.
30. Canova F. Methods for Applied Macroeconomic Research. Princeton University Press 2007.
31. Carroll K. The method of endogenous grid points for solving dynamic stochastic optimal problems. Economic letters. 2005;91:312–320.
32. Caselli, F., Koren, M., Lisicky, M., Tenreyro, S., 2011. Diversification through trade. Manuscript.
33. Chari VV, Kehoe P, McGrattan E. New Keynesian models: not yet useful for policy analysis. American Economic Journal: Macroeconomics. 2009;1(1):242–266.
34. Chatterjee S, Corbae D, Nakajima M, Ríos-Rull J-V. A quatitative theory of unsecured consumer credit with risk of default. Econometrica. 2007;75(6):1525–1589.
35. Chen B, Zadrozny P. Multi-step perturbation solution of nonlinear differentiable equations applied to an econometric analysis of productivity. Computational Statistics and Data Analysis. 2009;53(6):2061–2074.
36. Cho IC, Sargent TJ. Self-confirming equilibrium. In: Durlauf S, Blume L, eds. The New Palgrave Dictionary of Economics. Palgrave Macmillan 2008.
37. Chong Y, Hendry D. Econometric evaluation of linear macroeconomic models. The Review of Economic Studies. 1986;53(4):671–690.
38. Christiano L, Fisher D. Algorithms for solving dynamic models with occasionally binding constraints. Journal of Economic Dynamics and Control. 2000;24:1179–1232.
39. Christiano L, Eichenbaum M, Evans C. Nominal rigidities and the dynamic effects of a shock to monetary policy. Journal of Political Economy. 2005;113(1):1–45.
40. Christiano L, Eichenbaum M, Rebelo S. When is the government spending multiplier large? Journal of Political Economy. 2011;119(1):78–121.
41. Cogan J, Taylor L, Wieland V, Wolters M. Fiscal consolidation strategy. Journal of Economic Dynamics and Control. 2013;37:404–421.
42. Cogley, T., Sargent, T., Tsyrennikov, V., 2013. Wealth dynamics in a bond economy with heterogeneous beliefs. Manuscript.
43. Coibion O, Gorodnichenko Y. What can survey forecasts tell us about informational rigidities? Journal of Political Economy. 2008;120(1):116–159.
44. Coleman, W., 1992. Solving nonlinear dynamic models on parallel computers. Discussion Paper 66, Institute for Empirical Macroeconomics, Federal Reserve Bank of Minneapolis.
45. Collard F, Juillard M. Accuracy of stochastic perturbation methods: the case of asset pricing models. Journal of Economic Dynamics and Control. 2001;25:979–999.
46. Constantinides G. Intertemporal asset pricing with heterogeneous consumers and without demand aggregation. Journal of Business. 1982;55:253–267.
47. Creel M. User-friendly parallel computations with econometric examples. Computational Economics. 2005;26(2):107–128.
48. Creel M. Using parallelization to solve a macroeconomic model: a parallel parameterized expectations algorithm. Computational Economics. 2008;32:343–352.
49. Creel M, Goffe W. Multi-core CPUs, clusters, and grid computing: a tutorial. Computational Economics. 2008;32(4):353–382.
50. Davidson R, MacKinnon J. Estimation and Inference in-Econometrics. New York, Oxford: Oxford University Press; 1993.
51. Del Negro M, Schorfheide F, Smets F, Wouters R. On the fit of new Keynesian models. Journal of Business and Economic Statistics. 2007;25(2):123–143.
52. Den Haan W. The optimal inflation path in a Sidrauski-type model with uncertainty. Journal of Monetary Economics. 1990;25:389–409.
53. Den Haan W. Comparison of solutions to the incomplete markets model with aggregate uncertainty. Journal of Economic Dynamics and Control. 2010;34:4–27.
54. Den Haan, De Wind J. Nonlinear and stable perturbation-based approximations. Journal of Economic Dynamics and Control. 2012;36(10):1477–1497.
55. Den Haan W, Marcet A. Solving the stochastic growth model by parameterized expectations. Journal of Business and Economic Statistics. 1990;8:31–34.
56. Den Haan W, Marcet A. Accuracy in simulations. Review of Economic Studies. 1994;6:3–17.
57. Den Haan W, Judd KL, Juillard M. Computational suite of models with heterogeneous agents II: multicountry real business cycle models. Journal of Economic Dynamics and Control. 2011;35:175–177.
58. Dmitriev A, Roberts I. International business cycles with complete markets. Journal of Economic Dynamics and Control. 2012;36(6):862–875.
59. Doornik JA, Hendry DF, Shephard N. Parallel computation in econometrics: A simplified approach. In: Kontoghiorghes EJ, ed. Handbook of Parallel Computing and Statistics. London: Chapman & Hall/CRC; 2006:449–476.
60. Dotsey M, Mao CS. How well do linear approximation methods work? The production tax case. Journal of Monetary Economics. 1992;29:25–58.
61. Duffie D. Presidential address: asset pricing dynamics with slow-moving capital. Journal of Finance. 2010;LXV(4):1237–1267.
62. Durham, G., Geweke, J., 2012. Adaptive sequential posterior simulators for massively parallel computing environments. Manuscript.
63. Eaves B, Schmedders K. General equilibrium models and homotopy methods. Journal of Economic Dynamics and Control. 1999;23:1249–1279.
64. Ellison M, Sargent T. A defence of the FOMC. International Economic Review. 2012;53(4):1047–1065.
65. Evans GW, Honkapohja S. Learning and Expectations in Macroeconomics. Princeton University Press 2001.
66. Evans, R., Kotlikoff, L., Phillips, K., 2012. Game over: simulating unsustainable fiscal policy. In: Fiscal Policy after the Financial Crisis National Bureau of Economic Research, NBER Chapters.
67. Fair R, Taylor J. Solution and maximum likelihood estimation of dynamic nonlinear rational expectation models. Econometrica. 1983;51:1169–1185.
68. Feng, Z., Miao, J., Peralta-Alva, A., Santos, M., 2009. Numerical simulation of nonoptimal dynamic equilibrium models. Working papers Federal Reserve Bank of St. Louis 018.
69. Fernández-Villaverde J, Rubio-Ramírez J. Solving DSGE models with perturbation methods and a change of variables. Journal of Economic Dynamics and Control. 2006;30:2509–2531.
70. Fernández-Villaverde J, Rubio-Ramírez J. Estimating macroeconomic models: a likelihood approach. Review of Economic Studies. 2007;74:1059–1087.
71. Fernández-Villaverde, J., Gordon, G., Guerrón-Quintana, P., Rubio-Ramírez, J., 2012. Nonlinear adventures at the zero lower bound. NBER Working Paper 18058.
72. Fudenberg D, Levine D. Self-confirming equilibrium. Econometrica. 1993;61:523–545.
73. Fukushima, K., Waki, Y., 2011. A Polyhedral Approximation Approach to Concave Numerical Dynamic Programming. Manuscript.
74. Gallant, R.A., 2012. Parallelization strategies: hardware and software (two decades of personal experience). <http://www.duke.edu/arg>.
75. Gaspar J, Judd KL. Solving large-scale rational-expectations models. Macroeconomic Dynamics. 1997;1:45–75.
76. Gertler M, Leahy J. A Phillips curve with an Ss foundation. Journal of Political Economy. 2008;110(3):533–572.
77. Gertler, M., Kiyotaki, N., Queralto, A., 2011. Financial crises, bank risk exposure and government financial policy. Manuscript.
78. Geweke J. Monte Carlo simulation and numerical integration. In: Amman H, Kendrick D, Rust J, eds. Handbook of Computational Economics. Amsterdam: Elsevier Science; 1996:733–800.
79. Glover A., Heathcote, J., Krueger, D., Ríos-Rull, J.-V., 2011. Intergenerational redistribution in the great recession. NBER Working Paper 16924.
80. Golosov, M., Sargent, T., 2012. Taxation, redistribution, and debt with aggregate shocks. Manuscript.
81. Golosov, M., Troshkin, M., Tsyvinski, A., 2011. Optimal dynamic taxes. NBER Working Paper 17642.
82. Golub G, Van Loan C. Matrix Computations. Baltimore and London: The Johns Hopkins University Press; 1996.
83. Gomes F, Kotlikoff L, Viceira L. Optimal life-cycle investing with flexible labor supply: a welfare analysis of life-cycle funds. American Economic Review: Papers and Proceedings. 2008;98(2):297–303.
84. Gomme P, Klein P. Second-order approximation of dynamic models without the use of tensors. Journal of Economic Dynamics and Control. 2011;35:604–615.
85. Gorman W. Community preference field. Econometrica. 1953;21:63–80.
86. Graham L, Wright S. Information, heterogeneity and market incompleteness. Journal of Monetary Economics. 2009;57(2):164–174.
87. Guerrieri, L., Iacoviello, M., 2013. OccBin: A toolkit for solving dynamic models with occasionally binding constraints easily. Manuscript.
88. Guerrieri, V., Lorenzoni, G., 2011. Credit crises, precautionary savings, and the liquidity trap. NBER Working Papers 17583.
89. Guibaud, S., Nosbusch, Y., Vayanos, D., forthcoming. Bond market clienteles, the yield curve, and the optimal maturity structure of government debt. Review of Financial Studies.
90. Guvenen, F., 2011. Macroeconomics with heterogeneity: a practical guide. NBER Working Papers 17622.
91. Hall, R.E., 2012. Quantifying the Forces Leading to the Collapse of GDP after the Financial Crisis. Manuscript.
92. Hasanhodzic, J., Kotlikoff, L.J., 2013. Generational risk – is it a big deal?: Simulating an 80-period OLG model with aggregate shocks. NBER 19179.
93. Heathcote, J., Perri, F., 2013. The international diversification puzzle is not as bad as you think. Manuscript.
94. Heathcote J, Storesletten K, Violante G. Quantitative macroeconomics with heterogeneous households. Annual Review of Economics, Annual Reviews. 2009;1(1):319–354.
95. Heer B, Maußner A. Computation of business cycle models: a comparison of numerical methods. Macroeconomic Dynamics. 2008;12:641–663.
96. Heer B, Maußner A. Dynamic General Equilibrium Modeling. Berlin Heidelberg: Springer-Verlag; 2010.
97. Horvath M. Computational accuracy and distributional analysis in models with incomplete markets and aggregate uncertainty. Economic Letters. 2012;117(1):276–279.
98. Jin, H., Judd, K.L., 2002. Perturbation methods for general dynamic stochastic models. Stanford University. Manuscript.
99. Jirnyi, A., Lepetyuk, V., 2011. A reinforcement learning approach to solving incomplete market models with aggregate uncertainty. IVIE Working Paper, Series AD 21.
100. Judd K. Projection methods for solving aggregate growth models. Journal of Economic Theory. 1992;58:410–452.
101. Judd K. Numerical Methods in Economics. Cambridge, MA: MIT Press; 1998.
102. Judd, K., 2003. Perturbation methods with nonlinear changes of variables. Manuscript.
103. Judd K, Guu S. Perturbation solution methods for economic growth models. In: Varian H, ed. Economic and Financial Modeling with Mathematica. Springer Verlag 1993:80–103.
104. Judd K, Yeltekin S, Conklin J. Computing supergame equilibria. Econometrica. 2003;71(1239):1254.
105. Judd, K.L., Maliar, L., Maliar, S., 2009. Numerically stable stochastic simulation approaches for solving dynamic economic models. NBER Working Paper 15296.
106. Judd, K.L., Maliar, L., Maliar, S., 2010. A cluster-grid projection method: solving problems with high dimensionality. NBER Working Paper 15965.
107. Judd, K.L., Maliar, L., Maliar, S., 2011a. One-node quadrature beats Monte Carlo: a generalized stochastic simulation algorithm. NBER Working Paper 16708.
108. Judd KL, Maliar L, Maliar S. Numerically stable and accurate stochastic simulation approaches for solving dynamic models. Quantitative Economics. 2011b;2:173–210.
109. Judd, K.L., Maliar, L., Maliar, S., 2011d. How to solve dynamic stochastic models computing expectations just once. NBER Working Paper 17418.
110. Judd, K.L., Maliar, L., Maliar, S., 2012a. Merging simulation and projection approaches to solve high-dimensional problems. NBER Working Paper 18501.
111. Judd KL, Renner P, Schmedders K. Finding all pure-strategy equilibria in games with continuous strategies. Quantitative Economics. 2012b;3:289–331.
112. Judd, K.L., Maliar, L., Maliar, S., Valero, R., 2013. Smolyak method for solving dynamic economic models: Lagrange interpolation, anisotropic grid and adaptive domain. NBER 19326.
113. Juillard, M. 2011. Local approximation of DSGE models around the risky steady state. Wp.comunite 0087, Department of Communication, University of Teramo.
114. Juillard M, Villemot S. Multi-country real business cycle models: accuracy tests and testing bench. Journal of Economic Dynamics and Control. 2011;35:178–185.
115. Kabourov G, Manovskii I. Occupational mobility and wage inequality. Review of Economic Studies. 2009;76(2):731–759.
116. Kendrik D, Ruben Mercado P, Amman HM. Computational Economics. Princeton University Press 2006.
117. Kiefer J. On large deviations of the empiric D.F of vector change variables and a law of the iterated logarithm. Pacific Journal of Mathematics. 1961;11:649–660.
118. Kim J, Kim S, Schaumburg E, Sims CA. Calculating and using second-order accurate solutions of discrete time dynamic equilibrium models. Journal of Economic Dynamics and Control. 2008;32:3397–3414.
119. Kim S, Kollmann R, Kim J. Solving the incomplete market model with aggregate uncertainty using a perturbation method. Journal of Economics Dynamics and Control. 2010;34:50–58.
120. Klenow P, Kryvtsov O. State-dependent or time-dependent pricing: does it matter for recent US inflation? Quarterly Journal of Economics. 2008;3(CXXIII):863–904.
121. Kocherlakota N, Pistaferri L. Asset pricing implications of Pareto optimality with private information. Journal of Political Economy. 2009;117(3):555–590.
122. Kollmann R, Kim S, Kim J. Solving the multi-country real business cycle model using a perturbation method. Journal of Economic Dynamics and Control. 2011a;35:203–206.
123. Kollmann R, Maliar S, Malin B, Pichler P. Comparison of solutions to the multi-country real business cycle model. Journal of Economic Dynamics and Control. 2011b;35:186–202.
124. Krueger D, Kubler F. Computing equilibrium in OLG models with production. Journal of Economic Dynamics and Control. 2004;28:1411–1436.
125. Krueger D, Kubler F. Pareto-improving social security reform when financial markets are incomplete? American Economic Review. 2006;96(3):737–755.
126. Krusell P, Smith A. Income and wealth heterogeneity in the macroeconomy. Journal of Political Economy. 1998;106:868–896.
127. Krusell P, Ohanian L, Ríos-Rull J-V, Violante G. Capital-skill complementarity and inequality: a macroeconomic analysis. Econometrica. 1997;68(5):1029–1053.
128. Kubler F, Schmedders K. Tackling multiplicity of equilibria with Gröbner bases. Operations Research. 2010;58:1037–1050.
129. Lim G, McNelis P. Computational Macroeconomics for the Open Economy. Cambridge, Massachusetts, London, England: The MIT Press; 2008.
130. Lombardo, G., 2010. On approximating DSGE models by series expansions. European Central Bank Working Paper 1264.
131. Maliar, L., 2013. Assessing gains from parallel computation on supercomputers. Manuscript.
132. Maliar L, Maliar S. Heterogeneity in capital and skills in a neoclassical stochastic growth model. Journal of Economic Dynamics and Control. 2001;25:1367–1397.
133. Maliar L, Maliar S. The representative consumer in the neoclassical growth model with idiosyncratic shocks. Review of Economic Dynamics. 2003a;6:362–380.
134. Maliar L, Maliar S. Parameterized expectations algorithm and the moving bounds. Journal of Business and Economic Statistics. 2003b;21:88–92.
135. Maliar L, Maliar S. Solving nonlinear stochastic growth models: iterating on value function by simulations. Economics Letters. 2005a;87:135–140.
136. Maliar L, Maliar S. Parameterized expectations algorithm: how to solve for labor easily. Computational Economics. 2005b;25:269–274.
137. Maliar, L., Maliar, S. 2011. Perturbation with precomputation of integrals. Manuscript.
138. Maliar, L., Maliar, S. 2012a. Solving the multi-country real business cycle model using an envelope-condition method. Manuscript.
139. Maliar, L., Maliar, S., 2012b. Value function iteration for problems with high dimensionality: An envelope-condition method. Manuscript.
140. Maliar L, Maliar S. Envelope condition method versus endogenous grid method for solving dynamic programming problems. Economics Letters. 2013;120:262–266.
141. Maliar L, Maliar S, Valli F. Solving the incomplete markets model with aggregate uncertainty using the Krusell-Smith algorithm. Journal of Economic Dynamics and Control. 2010;34(Special issue):42–49.
142. Maliar S, Maliar L, Judd KL. Solving the multi-country real business cycle model using ergodic set methods. Journal of Economic Dynamic and Control. 2011;35:207–228.
143. Maliar L, Maliar S, Villemot S. Taking perturbation to the accuracy frontier: a hybrid of local and global solutions. Computational Economics. 2013;42:307–325.
144. Malin B, Krueger D, Kubler F. Solving the multi-country real business cycle model using a Smolyak-collocation method. Journal of Economic Dynamics and Control. 2011;35:229–239.
145. Manova K. Credit constraints, heterogeneous firms, and international trade. Review of Economic Studies. 2013;80:711–744.
146. Marcet, A., 1988. Solution of nonlinear models by parameterizing expectations. Carnegie Mellon University, Manuscript.
147. Marcet A, Lorenzoni G. The parameterized expectation approach: some practical issues. In: Marimon R, Scott A, eds. Computational Methods for Study of Dynamic Economies. New York: Oxford University Press; 1999:143–171.
148. Marcet A, Sargent T. Convergence of least-squares learning in environments with hidden state variables and private information. Journal of Political Economy. 1989;97:1306–1322.
149. Marimon R, Scott A. Computational Methods for Study of Dynamic Economies. New York: Oxford University Press; 1999.
150. MATLAB, 2011. MATLAB parallel computing toolbox. <http://www.mathworks.com/products/parallel-computing/description5.html>.
151. Mendoza, E.G., Bianchi, J., 2011. Overborrowing, financial crises and ‘macro-prudential’ policy? IMF Working Papers 11/24, International Monetary Fund.
152. Menzio, G., Telyukova, I., Visschers, L., 2012. Directed search over the life cycle. NBER Working Papers 17746.
153. Mertens, T., Judd, K.L., 2013. Equilibrium existence and approximation for incomplete market models with substantial heterogeneity. Manuscript.
154. Mertens, K., Ravn, M., 2011. Credit channels in a liquidity trap. CEPR Discussion Paper 8322.
155. Michelacci, C., Pijoan-Mas, J., 2012. Intertemporal labour supply with search frictions. Review of Economic Studies (2012) 79, 899–931.
156. Miranda M, Fackler P. Applied Computational Economics and Finance. Cambridge: MIT Press; 2002.
157. Miranda M, Helmberger P. The effects of commodity price stabilization programs. American Economic Review. 1988;78:46–58.
158. Moore GE. Cramming more components onto integrated circuits. Electronics. 1965;38(8):1965.
159. Morozov S, Mathur S. Massively parallel computation using graphics processors with application to optimal experimentation in dynamic control. Computational Economics. 2012;40:151–182.
160. Nadaraya EA. On Estimating Regression. Theory of probability and its applications. 1964;10:186–190.
161. Nagurney A. Parallel computation. In: Amsterdam: Elsevier; 1996:336–401. Amman HM, Kendrick DA, Rust J, eds. Handbook of Computational Economics. vol. 1.
162. Nagurney A, Zhang D. A massively parallel implementation of discrete-time algorithm for the computation of dynamic elastic demand and traffic problems modeled as projected dynamical systems. Journal of Economic Dynamics and Control. 1998;22(8–9):1467–1485.
163. Nakajima, M., Telyukova, I., 2011. Reverse mortgage loans: a quantitative analysis. Manuscript.
164. Niederreiter H. Random Number Generation and Quasi-Monte Carlo Methods. Philadelphia, Pennsylvania: Society for Industrial and Applied Mathematics; 1992.
165. Pagan Ullah. Nonparametric Econometrics. New York: Cambridge University Press; 1999.
166. Pakes A, McGuire P. Stochastic algorithms, symmetric Markov perfect equilibria, and the ‘curse’ of dimensionality. Econometrica. 2001;69:1261–1281.
167. Peralta-Alva A, Santos M. Accuracy of simulations for stochastic dynamic models. Econometrica. 2005;73:1939–1976.
168. Piazzesi, M., Schneider, M. 2012. Inflation and the price of real assets. Staff Report 423, Federal Reserve Bank of Minneapolis.
169. Pichler P. Solving the multi-country real business cycle model using a monomial rule Galerkin method. Journal of Economic Dynamics and Control. 2011;35:240–251.
170. Powell W. Approximate Dynamic Programming. Hoboken, New Jersey: Wiley; 2011.
171. Ravenna F, Walsh C. Welfare-based optimal monetary policy with unemployment and sticky prices: a linear-quadratic framework. American Economic Journal: Macroeconomics. 2011;3:130–162.
172. Reiter M. Solving heterogeneous-agent models by projection and perturbation. Journal of Economic Dynamics and Control. 2009;33(3):649–665.
173. Rios-Rull, J.V., 1997. Computing of equilibria in heterogeneous agent models. Federal Reserve Bank of Minneapolis Staff. Report 231.
174. Rust J. Numerical dynamic programming in economics. In: Amman H, Kendrick D, Rust J, eds. Handbook of Computational Economics. Amsterdam: Elsevier Science; 1996:619–722.
175. Rust J. Using randomization to break the curse of dimensionality. Econometrica. 1997;65:487–516.
176. Rust J. Dynamic programming. In: Durlauf S, Blume L, eds. The New Palgrave Dictionary of Economics. Palgrave Macmillan 2008.
177. Sanders J, Kandrot E. CUDA by Example: An Introduction to General-Purpose GPU Programming. Upper Saddle River, NJ: Addison-Wesley Professional; 2010.
178. Santos M. Numerical solution of dynamic economic models. In: Taylor J, Woodford M, eds. Handbook of Macroeconomics. Amsterdam: Elsevier Science; 1999:312–382.
179. Santos M. Accuracy of numerical solutions using the Euler equation residuals. Econometrica. 2000;68:1377–1402.
180. Schmitt-Grohé S, Uribe M. Solving dynamic general equilibrium models using a second-order approximation to the policy function. Journal of Economic Dynamics and Control. 2004;28(4):755–775.
181. Scott D, Sain S. Multidimensional density estimation. In: Rao C, Wegman E, Solka J, eds. Handbook of Statistics. Amsterdam: Elsevier B. V.; 2005:229–261. vol 24.
182. Sims C, Waggoner D, Zha T. Methods for inference in large-scale multiple equation Markov-switching models. Journal of Econometrics. 2008;142(2):255–274.
183. Smets F, Wouters R. An estimated dynamic stochastic general equilibrium model of the Euro area. Journal of the European Economic Association. 2003;1(5):1123–1175.
184. Smets F, Wouters R. Shocks and frictions in US business cycles: a Bayesian DSGE approach. American Economic Review. 2007;97(3):586–606.
185. Smith, A., 1991. Solving stochastic dynamic programming problems using rules of thumb. Queen’s University. Economics Department, Discussion Paper 816.
186. Smith A. Estimating nonlinear time-series models using simulated vector autoregressions. Journal of Applied Econometrics. 1993;8:S63–S84.
187. Smolyak S. Quadrature and interpolation formulas for tensor products of certain classes of functions. Soviet Mathematics, Doklady. 1963;4:240–243.
188. Song Z, Storesletten K, Zilibotti F. Rotten parents and disciplined children: a politico-economic theory of public expenditure and debt. Econometrica. 2012;80(6):2785–2803.
189. Stachursky J. Economic Dynamics: Theory and Computation. Cambridge: MIT Press; 2009.
190. Stroud A. Approximate Integration of Multiple Integrals. Englewood Cliffs, New Jersey: Prentice Hall; 1971.
191. Su CL, Judd KL. Constrained optimization approaches to estimation of structural models. Econometrica. 2012;80(5):2213–2230.
192. Swanson, E., Anderson, G., Levin, A., 2002. Higher-order perturbation solutions to dynamic, discrete-time rational expectations models. Manuscript.
193. Swanson, E., Anderson, G., Levin, A., 2006. Higher-order perturbation solutions to dynamic, discrete-time rational expectations models. Federal Reserve Bank of San Francisco working paper 1.
194. Tauchen G. Finite state Markov chain approximations to univariate and vector autoregressions. Economic Letters. 1986;20:177–181.
195. Tauchen G, Hussey R. Quadrature-based methods for obtaining approximate solutions to nonlinear asset pricing models. Econometrica. 1991;59:371–396.
196. Taylor J, Uhlig H. Solving nonlinear stochastic growth models: a comparison of alternative solution methods. Journal of Business and Economic Statistics. 1990;8:1–17.
197. Temlyakov V. Greedy Approximation. Cambridge: Cambridge University Press; 2011.
198. Tesfatsion L, Judd KL. Handbook of computational economics. In: Agent-Based Computational Economics. Amsterdam: Elsevier Science; 2006; Vol 2.
199. Tsitsiklis J. Asynchronous stochastic approximation and Q-Learning. Machine Learning. 1994;16:185–202.
200. Valero, R., Maliar, L., Maliar, S., 2013. Parallel speedup or parallel slowdown: is parallel computation useful for solving large-scale dynamic economic models? Manuscript.
201. Villemot, S. 2012. Accelerating the resolution of sovereign debt models using an endogenous grid method. Dynare working paper 17, <http://www.dynare.org/wp>.
202. Watson GS. Smooth regression analysis. Shankya Series A. 1964;26:359–372.
203. Weintraub G, Benkard CL, Roy BV. Markov perfect industry dynamics with many firms. Econometrica. 2008;2008:1375–1411.
204. Winschel V, Krätzig M. Solving, estimating and selecting nonlinear dynamic models without the curse of dimensionality. Econometrica. 2010;78(2):803–821.
205. Woodford M. Optimal monetary stabilization policy. In: Amsterdam: Elsevier; 2011:723–828. Friedman BM, Woodford M, eds. Handbook of Monetary Economics. vol. 3B.
206. Wright B, Williams J. The welfare effects of the introduction of storage. Quarterly Journal of Economics. 1984;99:169–192.
207. Young E. Solving the incomplete markets model with aggregate uncertainty using the Krusell-Smith algorithm and non-stochastic simulations. Journal of Economic Dynamics and Control. 2010;34:36–41.
1Heterogeneous agents models are studied in, e.g., Gaspar and Judd (1997), Krusell and Smith (1998), Kabourov and Manovskii (2009), Heathcote et al. (2009), Guvenen (2011), Guerrieri and Lorenzoni (2011), Michelacci and Pijoan-Mas (2012), Bai et al. (2012), Dmitriev and Roberts (2012), Cogley et al. (2013). Examples of models with multiple sectors and heterogeneous firms are Krusell et al. (1997), Altig et al. (2004), Klenow and Kryvtsov (2008), Gertler and Leahy (2008), Bloom (2009).
2Asset-pricing models are studied in, e.g., Kocherlakota and Pistaferri (2009), Duffie (2010), Borovička and Hansen (2012), Piazzesi and Schneider (2012); life-cycle models are studied in, e.g., Krueger and Kubler (2004, 2006), Gomes et al. (2008), Glover et al. (2011), Menzio et al. (2012), Guibaud et al. (forthcoming), Hasanhodzic and Kotlikoff (2013); international trade models are studied in, e.g., Caselli et al. (2011), Manova (2013), Heathcote and Perri (2013).
3New Keynesian models are studied in, e.g., Smets and Wouters (2003, 2007), Christiano et al. (2005, 2011), Del Negro et al. (2007), Chari et al. (2009), Woodford (2011), Mertens and Ravn (2011), Ravenna and Walsh (2011), Hall (2012), Cogan et al. (2013).
4Some examples from recent literature are climate change models (Cai et al., 2012), models of information and forecasts (Coibion and Gorodnichenko, 2008; Graham and Wright, 2009; Amador and Weil, 2010; Attanasio and Pavoni, 2011; Ellison and Sargent, 2012); fiscal policy models (Golosov et al., 2011; Golosov and Sargent, 2012; Evans et al., 2012); models with a risk of consumer default (Chatterjee et al., 2007); housing and mortgage models (Nakajima and Telyukova, 2011); resource war models (Acemoglu et al., 2011); political economy models (Song et al., 2012); financial crises models (Mendoza and Bianchi, 2011; Gertler et al., 2011).
5One example is a nested fixed-point estimation in econometrics, see, e.g., Fernández-Villaverde and Rubio-Ramírez (2007), Winschel and Krätzig (2010), Su and Judd (2012).
6Krusell and Smith (1998) focus on a related but mathematically different problem. They assume a continuum of agents distributed in the interval ![]() while we consider a finitely large number of agents
while we consider a finitely large number of agents ![]() . The framework of Krusell and Smith (1998) is designed for modeling the aggregate behavior of a very large number of agents that are identical in fundamentals (e.g., consumers or firms) while our framework allows for combinations of any agents (consumers, firms, government, monetary authority) as long as their total number is not too large. The computational approach of Krusell and Smith (1998) also differs from ours in that they replace the true state space (a joint distribution of individual state variables) with a reduced state space (moments of such a distribution) while we operate with the true state space.
. The framework of Krusell and Smith (1998) is designed for modeling the aggregate behavior of a very large number of agents that are identical in fundamentals (e.g., consumers or firms) while our framework allows for combinations of any agents (consumers, firms, government, monetary authority) as long as their total number is not too large. The computational approach of Krusell and Smith (1998) also differs from ours in that they replace the true state space (a joint distribution of individual state variables) with a reduced state space (moments of such a distribution) while we operate with the true state space.
7Codes are available from the authors’ web sites. In particular, a Fortran code for the Smolyak method is available at http://economics.sas.upenn.edu/![]() dkrueger/research.php; a MATLAB code for GSSA method is available at http://www.stanford.edu/
dkrueger/research.php; a MATLAB code for GSSA method is available at http://www.stanford.edu/![]() maliarl; C++ / DYNARE code for the perturbation-based hybrid solution methods is available at http://www.dynare.org/sebastien/; a C++/CUDA code for a value function iteration method is available at http://www.parallelecon.com.
maliarl; C++ / DYNARE code for the perturbation-based hybrid solution methods is available at http://www.dynare.org/sebastien/; a C++/CUDA code for a value function iteration method is available at http://www.parallelecon.com.
8The term curse of dimensionality was originally used by Richard Bellman (1961) to refer to an exponential increase in volume associated with adding extra dimensions to a mathematical space.
9Den Haan and Marcet (1990) find that the implementation of PEA that uses least-squares learning becomes problematic even for a second-degree polynomial. Specifically, a cross term in a polynomial function is highly correlated with other terms and must be removed from a regression.
10These points are extrema of a Chebyshev polynomial function but this fact is not essential for the Smolyak construction; we can use other unidimensional grid points instead, for example, uniformly spaced grid points.
11Again, the assumption of Chebyshev basis functions is convenient but not essential for the Smolyak construction.
12The name of Marcet’s (1988) method highlights the way in which it deals with uncertainty; namely, it parameterizes a conditional expectation function and approximates such a function from simulated data using a Monte Carlo integration method (combined with a least-squares learning).
13Christiano and Fisher (2000) found that multicollinearity can plague the regression step even with orthogonal (Chebyshev) polynomials as basis functions.
14For a description of methods for computing the SVD of a matrix, see, e.g., Golub and Van Loan (1996), pp. 448–460. Routines that compute the SVD are readily available in modern programming languages.
15Another decomposition of ![]() that leads to a numerically stable LS approach is a QR factorization; see, e.g., Davidson and MacKinnon (1993), pp. 30–31, and Golub and Van Loan (1996), p. 239.
that leads to a numerically stable LS approach is a QR factorization; see, e.g., Davidson and MacKinnon (1993), pp. 30–31, and Golub and Van Loan (1996), p. 239.
16There is another technique that can help us to increase the accuracy of perturbation methods, namely, computing Taylor expansions around stochastic steady state instead of deterministic one. Two variants of this technique are developed in Juillard (2011) and Maliar and Maliar (2011): the former paper computes the stochastic steady state numerically, while the latter paper uses analytical construction based on precomputation of integrals of Judd et al. (2011d). We do not survey this technique in detail because it is not yet tested in the context of large-scale models.
17See http://www.dynare.org and Adjemian et al. (2011) for more details on Dynare.
18In particular, in the comparison analysis of Kollmann et al. (2011b), the first- and second-order perturbation methods of Kollmann et al. (2011a) produce maximum residuals of 6.3% and 1.35% on a stochastic simulation, and they produce maximum residuals of 65% and 50% on a 30% deviation from the steady state. Moreover, perturbation quadratic solutions are up to three orders of magnitude less accurate than global quadratic solutions.
19Currently, NVIDIA graphical cards are the most developed ones for scientific computation, and they use a language that has a basis in C, called CUDA; see Sanders and Kandrot (2010).
20The comparison here is not completely fair. By default, MATLAB makes the use of multithreading capabilities of the computer. If we limit MATLAB to a single computational thread, all the reported speedups will increase by around a factor of 3–4.
21In total, there are four models, Models I–IV, studied in Kollmann et al. (2011b), and each of these models has symmetric and asymmetric specifications.
22Model I has a degenerate labor-leisure choice and Models III and IV are identical to Model II up to specific assumptions about preferences and technologies. Juillard and Villemot (2011) provide a description of all models studied in the comparison analysis of Kollmann et al. (2011b).
*Chapter prepared for Handbook of Computational Economics, Volume 3, edited by Karl Schmedders and Kenneth L. Judd.