Solving and Simulating Models with Heterogeneous Agents and Aggregate Uncertainty
Yann Algana, Olivier Allaisb, Wouter J. Den Haanc, d and Pontus Rendahle, aSciences Po, Paris, France, bINRA, UR1303 ALISS, Ivry-sur-Seine, France, cCentre for Macroeconomics, London School of Economics, London, UK, dCEPR, London, UK, eCentre for Macroeconomics, University of Cambridge, Cambridge, UK, a [email protected], b [email protected], d [email protected], e [email protected]
Abstract
Although almost nonexistent 15 years ago, there are now numerous papers that analyze models with both aggregate uncertainty and a large number—typically a continuum—of heterogeneous agents. These models make it possible to study whether macroeconomic fluctuations affect different agents differently and whether heterogeneity in turn affects macroeconomic fluctuations. This chapter reviews different algorithms to solve and simulate these models. In addition, it highlights problems with popular accuracy tests and discusses more powerful alternatives.
Keywords
Incomplete markets; Numerical solutions; Projection methods; Perturbation methods; Parameterized densities; Accuracy tests
JEL Classification Codes
C63; D52
1 Introduction
The development of computational algorithms to solve economic models with heterogeneous agents and aggregate uncertainty started in the second half of the 1990s. Early examples are Campbell (1998), Den Haan (1996, 1997), and Krusell and Smith (1997, 1998).1 The presence of aggregate uncertainty implies that the cross-sectional distribution of agents’ characteristics is time varying and, thus, has to be included in the set of state variables. This implies that the individual policy rules depend on a large number of arguments, unless the number of agents is small. In particular, under the common assumption that there is a continuum of agents, the set of state variables would be infinite dimensional. A common feature of existing algorithms is to summarize this infinite-dimensional object with a limited set of statistics that summarize the distribution.
Krusell and Smith (1998) consider a model in which employment risk is not fully insurable because of borrowing constraints and missing insurance markets. They show that in this environment the model satisfies the approximate aggregation property, that is, the mean of the capital stock is a sufficient statistic to predict next period’s prices accurately.2 The reason for this important finding is that the marginal propensity to save is very similar across agents with different income and wealth levels—except for the very poor. Since there are not many poor agents and their wealth is small, the similarity of the marginal propensity to save of the other agents implies that redistributions of wealth have no effect on aggregate savings and, thus, not on market prices. This is quite a general result and remains valid if, for example, the amount of idiosyncratic risk is increased. Important is that the amount of aggregate savings is endogenous. This implies that the average agent can build up a wealth level that is so high that the chance of the constraint being binding is small. Den Haan (1997) considers a model in which aggregate savings are zero. In this model, the borrowing constraint is more frequently binding and higher-order moments do matter. Krusell and Smith (2006) say in their conclusion that “we foresee important examples of such phenomena [i.e., quantitatively convincing models with large departures from approximate aggregation] to be discovered in future research.” Such models will, without doubt, be harder to solve, and as we move into solving more complex models, the need for alternative algorithms and careful testing of accuracy becomes more important.
Existing algorithms differ in important aspects from each other. While the first algorithms relied heavily on simulation procedures, the newer attempts try to build algorithms using building blocks proven to be fruitful in the numerical literature such as projection methods and perturbation techniques.
In addition to reviewing solution algorithms, this chapter also reviews different procedures to simulate economies with a continuum of agents. Simulations are an essential ingredient in several of the algorithms and typically are important even when the algorithms themselves do not rely on simulations. The reason is that many properties of the model can only be calculated through simulation. With a continuum of agents, simulation is nontrivial. In the most commonly used procedure, the continuum of agents is approximated with a large but finite number of agents. This introduces unnecessary sampling variation that may be substantial for some groups of the population. We review several alternative procedures that are more accurate and faster.
Another important topic of this chapter is a discussion on how to check for accuracy. The standard procedure to check for accuracy is to use the 
or the standard error of the regression, the two accuracy measures that Krusell and Smith (1998) focus on. Den Haan (2010a) shows that these are very weak measures. In particular, it is shown that aggregate laws of motion that differ substantially from each other in important dimensions can all have a very high 
and a low regression standard error. Den Haan (2010a) also proposes an alternative accuracy test that is more powerful. Note that Krusell and Smith (1996, 1998) actually consider several alternative accuracy measures. One of them, the maximum forecast error at a long forecast horizon, turns out to be much more powerful in detecting inaccuracies than the 
and the standard error.
This chapter is organized as follows. In Section 2, we describe the model that we use to illustrate the different algorithms. In Sections 3 and 6, we describe the numerical solution and the numerical simulation procedures, respectively. In Section 4, we discuss the importance of ensuring that the numerical solution satisfies market clearing. In Section 5, we discuss the result from Krusell and Smith (1998) that the mean capital stock is a sufficient statistic, i.e., approximate aggregation. In Section 7, we discuss accuracy tests, and in Section 8, we compare the properties of the different algorithms. The last section concludes.
2 Example Economy
The model described in this section is an extension of Krusell and Smith (1998).3 Its relative simplicity makes it very suitable to illustrate the key features of the different algorithms. Another reason to focus on this model is that its aggregation properties have been quite influential.
Problem for the Individual Agent
The economy consists of a continuum of ex ante identical households with unit mass. Each period, agents face an idiosyncratic shock 
that determines whether they are employed, 
, or unemployed, 
. An employed agent earns an after-tax wage rate of 
and an unemployed agent receives unemployment benefits 
.4 Markets are incomplete and agents can only save through capital accumulation. The net rate of return on investment is equal to 
, where 
is the rental rate and 
is the depreciation rate. Agent 
’s maximization problem is as follows:
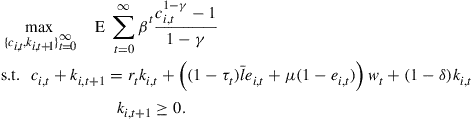(1)
Here 
is the individual level of consumption, 
is the agent’s beginning-of-period capital, and 
is the time endowment. We set 
equal to 1 to simplify the notation.
The Euler equation error, 
, is defined as
(2)
and the first-order conditions of the agent are given by
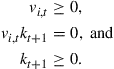(3)
Firm Problem
Markets are competitive and the production technology of the firm is characterized by a constant-returns-to-scale Cobb-Douglas production function. Consequently, firm heterogeneity is not an issue. Let 
and 
stand for the per capita capital stock and the employment rate, respectively. Per capita output is given by
(4)
and prices by
(5)
(6)
Aggregate productivity, 
, is an exogenous stochastic process that can take on two values, 
and 
.
Government
The only role of the government is to tax employed agents and to redistribute funds to the unemployed. We assume that the government’s budget is balanced each period. This implies that the tax rate is equal to
(7)
where 
denotes the unemployment rate in period 
.
Exogenous Driving Processes
There are two stochastic driving processes. The first is aggregate productivity and the second is the employment status. Both are assumed to be first-order Markov processes. We let 
stand for the probability that 
and 
when 
and 
. These transition probabilities are chosen such that the unemployment rate can take on only two values. That is, 
when 
and 
when 
with 
.5
Equilibrium
Krusell and Smith (1998) consider recursive equilibria in which the policy functions of the agent depend on his employment status, 
, his beginning-of-period capital holdings, 
, aggregate productivity, 
, and the cross-sectional distribution of capital holdings, 
.6 An equilibrium consists of the following elements:
1. Individual policy functions that solve the agent’s maximization problem for given laws of motion of 
and 
.
2. A rental and a wage rate that are determined by Eqs. (5) and (6), respectively.
3. A transition law for the cross-sectional distribution of capital that is consistent with the individual policy function. We let 
represent the beginning-of-period cross-sectional distribution of capital and the employment status after the employment status has been realized. The transition law can be written as
(8)
This law of motion reveals an advantage of working with a continuum of agents. The idea is to rely on a law of large numbers, so that conditional on 
there is no uncertainty about 
.7
3 Algorithms—Overview
There are now several algorithms to solve models with heterogeneous agents and aggregate uncertainty using a wide range of different tools from the numerical solution literature. They include algorithms that use only perturbation techniques like Preston and Roca (2006); algorithms that use only projection methods like Den Haan (1997) and Den Haan and Rendahl (2010); as well as several others that combine different tools such as Den Haan (1996), Krusell and Smith (1998), Algan et al. (2008), Reiter (2009), and Reiter (2010). This section is split in two parts. Section 3.1 discusses procedures that rely on projection approaches, possibly combined with a simulation procedure. These are global procedures in the sense that properties of the model in different parts of the state space affect the numerical solution. Section 3.2 discusses perturbation approaches in which the numerical solution is pinned down by the derivatives at one particular point. The purpose of this section is to explain—hopefully in an intuitive manner—the key aspects of the different algorithms.
3.1 Projection and Simulation Approaches
This section discusses four quite different approaches. It discusses the approach of Krusell and Smith (1998) in which simulations are used to determine the aggregate laws of motion; the approach developed in Den Haan (1996), which is a pure simulation approach; the approach of Algan et al. (2008), which is based mainly on projection methods8; and finally the approach developed in Den Haan and Rendahl (2010), which uses only projection methods. As discussed above, we focus on equilibria in which (i) individual policy functions depend on 
and (ii) the next period’s cross-sectional distribution is a time-invariant function of the current distribution and the aggregate shock. All existing algorithms summarize the information of the cross-sectional distribution with a finite set of elements.
3.1.1 Obtain Aggregate Policy Functions from Simulation
The most popular algorithm used in the literature is the one developed in Krusell and Smith (1998). They approximate the infinite-dimensional cross-sectional distribution with a finite set of moments, 
.9 An approximate solution then consists of an individual policy function (as a function of the vector 
) and a law of motion for 
of the form
(9)
The idea underlying this algorithm is fairly straightforward. Notice that the problem of solving for the individual policy rules is standard and one can use any of the available algorithms.10 In solving for the individual policy functions, one will run into the problem of evaluating next period’s prices, which depend on next period’s aggregate capital stock, but this can be calculated using the mapping 
. The algorithm then proceeds using the following iterative scheme:
1. Start with an initial guess for 
, say 
.
2. Using this guess, solve for the individual policy rule.
3. Construct a time series for 
. That is, using the solution for the individual policy rule, simulate the economy using one of the simulation techniques discussed in Section 6. For each period calculate the elements of 
from the cross-sectional distribution.
4. Use least squares to obtain a new estimate for the law of motion 
. This is 
.
is sufficiently close to 
.3.1.2 Obtain Aggregate and Individual Policy Functions Through Simulation
As in Krusell and Smith (1998), Den Haan (1996) also assumes that the cross-sectional distribution is characterized by a finite set of moments, 
. He solves for the individual policy rules from a simulation procedure, which avoids having to specify an approximating law of motion for the transition of 
.11
Den Haan (1996) parameterizes the conditional expectation, but it is also possible to approximate the consumption or the capital choice. With this approximation, the optimality conditions of the agent can be written as
(10)
(11)
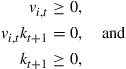(12)
where 
is a flexible functional form of order 
with coefficient vector 
.12 The algorithm works as follows:
1. Start with an initial guess for the parameterized conditional expectation, characterized by its coefficients, 
. Note that this is equivalent to having the individual policy functions for consumption and capital.
2. Use the individual policy rule to simulate a time series for 
and the choices for one agent. That is, we obtain a time series for 
. Prices can be calculated using the observed cross-sectional mean capital stock. Let 
be equal to
(13)
Note that
(14)
where 
is a prediction error that is orthogonal to the variables in the time 
information set.13 This means one can use nonlinear least squares to get a new estimate of 
.
have converged.This procedure is similar to the one used by Krusell and Smith (1998), but it does not require specifying an approximation to the law of motion for the moments that are used as state variables. The reason is the following. Krusell and Smith (1998) use the approximation to the aggregate law of motion to describe next period’s prices in terms of next period’s value of 
and this period’s moments. If one projects 
on 
, then this transition law is automatically taken into account without having specified a particular functional form to describe it.
3.1.3 Obtain Aggregates by Integrating over a Parameterized Distribution
Next, we discuss the algorithm of Den Haan (1997) and the improved version developed in Algan et al. (2008). As in Den Haan (1996), the conditional expectation of the individual agent is parameterized and the objective is to solve for the value of 
. Moreover, the cross-sectional distribution is characterized with a finite set of moments, 
, and the state variables are, thus, again given by 
, and 
. Nevertheless, these are very different algorithms. Whereas Den Haan (1996) is based on simulations, the algorithm of Den Haan (1997) uses textbook projection methods. A textbook projection procedure consists of (i) a grid in the state variables, (ii) a quadrature procedure to calculate the conditional expectation in Eq. (2), and (iii) an equation solver to find the coefficients of the approximating function for which the errors on the grid are equal to zero.14
For the type of problem considered in this paper, it is not straightforward to solve the model using standard projection techniques. Some additional information is required. To understand why, consider a particular grid point, that is, a particular combination of 
, and 
. Calculation of
requires knowing the aggregate capital stock, 
. To calculate 
at a particular grid point requires not only knowing 
(and 
), but typically requires knowing the actual distribution.15 Den Haan (1997) deals with this problem by parameterizing the cross-sectional distribution. Conditional on a particular functional form, say the exponential of an nth-order polynomial, there is a mapping between the 
values of 
and the coefficients of the approximating density, 
. For example, if one uses a second-order exponential, i.e., a Normal density, then the mean and the variance pin down the two elements of 
.16 Given the parameterization 
, the conditional expectation can be calculated using standard quadrature techniques and standard projection methods can be used to solve for the coefficients of the individual policy rule, 
.17
Reference Moments/Distribution
The description so far assumes that the order of the approximation of the cross-sectional density is directly related to the moments included. That is, if 
moments are used as state variables, then an nth-order approximation is used to approximate the cross-sectional density (and vice versa). But this may be inefficient. For example, it may be the case that only first- and second-order moments are needed as state variables, but that (for the particular class of approximating polynomials chosen) a much higher-order approximation is needed to get the shape of the cross-sectional distribution right.
Algan et al. (2008, 2010) improve upon Den Haan (1997) and deal with this inefficiency by introducing “reference” moments that are characteristics of the distribution exploited to pin down its shape, but are not used as state variables.18 Let 
, where 
consists of (lower-order) moments that serve as state variables and are used to construct the grid and where 
consists of higher-order reference moments. On the grid, the values of the reference moments, 
, are calculated as a function of 
and 
using an approximating function 
.19 Algan et al. (2008, 2010) find this mapping by simulating a time series for 
, but this is the only role for simulations in their algorithm. A numerical solution has to be such that the relationship between reference moments and other state variables is consistent with the one that comes out of the simulation.
Histogram as Reference Distribution
The algorithm of Reiter (2010) is similar to that of Algan et al. (2008, 2010), but differs in its implementation. Reiter (2010) characterizes the cross-sectional distribution using a histogram and obtains a complete reference distribution from the simulation. The reference distribution, together with the values of the moments included as state variables, is then used to construct a new histogram that is consistent with the values of the state variables and “close” to the reference distribution itself. Next period’s values of the cross-sectional moments are calculated by integrating over this histogram.
3.1.4 Obtain Aggregates by Explicit Aggregation
The idea of the algorithm of Den Haan and Rendahl (2010) is to derive the aggregate laws of motion directly from the individual policy rules simply by integrating them without using information about the cross-sectional distribution. Before we describe the algorithm, it will be useful to explain the relationship between the individual policy function and the set of moments that should be included as state variables in the exact solution. Krusell and Smith (2006) show that one often can get an accurate solution by using only first-order moments to characterize the distribution. The fact that individual policy functions of the models considered are close to being linear, except possibly for rare values of the state variables, is important for this result. Here we address the question how many moments one has to include to get the exact solution if the individual policy function is (nearly) linear or nonlinear.
Relationship Between Individual Policy Rule and Aggregate Moments to Include
Suppose that the individual policy functions for the employed and the unemployed agent can be written as
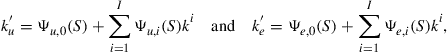(15)
where 
is a vector containing the aggregate state variables 
and 
. Note that (i) the individual policy functions are polynomials in the individual state variables, but the specification allows for more general dependence in the employment status and the aggregate state variables, and (ii) the left-hand side is the level of the capital stock and not, for example, the logarithm.20 Our argument does not rely on the use of polynomials. Other basis functions could be used, including those that generate splines. The logic of the algorithm is easiest understood, however, if the policy function are polynomials in the levels of the individual state variables.
The immediate objective is to calculate end-of-period values of the aggregate state, given the beginning-of-period values.21 For the policy function given in Eq. (15), which is linear in the coefficients of the 
terms, one can simply integrate across individuals to get
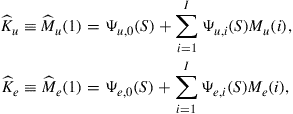(16)
where 
is the ith uncentered moment of beginning(end)-of-period capital holdings of agents with employment status 
.
The first lesson to learn from these expressions is that if the individual policy rule is an Ith-order polynomial, one has to include at least the first 
moments of both types of agents as state variables. Thus,
(17)
where 
is the ith cross-sectional moment of individual capital holdings for agents with employment status 
.
We now address the question whether this set of moments is enough. First, consider the case when 
, that is, the individual policy rule is linear in 
. Then 
is equal to 
and the expressions in (16) are—together with the value of 
—sufficient to calculate 
. Conditional on the individual policy rule being linear, the model with heterogeneous agents and aggregate uncertainty can be solved using standard projection techniques, without relying on simulation procedures or an approximation of the cross-sectional distribution.
The situation is substantially more complicated if there is just a little bit of nonlinearity. For simplicity, suppose that 
. From the discussion above we know that a minimum specification for 
would be 
. This means that to determine 
we need expressions for 
and 
. Using Eq. (15) with 
we get
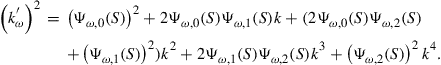(18)
Aggregation of this expression gives us the moments we need, but aggregation of the right-hand side implies that we have to include the first four moments instead of the first two as state variables, that is,
This means that to determine 
we need expressions for 
and 
, which in turn implies that we need even more additional elements in 
. The lesson learned is that whenever 
one has to include an infinite set of moments as state variables to get an exact solution, even if there are only minor nonlinearities.
Algorithm of Den Haan and Rendahl (2010)
The key step in the algorithm of Den Haan and Rendahl (2010) is to break the infinite regress problem by approximating the policy rules that are needed to determine next period’s aggregate state using lower-order polynomials. Consider again the case with 
. If we break the chain immediately at 
, then 
is obtained from the approximation
(19)
and not from Eq. (18). Note that 
in Eq. (19) is not equal to 
. The 
subscript in 
indicates that the coefficients in the approximating relationship in Eq. (19) are not obtained from the 
coefficients as in Eq. (18), but from a separate projection of 
on the space of included terms. The coefficients 
are chosen to get the best fit for 
according to some measure. Given that the excluded terms, i.e., 
and 
, are correlated with the included terms, these coefficients will also capture some of the explanatory power of the higher-order excluded terms. The key implication of using Eq. (19) instead of Eq. (18) is that aggregation of Eq. (19) does not lead to an increase in the set of aggregate state variables.
For 
the numerical algorithm consists of the following steps. The variables on the grid are 
. With the use of Eqs. (16) and (19), the error terms defined in Eq. (2) can be calculated given values for 
and 
. The algorithm chooses those values for the coefficients that minimize some objective function of the errors defined in Eq. (2).
To get expressions for next period’s aggregate variables using explicit aggregation, one has to break the infinite regress at some point. One could break it at 
as in the example above, but one also could break it at some higher level. For example, suppose again that the individual policy rule is approximated well with a second-order polynomial. One possibility would be to set 
and approximate 
, 
, 
, and 
using fourth-order polynomials. But an alternative would be to approximate 
with a second-order polynomial as above, using Eq. (18)—i.e., the exact expression given the policy rule for 
, to describe 
—and construct approximations for 
and 
using fourth-order polynomials.
Separate Individual Policy Rule for Aggregation
It is possible that a high-order polynomial is needed to accurately describe individual behavior for all possible values of 
. Using this algorithm would then require a lot of aggregate state variables, since every monomial in the approximating function corresponds to an additional aggregate state variable. However, one can use a complex approximation to describe individual behavior and one can use a simpler individual policy rule just to aggregate and obtain the aggregate laws of motion. In fact, Den Haan and Rendahl (2010) approximate individual policy rule with a spline,22 but obtain the aggregate law of motion by aggregating a simple linear approximation of the individual policy rule, and show that they can get an accurate solution with this approach.
3.2 Perturbation Approaches
In this section, we discuss two perturbation procedures. The procedure developed by Preston and Roca (2006) is a “pure” implementation of the perturbation procedure. We will see that the order of the implementation used implies which moments of the cross-sectional distribution should be included. For the perturbation procedure of Preston and Roca (2006), the nonstochastic steady state, around which the solution is perturbed, corresponds to the model solution when both aggregate and idiosyncratic uncertainty are equal to zero. The algorithm of Reiter (2009) combines a perturbation procedure with projection elements, which makes it possible to perturb the model around the solution of the model without aggregate uncertainty but with individual uncertainty.
Perturbation methods have the advantage of being fast and since they do not require the specification of a grid allow for many state variables. Also, projection methods require several choices of the programmer, especially in the construction of the grid, whereas implementation with perturbation techniques is more standard. Perturbation methods also have disadvantages. Since they are based on a Taylor series expansion around the steady state, the policy functions are required to be sufficiently smooth. Den Haan and De Wind (2009) discuss another disadvantage. Perturbation approximations are polynomials and, thus, display oscillations.23 As argued in Den Haan and De Wind (2009), the problem of perturbation procedures is that one cannot control where the oscillations occur.24 They could occur close to the steady state and lead to explosive solutions.
3.2.1 Perturbation Around Scalar Steady State Values
Preston and Roca (2006) show how to solve models with aggregate uncertainty and heterogeneous agents with a perturbation procedure. The steady state they consider is the solution of the model when there is no aggregate uncertainty and when there is no idiosyncratic uncertainty.
There are some particular features of the model described above that makes it less suited for perturbation procedures. So we will modify the problem slightly. The idea of perturbation procedures is to take a local approximation around the point where there is no uncertainty and then introduce the amount of uncertainty as an explicit variable in the policy function of the agent. Since perturbation techniques rely on the implicit function theorem, uncertainty should affect the problem in a smooth way. In the problem described in Section 2, one can characterize the amount of uncertainty with the probability of becoming unemployed. But even an increase in the probability of becoming unemployed from zero to a slightly positive number introduces sudden discontinuous jumps in the budget set if the individual employment status, 
, switches from 0 to 1. If one wants to use a perturbation technique, it is safer to let the support of 
increase continuously with the perturbation parameter that controls uncertainty.25 Preston and Roca (2006) assume that the law of motion for 
is given by
(20)
where 
has variance 
.26,27 Similarly, let the law of motion for 
be given by
(21)
Perturbation techniques cannot deal with inequality constraints, because they could never be captured with the derivatives at the steady state. The inequality constraint is, therefore, replaced by a smooth penalty function that makes it costly to have low capital levels. In particular, Preston and Roca (2006) assume that there is a utility cost of holding 
equal to 
.28 The first-order conditions of the agents can then be written as
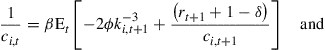(22)
(23)
The order of the perturbation approximation and the set of state variables are related to each other. If a second-order approximation is used then—as will be explained below—the state variables for the agent are 
with
(24)
where
(25)
(26)
(27)
(28)
That is, first- and second-order moments of the cross-sectional distribution are included. If a first-order approximation is used, then only first-order moments are included.
Let 
be the policy function for variable 
with 
. To get the perturbation solution, we write the model as follows:
(29a)
(29b)
(29c)
(29d)
(29e)
Here, 
is the steady-state value of capital and 
is a scalar parameter that scales both types of uncertainty, 
and 
. The variables 
, 
, and 
are given by
(30)
(31)
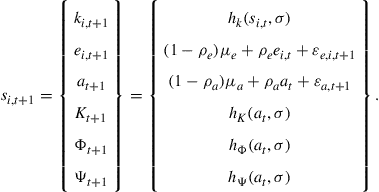(32)
Because of the aggregation constraints, i.e., Eqs. (29c), (29d), and (29e), it is important that the solution is specified in the nontransformed level of the variables and not, for example, in logs.29 If not, then the functional forms of 
, and 
would not be consistent with the functional forms of 
and 
. The aggregation constraint makes clear what the list of state variables should be for the particular approximation order chosen. That is, a particular approximation implies a particular law of motion for the cross-sectional income and wealth distribution, which in turn implies what the relevant state variables are.
Suppose that one uses a first-order approximation. Clearly, 
and 
matter for the individual policy functions. The agent also cares about prices and, thus, about 
, and future values of 
. When the savings function is linear in 
, and 
, then the aggregation restriction (together with the linearity of the policy function) implies that 
is linear in these variables as well, and that other moments of the cross-sectional distribution, thus, should not be included.
If the individual policy functions are second order and in particular include 
and 
, then the aggregation constraint implies that next period’s capital stock depends on 
and 
, which means that these should be included as state variables as well.30
When Eqs. (30)–(32) are used to substitute out 
, and 
, then Eq. (29) specifies a set of five equations in five functions: 
, 
, and 
. Sequentially differentiating the five equations and evaluating the expressions at the steady state gives the equations with which to solve for the coefficients of the Taylor expansions of the five policy functions. In the appendix, we give an example.
Perturbation approximations specify complete polynomials.31 This means that the term 
is not combined with any other state variables in a second-order approximation, because it is itself a second-order term. Similarly, 
and 
only appear by themselves since they are also second-order terms.
Comparison with Explicit Aggregation
The explicit aggregation algorithm of Den Haan and Rendahl (2010) and the perturbation algorithm of Preston and Roca (2006) seem to be at the opposite sides of the spectrum of solution algorithms. The algorithm of Den Haan and Rendahl (2010) is a “pure” implementation of projection methods and the algorithm of Preston and Roca (2006) is a “pure” implementation of perturbation techniques.32 There also seem to be nontrivial differences in terms of the structure of the algorithms. To be able to explicitly aggregate the individual policy functions, Den Haan and Rendahl (2010) have to derive additional approximations for the higher-order terms of the individual choices. No such step is present in the algorithm of Preston and Roca (2006).
But there is also a striking similarity between the algorithms: Both Preston and Roca (2006) and Den Haan and Rendahl (2010) derive the law of motion for the aggregate variables directly from the individual policy rules without relying on simulations or numerical integration techniques.
The algorithm of Den Haan and Rendahl (2010) does not take a stand on how to solve for the individual policy rules and these could, in principle, be solved for using perturbation techniques. To understand the connection between the two algorithms, consider the following implementation of the explicit aggregation algorithm. First, suppose the solution to the individual policy rule, 
, is obtained using perturbation techniques taking the aggregate policy rule as given. If nth-order perturbation is used, then one has to solve simultaneously for the higher-order policy rules, 
for 
. In perturbation software one would simply add 
as additional equations and the 
variables would appear as additional variables. This would result in a solution for the 
variables as a function of 
, that is, 
. When the aggregate policy rule is given, then this is typically a straightforward simple implementation of perturbation techniques and could be solved using standard software such as Dynare. Second, the solution for the aggregate policy rule is obtained by explicitly aggregating policy rules for 
and 
. Finally, one would iterate until convergence is achieved. In the appendix, we work out an example to show that the solution obtained with explicit aggregation is in this case identical to the one obtained with the algorithm of Preston and Roca (2006).
The explicit aggregation algorithm of Den Haan and Rendahl (2010) can, thus, be viewed as a general procedure that boils down to the algorithm of Preston and Roca (2006) if the individual policy rules are solved for using perturbation techniques. Moreover, if the individual policy rules are indeed solved with perturbation techniques, then—as was outlined above—the explicit aggregation algorithm suggests a simple way to solve the model using standard perturbation software such as Dynare.
3.2.2 Perturbation Around the Steady State Cross-Sectional Distribution
The procedure of Preston and Roca (2006) perturbs around the point where there is neither aggregate nor idiosyncratic uncertainty. The idea of the procedure in Reiter (2009) is to take a perturbation around the model solution with no aggregate uncertainty.33 This solution consists of a cross-sectional distribution for income and capital levels that is not time varying. We describe the algorithm as a general perturbation problem and in doing so deviate somewhat from the description in Reiter (2009), but the underlying idea is the same.
Consider a numerical solution to the model of Section 2,
(33)
where 
is a vector with the coefficients of the numerical solution for the capital policy function. 
is an approximating (but fixed) functional form, say an nth-order polynomial. Let the law of motion for 
be given by
(34)
The subscript 
makes clear that this law of motion depends on the solution of the individual policy function. That is, a different individual policy rule will imply a different law of motion for the cross-sectional distribution. It is assumed that 
is more than a limited set of moments, but pins down—possibly with additional assumptions—the complete cross-sectional distribution. For example, 
could be the values of a histogram defined on a fine grid.34 This assumption implies that—conditional on the individual policy function—the mapping 
is known, although implementing it may require some numerical procedures like quadrature integration. In other words, given the choice to approximate the savings function with 
and given the choice to characterize the cross-sectional distribution in a particular way, the only unknown is 
. As soon as 
is known, then all variables, including 
, can be calculated for a given set of initial values and realizations of the shock.
The individual policy function in Eq. (33) can be written without the aggregate state variables, but with time-varying coefficients. That is,
(35)
with
(36)
Let 
, let the dimension of 
be given by 
, and let 
be an 
vector with nodes for the employment status and capital levels.35 Evaluated at the nodes for the individual state variables, 
, the first-order conditions of the agent can be written as follows36:
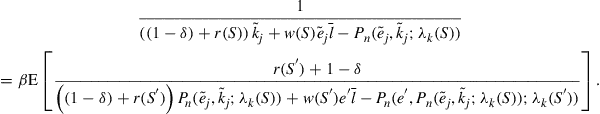(37)
In equilibrium, the endogenous part of 
, i.e., 
, is determined by
(38)
where, as mentioned above, 
is—conditional on knowing 
—a known function. Suppose that 
is constant and that 
characterizes the corresponding cross-sectional distribution. Evaluated at these constant values for 
and 
, Eq. (37) is then a standard set of 
equations to solve for the 
(constant) elements of 
. But to understand the procedure considered here, it is important to think of Eq. (37), with 
determined by Eq. (38), as a system that defines the vector-valued function 
.
It is important to understand what is fixed and what we are solving for in this system. First, 
has a known functional form, namely, the one chosen as a numerical approximation. In the example considered in Section 2, the stochastic variables 
and 
have discrete support, so there is an analytical expression for the conditional expectation in Eq. (37). If this is not the case, then a numerical integration procedure has to be used. But for every quadrature procedure chosen, Eq. (37) represents a fixed set of equations. The same is true for Eq. (38). It may be possible that 
is only implicitly defined by a set of equations. This does not matter. Essential is that there is a fixed set of equations that in principle determines 
.
Thus, Eq. (37), with 
determined by Eq. (38), is a system in which the coefficients of the approximating individual policy function, 
, are the variables. That is, instead of consumption and capital being variables, the coefficients of the policy function have become the variables. The idea is now to solve for these functions using the perturbation approach. That is, we write 
as 
and its Taylor expansion around the steady state as
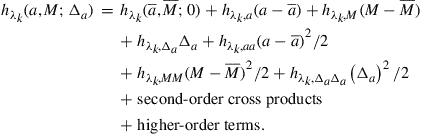(39)
As in standard perturbation procedures, we can find the coefficients of the Taylor expansion by taking successive derivatives of Eq. (37).
This procedure assumes that 
is more than a very limited set of moments such as the mean capital stock. The elements of 
should pin down the complete cross-sectional distribution. One possibility would be to let 
be the set of values of the CDF at a very fine grid. The value of 
is then very large and one has to find the policy function for many variables.37 This could be especially problematic if higher-order perturbation solutions are considered or if 
is a nonlinear function of 
. In this case it may be better to impose some structure on the functional form of the cross-sectional distribution, so that the cross-sectional distribution is fully determined by a smaller set of coefficients. In particular, in Algan et al. (2008) it is shown that a sixth-order polynomial (whose coefficients are pinned down by six moments) describes the cross-sectional distributions generated by the model described in Section 2 through time well.
4 Models with Nontrivial Market Clearing
As long as the numerical solutions for the model described in Section 2 do not violate the condition that the rental rate and the wage rate are equal to the corresponding marginal products, then the solution is consistent with market clearing in all markets. Using these prices, the firms demand exactly the amount of capital and labor offered by households.
In many other models, it is not true that markets automatically clear exactly for the numerical solution. Nevertheless, market clearing is an important property. Consider a bond economy in which bonds are in zero net supply. Suppose that aggregated across households, the demand for bonds is close to, but not exactly, zero at each point in the state space. It is very unlikely that these small deviations from market clearing will average out as an economy is simulated at a long horizon. Instead, the total amounts of bonds held in the economy are likely to move further and further away from its equilibrium value, and it is not clear how to interpret such an economy given that the solution is based on the economy being in equilibrium.
To understand why market clearing is not automatically imposed exactly when numerically solving a model, consider adding one-period zero-coupon bonds to the economy developed in Section 2 and let the bond price be equal to 
. One possibility would be to specify a law of motion for the bond price as a function of the aggregate state variables, that is, 
, and to solve for this law of motion. When simulating the economy, the bond price cannot adjust to ensure market clearing. Of course, a good numerical solution will be such that aggregate demand is close to zero, but—as pointed out above—we would need exact market clearing to prevent errors from accumulating.38
There are several ways to impose market clearing. One possibility would be to solve the individual problem using the approximation for 
to determine next period’s prices only and to treat the current-period price as a state variable for the individual problem. The individual policy functions are then a function of the bond price and in a simulation the price can be chosen such that the aggregate demand is equal to zero.
Instead of solving for the individual demand for bonds, 
, Den Haan and Rendahl (2010) propose to solve for the individual demand for bonds plus the bond price, that is, 
. The advantage of this approach is that the bond price does not have to be added to the set of state variables. Since aggregate demand is equal to zero in equilibrium, aggregation of these individual choices across individuals gives the bond price. That is,
(40)
If 
is used to determine the individual demand for bonds, then markets clear by construction.
5 Approximate Aggregation
Krusell and Smith (2006) point out that many models with heterogeneous agents and aggregate risk have the desirable property that the mean values of the cross-sectional distributions are sufficient statistics to predict next period’s prices. They also point out that this property is unlikely to be true for all models to be considered in the future.39 Given that approximate aggregation relies on a limited amount of variation across agents’ marginal propensities to save—a quite unrealistic property—this seems a safe prediction.
It is important to understand what approximate aggregation means and in particular what it does not mean. Approximate aggregation does not imply that the aggregate variables can be approximately described by a representative agent model in which the agent faces sensible preferences, and it definitely does not imply that the aggregate variables can be approximately described by a representative agent model in which the preferences of the representative agent are identical to the preferences of the individual agents in the model with heterogeneous agents.40
Approximate aggregation does not imply that there is perfect insurance and a perfect correlation of individual and aggregate consumption. In fact, even if agents start out with identical wealth levels, then the model of Section 2 generates a substantial amount of cross-sectional dispersion in individual consumption levels.
6 Simulation with a Continuum of Agents
In this section, we discuss different procedures to simulate an economy with a continuum of heterogeneous agents taking as given numerical solutions for the individual policy rules. The most common procedure approximates the continuum with a large but finite number of agents and uses a random number generator to draw both the aggregate and the idiosyncratic shocks. With a finite number of agents, there will be cross-sectional sampling variation in the simulated cross-sectional data, while—conditional on the aggregate shock—there should be none if the model has a continuum of agents. Even when a large total number of agents is used, then some subgroups may still have a low number of agents and their cross-sectional characteristics are measured with substantial sampling noise. For example, Algan et al. (2008) document that moments of the capital holdings of the unemployed of the model described in Section 2 are subject to substantial sampling variation and that some properties of the true of law motion are not noticeable, even if the total number of agents is as high as 100,000.
This is documented in Figures 1–3. Figure 1 plots the per capita capital stock of the unemployed when the total number of agents in the panel is equal to 10,000. The figure clearly documents the sampling uncertainty. Figure 2 zooms in on a subsample and adds the simulated path when there are 100,000 agents in the economy. Even with 100,000 agents in the economy there is still noticeable sampling uncertainty. Of course, the number of unemployed agents is substantially less than the total number of agents in the economy.
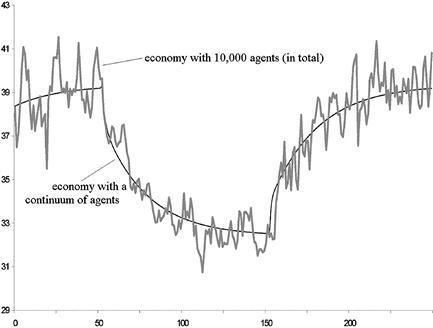
Figure 1 Simulated per capita capital of the unemployment. Notes: This graph plots the simulated aggregate capital stock of the unemployed using either a finite number (10,000) or a continuum of agents.
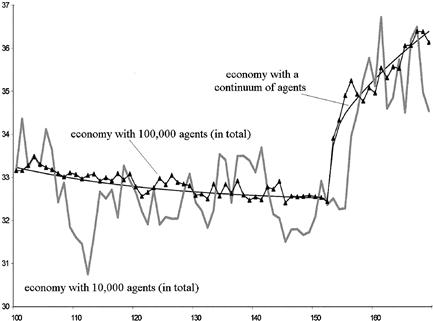
Figure 2 Simulated per capita capital of the unemployment. Notes: This graph plots the simulated aggregate capital stock of the unemployed using either a finite number (10,000) or a continuum of agents. It displays a subset of the observations shown in Figure 1.
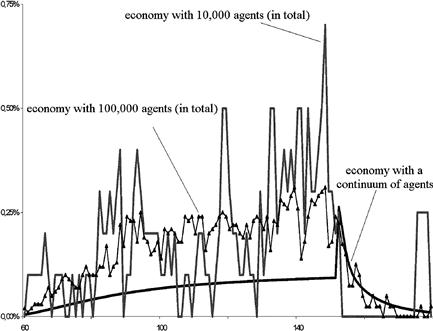
Figure 3 Simulated fraction of contrained agents. Notes: This graph plots the simulated fraction of unemployed agent at the borrowing constraint using either a finite number (10,000 or 100,000) or a continuum of agents.
Figure 3 plots the fraction of unemployed agents at the constraint. The sampling uncertainty in the time paths simulated with a finite number of agents is again striking, even when there are a total of 100,000 agents in the economy. In fact, the sampling uncertainty is so large that an interesting property of the model is completely dominated by sampling uncertainty. If the economy moves out of a recession into a boom, then the fraction of unemployed agents at the constraint increases according to the accurate simulation with a continuum of agents. The reason is that during a recession there is a higher chance that an unemployed agent was employed in the last period and employed agents never choose a zero capital stock.
This section discusses three procedures to simulate a time series of the cross-sectional distribution of a continuum of agents. The first two are grid methods that approximate the cross-sectional density with a histogram. One of these grid methods requires the inverse of the policy function, while the other does not. The third procedure uses polynomials. It imposes more structure on the functional form, but uses a lot fewer coefficients to characterize the distribution.
6.1 Grid Method I: Calculation of Inverse Required41
Consider a fine grid for the capital stock. This simulation procedure approximates at each point in time the CDF with a linear spline. This means that in between grid points the distribution is assumed to be uniform. Point mass at the borrowing constraint means that the value of the CDF at the first node is strictly positive. Calculating the CDF of the end-of-period capital holdings proceeds as follows. At each node, 
(which represents a value for the end-of-period capital holdings), calculate the value of the beginning-of-period capital stock, 
, that would have led to the value 
. That is, 
is the inverse of 
according to the individual policy function. The probability that the beginning-of-period capital stock is less than 
is then used to calculate the value of the CDF value at 
. Note that this last step requires the policy function to be monotone.
Information Used
The beginning-of-period 
distribution of capital holdings is fully characterized by the following:
• the fraction of unemployed agents with a zero capital stock, 
,
• the fraction of employed agents with a zero capital stock,42 
,
• the distribution of capital holdings of unemployed agents with positive capital holdings, and
• the distribution of capital holdings of employed agents with positive capital holdings.
The goal is to calculate the same information at the beginning of the next period. Besides these four pieces of information regarding the cross-sectional distribution, one only needs (i) the realizations of the aggregate shock this period and next period and (ii) the individual policy function.
Grid
Construct a grid and define the beginning-of-period distribution of capital as follows:
and 
, for 
.2. Let 
be the fraction of agents with employment status 
with a zero capital stock at the beginning of period 
.
3. For 
, let 
be equal to the mass of agents with a capital stock bigger than 
and less than or equal to 
. This mass is assumed to be distributed uniformly between grid points.
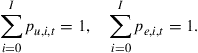
Denote this beginning-of-period distribution function by 
.
End-of-Period Distribution
The first step is to calculate the end-of-period distribution of capital. For the unemployed, calculate the level of capital holdings at which the agent chooses 
. If we denote this capital level by 
, then it is defined by43
(41)
This involves inverting the policy function and is the hardest part of the procedure. At each grid point, the period 
end-of-period values of the cumulative distribution function for the unemployed, 
, are given by
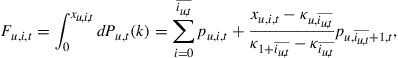(42)
where 
is the largest value of 
such that 
. The second equality follows from the assumption that 
is distributed uniformly between grid points.
A similar procedure is used to calculate the period 
end-of-period values of the cumulative distribution function for the employed, 
. That is,
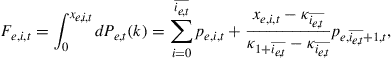(43)
is the largest value of 
such that 
.Next Period’s Beginning-of-Period Distribution
Let 
stand for the mass of agents with employment status 
that have employment status 
, conditional on the values of 
and 
. For each combination of values of 
and 
we have
(44)
This gives
(45)
and
(46)
(47)
6.2 Grid Method II: No Calculation of Inverse Required44
This method also uses a grid and approximates the cross-sectional distribution with a histogram. Now it is assumed, however, that the distribution only has mass at the grid points. In terms of the information used, the notation, and the specification of the grid, everything is identical to the first procedure.45 An important advantage of this procedure is that it does not require using the inverse of the policy function and the policy function does not have to be monotone.
End-of-Period Distribution
The first procedure goes through a grid for the end-of-period capital holdings and then calculates which beginning-of-period capital values lead to this or a smaller grid value. The second procedure goes through the same grid values, but they now represent the beginning-of-period capital holdings. It then calculates the chosen capital stock and assigns the probability associated with this beginning-of-period capital stock to the two grid points that enclose the end-of-period capital choice.
Let 
be the mass of agents with employment status 
that have a capital level equal to 
at the end of the period. It can be calculated as follows:
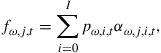(48)
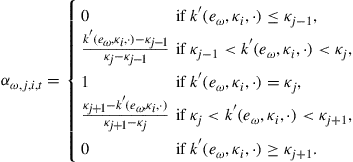(49)
The weights 
allocate the probabilities to the grid points and the magnitude of each weight is determined by the relative distance of 
to the two grid points that enclose 
.46
Next Period’s Beginning-of-Period Distribution
Given the end-of-period distribution, the distribution of next period’s beginning-of-period capital holdings can be calculated using Eq. (45). This step is identical to the one used for the first grid method.
6.3 Simulating Using Smooth Density Approximations
Algan et al. (2008) propose an alternative solution. Suppose that the beginning-of-period cross-sectional density is given by a particular density, 
, where 
contains the coefficients of the density characterizing the density of capital holdings of agents with employment status 
in period 1. 
and 
together with individual policy rules and the values of 
and 
are in principle sufficient to determine 
and 
. Algan et al. (2008) propose the following procedure. Let 
and 
be nth-order polynomials that describe the distributions in period 1. Below we will be more precise about the particular type of polynomial used, but this detail is not important to understand the main idea underlying the procedure.
Main Idea
The objective of the procedure is to generate a time series for the two cross-sectional distributions. Given that we use nth-order polynomials, this means generating the values of 
and 
. This is done as follows:
1. Use 
, for 
, together with individual policy rules to determine the first 
moments of capital holdings at the end of period 1, 
. Standard quadrature methods can be used to calculate these. Using the transition equations, it is then straightforward to calculate the moments of capital holdings at the beginning of period 2, 
.
2. Given the values of 
find the values of 
. That is, find the values of the coefficients of the approximating density that ensure that the moments of the approximating density are equal to the desired set of moments.
3. Iterating on this procedure generates a complete time series.
Implementation
The tricky part of this procedure is to find the coefficients that correspond with a set of specified moments, that is, Step 2. Algan et al. (2008) make this problem substantially easier by using a particular functional form for 
. In particular, they use
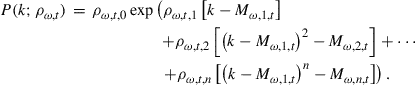(50)
We will now explain what the advantage of this particular functional form is.
Step 2 is a root finding problem. Its purpose is to find the values for 
that solve a set of equations. When the density is constructed in this particular way the coefficients, except for 
, can be found with the following minimization routine:
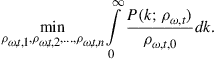(51)
This minimization exercise leads to the right answer, because the first-order conditions correspond exactly to the condition that the first 
moments of 
should correspond to the set of specified moments. The coefficient 
does not appear in these equations, but it is determined by the condition that the density integrates to 1.
One can always try to find the roots of an equation by using a minimization problem. The advantage of this particular minimization problem is that it has some desirable characteristics. The Hessian is given by
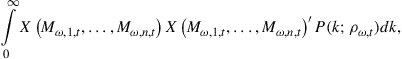(52)
where 
is an 
vector and the ith element is given by
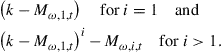(53)
The Hessian is positive semi-definite since 
does not depend on 
.47 Consequently, this is a convex optimization problem and, thus, avoids the need for good initial conditions.48
6.4 Comparison of Simulation Methods
Of the three methods, the procedure by Young (2010), i.e., the grid-based method that does not require calculating an inverse, is the easiest to program. Given the similarity with the other grid-based method, there does not seem to be a reason to prefer the more complicated one that does require calculating the inverse. The procedure proposed by Algan et al. (2008) is clearly not as easy to program as the procedure proposed by Young (2010). Moreover, it relies on smooth approximations of the density. It has one advantage over both grid-based methods, however, and that is that it uses substantially fewer coefficients to parameterize the cross-sectional distribution. For some applications this is useful. For example, in the solution procedure of Reiter (2009) all the coefficients of the cross-sectional distributions are variables of a perturbation procedure. When a grid-based method is used, then typically around 1,000 grid points are used to describe the cross-sectional distribution of the model described in Section 2. With so many variables, it is very difficult to use higher-order perturbation procedures.
The question arises how accurate the procedure of Algan et al. (2008) is, especially when the CDF is discontinuous. Algan et al. (2008) document that a very accurate simulated series can be obtained for the model of Section 2 by parameterizing the cross-sectional density with a (smooth) sixth-order polynomial. Since there are hardly any agents at the constraint in this model, the challenge is not that high. Algan et al. (2010), therefore, consider an example in which there are many large jumps in the CDF and a 10th-order polynomial is used to approximate the density. Although this approximation cannot capture the jumps, Algan et al. (2010) document that the implied CDF corresponding to their approximating density provides a good average fit of the true CDF. More importantly, they show that the generated time series for characteristics of the distribution such as moments and fraction of agents at the constraint are accurate.
7 Accuracy
Models with heterogeneous agents and aggregate uncertainty are complex models. As was pointed out in Section 2, it is not even clear for which class of models a recursive equilibrium exists for the set of state variables typically used in numerical analysis. This by itself would imply that careful accuracy tests are required. Another reason is that simulations play an essential role in several algorithms. Simulations are inefficient numerical tools, because sampling uncertainty disappears at a slow rate and because simulated data tend to cluster. Clustering is bad for function approximation. Chapter 6 in Judd (1998) shows that uniform convergence of the approximating polynomial to the truth requires nodes to be sufficiently spread out. Uniform convergence is guaranteed with Chebyshev nodes (under certain regularity conditions). In contrast, uniform is not guaranteed with equidistant nodes. Note that equidistant nodes are typically much more spread out than the points generated in a simulation, so uniform convergence is unlikely to be guaranteed when using simulated data.
Many Aspects of the Model to Check
Given the complexity of this type of model, there are many aspects that need to be checked for accuracy. In addition to the policy rules that characterize individual behavior, the policy functions of aggregate variables and the simulation procedure need to be checked. If the algorithm solves for an approximation of the cross-sectional distribution, then this needs to be checked as well. Below we will discuss some formal accuracy tests. It is important to realize, however, that accuracy tests have limitations. In particular, it has been shown that numerical solutions can fail accuracy tests and still generate very accurate predictions for most properties generated with the solution.49 Moreover, as will be shown below, it is also possible that numerical solutions pass accuracy tests and are not accurate at all.
It is, therefore, important to play around with different implementations of the algorithm and see whether the results one is interested in do not change. For example, one should check whether the results are robust to modifications such as a different range for the grid, a different order for the approximating function, and a different choice of the function to be approximated. Ideally, one would document as well that the results are robust to using a different type of algorithm. There are now definitely enough algorithms to choose from.
Conditional on the solution for the aggregate variables, the accuracy of individual policy can be evaluated using standard accuracy tests such as the maximum Euler equation error across a large set of grid points.50
Formal tests to check the accuracy of a simulated cross-section do not exist. A reasonable test would consist of increasing the number of nodes for the grid methods or the order of the approximating density for the nongrid method to see whether the generated series change. And generating the same set of results with both a grid and a nongrid method would be a persuasive indication that the generated series are accurate.
To check for accuracy of a parameterized distribution, one can check whether the parameterized cross-sectional distribution corresponds closely to the cross-sectional distribution observed in a simulated cross-section or one could check whether the approximating density has the same implications for a set of key characteristics such as the mean and the variance as those observed in the simulated data.
Problems of the 
as Accuracy Test
In most algorithms, the law of motion describing aggregate variables such as the mean capital stock plays a central role. Checking for its accuracy should, therefore, be done very carefully. Some authors are clearly aware of the difficulty in assessing accuracy of the aggregate law of motion. Krusell and Smith (1996, 1998), for example, perform a variety of accuracy tests, try out several different alternative approximating functional forms, and perform a careful economic analysis to explain why their preferred numerical solution, one in which only the mean matters for aggregate dynamics, is an accurate one. Unfortunately, Krusell and Smith (1998) put most emphasis on two weak accuracy tests and the subsequent literature has treated these as sufficient to evaluate the accuracy of the aggregate law of motion. In particular, Krusell and Smith (1998) estimate the aggregate law of motion with least-squares regression using simulated data. The two accuracy tests are the 
and the standard error of the regression, 
.
Den Haan (2010a) shows that the 
and the standard error of the regression are very weak accuracy tests and gives examples in which numerical solutions with an 
in excess of 0.9999 can still be inaccurate. The accuracy of many results in the literature is, thus, still undocumented. To focus the discussion, suppose that a researcher is interested in assessing the accuracy of the following approximating law of motion
(54)
where 
is the mean of the cross-sectional distribution of capital and 
is an aggregate shock. The standard procedure to calculate 
and the 
consists of the following steps. First, simulate a panel and for each period calculate the aggregate capital stock. The panel is generated using only the individual policy rules and should not rely in any way on the approximating aggregate law of motion. It is the law of motion of this aggregate capital stock that we are interested in. To highlight the key element of the argument we will refer to this capital stock as 
even though it is typically not calculated without any numerical error.51 The approximation in Eq. (54) would be a good approximation if 
follows 
closely. Are the 
and 
good measures for this?
The 
and 
are based on errors defined as
(55)
where 
is the capital stock predicted according to the approximation. So far, everything is fine. But when calculating the 
and 
, one uses 
as the argument in the approximating law of motion. That is,
(56)
(57)
That is, each period one starts with the true value and sees how the approximation performs starting at the truth. Consider the case when the approximating law of motion would want to push the observations away from the truth each period. The error terms defined this way underestimate the problem, because the true dgp is used each period to put the approximating law of motion back on track. This is the most troublesome feature of these two accuracy measures.
But these measures have other problems too. For example, the 
and 
are based on averages, but accuracy tests typically focus on the maximum error. Moreover, the 
inflates the measure of fit by scaling the sum of the errors with the variance of the dependent variable. To see why this matters, suppose that one focuses on 
instead of 
. The approximating law of motion is redefined accordingly as
(58)
After 
is subtracted from both sides of Eq. (54), the approximating law of motion is of course still the exact same law of motion and there is no reason to prefer Eq. (54) over Eq. (58). But this bit of trivial algebra does change the 
, revealing the arbitrary nature of the 
. The 
changes because the variance of 
is typically much lower than the variance of 
. The drop in the value of the 
can be substantial. Den Haan (2010a) gives examples in which the average 
is equal to 0.9952 when Eq. (54) is used and 0.8411 when Eq. (58) is used.
Examples
The weakness of the existing accuracy tests can be easily documented using the following example from Den Haan (2010a). Table 1 reports the 
and some properties of different aggregate laws of motion using a sample of 10,000 observations for the aggregate capital stock, 
. The series for 
are generated using the numerical solution of Young (2010) for the individual policy rules of the model described in Section 2. The first row corresponds to the fitted law of motion of the regression equation:
(59)
This equation has an 
equal to 0.99999729 and the estimated value for 
is equal to 0.96404. In the subsequent specifications, the value of 
is changed. The value of 
is adjusted to ensure that the mean error term of the regression equation remains equal to zero. This adjustment of 
also ensures that the implied mean for the (logarithm of the) aggregate capital stock remains the same.
Table 1
.
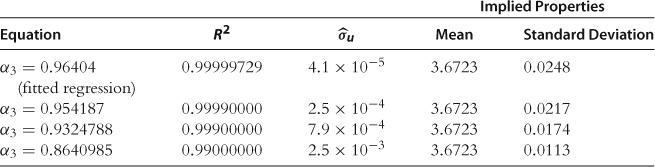
Notes: The first row corresponds to the fitted regression equation. The subsequent rows are based on aggregate laws of motion in which the value of 
is changed until the indicated level of the 
is obtained. 
is adjusted to keep the fitted mean capital stock equal.
As the value of 
is reduced, the value of the 
obviously goes down. But the changes in 
considered here are such that the 
remains quite high. In particular, 
is lowered until the 
is equal to 0.9999, 0.999, and 0.99. Despite the high 
values, the alternative aggregate laws of motion are very different laws of motion. This is made clear by the standard deviation of the aggregate capital stock that is implied by the three alternative aggregate laws of motion. The standard deviation implied by the original regression equation is equal to 0.0248, which corresponds very closely to the standard deviation of the underlying series. But as the value of 
is changed, the implied standard deviation plummets. For example, when 
is equal to 0.9324788 (0.8640985) then the true value of the standard deviation of the aggregate capital stock (the one implied by the individual policy rules) is 43% (119%) above the value implied by the approximating aggregate law of motion, even though the 
of the approximating laws of motion is equal to 0.999 (0.99). And when 
is adjusted so that the 
is equal to 0.9999, then there is still a 14% error for the standard deviation of aggregate capital.
More Powerful Accuracy Test
Den Haan (2010a) proposes an alternative accuracy procedure, which is a much more powerful accuracy test, in the sense of detecting differences between the truth and the approximating law of motion. It is also likely to be more insightful in determining where and why the approximation fails. It consists of the following steps:
1. Generate a time series for 
and choose an initial cross-sectional distribution. For algorithms that obtain the aggregate law of motion using simulated data, the time series for 
should not be the same draw as the one used to calculate the approximating law of motion.52
2. Generate a panel data set using only the individual policy function. From the panel construct a time series for 
.53
3. Generate a time series for 
using the approximating law of motion given in (54). This series is based on the same draw for 
and the same initial condition, i.e., 
, but is not related to 
in any other way.
(60)
where 
is generated by
(61)
Whereas the 
uses 
to predict next period’s capital stock, this accuracy test uses 
. By using 
instead of 
it is, of course, much more difficult to closely track 
.
5. Report the maximum error. If the variable is something like the log of capital, then no scaling is necessary. Otherwise the author should think about appropriate scaling.
6. Plot the two generated series. This is referred to in Den Haan (2010a) as the “essential accuracy plot.” Check in particular whether one series is systematically below the other and determine in which part of the state space the deviations are biggest.
Figure 4 gives an example of such an “essential accuracy plot.” The example is from Den Haan (2010a).54 The only difference between the true and the approximating law of motion for aggregate capital is that according to the true law of motion next period’s aggregate capital depends on this period’s and on last period’s capital, whereas according to the approximating law of motion next period’s aggregate capital only depends on this period’s capital stock. The approximating law of motion has a high 
, namely, 0.9953. But Figure 4 makes clear that the approximating law of motion is not accurate at all. There are enormous gaps between the time series generated by the approximating law of motion and the true series. The high 
of the approximating law of motion is only due to the fact that the true series are used as explanatory series each period.
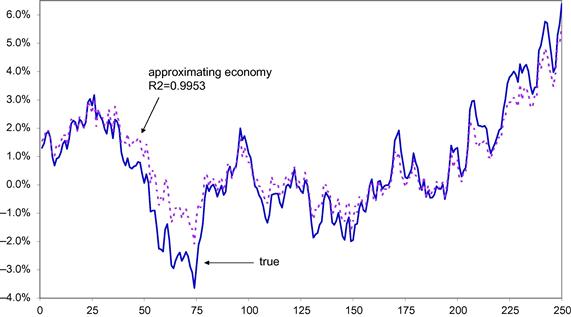
Figure 4 High 
and inaccurate law of motion. Notes: This graph plots the true aggregate capital stock and the one predicted by the approximate aggregate law of motion when the input of the approximation is the lagged value generated by the approximation and not the true lagged value (as is done when calculating the 
).
Den Haan (2010a) shows that the accuracy test proposed above is just as powerful as one of the tests considered by Krusell and Smith (1996, 1998), namely, the maximum 100-quarter ahead forecast error. The advantage of the “essential accuracy plot” is that it provides some useful insights. For example, suppose the panel data set is generated using a finite number of agents, which means that 
—which is used as a proxy for the true dgp—is actually generated with error. If one would find that 
fluctuates around a smooth time path for 
, then the deviations are likely to be due to errors in generating 
, not in the approximating law of motion. The essential accuracy plot would quickly make this clear.
Formal accuracy tests may often provide limited insights into why a particular approximation works or does not work.55 It is, therefore, important not to treat the model as a black box and take the generated numerical results simply as given. As stressed by Krusell and Smith (2006), in models with heterogeneous agents, it is particularly important to understand the relationship between individual policy rules and aggregate laws of motion. The problem is, of course, that solving the full model can be time consuming. As an alternative they suggest to first analyze a two-period version of the model in which one can vary the cross-sectional distribution exogenously. After studying this environment one can solve the full model.
8 Comparison
Den Haan (2010b) compares the properties of the solutions to the model of Section 2 using most of the algorithms discussed in this chapter. The perturbation algorithms are not considered, because the model has an inequality constraint, which would be difficult to handle for the perturbation procedures because of the discontinuities.56 Here we summarize the main findings.
The solutions turn out to differ substantially in several dimensions. This is surprising given the relatively simple nature of the model. Differences are most noticeable for the individual choices. Not only do the generated series differ during exceptional periods, such as particularly bad times, but there are even nontrivial differences between the implied first moments.
Several accuracy checks are performed. Figure 5 plots the essential accuracy plot for six algorithms. The figure compares the data generated by the aggregate law of motion with the corresponding time series from the simulated panel.57 For BInduc, the algorithm of Reiter (2010), for Param, the algorithm of Algan et al. (2010), for Xpa, the algorithm of Den Haan and Rendahl (2010), and for Penal, the algorithm of Kim et al. (2010), the results for the aggregate capital stocks conditional on the employment status are reported. For KS-num, the algorithm of Young (2010), and for KS-sim, the algorithm of Maliar et al. (2010), only the results for the aggregate capital stocks are reported. The reason is that KS-num and KS-sim only generate a law of motion for aggregate capital. Finding an accurate solution for the law of motion of the average capital stock across all agents is obviously easier than doing the same for the average capital stock of the unemployed, but should be comparable to obtaining the law of motion for the average capital stock of the employed.
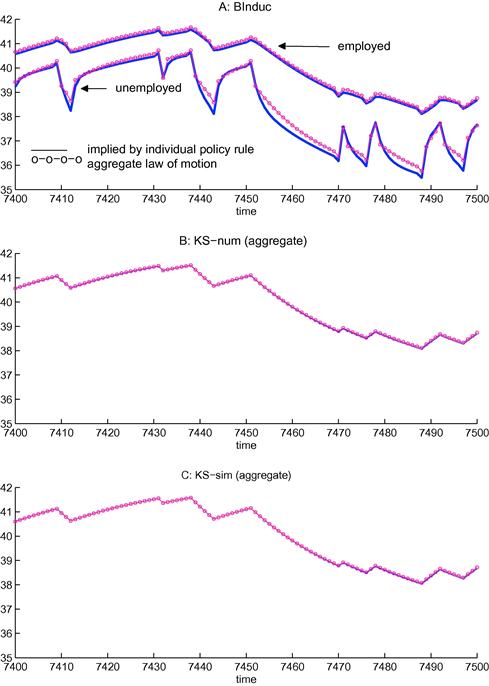
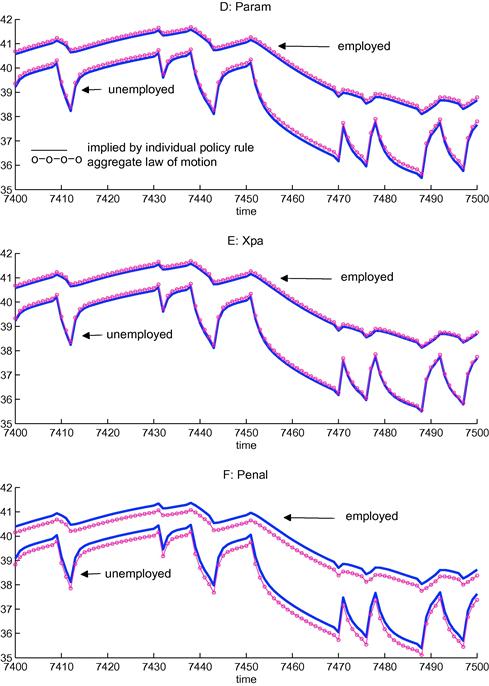
Figure 5 Accuracy aggregate law of motion for different algorithms. Notes: This graph plots the indicated mean capital stock according to the aggregate law of motion (line with open circles) and the value that is obtained if the individual policy rules are used to simulate a cross-sectional distribution (solid line). Note that the figures for KS-num and KS-sim do plot the two lines, but that they are basically indistinguishable. BInduc: The algorithm of Reiter (2010); Param: The algorithm of Algan et al. (2010); Xpa: The algorithm of Den Haan and Rendahl (2010); Penal: The algorithm of Kim et al. (2010); KS-num: The algorithm of Young (2010); KS-sim: The algorithm of Maliar et al. (2010).
Regarding the aggregate law of motion, the best performance is by KS-num and KS-sim. Both algorithms obtain the coefficients of the law of motion for the aggregate capital stock by using simulated data in a least-squares regression. KS-num simulates using a continuum of agents and KS-sim with a large finite number of agents. The graph clearly documents the excellent fit for KS-num and KS-sim. The errors of Param and Xpa are small, but the aggregate law of motion generates data that are consistently above the simulated series in this part of the sample. The aggregate laws of motion of BInduc do well during a boom, but the aggregate law of motion for the average capital stock of the unemployed clearly does poorly during a downturn. For Penal the aggregate law of motion consistently lies below the one implied by the simulation, which makes sense given that this law of motion is simply the capital choice of a representative agent that does not face idiosyncratic risk and incomplete markets.
Overall, the algorithm of Reiter (2010) performs best in terms of accuracy. It clearly performs the best in terms of the accuracy of the individual policy rules and it performs close to the best in terms of the accuracy of the aggregate law of motion.58 The performance of the algorithm of Den Haan and Rendahl (2010) is close to the performance of Reiter (2010) in terms of accuracy. Computing times are reported in Table 2, which reports the time it takes for the different algorithms to solve the model when 
is equal to 1.1, taking as initial conditions the solution of the model when 
is equal to 1.59
Table 2
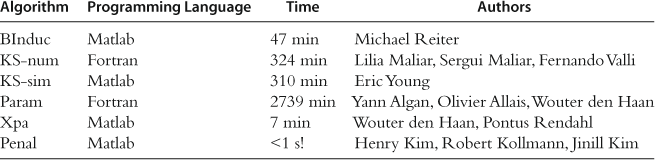
Notes: This table reports the time it takes to solve the model when 
, starting at the solution for 
.
Interestingly, the algorithms of Den Haan and Rendahl (2010) and Reiter (2010), which do best in terms of accuracy, are also the fastest, with the algorithm of Den Haan and Rendahl (2010) roughly seven times as fast as the algorithm of Reiter (2010).60 This discussion ignores programming complexity. The Krusell-Smith algorithm and the algorithm of Den Haan and Rendahl (2010) are very easy to program. The algorithms of Reiter (2010) and Algan et al. (2008) are much more involved.
The fact that the different algorithms generate results that are not that similar for such a relatively simple model should motivate us to be careful in numerically solving these models. There are several useful lessons that can be learned from this comparison project. Those are the following:
• It is essential to have an algorithm for the individual problem that does well in terms of accuracy as well as speed. Standard lessons from the numerical literature should not be ignored. For example, time iteration is typically faster and more reliable than fixed-point iteration.61 Also, the lower and upper bounds of the grid should be chosen with care in order not to miss or waste grid points. Den Haan (2010b) reports that algorithms that use the largest range for individual capital also have lower accuracy. Finally, the method of endogenous grid points, proposed in Carroll (2006), is recommended. It is not clear whether this leads to a more accurate solution, but it is definitely faster and makes it, for example, easy to implement time iteration.
• It is important to realize that the properties of an algorithm found when solving for individual policy rules in the model without aggregate uncertainty, i.e., for a fixed aggregate capital stock level, do not carry over to the model with aggregate uncertainty, even when taking as given the law of motion for aggregate capital. In particular, Den Haan (2010b) finds that it is more difficult to get accurate individual policy rules in the model with aggregate uncertainty than in the model without even when taking the aggregate law of motion as given.
• In solving models with a representative agent, it is typically possible to achieve arbitrary accuracy. None of the algorithms considered in the comparison project does extremely well in terms of all the accuracy tests. Especially the outcomes of the accuracy test for the aggregate policy rule are somewhat disappointing.62 The maximum errors in a simulation of 10,000 observations vary across algorithms from 0.156% to 1.059%. Ideally, they should be at least a factor 10 smaller than the smallest numbers found here.
• Given that it is not (yet) easy to generate numerical solutions with arbitrary accuracy, it is important to perform accuracy tests. The role of a good accuracy procedure consists not only of providing a measurement of the accuracy of the solution, but also of making clear which aspect of the solution is inaccurate under what conditions and whether the inaccuracies found matter.
9 Other Types of Heterogeneity
This chapter has focused on models with a continuum of agents. From a practical point of view, it does not matter whether one has a continuum of agents or, say, several million. Using a continuum is mathematically more elegant, however, because with a continuum any cross-sectional variation is only due to aggregate uncertainty.
There are also models in which there are enough heterogeneous agents to make the problem numerically challenging, but not enough to approximate them with a continuum. An example would be a multi-country model. Algorithms to solve these types of models are discussed in a special issue of the Journal of Economic Dynamics and Control.63 There are two key differences between models with a continuum of agents and models with a finite number of heterogeneous agents.
The first difference is that idiosyncratic risk does not average out in models with a finite number of agents. Typically this means that one faces integrals over many random variables. The second difference is that the state consists of a finite but large number of elements in models with a finite number of agents. It is an open question at what point the number of elements becomes so large that it becomes worthwhile to approximate the distribution with summary statistics instead of including the complete set.
The problem of having a high-dimensional state space and the problem of having expectations over many random variables are related. Both problems require thinking carefully about how to choose relevant points in large spaces. We refer the reader to Kollmann et al. (2011), Malin et al. (2011), Maliar et al. (2011), and Pichler (2011) for discussions on recent techniques to deal with these problems.
10 Concluding Comments
There are many macroeconomic models with heterogeneous agents and aggregate uncertainty. Often, the computational complexity is reduced by making particular ad hoc assumptions. For example, in models with a financial accelerator, as in Carlstrom and Fuerst (1997) or Bernanke et al. (1999), the assumption is made that the production function is linear in the sector in which agents face financial frictions and that there are no financial frictions in the sector in which the production function is not linear. This makes it possible to aggregate and model a representative firm, even though in the underlying model firms face idiosyncratic shocks and a fraction of firms go bankrupt each period. Similarly, aggregation is possible in standard New-Keynesian models with Calvo pricing if one restricts attention to the linearized solution.
The question arises how sensible these assumptions are and whether the predictions of the models in which these restrictive assumptions are not made are different. With the algorithms that have been developed, it has become possible to check these assumptions and to have models with financial frictions and sticky prices in more general environments.
We end this chapter expressing a concern about current practice in the quantitative analysis of dynamic stochastic models. It is a deplorable fact that results based on numerical solutions are often not properly checked for accuracy. Properties of the algorithm established in simpler environments are simply believed to carry over to more complex environments without a proper discussion. If this practice continues, then it is only a matter of time that the quantitative economics literature will face its own crisis, instead of being able to provide useful answers to pressing problems like the current financial crisis.
Acknowledgments
The authors would like to thank Ken Judd, Michel Juillard, Alex Ludwig, Karl Schmedders, and an anonymous referee for useful comments.
A Explicit Aggregation and Perturbation Techniques
In this section, we work out an example to document that the explicit aggregation algorithm of Den Haan and Rendahl (2010) boils down to the same algorithm as the one proposed by Preston and Roca (2006) if the individual problem is solved using perturbation techniques. We consider the following simple example in which the model equations are given by
(62)
and
(63)
The solutions we seek can be written as
(64)
and
(65)
where 
consists of a finite set of higher-order uncentered moments.
First-Order Perturbation
When first-order perturbation is used, then the solutions are of the form 
and 
. Using this, the model equations can be written as
(66)
The first-order Taylor expansion of the solution is given by
(67)
Differentiating Eq. (66) with respect to 
and 
and evaluating the expressions at the steady state gives the following two equations:
(68)
and
(69)
There are three unknowns in these equations, namely, 
, and 
. If the explicit aggregation algorithm of Den Haan and Rendahl (2010) is used, then the policy rule for 
is given by
(70)
That is,
(71)
Equations (68), (69), and (71) can then be used to solve for the three unknowns.
The algorithm of Preston and Roca (2006) would also use Eqs. (68) and (69). It would solve for 
from the aggregation equation:
(72)
Differentiating and evaluating at the steady state give
(73)
or
(74)
or
(75)
which is equivalent to Eq. (71), the equation obtained using the explicit aggregation algorithm of Den Haan and Rendahl (2010).
Second-Order Perturbation
The solutions are now of the form 
, and the model equations can be written as
(76)
The second-order Taylor expansion of the solution is given by
(77)
Note that 
is a second-order term, and is, thus, not combined with any other terms. When using the explicit aggregation algorithm of Den Haan and Rendahl (2010), we also need a second-order solution for 
, which we write as
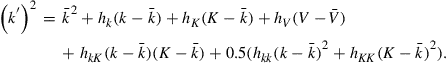(78)
The additional equation for the additional variable, 
, is given by
(79)
Explicitly aggregating the two policy rules gives the laws of motion for the two aggregate state variables, 
and 
. Thus,
(80)
and
(81)
That is, using explicit aggregation gives
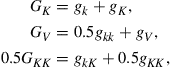(82)
and
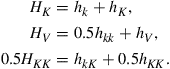(83)
The question arises whether the procedure of Preston and Roca (2006) gives the same system of equations. The law of motion for 
satisfies
(84)
By taking the second-order Taylor expansion around the steady state on both sides we get
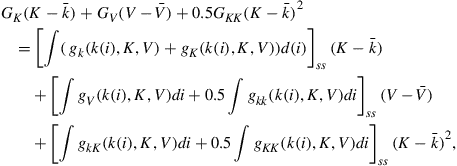(85)
where 
indicates that the expression is evaluated at steady-state values. This gives indeed the same values for 
, and 
as those implied by explicit aggregation.
The law of motion for 
satisfies
(86)
By taking the second-order Taylor expansion around the steady state on both sides we get
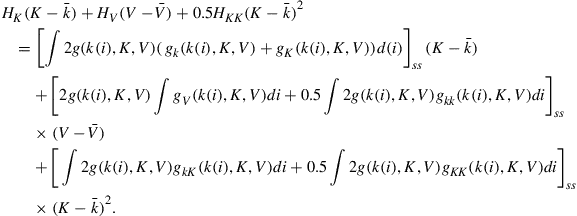(87)
This leads to the following set of solutions for the coefficients of 
:
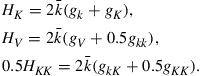(88)
The final question is whether these second-order perturbation solutions for 
are equal to the solutions one gets with explicit aggregation, as given in Eq. (83). The answer is yes. Using that 
or 
we get that
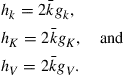(89)
Using these expressions, we see that the explicit aggregation algorithm of Den Haan and Rendahl (2010) gives the exact-same policy rules as the procedure of Preston and Roca (2006), if the individual policy rules are solved using perturbation.
References
1. Algan Y, Allais O, Den Haan WJ. Solving heterogeneous-agent models with parameterized cross-sectional distributions. Journal of Economic Dynamics and Control. 2008;32:875–908.
2. Algan Y, Allais O, Den Haan WJ. Solving the incomplete markets model with aggregate uncertainty using parameterized cross-sectional distributions. Journal of Economic Dynamics and Control. 2010;34:59–68.
3. Bernanke B, Gertler M, Gilchrist S. The financial accelerator in a quantitative business cycle framework. In: Taylor J, Woodford M, eds. Handbook of Macroeconomics. Elsevier Science B.V. 1999:1341–1393.
4. Campbell JR. Entry, exit, embodied technology, and business cycles. Review of Economic Dynamics. 1998;1:371–408.
5. Carlstrom CT, Fuerst TS. Agency costs, net worth, and business fluctuations: a computable general equilibrium analysis. American Economic Review. 1997;87:893–910.
6. Carroll CD. The method of endogenous gridpoints for solving dynamic stochastic optimization problems. Economic Letters. 2006;91:312–320.
7. Den Haan WJ. Heterogeneity, aggregate uncertainty and the short-term interest rate. Journal of Business and Economic Statistics. 1996;14:399–411.
8. Den Haan WJ. Solving dynamics models with aggregate shocks and heterogeneous agents. Macroeconomic Dynamics. 1997;1:355–386.
9. Den Haan WJ. Assessing the accuracy of the aggregate law of motion in models with heterogeneous agents. Journal of Economic Dynamics and Control. 2010a;34:79–99.
10. Den Haan WJ. Comparison of solutions to the incomplete markets model with aggregate uncertainty. Journal of Economic Dynamics and Control. 2010b;34:4–27.
11. Den Haan, W.J., De Wind, J., 2009. How Well-Behaved are Higher-Order Perturbation Solutions? Unpublished manuscript, University of Amsterdam.
12. Den Haan WJ, Judd KL, Juillard M. Computational suite of models with heterogeneous agents I: incomplete markets and aggregate uncertainty. Journal of Economic Dynamics and Control. 2010;34:1–3.
13. Den Haan WJ, Judd KL, Juillard M. Computational suite of models with heterogeneous agents II: multi-country real business cycle models. Journal of Economic Dynamics and Control. 2011;35:175–177.
14. Den Haan WJ, Marcet A. Accuracy in simulations. Review of Economic Studies. 1994;61:3–18.
15. Den Haan WJ, Rendahl P. Solving the incomplete markets model with aggregate uncertainty using explicit aggregation. Journal of Economic Dynamics and Control. 2010;34:69–78.
16. Heathcote J. Fiscal policy with heterogeneous agents and incomplete markets. Review of Economics Studies. 2005;72:161–188.
17. Judd KL. Projection methods for solving aggregate growth models. Journal of Economic Theory. 1992;58.
18. Judd KL. Numerical Methods in Economics. Cambridge, Massachusetts: The MIT Press; 1998.
19. Kim S, Kollmann R, Kim J. Solving the incomplete markets model with aggregate uncertainty using a perturbation method. Journal of Economic Dynamics and Control. 2010;34:50–58.
20. Kollmann R, Kim J, Kim SH. Solving the multi-country real business cycle model using a peturbation method. Journal of Economic Dynamics and Control. 2011;35:203–206.
21. Krueger D, Kubler F. Computing equilibrium in OLG models with stochastic production. Journal of Economic Dynamics and Control. 2004;28:1411–1436.
22. Krusell, P., Smith Jr., A.A., 1996. Income and Wealth Heterogeneity in the Macroeconomy, Working paper version.
23. Krusell P, Smith Jr AA. Income and wealth heterogeneity, portfolio choice, and equilibrium asset returns. Macroeconomic Dynamics. 1997;1:387–422.
24. Krusell P, Smith Jr AA. Income and wealth heterogeneity in the macroeconomy. Journal of Political Economy. 1998;106:867–896.
25. Krusell P, Smith Jr AA. Quantitative macroeconomic models with heterogeneous agents. In: Blundell R, Newey W, Persson T, eds. Advances in Economics and Econometrics: Theory and Applications, Ninth World Congress. Cambridge University Press: Econometric Society Monographs; 2006:298–340.
26. Maliar L, Maliar S, Valli F. Solving the incomplete markets model with aggregate uncertainty using the Krusell-Smith algorithm. Journal of Economic Dynamics and Control. 2010;34:42–49.
27. Maliar S, Maliar L, Judd KJ. Solving the multi-country real business cycle model using ergodic set methods. Journal of Economic Dynamics and Control. 2011;35:207–228.
28. Malin BA, Krueger D, Kubler F. Solving the multi-country real business cycle model using a Smolyak-collocation method. Journal of Economic Dynamics and Control. 2011;35:229–238.
29. Miao J. Competitive equilibria of economies with a continuum of consumers and aggregate shocks. Journal of Economic Theory. 2006;128:274–298.
30. Pichler P. Solving the multi-country real business cycle model using a monomial rule Galerkin method. Journal of Economic Dynamics and Control. 2011;35:240–251.
31. Preston, B., Roca, M., 2006. Incomplete Markets, Heterogeneity and Macroeconomic Dynamics, Unpublished manuscript,Columbia University.
32. Reiter, M., 2001. Estimating the Accuracy of Numerical Solutions to Dynamic Optimization Problems, Unpublished manuscript, Universitat Pompeu Fabra.
33. Reiter M. Solving heterogeneous-agent models by projection and perturbation. Journal of Economic Dynamics and Control. 2009;33:649–665.
34. Reiter M. Solving the incomplete markets economy with aggregate uncertainty by backward induction. Journal of Economic Dynamics and Control. 2010;34:28–35.
35. Ríos-Rull JV. Computation of equilibria in heterogeneous agent models. Federal Reserve Bank of Minneapolis Staff Report. 1997;231:238–264.
36. Santos M. Accuracy of numerical solutions using the Euler equations residual. Econometrica. 2000;68:1377–1402.
37. Santos MS, Peralta-Alva A. Accuracy of simulations for stochastic dynamic models. Econometrica. 2005;73:1939–1976.
38. Taylor JB, Uhlig H. Solving nonlinear stochastic growth models: a comparison of alternative solution methods. Journal of Business and Economic Statistics. 1991;8:1–17.
39. Young ER. Solving the incomplete markets model with aggregate uncertainty using the Krusell-Smith algorithm and non-stochastic simulations. Journal of Economic Dynamics and Control. 2010;34:36–41.
1Recently, the Journal of Economic Dynamics and Control devoted a special issue to these models. See Den Haan et al. (2010a) for further information.
2Here and in the remainder of this chapter, the phrase “sufficient (set of) statistic(s)” means that a sufficiently accurate approximation can be achieved with this (set of) statistic(s).
3The version described here includes labor taxes that are used to finance unemployment benefits. These are not present in Krusell and Smith (1998).
4Krusell and Smith (1998) set 
equal to zero. To ensure that the constraint is occasionally binding, we assume that 
is positive.
5See Krusell and Smith (1998) for details.
6Miao (2006) shows the existence of a recursive equilibrium, but also uses expected payoffs as state variables. He also shows the existence of a recursive solution that is a function of the smaller set of state variables used by Krusell and Smith (1998), but under an assumption that cannot be checked from primitives. It remains, therefore, not clear whether a recursive equilibrium exists when the smaller set of state variables is used. For a numerical solution this is less important in the sense that approximation typically entails not using all information.
7Experience indicates that invoking a law of large numbers is not problematic in practice. A priori, however, it is difficult to know whether the necessary regularity conditions are satisfied since both 
and 
are endogenous.
8This algorithm is an improved version of Den Haan (1997).
9The aggregate capital stock, 
, is either an element of 
or can be calculated from 
(and possibly 
).
10Several of the procedures discussed in Taylor and Uhlig (1991) are still in use. See Judd (1998) for a thorough discussion of alternative algorithms.
11In contrast to the algorithm of Krusell and Smith (1998), this algorithm does not require that the aggregate capital stock is an element of or can be calculated from 
. For example, 
could only include a set of percentiles.
12Throughout this paper, we use 
to indicate a flexible functional form of order 
with coefficients 
. The notation will not make clear that different types of functional forms may be used for different objects.
13If the orthogonality property is not satisfied, then it is possible to construct better forecasts; consequently, 
cannot be the conditional expectation.
14Or a minimization routine to minimize some loss criterion in case there are more grid points than coefficients.
15As discussed in Section 3.1.4, the algorithm of Den Haan and Rendahl (2010) makes clear that for some functional forms aggregation is possible without knowing the cross-sectional distribution.
16Algan et al. (2008) propose a particular approximating functional form, which makes it easy to establish the mapping between moments and the approximating functional form. This will be discussed in Section 6.
17The procedure used in Algan et al. (2008) is actually more cumbersome than necessary. They solve the individual policy rule taking as given an aggregate law of motion for the transition of the moments, 
. Next, they use the procedure described in the text to update 
. Next, they iterate between the two problems until there is convergence in the aggregate law of motion, similar to the procedure used by Krusell and Smith (1998). Note, however, that one does not need to specify an aggregate law of motion as an intermediate step.
18The idea of reference moments was first proposed in Reiter (2010).
19In Algan et al. (2008) the simplifying assumption is made that 
only depends on 
, because dependence on 
turned out to be not important.
20The discrete nature of the employment status makes it feasible to specify separate approximating functions for 
for each realization of the employment status. If individual productivity has continuous support, 
would be a polynomial in both individual state variables.
21Given the transition laws of the employment status, the next period’s distribution of beginning-of-period capital levels follows directly from this period’s distribution of end-of-period capital levels and the values of 
and 
.
22Since a spline can be written as a weighted combination of basis functions, explicit aggregation is possible with splines. But splines typically have many nodes, which would correspond with a large number of basis functions, and thus, many aggregate state variables.
23For example, every second-order approximation is nonmonotone even if the truth is monotone.
24With projection methods, oscillations of approximating polynomials typically occur outside the grid. So by choosing the grid one controls where the oscillations occur.
25In the model discussed above this can be accomplished by letting both the probability and the drop in income increase continuously with the parameter that controls the amount of uncertainty.
26Below, it will become clear that the analysis relies on implementing the perturbation procedure without the standard log transformation of the variables. By assuming that the laws of motion for the stochastic variables, 
and 
, are linear in levels instead of logs one avoids having to take an approximation of this exogenous law of motion. As long as the uncertainty is not too large, one would not run into problematic negative values.
27One could allow this law of motion to depend on the aggregate state. This specification implies that aggregate labor, 
, is constant, but one could let 
depend on the aggregate state.
28Instead of assuming a utility cost, one can also assume that the cost enters the budget constraint. The penalty term in the Euler equation is then multiplied by the marginal utility of consumption, which makes it less powerful because the marginal utility tends to be high when the agent lowers his capital holdings and it is not clear what will happen with the cross product.
29This would not be true if one would approximate the aggregation constraints as well. Accurately approximating the aggregation constraints may not be that easy. At the nonstochastic steady state, agents are equally rich, which would imply that the values of the individual variable across agents get the same weight in constructing the aggregate. This could very well be inaccurate, given that at each point in time there typically are large differences in individual wealth levels in this type of model.
30The integral of other products can be simplified. For example, 
equals 
.
31A complete polynomial of order 
in 
and 
includes all terms 
such that 
.
32In contrast, the other algorithms combine elements of both. Moreover, the other algorithms explicitly approximate additional aspects such as the cross-sectional distribution and/or add simulation features.
33This algorithm is closely related to the algorithm used in Campbell (1998). This algorithm approximates the information of the cross-sectional distribution with a finite set of elements and linearizes the resulting set of equations. See the computational appendix of Campbell (1998) for more details.
34
could be a set of moments, but then it has to be accompanied by a functional form assumption so that the cross-sectional density is pinned down as discussed in Section 6.3.
35That is, we consider here the case where there are exactly enough grid points to determine the elements of 
.
36For simplicity, we assume that unemployment benefits are zero and there is no binding constraint on capital.
37This could easily be 1,000 coefficients/variables or more.
38See Den Haan (1997) and Krusell and Smith (1997).
39One notable model in which approximate aggregation does not hold is the OLG model of Krueger and Kubler (2004).
40The latter property may be true in some models. In fact, Krusell and Smith (2006) point out that the latter property is true for the simplest version of the model in Krusell and Smith (1998), but that it is not true for the version of their model with stochastic discount rates.
41This procedure is proposed by Ríos-Rull (1997) and used in, e.g., Heathcote (2005) and Reiter (2009).
42Employed agents never choose a zero capital stock, but some unemployed agents that chose a zero capital stock last period are employed in the current period.
43This is a nonlinear problem (and has to be calculated at many nodes), but it should be a well-behaved problem.
44This procedure is proposed by Young (2010).
45Except that the probability always refers to the probability at a grid point, not to the mass in between grid points.
46The dependence on time comes through the aggregate state variables, which are suppressed here to economize on notation.
47Note that evaluated at the solution for 
, the Hessian is a covariance matrix.
48As an alternative, Algan et al. (2008) use standard exponentials to parameterize the density and an equation solver to find the coefficients. This version of the algorithm often got stuck and had to be restarted with better initial conditions.
49See Den Haan and Marcet (1994).
50See Judd (1992).
51For example, the number of agents used in a simulation with a finite number of agents may not be high enough to eliminate all sampling uncertainty. Alternatively, the grid to construct the histogram for the cumulative distribution function may not be fine enough.
52It is obviously cleaner to use a fresh draw. This would not be very important, however, if long enough samples are used to estimate the coefficients of the approximating law of motion.
53We remind the reader that 
refers to the aggregate capital stock that is based on the individual policy functions. The superscript “truth” is used, because it is the law of motion of this capital stock that one is trying to approximate. But the superscript is misleading, because (taking the individual policy functions as given) this measure is typically not calculated without any numerical error.
54Namely, Experiment 1.2.
55Some accuracy tests are directly linked to properties of interest, but this is unusual. Santos (2000) relates the Euler equation residual to errors in the policy function. Reiter (2001) and Santos and Peralta-Alva (2005) construct a relationship between the size of the errors found and an upper bound on the error for objects economists could be interested in such as the obtained utility level or moments.
56Kim et al. (2010) implement the inequality constraint with a penalty function, but they are not very successful in doing so.
57The figure plots the series in that part of the sample where BInduc obtains its largest errors (excluding the initial period) for the average capital stocks conditional on employment status. BInduc does not automatically generate a law of motion for the average capital stocks conditional on employment status, but it is possible to do so. The errors for the conditional means are substantially larger than the errors for the per capita capital stock. The proxy distribution in BInduc takes the role of the aggregate law of motion in the other algorithms. The proxy distribution does not take care well of how capital is split between employed and unemployed, but does predict aggregate capital well.
58The Krusell-Smith algorithm achieved the highest accuracy for the aggregate law of motion.
59The programs were run on a Dell Latitude D410 with an Intel Pentium M processor (2.00 GHz, 798 MHz FSB).
60The algorithm of Kim et al. (2010) is even faster, but this algorithm does not solve the actual model specified with heterogeneous agents.
61See Judd (1998) for a discussion on the differences between these two procedures.
62A much more demanding accuracy test than the 
is used.
63See Den Haan et al. (2011) for more information.