7.2.3 Shall We Use the Envelope Condition with Endogenous Grid?
Four combinations are possible to obtain from two alternative conditions for 
(i.e., FOC (83) and envelope condition (92)) and two alternative grids (i.e., exogenous and endogenous). So far, we have distinguished two competitive methods: one is EGM of Carroll (2005) (FOC (83) and endogenous grid) and the other is our ECM (envelope condition (92) and exogenous grid). Conventional VFI (FOC (83) and exogenous grid) is not competitive. Therefore, we are left to check the remaining combination (envelope condition (92) and endogenous grid).
given 
.Solving (94) involves costly evaluation of 
for many candidate solution points 
. We conclude that the combination of the envelope condition and endogenous grid does not lead to a competitive method. Our results are suggestive for other applications.
7.2.4 EGM and ECM in a Model with Elastic Labor Supply
Maliar and Maliar (2013) apply ECM and EGM for solving the one-agent model with elastic labor supply under assumption (17). Under EGM, Carroll’s (2005) change of variables does not avoid rootfinding in the model with elastic labor supply. The variable 
depends on future labor 
, and 
cannot be computed without specifying a labor policy function. Barillas and Fernández-Villaverde (2007) propose a way of extending EGM to the model with elastic labor supply. Namely, they fix a policy function for labor 
, construct the grid of 
, solve the model on that grid holding 
fixed, and use the solution to reevaluate 
; they iterate on these steps until 
converges. See also Villemot (2012) for an application of EGM for solving a model of sovereign debt.
The implementation of EGM in Maliar and Maliar (2013) for the model with elastic labor supply differs from that in Barillas and Fernández-Villaverde (2007). First, Maliar and Maliar (2013) use future endogenous state variables for constructing grid points but they do not use Carroll’s (2005) change of variables. Second, to deal with rootfinding, Maliar and Maliar (2013) use a numerical solver, while Barillas and Fernández-Villaverde (2007) iterate on a state contingent policy function for labor 
. Maliar and Maliar (2013) find that ECM and EGM have very similar performances in that they produce solutions of similar (high) accuracy and have similar computational expenses. Even though neither ECM nor EGM allows us to solve the system of intratemporal choice conditions in a closed form, these two methods still lead to far simpler systems of equations than does conventional VFI.
7.3 Increasing the Accuracy of Dynamic Programming Methods
So far, we have been concerned with the inner loop: all the methods we have considered differ in the way in which they solve for the intratemporal choice. Maliar and Maliar (2012b, 2013) modify the outer loop as well by introducing versions of EGM and ECM that solve for the derivative of value function, 
, instead of or in addition to the value function itself 
. Since only the derivative of the value function enters optimality conditions (83) and (92) but not the value function itself, we can find a solution to problem (82)–(84) without computing 
explicitly.
In terms of our example, combining (83) and (92) yields
(95)
This equation is used in Maliar and Maliar (2012b, 2013) to implement iteration on the derivative of the value function similar to the one we implement for value function using the Bellman equation. Iteration on the derivative of the value function is compatible with all previously described DP methods such as conventional VFI, EGM, and ECM. In particular, ECM modifies as follows:
In some experiments, Maliar and Maliar (2012a,b) approximate the value function 
and its derivative 
jointly. A robust finding is that methods approximating derivatives of value function lead to far more accurate solutions than the methods approximating the value function itself.
7.4 Numerical Illustration of Dynamic Programming Methods
Under Maliar and Maliar’s (2012a) implementation, the rootfinding problems under EGM and ECM are comparable in their complexity. In both cases, we must find a solution to a nonlinear equation in each grid point. Such an equation does not involve either interpolation or approximation of expectations. Below, we reproduce from Maliar and Maliar (2013) the results about a numerical comparison of ECM with EGM in the context of the model with elastic labor supply parameterized by (17).
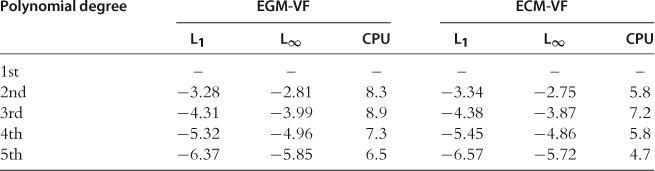
We first solve for 
by iterating on the Bellman equation (82)–(84) ; we refer to the corresponding methods as EGM-VF and ECM-VF. The results are shown in Table 12. The performance of EGM-VF and ECM-VF is very similar. EGM-VF produces slightly smaller maximum residuals, while ECM-VF produces slightly smaller average residuals. EGM-VF is somewhat slower than ECM-VF.
Table 12
Accuracy and speed of EGM-VF and ECM-VF in the one-agent model with elastic labor supply.a
aNotes: 
and 
are, respectively, the average and maximum of absolute residuals across optimality condition and test points (in log10 units) on a stochastic simulation of 10,000 observations; CPU is the time necessary for computing a solution (in seconds). These results are reproduced from Maliar and Maliar (2013), Table 1.
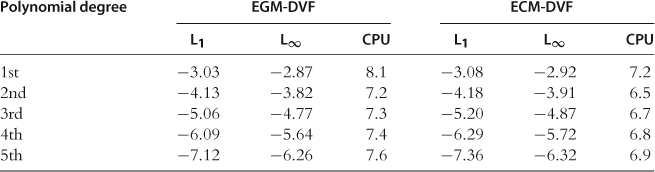
We next solve for 
by iterating on (95); we call the corresponding methods EGM-DVF and ECM-DVF. The results are provided in Table 13. Again, EGM-DVF and ECM-DVF perform very similarly. Both methods deliver accuracy levels that are about an order of magnitude higher than those of EGM-VF and ECM-VF.
Table 13
Accuracy and speed of EGM-DVF and ECM-DVF in the one-agent model with elastic labor supply.a
aNotes: 
and 
are, respectively, the average and maximum of absolute residuals across optimality condition and test points (in log10 units) on a stochastic simulation of 10,000 observations; CPU is the time necessary for computing a solution (in seconds). These results are reproduced from Maliar and Maliar (2013), Table 2.
Iterating on (95) produces more accurate solutions than iterating on (82) because the object that is relevant for accuracy is 
and not 
(
identifies the model’s variables via (83), (85), and (92)). Approximating a supplementary object 
and computing its derivative 
involves an accuracy loss compared to the case when we approximate the relevant object 
directly. For example, if we approximate 
with a polynomial, we effectively approximate 
with a polynomial which is one degree lower, i.e., we “lose” one polynomial degree. In our experiments, EGM-DVF and ECM-DVF attain accuracy levels that are comparable to the highest accuracy attained by the Euler equation methods.
8 Precomputation Techniques
Precomputation is a technique that computes solutions to some model’s equations outside the main iterative cycle. Precomputation techniques can be analytical, numerical, or a combination of both. We describe two numerical techniques: a technique of precomputing integrals in the intratemporal choice introduced in Judd et al. (2011d) and a technique of precomputing the intratemporal choice manifolds introduced in Maliar and Maliar (2005b) and developed in Maliar et al. (2011). We then briefly discuss an analytical technique of imperfect aggregation of Maliar and Maliar (2001, 2003a) which allows us to characterize aggregate behavior of certain classes of heterogeneous-agent economies in terms of one-agent models.
8.1 Precomputation of Integrals
In existing iterative methods for solving dynamic stochastic models, a conditional expectation function is computed in each iteration. Recomputing expectations in each iteration is costly. Judd et al. (2011d) show a simple technique that makes it possible to compute conditional expectation functions just once, in the stage of initialization. The proposed technique is called precomputation of integrals. We first show how to precompute the expectation for polynomial functions, and we then use the resulting polynomial functions to approximate expectations in the Euler and Bellman equations outside the main iterative loop.
8.1.1 Precomputation of Expectations for Polynomial Functions
Let us consider the one-agent model (1)–(3). Consider a complete ordinary polynomial function in terms of the current state 
,
(96)
where 
is a vector of polynomial coefficients, and 
is a polynomial degree. Taking into account that 
is known at present and that 
, we can represent the conditional expectation of 
as follows:
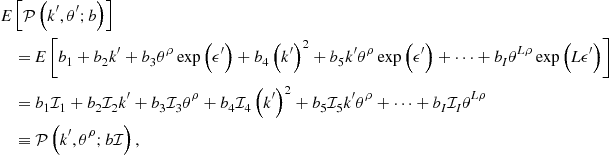(97)
where 
, and 
, 
with
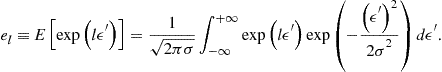(98)
The integrals 
can be computed up-front without solving the model (i.e., precomputed). Once 
’s are computed, an evaluation of conditional expectation becomes very simple. Namely, the conditional expectation of a polynomial function is given by the same polynomial function but evaluated at a different coefficient vector, i.e., 
. Effectively, precomputation of integrals converts a stochastic problem into a deterministic one.
8.1.2 Precomputation of the Expectation in the Euler Equation
We now show how to precompute conditional expectation functions in Euler equation (74). Let us parameterize a variable inside the conditional expectation function with a polynomial function,
(99)
By (99), we can write Euler equation (74) as
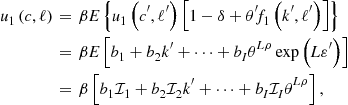(100)
where 
are integrals that are known (precomputed) using (98). With this result, we formulate a system of four equations to feed into a grid-based Euler equation method:
(101)
(102)
(103)
(104)
We can now implement the following iterative scheme: fix some 
, use the intratemporal choice equations 101, 102, (103) to solve for 
in each grid point 
, and use the intertemporal choice equation (104) to recompute 
. There is an explicit OLS formula for 
, namely, 
, where 
is a matrix of the coefficients and 
is a vector of marginal utilities. However, the OLS method can be numerically unstable, and we may need to use regression methods that are robust to ill-conditioning studied in Section 4.2.
With precomputation of integrals, we can also construct a version of the Euler equation method that operates on an endogenous grid 
and that is analogous to Carroll’s (2005) EGM. The iterative scheme modifies as follows: fix some 
, use the intratemporal choice equations (102)–(104) to solve for 
in each grid point 
, and use the intertemporal choice condition (101) to recompute 
. Again, there is an explicit OLS formula for 
, where 
is a matrix of the coefficients and variable 
is defined as 
.
8.1.3 Precomputation of the Expectation in the Bellman Equation
We now show how to precompute conditional expectation functions in Bellman equation 8,9 and 10. Let us parameterize the value function with complete ordinary polynomial,
(105)
Then, according to (97), expectation 
can be precomputed as
(106)
With this result, we rewrite the Bellman equation (8) as
(107)
The system of the optimality conditions under precomputation of integrals becomes
(108)
(109)
(110)
(111)
A version of ECM with precomputation of integrals is as follows: fix some 
, use intratemporal choice equations (108)–(110) to solve for 
in each grid point 
, and use the intertemporal choice equation (111) to recompute 
; iterate until convergence.
Precomputation of integrals can also be performed for the DP methods iterating on derivatives of value function as discussed in Section 7. Interestingly, a method that iterates on a derivative of value function coincides with the previously described Euler equation method that solves (101)–(104). This is because in this specific example, a variable in (99) which is parameterized to precompute the expectations in the Euler equation (74) coincides with the derivative 
. However, precomputation of integrals in the Euler equation is possible even for those problems for which we do not have a Bellman equation.
Similar to the Euler equation case, there is an explicit OLS formula for 
, where 
is a matrix of coefficients, and 
is a vector of values of the utility functions. Finally, we can construct a version of Carroll’s (2005) EGM with precomputation of integrals. In this case, we compute the intratemporal choice 
on the grid 
to satisfy (109)–(111), and we use (108) to recompute 
.
8.1.4 Relation of Precomputation of Integrals to the Literature
Effectively, precomputation of integrals allows us to solve stochastic economic models as if they were deterministic, with the corresponding reduction in cost. Precomputation of integrals is a very general technique that can be applied to any set of equations that contains conditional expectations, including the Bellman and Euler equations. Furthermore, precomputation of integrals is compatible with a variety of approximating functions, solution domains, integration rules, fitting methods, and iterative schemes for finding unknown parameters of approximating functions. That is, apart from precomputation of integrals, the rest of our solution procedure is standard. Finally, given that we must approximate integrals just once, we can use very accurate integration methods that would be intractable if integrals were computed inside an iterative cycle.
We must emphasize that, in order to precompute integrals, it is critical to parameterize the integrand, i.e., the expression inside the expectation function. Other parameterizations such as the capital function or the expectation function do not allow us to precompute integrals using accurate deterministic integration methods.
There are two other methods of approximating integrals that have similar computational complexity as does the method of precomputation of integrals (they also evaluate integrals in just one point). First, Marcet (1988) approximates an expectation function in each simulated point using a next-period realization of the integrand (which is a version of a Monte Carlo method with one random draw); the accuracy of this approximation is low and limits dramatically the accuracy of solutions; see our discussion in Section 5.8. Second, Judd et al. (2011a) propose to use a one-node Gauss-Hermite quadrature method, which approximates the integral with the expected value of the integrand; this method is far more accurate than the one-node Monte Carlo integration and is even more accurate than Monte Carlo integration with thousands of random nodes in the class of problems studied. Still, for high-degree polynomials, the one-node quadrature method limits the accuracy of solutions. In contrast, the method of precomputation of integrals delivers the highest possible accuracy that can be produced by deterministic integration methods at the lowest possible cost.
8.1.5 Numerical Illustration of the Precomputation Methods
In Table 14, we provide the results for the model with inelastic labor supply parameterized by (18) that are delivered by the Bellman and Euler equation methods with precomputation of integrals (these results are reproduced from Judd et al. (2011d)).
Table 14
Accuracy and speed of the Bellman equation algorithm in the one-agent model with inelastic labor supply.a
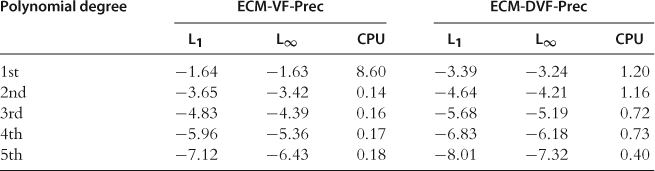
aNotes: 
and 
are, respectively, the average and maximum of absolute residuals across optimality condition and test points (in log10 units) on a stochastic simulation of 10,000 observations; CPU is the time necessary for computing a solution (in seconds). The results for ECM-VF-Prec and ECM-DVF-Prec are reproduced from Judd et al. (2011d), Table 1 and 2, respectively.
As we can see, the residuals decrease with each polynomial degree by one or more orders of magnitude. High-degree polynomial solutions are very accurate. Under ECM-VF-Prec (which is a DP algorithm), the maximum residuals for the fifth-degree polynomial approximations are of the order 
. Under ECM-DVF-Prec (which is an Euler equation algorithm), the maximum residuals are about one order of magnitude smaller. The tendencies are similar to those we observe for the corresponding methods without precomputation; see Tables 12 and 13 for a comparison.
8.2 Precomputation of Intratemporal Choice Manifolds
The precomputation technique of intratemporal choice manifolds constructs solutions to the intratemporal choice conditions outside the main iterative cycle and uses the constructed solutions to infer the intratemporal choice inside the main iterative cycle. Consider the intratemporal choice conditions for model (1)–(3) under parameterization (17)
(112)
(113)
We denote a solution for 
and 
for given 
as 
and 
, respectively, and we call 
and 
solution manifolds.
Observe that it is sufficient for us to construct a manifold for labor 
since we can infer consumption from (113) if labor is given. To compute the intratemporal choice inside the main iterative cycle, first we use 
to find 
and 
; then we use 
to compute 
and 
; and, finally, we can get 
and 
from (113). In the remainder of the section, we focus on constructing 
.
In simple cases, the intratemporal choice manifolds can be constructed analytically. Consider the following example.
Example 18
Assume (17) under 
. Then, system (112), (113) admits a closed-form solution in the form
(114)
However, under more general parameterizations, 
cannot be constructed analytically from (112), (113). We therefore construct it numerically.
Example 19
Assume (17). Consider system (112), (113). We proceed as follows:– Outside the main iterative cycle:
within the relevant range.
, compute the values of 
and 
that satisfy 
(by fitting 
to some parametric function, such as polynomial function, splines, etc., on the grid 
).In the above example, we had to compute values for labor using a numerical solver. We now show how to “invert” the problem and to precompute the same manifold but without using a solver.
within the relevant range.
, compute analytically the values of 
from 
(by fitting the values 
to a polynomial function, splines, etc., on the grid 
).Maliar and Maliar (2005b) show an example of precomputation of the labor choice in a similar model but assuming that the intertemporal choice is parameterized with a consumption decision function instead of a capital decision function. In this case, the labor choice can be precomputed in terms of just one artificial variable and, thus, is easier to construct in the main iterative cycle; see the example below.
Example 21
Assume (17). Consider the system (112), (113). Let us define a new variable 
by
(117)
We proceed as follows:– Outside the main iterative cycle:
(i) Take a grid 
within the relevant range.
(ii) For each grid point 
, compute the value of variable 
satisfying (117).
(iii) Construct a labor manifold 
(by fitting the values 
to a polynomial function, splines, etc., on the grid 
).
Inside the main iterative cycle, given a value of 
, we compute 
using the precomputed manifolds 
, and we compute 
using (113).
We can also invert the task and construct the same manifold by choosing a grid for 
and by solving for 
using (117), in which case a numerical solver is not needed. See Maliar et al. (2011) for examples of precomputation of the intratemporal choice manifolds for heterogeneous-agent economies.
Three comments are in order: First, the solution manifold 
depends on three arguments 
instead of the conventional decision function that depends on two arguments 
: the relation between these objects is given by 
, where 
is the optimal capital decision function; see Maliar et al. (2011) for a discussion. Second, there are many ways to define the intertemporal (and thus, intratemporal) choice manifolds; it is possible to fix any three variables in (112), (113) and solve for the remaining two variables; for example, we can fix 
and find 
. Finally, precomputation of the intratemporal choice can also be implemented in the context of DP methods described in Section 7.
8.3 Precomputation of Aggregate Decision Rules
Maliar and Maliar (2001, 2003a) study complete-market heterogeneous-agents economies in which agents differ in initial endowments and labor productivities (under some parameterizations, their model is identical to the multicountry model studied in Section 11). In particular, they show that under the standard assumptions of the CRRA or addilog utility functions and the Cobb-Douglas production function, it is possible to characterize the aggregate behavior of a heterogeneous-agents economy in terms of a one-agent model. This kind of result is referred to as imperfect aggregation and is in effect an analytical precomputation of some aggregate decision functions outside the main iterative cycle.
Imperfect aggregation is not an aggregation result in the traditional sense of Gorman (1953) since the behavior of the composite consumer does depend on a joint distribution of heterogeneity parameters. It is a special case of the aggregation in equilibrium point by Constantinides (1982) in which the social utility function can be constructed analytically. (In general, such utility function depends on the distribution of individual characteristics in a manner which is difficult to characterize). Models derived from aggregation are of additional interest because having explicit conditions relating aggregate variables is convenient for numerical work. See Maliar et al. (2011) for imperfect aggregation results in the context of the multicountry models studied in the JEDC comparison analysis.
9 Local (Perturbation) Methods
A local perturbation method computes a solution to an economic model in just one point—a deterministic steady state—using Taylor expansions of optimality conditions. Perturbation methods are introduced to economics in Judd and Guu (1993) and became a popular tool in the literature. The main advantage of perturbation methods is their low computational expense. The main shortcoming is that the accuracy of perturbation solutions may decrease rapidly away from the steady state. In this section, we discuss two techniques that can increase the accuracy of perturbation methods: a change of variables introduced in Judd (2003) and a hybrid of local and global solutions advocated in Maliar et al. (2013).16 We present these techniques in the context of Euler equation methods; however, our results apply to DP methods as well. See Judd (1998) for perturbation methods in the context of value function iteration.
9.1 Plain Perturbation Method
To present the perturbation techniques, we use a version of the one-agent model (1)–(3) with inelastic labor supply:
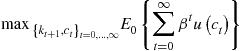(118)
(119)
(120)
where 
is given. This model’s presentation differs from that in (1)–(3) in two respects: First, we use a separate notation for a net of depreciation production function 
, where 
is the gross production function. This helps us to simplify the presentation. Second, we explicitly introduce 
into the process for productivity (120). This is done because we compute a Taylor expansion not only with respect to the two state variables 
but also with respect to parameter 
. In addition, we assume that 
.
We approximate the capital decision function in the form 
using the Taylor expansion around the deterministic steady state 
, as follows:
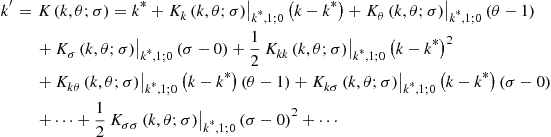
In this section, notation of type 
and 
stands for the first-order partial derivative of a function 
with respect to a variable 
and the second-order partial derivative with respect to variables 
and 
, respectively. The steady-state value 
follows by (120).
To identify the derivatives of 
, we use a procedure suggested by an implicit function theorem. We write the Euler equation of problem (118)–(120) as follows:
(121)
where 
is determined by (120), and 
and 
are determined by (119) in the current and next periods, respectively,
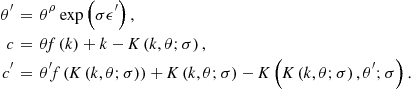
By definition, 
is a zero function in the true solution since the Euler equation must be satisfied exactly for any 
. In particular, the value of 
must be zero in the steady state, 
, and all the derivatives of 
must be also zero in the steady state, 
, etc. This fact suggests a procedure for approximating a solution to the model. Namely, we evaluate the value of 
and its derivatives in the steady state and set them to zero to identify the unknown coefficients in the capital decision function 
.
We start by finding the steady state. Given 
, (121) implies 
, which identifies 
and 
). Let us show how to derive the first-order perturbation solution.
First, 
is given by
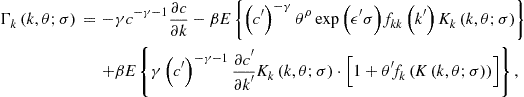
where
Note that 
. Evaluating 
in the steady state and equalizing it to zero, we obtain
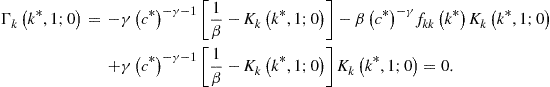
Rearranging the terms yields
This is a quadratic equation in one unknown, 
.
Second, 
is given by
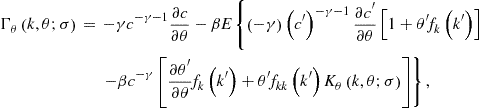
where
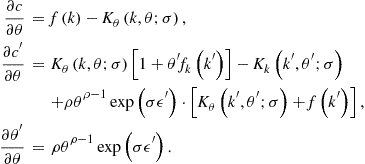
Evaluating 
in the steady state and equalizing it to zero, we obtain
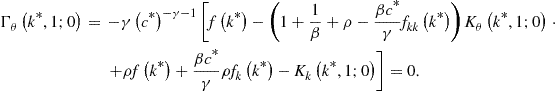
This gives us a solution for 
:
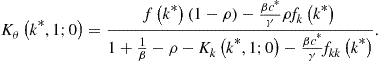
Finally, 
is given by
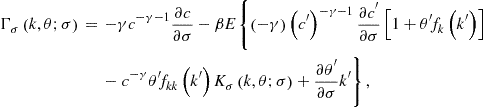
where
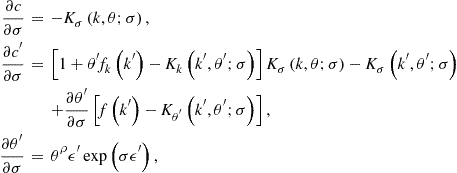
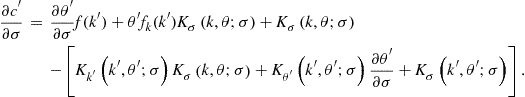
Evaluating 
in the steady state and equalizing it to zero, we obtain
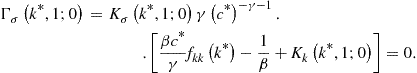
.After all the derivatives of 
are found, we can form a first-order perturbation solution for capital,
(122)
Similarly, we can write a first-order perturbation solution for consumption 
,
(123)
where 
, and 
. Finally, the first-order perturbation approximation for the productivity shocks 
is
(124)
where 
and 
. The first-order terms 
, and 
are equal to zero in (122),(123)and(124), respectively. However, the higher-order derivatives of 
, and 
with respect to 
are not equal to zero, which makes higher-order perturbation solutions depend on the volatility of shocks.
9.2 Advantages and Shortcomings of Perturbation Methods
Constructing perturbation solutions by hand is tedious even in the case of first-order approximation, as our example demonstrates. Fortunately, perturbation methods can be easily automated. Perturbation software commonly used in economics is Dynare. This software platform can solve, simulate, and estimate a wide class of economic models and delivers standard perturbation solutions up to the third order.17 Automated software for solving economic models is also developed by Jin and Judd (2002), Swanson et al. (2002), and Schmitt-Grohé and Uribe (2004). There are perturbation methods that can solve models with kinks using penalty functions; see Kim et al. (2010) and Mertens and Judd (2013).
An important advantage of perturbation methods is that they have low computational expense, which makes them an ideal candidate for solving problem with high dimensionality. The shortcoming of perturbation methods is that the accuracy of local solutions may decrease rapidly away from the steady state. To provide an illustration, we reproduce some results from Judd and Guu (1993). In Figure 8, we plot the size of unit-free residuals in the Euler equation (in 
units) depending on how far we deviate from the steady state where the solution is computed (in this figure, 
denotes an order of approximation).
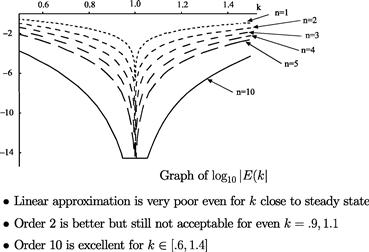
Figure 8 Global Quality of Asymptotic Approximations. Notes: Reproduced from Judd and Guu (1993) with kind permission from Springer Science+Business.
We observe that the linear perturbation solutions are very inaccurate. The quadratic perturbation solutions are more accurate but are still not acceptable even in a relatively small range around the steady state (e.g., 
). The perturbation solutions of order 10 are of acceptable accuracy in a large range (e.g., 
). Thus, high-order approximations are needed to attain accurate solutions. See also Kollmann et al. (2011b) and Judd et al. (2012) for the accuracy results of perturbation methods in the context of a large-scale multicountry model and a new Keynesian model, respectively.18
9.3 Change of Variables
Judd (2003) shows that the accuracy of perturbation methods can be considerably increased using a nonlinear change of variables. Specifically, he shows that the ordinary Taylor series expansion can be dominated in accuracy by other expansions implied by changes of variables. All the expansions are locally equivalent but differ globally. We must choose the one that performs best in terms of accuracy on the domain of interest. In the context of a deterministic optimal growth model, Judd (2003) finds that using alternative expansions can increase the accuracy of the conventional perturbation method by two orders of magnitude. Fernández-Villaverde and Rubio-Ramírez (2006) show how to apply the method of change of variables to a model with uncertainty and elastic labor supply.
9.3.1 An Example of the Change of Variables Technique
Let us consider the one-agent model (118)–(120) with inelastic labor supply as an example. Suppose 
is approximated as was discussed in Section 9 and that we have computed all the derivatives 
, and 
. The objective is to find a change of variables 
and 
, with 
being a new variable, such that a Taylor approximation (122) of 
in terms of a new variable 
has two properties: (i) the derivatives are the same in the steady state; and (ii) the accuracy declines less rapidly when we deviate from the steady state.
Using the identity, 
, we rewrite the capital function 
as 
. With this result, we obtain a decision function for 
(125)
Let us find a first-order Taylor expansion of the decision function for 
(125) around 
, and 
:
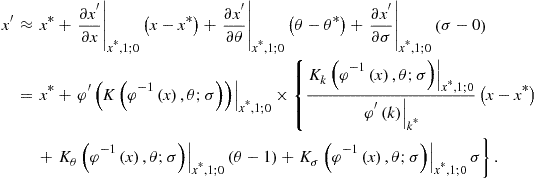
Substituting the steady-state value 
instead of 
, we obtain the formula for the change of variables
(126)
Consider now specific examples. In the trivial case, 
, we have 
, and we are back to (122). Under a logarithmic transformation of, i.e., 
, condition (126) implies
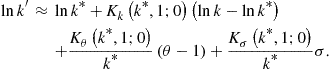(127)
For a power transformation 
, we obtain
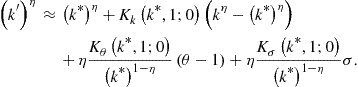(128)
In this way, we can try many different transformations (at a low cost). For each candidate change of variables, we evaluate accuracy using a selected accuracy test (e.g., we can evaluate the Euler equation residuals on a stochastic simulation), and we choose the representation that yields the most accurate solution globally.
Three observations are in order. First, we need not compute anything new to implement the change of variables: the derivatives 
, and 
which determine the coefficients in (127) and (128) are the same as that we found in Section 9.1 using the plain perturbation method. Second, in the above example, we apply the same change of variables to 
and 
. More generally, we can use other transformations. For example, for 
, we may keep the same transformation as before, 
, but for 
, we may use a different transformation 
so that 
. Finally, we may also apply some changes of variables to 
and 
. Ideally, a selection of the right change of variables must be automated; see Judd (2003) for more details.
9.3.2 Numerical Illustration of the Change of Variables Technique
For a simple one-agent model with inelastic labor supply, Judd (2003) shows that logarithmic and power transformations of the variables may decrease the maximum residuals in the optimality conditions by several orders of magnitude. In Table 15, we reproduce his results for the logarithmic transformations of 
and 
(perturbation in logarithms) compared to ordinary perturbation in levels. As we can see, perturbation in logarithms produces significantly more accurate approximations than perturbation in levels; however, this accuracy ranking is model-specific and does not need to hold for other models.
Table 15
Perturbation in levels and logarithms in the one-agent model.a
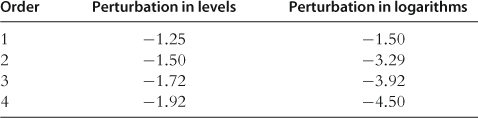
aNotes: The numbers in the table are the maximum absolute Euler equation residuals (in log10 units); 
. These results are reproduced from Judd (2003), Table 2.
9.4 Hybrid of Local and Global Solutions
Maliar et al. (2013) develop a hybrid perturbation-based solution method that combines local and global approximation techniques. (The term hybrid method indicates that we combine policy functions produced by different solution methods.) This hybrid method computes a plain perturbation solution, fixes some perturbation functions, and replaces the rest of the perturbation functions by new functions that are constructed to satisfy the model’s conditions exactly. The construction of these new functions mimics global solution methods: for each point of the state space considered, we solve nonlinear equations either analytically (when closed-form solutions are available) or with a numerical solver. If the perturbation functions that were used to construct a hybrid solution are accurate, then the entire hybrid solution will inherit their high accuracy; such a hybrid solution may be far more accurate than the original perturbation solution. The cost of the hybrid method is essentially the same as that of the standard perturbation method. The hybrid method of Maliar et al. (2013) encompasses previous examples constructed on the basis of the standard loglinearization method in Dotsey and Mao (1992) and Maliar et al. (2011).
9.4.1 Description of the Hybrid Method
To exposit the idea of the hybrid method, we use the one-agent model (118)–(120) with inelastic labor supply. We assume that a plain perturbation method delivers an approximate solution in the form of two decision functions 
and 
, such as (122), (123) constructed in Section 9.1. Let us assume that the decision functions are not sufficiently accurate for our purpose.
We attempt to improve on the accuracy in the following way. We fix one decision function from the benchmark solution, for example, 
, and we solve for the other decision function, 
, to satisfy some model’s nonlinear optimality conditions taking 
as given.
For model (118)–(120), we have two optimality conditions,
(129)
(130)
By considering all possible combinations of the two decision functions and the two optimality conditions, we construct four hybrid solutions 
, and 
, as follows:
HYB1: Fix 
and define 
using (130),
HYB2: Fix 
and define 
using (129),
HYB3: Fix 
and define 
using (130),
HYB4: Fix 
and define 
using (129),
On the basis of this example, we can make the following observations: first, multiple hybrid solutions can be constructed for a given benchmark solution; in our example, there are four hybrid solutions. Second, the hybrid method mimics global solution methods in a sense that functions 
, 
, and 
are defined to satisfy the corresponding nonlinear optimality conditions globally, for any point 
of the state space considered. Third, a hybrid solution can be either more accurate or less accurate than the benchmark solution. Assume that in the benchmark solution, 
is accurate and 
is not. Then, the hybrid solutions based on 
(i.e., HYB1 and HYB2) will be more accurate, while the hybrid solutions based on 
(i.e., HYB3 and HYB4) will be less accurate than the benchmark solution. Finally, hybrid solutions can differ in cost considerably. In our example, HYB1 and HYB3 are obtained using simple closed-form expressions, while HYB2 and HYB4 are defined implicitly and are far more costly to compute.
9.4.2 Numerical Illustration of the Hybrid Method
A potential usefulness of the hybrid solution method is well seen in examples constructed using the standard loglinearization method. In particular, Maliar et al. (2011) take the capital decision function produced by the standard loglinearization method and accurately solve for consumption and labor to satisfy the intertemporal choice conditions (using the iteration-on-allocation method) in the context of a two-agent version studied in the JEDC comparison analysis. In Table 16, we compare the accuracy of the resulting hybrid method, HYB, with that of the plain first-order and second-order perturbation methods (in levels), denoted PER1 and PER2, respectively. As the table indicates, the first-order hybrid method produces more accurate linear approximations (by more than an order of magnitude) than PER1. In terms of the maximum residuals, it is even more accurate than PER2.
Table 16
Perturbation method versus hybrid method in the two-agent model.a
aNotes: 
and 
are, respectively, the average and maximum of absolute residuals across optimality conditions and test points (in log10 units). PER1 and PER2 are the first- and second-order perturbation solutions (in levels), and HYB are the hybrid solutions. These results are reproduced from Maliar et al. (2011), Table 5.
9.5 Numerical Instability of High-Order Perturbation Solutions in Simulation
An important shortcoming of plain perturbation methods is a numerical instability in simulation. The instability occurs because perturbation methods produce an approximation that is valid only locally, i.e., in the steady-state point and its small neighborhood. If we use this approximation for simulation, there is a chance that the simulated series become explosive when some realizations of shocks drive the process outside the accuracy range. The chance of nonstationary behavior is higher if the model has a high degree of nonlinearity.
Pruning methods try to address this shortcoming of the standard perturbation methods. The term pruning is introduced by Kim et al. (2008) who point out that a simulation of high-order perturbation solutions may produce explosive time series. To restore numerical stability, they propose to replace cross-products of variables in the second-order perturbation solution with cross-products of variables obtained from the first-order perturbation solution. Other papers that focus on stabilizing perturbation methods are Lombardo (2010) and Den Haan and De Wind (2012). In particular, the latter paper uses a fixed-point iteration technique that is similar in spirit to iteration-on-allocation described in Maliar et al. (2010, 2011) for constructing hybrid-like solutions.
10 Parallel Computation
Technological progress constantly increases the speed of computers. Moore (1965) made an observation that the number of transistors on integrated circuits doubles approximately every 2 years, and the speed of processors doubles approximately every 18 months (both because the number of transistors increases and because transistors become faster). The Moore law continues to hold meaning that in 10 years, computers will become about 100 times faster.
What happens if we cannot wait for 10 years or if a 100-time increase in speed is not sufficient for our purpose? There is another important source of growth of computational power that is available at present, namely, parallel computation: we connect a number of processors together and use them to perform a single job. Serial desktop computers have several central processing units (CPUs) and may have hundreds of graphics processing units (GPUs), and a considerable reduction in computational expense may be possible. Supercomputers have many more cores (hundreds of thousands) and have graphical cards with a huge number of GPUs. Each processor in a supercomputer is not (far) more powerful than a processor on our desktop but pooling their efforts gives them a high computational power. Running a job on 10,000 cores in parallel can increase the speed of our computation up to a factor of 10,000. This is what supercomputers are.
Early applications of parallel computation to economic problems are Amman (1986, 1990), Chong and Hendry (1986), Coleman (1992), Nagurney (1996), Nagurney and Zhang (1998). More recent applications include Doornik et al. (2006), Creel (2005, 2008), Creel and Goffe (2008), Sims et al. (2008), Aldrich et al. (2011), Morozov and Mathur (2012), Durham and Geweke (2012), Cai et al. (2012), Valero et al. (2013), and Maliar (2013), among others.
The possibility of parallel computation raises new issues. First, to take advantage of this technology, we must design algorithms in a manner which is suitable for parallelization. Second, we need hardware and software that support parallel computation. Finally, we must write a code that splits a large job into smaller tasks, that exchanges information between different cores in the process of computation, and that gathers the information to produce final output. We discuss these issues in the remainder of the section.
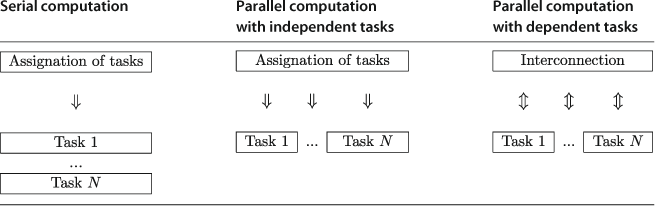
10.1 Serial Versus Parallel Computation
Assume that we must execute 
tasks. Traditional, one-core serial computation requires us to process the tasks one-by-one. The running time for executing 
tasks is 
times larger than that for executing one task. If we have multiple cores, we can parallelize the computation. The easiest case for parallelization is when tasks are independent and no information is shared (exchanged) during the process of computation. This case is known in computer science literature as naturally parallelizable jobs. A more general case requires us to exchange information between the cores (implementing different tasks) during the computational process; see Table 17.
A coordinating unit, called a core 0 or master, assigns tasks to multiple cores (workers) and performs the information exchange if needed. Assuming that the implementation of parallel computation has no additional cost, the parallelized algorithm is 
times faster than the serial one if tasks are independent. When the information exchange is needed, the gain from parallelization depends on a specific application and a specific way in which the code is implemented.
10.1.1 Applications with Independent Tasks
The restriction that tasks are independent is obviously limiting. Still, there are many interesting applications for which this restriction is satisfied. In econometrics, we may need to run many regressions of a dependent variable on different combinations of independent variables, and we may run each such a regression on a separate core; see Doornik et al. (2006) for a review of applications of parallel computation in econometrics. In a similar vein, we may need to solve an economic model under a large number of different parameterizations either because we want to study how the properties of the solution depend on a specific parameterization (sensitivity analysis) or because we want to produce multiple data sets for estimating the model’s parameters (e.g., nested fixed-point estimation; see Fernández-Villaverde and Rubio-Ramírez (2007), Winschel and Krätzig (2010), and Su and Judd (2012) for related examples). In this case, we solve a model under each given parameter vector on a separate core. Other examples of naturally parallelizable jobs are matrix multiplication, exhaustive search over a discrete set of elements, optimization of a function over a region of state space, etc.
10.1.2 Applications with Dependent Tasks
In general, a given problem will contain some tasks that can be parallelized, some tasks that cannot be parallelized, and some tasks that can be parallelized but will require information exchange during their implementation (dependence). This is in particular true for the solution methods described in Sections 4–9. Loops are an obvious candidate for parallelization. However, after each iteration on a loop, we must typically gather the output produced by all workers and to combine it in order to produce an input for the next iteration. Some of the surveyed computational techniques are designed to be parallelizable. In particular, Maliar et al. (2011) and Maliar and Maliar (2013) propose a separation of the model’s equations into the intratemporal and intertemporal choice equations under the Euler equation and dynamic programming methods. Such a separation provides a simple way to parallelize computation. Namely, we can first produce current and future endogenous state variables in all grid points and or integration nodes, and we can then solve for the intratemporal choice in each grid point and integration node using a separate core; see Sections 6 and 7 for a discussion.
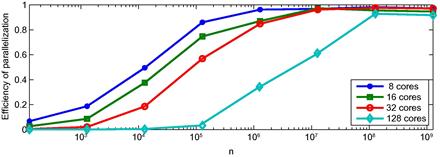
10.1.3 Speedup and Efficiency of Parallelization
Two measures that are used to characterize gains from parallelization are the speedup and efficiency of parallelization. The speedup is defined as a ratio
(131)
where 
and 
are the times for executing a job on one core and 
cores, respectively. In turn, the efficiency of parallelization is defined as
(132)
The efficiency shows gains from parallelization 
relative to the number of cores used 
. The upper bounds of (131) and (132) are 
and 
, and they are attained if a job is perfectly parallelizable and the cost of information transfers is zero.
The typical code has some parts that are parallelizable and other parts that must be executed serially. Nonparallelizable parts of the code restrict the speedup and efficiency of parallelization that can be attained in a given application. Moreover, the speedup and efficiency of parallelization depend on the cost of implementing the parallelization procedure and information transfers.
Consider the case when the parallelizable part of the code consists of a number of tasks that require the same execution time. The following condition can be used to characterize the speedup
(133)
where 
and 
denote the execution times for parallelizable and nonparallelizable parts of the code, respectively, 
, and 
denotes the time for information transfers. The measure (133) is a version of Amdahl’s (1967) law, which we augment to include the cost of information transfers 
; see Nagurney (1996) for a further discussion.
Two implications of the Amdahl’s (1967) law are the following. First, (133) implies that 
, i.e., the fraction of the code that is not parallelizable, 
, is a bottleneck for the speedup. For example, if 
of the code is not parallelizable, i.e., 
, we can reduce the running time of a code at most by a factor of 2, no matter how many cores we employ. Second, (133) shows that the speedup can be smaller than 1 (which is parallel slowdown) if the cost of information transfers 
is very large.
It is straightforward to describe the implications of Amdahl’s (1967) law for the efficiency measure (132). Namely, efficiency of parallelization decreases with the number of cores 
reaching zero in the limit 
, which is another way to say that the gains from parallelization are bounded from above by the execution time of tasks that cannot be parallelized. Furthermore, 
decreases with the costs of parallelization and transfer, and it can be arbitrary close to zero if such costs are very large.
Finally, different tasks executed in a parallel manner may differ in the amount of time necessary for their execution. For example, when searching for a maximum of a function over different regions of state space, a numerical solver may need considerably more time for finding a maximum in some regions than in others. The most expensive region will determine the speedup and efficiency of parallelization since all the workers will have to wait until the slowest worker catches up. The cost of information transfers may also differ across parallelizable tasks in some applications. These issues must be taken into account when designing codes for parallel computation.
10.2 Parallel Computation on a Desktop Using MATLAB
Most economic researchers write codes for solving dynamic economic models using a desktop and serial MATLAB software. The advantages of this choice are three: first, the user can concentrate exclusively on computations without being concerned with all subtle issues related to the operational system and computer architecture. Second, communication among multiple cores of a desktop is very fast, and can be much faster than that among cores in a cluster or supercomputer. Finally, MATLAB itself is a convenient choice. It is widespread, well-supported, and has an extensive documentation; it is easy to learn and to use; and it has many preprogrammed routines that can be easily integrated into other codes.
In particular, MATLAB provides a simple way to parallelize computations on either CPUs or GPUs; no additional software is needed. Valero et al. (2013) survey parallel computation tools available in MATLAB; below, we reproduce some discussion from this paper.
First, MATLAB has a “Parallel Computing Toolbox” which allows us to allocate the computational effort in different CPUs on multicore computers; see MATLAB (2011). Parallelizing in MATLAB is simple, we just need to replace “for” with its parallel computing version “parfor.” To use it, we must tell to the computer what part of the code we want to parallelize and when we want to finish parallel computation and to gather the output; this is done using “matlabpool open/matlabpool close.” Some restrictions must be imposed on variables that are used in parallel computing.
Second, MATLAB has tools for working with GPUs. Functions “gpuArray” and “gather” transmit data from CPUs to GPUs and vice versa, respectively. It is also possible to generate the data directly in GPUs which can help to save on transfer time, for example, “parallel.gpu.GPUArray.zeros 
” creates an array of zeros of dimension 
in GPUs. Once you allocate an array in a GPU, MATLAB has many functions which allow you to work directly there. A useful function in MATLAB is “arrayfun” which, instead of multiple calls to perform separate GPU operations, makes one call to a vectorized GPU operation (it is analogous to MATLAB’s vectorized operations). MATLAB has functions that allow us to use native languages for GPU programming; for example, it allows us to use CUDA with the NVIDIA graphical card.19
Finally, MATLAB has other tools that are useful for parallel computation. “Jacket” and “GPUMat” toolboxes are useful alternatives to the standard “Parallel Computation Toolbox.” Another useful tool is “deploytool” which allows us to convert MATLAB codes into executable files. Also, MATLAB codes can be translated to other languages such as C/C++ or Fortran source code using the “mex” tool. Depending on a specific version of MATLAB, different software may be needed to create the mex files; we use a Microsoft Windows SDK 7.1 with NET Framework 4.0. Function “coder.extrinsic” makes it possible to export to other languages some functions that are specific to MATLAB, e.g., “tic” and “toc.” The above tools allow us to run MATLAB codes on machines that do not have MATLAB installed.
The drawbacks of MATLAB are typical for high-level programming languages: it is relatively slow and does not take into account the hardware characteristics to optimize computations. Also, MATLAB is not free software and can be executed only on those machines that have licenses.
Many other programming languages can be used on a desktop instead of MATLAB. Octave is almost identical to MATLAB and is freeware. Another freeware is Python, a high-level language that is growing in popularity. Significant speedups of calculations can be obtained using low-level languages such as C or Fortran. However, these languages may be more complicated to learn and to use. There are also languages that are specially designed to work with GPUs. A pioneering paper by Aldrich et al. (2010) shows how to apply GPUs using CUDA for solving economic problems; see also Morozov and Mathur (2012). CUDA can only be used with NVIDIA GPUs. However, there is software that can manage other kinds of GPUs, for example, OPEN CL (see http://www.khronos.org), VIENNA CL (http://viennacl.sourceforge.net); see Gallant’s (2012) conference slides for a concise and informative discussion and further references.
10.2.1 Numerical Example of GPU Computation Using MATLAB
The following example is borrowed from Valero et al. (2013). Consider a function with a unique input 
, which is randomly drawn from a uniform distribution 
(134)
We approximate the expectation of 
using a Monte Carlo integration method 
.
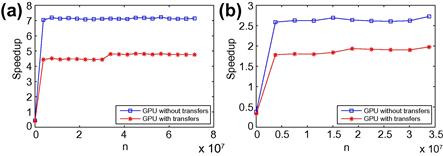
The calculations are implemented in GPUs using MATLAB. We report separately the cases with a single and double precision because the precision significantly affects the speed of GPU computations. To illustrate the cost of transfers between CPUs and GPUs, we report two speedups (a ratio of CPU to GPU running times, see definition (131)): the speedup without information transfers between CPUs and GPUs and that with such transfers.20 We first report the results obtained with “gpuArray” and “gather” functions in Figure 9a and b for the single and double precision cases, respectively.
If the transfer time is included, we observe speedups of order 4.5 and 1.7 under the single and double precision, respectively, when 
is sufficiently large (for small 
, the speedup is negative as the gain from GPUs does not compensate for the high cost of transferring information between CPUs and GPUs).
We next repeat the computations using a vectorized version of the code built on “arrayfun”; see Figure 10a and 10b for single and double precision, respectively.
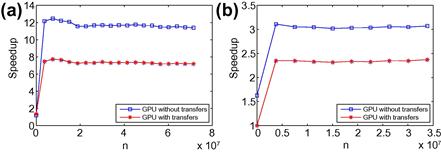
Figure 10 (a) Speedup with GPUs (vectorized): single precision. (b) Speedup with GPUs (vectorized): double precision.
This improves the performance of GPUs considerably. Now, the speedups are of order 7 and 2.4 under the single and double precision, respectively. “Arrayfun” also allows for better allocations of memory. Our hardware for GPU computations is: Intel(®) Core(TM) i7-2600 CPU @ 3.400 GHz with RAM 12.0 GB and GPU GeFoce GT 545, and we use MATLAB 2012a.
10.3 Parallel Computation on Supercomputers
Clusters of computers and supercomputers can solve certain problems of very large size. Clusters are networks that have 16–1,000 cores, and supercomputers may have hundreds of thousands of cores, as well as graphical cards with a huge number of GPUs. However, two issues must be mentioned. First, the information exchange between CPUs or GPUs is generally slower than that between cores on a desktop, which may reduce the gains from parallelization in some applications. Second, using supercomputers requires certain knowledge of the computer architecture and the operational system (typically, Unix), as well as software that distributes and exchanges information among different cores, and the programming can be a nontrivial task.
Three different types of supercomputers are distinguished in the computer science literature; see Blood (2011).
1. High-performance computing (HPC) runs one large application across multiple cores. The user is assigned a fixed number of processors for a fixed amount of time, and this time is over if not used.
2. High-throughput computing (HTC) runs many small applications at once. The user gets a certain number of cores that are available at that time, and this computer time would be wasted otherwise.
3. Data-intensive computing focuses on input-output operations, where data manipulation dominates computation.
We are primarily interested in the first two types of supercomputing, HPC and HTC. An important issue for parallel computation is how to share the memory. Two main alternatives are shared memory and distributed memory.
• Shared memory programming. There is a global memory which is accessible by all processors, although processors may also have their local memory. For example, OpenMP software splits loops between multiple threads and shares information through common variables in memory; see http://www.openmp.org.
• Distributed memory programming. Processors possess their own memory and must send messages to each other in order to retrieve information from memories of other processors. MPI is a commonly used software for passing messages between the processors; see http://www.mpi-forum.org.
The advantage of shared memory is that it is easier to work with and it can be used to parallelize already existing serial codes. The drawbacks are that the possibilities of parallelization are limited and that sharing memory between threads can be perilous. The advantage of distributed memory is that it can work with a very large number of cores and is ubiquitous but it is also more difficult to program. There are also hybrids that use distributed memory programming for a coarse parallelization and that use shared memory programming for a fine parallelization.
High computational power becomes increasingly accessible to economists. In particular, the eXtreme Science and Engineering Discovery Environment (XSEDE) portal financed by the NSF provides access to supercomputers for US academic/nonprofit institutions. Currently, XSEDE is composed of 17 service providers around the world; see https://portal.xsede.org. We discuss two examples of supercomputers within the XSEDE portal, namely, Blacklight and Condor; see http://www.psc.edu/index.php/computing-resources/blacklight and https://www.xsede.org/purdue-condor, respectively.
Blacklight is an example of an HPC machine. It consists of 256 nodes each of which holds 16 cores, 4096 cores in total. Each core has a clock rate of 2.27 GHz and 8 Gbytes of memory. The total floating point capability of the machine is 37 Tflops, and the total memory capacity of the machine is 32 Tbytes. Blacklight has many software packages installed including C, C++, Fortran, R, Python, MATLAB, etc., as well as facilities for running MPI and OpenMP programs. See Maliar (2013) for an assessment of the efficiency of parallelization using MPI and OpenMP on a Blacklight supercomputer.
Condor is an example of an HTC machine. It is composed of a large net of computers. Computers in the net belong to priority users and are not always free (our own computers can become a part of the Condor network if we give them a permission). Condor software detects computers that are not currently occupied by priority users and assigns tasks to them. It passes messages between masters and workers, queues the tasks, detects failures and interruptions, collects the output, and delivers it to users. The Condor network is slower than that of HPC machines but the speed of communication is not essential for many applications, in particular, for those that are naturally parallelizable. Cai et al. (2013a,b) show how to use the Condor network to solve dynamic programming problems.
Computer time can be also bought in the Internet at relatively low prices. For example, Amazon Elastic Compute Cloud provides the possibility to pay for computing capacity by the hour; see http://aws.amazon.com/ec2/#pricing.
MATLAB is of a limited use on supercomputers. For example, at the moment, Blacklight has MATLAB licenses just on 32 cores, meaning that only a tiny fraction of its total capacity is available to MATLAB users. Such users have two alternatives. The first one is to convert MATLAB files into executable files as was discussed earlier (this can work well if we have independent tasks). The other alternative is to use Octave, which is a freeware clone of MATLAB. The problem is that there are still some differences between MATLAB and Octave, and it could happen that the MATLAB code does not work under Octave as expected. For working with a supercomputer, a better alternative is to use languages that are freeware and have no restrictions on the number of licenses (C, R, Python, etc.). These languages have developed parallel programming tools that can be used with MPI or OpenMP.
10.3.1 Numerical Example of Parallel Computation Using a Blacklight Supercomputer
For desktops, the information exchange between CPUs is very fast. For supercomputers, the information exchange is far slower and may reduce dramatically gains from parallelization even in applications that are naturally suitable for parallelization. It is therefore of interest to determine how large a task per core should be to obtain sufficiently high gains from parallelization on supercomputers.
In the following example, we assess the efficiency of parallelization using MPI on a Blacklight supercomputer; this example is borrowed from Maliar (2013). Let us again consider the problem of approximating the expectation of 
, defined in (134) using Monte Carlo integration. The calculations are implemented on Blacklight using C and MPI (with point-to-point communication). In the code, each core (process) runs a copy of the executable (single program, multiple data), takes the portion of the work according to its rank, and works independently of the other cores, except when communicating. For each simulation length 
(the size of the problem), we run four experiments in which we vary the number of cores, 1, 16, 32, and 128. In each experiment, we solve the problem of the same size 
. That is, depending on the number of cores assumed, each core performs tasks of the corresponding size. For example, if the number of cores is 16, each core processes 
observations (we use 
which are multiples of 128). The results are provided in Figure 11.
In the figure, we compute the efficiency of parallelization as defined in (132). For small 
, the efficiency of parallelization is low because the cost of information transfer overweighs the gains from parallelization. However, as 
increases, the efficiency of parallelization steadily increases, approaching unity. We also observe that the efficiency of parallelization depends on the number of cores used: with 16 cores, the efficiency of parallelization of 90% is reached for 20 s problem (2.5 s per core), while with 128 cores, a comparable efficiency of parallelization is reached only for 2,000 s problem (15.6 s per core). Our sensitivity experiments (not reported) had shown that for larger numbers of cores, the size of the task per core must be a minute or even more to achieve high efficiency of parallelization.
11 Numerical Analysis of a High-Dimensional Model
In the previous sections, we have surveyed a collection of efficient computational techniques in the context of simple examples. Now, we show how these techniques can be combined into numerical methods that are suitable for solving large-scale economic models.
11.1 The Model
As an example of a high-dimensional problem, we consider a stylized stochastic growth model with 
heterogeneous agents (interpreted as countries). Each country is characterized by a capital stock and a productivity level, so that there are 
state variables. By varying 
, we can control the dimensionality of the problem. In addition to a potentially large number of state variables, the model features elastic labor supply, heterogeneity in fundamentals, and adjustment cost for capital.
Time is discrete, and the horizon is infinite, 
. The world economy consists of a finite number of countries, 
, and each country is populated by one (representative) consumer. A social planner maximizes a weighted sum of expected lifetime utilities of the consumers
(135)
subject to the aggregate resource constraint, i.e.,
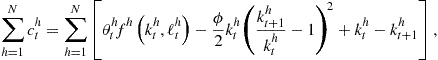(136)
where 
is the operator of conditional expectation conditional on 
and 
, and 
are consumption, labor, end-of-period capital, productivity level, utility function, production function, and welfare weight of a country 
, respectively; 
is the discount factor; 
is the adjustment-cost parameter; and 
is the depreciation rate. Initial condition, 
and 
, is given. We assume that 
and that 
and 
are strictly increasing and strictly concave and satisfy the Inada types of conditions for all 
. To simplify the presentation, we consider the production function net of depreciation 
, where 
is a gross production function and 
is the depreciation rate, 
.
Future productivity levels of countries are unknown and depend on randomly drawn productivity shocks,
(137)
where 
is the autocorrelation coefficient of the productivity level; 
determines the standard deviation of the productivity level; and 
is a vector of productivity shocks with 
being a vector of zero means and 
being a variance-covariance matrix. Thus, we allow for the case when productivity shocks of different countries are correlated. A planner’s solution is given by decision functions 
, and 
, where 
and 
.
11.2 Methods Participating in the JEDC Project
Model (135)–(137) has been studied in the February 2011 special issue of the Journal of Economic Dynamics and Control. Detailed descriptions of the numerical methods that participate in the JEDC comparison analysis can be found in the individual papers of the participants of the JEDC project. In this section, we provide a brief description of these algorithms and summarize their main implementation details in Table 18.
Table 18
Implementation of the algorithms participating in the JEDC project.a
aNotes: 
is the decision function for investment of country 
is the decision function for aggregate consumption; 
is the model’s dimensionality. A part of this table is reproduced from Kollmann et al. (2011b), Table 2.
Perturbation Methods, PER
The first- and second-order perturbation methods (PER1) and (PER2) of Kollmann et al. (2011a) compute perturbation solutions in logarithms of the state variables. These two methods approximate the decision functions of all individual variables (consumption, labor, capital, investment) and the Lagrange multiplier associated with the aggregate resource constraint using Taylor expansions of the equilibrium conditions.
Stochastic Simulation Algorithm, SSA
The stochastic simulation algorithm (SSA) of Maliar et al. (2010) is a variant of GSSA that computes linear polynomial approximations using a one-node Monte Carlo integration method. It parameterizes the capital decision functions of all countries, solves for polynomial coefficients of approximating functions using FPI, and solves for consumption and labor nonparameterically, using iteration-on-allocation.
Cluster Grid Algorithm, CGA
The cluster grid algorithm (CGA) of Maliar et al. (2011) constructs a grid for finding a solution using methods from cluster analysis; see our discussion in Section 4.3.3. CGA computes quadratic polynomial approximations. It parameterizes the capital decision functions of all countries and it finds the coefficients using FPI. For integration, it uses a monomial rule. CGA computes consumption and labor nonparameterically, using iteration-on-allocation.
Monomial Rule Galerkin Method, MRGAL
The monomial rule Galerkin algorithm (MRGAL) of Pichler (2011) uses a set of points produced by monomial rules both as a grid for finding a solution and as a set of nodes for integration. MRGAL uses second-degree Chebyshev polynomials of state variable to approximate the decision functions for capital of all countries and the aggregate consumption function. It solves for the polynomial coefficients using a Newton-type solver that minimizes a weighted sum of residuals in the equilibrium conditions.
Smolyak Method, SMOL-MKK
The Smolyak-collocation method (SMOL-MKK) of Malin et al. (2011) solves the model on a Smolyak grid with an approximation level 
. SMOL-MKK approximates the capital decision functions of all countries and the consumption decision function of the first country using a second-degree Smolyak polynomial function of state variables. It uses monomial rules to approximate integrals, and it uses time iteration to compute fixed-point polynomial coefficients.
11.3 Global Euler Equation Methods
We implement several other methods for solving model (135)–(137), in addition to the six solution methods studied in the JEDC comparison analysis. Below, we elaborate a description of the three global Euler equation methods, SMOL-JMMV, GSSA, and EDS, outlined in Sections 4.1, 4.2, and 4.3, respectively. We compute both second- and third-degree polynomial approximations whereas the solution methods of the JEDC project are limited to second-degree polynomial approximations. We summarize the implementation of these methods in Table 19
Table 19
Implementation of our Euler equation algorithms.a
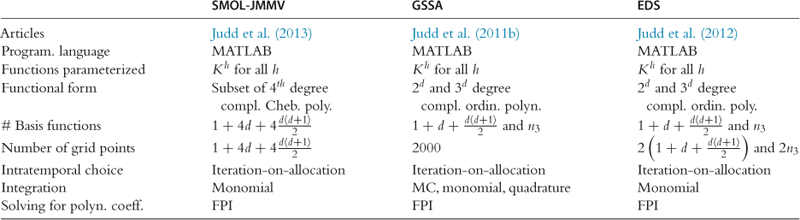
aNotes: “MC” means Monte Carlo integration; 
is the model’s dimensionality, 
; FPI means fixed-point iteration; 
is the number of basis functions in complete ordinary polynomial of degree 3.
11.3.1 First-Order Conditions
We assume that the planner’s solution to model (135)–(137) is interior and, hence, satisfies the FOCs given by
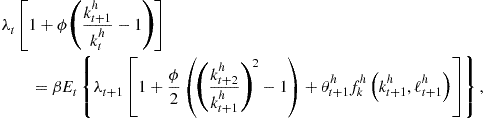(138)
(139)
(140)
where 
is the Lagrange multiplier associated with aggregate resource constraint (136). Here, and further on, notation of type 
stands for the first-order partial derivative of a function 
with respect to a variable 
.
11.3.2 Separating the Intertemporal and Intratemporal Choices
The global Euler equation methods aim at solving (136)–(140). We separate the equilibrium conditions into the intertemporal and intratemporal choice conditions as described in Section 6.
Regarding the intertemporal choice, we combine (138) and (139) to eliminate 
, premultiply both sides with 
, and rearrange the terms to obtain
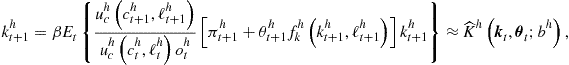(141)
where new variables 
and 
are introduced for compactness,
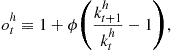(142)
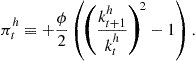(143)
We parameterize the right side of (141) with a flexible functional form. Our goal is to find parameters vectors 
such that 
solves (141) for 
. This representation of the intratemporal choice follows Example 11 in Section 6 and allows us to implement FPI without the need of a numerical solver. All three global Euler equation methods described in this section use parameterization (141) for characterizing the intertemporal choice.
Concerning the intratemporal choice, we do not use state contingent functions but solve for quantities 
that satisfy (136), (139), and (140). In principle, this can be done with any numerical method that is suitable for solving systems of nonlinear equations, for example, with a Newton’s method. However, we advocate the use of derivative-free solvers; see Section 6 for a discussion. In Section 11.6, we show how to implement one such method, iteration-on-allocation, for the studied multicountry model.
11.3.3 Smolyak Method with Iteration-on-Allocation and FPI
We consider a version of the Smolyak algorithm, SMOL-JMMV, that builds on Judd et al. (2013). Also, Valero et al. (2013) test this algorithm in the context of a similar multicountry model. This method differs from the SMOL-MKK of Malin et al. (2011) in three respects. SMOL-JMMV solves for the intratemporal choice in terms of quantities (instead of state-contingent functions); this increases the accuracy of solutions. SMOL-JMMV solves for equilibrium decision rules using FPI (instead of time iteration); this decreases computational expense. Finally, SMOL-JMMV constructs the interpolation formula in a way that avoids costly repetitions of grid points and polynomial terms and computes the polynomial coefficients from a linear system of equations (instead of the conventional interpolation formula with repetitions); see Section 4 for a discussion.
Steps of SMOL-JMMV
(a) Choose approximation level 
.
(b) Parameterize 
with Smolyak polynomials 
constructed using Chebyshev unidimensional basis functions.
(c) Construct a Smolyak grid 
on the hypercube 
using the Smolyak interpolation method described in Section 4.1, where 
and 
.
(d) Compute the Smolyak basis functions 
in each grid point 
. The resulting 
matrix is 
.
(e) Choose the relevant ranges of values for 
on which a solution is computed. The resulting hypercube is 
.
(f) Construct a mapping between points 
in the original hypercube 
and points 
in the normalized hypercube 
using a linear change of variables:
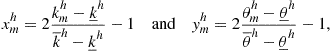(144)
and 
.(g) Choose integration nodes, 
, and weights, 
, 
.
(h) Construct next-period productivity, 
with 
for all 
and 
.
(i) Make an initial guess on the coefficient vectors 
.
• Iterative cycle. At iteration 
, given 
, perform the following steps.
• Step 1. Computation of the capital choice.
Compute 
, where 
is the 
th row of 
for 
.
• Step 2. Computation of the intratemporal choice.
Compute 
satisfying (136), (139), and (140) given 
for 
.
• Step 3. Approximation of conditional expectation.
For 
,
– 
that correspond to 
using the inverse of the transformation (144);
– the Smolyak basis functions 
in each point 
; the resulting 
matrix is 
;
– 
, where 
is a vector of basis functions evaluated in 
using the transformation (144) for all 
;
– 
satisfying (136), (139), and (140) given 
for 
;
(b) evaluate conditional expectation:
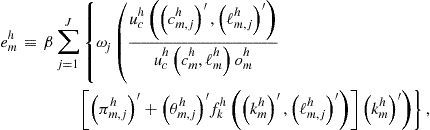
where 
and 
are given by (142) and (143), respectively.
• Step 4. Computation of the intertemporal choice.
Find 
that solves 
, i.e., 
.
• Step 5. Updating of the coefficient vectors.
For each 
, compute the coefficient vector for the subsequent iteration 
using fixed-point iteration,
(145)
where 
is a damping parameter.
Iterate on Steps 1–5 until convergence of the solution,
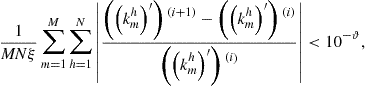(146)
where 
and 
are the 
th country’s capital choices on the grid obtained on iterations 
and 
, respectively, and 
.
Computational Details
To start iterations, we use an arbitrary initial guess on the capital decision function, 
, for all 
(this guess matches the steady-state level of capital). We use a Smolyak polynomial function with an approximation level 
(such a function has four times more coefficients than the ordinary polynomial function of degree two). We transform 
into 
using a linear change of variable (144) because unidimensional Chebyshev basis functions are defined in the interval 
and, thus, the Smolyak grid 
is constructed inside a hypercube 
, whereas the original capital and productivity levels are not necessarily in this range. To approximate integrals, we use a monomial integration rule 
with 
nodes. We set the damping parameter in FPI (145) at 
, and we set the tolerance parameter at 
in convergence criterion (147).
11.3.4 Generalized Stochastic Simulation Algorithm
In the JEDC comparison analysis, Maliar et al. (2011) implement a version of the GSSA algorithm that computes linear solutions using a one-node Monte Carlo integration method (we refer to this method as SSA). In this section, we implement other versions of GSSA, those that use Monte Carlo, Gauss-Hermite quadrature and monomial rules. Also, we compute polynomial approximations up to degree 3. In particular, these choices allow us to assess the role of approximation and integration methods in the accuracy and speed of GSSA.
Steps of GSSA
(a) Parameterize 
with a flexible functional form 
.
(b) Fix simulations length 
and initial condition 
. Draw a sequence of productivity shocks 
. Compute and fix the sequence of productivity levels 
using equation (137).
(c) Choose integration nodes, 
, and weights, 
, 
.
with 
for all 
.
.Iterative cycle. At iteration 
, given 
, perform the following steps.
• Step 1. Simulation of the solution.
Use the assumed capital decision functions 
, to recursively calculate a sequence of capital stocks 
corresponding to a given sequence of productivity levels 
.
• Step 2. Computation of the intratemporal choice.
Compute 
satisfying (136), (139), and (140) given 
for 
.
• Step 3. Approximation of conditional expectation.
For 
,
for all 
;– 
satisfying (136), (139), and (140) for given 
;
(b) evaluate conditional expectation:
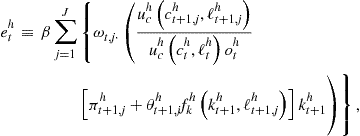
where 
and 
are given by (142) and (143).
• Step 4. Computation of the intertemporal choice.
Find 
such that
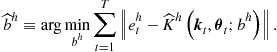
• Updating of the coefficients vectors. For each 
, compute the coefficient vector for the subsequent iteration 
using FPI (145).
Iterate on Steps 1–5 until convergence,
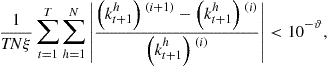(147)
where 
and 
are the 
th country’s capital stocks obtained on iterations 
and 
, respectively, and 
.
Computational Details
To start the iterative process, we use the same (arbitrary) initial guess as in the Smolyak method: 
for all 
. The simulation length for finding solutions is 
. Initial capital and productivity level are set at their steady-state values: 
and 
for all 
. We compute complete ordinary polynomial approximations of degrees 2/3. In Step 4, we approximate integrals using three different methods: a one-node Monte Carlo integration method, a one-node Gauss-Hermite quadrature rule (i.e., we assume that the future has just one possible state 
for all 
), and a monomial rule 
with 
nodes. In Step 5, we use a least-squares truncated QR factorization method, which is robust to ill-conditioning. We set the damping parameter in FPI (145) at 
and we set the tolerance parameter at 
in convergence criterion (147).
11.3.5 
-Distingishable Set Algorithm
We consider a version of the EDS algorithm studied in Judd et al. (2012). The number of grid points in the EDS grid is smaller than the number of simulated points considered by GSSA; namely, we set the number of grid points, which is two times larger than the number of polynomial coefficients to estimate. This allows us to substantially reduce the cost relative to GSSA.
Steps of EDS
(a) Parameterize 
with a flexible functional form 
.
(b) Fix simulations length 
and initial condition 
. Draw 
. Compute and fix 
using equation (137).
(c) Choose integration nodes, 
, and weights, 
, 
.
(d) Make an initial guess on the coefficient vectors 
.
• Step 1. Construction of a grid and the corresponding next-period productivity.
(a) Use the assumed capital decision functions 
, to recursively calculate a sequence of capital stocks 
corresponding to a given sequence of productivity levels 
.
(b) Construct a grid 
using the EDS algorithm described in Section 4.3.
with 
for all 
and 
.Iterative cycle. At iteration 
, given 
, perform the following steps.