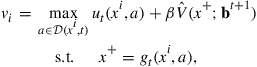Advances in Numerical Dynamic Programming and New Applications
Yongyang Cai and Kenneth L. Judd, Hoover Institution & NBER, USA, [email protected], [email protected]
Abstract
Dynamic programming is the essential tool in dynamic economic analysis. Problems such as portfolio allocation for individuals and optimal economic growth are typical examples. Numerical methods typically approximate the value function. Recent work has focused on making numerical methods more stable, and more efficient in its use of information. This chapter presents two examples where numerical dynamic programming is applied to high-dimensional problems from finance and the integration of climate and economic systems.
Keywords
Numerical dynamic programming; Value function iteration; Shape preservation; Hermite interpolation; Parallel computing; Optimal growth; Dynamic portfolio optimization; Climate change; Stochastic IAM
JEL Classification Codes
C61; C63; G11; Q54; D81
1 Introduction
All dynamic economic problems are multistage decision problems, and their nonlinearities make them numerically challenging. Dynamic programming is the standard approach for any time-separable problem. If state variables and control variables are continuous, and the problem is a concave maximization problem, then its value function is continuous, concave, and often differentiable. Any numerical procedure needs to approximate the value function, but any such approximation will be imperfect since computers cannot model the entire space of continuous functions. Many dynamic programming problems are solved by value function iteration, where the period ![]() value function is computed from the period
value function is computed from the period ![]() value function, and the value function at the terminal time
value function, and the value function at the terminal time ![]() is known.
is known.
Dynamic programming problems can generally be formulated by the following Bellman equation (Bellman, 1957):
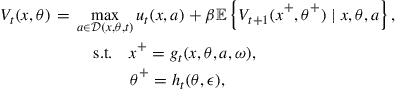 (1)
(1)
where ![]() is the vector of continuous state variables in
is the vector of continuous state variables in ![]() , and
, and ![]() is an element of the set of discrete state vectors,
is an element of the set of discrete state vectors, ![]() (where
(where ![]() is the number of different discrete state vectors in
is the number of different discrete state vectors in ![]() ).
). ![]() is the value function at time
is the value function at time ![]() , and the terminal value function,
, and the terminal value function, ![]() , is given. The decision maker chooses a vector of action variables,
, is given. The decision maker chooses a vector of action variables, ![]() , where the choice is constrained by
, where the choice is constrained by ![]() . We let
. We let ![]() denote the value of the continuous state variables in the next period, and assume that the law of motion is a time-specific function
denote the value of the continuous state variables in the next period, and assume that the law of motion is a time-specific function ![]() at time
at time ![]() . Similarly,
. Similarly, ![]() is the next-stage discrete state vector in
is the next-stage discrete state vector in ![]() with a transition function
with a transition function ![]() at time
at time ![]() . The state transitions may be affected by random shocks,
. The state transitions may be affected by random shocks, ![]() and
and ![]() . At time
. At time ![]() , the payoff flow is
, the payoff flow is ![]() , and the overall objective is to maximize the expected discounted sum of utility, using
, and the overall objective is to maximize the expected discounted sum of utility, using ![]() as the discount factor. We let
as the discount factor. We let ![]() denote the expectation operator.
denote the expectation operator.
To explain computational ideas that arise often in applications of dynamic programming in economics, we will often use the simple case with no discrete states and no random shocks, assumptions that simplify the Bellman equation (1) to
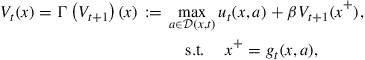 (2)
(2)
where ![]() is the Bellman operator that maps the period
is the Bellman operator that maps the period ![]() value function
value function ![]() to the period
to the period ![]() value function
value function ![]() . The Bellman operator is possibly different at each time
. The Bellman operator is possibly different at each time ![]() , and should be denoted
, and should be denoted ![]() .
.
This chapter focuses on the computational challenges of solving dynamic programming problems. We first address the concerns over the “curse of dimensionality” often raised in theoretical discussions of the computational complexity of solving dynamic programming problems. If the curse of dimensionality were present in nearly all dynamic programming problems then there would be little point in even attempting to solve multidimensional problems. We review the results in the complexity literature but point out the features of a dynamic programming problem that may keep it from being a victim of the curse of dimensionality. Sections 3 and 4 review the range of methods from numerical analysis that we can use to construct efficient algorithms. Section 5 discusses the importance of shape-preservation for constructing stable numerical implementations of value function iteration. Section 6 discusses the use of massive parallelism to solve large dynamic programming problems.
The combination of shape-preserving approximation methods and massive parallelism allows us to solve problems previously considered too challenging for dynamic programming. These ideas are being incorporated in work that extends the range of problems analyzed by stochastic dynamic programming models. Section 7 discusses recent work on portfolio decision making when there are transaction costs. The multidimensional finite-horizon analysis of Section 7 shows us that we can now analyze life-cycle problems far more realistically than is currently the practice in quantitative economic analysis. Section 8 presents a stochastic dynamic general equilibrium extension of DICE, a basic model of interactions between climate and the economy. Previous analyses have been limited by computational tools to examine only deterministic models of global climate change. Section 8 shows that we can now analyze models that come far closer to analyzing risks and uncertainty that are inherent in any discussion of climate change policy.
2 Theoretical Challenges
There are two challenges in solving difficult dynamic programming problems. First, numerical methods do not necessarily inherit the contraction properties of the Bellman operator. This creates stability problems that become increasingly challenging as one increases dimension. Second, dynamic programming is often said to suffer from the “curse of dimensionality”; that is, the cost of solving a dynamic programming problem may grow exponentially as the dimension increases. In this section we describe recent theoretical work on these issues.
Rust (1997) and Rust et al. (2002) are two recent papers that prove that the curse of dimensionality is a problem for large classes of dynamic programming problems. However, before one becomes too pessimistic about solving high-dimensional dynamic programming problems, he should remember how the curse of dimensionality is defined. First, it is always a statement about a set of dynamic programming problems, and, second, it says that there is a sequence of problems in that set where the cost explodes exponentially as the dimension rises. The underlying approach is the worst-case analysis. More precisely, it means that for any algorithm, there is a sequence of dynamic programming problems of increasing dimension such that the cost rises exponentially in the dimension. Even if there is only one such example, we still say that there is a curse of dimensionality.
This need not be a major concern. A proof of exponential complexity says nothing about the average cost of using an algorithm to solve a problem. One way to proceed is to find algorithms that grow polynomially on average as dimension increases. This would be a difficult direction, requiring the development of deep mathematical analysis. The other, and more practical, way to proceed is to find formulations of economics problems that avoid the curse of dimensionality. Complexity theory provides guidance on that issue. While the literature is large, a very general treatment is in Griebel and Wozniakowski (2006) which shows that, as long as an unknown function has sufficient smoothness, then there is no curse of dimensionality in computing its derivatives or in approximating it from a finite sample of its values. Therefore, problems with smooth payoffs, smooth transitions, and smooth value functions can avoid the curse of dimensionality. Many problems in economics have no difficulty in satisfying these requirements.
A second problem that arises in numerical solutions is that numerical value function iteration may not be stable. To understand this issue, we need to recall the key property of the Bellman operator. Assume that the Bellman operator ![]() maps a bounded value function
maps a bounded value function ![]() to a bounded function, where the state space of
to a bounded function, where the state space of ![]() is compact. The critical feature of value function iteration is that
is compact. The critical feature of value function iteration is that ![]() is a contraction in
is a contraction in ![]() , i.e.,
, i.e., ![]() , for any continuous and bounded functions
, for any continuous and bounded functions ![]() and
and ![]() on the compact state space, if
on the compact state space, if ![]() . Numerical methods cannot represent
. Numerical methods cannot represent ![]() perfectly. Let
perfectly. Let ![]() denote the method used to approximate
denote the method used to approximate ![]() , implying that the approximation of
, implying that the approximation of ![]() is denoted by
is denoted by ![]() . Various errors in approximation and computing expectations can prevent
. Various errors in approximation and computing expectations can prevent ![]() from being a contraction even though
from being a contraction even though ![]() is. This can lead to nonconvergence or even divergence for numerical value function iteration based on
is. This can lead to nonconvergence or even divergence for numerical value function iteration based on ![]() . Stachurski (2008) discusses approximation structures in dynamic programming problems and their impact on the stability of value function iteration. Stachurski shows that if
. Stachurski (2008) discusses approximation structures in dynamic programming problems and their impact on the stability of value function iteration. Stachurski shows that if ![]() is nonexpansive, i.e.,
is nonexpansive, i.e., ![]() , then the operator
, then the operator ![]() is also a contraction mapping. He exploits the contractiveness of
is also a contraction mapping. He exploits the contractiveness of ![]() to obtain error bounds for the approximate value functions for general nonexpansive approximation methods.
to obtain error bounds for the approximate value functions for general nonexpansive approximation methods.
Even though Stachurski discusses stationary infinite-horizon problems, these considerations are equally important in finite-horizon dynamic programming, which is the focus of this chapter. Even if the Bellman operator ![]() is different at each time
is different at each time ![]() , it is still a contraction operator on its domain. We still want each approximate Bellman operator
, it is still a contraction operator on its domain. We still want each approximate Bellman operator ![]() to have that same property. If, instead, the approximation method implies a possibly expansive operator
to have that same property. If, instead, the approximation method implies a possibly expansive operator ![]() , then successive applications of the
, then successive applications of the ![]() operators may generate spurious numerical errors and prevent accurate approximations of the value and policy functions. Therefore, the expansiveness considerations in Stachurski (2008) apply to stability issues in finite-horizon dynamic programming.
operators may generate spurious numerical errors and prevent accurate approximations of the value and policy functions. Therefore, the expansiveness considerations in Stachurski (2008) apply to stability issues in finite-horizon dynamic programming.
Nonexpansiveness is related to the concept of shape-preserving approximation. Judd and Solnick (1994) highlighted the computational advantages of such approximations, where the “shapes” of greatest interest are monotonicity and convexity (or concavity). Piecewise linear interpolation is an example of an approximation method which is both nonexpansive and shape-preserving in one dimension. Stachurski (2008) points out that some shape-preserving quasi-interpolants are also nonexpansive.
3 Numerical Methods for Dynamic Programming
If state and control variables in a dynamic programming problem are continuous, then the value function is a function in ![]() , and must be approximated in some computationally tractable manner. It is common to approximate value functions with a finitely parameterized collection of functions; that is, we choose some functional form
, and must be approximated in some computationally tractable manner. It is common to approximate value functions with a finitely parameterized collection of functions; that is, we choose some functional form ![]() , where
, where ![]() is a vector of parameters, and approximate a value function,
is a vector of parameters, and approximate a value function, ![]() , with
, with ![]() for some parameter value
for some parameter value ![]() . For example,
. For example, ![]() could be a linear combination of polynomials where
could be a linear combination of polynomials where ![]() would be the weights on polynomials. After the functional form is fixed, a numerical method focuses on finding the vector of parameters,
would be the weights on polynomials. After the functional form is fixed, a numerical method focuses on finding the vector of parameters, ![]() , such that
, such that ![]() approximately satisfies the Bellman equation for all times
approximately satisfies the Bellman equation for all times ![]() .
.
3.1 Outline of the Basic Value Function Iteration Algorithm
Algorithm 1 presents the traditional value function iteration for solving the simple Bellman equation (2). In Algorithm 1, a numerical solution needs only to approximate the value function and solve the optimization problem at a finite number of values for the state variable.
The more general case of stochastic dynamic programming and discrete state variables is presented in Algorithm 2. The presence of stochastic disturbances implies the need to compute the expected value function at the next period, which presents a new computational challenge. The presence of discrete states does not create new computational challenges because the representation of the value function is to create an approximation over the continuous states ![]() for each distinct discrete state. In particular, discrete states do not increase the number of dimensions of the continuous portions of the value function.
for each distinct discrete state. In particular, discrete states do not increase the number of dimensions of the continuous portions of the value function.
Algorithm 2 includes three types of numerical problems. First, we need to solve a maximization problem at each node ![]() and
and ![]() . Second, the evaluation of the objective requires us to compute an expectation. Third, we need to efficiently take the data and compute the best fit for the new value function. The challenge is not only to use good numerical methods for each of these steps but also to choose methods that are compatible with each other and jointly lead to efficient algorithms. The next section describes these choices in more detail. More detailed discussion can be found in Cai (2010), Judd (1998), and Rust (2008).
. Second, the evaluation of the objective requires us to compute an expectation. Third, we need to efficiently take the data and compute the best fit for the new value function. The challenge is not only to use good numerical methods for each of these steps but also to choose methods that are compatible with each other and jointly lead to efficient algorithms. The next section describes these choices in more detail. More detailed discussion can be found in Cai (2010), Judd (1998), and Rust (2008).
3.2 Typical Applications
Dynamic programming has been applied to numerous economic problems. For the purposes of this chapter, we use two basic applications familiar to readers. These examples will allow us to later illustrate numerical methods in a clear manner.
3.2.1 Optimal Growth Example
We first illustrate our methods with a discrete-time optimal growth problem with one good and one capital stock.1 The objective is to find the optimal consumption function and the optimal labor supply function such that the total utility over the ![]() -horizon time is maximal, i.e.,
-horizon time is maximal, i.e.,
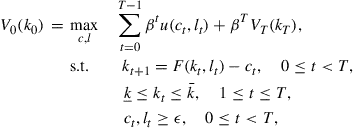 (4)
(4)
where ![]() is the capital stock at time
is the capital stock at time ![]() with
with ![]() given,
given, ![]() is the consumption of the good,
is the consumption of the good, ![]() is the labor supply,
is the labor supply, ![]() and
and ![]() are given lower and upper bound of
are given lower and upper bound of ![]() is the discount factor,
is the discount factor, ![]() with
with ![]() the aggregate net production function,
the aggregate net production function, ![]() is a given terminal value function, and
is a given terminal value function, and ![]() is the utility function, and
is the utility function, and ![]() is a small positive number to avoid the nonpositive consumption or labor supply.
is a small positive number to avoid the nonpositive consumption or labor supply.
The dynamic programming version of the discrete-time optimal growth problem is the Bellman equation:
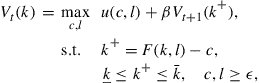 (5)
(5)
for ![]() , where
, where ![]() is the previously given terminal value function. Here
is the previously given terminal value function. Here ![]() is the state variable and
is the state variable and ![]() are the control variables.
are the control variables.
Using dynamic programming does not make more traditional methods obsolete; in fact, careful applications of dynamic programming will use traditional methods to check solutions. For the finite-horizon optimal growth problem (4), when ![]() is small, we can use a good large-scale optimization package to solve the problem directly, and its solution could be better than the solution of the dynamic programming model (5) given by numerical dynamic programming algorithms because of the numerical approximation errors. Numerical dynamic programming is a problem in infinite-dimensional function spaces and we do not know a priori how flexible our finite-dimensional approximations need to be. Comparing our dynamic programming solution to the solutions from conventional optimization methods can help us determine the amount of flexibility we need to solve for the value function.
is small, we can use a good large-scale optimization package to solve the problem directly, and its solution could be better than the solution of the dynamic programming model (5) given by numerical dynamic programming algorithms because of the numerical approximation errors. Numerical dynamic programming is a problem in infinite-dimensional function spaces and we do not know a priori how flexible our finite-dimensional approximations need to be. Comparing our dynamic programming solution to the solutions from conventional optimization methods can help us determine the amount of flexibility we need to solve for the value function.
When we turn to stochastic versions of the growth model, dynamic programming must be used since conventional optimization methods can no longer be used when either the horizon or number of random states is large. However, as long as the complexity of the value function is only moderately affected by the stochastic terms, the information obtained from conventional methods applied to the deterministic problem will tell us much about the value function for the stochastic problem.
3.2.2 Multistage Portfolio Optimization Example
We also illustrate our methods with a multistage portfolio optimization problem. Let ![]() be an amount of money planned to be invested at time
be an amount of money planned to be invested at time ![]() . Assume that available assets for trading are
. Assume that available assets for trading are ![]() stocks and a bond, where the stocks have a random return vector
stocks and a bond, where the stocks have a random return vector ![]() and the bond has a risk-free return
and the bond has a risk-free return ![]() for each period. If
for each period. If ![]() is a vector of money invested in the
is a vector of money invested in the ![]() risky assets at time
risky assets at time ![]() , then money invested in the riskless asset is
, then money invested in the riskless asset is ![]() , where
, where ![]() is a column vector of
is a column vector of ![]() s. Thus, the wealth at the next stage is
s. Thus, the wealth at the next stage is
![]() (6)
(6)
for ![]() .
.
A simple multistage portfolio optimization problem is to find an optimal portfolio ![]() at each time
at each time ![]() such that we have a maximal expected terminal utility, i.e.,
such that we have a maximal expected terminal utility, i.e.,
![]() (7)
(7)
where ![]() is the terminal wealth derived from the recursive formula (6) with a given
is the terminal wealth derived from the recursive formula (6) with a given ![]() , and
, and ![]() is the terminal utility function, and
is the terminal utility function, and ![]() is the expectation operator.
is the expectation operator.
The dynamic programming model of this multistage portfolio optimization problem is
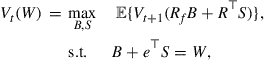 (8)
(8)
for ![]() , where
, where ![]() is the state variable and
is the state variable and ![]() is the control variable vector, and the terminal value function is
is the control variable vector, and the terminal value function is ![]() . We should add
. We should add ![]() and
and ![]() as bound constraints in the above dynamic programming model, if neither shorting stock nor borrowing bond is allowed.
as bound constraints in the above dynamic programming model, if neither shorting stock nor borrowing bond is allowed.
For small portfolio problems, conventional methods can be used. In the portfolio optimization problem (7), if we discretize the random returns of ![]() stocks as
stocks as ![]() with probability
with probability ![]() for
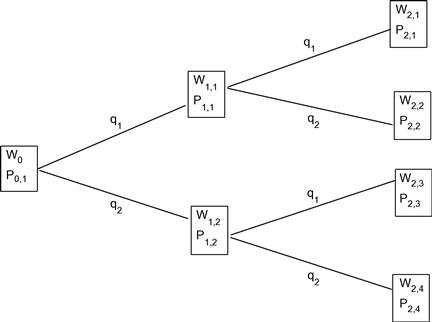
for ![]() , then it becomes a tree. Figure 1 shows one simple tree with
, then it becomes a tree. Figure 1 shows one simple tree with ![]() and
and ![]() for a portfolio with one bond and one stock. The stock’s random return has a probability
for a portfolio with one bond and one stock. The stock’s random return has a probability ![]() to have a return
to have a return ![]() , and the probability
, and the probability ![]() to have a return
to have a return ![]() . So there are two scenarios at time 1:
. So there are two scenarios at time 1: ![]() and
and ![]() , and four scenarios at time 2:
, and four scenarios at time 2: ![]() .
.
In a mathematical formula, the probability of scenario ![]() at time
at time ![]() is
is
![]()
and the wealth at scenario ![]() and time
and time ![]() is
is
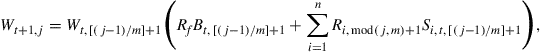
for ![]() and
and ![]() . Here,
. Here, ![]() is a given initial wealth,
is a given initial wealth, ![]() is the remainder of division of
is the remainder of division of ![]() by
by ![]() , and
, and ![]() is the quotient of division of
is the quotient of division of ![]() by
by ![]() . The goal is to choose optimal bond allocations
. The goal is to choose optimal bond allocations ![]() and stock allocations
and stock allocations ![]() to maximize the expected terminal utility, i.e.,
to maximize the expected terminal utility, i.e.,
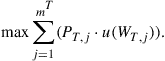 (9)
(9)
We should add ![]() and
and ![]() for all
for all ![]() as bound constraints in the tree model, if neither shorting stock or borrowing bond is allowed. This tree method includes all possible scenarios with their assigned probabilities.
as bound constraints in the tree model, if neither shorting stock or borrowing bond is allowed. This tree method includes all possible scenarios with their assigned probabilities.
The disadvantage of the tree method is that when ![]() or
or ![]() is large, the problem size will exponentially increase and it will not be feasible for a solver to find an accurate solution. In contrast, dynamic programming algorithms have no such disadvantage. As with the growth model example, the cases where we can solve the portfolio problem exactly can be used to evaluate the quality of our numerical dynamic programming methods.
is large, the problem size will exponentially increase and it will not be feasible for a solver to find an accurate solution. In contrast, dynamic programming algorithms have no such disadvantage. As with the growth model example, the cases where we can solve the portfolio problem exactly can be used to evaluate the quality of our numerical dynamic programming methods.
Both of these examples are simple one-dimensional problems. Our examples below will also discuss solutions to multidimensional versions of both the growth model and the portfolio model.
4 Tools from Numerical Analysis
The previous section outlined the basic numerical challenges. In this section, we review the tools from numerical analysis that we use to produce stable and efficient algorithms. There are three main components in numerical dynamic programming: optimization, approximation, and numerical integration.
4.1 Optimization
For value function iteration, the most time-consuming portion is the optimization step. There are ![]() optimization tasks at time
optimization tasks at time ![]() in Algorithm 1, one for each approximation node. If the number of value function iterations is
in Algorithm 1, one for each approximation node. If the number of value function iterations is ![]() , then the total number of optimization tasks is
, then the total number of optimization tasks is ![]() . All these optimization tasks are relatively small problems with a small number of choice variables. Algorithm performance depends on how quickly these problems are solved.
. All these optimization tasks are relatively small problems with a small number of choice variables. Algorithm performance depends on how quickly these problems are solved.
If the value function approximation is not smooth, then the objective function of the optimization problem in the maximization step is not smooth, forcing us to use methods that can solve nonsmooth problems. If the value function approximation is smooth, we can use Newton’s method and related methods for constrained nonlinear optimization problems, which have a locally quadratic convergence rate.
We often use NPSOL (Gill et al., 1994), a set of Fortran subroutines for minimizing a smooth function subject to linear and nonlinear constraints. The NPSOL libraries may be called from a driver program in Fortran, C/C++, or MATLAB. NPSOL is an appropriate optimization solver for dynamic programming applications in economics and finance, since the optimization tasks in numerical dynamic programming are small-size smooth problems.
4.2 Numerical Integration
In the objective function of the Bellman equation, we often need to compute the conditional expectation of ![]() . When the random variable is continuous, we have to use numerical integration to compute the expectation. Gaussian quadrature rules are often applied in computing the integration.
. When the random variable is continuous, we have to use numerical integration to compute the expectation. Gaussian quadrature rules are often applied in computing the integration.
4.2.1 Gauss-Hermite Quadrature
In the expectation operator of the objective function of the Bellman equation, if the random variable has a normal distribution, then it will be good to apply the Gauss-Hermite quadrature formula to compute the numerical integration. That is, if we want to compute ![]() where
where ![]() has a distribution
has a distribution ![]() , then
, then
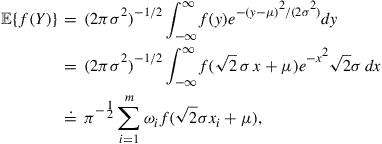
where ![]() and
and ![]() are the Gauss-Hermite quadrature with
are the Gauss-Hermite quadrature with ![]() weights and nodes over
weights and nodes over ![]() . If
. If ![]() is log normal, i.e.,
is log normal, i.e., ![]() has a distribution
has a distribution ![]() , then we can assume that
, then we can assume that ![]() , where
, where ![]() , thus
, thus
![]()
See Judd (1998) for more details.
If we want to compute a multidimensional integration, we could apply the product rule. For example, suppose that we want to compute ![]() , where
, where ![]() is a random vector with multivariate normal distribution
is a random vector with multivariate normal distribution ![]() over
over ![]() , where
, where ![]() is the mean column vector and
is the mean column vector and ![]() is the covariance matrix, then we could do the Cholesky factorization first, i.e., find a lower triangular matrix
is the covariance matrix, then we could do the Cholesky factorization first, i.e., find a lower triangular matrix ![]() such that
such that ![]() . This is feasible as
. This is feasible as ![]() must be a positive semi-definite matrix from the covariance property.
must be a positive semi-definite matrix from the covariance property.
4.3 Approximation
An approximation scheme consists of two parts: basis functions and approximation nodes. Approximation nodes can be chosen as uniformly spaced nodes, Chebyshev nodes, or some other specified nodes. From the viewpoint of basis functions, approximation methods can be classified as either spectral methods or finite element methods. A spectral method uses globally nonzero basis functions ![]() such that
such that ![]() is a degree-
is a degree-![]() approximation. Examples of spectral methods include ordinary polynomial approximation, Chebyshev polynomial approximation, and shape-preserving Chebyshev polynomial approximation (Cai and Judd, 2013). In contrast, a finite element method uses locally basis functions
approximation. Examples of spectral methods include ordinary polynomial approximation, Chebyshev polynomial approximation, and shape-preserving Chebyshev polynomial approximation (Cai and Judd, 2013). In contrast, a finite element method uses locally basis functions ![]() that are nonzero over subdomains of the approximation domain. Examples of finite element methods include piecewise linear interpolation, cubic splines, and B-splines. See Cai (2010), Cai and Judd (2010), and Judd (1998) for more details.
that are nonzero over subdomains of the approximation domain. Examples of finite element methods include piecewise linear interpolation, cubic splines, and B-splines. See Cai (2010), Cai and Judd (2010), and Judd (1998) for more details.
4.3.1 Chebyshev Polynomial Approximation
Chebyshev polynomials on ![]() are defined as
are defined as ![]() . Economics problems typically live on an interval
. Economics problems typically live on an interval ![]() ; if we let
; if we let
![]()
then ![]() are Chebyshev polynomials adapted to
are Chebyshev polynomials adapted to ![]() for
for ![]() These polynomials are orthogonal under the weighted inner product:
These polynomials are orthogonal under the weighted inner product: ![]() with the weighting function
with the weighting function ![]() . A degree
. A degree ![]() Chebyshev polynomial approximation for
Chebyshev polynomial approximation for ![]() on
on ![]() is
is
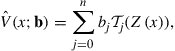 (10)
(10)
where ![]() are the Chebyshev coefficients.
are the Chebyshev coefficients.
If we choose the Chebyshev nodes on ![]() with
with ![]() for
for ![]() , and Lagrange data
, and Lagrange data ![]() are given (where
are given (where ![]() ), then the coefficients
), then the coefficients ![]() in (10) can be easily computed by the following formula,
in (10) can be easily computed by the following formula,
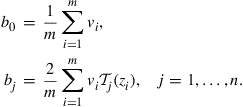 (11)
(11)
The method is called the Chebyshev regression algorithm in Judd (1998).
When the number of Chebyshev nodes is equal to the number of Chebyshev coefficients, i.e., ![]() , then the approximation (10) with the coefficients given by (11) becomes Chebyshev polynomial interpolation (which is a Lagrange interpolation), as
, then the approximation (10) with the coefficients given by (11) becomes Chebyshev polynomial interpolation (which is a Lagrange interpolation), as ![]() , for
, for ![]() .
.
4.3.2 Multidimensional Complete Chebyshev Polynomial Approximation
In a ![]() -dimensional approximation problem, let the domain of the value function be
-dimensional approximation problem, let the domain of the value function be
![]()
for some real numbers ![]() and
and ![]() with
with ![]() for
for ![]() . Let
. Let ![]() and
and ![]() . Then we denote
. Then we denote ![]() as the domain. Let
as the domain. Let ![]() be a vector of nonnegative integers. Let
be a vector of nonnegative integers. Let ![]() denote the product
denote the product ![]() for
for ![]() . Let
. Let
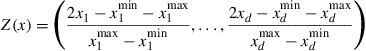
for any ![]() .
.
Using these notations, the degree-![]() complete Chebyshev approximation for
complete Chebyshev approximation for ![]() is
is
![]() (12)
(12)
where ![]() for the nonnegative integer vector
for the nonnegative integer vector ![]() . So the number of terms with
. So the number of terms with ![]() is
is ![]() for the degree-
for the degree-![]() complete Chebyshev approximation in
complete Chebyshev approximation in ![]() .
.
4.3.3 Shape-Preserving Chebyshev Interpolation
One problem for Chebyshev interpolation is the absence of shape-preservation in the algorithm. To solve this, Cai and Judd (2013) create an optimization problem that modifies the Chebyshev coefficients so that concavity and monotonicity of the value function will be preserved. We begin with the Lagrange data ![]() generated by the maximization step of Algorithm 1, where
generated by the maximization step of Algorithm 1, where ![]() are the approximation nodes and
are the approximation nodes and ![]() is the value of the unknown function at
is the value of the unknown function at ![]() . If theory tells us that the true value function is strictly increasing and concave, then add constraints to the fitting criterion that will impose shape restrictions.
. If theory tells us that the true value function is strictly increasing and concave, then add constraints to the fitting criterion that will impose shape restrictions.
Specifically, we approximate the value function using the functional form
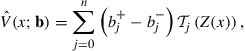 (13)
(13)
where we replaced ![]() in the Eq. (10) by
in the Eq. (10) by ![]() with
with ![]() , and we use the Chebyshev nodes
, and we use the Chebyshev nodes ![]() as approximation nodes. We choose some points
as approximation nodes. We choose some points ![]()
![]() , called shape nodes, and impose the requirement that
, called shape nodes, and impose the requirement that ![]() satisfies the shape conditions at the shape nodes. We want to choose the parameters
satisfies the shape conditions at the shape nodes. We want to choose the parameters ![]() to minimize approximation errors but also satisfy the shape conditions. We can get a perfect fit and satisfy shape conditions if we allow
to minimize approximation errors but also satisfy the shape conditions. We can get a perfect fit and satisfy shape conditions if we allow ![]() to be sufficiently large, but the problem may have too many solutions. We can be sure to get a shape-preserving Chebyshev interpolant by adding enough shape-preserving constraints and using a sufficiently high degree (bigger than
to be sufficiently large, but the problem may have too many solutions. We can be sure to get a shape-preserving Chebyshev interpolant by adding enough shape-preserving constraints and using a sufficiently high degree (bigger than ![]() ) polynomial, but we again could have multiple solutions and end up with a more complex polynomial than necessary.
) polynomial, but we again could have multiple solutions and end up with a more complex polynomial than necessary.
To allow for the flexibility necessary to have both interpolation and shape properties, we penalize the use of high-order polynomials. Therefore, we solve the following linear programming problem:
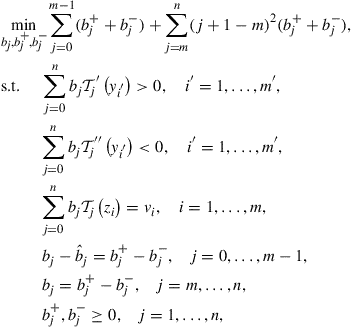 (14)
(14)
where ![]() for
for ![]() .
.
This problem includes interpolation among the constraints as well as the shape conditions, but chooses the polynomial with the smallest total weighted penalty, and is biased toward low-degree polynomials since a higher degree term is penalized more. The expression ![]() represents
represents ![]() with
with ![]() , implying
, implying ![]() . The simple Chebyshev interpolation coefficients
. The simple Chebyshev interpolation coefficients ![]() give us a good initial guess. Therefore, we actually solve for the deviations of the Chebyshev coefficients from the simple Chebyshev interpolation coefficients.
give us a good initial guess. Therefore, we actually solve for the deviations of the Chebyshev coefficients from the simple Chebyshev interpolation coefficients.
The ![]() are pre-specified shape nodes in
are pre-specified shape nodes in ![]() for shape-preserving constraints. We often need to use more shape points than just the
for shape-preserving constraints. We often need to use more shape points than just the ![]() approximation nodes since polynomial approximation need not preserve shape. There is no obvious best way to choose these points. One logical possibility is to use Chebyshev nodes corresponding to the zeroes of a degree
approximation nodes since polynomial approximation need not preserve shape. There is no obvious best way to choose these points. One logical possibility is to use Chebyshev nodes corresponding to the zeroes of a degree ![]() Chebyshev polynomial; however, we have no reason to think this is the best. The strong approximation properties of Chebyshev interpolation do not apply directly since shape-preservation is a one-sided inequality condition whereas Chebyshev interpolation is excellent for
Chebyshev polynomial; however, we have no reason to think this is the best. The strong approximation properties of Chebyshev interpolation do not apply directly since shape-preservation is a one-sided inequality condition whereas Chebyshev interpolation is excellent for ![]() approximation, a two-sided concept. Another choice, one that we use in our examples, is to use
approximation, a two-sided concept. Another choice, one that we use in our examples, is to use ![]() equally spaced points. For any method we use, we may not know how many we need when we begin, so one must test the resulting solution on many more points, and increase the set of shape nodes if shape has not been preserved. As long as the value function has bounded derivatives, it is obvious that there is some finite number of shape constraints that will impose shape.
equally spaced points. For any method we use, we may not know how many we need when we begin, so one must test the resulting solution on many more points, and increase the set of shape nodes if shape has not been preserved. As long as the value function has bounded derivatives, it is obvious that there is some finite number of shape constraints that will impose shape.
Moreover, the interpolation constraints imply that ![]() , the number of Chebyshev polynomials used in the value function approximation, needs to be greater than the number of interpolation nodes since we need to satisfy
, the number of Chebyshev polynomials used in the value function approximation, needs to be greater than the number of interpolation nodes since we need to satisfy ![]() interpolation equality constraints and
interpolation equality constraints and ![]() shape-preserving constraints in (14).
shape-preserving constraints in (14).
4.3.4 Shape-Preserving Hermite Interpolation
The shape-preserving Chebyshev interpolation imposes many additional shape-preserving constraints in the fitting problem and are computationally more demanding than desirable. There has been much effort developing shape-preserving and Hermite interpolation; see, for example, the survey paper in Goodman (2001). Most methods produce splines and are global, with all spline parameters depending on all the data. Judd and Solnick (1994) applied Schumaker shape-preserving polynomial splines (Schumaker, 1983) in optimal growth problems, but Schumaker splines are costly because they require creating new nodes each time a value function is constructed.
Cai and Judd (2012a) present an inexpensive shape-preserving rational function spline Hermite interpolation for a concave, monotonically increasing function. Suppose we have the Hermite data ![]() , where
, where ![]() are the approximation nodes,
are the approximation nodes, ![]() is the value of the unknown function at
is the value of the unknown function at ![]() , and
, and ![]() is its slope at
is its slope at ![]() . With these data, we approximate the value function on the interval
. With these data, we approximate the value function on the interval ![]() with
with
![]() (15)
(15)
for ![]() , where
, where
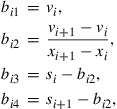 (16)
(16)
for ![]() .
. ![]() is obviously
is obviously ![]() on each interval
on each interval ![]() , and
, and ![]() globally.
globally.
This is a local method because the rational function interpolant on each interval ![]() depends only on the level and slope information at the endpoints. Moreover,
depends only on the level and slope information at the endpoints. Moreover, ![]() is shape-preserving. If the data is consistent with a concave increasing value function, i.e.,
is shape-preserving. If the data is consistent with a concave increasing value function, i.e., ![]() , then straightforward computations show that
, then straightforward computations show that ![]() and
and ![]() for all
for all ![]() , that is, it is increasing and concave in the interval
, that is, it is increasing and concave in the interval ![]() . It is also cheaply computed since the approximation on each interval depends solely on the data at its endpoints. This approach does not require adding new nodes to the spline or the determination of free parameters, features that are common in the shape-preserving polynomial spline literature.
. It is also cheaply computed since the approximation on each interval depends solely on the data at its endpoints. This approach does not require adding new nodes to the spline or the determination of free parameters, features that are common in the shape-preserving polynomial spline literature.
5 Shape-preserving Dynamic Programming
Algorithm 1 is a general method for solving deterministic dynamic programming problems, but it may fail. Theory tells us that if ![]() is concave and monotone increasing then
is concave and monotone increasing then ![]() is also concave and monotone increasing. However, this may fail in Algorithm 1. Theory assumes that we solve the maximization step at each state but Algorithm 1 solves the maximization step at only a finite number of states and produce a finite amount of Lagrange data
is also concave and monotone increasing. However, this may fail in Algorithm 1. Theory assumes that we solve the maximization step at each state but Algorithm 1 solves the maximization step at only a finite number of states and produce a finite amount of Lagrange data ![]() . This data may be consistent with concavity, but many methods of fitting a curve to the data will produce approximations for
. This data may be consistent with concavity, but many methods of fitting a curve to the data will produce approximations for ![]() that violate either monotonicity or concavity, or both. If
that violate either monotonicity or concavity, or both. If ![]() is not concave or monotone increasing, then those errors will produce errors when we compute
is not concave or monotone increasing, then those errors will produce errors when we compute ![]() . These problems may create significant errors in approximating the value functions as we iterate backward in time. This is not just a theoretical possibility; an example in Section 5.1 illustrates how these problems can arise easily. In any case, if the value function approximations violate basic shape properties that we know are satisfied by the true solution, we know that we have bad approximations.
. These problems may create significant errors in approximating the value functions as we iterate backward in time. This is not just a theoretical possibility; an example in Section 5.1 illustrates how these problems can arise easily. In any case, if the value function approximations violate basic shape properties that we know are satisfied by the true solution, we know that we have bad approximations.
This possibly explains the tendency of economists to use piecewise linear approximations of value functions since piecewise linear approximations automatically preserve shape. While this may solve the shape problems, it causes other problems. If one uses piecewise linear approximations, then one needs to use many nodes to construct a good approximation, and the optimization problems in Algorithm 1 have nondifferentiable objective functions, a feature that rules out the use of fast Newton-type solvers. The alternatives, such as bisection, will be much slower. Also, the piecewise linear approximation approach only works for one-dimensional problems.
Dynamic programming problems in economics often make assumptions that imply monotone increasing, concave, and ![]() value functions. It is natural to impose those properties on the value function approximations in Algorithm 1. The optimization step will be a smooth convex optimization problem for which it is easy to find the global optimum.
value functions. It is natural to impose those properties on the value function approximations in Algorithm 1. The optimization step will be a smooth convex optimization problem for which it is easy to find the global optimum.
5.1 Application in Optimal Growth Problems
We use the following numerical examples of the finite-horizon optimal growth model (4) to illustrate the importance of the shape-preserving property. In the following examples, we let ![]() , and
, and ![]() . Let the range of
. Let the range of ![]() be
be ![]() , i.e.,
, i.e., ![]() and
and ![]() . And we choose
. And we choose ![]() in the model (4). The production function is
in the model (4). The production function is ![]() , and the utility function is a power utility with the following form
, and the utility function is a power utility with the following form
![]()
Thus the steady state of the infinite-horizon deterministic optimal growth problems is ![]() while the optimal consumption and the optimal labor supply at
while the optimal consumption and the optimal labor supply at ![]() are, respectively,
are, respectively, ![]() and
and ![]() . Moreover, the utility at the steady state is 0 and then the true value function at the steady state is also 0. This normalization of the typical power utility from the economic literature not only helps avoid scaling issues but also gives us a simple criterion to check if a numerical solution is close to the true solution.
. Moreover, the utility at the steady state is 0 and then the true value function at the steady state is also 0. This normalization of the typical power utility from the economic literature not only helps avoid scaling issues but also gives us a simple criterion to check if a numerical solution is close to the true solution.
We choose the terminal value function as
![]()
We see that the terminal value function is smooth and concave, and the optimal controls will not be binding at least at the next-to-the-last stage ![]() . Thus, it is supposed that polynomial approximation methods could approximate the value functions well. We use the solutions given by directly applying SNOPT (Gill et al., 2005) in the model (4) as the true solutions.
. Thus, it is supposed that polynomial approximation methods could approximate the value functions well. We use the solutions given by directly applying SNOPT (Gill et al., 2005) in the model (4) as the true solutions.
Figure 2 illustrates how Chebyshev interpolation without shape-preservation produces bad approximations. Figure 2 contains four graphs corresponding to combinations of ![]() and
and ![]() norms with the controls, consumption, and labor supply. Each graph contains two lines; the solid line displays errors for Chebyshev interpolation without shape-preservation, and the broken line displays errors with shape-preservation. Each line shows the relative errors of consumption or labor supply using either the
norms with the controls, consumption, and labor supply. Each graph contains two lines; the solid line displays errors for Chebyshev interpolation without shape-preservation, and the broken line displays errors with shape-preservation. Each line shows the relative errors of consumption or labor supply using either the ![]() or the
or the ![]() norm. Shape was imposed at
norm. Shape was imposed at ![]() equally spaced nodes in (14).
equally spaced nodes in (14).
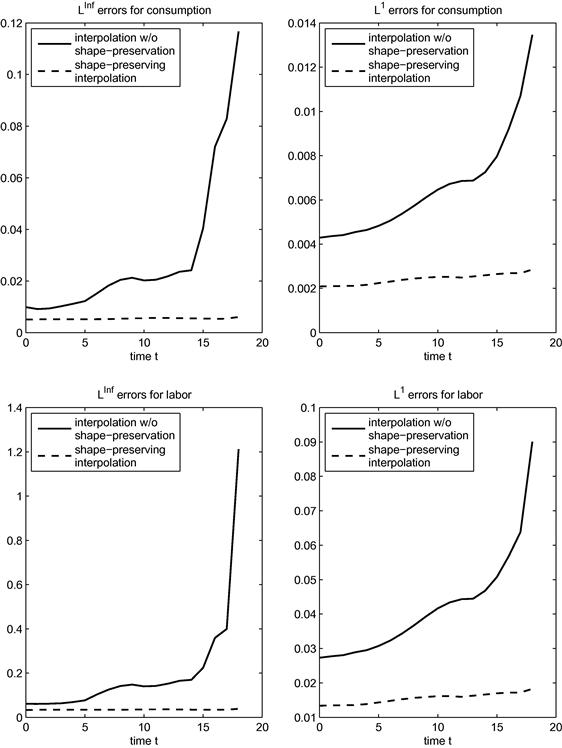
Figure 2 Errors of numerical dynamic programming with Chebyshev interpolation with/without shape-preservation for growth problems.
Figure 2 first shows that the errors are substantial when we ignore shape constraints. The errors are particularly large for later periods, and do decrease as we iterate backwards in time but they do not disappear. This example is a relatively easy problem, with infinitely smooth utility and production functions.
The second conclusion from Figure 2 is that shape-preservation substantially reduces the errors. Furthermore, the errors are uniformly small across time. The functional form of the approximation is a degree-9 polynomial for both methods in Figure 2; hence, the problem when we ignore shape constraints is not that there is no good degree-9 polynomial approximation of the value function. The only difference between the two procedures is the imposition of shape constraints, constraints that we know are satisfied by the true value function.
5.2 Application in Multistage Portfolio Optimization Example
We use the multistage portfolio optimization model (7) with one stock and one bond available for investment to show the shape-preservation is even more crucial when there is a kink in the optimal solutions. We assume that the number of periods is ![]() , the bond has a risk-free return
, the bond has a risk-free return ![]() , and the stock has a discrete random return
, and the stock has a discrete random return
 (17)
(17)
Let the range of initial wealth ![]() be
be ![]() . The terminal utility function is
. The terminal utility function is
![]()
with ![]() and
and ![]() so that the terminal wealth should be always bigger than 0.2. Moreover, we assume that borrowing or shorting is not allowed in this example, i.e.,
so that the terminal wealth should be always bigger than 0.2. Moreover, we assume that borrowing or shorting is not allowed in this example, i.e., ![]() and
and ![]() for all
for all ![]() .
.
Since the terminal utility function is ![]() , we know that the terminal wealth
, we know that the terminal wealth ![]() must be always larger than
must be always larger than ![]() . It follows that we should have
. It follows that we should have ![]() . Thus, since shorting or borrowing is not allowed and
. Thus, since shorting or borrowing is not allowed and ![]() is bounded, we choose the ranges
is bounded, we choose the ranges ![]() for approximating value functions as
for approximating value functions as
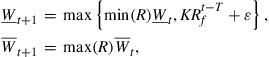 (18)
(18)
with a given initial wealth bound ![]() , where
, where ![]() is a small number.
is a small number.
Specifically, for the numerical example with ![]() ,
, ![]() , and
, and ![]() , after we choose
, after we choose ![]() and
and ![]() , we have
, we have
![]()
We see that the ranges are expanding exponentially along time ![]() . If we use a fixed range along time
. If we use a fixed range along time ![]() in our numerical dynamic programming algorithms, then it will definitely reduce the accuracy of solutions. So here we choose the above ranges at times
in our numerical dynamic programming algorithms, then it will definitely reduce the accuracy of solutions. So here we choose the above ranges at times ![]() .
.
5.2.1 Numerical Results of Shape-Preserving Rational Spline Hermite Interpolation
We use the shape-preserving rational function spline Hermite interpolation (15) to solve the multistage portfolio optimization problem (7), and compare it with earlier methods. To evaluate the accuracy of our method, we compare it to the true solution. The value function has no closed-form expression because of the borrowing constraints. An example with a closed-form solution would have been too easy for our method to solve. The borrowing constraint makes this more challenging because the bond strategy has a kink at the largest wealth where it binds. However, we can compute the true solution for any initial wealth using the tree method (9). The tree method solves for the state-contingent values of all variables at all nodes in the decision tree. We solve the tree model using MINOS (Murtagh and Saunders, 1982) in AMPL code (Fourer et al., 1990) via the NEOS server (Czyzyk et al., 1998). We use the true solution to measure the accuracy of our dynamic programming algorithm and compare it with the accuracy of other methods. The presence of a borrowing constraint also means we should approximate the value function, which will be ![]() , not the policy function which may only be
, not the policy function which may only be ![]() . Polynomial approximation theory tells us to focus on approximating the smoother function.
. Polynomial approximation theory tells us to focus on approximating the smoother function.
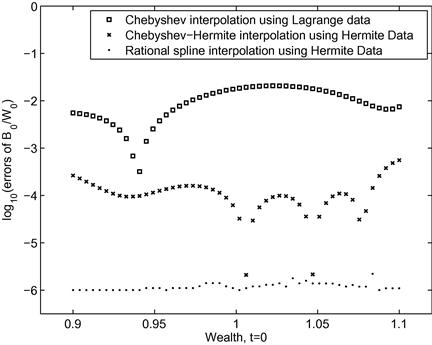
Figure 3 shows relative errors for bond allocations of alternative dynamic programming algorithms. The squares are errors of solutions of dynamic programming with Chebyshev interpolation using Lagrange data, the x-marks are errors of dynamic programming with Chebyshev-Hermite interpolation using Hermite data, and the solid points are errors of dynamic programming with the rational function spline interpolation using Hermite data. All the computational results are given by MINOS (Murtagh and Saunders, 1982) in AMPL (Fourer et al., 1990) via the NEOS server (Czyzyk et al., 1998). For dynamic programming with Chebyshev interpolation or dynamic programming with Chebyshev-Hermite interpolation, we use ![]() Chebyshev nodes and degree-9 or degree-19 Chebyshev polynomials, respectively. For the rational function spline interpolation, we use
Chebyshev nodes and degree-9 or degree-19 Chebyshev polynomials, respectively. For the rational function spline interpolation, we use ![]() equally spaced nodes.
equally spaced nodes.
We see that the errors are about ![]() or
or ![]() for Chebyshev interpolation using Lagrange data, while they are about
for Chebyshev interpolation using Lagrange data, while they are about ![]() or
or ![]() for Chebyshev-Hermite interpolation (Cai and Judd, 2012b) using Hermite data. However, the errors of the rational function spline Hermite interpolation is always about
for Chebyshev-Hermite interpolation (Cai and Judd, 2012b) using Hermite data. However, the errors of the rational function spline Hermite interpolation is always about ![]() , showing that it has the best performance for approximating value functions.
, showing that it has the best performance for approximating value functions.
Table 1 lists numerical errors of optimal bond allocations from dynamic programming with the rational function spline interpolation, for various values of ![]() . We see that even for large
. We see that even for large ![]() , the solutions from dynamic programming with the rational function spline interpolation are still good.
, the solutions from dynamic programming with the rational function spline interpolation are still good.
Our new approximation method was always as fast as any of the other algorithms. Therefore, the shape-preserving rational function spline Hermite interpolation is reliable and often substantially better than other approximation methods.
5.2.2 Other Shape-preserving Methods
There are many methods for preserving shape (see Goodman, 2001) but many are not suitable for our purposes. The one-dimensional Schumaker shape-preserving interpolation method (Schumaker, 1983) was applied to dynamic programming in Judd and Solnick (1994) and Cai (2010). However, the approximation is more complex than the ones discussed above, and is at best ![]() whereas Newton solvers really prefer
whereas Newton solvers really prefer ![]() or smoother value function approximations. Wang and Judd (2000) applied a bivariate shape-preserving spline interpolation method (Costantini and Fontanella, 1990) in numerical dynamic programming to solve a savings allocation problem. However, the bivariate method only preserved shape along the coordinate axes, whereas the shape-preserving Chebyshev interpolation method (Cai and Judd, 2013) can be generalized to higher dimensions and impose shape restrictions in any direction. The mathematics literature on shape-preserving approximation is mostly focused on one- or two-dimensional problems, forcing economists to develop their own methods when solving higher dimensional dynamic programming problems.
or smoother value function approximations. Wang and Judd (2000) applied a bivariate shape-preserving spline interpolation method (Costantini and Fontanella, 1990) in numerical dynamic programming to solve a savings allocation problem. However, the bivariate method only preserved shape along the coordinate axes, whereas the shape-preserving Chebyshev interpolation method (Cai and Judd, 2013) can be generalized to higher dimensions and impose shape restrictions in any direction. The mathematics literature on shape-preserving approximation is mostly focused on one- or two-dimensional problems, forcing economists to develop their own methods when solving higher dimensional dynamic programming problems.
6 Parallelization
Many dynamic programming problems in economics involve many states, and solving them will face the “curse of dimensionality.” Even if one uses approximation and quadrature methods that avoid the curse of dimensionality, dynamic programming problems with many states are expensive to solve. If parallelization can be used, it is the natural way to make otherwise intractable problems tractable. Many modern computer systems now offer researchers parallel computing tools. Fortunately, dynamic programming problems do have a structure that facilitates the use of parallelization.
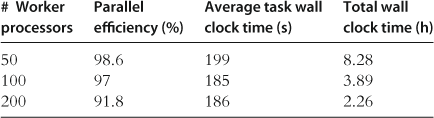
Cai et al. (2013b) implement a parallel dynamic programming algorithm on a computational grid consisting of loosely coupled processors, possibly including clusters and individual workstations. The grid changes dynamically during the computation, as processors enter and leave the pool of workstations. The algorithm is implemented using the Master-Worker library running on the HTCondor grid computing platform. We implement value function iteration for large optimal growth problems. We present examples that solve in hours on HTCondor but would take weeks if executed on a single workstation. The use of HTCondor can increase a researcher’s computational productivity by at least two orders of magnitude.
In the value function iteration, a set of discrete and approximation nodes will be chosen and the period ![]() value function at those nodes will be computed and then we can use some approximation methods to approximate the value function. For every approximation node, there is a time-consuming optimization problem to be solved. Moreover, these optimization problems are independent, allowing them to be solved efficiently in parallel.
value function at those nodes will be computed and then we can use some approximation methods to approximate the value function. For every approximation node, there is a time-consuming optimization problem to be solved. Moreover, these optimization problems are independent, allowing them to be solved efficiently in parallel.
6.1 The Variety of Parallel Programming Architectures
There are three basic approaches to massive parallelism. Supercomputing is a well-known example of massive parallelism. Supercomputers combine large numbers of identical processors with specialized communication hardware that allows for rapid communication among processors. This is called high-performance computing (HPC). Supercomputers are able to solve some very large problems at high efficiency. However, attaining these speeds puts rigid requirements on problems. Users of supercomputers are generally given a fixed block of processors for a fixed amount of time. This structure requires that users reserve supercomputer time, and the lag time between requests and the actual allocation will increase with the number of desired processors and requested time. Moreover, economists face substantial bureaucratic hurdles in getting access to supercomputer time because the people who control supercomputers impose requirements that are met by few economists. In particular, the authors have been told that US Department of Energy supercomputers available to the general scientific community are not available to economists who want to analyze policy issues, such as taxation problems.
Second, there is high-throughput computing (HTC) which may be slower but is a paradigm with much greater flexibility and lower cost. HTCondor is an example of HTC and a valuable alternative to HPC. The HTCondor system is an open-source software framework for distributed parallelization of computationally intensive tasks on a cluster of computers. HTCondor accumulates a set of desired tasks from users, and then allocates them to those computers that are not being used at the moment. HTCondor acts as a management tool for identifying, allocating, and managing available resources to solve large distributed computations. For example, if a workstation on a network is currently unused, HTCondor will detect that fact, and send it a task. HTCondor will continue to use that workstation until a higher-priority user (such as a student sitting at the keyboard) appears, at which time HTCondor ends its use of the workstation. This is called “cycle scavenging” and allows a system to take advantage of essentially free computing time. The marginal social cost of CPU time used in HTCondor is essentially zero because it is using CPU time that otherwise would go unused. HTCondor manages the number of processors being used in response to processor availability and the needs of the computational procedure. HTC is opportunistic, utilizing any resource that becomes available and does not force the user to make reservations. The disadvantage of HTC is that interprocessor communication will be only as fast as communication among computers in a cluster, a speed considerably slower than that in supercomputers. While this does limit the amount of parallelization that can be exploited, HTC environments can still efficiently use hundreds of processors for many problems.
The HTCondor team at the University of Wisconsin-Madison has developed several “flavors” of HTCondor, each fine-tuned for some specific type of parallel programming. For our dynamic programming problems, we used the HTCondor Master-Worker (MW) system. The HTCondor MW system consists of two entities: a master process and a cluster of worker processes. The master process decomposes the problem into small tasks and puts those tasks in a queue. Each worker process first examines the queue, takes the “top” problem off the queue, and solves it. The worker then sends the results to the master, examines the queue of unfinished tasks, and repeats this process until the queue is empty. The workers’ execution is a simple cycle: take a task off master’s queue, do the task, and then send the results to the master. While the workers are solving the tasks, the master collects the results and puts new tasks on the queue. This is a file-based, remote I/O scheme that serves as the message-passing mechanism between the master and the workers.
Third, there is grid computing which spreads work across computers connected only by the Internet. While the authors are not aware of any economics applications of grid computing, it is used extensively in the sciences. See BOINC (http://boinc.berkeley.edu) for a discussion of grid computing applied to scientific projects.
Based on our experiences, we believe that all three forms of massive parallelism can be used to solve large dynamic programming problems. Our discussion below will focus on our use of HTCondor, but the same basic approach will work on both supercomputers and grid computing.
6.2 Parallel Dynamic Programming
The numerical dynamic programming algorithms can be applied easily in the HTCondor MW system for dynamic programming problems with multidimensional continuous and discrete states. To solve these problems, numerical dynamic programming algorithms with value function iteration have the maximization step that is mostly time-consuming in numerical dynamic programming. Equation (3) in Algorithm 2 computes ![]() for each approximation point
for each approximation point ![]() in the finite set
in the finite set ![]() and each discrete state vector
and each discrete state vector ![]() , where
, where ![]() is the number of points of
is the number of points of ![]() and
and ![]() is the number of points of
is the number of points of ![]() , resulting in
, resulting in ![]() small maximization problems. If the
small maximization problems. If the ![]() is large, as it is for high-dimensional problems, then these maximization steps will consume most of the time used in any algorithm. However, these
is large, as it is for high-dimensional problems, then these maximization steps will consume most of the time used in any algorithm. However, these ![]() small-size maximization problems can be naturally parallelized in the HTCondor MW system, in which one or several maximization problem(s) could be treated as one task.
small-size maximization problems can be naturally parallelized in the HTCondor MW system, in which one or several maximization problem(s) could be treated as one task.
We first present an example where we parallelize the problem across the discrete states. After that presentation, we will indicate how to parallelize in the continuous dimensions of the state space.
When ![]() is large but the number of approximation nodes,
is large but the number of approximation nodes, ![]() , is of medium size, it is natural to separate the
, is of medium size, it is natural to separate the ![]() maximization problems into
maximization problems into ![]() tasks, where each task corresponds to a discrete state vector
tasks, where each task corresponds to a discrete state vector ![]() and all continuous state nodes set
and all continuous state nodes set ![]() . Algorithm 3 is the architecture for the master processor, and Algorithm 4 is the corresponding architecture for the workers.
. Algorithm 3 is the architecture for the master processor, and Algorithm 4 is the corresponding architecture for the workers.
Algorithm 3 describes the master’s function. Suppose that the value function for time ![]() is known, and the master wants to solve for the value function at period
is known, and the master wants to solve for the value function at period ![]() . For each point
. For each point ![]() , the master gathers all the Bellman optimization problems associated with that
, the master gathers all the Bellman optimization problems associated with that ![]() , together with the solution for the next period’s value function, and sends that package of problems to a worker processor. It does this until all workers are working on some such package. When the master receives the solutions from a worker, it records those results and sends that worker another package of problems not yet solved. This continues until all
, together with the solution for the next period’s value function, and sends that package of problems to a worker processor. It does this until all workers are working on some such package. When the master receives the solutions from a worker, it records those results and sends that worker another package of problems not yet solved. This continues until all ![]() specific packages have been solved, at which point the master repeats this for period
specific packages have been solved, at which point the master repeats this for period ![]() .
.
Algorithm 4 describes the typical worker task. It takes the ![]() package from the master, solves the Bellman optimization problem for each node in
package from the master, solves the Bellman optimization problem for each node in ![]() , and computes the new value for
, and computes the new value for ![]() , the coefficients for the value function in the
, the coefficients for the value function in the ![]() dimension, and sends those coefficients back to the master.
dimension, and sends those coefficients back to the master.
The case where we parallelize only across the discrete dimensions is easy to implement, and is adequate if the number of available workers is small relative to the number of points in ![]() . If we have access to more workers, then we will also parallelize across points in
. If we have access to more workers, then we will also parallelize across points in ![]() . The key difference in that case is that each worker can only compute some of the
. The key difference in that case is that each worker can only compute some of the ![]() values needed to determine
values needed to determine ![]() . One way to proceed is to send all the
. One way to proceed is to send all the ![]() values to the master which then executes the fitting step, or, if that is too demanding, the master will send that task to a worker to compute
values to the master which then executes the fitting step, or, if that is too demanding, the master will send that task to a worker to compute ![]() . See Cai et al. (2013b) for more details on this case.
. See Cai et al. (2013b) for more details on this case.
Our parallelization examples of economic problems, as described above, have used only the most basic techniques for coordinating computation among processors. There are many other places where parallelization might be useful. For example, if the Bellman optimization problem corresponding to a single point ![]() in the state space were itself a large problem, and we had a large number of processors, then it might be useful to use a parallel algorithm to solve each such state-specific problem. There are many possible ways to decompose the big problem into smaller ones and exploit the available processors. We have discussed only the first two layers of parallelization that can be used in dynamic programming. How fine we go depends on the number of processors at our disposal and the communication times across computational units.
in the state space were itself a large problem, and we had a large number of processors, then it might be useful to use a parallel algorithm to solve each such state-specific problem. There are many possible ways to decompose the big problem into smaller ones and exploit the available processors. We have discussed only the first two layers of parallelization that can be used in dynamic programming. How fine we go depends on the number of processors at our disposal and the communication times across computational units.
6.3 Application to Stochastic Optimal Growth Models
We consider a multidimensional stochastic optimal growth problem. We assume that there are ![]() sectors, and let
sectors, and let ![]() denote the capital stocks of these sectors which is a
denote the capital stocks of these sectors which is a ![]() -dimensional continuous state vector at time
-dimensional continuous state vector at time ![]() . Let
. Let ![]() denote current productivity levels of the sectors which is a
denote current productivity levels of the sectors which is a ![]() -dimensional discrete state vector at time
-dimensional discrete state vector at time ![]() , and assume that
, and assume that ![]() follows a Markov process with a stable probability transition matrix, denoted as
follows a Markov process with a stable probability transition matrix, denoted as ![]() where
where ![]() are i.i.d. disturbances. Let
are i.i.d. disturbances. Let ![]() denote elastic labor supply levels of the sectors which is a
denote elastic labor supply levels of the sectors which is a ![]() -dimensional continuous control vector variable at time
-dimensional continuous control vector variable at time ![]() . Assume that the net production function of sector
. Assume that the net production function of sector ![]() at time
at time ![]() is
is ![]() , for
, for ![]() . Let
. Let ![]() and
and ![]() denote, respectively, consumption and investment of the sectors at time
denote, respectively, consumption and investment of the sectors at time ![]() . We want to find an optimal consumption and labor supply decisions such that expected total utility over a finite-horizon time is maximized, i.e.,
. We want to find an optimal consumption and labor supply decisions such that expected total utility over a finite-horizon time is maximized, i.e.,
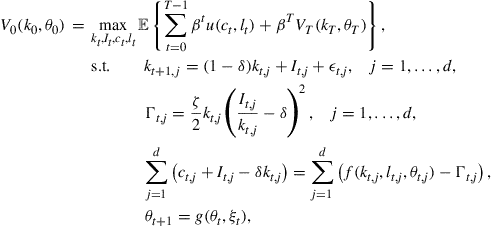
where ![]() and
and ![]() are given,
are given, ![]() is the depreciation rate of capital,
is the depreciation rate of capital, ![]() is the investment adjustment cost of sector
is the investment adjustment cost of sector ![]() , and
, and ![]() governs the intensity of the friction,
governs the intensity of the friction, ![]() are serially uncorrellated i.i.d. disturbances with
are serially uncorrellated i.i.d. disturbances with ![]() , and
, and ![]() is a given terminal value function. This model is the finite-horizon version of the problems introduced in Den Haan et al. (2011), and Juillard and Villemot (2011).
is a given terminal value function. This model is the finite-horizon version of the problems introduced in Den Haan et al. (2011), and Juillard and Villemot (2011).
6.3.1 Dynamic Programming Model
The dynamic programming formulation of the multidimensional stochastic optimal growth problem is
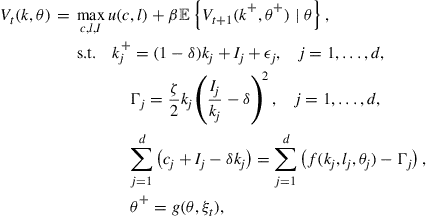
for ![]() , where
, where ![]() is the continuous state vector and
is the continuous state vector and ![]() is the discrete state vector,
is the discrete state vector, ![]() ,
, ![]() , and
, and ![]() are control variables,
are control variables, ![]() are i.i.d. disturbance with mean 0, and
are i.i.d. disturbance with mean 0, and ![]() and
and ![]() are the next-stage state vectors. Numerically,
are the next-stage state vectors. Numerically, ![]() is approximated with given values at finite nodes, so the approximation is only good at a finite range. That is, the state variable must be in a finite range
is approximated with given values at finite nodes, so the approximation is only good at a finite range. That is, the state variable must be in a finite range ![]() , then we should have the restriction
, then we should have the restriction ![]() . Here
. Here ![]() , and
, and ![]() denotes that
denotes that ![]() for all
for all ![]() . Moreover, we should add
. Moreover, we should add ![]() and
and ![]() in the constraints.
in the constraints.
6.3.2 Numerical Example
In the following numerical example, we see the application of parallelization of numerical dynamic programming algorithms for the dynamic programming model of the multidimensional stochastic optimal growth problem. We let ![]() ,
, ![]() with
with ![]() and
and ![]() , for
, for ![]() , and
, and
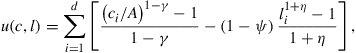
In this example, we let ![]() . So this is a dynamic programming example with four-dimensional continuous states and four-dimensional discrete states. Here we assume that the possible values of
. So this is a dynamic programming example with four-dimensional continuous states and four-dimensional discrete states. Here we assume that the possible values of ![]() are in
are in ![]() . We assume that if the current state is
. We assume that if the current state is ![]() then there is a 25% chance of moving to
then there is a 25% chance of moving to ![]() , 25% chance of moving to
, 25% chance of moving to ![]() , and 50% chance of staying, except at the boundaries where there is a reflecting boundary. We assume that
, and 50% chance of staying, except at the boundaries where there is a reflecting boundary. We assume that ![]() are independent of each other. In addition, we assume that
are independent of each other. In addition, we assume that ![]() are i.i.d., and each
are i.i.d., and each ![]() has possible discrete values in
has possible discrete values in ![]() , while their probabilities are
, while their probabilities are ![]() , and
, and ![]() , respectively.
, respectively.
The continuous value function approximation is the complete degree-![]() Chebyshev polynomial approximation method (12) with
Chebyshev polynomial approximation method (12) with ![]() Chebyshev nodes for continuous state variables, the optimizer is NPSOL (Gill et al., 1994), and the terminal value function is chosen as
Chebyshev nodes for continuous state variables, the optimizer is NPSOL (Gill et al., 1994), and the terminal value function is chosen as
![]()
where ![]() is the vector with
is the vector with ![]() ’s everywhere. Here
’s everywhere. Here ![]() is chosen because it is the steady-state labor supply for the corresponding infinite-horizon problem and is also the average value of
is chosen because it is the steady-state labor supply for the corresponding infinite-horizon problem and is also the average value of ![]() .
.
6.3.3 Parallelization Results
We use the master Algorithm 3 and the worker Algorithm 4 to solve the optimal growth problem. Since the number of possible values of ![]() is
is ![]() for
for ![]() , the total number of HTCondor-MW tasks for one value function iteration is
, the total number of HTCondor-MW tasks for one value function iteration is ![]() , and each task computes
, and each task computes ![]() small-size maximization problems as there are
small-size maximization problems as there are ![]() Chebyshev nodes.
Chebyshev nodes.
Under HTCondor, we assign ![]() workers to do this parallel work. Table 2 lists some statistics of our parallel dynamic programming algorithm under HTCondor-MW system for the growth problem after running three value function iterations (VFI). The last line of Table 2 shows that the parallel efficiency of our parallel numerical dynamic programming method is very high (up to 98.6%) for this example. We see that the total CPU time used by all workers to solve the optimal growth problem is nearly 17 days, i.e., it will take nearly 17 wall clock days to solve the problem without using parallelism. However, it takes only 8.28 wall clock hours to solve the problem if we use the parallel algorithm and 50 worker processors.
workers to do this parallel work. Table 2 lists some statistics of our parallel dynamic programming algorithm under HTCondor-MW system for the growth problem after running three value function iterations (VFI). The last line of Table 2 shows that the parallel efficiency of our parallel numerical dynamic programming method is very high (up to 98.6%) for this example. We see that the total CPU time used by all workers to solve the optimal growth problem is nearly 17 days, i.e., it will take nearly 17 wall clock days to solve the problem without using parallelism. However, it takes only 8.28 wall clock hours to solve the problem if we use the parallel algorithm and 50 worker processors.
Table 2
Statistics of parallel dynamic programming under HTCondor-MW for the growth problem.
| Wall clock time for three VFIs | 8.28 h |
| Total time workers were assigned | 16.9 days |
| Average wall clock time per task | 199 s |
| Number of (different) workers | 50 |
| Overall parallel performance | 98.6% |
Table 3 gives the parallel efficiency with various numbers of worker processors for this optimal growth model. We see that it has an almost linear speed-up when we add the number of worker processors from 50 to 200. We see that the wall clock time to solve the problem is only 2.26 h now if the number of worker processors increases to 200.
Parallel efficiency drops from 99% to 92% when we move from 100 processors to 200. This is not the critical fact for a user. The most important fact is that requesting 200 processors reduced the waiting time from submission to final output by 1.6 h. Focusing on the user’s waiting time is one of the values of the HTC approach to parallelization.
7 Dynamic Portfolio Optimization with Transaction Costs
Any investment strategy involves dynamic management of assets, spelling out when one trades assets for other assets—rebalancing a portfolio—or for cash to finance consumption. Conventional theory assumes there are no costs to asset trades. This is not true of real markets. Even if conventional brokerage fees are small, the presence of any bid-ask spread is essentially a transaction cost since the sale price is less than the purchase price. The presence of even small transaction costs can have significant impact on investment strategies; for example, Judd et al. (2012) show that even infinitesimal transaction costs reduce bond portfolio rebalancing to nearly zero. Therefore, any examination of real-world dynamic portfolio management needs to consider these frictions.
Multistage portfolio optimization problems with transaction costs have been studied in many papers (see Abrams and Karmarkar, 1980; Boyle and Lin, 1997; Brown and Smith, 2011; Constantinides, 1976, 1979, 1986; Gennotte and Jung, 1994; Kamin, 1975; Zabel, 1973, etc.). The key insight is that transaction costs create a “no-trade region” (NTR); that is, no trading is done if the current portfolio is inside the no-trade region, and otherwise the investor trades to some point on the boundary of the no-trade region.
Multistage portfolio optimization problems with transaction costs assume that there are ![]() risky assets (“stocks”) and/or a riskless asset (“bank account” paying a fixed interest rate
risky assets (“stocks”) and/or a riskless asset (“bank account” paying a fixed interest rate ![]() ) traded during the period
) traded during the period ![]() . In our discrete-time analysis, portfolio adjustments are made at time
. In our discrete-time analysis, portfolio adjustments are made at time ![]() . Trades are made to maximize the investor’s expected utility over terminal wealth (
. Trades are made to maximize the investor’s expected utility over terminal wealth (![]() is the terminal time) and/or consumption during
is the terminal time) and/or consumption during ![]() . If the major transaction cost is the bid-ask spread, then a proportional transaction costs is the correct case to study.
. If the major transaction cost is the bid-ask spread, then a proportional transaction costs is the correct case to study.
Cai (2010), Cai and Judd (2010), and Cai et al. (2013c) introduce application of numerical dynamic programming algorithms in multistage portfolio optimization problems with transaction costs, and showed that the method performs very well for the problems with three or more risky assets and ![]() with general utility functions. We assume that an investor begins with some wealth
with general utility functions. We assume that an investor begins with some wealth ![]() and initial investment allocation
and initial investment allocation ![]() accros several risky assets, and manages it so as to maximize the expected utility of wealth at time
accros several risky assets, and manages it so as to maximize the expected utility of wealth at time ![]() , while there exist transaction costs at each rebalancement time. We assume a power utility function for terminal wealth,
, while there exist transaction costs at each rebalancement time. We assume a power utility function for terminal wealth, ![]() where
where ![]() and
and ![]() . A multistage portfolio optimization problem with transaction costs is to find an optimal portfolio
. A multistage portfolio optimization problem with transaction costs is to find an optimal portfolio ![]() at each time
at each time ![]() such that we have a maximal expected terminal utility, i.e.,
such that we have a maximal expected terminal utility, i.e.,
![]()
where ![]() is the terminal wealth with the given initial wealth
is the terminal wealth with the given initial wealth ![]() and initial allocation
and initial allocation ![]() in the risky assets.
in the risky assets.
Let ![]() be the random one-period return of
be the random one-period return of ![]() risky assets, and
risky assets, and ![]() be the return of the riskless asset. The portfolio share for asset
be the return of the riskless asset. The portfolio share for asset ![]() at the beginning of a period is denoted
at the beginning of a period is denoted ![]() . The state variables are the wealth
. The state variables are the wealth ![]() and allocations
and allocations ![]() invested in the risky assets at the beginning of a period. The difference between wealth and the wealth invested in stocks is invested in bonds. We assume a proportional transaction cost
invested in the risky assets at the beginning of a period. The difference between wealth and the wealth invested in stocks is invested in bonds. We assume a proportional transaction cost ![]() for all sales and purchases of the risky assets. Let
for all sales and purchases of the risky assets. Let ![]() denote the amount of asset
denote the amount of asset ![]() purchased, expressed as a fraction of wealth, and let
purchased, expressed as a fraction of wealth, and let ![]() denote the amount sold, where
denote the amount sold, where ![]() . Let
. Let ![]() denote the column vector where
denote the column vector where ![]() for all
for all ![]() .
.
The dynamic programming problem becomes
![]()
where ![]() is time
is time ![]() wealth in asset
wealth in asset ![]() where
where ![]() is the change in bond holding,
is the change in bond holding, ![]() is time
is time ![]() wealth, and
wealth, and ![]() is the vector of risky asset allocations. Given the isoelasticity of
is the vector of risky asset allocations. Given the isoelasticity of ![]() , we know that
, we know that ![]() , for some functions
, for some functions ![]() ,
, ![]() . The numerical task reduces to approximating the
. The numerical task reduces to approximating the ![]() functions.
functions.
7.1 Numerical Example
We assume three stocks and one bond, where the stock returns are log-normally distributed, ![]() , and
, and

We assume a power terminal value function with ![]() , a transaction cost of
, a transaction cost of ![]() and
and ![]() . We use the degree-
. We use the degree-![]() complete Chebyshev polynomial approximation method and a multidimensional product Gauss-Hermite quadrature rule with
complete Chebyshev polynomial approximation method and a multidimensional product Gauss-Hermite quadrature rule with ![]() nodes in each dimension to compute expectations. We assume a
nodes in each dimension to compute expectations. We assume a ![]() investment horizon.
investment horizon.
The key property of the solution is a no-trade region ![]() for
for ![]() . When
. When ![]() , the investor will not trade at all, and when
, the investor will not trade at all, and when ![]() , the investor will trade to some point on the boundary of
, the investor will trade to some point on the boundary of ![]() . Since the value function has the form
. Since the value function has the form ![]() , the optimal portfolio rules and the “no-trade” regions
, the optimal portfolio rules and the “no-trade” regions ![]() are independent of
are independent of ![]() . Figure 4 shows the no-trade regions for periods
. Figure 4 shows the no-trade regions for periods ![]() . We see that the no-trade region grows as
. We see that the no-trade region grows as ![]() approaches
approaches ![]() . This corresponds to the intuition that an investor is not likely to adjust his portfolio if he has to pay transaction costs and the holding time is short.
. This corresponds to the intuition that an investor is not likely to adjust his portfolio if he has to pay transaction costs and the holding time is short.
8 Dynamic Stochastic Integration of Climate and Economy
The examples presented above are simple ones that do not require the most advanced computational tools. In this section we described a far more ambitious use of numerical dynamic programming, and is a much better demonstration of the potential power of efficient dynamic programming.
There is growing concern about the impact of human activity on the climate. The global climate system is complex and its response to future increases in anthropogenic GHGs is poorly understood. Any rational policy choice must take into account the uncertainty about the magnitude and timing of climate change on economic productivity. This section describes the use of numerical dynamic programming algorithms to solve DSICE (Cai et al., 2012b, 2013a), a model of dynamic stochastic integration of climate and economy. DSICE is a DSGE extension of the DICE2007 model of William Nordhaus (Nordhaus, 2008). It is a well-known model used to examine various issues. One focus of research is estimating the expected social marginal cost of an extra ton of carbon in the atmosphere. This was, for example, the application of DICE used by IWG (2010).
The major contribution of DSICE is the ability to flexibly consider the importance of social attitudes toward risk. We know from the equity premium literature (Mehra and Prescott, 1985) that the standard, time-separable specifications of consumer preferences are incapable of modeling how people feel about risk. Kreps and Porteus (1978) have argued that there could be value in early resolution of uncertainty, and Epstein and Zin (1989) preferences have explored the implications of this for asset pricing.
Cai et al. (2012b, 2013a) build on Cai et al. (2012a) and combine standard features of DSGE models—productivity shocks, dynamic optimizing agents, and short time periods—with DICE2007, and adds uncertainty about the climate’s response to greenhouse gases. Specifically, it examined the impact of “tipping points” (see also Lontzek et al., 2012). A tipping point is an event that is triggered by warming and has a permanent impact on economic productivity. Lenton et al. (2008) discuss examples of possible tipping points.
8.1 A Stochastic IAM with Epstein-Zin Preferences
This section briefly describes the DSICE model and summarizes its conclusions. See Cai et al. (2012b, 2013a), for more details.
Let ![]() be a three-dimensional vector describing the carbon concentrations in the atmosphere, and upper and lower levels of the ocean. These concentrations evolve over time according to:
be a three-dimensional vector describing the carbon concentrations in the atmosphere, and upper and lower levels of the ocean. These concentrations evolve over time according to:
![]()
where ![]() is a linear transition matrix, and
is a linear transition matrix, and ![]() is the annual total carbon emissions dependent on the capital
is the annual total carbon emissions dependent on the capital ![]() and the fraction of potential emissions that are mitigated,
and the fraction of potential emissions that are mitigated, ![]() . The anthropogenic sources of carbon are represented by the
. The anthropogenic sources of carbon are represented by the ![]() , which will be specified below. The DICE climate system also includes temperatures of the atmosphere and ocean, represented by
, which will be specified below. The DICE climate system also includes temperatures of the atmosphere and ocean, represented by ![]() . The temperatures follow the law of motion
. The temperatures follow the law of motion
![]()
where ![]() is a linear transition matrix. Atmospheric temperature is affected by the total radiative forcing,
is a linear transition matrix. Atmospheric temperature is affected by the total radiative forcing, ![]() , dependent on the atmospheric carbon concentration.
, dependent on the atmospheric carbon concentration.
The impact of global warming on the economy is reflected by a simple damage function in DICE. Our damage function includes a term ![]() which represents damage to output due to the tipping point.
which represents damage to output due to the tipping point. ![]() if tipping has not occurred by time
if tipping has not occurred by time ![]() , and
, and ![]() at all times
at all times ![]() after a tipping event. The likelihood of tipping depends on current temperature. Thus, the stochastic damage factor in DSICE is
after a tipping event. The likelihood of tipping depends on current temperature. Thus, the stochastic damage factor in DSICE is
![]()
where the denominator represents the standard damage function from the DICE2007 model.
Capital ![]() follows the rule
follows the rule
![]()
where ![]() denotes the consumption level and
denotes the consumption level and ![]() denotes the production function, which is affected by the damage factor,
denotes the production function, which is affected by the damage factor, ![]() , the capital
, the capital ![]() , and the emission control rate
, and the emission control rate ![]() .
.
8.2 Dynamic Programming with Epstein-Zin Preferences
The standard separable utility function in the finite-horizon DICE2007 class of models is
![]() (19)
(19)
where ![]() is the total labor supply (and population). DSICE assumes a social planner maximizes the present-discounted utility stream up to a terminal time
is the total labor supply (and population). DSICE assumes a social planner maximizes the present-discounted utility stream up to a terminal time ![]() (600 years), using Epstein-Zin preferences.
(600 years), using Epstein-Zin preferences.
The dynamic optimization problem has six continuous state variables: the capital stock, ![]() , the three-dimensional carbon system,
, the three-dimensional carbon system, ![]() , and the two-dimensional temperature vector,
, and the two-dimensional temperature vector, ![]() . Furthermore,
. Furthermore, ![]() is the discrete shock to the climate. The recursive formulation of the social planner’s objective is
is the discrete shock to the climate. The recursive formulation of the social planner’s objective is
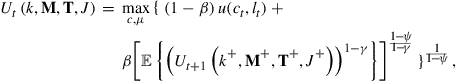
where ![]() is the inverse of the intertemporal elasticity of substitution,
is the inverse of the intertemporal elasticity of substitution, ![]() is the risk aversion parameter, and
is the risk aversion parameter, and ![]() is the discount factor. The actual risk premium will depend on interactions between
is the discount factor. The actual risk premium will depend on interactions between ![]() and
and ![]() . The special case of
. The special case of ![]() is the time-separable specification where both parameters represent both risk aversion and the elasticity of substitution. In general, increasing
is the time-separable specification where both parameters represent both risk aversion and the elasticity of substitution. In general, increasing ![]() will correspond to a greater willingness to sacrifice consumption to avoid risk. We use Epstein-Zin preferences because they are better at explaining the willingness to pay to reduce risk. This is the conclusion from the literature on the equity premium puzzle.
will correspond to a greater willingness to sacrifice consumption to avoid risk. We use Epstein-Zin preferences because they are better at explaining the willingness to pay to reduce risk. This is the conclusion from the literature on the equity premium puzzle.
The dynamic optimization problem can be formulated in terms of the value function
![]()
which implies the following Bellman equation:
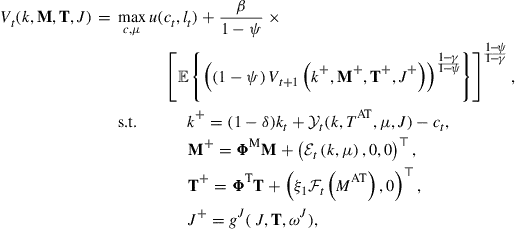 (20)
(20)
for ![]() . The terminal value function
. The terminal value function ![]() is the terminal value function given in Cai et al. (2012a).
is the terminal value function given in Cai et al. (2012a).
8.3 Numerical Examples
We implement our numerical dynamic programming to analyze how the optimal carbon tax is affected by different preference parameters combined with various tipping point events. We first solve a benchmark case with standard parameter assumptions. We cover a broad range of values for the degree of risk aversion ![]() and the reciprocal of the intertemporal elasticity of substitution
and the reciprocal of the intertemporal elasticity of substitution ![]() , representing empirical work that aims to estimate these parameters. In this section, we present the qualitative results of the benchmark case. The reader is referred to Cai et al. (2013a) for the specific parameter values and results of other cases.
, representing empirical work that aims to estimate these parameters. In this section, we present the qualitative results of the benchmark case. The reader is referred to Cai et al. (2013a) for the specific parameter values and results of other cases.
Figure 5 illustrates the typical dynamic path for the carbon tax. The lower dotted line represents the optimal carbon tax if no tipping were expected. The upper envelope in Figure 5 represents at each time t, the carbon tax if there has not yet been a tipping event. We call this the pre-tipping carbon tax. In contrast, the lower envelope in general represents the carbon tax in the post-tipping regime. Figure 5 also displays the timing of some sample tipping events. For example, the first drop (which is at year 2025 in Figure 5) is the first tipping out of our 1000 simulations. By the middle of this century about 5% of the simulated paths have generated a tipping point and by the end of the 21st century more than 20% of the paths have exhibited a tipping point.
The key fact to note in Figure 5 is the effect of the possible tipping event on the carbon tax. At the initial period (year 2005), the optimal carbon tax is $54, while it is $37 in the case when the tipping point does not exist, a significant increase. Furthermore, note that the extra carbon tax due to the anticipated tipping event is roughly constant. Figure 5 illustrates an unexpected decomposition of the optimal carbon tax: the deterministic component of damages implies a growing carbon tax in the optimal policy, but the stochastic damages caused by the uncertain time of tipping imply a near constant increase in the optimal carbon tax.
Different assumptions about tastes, technology, and climate will produce different optimal carbon tax paths. However, the example in Figure 5 as well as many others in Cai et al. (2012a) clearly show that the stochastic component must be modeled explicitly via stochastic dynamic programming. No certainty equivalent can make the distinction between the sure damages and the uncertain damages. This is a clear example of where multidimensional dynamic programming is essential to arrive at an important insight regarding greenhouse gas policy.
9 Conclusions
Dynamic economic problems are analyzed with dynamic programming methods. Solving the complex economic multidimensional problems that economists study requires reliable and efficient algorithms. This chapter has reviewed a few of the key elements of any such effort, but recognizes that there is much left to be done regarding both mathematical methods and efficient utilization of available hardware.
For example, further development of multidimensional approximation methods is needed. Using sparse grid methods (Malin et al. (2011) contains an informative discussion of Smolyak’s method, a sparse grid method used in economics) would dramatically reduce the number of points we use in our state space, but perhaps at the cost of not preserving shape. Numerical dynamic programming presents novel mathematical challenges due to the multiple objectives of using few points, computing an approximation that has small errors in a traditional metric such as ![]() , as well as computing an approximation that satisfies qualitative criteria such as monotonicity and curvature constraints. We suspect that algorithms that find efficient solutions to such approximation problems will themselves be computationally intensive, but in developing those methods we should remember that intensive computations will be worth the effort if the resulting value functions are evaluated thousands, or even millions, of times in later iterations.
, as well as computing an approximation that satisfies qualitative criteria such as monotonicity and curvature constraints. We suspect that algorithms that find efficient solutions to such approximation problems will themselves be computationally intensive, but in developing those methods we should remember that intensive computations will be worth the effort if the resulting value functions are evaluated thousands, or even millions, of times in later iterations.
By its definition, computational methods depend on the properties of computers, the hardware. As hardware changes, we will want to exploit novel features and capabilities. For example, the newest innovation in basic hardware is the exploding use of graphical processing units (GPUs) and the potential partnerships between GPUs and conventional CPUs in supercomputers. Hardware innovations are an essential part of the evolution of computational methods, and those developing methods will often find that new hardware alters the tradeoffs that must be balanced when creating numerical methods.
Hopefully this chapter will suffer the same fate as many other such chapters reviewing the state-of-the-art in computational tools and soon be viewed as being primitive and hopelessly out of date. Such is the nature of computational science.
Acknowledgments
Cai and Judd gratefully acknowledge NSF support (SES-0951576), and thank Karl Schmedders and three anonymous referees for their helpful comments.
References
1. Abrams RA, Karmarkar US. Optimal multiperiod investment-consumption policies. Econometrica. 1980;48(2):333–353.
2. Bellman R. Dynamic Programming. Princeton University Press 1957.
3. Boyle PP, Lin X. Optimal portfolio selection with transaction costs. North American Actuarial Journal. 1997;1(2):27–39.
4. Brown DB, Smith JE. Dynamic portfolio optimization with transaction costs: heuristics and dual bounds. Management Science. 2011;57(10):1752–1770.
5. Cai Y. Dynamic Programming and Its Application in Economics and Finance. PhD Thesis Stanford University 2010.
6. Cai Y, Judd KL. Stable and efficient computational methods for dynamic programming. Journal of the European Economic Association. 2010;8(2–3):626–634.
7. Cai Y, Judd KL. Dynamic programming with shape-preserving rational spline Hermite interpolation. Economics Letters. 2012a;117(1):161–164.
8. Cai, Y., Judd, K.L., 2012b. Dynamic programming with Hermite approximation. NBER Working Paper No. 18540.
9. Cai Y, Judd KL. Shape-preserving dynamic programming. Mathematical Methods of Operations Research. 2013;77(3):407–421.
10. Cai, Y., Judd, K.L., Lontzek, T.S., 2012a. Continuous-time methods for integrated assessment models. NBER Working Paper No. 18365.
11. Cai, Y., Judd, K.L., Lontzek, T.S., 2012b. DSICE: a dynamic stochastic integrated model of climate and economy. RDCEP Working Paper No. 12-02.
12. Cai, Y., Judd, K.L., Lontzek, T.S., 2013a. The social cost of stochastic and irreversible climate change. NBER Working Paper No. 18704.
13. Cai, Y., Judd, K.L., Thain, G., Wright, S., 2013b. Solving dynamic programming problems on a computational grid. NBER Working Paper No. 18714.
14. Cai, Y., Judd, K.L., Xu, R., 2013c. Numerical solution of dynamic portfolio optimization with transaction costs. NBER Working Paper No. 18709.
15. Constantinides GM. Optimal portfolio revision with proportional transaction costs: extension to HARA utility functions and exogenous deterministic income. Management Science. 1976;22(8):921–923.
16. Constantinides GM. Multiperiod consumption and investment behavior with convex transaction costs. Management Science. 1979;25:1127–1137.
17. Constantinides GM. Capital market equilibrium with transaction costs. Journal of Political Economy. 1986;94(4):842–862.
18. Costantini P, Fontanella F. Shape-preserving bivariate interpolation. SIAM Journal of Numerical Analysis. 1990;27:488–506.
19. Czyzyk J, Mesnier M, Moré J. The NEOS Server. IEEE Journal on Computational Science and Engineering. 1998;5:68–75.
20. Den Haan WJ, Judd KL, Juillard M. Computational suite of models with heterogeneous agents II: multi-country real business cycle models. Journal of Economic Dynamics & Control. 2011;35:175–177.
21. Epstein LG, Zin SE. Substitution, risk aversion, and the temporal behavior of consumption and asset returns: a theoretical framework. Econometrica. 1989;57(4):937–969.
22. Fourer R, Gay DM, Kernighan BW. Modeling language for mathematical programming. Management Science. 1990;36:519–554.
23. Gennotte G, Jung A. Investment strategies under transaction costs: the finite horizon case. Management Science. 1994;40(3):385–404.
24. Gill, P., Murray, W., Saunders, M.A., Wright, M.H., 1994. User’s Guide for NPSOL 5.0: a Fortran Package for Nonlinear Programming. Technical Report, SOL, Stanford University.
25. Gill P, Murray W, Saunders MA. SNOPT: an SQP algorithm for largescale constrained optimization. SIAM Review. 2005;47(1):99–131.
26. Goodman, T.N.T., 2001. Shape preserving interpolation by curves. In: Proceedings of the 2001 International Symposium, pp. 24–35.
27. Griebel M, Wozniakowski H. On the optimal convergence rate of universal and nonuniversal algorithms for multivariate integration and approximation. Mathematics of Computation. 2006;75(255):1259–1286.
28. Interagency Working Group on Social Cost of Carbon, 2010. Social Cost of Carbon for Regulatory Impact Analysis under Executive Order 12866. United States Government. <http://www.whitehouse.gov/sites/default/files/omb/inforeg/for-agencies/Social-Cost-of-Carbon-for-RIA.pdf>.
29. Judd KL. Numerical Methods in Economics. The MIT Press 1998.
30. Judd KL, Solnick A. Numerical dynamic programming with shape-preserving splines. Hoover Institution 1994.
31. Judd KL, Kubler F, Schmedders K. Bond ladders and optimal portfolios. Review of Financial Studies. 2012;24(12):4123–4166.
32. Juillard M, Villemot S. Multi-country real business cycle models: accuracy tests and test bench. Journal of Economic Dynamics & Control. 2011;35:178–185.
33. Kamin JH. Optimal portfolio revision with a proportional transaction cost. Management Science. 1975;21(11):1263–1271.
34. Kreps DM, Porteus EL. Temporal resolution of uncertainty and dynamic choice theory. Econometrica. 1978;46(1):185–200.
35. Lenton TM, Held H, Kriegler E, et al. Tipping elements in the Earth’s climate system. PNAS. 2008;105:1786–1793.
36. Lontzek, T.S., Cai, Y., Judd, K.L., 2012. Tipping Points in a Dynamic Stochastic IAM. RDCEP Working Paper No. 12-03.
37. Malin BA, Krueger D, Kubler F. Solving the multi-country real business cycle model using a Smolyak collocation method. Journal of Economic Dynamics & Control. 2011;35:229–239.
38. Mehra R, Prescott EC. The equity premium: a puzzle. Journal of Monetary Economics. 1985;15(2):145–161.
39. Murtagh B, Saunders M. A projected Lagrangian algorithm and its implementation for sparse nonlinear constraints. Mathematical Programming Study. 1982;16:84–117.
40. Nordhaus WD. A Question of Balance: Weighing the Options on Global Warming Policies. Yale University Press 2008.
41. Rust J. Using randomization to break the curse of dimensionality. Econometrica. 1997;65(3):487–516.
42. Rust J. Dynamic programming. In: Durlauf Steven N, Blume Lawrence E, eds. New Palgrave Dictionary of Economics. second ed. Palgrave Macmillan 2008.
43. Rust J, Traub JF, Wozniakowski H. Is there a curse of dimensionality for contraction fixed points in the worst case? Econometrica. 2002;70(1):285–329.
44. Schumaker L. On shape-preserving quadratic spline interpolation. SIAM Journal of Numerical Analysis. 1983;20:854–864.
45. Stachurski J. Continuous state dynamic programming via nonexpansive approximation. Computational Economics. 2008;31:141–160.
46. Wang S-P, Judd KL. Solving a savings allocation problem by numerical dynamic programming with shape-preserving interpolation. Computers & Operations Research. 2000;27(5):399–408.
47. Zabel E. Consumer choice, portfolio decisions, and transaction costs. Econometrica. 1973;41(2):321–335.
1Please see Judd (1998) for a detailed description of this.