Learning About Learning in Dynamic Economic Models*
David A. Kendricka, Hans M. Ammanb and Marco P. Tuccic, aDepartment of Economics, University of Texas, Austin, Texas 78712, USA, bUtrecht School of Economics, Utrecht University, Heidelberglaan, 8, Utrecht, 3584 CS, The Netherlands, cDipartimento di Economia Politica, Università di Siena, Piazza S. Francesco, 7, Siena, 53100, Italy, [email protected], [email protected], [email protected]
Abstract
This chapter of the Handbook of Computational Economics is mostly about research on active learning and is confined to discussion of learning in dynamic models in which the system equations are linear, the criterion function is quadratic, and the additive noise terms are Gaussian. Though there is much work on learning in more general systems, it is useful here to focus on models with these specifications since more general systems can be approximated in this way and since much of the early work on learning has been done with these quadratic-linear-gaussian systems.
We begin with what has been learned about learning in dynamic economic models in the last few decades. Then we progress to a discussion of what we hope to learn in the future from a new project that is just getting underway. However before doing either of these we provide a short description of the mathematical framework that will be used in the chapter.
Keywords
Active learning; Dual control; Optimal experimentation; Stochastic optimization; Time-varying parameters; Forward looking variables; Numerical experiments
JEL Classification Codes
C63; E61
1 Introduction
It is common sense that one can learn about an economic system as time passes. One can observe the inputs and outputs of the system and make inferences about the relationship between the variables that characterize the system. An example is a macroeconomics model with inputs like government expenditure, taxes, and the money supply and outputs like gross domestic product, inflation, and unemployment. Another example is a microeconomic model with inputs like the price level and resources such as capital, labor, and energy and outputs like production, sales, and profit.
In the control theory framework one can model the inputs as control variables and the outputs as state variables and characterize the relationship between the two with the functional form of the system equations and the parameters of those equations. In this context previously obtained data may be used to calculate the means and variances of the estimates of the parameters and of the additive noise terms in the system equations. Learning then occurs as more observations are obtained with the passage of time and these observations are used to modify the means and to reduce the variances of the estimates of the parameters and of the additive noise terms. This is called passive learning because no deliberate attempt is made to increase the learning done in each period.
In contrast active learning occurs when the control variables are chosen in each period in such a way as to perturb the system and thus increase the speed of learning.1 However, this is done only at some cost in moving the economic system away from the paths that would otherwise be followed.
This chapter is mostly about research on active learning and is confined to discussion of learning in dynamic models in which the systems equations are linear, the criterion function is quadratic, and the additive noise terms are Gaussian. Though there is much work on learning in more general systems, it is useful here to focus on models with these specifications since more general systems can be approximated in this way and since much of the early work on learning has been done with these quadratic-linear-gaussian systems.
We begin with what has been learned about learning in dynamic economic models in the last few decades. Then we progress to a discussion of what we hope to learn in the future from a new project that is just getting underway. However, before doing either of these it is useful to provide a short description of the mathematical framework that will be used in the chapter.
2 The Framework
The framework consists of two parts: an optimization part and a learning part. The optimization part of the framework consists of an objective that has to be minimized, the criterion value, and the constraints that bind this objective. In economics the constraints define the dynamics of the system (state). We start with the constraints.
As mentioned above, optimal control models, like those used in Kendrick (1980, 1981, 2002), have linear system equations of the form
(1)
where 
is the (discrete) time index, 
a state vector, 
a control vector, 
an independently and identically distributed (i.i.d.) additive noise term with 
, 
a transition matrix, 
a control coefficient matrix, and 
an exogenous variables vector. The vector 
is a vector containing the subset of the coefficients in 
, 
, and 
that are treated as uncertain. The matrix 
is a function of the subset of the uncertain coefficients in 
which come from that matrix. The same applies to 
and 
.
This class of models permits consideration of situations that are common in economics where the state variables 
may not all be directly observed or may not be observed without noise. The equations for this specification are called the measurement equations and may be written as
(2)
where 
is a measurement vector, 
a measurement coefficient matrix, and 
an i.i.d. measurement noise vector with 
.
The parameter estimates 
of the true 
change over time,2 while in most specifications of this class of models the true values of the parameters are assumed to remain constant. However, in some specifications the true values of the parameters are themselves assumed to be time varying. In these cases one can use parameter evolution equations of the form
(3)
where 
the parameter evolution matrix and 
an i.i.d. additive noise term 
. When a more general form of Eq. (3) is needed, the law of motion of the time-varying parameters can be written as
(4)
where 
is the identity matrix and 
is the unconditional mean of the stochastic parameter. This is the form used by Tucci (1997, 1998, 2004) to model a wide variety of time-varying parameter specifications. For example, when 
, Eq. (4) reduces to Eq. (3). Also, when 
and 
are zero, 
becomes the usual time-invariant case. In contrast, if 
is equal to zero, but 
is nonzero, then Eq. (4) describes a random parameter, i.e., a parameter varying randomly about the fixed mean 
. If, on the other hand, 
is equal to zero, Eq. (4) models a vector-autoregressive process of order one with mean zero. Also, random walk parameters may be modeled by setting 
equal to one. Finally, Eq. (4) can be used to represent a lack of knowledge about the parameters. For example, when the true parameter associated with the control variable is constant, but unknown, then setting 
equal to zero and 
not equal to zero allows one to interpret 
as the time-varying estimate of the unknown constant parameter 
based on observations through period 
. When this is the case, one can interpret 
as the covariance of the estimates based on all information available at time 
.
The initial conditions for the systems equation and the parameter evolution equations model are
(5)
where 
is the expectations operator. The expected states at 
, and their covariances 
are assumed to be known.3
The criterion function for this class of finite horizon models may be written with discounting terms as in Amman and Kendrick (1999b) as
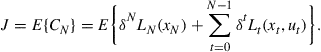(6)
is the (scalar) value of the criterion, a discount factor 
usually defined on the interval 
, 
the criterion function, and 
the terminal period.4 The two terms on the right-hand side of Eq. (6) are defined as
(7)
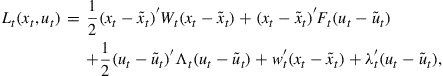(8)
where 
the desired state vector and 
the desired control vector. 
, and 
are penalty matrices on the deviation of states and controls from their desired paths. 
is assumed to be semi-positive definite and 
to be positive definite. 
and 
are penalty vectors on the deviation of states and controls from their desired paths.
In summary, the stochastic optimal control model is specified to find the set of control variables 
that will minimize the criterion function (6) subject to (7) and (8), the system Eqs. (1), the measurement Eq. (2), the parameter evolution Eq. (3) or (4), and the initial conditions (5).
This brings us to the second part of the framework. After the optimal control vector 
is chosen in each time period, the outputs of the system are observed and the means and variances of the parameters and of the state vectors are updated.
In this optimization procedure the original state vector 
is augmented with the parameter vector 
to create a new state
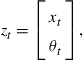(9)
thus the corresponding covariance matrix for the augmented state is written as
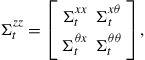(10)
where 
is the covariance for the parameter estimates as previously defined. In general, 
is not known and has to be estimated. Hence, we have
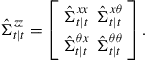(11)
Also, for all four elements of the covariance matrix 
a distinction will be made between the current period covariance 
, the projected covariance next period before new measurements are made 
, and the projected variance next period after new measurements are made 
.5
The estimation process used in Kendrick (1981, 2002) is the Kalman filter. The mathematical expression for updating the means of the uncertain parameters is6
(12)
where
(13)
From these equations one can see that the change in the parameter estimate from the projection 
to the post-measurement updated values 
depends on the difference between the actual measurement 
and the expected measurement 
via the measurement Eq. (2). From Eq. (12) one can see that the magnitude of this adjustment depends positively on the estimated covariance of the original state vector 
and the parameter vector 
in 
. Also, Eq. (13) shows that the magnitude of the adjustment depends inversely on the estimated degree of uncertainty about the original states 
and the variance of the i.i.d. additive noise term in the measurement equations, which is 
.
In parallel to the updating equation for the parameter means is the updating equation for the parameter covariances which is shown below
(14)
Note that the degree of learning in period t is represented by the decrease in the covariance from the prior projection 
to the posterior measurement update 
. Furthermore, in Eq. (14), this is positively related to the covariance of the original state vector 
and the parameter vector 
as represented by the estimated matrix 
. Also, from (13) and (14) the learning is inversely related to the degree of uncertainty about the original states 
and the additive noise term in the measurement equations, that is, 
.
This completes the discussion of the mathematical framework so, with this framework in mind, we turn to a discussion first of what has already been learned about learning in this type of dynamic economic model.
3 What We Have Learned
Research on passive and active learning stochastic control of economic models has been underway for more than 30 years dating back to the early work of Prescott (1972), MacRae (1972), and Taylor (1974) and including work by Norman (1976), Kendrick (1976, 1980, 1981), Easley and Kiefer (1988), Kiefer (1989), Kiefer and Nyarko (1989), Tucci (1989), Mizrach (1991), Aghion et al. (1991), Amman (1996), Amman and Kendrick (1995, 1997), Wieland (2000a,b), Beck and Wieland (2002), Tucci (2004), Cosimano and Gapen (2005a,b), Cosimano (2008), Tesfaselassie et al. (2007), and others. What have we learned about learning from this research?
3.1 Active Perturbation
The most basic expectation about active learning comes in comparing it to passive learning. For example, compare Expected Optimal Feedback (EOF) with Dual Control (DC).7 In EOF the choice of control takes into account the uncertainty in the parameter estimates and may therefore exhibit a tendency toward caution as compared to methods that do not consider the parameter uncertainty. However, in EOF no consideration is given to the impact of the current choice of control on future decreases in the uncertainty of the parameter estimates. In contrast, in the DC method the choice of control in each period depends on projections of the future covariance matrices of the parameters 
for all future time periods.
Thus one expects that the control variables will be more active in the early time periods in the active control (DC) solutions than in the passive control (EOF) solutions. Our experience is that this expectation proves to be true. In fact, it appears that the perturbations in the control variables with the DC method are used not to learn all parameters equally but rather to learn more quickly those parameters that are most crucial to the effective control of the system. Neither we nor, so far as we know, others have yet quantified these kinds of results; however, our causal observations of the models we have used suggest that this class of results holds.
3.2 Rapid Decrease in Parameter Variances in the First Few Periods
Also, we have observed that in most active learning solutions there is a very sharp decrease in the elements of the covariance matrix of the parameters, 
, in the first few time periods. Of course, the speed of this learning is related to the cost of the perturbations in driving the state variables further away from their desired paths than would otherwise occur. If this cost is high, the learning will progress more slowly. In addition, when the cost of control is high, i.e., in situations where the penalty weights in the 
matrix in the criterion function are relatively large, then the control will not be very active and the learning will be slower, i.e., the elements in the 
matrix will decline more slowly over time.
Conversely, if there is large initial uncertainty in the parameter estimates, 
, then it is difficult to effectively control the system and there is reason to provide larger perturbations in order to quickly reduce this uncertainty. Exactly how this trade-off will play out in macroeconomic and microeconomic systems is a matter that deserves substantial attention in future research.
3.3 Nonconvexities
Also, we have learned that the 
matrices play a major role in determining whether or not there are nonconvexities in the cost-to-go function. As we have related elsewhere, Kendrick (2005), in the early work on dual control we did not expect that the cost-to-go function would exhibit nonconvexities and we did not make any allowance for this. However, we accidentally discovered that local optima existed in the cost-to-go functions, Kendrick (1978), Norman et al. (1979), and this was confirmed by theoretical research by Mizrach (1991) and by numerical research by Amman and Kendrick (1995). Also, the presence of the nonconvexities has been confirmed by Wieland (2000a) using a different solution method, namely value function iteration.
Therefore as a guard against the nonconvexity problem we have incorporated grid search methods into our DualPC software systems.8 However the unvarnished grid search system may be inefficient. This occurs because in our experience the nonconvexities are most likely to occur in the first few periods when the 
matrix elements are relatively large. We have come to this realization in part by the way that the cost-to-go is divided into three components in the Tse and Bar-Shalom (1973) framework that we have used. These three components are labeled deterministic, caution, and probing. In our experience the deterministic term is always convex and the cautionary term is almost always convex so these two terms do not generally cause a problem. However, the third component, namely the probing cost term, can have a concave shape when the elements of 
are large. In this situation the sum of the deterministic, caution, and probing terms may be a nonconvex function with local optima and grid search methods or some global search optimization must be used.
However, in the cases where the 
declines rapidly over time the probing term diminishes in size relative to the other two terms and changes to a less pronounced concave shape. Thus the cost-to-go function will be nonconvex in the first few periods but will become convex in later time periods. In this situation one would like to use a global optimization procedure that checks in each time period to see whether or not nonconvexities are present. In those time periods where nonconvexities are present, time-consuming and thorough grid search methods must be used.
In contrast, in time periods where the cost-to-go function is apparently convex, efficient gradient methods can be used.9 We are still in the early stages of gaining experience with these approaches; however, it appears that they may be extremely useful in permitting the rapid solution of active learning control problems with substantial numbers of Monte Carlo runs in situations where there are nonconvexities in the cost-to-go function.
Sometimes mathematical results derived for one purpose have the fortunate side effect that they can later be used for another purpose. Such is the case of the analytical results that were originally derived to track down the sources of nonconvexities in small models. These results in Mizrach (1991) and Amman and Kendrick (1994b, 1995) allow one to fully characterize the three components of the cost-to-go function for the simplest one-state, one-control, one unknown parameter, quadratic linear adaptive control problem with a time horizon of two periods. Therefore, in Tucci et al. (2010) we have used these results as a starting point to compare the average or representative cost-to-go with different parameter sets and thus to analyze the effects of these different parameter sets on individual runs of a Monte Carlo experiment.10 The representative cost-to-go helps to sort out the basic characteristics of the different parameter sets. The Monte Carlo results are useful in reconciling the theoretical results in Mizrach (1991) and Amman and Kendrick (1994a, 1995) with the computational findings in Tucci (1998, 2004), and to shed some light on the outlier problem discussed in Amman et al. (2008).
3.4 Rankings
One of the key questions in the field of learning in dynamic economic models is whether there is enough difference between the solutions provided by different methods to justify coping with the complexity of the more sophisticated methods. We have addressed this question primarily by comparing three methods: Optimal Feedback (OF), Expected Optimal Feedback (EOF), and Dual Control (DC). We have discussed these methods in detail in Amman et al. (2008); however, the basic difference can be outlined in a few sentences.
The OF method is the most simple since it ignores the uncertainty in the parameter matrix and considers only the additive noise uncertainty 
in the system equations. Thus the solution method is very fast. The EOF method considers the uncertainty in both the additive noise term in the system equations and in the parameters in the 
vector which are elements from the 
and 
matrices and the C vector from the system equations. The EOF is more complex than the OF method, but is still computationally very efficient. However, this method does not consider the potential effect of change in the control today on the future uncertainty of the parameter estimates as represented in the 
matrices—matters that are considered in the DC method. The DC method is substantially more complex mathematically than the first two and is also much less efficient computationally—especially so in cases where nonconvexities arise.
When we first started learning about learning we expected that there would be a clear ranking between these three methods as measured by the criterion function values from the three solution methods over substantial numbers of Monte Carlo runs. We thought that DC would be clearly better than EOF which in turn would be clearly better than OF. Our experience so far has turned out to be more complex.
In each case when we compare the methods we have done it in two ways. One way is to count the percentage on the Monte Carlo runs in which each method had the lowest average criterion value across Monte Carlo runs when compared to the other two methods. The other way is to compute the average criterion value for each of the three methods over the Monte Carlo runs. A recent example of our work in this realm can be found in Amman et al. (2008) where we compare the three methods over solutions to the models from Beck and Wieland (2002). These results are typical of those that we have obtained with other models as well. Basically we find that the simple OF method does well relative to the more complex EOF and DC methods when the “number of runs” comparison is used. In contrast, the DC method does better than the EOF method which does better than the OF method when one compares average values.
We believe that the difference between these two types of results can be explained in rather simple terms. It appears that the less sophisticated OF method may work better in most cases; however in situations where it does not work well, it does very poorly. For example, in a Monte Carlo run where the initial values of the parameter estimates from the random drawing are relatively close to the true values, the OF method does well relative to the EOF and DC methods. However, when the initial values of the parameter estimates are away from the true values then there is a premium on treating those values with caution, as is done in the EOF method, or of actively perturbing the system in order to increase the rate of learning and thereby obtaining parameter estimates closer to the true values in later periods as is done in the DC method.
Since in our judgment the average value method is the most useful approach in most situations where learning occurs we believe that the DC method is better than the EOF and OF methods. However, this leaves open the question of how much better. If we compute the variance of the criterion values we usually find that the difference between the DC method and the EOF method is statistically significant; however, one may want to address this question in a larger realm than purely one of statistical significance.
Also, our experience is that the ranking between these three methods can be very model dependent.11 With some models one may get the expected ranking of DC better than EOF better than OF; however, with other models this ranking may be different. We do not yet have enough experience with different models to say much about which properties of models affect the rankings; however, we will address this question more in the following section of this chapter.
3.5 Time-Varying Parameters
There is one other more subtle question that we have begun to consider in this area. This comes from comparison of the methods across two versions of the same model, one without and one with time-varying parameters. (Here we mean time-varying values of the true parameters and not of the parameter estimates since in all learning situations there are time-varying values of the parameter estimates.) The Beck and Wieland (2002) model offers a good laboratory for this kind of experiment since it has both constant parameter and time-varying parameter versions.12 Using the “average value” approach it would seem that the difference between the DC method and the EOF method might diminish when one moves from the constant parameter to the time-varying parameter version of the model. This occurs because the gain from learning diminishes when the true values of the parameters themselves change over time. Our results in Amman et al. (2008) are of this variety.
However, it can also be argued that in situations where the true values of the parameters are time varying it will be even more important to perturb the system to try to continue to track those changing true values. Thus the jury may be out on this more subtle question for some time to come.
3.6 Model Sizes
Our experience with learning about learning is so far limited to small models with only a few equations and unknown parameters. However, as the speed of computers continues to increase it may well be possible to do large numbers of Monte Carlo runs using even the more sophisticated DC methods and even here in cases where there may be some nonconvexities in the cost-to-go function.13 The crucial issue will probably not be so much the number of uncertain parameters but rather the number of control variables since this governs the number of dimensions in which one must search in cases where there are nonconvexities.
4 What We Hope to Learn
The field of learning in dynamic economic models got off to a strong start 20/30 years ago but then went through a period when there was less interest among economists in the subject. That has changed in recent years with an increase in contributions from two groups, one at the Goethe University Frankfurt led by Volker Wieland and one at Notre Dame University led by Thomas Cosimano. These two groups and our own each use different methods for solving learning models so we have launched a small and informal project to compare the three methods and thus to learn their comparative advantage.
The first session of the project included presentation of the three methods. Wieland presented a dynamic programming method with numerical approximation of optimal decision rules, Wieland (2000a,b), that is based on previous work on authors such as Prescott (1972), Taylor (1974), and Kiefer (1989). Cosimano discussed his perturbation method applied in the neighborhood of the augmented linear regulator problem (see Cosimano, 2008 and Cosimano and Gapen, 2005a,b), which drew on the work by Hansen and Sargent (2001, 2004, 2008). We talked about the adaptive control method (see Kendrick, 1981, 2002, and Amman and Kendrick, 1999a,d, 2003) that drew on earlier work in the engineering literature by Tse (1973), Tse and Athans (1972), Tse and Bar-Shalom (1973), and Tse et al. (1973).
After the session we decided to use all three methods to solve the same model and thus to begin a new phase of learning about learning in dynamic economic models. The first model we selected to solve was the Beck and Wieland (2002) model with both constant parameter and time-varying parameter versions. In this work Gunter Beck has joined with Volker Wieland, Michael Gapen is working with Thomas Cosimano, and Marco Tucci has become a member of our group.
The focus of this Methods Comparison project will be to study the comparative advantage of the three methods in a number of dimensions including accuracy and efficiency and to use the three methods to further explore a number of questions about learning. These questions are what characteristics of models cause different rankings among OF, EOF, and DC methods, whether or not nonconvexities will turn out to be a common or an uncommon problem in economic models, whether measurement errors are large enough that they should be routinely included in learning models, and whether the use of constant or time-varying parameters in the models changes the answers to any of the questions above.
4.1 Accuracy
It would appear that the dynamic programming method used by Wieland and Beck will produce more accurate solutions than either of the other two approaches since they both use approximation methods. However, it remains to be seen how large this loss of accuracy is for each method relative to the dynamic programming methods.
4.2 Efficiency
It would also appear that the approximation methods used by (1) Cosimano and Gapen and (2) our group will be more efficient and thus be able to solve larger models and do larger numbers of Monte Carlo runs on those models. However, it remains to be seen whether or not that difference is substantial and what dimensions of the models are most important in determining this relative efficiency. It may be that it is not the number of state variables or control variables that is the crucial measure of size here but rather the number of parameters that are treated as unknown. For example, a relatively large model might have only a few parameters that need to be learned and thus the least efficient of the three methods will still be very useful for that model.
4.3 Rankings
In the process of applying the three methods to a number of different economic models we hope to begin to sort out the question of what characteristics of different economic models result in differences in the rankings between the OF, EOF, DC, and related methods. From the discussion above it appears likely that the size of the initial parameter uncertainty in 
will be a crucial element; however, it also seems likely that the nature of the 
matrix and the degree of controllability of the model may also be very important. Likewise it may be that the nature and size of the measurement errors may play a large role in determining the rankings of different methods on various types of models.
4.4 Nonconvexities
As discussed above, it appears that the size of the elements in the initial estimate of the parameter covariance matrix 
plays a crucial role in determining whether or not there are nonconvexities in the cost-to-go function. If the elements in this matrix are relatively small in macroeconomic, finance or microeconomic models, then there will probably be little or no problem with local optima in those models. On the other hand if these elements are relatively large in models from some applications areas then it will be necessary to redouble our efforts to include efficient global search methods in our computer codes.
For models with a single control, grid search methods may prove to be an effective way to obtain the global optimal solution, even though these methods may not be the most efficient methods. However in models with more than one control—and even in some models with a single control—it may be wise to use more sophisticated global search methods. Our experience suggests that nonconvexities are much more common and subtle than what the theoretical results suggest. For example, Amman and Kendrick (1995, page 465) found that when the MacRae (1972) parameter set is used the cost-to-go function becomes nonconvex when the variance of the estimated parameter is set to 
. However, Tucci (1998, 2004) found nonconvexities in 28% of the cases of a Monte Carlo experiment with the same parameter set and a variance equal to 0.5 for the unknown parameter. Thus it may be wise to employ sophisticated global optimization methods with most models until one has gained some confidence that nonconvexities are not present.
4.5 Measurement Errors
Measurement errors have not been commonly considered in economic models, yet it seems likely that they may serve as an important limitation of learning in economic models. The good news here is that stochastic control methods commonly are equipped to handle measurement errors and we have included them in the models we have experimented with for some years. Also, there is recently new attention to this area of economics as in the work of Coenen et al. (2005).
4.6 Time-Varying Parameters
The methods used by all three groups include, to various degrees, the ability to handle time-varying parameter specifications. In particular, Tucci (1989, 2004) has done considerable work in this area and has laid the groundwork for exploration of the effects of time-varying parameters on the rankings of OF, EOF, and DC methods and of the relative efficiency of different approaches to solving economic models with learning.
4.7 Monte Carlo Runs
While much useful knowledge can be obtained from analysis of representative runs of stochastic control models, when comparison of solution methods is being considered, Monte Carlo experiments have been the method of choice. For each Monte Carlo run random values of the system noise 
and the initial parameter estimate 
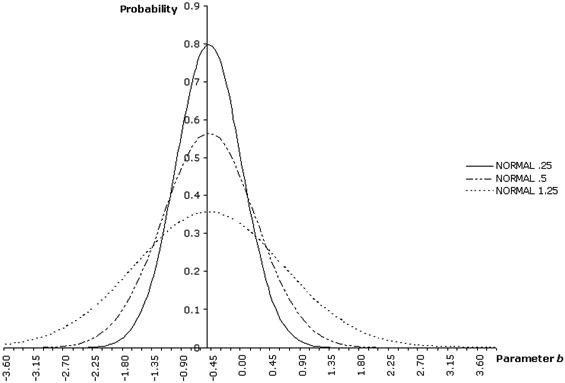
are generated using the means and covariances described above. This corresponds to running the model repeatedly with different additive noise terms and with different initial values of the estimate of the parameter 
. Figure 1 shows (for a model with a single uncertain parameter) the probability density function of the initial parameter estimate for selected values of its covariance. It highlights the effect of this quantity on the actual values of the uncertain parameter used in a Monte Carlo experiment. 14
when 
, 
, and 
.Therefore it is important to analyze the shape of the approximate cost-to-go function when the initial parameter estimate takes on values in different intervals. Recall that even though the probability that the parameter will take on a specific value is zero, the probability that it will fall in a certain interval is not zero. In studying the effect of changes in the parameter (when that parameter is the one multiplied by the control variable) Amman and Kendrick (1995, page 470) observed that for the MacRae (1972) model the cost-to-go function will be convex for values either substantially above or below zero but will be nonconvex for values close to zero. However, they did not investigate the relationship between this result and the outcomes of the Monte Carlo experiments. In Tucci et al. (2010) we have moved in this direction studying more closely this model. However, more general models should also be considered.
5 Algorithms and Codes
One of the most important aspects of research in this area is that the mathematics of the algorithms for learning in dynamic economic models is complex. It is not difficult but it is complex—both in the sense of there being a lot of it and in the sense of requiring close attention to a substantial amount of detail. The mathematics has cost-to-go functions, Riccati equations, Kalman filters, and other components that are themselves not difficult; however, when they are combined in an active learning framework the whole requires prolonged and careful work to master.
Also, this is reflected in the computer codes. They too are not inherently difficult to understand but they require the development of many substantive subroutines that must be integrated carefully.
The result of this situation is that until recently there have not been many alternative algorithms and codes developed in this area. This meant that it has been difficult to cross-check both mathematical and numerical results and therefore to increase the probability that both the math and the codes are error free. However, this is now changing. Within our own group Tucci (2002) has developed a variant of the adaptive control code which includes a variety of ways to specify time-varying parameters. In the process he has modified the mathematics in Kendrick (1981, 2002) and thus provided an independent derivation of the many mathematical results. Also, Beck and Wieland (2002), Cosimano (2008), and Cosimano and Gapen (2005a,b) have provided detailed results and derivations of those results that permit cross checking of aspects of the mathematics. A small beginning of cross checking of mathematical results is in Kendrick et al. (2008) which compares results obtained by Beck and Wieland (2002) with those obtained by our group.
Also, we now have a variety of computer codes available that permit cross checking of numerical results. The original Dual code by Kendrick has been extensively revised and updated by Hans Amman to create DualPC which is an efficient code in Fortran. Kendrick has developed a Windows version of Dual in the C language with an easy-to-use interface (DualI) to permit low-cost entry to the field. Amman has developed code in MATLAB that is useful for solving models with rational expectations. Tucci has created a version of Dual with a variety of time-varying parameter specifications (DualTVP). We have found it most useful to run these codes against one another in a continuing process of checking numerical results.
Also Wieland has developed code in Fortran to implement his algorithm and has made it available at his web site (http://www.volkerwieland.com) and Cosimano and Gapen have developed code in MATLAB to implement their algorithm. We anticipate in the future that all three groups will be able to solve a number of different macroeconomic and financial models and thus facilitate numerical checking across codes. As an example of this, in the following section we report on work we have done recently on the Beck and Wieland (2002) model.
Recently, a research group headed by Reinhard Neck at Klagenfurt University in Austria has extended their OPTCON code for models with nonlinear system equations to include a Kalman filter for learning parameters.15 They have informally reported that they have been able to replicate results from two test models in the DualI software for both OF and EOF solutions.
6 A Showcase on Active Learning
In this section we will present a simple model that fits into the framework we have presented in Section 2 and we focus on the issue of rankings as discussed in Section 3.4. Thus we compare Optimal Feedback (OF), Expected Optimal Feedback (EOF), and Dual Control (DC) methods. We begin with a brief presentation of the BW model followed by the results for the constant parameter version of the model and then progress to the results for the version with time-varying parameters.
6.1 Outline of the Beck and Wieland Model
Following Beck and Wieland (2002) the decision maker is faced with a linear stochastic optimization problem of the form
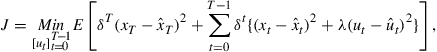(15)
(16)
(17)
In fact the model goes back to an earlier strand of literature in the early 1970s; see MacRae (1975). The model contains one uncertain parameter 
, with an initial estimate of its value 
, and an initial estimate of its variance 
. The parameters 
and 
are constant, 
, and 
. Beck and Wieland assume in their paper that 
. In contrast, we will assume that the planning horizon is finite, hence 
. Furthermore, we have adopted the timing convention from Kendrick (1981, 2002) where the control, 
, has a lagged response on the state 
.
For the simulations in the next paragraphs we will use the following numerical values for experiments: 
, 
, 
for the constant parameter case, and 
for the time-varying parameter case (see the next two sections). Furthermore, 
, and 
.
With this set of parameters, the above model can be solved in DualPC (see Amman et al., 2008), allowing us to simulate the various situations in the next sections.
6.2 Constant Parameters
We make a distinction, at each time step, between the true parameters, 
, and the estimates of those parameters, 
. In this version of the model the true values of the parameters are constant but the estimates change over time. In contrast, in the time-varying parameter version of the model in Section 6.3, both the true parameters and the estimates change over time.
The parameters are the same as those used with the versions of the model solved with DualI except for the discount factor, 
, which is set at 0.95 in the DualI versions and at 1.00 in the DualPC versions. The reason for this is that the DualPC software does not yet support discounting.
We used the DualPC software to run 10,000 Monte Carlo in which we compared the criterion values obtained with three different methods: OF, EOF, and DC. As indicated above, the first two methods are described in the complementary paper, Kendrick and Tucci (2006). For each Monte Carlo run, random values of the system noise 
and the initial parameter estimate 
are generated using the means and covariances described above. This corresponds to running the model repeatedly with different additive noise terms and with different initial values of the estimate of the parameter 
.
The DC (adaptive control) method used here is the one described in Chapters 9 and 10 of Kendrick (2002). In addition, the DualPC software includes a grid search method that is designed to deal with possible nonconvexities in the cost-to-go function. This is a two-level grid search that begins in the neighborhood of the OF solution. The best grid point obtained in the first search then provides the starting point for the second level search which is done in finer detail over a lesser range than the first grid search.
When we applied the OF, EOF, and DC methods to the BW model we found that in a substantial number of runs the criterion value for one or more of the methods was unusually large. Or, to say this in another way, the distribution of criterion values had a long right tail.
This outlier problem may be caused by the initial parameter estimates for the uncertain parameter, which are themselves outliers in either the right or left tail of that distribution. Assuming that the uncertain parameter has mean −0.5 and variance 1.25 implies that the initial value used in the Monte Carlo runs is in the interval (−1.62, 0.62) in approximately 68% of the cases, and in the intervals (−2.74, 1.74) and (−3.86, 2.86) in approximately 95% and 99%, respectively, of the cases. Alternatively put, the initial estimate of the unknown parameter is outside the narrower interval (−1.62, 0.62) approximately 32% of times and this is obviously reflected in the associated value of the criterion function. To see how the various methods perform in the different situations we decided to run the comparison three times. In the first test we kept the runs in which the criterion value for all of the three methods was less than or equal to 100. In the second test we set this boundary at 200 and in the third run we set the boundary at 500. Thus in the three tests we include a larger and larger number of the runs that we are uneasy about. Therefore we are inclined to give more credence to the test with the lower cutoff values.
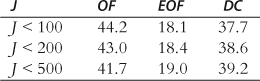
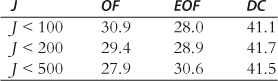
Our calculations were performed on a 64-bit AMD Dual Opteron Linux machine. Each simulation run of 10,000 Monte Carlo runs took about an hour of processing time on one processor. In comparing the results we looked first at the percentage of runs in which each method proved to have the lowest criterion value. These results are shown in Table 1.
The first line of Table 1 shows that for the 
case the percentage of Monte Carlo runs for which each method obtained the lowest criterion value was OF 44%, EOF 18%, and DC 38%. These results proved to be relatively constant across the three rows of Table 1 which indicated that the outlier problem does not seem to affect the relative performance of the three methods.
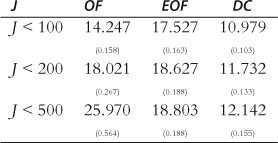
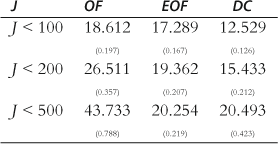
The second way we compared the results was by examining the average criterion value for each method with their standard errors.16 These results are shown in Table 2.
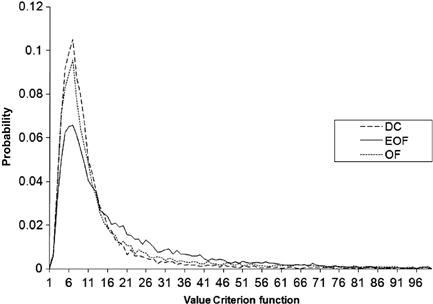
The first row in Table 2 shows that the OF and EOF methods do not do as well as the DC method in the 
case. This is the result to which we currently assign the most credence because it describes a situation where the estimated parameter is not “too far” from the true unknown value. The simulated probability density function for OF, EOF, and DC, 
, is plotted in Figure 2.
Looking down the columns in Table 2 we see, not unexpectedly, that the average criterion values increase as more of the outliers are included. However, it is worth noting that the criterion values in the EOF column do not increase as rapidly as do those in the OF column. This is consistent with our results in Amman and Kendrick (1999d), that when the OF solutions are bad they may be really bad, i.e., when you have an outlier estimate for the parameter value and treat it as though you trust that it is correct one can get a seriously bad solution. In these cases EOF is better, because it is cautious, and DC is better yet, because it devotes a part of the control energy to experiments to help learn the parameter value. Next we turn to the version of the BW model with time-varying parameters.
6.3 Time-Varying Parameters Version
In this version of the BW model the true value of the parameter is time varying and follows a first-order Markov process. The major change from the first version of the model is that the variance of the additive noise term in the parameter evolution equation, 
, is not zero, as in the previous version, but is 
. Also, recall that for both versions of the model solved with the DualPC software, the discount factor, 
, is not 0.95 but rather 1.00.
Just as with the constant parameter version of the model, in comparing the results we looked first at the percentage of the 10,000 Monte Carlo runs in which each method proved to have the lowest criterion value. These results are shown in Table 3.
The first line of Table 3 shows that for the 
case the OF method and the EOF method each had the lowest criterion valve in roughly 30% of the Monte Carlo runs and that the DC method had the lowest criterion value in roughly 40% of the runs. So the DC method proves to be the best of the three when the comparison is done in this way.
Then a comparison of the second and third rows in Table 3 to each other and to the first row shows that the percentage of the Monte Carlo runs in which each method had the lowest criterion value was not affected much by the number of outliers that were included. Again the outliers do not seem to affect the relative performance of OF, EOF, and DC.
The second way we compared the results was by examining the average criterion value. These results with their standard errors are shown in Table 4.17
The first row in Table 4 shows that the OF method does not do as well as the EOF method which in turn does not do as well as the DC method in the 
case. This is the result to which we currently assign the most credence.
Looking down the columns in Table 4 shows, not unexpectedly, that the average criterion values increase as more of the outliers are included. However, it is worth noting that the criterion values in the EOF column do not increase as rapidly as do those in either of the other columns.
Overall the most important result from these Monte Carlo experiments to provide ranking among methods using the Beck and Wieland model is that the Dual Control (DC) method is better than the Expected Optimal Feedback (EOF) and the Optimal Feedback (OF) method in the constant parameter case. Also, in the time-varying parameter case the DC method is better than the EOF method which in turn is better than the OF method.
7 Learning with Forward Looking Variables
In the mid-1970s the use of optimal control techniques for deriving an optimal macroeconomic policy, e.g., Pindyck (1973) and Chow (1975), came under scrutiny. The critique by Lucas (1976) argued that it is difficult to determine optimal macroeconomic policies because the announcement of these policies results in changes in behavior by economic agents and thus changes in the parameters on which the optimal policy was based.
In this view one of the major drawbacks was that control methods could not deal with forward looking variables or rational expectations (RE). Subsequently a number of generic methods to solve models with forward looking variables were developed. For instance, Fair and Taylor (1983) used an iterative method for solving RE models and, in the tradition of Theil (1964) and Fisher et al. (1986) used a method based on stacking the model variables. Blanchard and Kahn (1980) and Anderson and Moore (1985) both presented methods based on the saddle point property.
A computational attractive and widely applicable method was introduced by Sims (2001) and applied in a control framework by Amman and Kendrick (2003). Sims solves forward looking models by using a generalized inverse approach based on the QZ decomposition. In the following subsection we will show how Sims’ approach can be used with forward looking models that include learning.
7.1 Extending the Framework
The state Eq. (1) can be augmented to accommodate forward looking variables like this
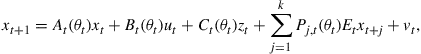(18)
where additionally to Section 2 the matrix 
is a parameter matrix, 
is a parameter matrix for the exogenous variables, 
is the vector of exogenous variables, and 
is the expected state for time 
at time 
being the maximum lead in the expectations formation.
In order to compute the admissible set of instruments we have to eliminate the rational expectations from the model. In order to apply Sims’ method we first put (18) in the form
(19)
where
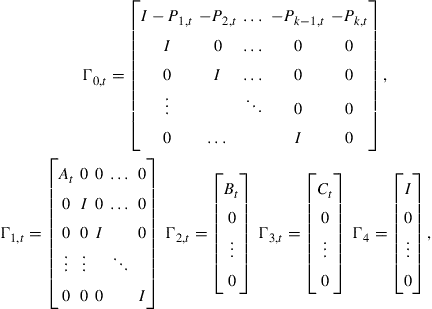
and the augmented state vector
(20)
Taking the generalized eigenvalues of (19) allows us to decompose the system matrices 
and 
in the following manner, viz. Coleman and Van Loan (1988) or Moler and Stewart (1973),
with 
and 
. The matrices 
and 
are upper triangular matrices and the generalized eigenvalues are 
. If we use the transformation 
and 
we can write (19)
(21)
It is possible to reorder the matrices 
and 
in such a fashion that the diagonal elements of the matrices 
and 
contain the generalized eigenvalues in ascending order. In that case we can write (21) as follows
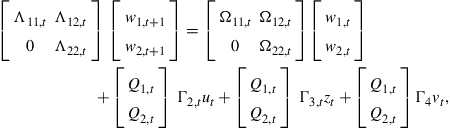(22)
where the unstable eigenvalues are in the lower right corner, that is, the matrices 
and 
. By forward propagation and taking expectations, it is possible to derive 
as a function of future instruments and exogenous variables
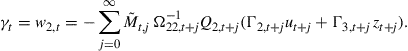(23)
The matrix 
is defined as
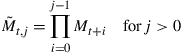
and
with
Given the fact that 
contains the eigenvalues outside the unit circle, we have applied the following condition in deriving (23)
In contrast to Sims, 
is not time invariant since we explicitly want to allow for time-dependent matrices in the model. Reinserting (23) into (22) gives us
(24)
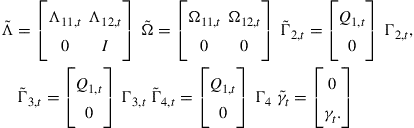
Knowing that 
and 
we can write (24) as
(25)
with
(26)
and
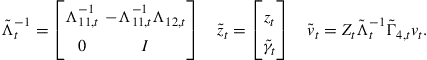(27)
Now that we have the augmented state Eq. (18) in the form of Eq. (25) we can compute the admissible controls as a function of the expected future states
(28)
Once we have applied these controls, we can go back to the augmented system and compute the expected future state 
and estimate the parameters 
when new information on the state 
becomes available. Hence, like with the controls 
the same holds for the estimation of the parameter that is a function of expected future states.
(29)
More detail about the corresponding algorithm is presented in Amman and Kendrick (1999a).
7.2 An Example
In an earlier paper, Amman and Kendrick (2003), we introduced a model in which one can address the question of how best to do macroeconomic policy formulation in an environment in which agents may change their behavior over time, as well as in response to economic policy pronouncements. To mimic the Lucas critique in our example we will assume that the random vector 
is influenced by the real money supply in the following way
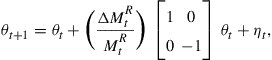(30)
which means that an increase in the real money supply has an increasing effect on inflation and a decreasing effect on output.18 The policy maker will be unaware of this relationship and will try to estimate 
based on the random walk assumption.
Consider first the unrealistic case in which the policy maker knows exactly the component of the drift in the parameters which is due to policy changes. We call this scenario Known Parameters. This is accomplished in the model by correcting the estimation of the parameters each time period when the updating occurs as in Eqs. (12) and (13), that is,
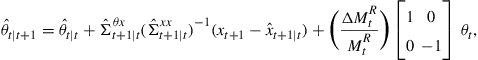(31)
so the policy maker is aware of the parameter shifts described in Eq. (30). Also, the parameters in this scenario are stochastic and time varying due to 
. Note that Eq. (31) is slightly simpler than Eq. (12) due to the fact there is no measurement error and therefore 
and 
. While, in reality, it would be impossible for policy makers to know exactly the parameter shifts like those modeled in Eq. (30) the known parameters case provides us with an infeasible but useful standard with which to compare other policy selection methods.
In the face of the fact that parameter drift may be occurring in the economy, policy may be determined in a deterministic manner treating all parameters as known and constant—i.e., a Deterministic scenario. In this case the true values of the parameters drift but the policy maker does not know what these values are and does not modify his or her policy in any way because of the stochastic elements of the model. One can then compare these two cases to asks whether or not knowing the parameter drift makes a difference. In order to do this we performed 1000 Monte Carlo runs with the model above and obtained the results shown in Table 5.
In both of these cases the true parameters are drifting over time and changing in response to shifts in policy values; however, in the known parameters case the policy maker knows the effect of policy changes on the drift and in the deterministic case he or she uses parameter values which are not correct, but treats those values as though (1) they are correct and (2) there is no uncertainty attached to the parameter estimates. Not surprisingly, the average criterion value is better at 1.638 for the known parameters case than at 1.675 for the deterministic case. Also from the max and min comparisons one can see that there is considerably more variability in the deterministic case than in the known parameters case, and this is confirmed in the last column which shows the standard deviation of the criterion values across the 1000 Monte Carlo runs.
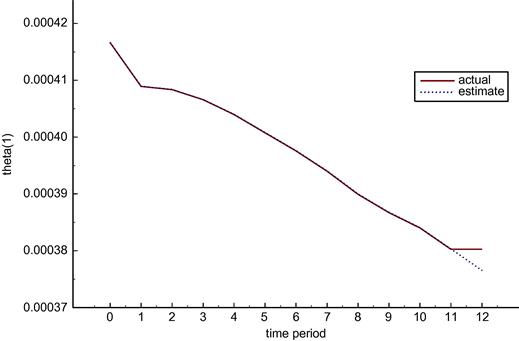
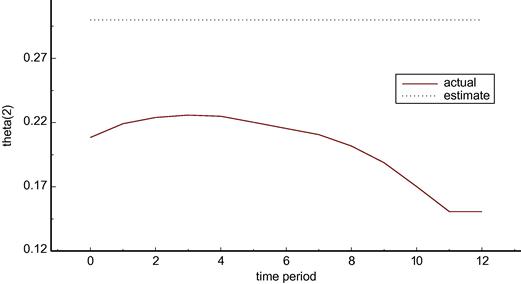
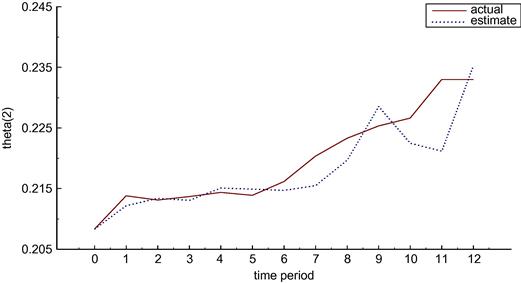
As an example of the nature of these results, compare Figures 3 and 4 which show the values of parameter 
in the two cases. The actual value of the parameter drifts down in both cases but changes by different amounts because the use of the policy variables is not the same in the two cases. In contrast the estimated value tracks the actual very closely in the known parameters case but does not track and indeed does not change in the deterministic case.
(1)).
(1)).So for the example at hand, the scenario of known parameters is better than the scenario of ignoring the fact of the unknown parameters in the deterministic case. Thus the Lucas critique is valid in this case. Ignoring the fact that the parameters are drifting and changing in response to policy pronouncements results in higher loss functions for the performance of the economy.
Would it be possible to do better with some other policy formulation method? One alternative approach would be to use game theory between the policy makers and the agents. Another, and the one which is examined here, is for the policy makers to (1) treat seriously the fact that they are using parameter estimates rather than the true parameter values when making policy and (2) update parameter estimates as the true values of the parameters drift over time and shift in response to policy announcements. We call this scenario the Learning approach. One can then ask whether the learning approach is indeed better than the deterministic case. This comparison is provided in Table 6.
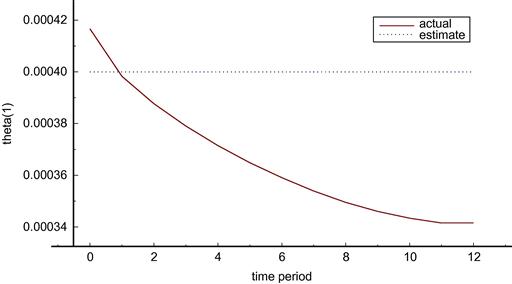
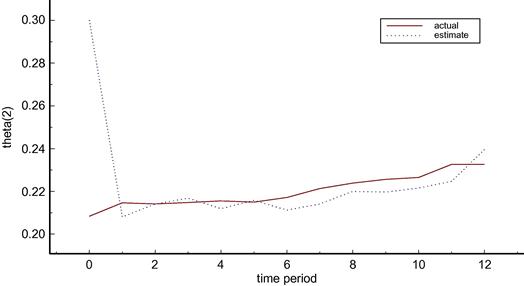
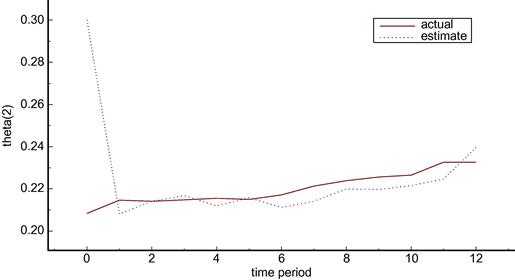
The average value of the criterion function over the 1000 Monte Carlo runs is better at 1.646 for the learning case than at 1.675 for the deterministic case. Also, the variability is lower for the learning case than the deterministic case as is shown in the remaining three columns of Table 6. Thus, for the case at hand, it is better to take account of the uncertainty in the parameters when determining policy in an environment where parameters are changing. Figures 5 and 6 show the true and estimated parameter estimates for the deterministic and learning scenarios—this time for parameter 
.
(2)).
(2)).As before, in the deterministic case there is no change in the parameter estimate in Figure 5. In contrast Figure 6 shows that there is a very rapid learning of the 
parameter in the learning scenario and that this parameter estimate then tracks closely the drift in the actual parameter over time.
Finally, one can ask whether the Lucas critique still carries heavy weight when policy makers treat seriously the uncertainty of parameter estimates in determining policy levels. Table 7 provides an indication of how this question may be answered by providing a comparison of the known parameters and the learning scenarios.
There is little difference between these two cases in either the means in the first column or in the indicators of variance in the remaining three columns. Thus for this commonly used small macroeconomic model, the effects of the Lucas critique are substantially mitigated if one uses policy determination methods which treat the uncertainty in parameter estimates seriously and track the drifting parameters over time by using Kalman filter estimators. Moreover, it is not possible for policy makers to have as much knowledge about parameter drift as the known parameters method implies; therefore, the difference between the learning method and a feasible method similar to the known parameters method would be even smaller.
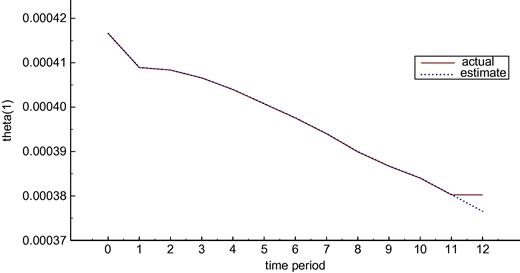
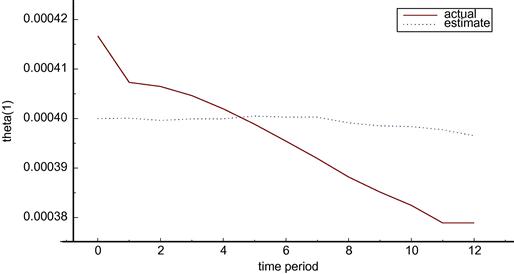
A comparison of Figures 7 and 8 shows that the known parameters scenario provides a better tracking of 
than does the learning scenario. However, a comparison of Figures 9 and 10 shows that the learning method does almost as well at tracking 
as does the known parameters method.
(1)).
(1)).
(2)).
(2)).In summary, forward variables and the effects of policy choices on the parameters modeling agent behavior can be included in stochastic control settings with learning. Furthermore, these methods can be used to mitigate the effects of the Lucas critique.
8 Other Applications of Active Learning
A referee has suggested that we add a section to our original paper that would provide a list of areas of applications with references to a number of articles that study learning and control in both microeconomic and macroeconomic applications. Apparently many of these applications use bandit-type frameworks where unknown parameters are known to take on only one of two possible values. However, in the referee’s opinion some of these might be improved with the methods presented in this article. The areas and the articles are as follows:
• Monopolistic profit maximization with unknown demand: Kiefer (1989) or Trefler (1993).
• Experimental consumption, drug use: Crawford and Shum (2005) or Grossman et al. (1977).
• Investment and growth under uncertainty: El-Gamal and Sundaram (1993) or Bertocchi and Spagat (1998).
• Inflation targeting and monetary policy: Wieland (2006), Ellison (2006) or Svensson and Williams (2007).
9 Summary
Thus looking back one can see that much has been learned about learning in dynamic economic models. It has been confirmed that in many cases the expected ranking between Optimal Feedback, Expected Optimal Feedback, and Dual Control methods holds, but we have also learned that this is not always the case. We have been surprised to find that nonconvexities can occur in the cost-to-go function but have been able to track down in the mathematics the reasons that this occurs and have been able to confirm numerically in the computer codes that these effects are significant. We have developed algorithms and computer codes for global search methods that are specifically tailored to deal with the way that nonconvexities appear in economic models in early time periods but disappear in the later time periods of the same model.
We have also learned how to incorporate forward variables and the effects of policy choices on the parameters that model agent behavior into stochastic control models with learning and time-varying parameters. And, in addition, we have found that models in this class can be used to show how one can mitigate the effects of the Lucas critique.
However, we have not yet been able to learn the characteristics of various economic models which change the ranking among the methods. We do not yet know whether or not nonconvexities will occur in most economic models or in only a few models. We do not yet know whether measurement errors will be large enough in many economic settings to substantially alter the results when they are included or excluded.
There are now a number of research groups actively working in this field and this has opened the possibility for fruitful checking of both mathematical and numerical results across algorithms and codes as well as the development and use of a variety of models from different fields of economics in order to learn more about learning.
References
1. Aghion P, Bolton P, Harris C, Jullien B. Optimal learning by experimentation. Review of Economic Studies. 1991;58:621–654.
2. Amman HM. Numerical methods for linear-quadratic models. In: Amman HM, Kendrick DA, Rust J, eds. Handbook of Computational Economics. Amsterdam, The Netherlands: North-Holland Publishers (Elsevier); 1996:579–618. Handbook in Economics vol. 13.
3. Amman HM, Kendrick DA. Active learning: Monte Carlo results. Journal of Economic Dynamics and Control. 1994a;18:119–124.
4. Amman HM, Kendrick DA. Nonconvexities in stochastic control problems: An analysis. In: Cooper WW, Whinston AB, eds. New Directions in Computational Economics. Dordrecht, The Netherlands: Kluwer Academic Publishers; 1994b:57–94. Advances in Computational Economics vol. 4.
5. Amman HM, Kendrick DA. Nonconvexities in stochastic control models. International Economic Review. 1995;36:455–475.
6. Amman HM, Kendrick DA. Active learning: A correction. Journal of Economic Dynamics and Control. 1997;21:1613–1614.
7. Amman HM, Kendrick DA. Linear-quadratic optimization for models with rational expectations. Macroeconomic Dynamics. 1999a;3:534–543.
8. Amman HM, Kendrick DA. Matrix methods for solving nonlinear dynamic optimization models. In: Heijmans RJ, Pollock DSG, Satorra A, eds. Innovations in Multivariate Statistical Analysis. Dordrecht, The Netherlands: Kluwer Academic Publishers; 1999b:257–276. Advanced Studies in Theoretical and Applied Econometrics vol. 30.
9. Amman, H.M., Kendrick, D.A., 1999c. The DualI/DualPC software for optimal control models: User’s guide, Working paper, Center for Applied Research in Economics, University of Texas, Austin, Texas, USA.
10. Amman HM, Kendrick DA. Should macroeconomic policy makers consider parameter covariances? Computational Economics. 1999d;14:263–267.
11. Amman HM, Kendrick DA. Mitigation of the Lucas critique with stochastic control methods. Journal of Economic Dynamics and Control. 2003;27:2035–2057.
12. Amman HM, Kendrick DA, Tucci MP. Solving the Beck and Wieland model with optimal experimentation in DUALPC. Automatica. 2008;44:1504–1510.
13. Anderson G, Moore G. A linear algebraic procedure for solving linear perfect foresight models. Economic Letters. 1985;17:247–252.
14. Beck G, Wieland V. Learning and control in a changing economic environment. Journal of Economic Dynamics and Control. 2002;26:1359–1377.
15. Bertocchi G, Spagat M. Growth under uncertainty with experimentation. Journal of Economic Dynamics and Control. 1998;23:209–231.
16. Blanchard OJ, Kahn CM. The solution of linear difference models under rational expectations. Econometrica. 1980;48:1305–1311.
17. Blueschke-Nikolaeva V, Blueschke D, Neck R. Optimal control of nonlinear dynamic econometric models: An algorithm and an application. Computational Statistics and Data Analysis. 2010;56(11):3230–3240.
18. Chow GC. A solution to optimal control of linear systems with unknown parameters. Review of Economics and Statistics. 1975;57(3):338–345 In: <http://www.jstor.org/stable/1923918?origin=JSTOR-pdf>; 1975.
19. Coenen G, Levin A, Wieland V. Data uncertainty and the role of money as an information variable for monetary policy. European Economic Review. 2005;49:975–1006.
20. Coleman TF, Van Loan C. Handbook for matrix computations. Philadelphia, Pennsylvania, USA: SIAM; 1988.
21. Cosimano TF. Optimal experimentation and the perturbation method in the neighborhood of the augmented linear regulator problem. Journal of Economics, Dynamics and Control. 2008;32:1857–1894.
22. Cosimano TF, Gapen MT. Program notes for optimal experimentation and the perturbation method in the neighborhood of the augumented linear regulator problem. Working paper: Department of Finance, University of Notre Dame, Notre Dame, Indiana, USA; 2005a.
23. Cosimano TF, Gapen MT. Recursive methods of dynamic linear economics and optimal experimentation using the perturbation method. Working paper: Department of Finance, University of Notre Dame, Notre Dame, Indiana, USA; 2005b.
24. Crawford G, Shum M. Uncertainty and learning in pharmaceutical demand. Econometrica. 2005;73:1137–1173.
25. Easley D, Kiefer NM. Controlling a stochastic process with unknown parameters. Econometrica. 1988;56:1045–1064.
26. El-Gamal M, Sundaram R. Bayesian economists …bayesian agents. Journal of Economic Dynamics and Control. 1993;17:355–383.
27. Ellison M. The learning cost of interest rate reversals. Journal of Monetary Economics. 2006;53:1895–1907.
28. Fair RC, Taylor JB. Solution and maximum likelihood estimation of dynamic rational expectations models. Econometrica. 1983;51:1169–1185.
29. Fisher PG, Holly S, Hughes-Hallett AJ. Efficient solution techniques for dynamic non-linear rational expectations models. Journal of Economic Dynamics and Control. 1986;10:139–145.
30. Glasserman P. Monte Carlo Methods in Financial Engineering. New York: Springer; 2004.
31. Grossman S, Kihlstrom R, Mirman L. A bayesian approach to the production of information and learning by doing. Review of Economic Studies. 1977;44:533–547.
32. Hansen LP, Sargent TJ. Robustness. Princeton, NJ, USA: Princeton University Press; 2008.
33. Hansen, L.P., Sargent, T.J., 2001. Elements of robust control and filtering for macroeconomics. Draft downloaded from Sargent’s web site at <www.stanford.edu/sargent>, version of 23 March 2001.
34. Hansen, L.P., Sargent, T.J., 2004. Recursive models of dyanmic linear economies. Univesity of Chicago manuscript, Department of Economics.
35. Kendrick DA. Applications of control theory to macroeconomics. Annals of Economic and Social Measurement. 1976;5:171–190.
36. Kendrick DA. Non-convexities from probing in adaptive control problems. Economic Letters. 1978;1:347–351.
37. Kendrick DA. Control theory with application to economics. In: Arrow KJ, Intriligator MD, eds. Handbook of Mathematical Economics. Amsterdam, The Netherlands: North-Holland Publishers (Elsevier); 1980:111–158. Handbook in Economics vol. 1 Chapter 4.
38. Kendrick DA. Stochastic Control for Economic Models. first ed. New York, USA: McGraw-Hill Book Company; 1981; (See also Kendrick (2002)).
39. Kendrick DA. The DualI/DualPC software for optimal control models. In: Amman HM, Rustem B, Whinston AB, eds. Computational Approaches to Economic Problems. Dordrecht, The Netherlands: Kluwer Academic Publishers; 1997:363. Advances in Computational Economics vol. 6.
40. Kendrick DA. Stochastic Control for Economic Models. second ed. University of Texas 2002; In: <http://www.utexas.edu/cola/depts/economics/faculty/dak2>; 2002.
41. Kendrick DA. Stochastic control for economic models: Past, present and paths ahead. Journal of Economic Dynamics and Control. 2005;29:3–30.
42. Kendrick DA, Amman HM. A classification system for economic stochastic control models. Computational Economics. 2006;27:453–481.
43. Kendrick, D.A., Tucci, M.P., 2006. The Beck and Wieland model in the adaptive control framework, Working paper, Department of Economics, University of Texas, Austin, Texas, USA.
44. Kendrick DA, Tucci MP, Amman HM. Duali: software for solving stochastic control problems. In: Kontoghiorghes EJ, Rustem B, Winker P, eds. Computational Methods in Financial Engineering. Springer, Berlin: Essays in Honor of Manfred Gilli; 2008:393–419.
45. Kiefer N. A value function arising in the economics of information. Journal of Economic Dynamics and Control. 1989;13:201–223.
46. Kiefer N, Nyarko Y. Optimal control of an unknown linear process with learning. International Economic Review. 1989;30:571–586.
47. Lucas RE. Econometric policy evaluation: A critique. In: Brunner K, Meltzer A, eds. The Phillips Curve and the Labor Markets. 1976:19–46. Supplementary Series to the, Journal of Monetary Economics.
48. MacRae EC. Linear decision with experimentation. Annals of Economic and Social Measurement. 1972;1:437–448.
49. MacRae EC. An adaptive learning role for multiperiod decision problems. Econometrica. 1975;43:893–906.
50. Mathur S, Morozov S. Massively parallel computation using graphics processors with application to optimal experimentation in dynamic control. University of Munich Personal RePec Archive 2009; In: <http://mpra.ub.uni-muenchen.de/16721>; 2009.
51. Matulka J, Neck R. An algorithm for the optimal control of nonlinear stochastic models. Annals of Operations Research. 1992;37:375–401.
52. Mizrach B. Non-convexities in an stochastic control problem with learning. Journal of Economic Dynamics and Control. 1991;15:515–538.
53. Moler CB, Stewart GW. An algorithm for for generalized matrix eigenvalue problems. SIAM Journal on Numerical Analysis. 1973;10:241–256.
54. Neck R. Stochastic control theory and operational research. European Journal of Operations Research. 1984;17:283–301.
55. Norman AL. First order dual control. Annals of Economic and Social Measurement. 1976;5:311–322.
56. Norman AL, Norman MR, Palash CJ. Multiple relative maxima in optimal macroeconomic policy: an illustration. Southern Economic Journal. 1979;46:274–729.
57. Pindyck RS. Optimal planning for economic stabilization. Amsterdam, The Netherlands: North-Holland; 1973.
58. Prescott EC. The multi-period control problem under uncertainty. Econometrica. 1972;40:1043–1058.
59. Sims CA. Solving linear rational expectations models. Computational Economics. 2001;20:1–20.
60. Svensson, L., Williams, N., 2007. Bayesian and adaptive optimal policy under model uncertainty, NBER Working Paper 13414, NBER.
61. Taylor JB. Asymptotic properties of multiperiod control rules in the linear regression model. International Economic Review. 1974;15:472–482.
62. Tesfaselassie, M.F., Schaling, E., Eijffinger, S., 2007. Learning about the term structure and optimal rules for inflation targeting, Working paper, Tilburg University, Tilburg, The Netherlands.
63. Theil H. Optimal Decision Rules for Government and Industry. Amsterdam, The Netherlands: North-Holland; 1964.
64. Trefler D. The ignorant monopolist: Optimal learning with endogenous information. International Economic Review. 1993;34:565–581.
65. Tse E. Further comments on adaptive stochastic control for a class of linear systems. IEEE Transactions on Automatic Control. 1973;18:324–326.
66. Tse E, Athans M. Adaptive stochastic control for a class of linear systems. IEEE Transactions on Automatic Control. 1972;17:38–52.
67. Tse E, Bar-Shalom Y. An actively adaptive control for linear systems. IEEE Transactions on Automatic Control. 1973;18:109–117.
68. Tse E, Bar-Shalom Y, Meier L. Wide sense adaptive dual control for nonlinear stochastic systems. IEEE Transactions on Automatic Control. 1973;18:98–108.
69. Tucci MP. Time-varying Parameters in Adaptive Control. PhD thesis Austin, Texas, USA: Department of Economics, University of Texas; 1989.
70. Tucci MP. Adaptive control in the presence of time-varying parameters. Journal of Economic Dynamics and Control. 1997;22:39–47.
71. Tucci MP. The nonconvexities problem in adaptive control models: A simple computational solution. Computational Economics. 1998;12:203–222.
72. Tucci MP. A note on global optimization in adaptive control, econometrics and macroeconomics. Journal of Economic Dynamics and Control. 2002;26:1739–1764.
73. Tucci MP. The Rational Expectation Hypothesis. Springer, Dordrecht, The Netherlands: Time-varying Parameters and Adaptive Control; 2004.
74. Tucci MP, Kendrick DA, Amman HM. The parameter set in an adaptive control Monte Carlo experiment: some considerations. Journal of Economic Dynamics and Control. 2010;34:1531–1549.
75. Tucci MP, Kendrick DA, Amman HM. Expected optimal feedback with time-varying parameters. Computational Economics. 2013;42:351–371.
76. Wieland V. Learning by doing and the value of optimal experimentation. Journal of Economic Dynamics and Control. 2000a;24:501–543.
77. Wieland V. Monetary policy, parameter uncertainty and optimal learning. Journal of Monetary Economics. 2000b;46:199–228.
78. Wieland V. Monetary policy and uncertainty about the natural unemployment rate: Brainard-style conservatism versus experimental activism. Advances in Macroeconomics. 2006;6:1–34.
1A more recent term for active learning is optimal experimentation; see, for instance, Beck and Wieland (2002).
2Following Bayesian literature, we make a distinction between prior estimates 
and posterior estimates 
of the true parameter vector 
.
3For simulation purposes we usually start with (good) estimates of the variables 
, and 
and update their prior and posterior estimates when new information becomes available. See Eqs. (12) and (14).
4A referee has noted that as 
there should exist a unique time-independent function 
(the value function or the expected cost-to-go) where 
is the optimal decision rule (active learning). See Kiefer and Nyarko (1989) for a proof of the existence of this function.
5Like in footnote (2), 
is called the prior estimate and 
the posterior estimate of the covariance matrix 
.
6Equations (12), (13), and (14)) are based on Kendrick (1981, 2002), Eqs. (10.61), (10.68), and (10.69).
7For a classification of the various methods that are used in stochastic control of economic models and the nomenclature that is associated with these methods see Kendrick and Amman (2006).
8See Kendrick (1997) and Amman and Kendrick (1999c).
9Marco Tucci has devised just such an optimization procedure, viz Tucci (1998, 2004).
10The term parameter set is used here to include both the parameters and their covariance and the values used for the penalty matrices, desired paths for the states and controls and the initial states.
11See the discussion in Section 8 of Tucci et al. (2010).
12Tucci et al. (2013) derive the appropriate formulae for the determination of EOF control in the presence of parameters following a Return to Normality model.
13A recent paper on computational speed in this arena is Mathur and Morozov (2009).
14For further discussion of these issues see Tucci et al. (2010).
15See Neck (1984), Matulka and Neck (1992), and Blueschke-Nikolaeva et al. (2010).
16The standard errors are printed between parentheses and defined as 
where 
is the standard deviation in the sample and 
the number of Monte Carlo runs. With the help of the standard errors it is possible to compute the confidence intervals for the various methods. For instance, the 
confidence for the mean of the DC solution is 
; cf. Glasserman (2004, page 541).
17The standard errors are given between parentheses. See also Footnote 16.
18A referee has observed that we use a Lucas style supply curve (inverted as an equation determining inflation at time 
, conditional on 
expectation of time 
inflation) in the Amman and Kendrick (2003) article. The referee suggested that the extension to the New-Keynesian Phillips curve (current inflation is then a function of current time 
expectation of 
inflation) would be interesting and could in principle be done with the methods we use (that is, with the Sims (2001) method for solving RE models that we have integrated into the DC algorithm).
*We are indebted to a referee for many helpful comments and suggestions.