CASE STUDY 1

Global Evidence on the Equity Risk Premium

Elroy Dimson, Paul Marsh and Mike Staunton

Today, investors have more cause than ever to ask what returns they can expect from equities, and what the future risk-reward tradeoff is likely to be. Corporate managers, too, need to know what returns their shareholders require for projects of differing risk. And regulators have to know the cost of equity capital in order to set “fair” rates of return for regulated industries. In fact, the magnitude of the equity risk premium – the incremental return that shareholders require to hold risky equities rather than risk-free securities – is one of the most important issues in corporate finance. It drives future equity returns and is a key determinant of the cost of capital.

This article sheds light on the equity risk premium by addressing two fundamental questions: How big has the equity risk premium been historically? And what can we expect for the future? To answer these questions, we need to look at long periods of capital market history, and to extend our horizons beyond just the United States. We start by examining equity returns in 16 different countries over the 103-year period from 1900 to 2002.

THE NEED FOR A LONG-RUN PERSPECTIVE

The dangers of focusing just on recent stock market history are easily demonstrated. Over the last decade of the 20th century, U.S. equity investors achieved a total return (capital gain plus reinvested dividends) of 17.6% per annum, thus increasing their initial stake by a factor of five. During the last five years of the 1990s, U.S. equities achieved high returns every year, ranging from 21% in 1996 to as much as 36% in 1995. Investors became convinced that high corporate growth rates could be extrapolated into the foreseeable future. In fact, surveys suggested that many investors expected long-run stock market returns to continue at double-digit percentage rates indefinitely. With strong growth rates, equity risk appeared lower. As a result, the premium sought by investors to compensate for exposure to equity market risk seemed to decline. This drove stock prices further onward and upward.

Then the technology bubble burst. Because growth projections had proved unrealistic, high growth was perceived to be associated with high risk. Investors demanded a larger reward for equity market risk exposure. Stock prices fell for three successive years from 2000–2002. With markets falling, investors started to project lower returns for the future. Yet it is wrong to overreact to recent stock market performance in projecting future required returns. Just because equities had delivered poor returns since 2000 did not mean that there had been a substantial change in the long-term expected equity premium.

Figure C1.1 compares U.S. real equity returns to those in 15 other countries and a world index. The figure shows annualized real equity returns over 2000–2002, and in all 16 countries, equities suffered negative returns. In contrast, government securities (not shown in Figure C1.1) generally performed well, so that equities markedly underperformed both bonds and bills in all 16 countries over 2000–2002. Estimating the expected risk premium from the performance of equities relative to bills or bonds over this period would clearly be nonsense. Investors cannot have required or expected a negative return for assuming risk. Instead, this was simply a very disappointing period for equities. Yet it would be equally misleading to estimate future risk premiums from data for 1990–1999. Figure C1.1 shows that over this period, equity returns (except in Japan and South Africa) were quite high. The 1990s represented a golden age for stocks, and golden ages, by definition, recur only infrequently.

To understand the risk premium – which is the principal objective of this article – we need to examine periods that are much longer than a few years or even a decade. Stock markets are volatile, with significant variation in year-to-year returns. In order to make inferences, we need a long time series that incorporates bad times as well as good. Figure C1.1 shows real equity returns over the 103-year period 1900–2002 (and which we describe in more detail later); these data provide insight into the perspective that longer periods of history can bring. Clearly, these 103-year returns are much lower than the returns during the 1990s, but they also contrast favorably with the disappointing returns over 2000–2002.

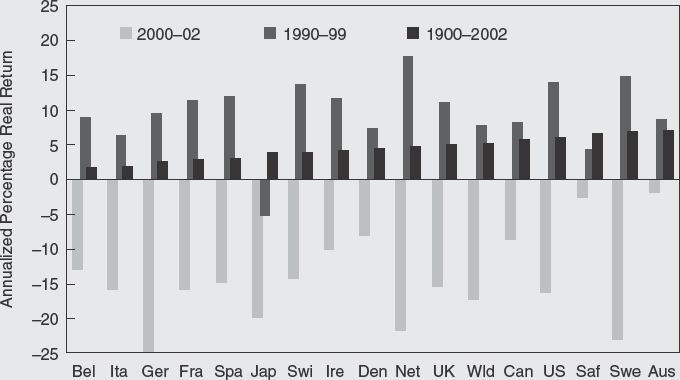
Figure C1.1 Short-term and long-run real returns on equities around the world
The country names listed in abbreviated form along the horizontal axis are (from left to right) Belgium, Italy, Germany, France, Spain, Japan, Switzerland, Ireland, Denmark, The Netherlands, The United Kingdom, the world (the weighted average of the 16 individual countries), Canada, The United States, South Africa, Sweden, and Australia.
Source: E. Dimson, P. Marsh, and M. Staunton, Triumph of the Optimists: 101 Years of Global Investment Returns (New Jersey: Princeton University Press, 2002) and Global Investment Returns Yearbook (ABN AMRO/London Business School, 2003).

PRIOR ESTIMATES OF THE RISK PREMIUM

To be fair, financial economists generally measure the equity premium over quite long periods. Standard practice, however, draws heavily on the United States, with most textbooks citing only the U.S. experience. By far the most widely cited U.S. source prior to the end of the technology bubble was Ibbotson Associates,¹ whose equity premium history started in 1926. For the period 1926–1999, they estimated an annualized return on equities of 11.3%, and a risk-free return of 3.8%. This implies a geometric premium relative to bills of 7.3% (1.113/1.038 = 1.073). References to other countries are few and far between, although some textbooks also cite U.K. evidence. Before the publication of our research, the most widely cited sources for the United Kingdom were studies published by Barclays Capital and Credit Suisse First Boston (CSFB)² which estimated annualized equity and risk-free returns from start-1919 to start-1999 of 12.2% and 5.5%, respectively, implying a geometric risk premium relative to bills of 6.4%.

In citing these estimates, financial economists are generally making the implicit assumption that the historical risk premium, measured over many decades, offers an unbiased estimate of the future premium, provided the data are of sufficient quality. Yet the 20th century proved to be a period of remarkable growth in U.S. economy, probably exceeding the expectations held in 1926 by U.S. investors. Similar arguments apply to the United Kingdom and the likely expectations of U.K. investors in 1919.

In recent years, practitioners and researchers alike have become increasingly suspicious that these widely cited estimates are too high. Apart from biases in index construction, the finger of suspicion has pointed mainly at success and survivorship bias.³ One influential study asserted “the high equity premium obtained for U.S. [and, by implication, U.K.] equities appears to be the exception rather than the rule.”⁴ Recently, well-known finance scholar Zvi Bodie argued that high U.S. and U.K. premiums are likely to be anomalous, and underlined the need for comparative international evidence. He pointed out that long-run studies are always of U.S. or U.K. premiums: “There were 36 active stock markets in 1900, so why do we only look at two? I can tell you – because many of the others don't have a 100-year history, for a variety of reasons.”⁵

What Do the Experts Say?

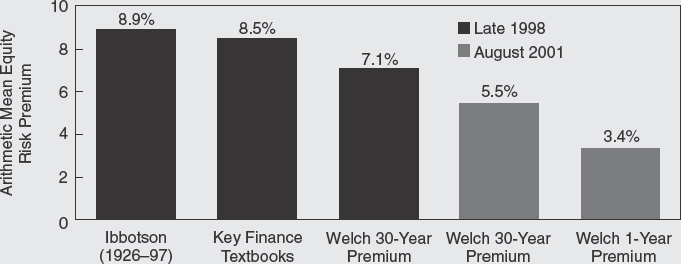
The question of the equity premium has thus been a source of controversy even among the “experts.” In late 1998, Ivo Welch studied the opinions of 226 financial economists who were asked to forecast the average annual risk premium over the next 30 years.⁶ Their mean forecast was 7.1%; the median was 7.0%; and the range ran from 1% to 15%. Interestingly, the spread in their distribution of forecasts indicated that the uncertainty among financial experts about the risk premium was as great as the uncertainty that arises from standard statistical analysis of historical returns.

Most respondents to the Welch survey would have regarded the Ibbotson Associates Yearbook as the definitive study of the historical U.S. risk premium. At that time, the most recent Yearbook was the 1998 edition, covering the period 1926–1997. The first bar of Figure C1.2 shows that the arithmetic mean risk premium based on the Ibbotson Yearbook data was 8.9% per year.⁷ The second bar shows that the key finance textbooks were on average suggesting a premium of 8.5%, a little below the Ibbotson mean. The textbook authors may have based their views on earlier, slightly lower, Ibbotson estimates, or perhaps they were simply shading the Ibbotson estimates downward. The Welch survey mean is in turn lower than the textbook figures, but since the respondents claimed to lower their forecasts when the equity market rises, this difference may be attributable to the market's strong performance in the 1990s.

The survey and textbook figures represent what was being taught at the end of the 1990s in the world's leading business schools and economics departments in the United States and around the world. As such, these estimates were widely used by investors, finance professionals, corporate executives, regulators, lawyers, and consultants. Their influence extended from the classroom to the deal room, to the boardroom, and to the courtroom.

By 2001, however, longer-term estimates of the U.S. arithmetic mean equity premium were gaining publicity. Our own estimate⁸ of a 7.7% mean premium over the longer period from 1900–2000 was 1.2% lower than the Ibbotson estimate of 8.9% for 1926–1997. In August 2001, Welch updated his earlier survey, receiving responses from 510 finance and economics professors.⁹ He found that the respondents to the follow-up questionnaire had revised their estimates downward by an average of 1.6%. They now estimated an equity premium averaging 5.5% over a 30-year horizon, and 3.4% over a one-year horizon (see Figure C1.2). Those who had participated in the earlier survey and those who were taking part for the first time estimated the same mean premiums. Although respondents to the earlier survey had indicated that, on average, a bear market would raise their equity premium forecast, Welch reports that “this is in contrast with the observed findings: it appears as if the recent bear market correlates with lower equity premium forecasts, not higher equity premium forecasts.”

Still, predictions of the long-term equity premium should not be so sensitive to short-term stock market fluctuations. The changing consensus might reflect new approaches to estimating the premium or new facts about long-term stock market performance, such as evidence that other countries have typically had historical premiums that were lower than in the United States.

Figure C1.2 Estimated arithmetic mean risk premiums relative to bills, 1998 and 2001

NEW EVIDENCE

The wide dispersion of estimates, together with the dramatic decline in the “expert” consensus premium between 1998 and 2001, reinforces the need to better understand the historical record. Our research helps fill the gap by providing a 103-year history of risk premiums for markets in 16 countries. The evidence on long-run risk premiums presented in this article is derived from a unique new database comprising annual returns on stocks, bonds, bills, inflation, and currencies for 16 countries over the period 1900–2002. The countries include the United States and Canada, the United Kingdom, seven markets from what is now the Euro currency area, three other European markets, two Asia-Pacific markets, and one African market. Together, these countries made up 94% of the free float market capitalization of all world equities at the beginning of 2003, and we estimate that they constituted over 90% by value at the start of our period in 1900.¹⁰

To compile this database, we assembled the best quality indexes and returns data available for each national market from previous studies and other sources.¹¹ Many early equity indexes measure just capital gains and ignore dividends, thereby introducing a serious downward bias. Similarly, many early bond indexes record just yields, ignoring price movements. Unlike most previous long-term studies of global markets, however, our investment returns include reinvested gross income as well as capital gains. Our database is thus more comprehensive and accurate than previous research and spans a longer period.¹² Furthermore, we can now set the U.S. risk premium data alongside comparable 103-year risk premiums for 15 other countries, and make international comparisons that help put the U.S. experience in perspective.

Table C1.1 shows the historical equity risk premiums for the 16 countries over the 103-year period 1900–2002. We also display equity premiums for our world equity index, which is a 16-country, common-currency (here taken as U.S. dollars) equity index with each country weighted by its beginning-of-period market capitalization or (in earlier years) its GDP.¹³ The left half of Table C1.1 shows equity premiums measured relative to the return on Treasury bills or the nearest equivalent short-term instrument; the right half shows premiums calculated using the same equity returns, but relative to the return on long-term government bonds. Since the world index is computed here from the perspective of a U.S. (dollar) investor, the world equity risk premium relative to bills is calculated with reference to the U.S. risk-free (Treasury bill) rate. The world equity premium relative to bonds is calculated relative to a GDP-weighted, 16-country, common-currency (here taken as U.S. dollars) world bond index.

In each half of the table we show three measures. These are the annualized risk premium, or geometric mean, over the entire 103 years; the arithmetic mean of the 103 one-year premiums; and the standard deviation of the 103 one-year premiums. While the United States and the United Kingdom have indeed performed well, there is no indication that they are hugely out of line compared to other markets.

Table C1.1 Equity risk premiums* around the world 1900–2002

Over the entire 103-year period, the annualized (geometric) equity risk premium, relative to bills, was 5.3% for the United States and 4.2% for the United Kingdom. Averaged across all 16 countries, the risk premium relative to bills was 4.5%, while the risk premium on the world equity index was 4.4%. Relative to long bonds, the story is similar. The annualized U.S. equity risk premium relative to bonds was 4.4%, and the corresponding figure for the United Kingdom was 3.8%. Across all 16 countries, the risk premium relative to bonds averaged 3.8%, and for the world index it was also 3.8%.¹⁴

The annualized equity risk premiums are plotted in Figure C1.3. In this figure, countries are ranked by the equity premium relative to bonds, displayed as bars. The line-plot presents each country's risk premium relative to bills. It can be seen that the United States does indeed have a historical risk premium above the world average, but it is by no means the country with the largest recorded premium. The equity premium for the United Kingdom is closer to the worldwide average. While U.S. and U.K. equities have performed well, both countries are toward the middle of the distribution of worldwide equity premiums.

Commentators have suggested that survivor bias may have led to unrepresentative equity premiums for the United States and the United Kingdom. While legitimate, these concerns are somewhat overstated. Rather, the critical factors are the period over which the risk premium is estimated, together with the quality of the index series. Investors have therefore probably not been greatly misled by a focus on the U.S. and U.K. experiences.

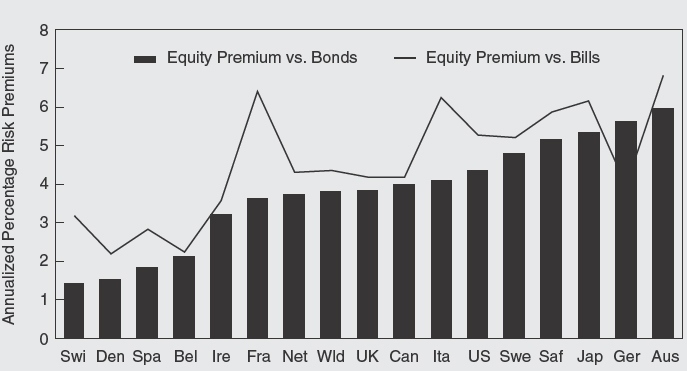
Figure C1.3 Worldwide annualized equity risk premiums 1900–2002 Germany excludes 1922–23.
Source: Dimson, Marsh, and Staunton, Triumph of the Optimists: 101 Years of Global Investment Returns (Princeton University Press, 2002) and Global Investment Returns Yearbook (ABN AMRO/London Business School, 2003).

The 103-year historical estimates of equity premiums reported here are lower than was previously thought and other studies suggest. Nonetheless, the historical record may still overstate expectations. First, even if we have been successful in avoiding survivor bias within each index, we still focus on markets that survived, omitting countries such as Poland, Russia, or China whose compound rate of return was −100%. Although these markets were relatively small in 1900,¹⁵ their omission probably leads to an overestimate of the worldwide risk premium.¹⁶ Second, our premiums are measured relative to bills and bonds, which in a number of countries yielded markedly negative real returns. Since these “risk-free” returns likely fell below investor expectations, the corresponding equity premiums are probably overstated.¹⁷

Although there is certainly room for debate, we do not consider market survivorship to be the most important source of bias when inferring expected premiums from the historical record. There are cogent reasons for suggesting that investors expected a lower premium than they actually received. However, this has more to do with a failure to fully anticipate improvements in business and investment conditions during the second half of the last century, an issue that we will return to later.

VARIATION IN RISK PREMIUMS OVER TIME

The historical equity premiums shown in Figure C1.3 are the annualized or geometric means of 103 separate one-year premiums that vary a great deal. The bars in Figure C1.4 show the year-by-year premiums on U.S. equities relative to bills.¹⁸ The lowest was −45% in 1931, when equities earned −44% and Treasury bills 1.1%; the highest was 57% in 1933, when equities earned 57.6% and bills 0.3%. Over the 103-year period spanned by Figure C1.4, the mean annual excess return was 7.2%, while the standard deviation was 19.8% (see Table C1.1). On average, therefore, U.S. investors received a positive, and quite large, reward for exposure to equity market risk.

Because the range of excess returns encountered on a year-to-year basis is very broad, however, it can be misleading to label them “risk premiums.” As already noted, investors cannot have expected, let alone required, a negative risk premium from investing in equities, otherwise they would simply have avoided them. All of the negative and many of the very low premiums plotted in Figure C1.4 must therefore reflect unpleasant surprises. Nor could investors have required premiums as high as the 57% achieved in 1933. Such numbers are implausible as a required reward for risk, and the high realizations must therefore reflect pleasant surprises. As a result, many writers choose not to refer to historical excess returns as “risk premiums.” To avoid confusion, we refer to the expected or “prospective” risk premium when we are looking to the future. When we measure the excess return over a period in the past, we generally refer to it as the “historical” risk premium.

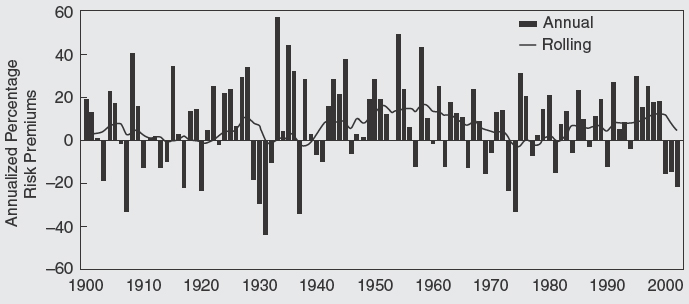
Figure C1.4 Annual and rolling ten-year U.S. premiums relative to bills, 1900–2002
Source: E. Dimson, P. Marsh, and M. Staunton, Triumph of the Optimists: 101 Years of Global Investment Returns (New Jersey: Princeton University Press, 2002) and Global Investment Returns Yearbook (ABN AMRO/London Business School, 2003).

Because one-year excess returns are so variable, we need to examine longer periods in the hope that good and bad luck might cancel out. A common choice of time frame is a decade. Figure C1.4 therefore also shows the U.S. equity risk premium measured over a sequence of rolling ten-year periods, superimposed on the annual returns since 1900. This line-plot shows that there is clearly less volatility in the ten-year measures.

Even over ten-year periods, however, historical excess returns were sometimes negative, most recently in the 1970s and early 1980s. Figure C1.4 also reveals several cases of double-digit ten-year premiums. Clearly, a decade is still too short a period for good and bad luck to cancel out, or for drawing inferences about investor expectations. Indeed, even with a full century of data, market fluctuations have an impact. Taking the United Kingdom as an illustration, we find that the arithmetic mean annual excess return for the first half of the 20th century was only 3.1%, compared to 8.6% from 1950 to date. As over a single year, all we are reporting is the excess return that was realized over a period in the past.

Imprecise Estimates

We have seen that very long series of stock market data are needed for estimating risk premiums. But even with 103 years of data, the potential inaccuracy in historical risk premiums is still fairly high. The standard error is a measure of this inaccuracy. It equals approximately one-tenth of the annual standard deviation of returns reported in Table C1.1. The standard error for the United States is 1.9%, and the range runs from 1.7% (Australia and Canada) to 3.5% (Germany). This means that while the U.S. arithmetic mean premium (relative to bills) has a best estimate of 7.2% (from Table C1.1), we can be only two-thirds confident that the true mean lies within one standard error of this estimate, namely within the range 7.2% ± 1.9%, or 5.3% to 9.1%. Similarly, there is a 19-out-of-20 probability that the true mean lies within two standard errors – that is, 7.2% ± 3.8%, or 3.4% to 11.0%.

FROM THE PAST TO THE FUTURE

To estimate the equity risk premium to use in discounting future cash flows, we need the expected future risk premium, which is the arithmetic mean of the possible premiums that may occur. Suppose future returns are drawn from the same distribution as those that occurred in the past. In this case, the expected risk premium is the arithmetic mean (or simple average) of the one-year historical premiums.

In Figure C1.5, the gray bars show the historical arithmetic mean premium relative to bills for each country. The U.S. equity premium is 7.2%, while the world equity risk premium is 5.7%. The arithmetic mean premiums are noticeably higher than the geometric mean premiums (shown by the grey bars) because whenever there is any variability in annual premiums, the arithmetic mean will exceed the geometric mean (or annualized) risk premium.¹⁹ The difference is largest (in both absolute terms and relative to the geometric mean) for the countries that experienced the greatest volatility of returns over the last century (see Table C1.1).

When returns are lognormally distributed, the arithmetic mean return will exceed the geometric mean return by half the variance. The historical arithmetic means plotted in Figure C1.5 are obviously affected by the historical variances. The latter, however, can be poor predictors of future volatility. This will be especially true for countries with very high levels of historical volatility, where some sources of extreme volatility (such as those arising from hyperinflation and the world wars) are unlikely to recur. We therefore need estimates of expected future risk premiums that are conditional on current predictions of market volatility.

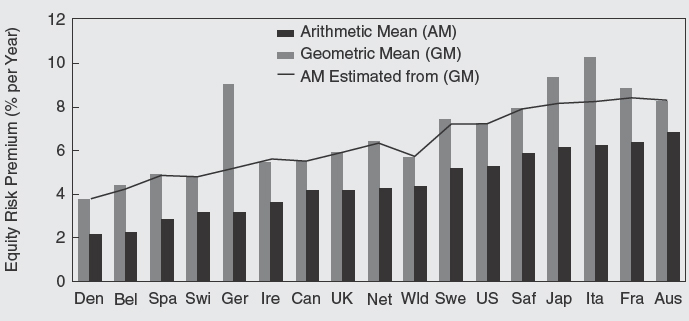
Figure C1.5 Adjustments to historical arithmetic mean equity risk premiums relative to bills, 1900–2002
Source: E. Dimson, P. Marsh, and M. Staunton, Triumph of the Optimists: 101 Years of Global Investment Returns (New Jersey: Princeton University Press, 2002) and Global Investment Returns Yearbook (ABN AMRO/London Business School, 2003).

In looking to the future, let us assume for the moment that investors in each country expect the same annualized (geometric mean) risk premium that they have received in the past. We can then estimate the expected future arithmetic mean premium for each country by replacing the historical difference between the geometric and arithmetic means with a difference based on a contemporary, rather than the historical, risk estimate.

Historically, the U.S. and U.K. markets both had volatility levels of 20%. If we take this figure as our contemporary risk estimate, and assume that all countries with historical volatilities in excess of this will have a future volatility of 20%, we can then estimate the expected future arithmetic mean premium for each country. The resulting estimates are shown by the line-plot in Figure C1.5. Note that we have left the historical estimates unchanged for countries with historical volatilities of 20% or below.

For those wishing to forecast future arithmetic mean risk premiums by extrapolating from the long-run historical annualized premiums, the adjusted premiums shown by the line-plot in Figure C1.5 are superior to the raw historical arithmetic means. Using historical volatility estimates, the figures for the United States and the world index remain unchanged at 7.2% and 5.7%, respectively. However, Figure C1.5 shows that the downward adjustments needed for several other countries, such as Japan, Italy, France, and especially Germany, are quite large.

REVISITING HISTORY

But since history may have turned out to be unexpectedly kind to (or harsh on) stock market investors, there are cogent arguments for going beyond raw historical estimates. First, the whole idea of using the achieved risk premium to forecast the future required risk premium depends on having a long enough period to iron out good and bad luck – yet as we noted earlier, our estimates are imprecise even with 103 years of data. Second, the expected equity risk premium could for good reasons vary over time. Third, we must take account of the fact that stock market outcomes are influenced by many factors, some of which (like removal of trade and investment barriers) may be nonrecurring, which implies projections for the future premium that differ from the past.

A comparison of equity returns between the first and second halves of our 103-year period makes the point. Over the first half of the 20th century, the arithmetic average annual real return on the world equity index was 5.1%, whereas over the period 1950–2002 it was 8.4%. Fourteen of the 16 countries had lower mean premiums in the first half-century,²⁰ with Australia and South Africa being the only exceptions. The 16-country (unweighted) mean annual real return on equities in the first half of the 20th century was 5.1%, versus 9.0% over the next 53 years.

The larger equity returns earned during the second half of the 20th century are attributable to at least four factors. First, there was rapid technological change, unprecedented growth in productivity and efficiency, and enhancements to the quality of management and corporate governance. As Europe, North America, and the Asia-Pacific region emerged from the turmoil of World War II, expectations for improvement were limited to what could be imagined. Reality almost certainly exceeded investor expectations. Corporate cash flows grew faster than investors anticipated, and this higher growth is now known to the market and reflected in higher stock prices. Second, transaction and monitoring costs fell over the course of the century, and this underpinned rising stock prices.²¹ Third, in the last two decades of the century, inflation rates generally declined and real interest rates rose, and this had a further impact on the stock market.

Finally, stock prices have also risen because of a fall in the required rate of return due to diminished business and investment risk. Business risk declined as the economic and political lessons of the 20th century were absorbed, international trade flows increased, and the Cold War ended. Investment risk diminished over time as investors gained the benefits of diversification, both domestically (through a wider range of quoted securities and industries, and through intermediaries such as mutual funds²²) and internationally (with the disappearance of impediments to foreign investment). Diversification allows investors to lower their risk exposure without detriment to expected returns. Factors such as these, which led to a reduction in the required risk premium, have contributed further to the upward re-rating of stock prices.

To convert a pure historical estimate of the risk premium into a forward-looking projection, we would like to reverse-engineer the factors that drove up stock markets over the last 103 years. In principle, we need to identify the influence of factors such as those described above – cash flow improvements, cost reductions, interest rate shocks, and improved diversification opportunities. To illustrate the latter, consider the dramatic change since 1900 in the valuation basis for equity markets. The price/dividend ratio (the reciprocal of the dividend yield) at the start of 1900 was 23 in both the United States and the United Kingdom; but by the start of 2002, the U.S. ratio had risen to 64 and the U.K. ratio to 32. Undoubtedly, this change is in part a reflection of expected future growth in earnings and thus real dividends, so we could in principle decompose the impact of this valuation change into two elements: one that reflects changes in required rates of return and one that reflects enhanced growth expectations.

To keep things simple, assume that the increase in the price/dividend ratio is attributable solely to a long-term fall in the required risk premium for equity investment.²³ Given this assumption, the stock price impact of the rerating since 1900 is estimated to be 1.0% per year in the United States and 0.3% per year in the United Kingdom. For the world portfolio, based on all 16 countries, the impact of the re-rating of equities is 0.8%. To estimate expected risk premiums, we deduct from our historical premiums the estimated impact of the re-rating of equities. For the U.S., U.K., and world, this adjustment gives rise to estimated risk premiums of 4.3%, 3.9%, and 3.5% respectively. On a forward-looking basis, these expected geometric risk premiums are similar to the estimates obtained recently by Eugene Fama and Kenneth French using a related approach.²⁴

EXPECTED RISK PREMIUMS

If they are to be used as prospective risk premiums, however, our annualized figures need to be converted into arithmetic means. Using a projected standard deviation for U.S. and U.K. equities equal to their historical standard deviation of 20%, the prospective arithmetic risk premium for the United States is 6.3% (i.e., 4.3 + 2.0%),²⁵ while the premium for the United Kingdom is 5.9% (i.e., 3.9 + 2.0%). Using a slightly lower standard deviation for the world index of 16%, again in line with the historical experience, the prospective arithmetic risk premium for the world index is 4.8% (i.e., 3.5 + 1.3%). If stock market volatility in the future is expected to be lower than in the past, then the risk premium estimates would be lower than those presented above. But even without any further downward adjustment, our forward-looking predictions for the equity risk premium are lower than the historically based projections reviewed earlier, whichever country one focuses on.

Further adjustments should almost certainly be made to historical risk premiums to reflect long-term changes in capital market conditions. Since, in most countries, corporate cash flows historically exceeded investor expectations, a further downward adjustment to the equity risk premium is in order. A plausible, forward-looking risk premium for the world's major markets would probably be on the order of 3% on a geometric mean basis, while the corresponding arithmetic mean risk premium would be around 5%.²⁶

A literal interpretation of country-by-country historical averages might suggest that France has a higher equity risk premium, while Denmark's is lower. But while there are certainly differences in risk between markets, they are unlikely to account for cross-sectional differences in historical premiums. Indeed, much of the cross-country variation in historical equity premiums is attributable to country-specific historical events that are unlikely to recur. When making future projections, there is a strong case, particularly given the increasingly integrated nature of international capital markets, for taking a global rather than a country-by-country approach to determining the prospective equity risk premium.

However, just as there must be some true differences across countries in their riskiness, there must also be variation over time in levels of stock market risk. It is well known that stock market volatility wanders over time, and it is likely that the “price” of risk – namely the risk premium – also fluctuates over time. In the days following September 11, 2001, for example, financial market risk was high, and the equity premium demanded by investors was probably also high. This depressed the market. If the terror had escalated, the market may have collapsed; but Armageddon did not arrive and the market recovered. Clearly, risk premiums at such times are above average. However, it is difficult to infer changes in expected premiums from any analysis of historical excess returns. For corporate capital budgeting purposes, it may be better to use a “normal” equity premium most of the time, and to deviate from this predication only when there are compelling economic reasons to suppose that expected premiums are unusually high or low.

CONCLUSION

The equity risk premium is the difference between the return on risky stocks and the return on safe bonds or bills; it is central to corporate finance and investment, and it is often described as the most important number in finance. Yet it is not clear how big the equity premium has been in the past or how large it is today.

This article presents new evidence on the historical risk premium for 16 countries over 103 years. Our estimates are lower than frequently quoted historical averages such as the Ibbotson Associates Yearbook figures for the United States, and the earlier Barclays Capital and CSFB studies for the United Kingdom.²⁷ The differences arise from bias in previous index construction for the United Kingdom and, for both countries, from our use of a longer time frame (1900–2002) that incorporates the earlier part of the 20th century as well as the opening years of the new millennium. Our global focus also results in rather lower risk premiums than hitherto assumed. Prior views have been heavily influenced by the experience of the United States, yet we find that the U.S. risk premium is somewhat higher than the average for the other 15 countries.

The historical equity premium is often presented as an annualized geometric mean rate of return, which summarizes past performance in one number. Looking ahead, for capital budgeting purposes, what is required is the arithmetic mean of the distribution of possible equity premiums. The arithmetic mean of past equity premiums may exceed the geometric mean premium by several percentage points due to market volatility. In forecasting the future arithmetic mean premium, then, investors or corporate managers who believe they can expect the same annualized risk premium that they have observed in the past still need to adjust for differences in volatility. And, for many countries, the volatility that we might anticipate today is probably very different from historical market volatility.

More fundamentally, however, we have argued that past returns have been advantaged by a re-rating due to a general decline in the risk faced by investors as the scope for diversification has increased. We have illustrated one approach that can be used to obtain an estimate of the amount by which the required rate of return has fallen. In addition, we have argued that past returns have also been inflated by the impact of good luck. Since the middle of the last century, equity cash flows have almost certainly exceeded expectations. Stock markets have therefore risen for reasons that are unlikely to be repeated. This means that when developing forecasts for the future, investors and managers should adjust historical risk premiums downward for the impact of these factors.

A plausible, forward-looking risk premium for the world's major markets would be on the order of 3% on a geometric mean basis, while the corresponding arithmetic mean risk premium would be around 5%. These estimates are lower than the historical premiums quoted in most textbooks or cited in surveys of finance academics. Nonetheless, they represent our best estimate of the equity risk premium for corporate capital budgeting and valuation applications.

NOTES

This paper draws on, extends, and updates the research that underpinned our recent book, Triumph of the Optimists: 101 Years of Global Investment Returns (New Jersey: Princeton University Press, 2002). We are very grateful to ABN AMRO for their extensive support and to our many international data contributors – too numerous to mention here, but all of whom are listed and cited in our book. We also benefited from the many helpful comments received from participants at numerous academic and practitioner seminars held around the world.

1. See Ibbotson Associates, Stocks, Bonds, Bills and Inflation Yearbook (Chicago: Ibbotson Associates, 2000).

2. Barclays Capital, Equity-Gilt Study (1999); and Credit Suisse First Boston, The CSFB Equity-Gilt Study (1999).

3. The U.K. evidence turned out to be based on a retrospectively constructed index whose composition up to 1955, was tainted by survivor bias and narrow coverage.

4. P. Jorion and W. Goetzmann, “Global Stock Markets in the Twentieth Century,” Journal of Finance, Vol. 54 (1999), pp. 953–980.

5. Z. Bodie, “Longer Time Horizon ‘Does Not Reduce Risk,’ “ Financial Times, January 26, 2002.

6. I. Welch, “Views of Financial Economists on the Equity Premium and Other Issues,” Journal of Business, Vol. 73 (2000), pp. 501–537.

7. This figure is the arithmetic mean of the one-year geometric risk premiums. The arithmetic mean of the one-year arithmetic risk premiums, i.e., the average annual difference between the equity return and the Treasury bill return was slightly higher at 9.1%.

8. E. Dimson, P. Marsh, and M. Staunton, Millennium Book II: 101 Years of Global Investment Returns (ABN AMRO/London Business School, 2001).

9. I. Welch, “The Equity Premium Consensus Forecast Revisited,” Working paper, Yale School of Management, September 2001.

10. The Dimson-Marsh-Staunton Global Returns data module is available from Ibbotson Associates, Chicago, IL.

11. Details of our data sources for all 16 countries together with full citations are provided in E. Dimson, P. March, and M. Staunton, Triumph of the Optimists: 101 Years of Global Investment Returns (New Jersey: Princeton University Press, 2002) and Global Investment Returns Yearbook (ABN AMRO/London Business School, 2003). Where possible, we used data from peer-reviewed academic papers, although some studies were previously unpublished. To span the full period from 1900 onward, we typically linked more than one index series. For the United Kingdom, we constructed our own indexes, since hitherto there was no satisfactory record of long-run returns. For the period since 1955, we used the London Business School Share Price Database to construct an index covering the entire U.K. equity market (see E. Dimson and P. Marsh, “U.K. Financial Market Returns 1955–2000,” Journal of Business, Vol. 74, pp. 1–31). From 1900–1955, we constructed an index of the performance of the largest 100 companies by a process of painstaking financial archaeology, collecting data from archives in the City of London. We also used archive data to construct indexes for several other countries (such as Canada, Ireland, South Africa, and Switzerland) for periods for which no data were previously available.

12. Interestingly; after publication of our research, Barclays Capital (but not CSFB) corrected their pre-1955 estimates of U.K. equity returns for bias and extended their index series back to 1900.

13. We use market capitalization weights from 1968 onward and GDP (gross domestic product) weights before then due to the lack of reliable comprehensive data on country capitalizations prior to that date.

14. Table C1.1 shows that the annualized world equity risk premium relative to bills was 4.4%, compared with 5.3% for the United States. Part of this difference, however, reflects the strength of the dollar over the period 1900–2002. The world risk premium is computed here from the world equity index expressed in dollars, in order to reflect the perspective of a U.S.-based global investor. Since the currencies of most other countries depreciated against the dollar over the 20th century, this lowers our estimate of the world equity risk premium relative to the (weighted) average of the local-currency-based estimates for individual countries.

15. See R. Rajan and L. Zingales, “The Great Reversals: The Politics of Financial Development in the 20^th Century,” Working paper No. 8178. (Cambridge MA: National Bureau of Economic Research, 2001), and our book, cited earlier.

16. We say omitting non-surviving markets “probably” gives rise to overestimated risk premiums because of the possibility that some defaulting countries have returns of −100% on bonds, while equities retain some residual value. For such countries, the ex post equity premium would be positive.

17. We again say low risk-free rates “probably” give rise to overstated risk premiums because equity returns would presumably have been higher if economic conditions had not given rise to markedly negative real fixed-income returns. If economic conditions had been better, it is possible that the equity premium would then have been larger.

18. Our U.S. equity returns data are described in E. Dimson, P. Marsh, and M. Staunton, Triumph of the Optimists: 101 Years of Global Investment Returns (New Jersey: Princeton University Press, 2002). From 1900–1925, we use the equity returns reported in J. Wilson and C. Jones. “An Analysis of the S&P 500 Index and Cowles's Extensions: Price Indexes and Stock Returns, 1870–1999,” Journal of Business, Vol. 75 (2002), pp. 505–533; from 1926–1970, we use the CRSP capitalization-weighted index; and from 1971 onward, we employ the Wilshire 5000 Index.

19. For example the arithmetic mean of two equally likely returns of + 25% and −20% is (+25 − 20)/2 =2½ %, while their geometric mean is zero since (1 + 25/100) × (1 − 20/100) − 1 = 0.

20. Because year-to-year stock returns are very volatile (see Table C1.1), these differences are statistically significant at the 95% level for only three of these 14 countries. In economic terms, however, the differences are clearly large.

21. See Y. Amihud and H. Mendelsohn, “The Liquidity Route to a Lower Cost of Capital,” Journal of Applied Corporate Finance, Vol. 12, No. 4 (1999).

22. At the start of our research period in 1900, U.S. domestic investors would have found it much harder than today to construct a well-diversified portfolio. At the start of 1900, there were just 123 stocks listed on the New York Stock Exchange, and the railroad industry alone accounted for 63% of their total market value. See Chapter 2 of our book.

23. In the United States, a confounding factor is the rapid growth of stock repurchases and the trend toward lower dividends; see, for example, E. Fama and K. French, “Disappearing Dividends: Changing Firm Characteristics or Lower Propensity to Pay,” Journal of Financial Economics, Vol. 60 (2001), pp. 3–43. However, in contrast with the United States, stock repurchases have been far less prevalent in the other countries. In Europe, the United Kingdom has the highest level of buybacks, but even U.K. repurchases are rather small (see Section 11.6 of our book).

24. E. Fama and K. French, “The Equity Premium,” Journal of Finance, Vol. 57 (2002), pp. 637–659. In their examination of dividend yields and dividend growth estimates, Fama and French use the Gordon model to compute the U.S. equity premium from 1872–1999. They find a premium of 3.8% before 1949, and a premium of 3.4% for the subsequent period. They argue that the difference between these estimates and the larger ex post risk premium based on historical realized returns is attributable to a reduction since 1949 in investors' required rates of return.

25. Assuming lognormally distributed returns, the arithmetic mean exceeds the geometric mean by ½ × variance = ½ × 0.20² = 0.02 = 2%.

26. For illustrative estimates, see Section 13.7 of our book.

27. Note that these organizations have recently lowered their single-country estimates of the equity risk premium. See R. Ibbotson and P. Chen, “Long-Run Stock Returns: Participating in the Real Economy,” Financial Analysts Journal, Vol. 59 (2003), pp. 88–98, and the 2003 updates to the reports cited in footnote 2.