3
Philosophy of Security by Cryptostakes Schemes
Hemant Kumar Saini
Rajasthan Technical University, Kota, Rajasthan, India
Abstract
The study of asymmetric cryptosystem is done depicting the public key and private key pairing to get the best technique. Also the RSA proofing and modular arithmetic resolve the computation complexity to solve the p-k system. On the other hand, to get sharing Diffie–Helman proved the algorithm with its own color symmetry.
Keywords: P-K system, RSA, trapdoor, SSL, CRT, man in middle attack, DH key, DES key
3.1 Philosophy of Public Key Cryptosystems (p-k Cryptography)
Public-key cryptography is a fundamental disappearance beginning the entire that has vanished by. From the ancient beginning 1960s to today’s complete cryptography is based on substitution and permutation [1]. It is also known by its other name asymmetric cryptography since it uses individual encryption key and another diverse except connected decryption key as shown in Figure 3.1.
Characteristics:
- It is impracticable to decide the decryption key just get merely information procedure and the encryption key.
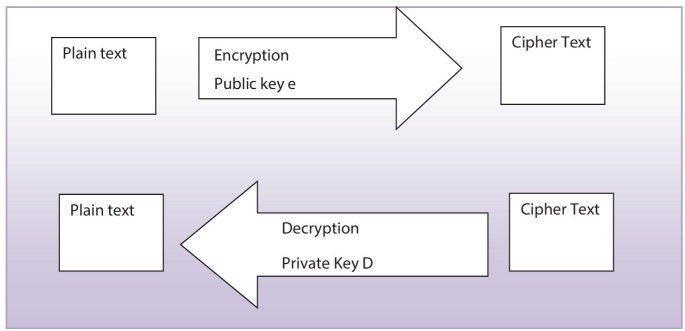
Figure 3.1 Principle of P-k cryptography.
- Among associated keys would be utilized for encryption, if one for encryption then other will be automatically decrypts it.
For any p-k process, the following are the basic main requirements.
- Plain text: any readable information, i.e., provide for enter.
- Encryption algorithm: for converting the plaintext.
- Encryption and decryption keys: pairs of keys if one intended for making cipher, the further is for re-originating plain text. The precise changes executed by the procedure rely on keys offered like participation.
- Cipher text: it is output in mess up form which relies on the puretext and key in support of same communication, with two dissimilar keys two disparate ciphers can be created.
- Decryption algorithm: production of original message with the decryption key and cipher.
Note: Each key used has significance in p-k processing. Since Public key of a user A is available for world then it is used in encryption for secrecy and the same is used for decryption for authentication purposes. Whilst the private key seeded in decryption with both reasons: secrecy plus authentication as private hold only by owner.
In this, if only one of the authentication/confidentiality is considered then there would be chances to breach. Hence the pk process with aggregation of both gives the better unbreakable way. With the deeper into details consider Figure 3.2(a) in which we can see the opponent can easily determine message with the private key of receiver B. Also Figure 3.2(b) gives us the idea of beaching the authenticity as the text was arranged using A’s private key where A’s public key known by everyone so opponent can easily determine the private key of sender A. There it is decided in modern cryptography that p-k inbuilt both and secure the message by first encrypting by senders private key then again encrypt second time by the receivers public key, which brings confidentiality as seen in Figure 3.2(c). But this produces the complexity as the same algorithm processed four times [2, 3].
3.2 RSA Algorithm
It was given by Ron Rivest, Adi Shamir, and Len Adleman at MIT in 1978. The RSA is a chunk where the message and cipher are numbers from 0 to n − 1. RSA uses exponentials to encrypt the plain text into blocks having a binary value < n.
From ancient times, messages are encrypted using specific key to cipher text message. To regaining the message we need same key toward the mapping. Hence to communicate securely both sender and receiver both need to share the identical keys. On the way, sender has to share each identical key with each receiver and hence it has to manage the ring of identical keys to manage and also there would an extra overhead communication to share those keys. In 1970, James Alice gives a clever concept based on lock and unlocks which is inverse operation of each other. He said sender purchase a lock open it and send to receiver. On receiving the lock now the receiver lock it and send the message to sender where the sender can unlock it and read message, no keys were exchanged as seen in Figure 3.3(a). But in this opponent may also become a recipient and get the key. So it extended the concept by developing the keys inverse of each other [4]. The idea of inverse keys can be simplified by explaining with color mixing. The inverse of some color is the complementary color which one added to it produces white. Sender must randomly select an private key say red, next using the complementary color of red, i.e., cyan sends as an public key on non secured communication channel if an intruder traps then it gets cyan as shown in Figure 3.3(b). Let us say now receiver wants to send secret yellow so he mix it with cyan and form a new green which is sent back to sender, where intruders traps this green also. Now sender adds private color red to green and gets yellow which the receiver sent. So with the more advances Ron Rivest, Adi Shamir, and Len Adleman together gives an algorithm which is given in Table 3.1 fundamentally uses the prime factorization one way function which is quite hard to reverse and it takes hundreds of years to break. As such sender after computing all the x, y, n, Ф(n), e, and d sends only the n and e as a public key acting as an open lock where intruder traps n, e [5]. At receiver side, receiver locks by C, and sent back to sender so now the intruder trapped n, e, and C. But it must be notified that none can find the M without f(n) which requires prime factorization of n and which cannot be solved long years [6]. Illustration:

Figure 3.2 (a) p-k secrecy, (b) p-k authentication, (c) p-k confidential + authentication.
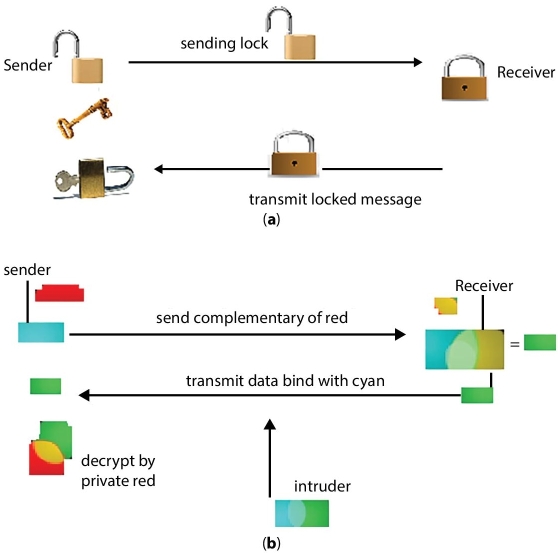
Figure 3.3 (a) Way of locking and unlocking in RSA, (b) RSA analogy to inverse color.
- choose x = 11, y = 19
- compute n = xy = 11 × 19 = 209
- compute f(n) = (x − 1)(y − 1) = 180.
- decide on e, relatively prime to and less than f(n), say e = 17.
Table 3.1 Algorithm for RSA stepwise.
| Key generation |
| choose prime x and y |
| compute n = x y |
| Compute f(n) = (x−1)(y−1) |
| choose integer e such that HCF(Ф(n),e) =1 but 1<e< f(n) |
| Compute d = e−1 mod f(n) or we say de = f(n) |
| Public key {e,n} |
| Private key {d,n} |
| Encryption |
| Message M |
| Cipher C = Me mod f(n) |
| Decryption |
| Cipher C = Me mod f(n) |
| Original message M = Cd mod f(n) |
- establish d such that de = 1 (mod 180) and d < 180.
- The accurate assessment for d is 77 as 77 × 17 = 1309 = 7 × 180 + 49 (using the extended version of Euclid’s algorithm)
3.3 Security Analysis of RSA
RSA obtains security by the complexity of factoring large numbers. Recuperating the message with single key and the cipher is two prime product factors. Therefore RSA can be break by the following attacks of determining the d while considering e and n.
- Swine Force: Attempt finally probable keys. Typical protection is a bulky key to get better higher encryption key and decryption key.
- Arithmetical attacks (trapdoor): Bifurgate the number n into two so permit computation of f(n) and the encryption key e = d−1 (mod f(n)). The most excellent RSA algorithm is utilized to ratio n into:
This take much large years to break but new factorization methods also eases to this.
- Time attacks: Kocher explained a novel assault on RSA where intruder know sender A hardware in enough feature moreover intelligent to determine the decryption period for frequent known ciphers, A can infer the d rapidly. This bother be functional beside the RSA. During Boneh and Brumley attacks over 2003 revealed a more sensible attack competent of recuperating RSA used in a system, e.g., by a Secure Socket Layer (SSL)-enabled web server. Such information is gained escaped by the CRT principle optimization taken by countless RSA accomplishments.
But new method of choosing r with sightless technique, the decryption period is nix lengthy correlated to the inputted cipher and so the timing attack is unsuccessful.
3.4 Exponentiation in Modular Arithmetic
In modular arithmetic, digits are by no means larger than the “modulus”. For instance, for “mod 12” digits are in no way superior than 11. The easiest technique to adapt digits in modular arithmetic is by separating at pleasing the remainder. Obtain 17/3. That is 5 with a remainder of 2, while it said “mod 17” that way that the intact phrase is modular, not presently the preceding number. Like is there would be an large multiplicative expression in modular arithmetic then before multiplication reduce into mod reduction and then solve this is the loveliness of modular arithmetic that the digits stay convenient.
- Example: 12 * 29 * 408 mod 13
- 12 mod 13 = 12
- 29 mod 13 = 3
- 408 mod 13 = 5
- Solution: 12 * 3 = 36, but “mod 13” it is 10
- Then 10 * 5 = 50 but “mod 13” that is 11, which is our answer.
- →12 * 29 = 348 348 * 408 = 141,984 mod 13 = 11 so we get in above.
This is how a mod reduction can be applied.
However the exponentiation function and the logarithm function are reverse of each other which is a modular arithmetic. As we already discussed about the modular arithmetic in unit first so we do not repeat its details. The logarithm of any number is significant (except 1) that have to be lift so as to the same the integer. explicitly, for p and for q,
If we consider k = l (mod s) for some l, where 0 <l < (s − 1) then with the properties of logarithm we can discover a sole exponent as k = ai(mod s) where 0 < i < (s − 1). So the discrete logarithm for the base a (mod s), which is dloga,s (k)10.
This can be seen as dlog a,s (a) = 1 because a1 mod s = a.
Fortunately with the previous example of 12 * 29 * 408 mod 13 it is already clear that proviso the exponentiation is ended above the integers plus next it must be condensed to modulo n, which is deducted as:
Example: watch M11 = M1+2+8 = (M)(M2)(M8). First calculate M mod n, M2 mod n, M4 mod n, and M8 mod n and get [(M mod n) × (M2 mod n) × (M8 mod n)] mod n.
In general, ab would found with m positive integers where b is a binary number such that
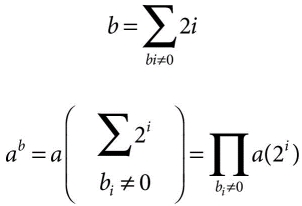
Therefore
We can follow the algorithm to find for computing abmod n.
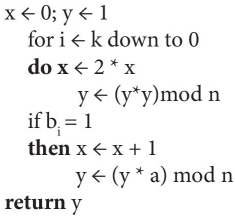
Solve itself: 37 * 10 mod 53; 56 mod 23
3.5 Distribution of Public Keys
There are numerous method have been planned for the sharing of public keys in the history. Those proposals can be grouped into four.
A. Public announcement
Public key since announced publicly and it is an uncontrolled way of sending and sharing the key publicly. This can be easily forged, namely, various consumer might imagine user A to send a encryption key to a new member or transmit such a encryption key.
B. Publicly available directory.
More security is provided by upholding a publicly accessible active index keys though preservation with the sharing of the community directory would contain to be liable of have confident organization. The authority maintains each entry by {name, public key} which is registered to the participant in a secure way. It is much secure but still fails when an opponent thrive in attain or calculate the confidential key of the index influence, the opponent might confidently passing the imitation public keys and snoop on post propel to any member an additional approach to reach the similar ending at challenger tampering influencing with account.
Example: Modular Exponentiation Algorithm for ab mod n, where a = 7, b = 560 = 1000110000, and n = 561.
| i | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| Bi | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| x | 1 | 2 | 4 | 8 | 17 | 35 | 70 | 140 | 280 | 560 |
| y | 7 | 49 | 157 | 526 | 160 | 241 | 298 | 166 | 67 | 1 |
C. Public-key authority
Since every contributor consistently knows a public key for the authority, by means of merely the authority meaningful the matching private key, the sharing of public keys commencing the directory is strongly controlled. However it is not safe as a user have to plea to the authority for a public key for each further user so as to it needs to call. Moreover the index of names in addition to public keys preserve by the authority is susceptible to tampering.
D. Public-key certificates
An unconventional loom where the participants uses certificates to swap keys devoid of drop a line to a public-key authority demonstrated in Figure 3.4. Certification authority (CA) attach public key to picky participant P, i.e., P (person, router) list its public key with CA by only if “proof of identity” to CA and CA generate certificate attaching P to its public key. This credential hold P’s public key digitally marked by CA or CA says “this is E’s public key”.
Thereafter, certificate authority generated the certificates, which are known by the applicant with the corresponding confidential key. A contributor broadcasts its credential to express its entered information and other participants can validate that the certificate was shaped by the ability. Here certificate authority (CA) configures the entire nodes. When participant A wants participant B’s public key it gets B’s certificate and apply CA’s public key to B’s certificate, so what verifying B’s public key which has been demonstrated mathematically in Figure 3.5.

Figure 3.4 Mark verification by CA
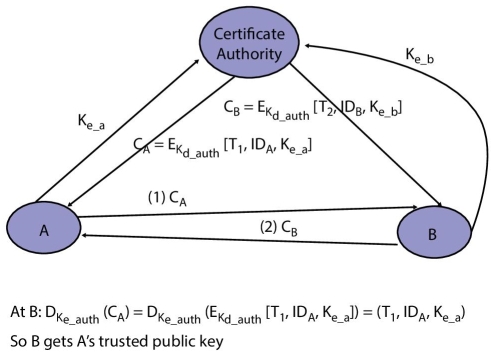
Figure 3.5 Mathematical Exchange of PK certificates
{source: http://flylib.com/books/3/190/1/html/2/images/10fig04.jpg}.
3.6 Distribution of Secret Keys Using Public Key Cryptosystems
Since the public-key are incompetent intended for huge post because secret keys used conventionally are attribute ally small. But if conservative confidential keys are considered like a message, the encryption of the input by means of a pk scheme will not be an overhead at the dispensation for a processor. Therefore, their combined employ a predictable and public-key cryptography be worn that offer verification, veracity, and privacy in a competent way [6].
Suppose sender sending a marked, secret message to a recipient. Sender primary add a digital signature as a purpose of the sender’s confidential input and message digest. With this, sender also breeds a predictable surreptitious key, and uses it to convert the message into miscible form. Successively, the sender converts the confidential key via the receiver’s public key. The sender lastly adds the encode the secret key and the digital signature to the miscible format, and put on the air the data to the receiver as shown in Figure 3.6.
On receiving, recipient’s decrypt the secret key with its private key. Now this secret key is worn dto decrypt the cipher. Hence the receivers authenticate the message signature as a purpose of the signature and the originator’s public key.
- So it surefire confidentiality as the receivers private key is the only way to decrypt the secret key which is further required to decrypt the message.
- It also guaranteed veracity as the digital signature was produced by a digest of the inventive plaintext message.
- Last, verification proved since digital signature proves that pain text comes is from original sender only and not being forged.
But with this some disadvantages are also held:
- public-key encryption shared might corrupt network since it comparatively lofty computational weight of public-key encryption and decryption. This can be minimizing, since a predictable scheme (e.g., DES) is worn to convert the plain text. Merely the encoding the confidential key (e.g., the DES key) entails a public-key algorithm.
- incapability to propel a message to many recipients. Proviso the message is spread to numerous receivers, the inventor encoding the confidential key one instant per receiver, by means of that recipient’s public-key such as, if a text is propel to five participants, five unusual encodings of the private key might be affixed to the plain text.
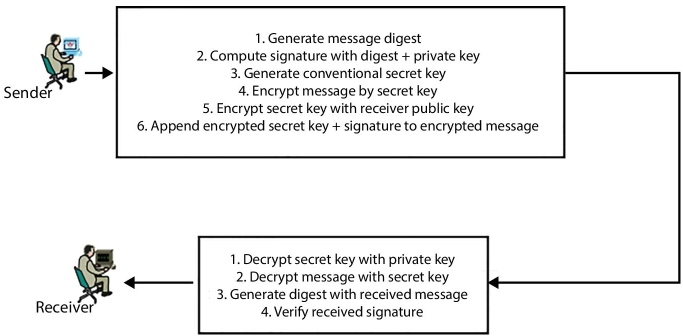
Figure 3.6 Circulation of confidential keys using Public Key phenomenon.
3.7 Discrete Logarithms
These are the basis of the asymmetric key including Diffie–Hellman key swap with the digital signature algorithm (DSA). Recalling from Euler’s theorem, for each prime a and n.
where Ф(n) is Euler’s totient function < n.
In general, am = 1 (mod n) means that there is no less than one integer m that satisfies it M = Ф(n).
- For example, 7 mod 19.
71 = 7 (mod 19)
72 = 49 = 11 (mod 19)
73 = 343 = 1 (mod 19)
74 = 2401 = 7 (mod 19)
75 = 16807 = 11 (mod 19).
Here is no point in enduring for the reason that the progression is recurring.
This can be proven by noting 73 = 343 = 1 (mod 19) whichever 73 + j = 737j = 7j (mod 19) so, any two powers of 7 whose exponents vary by 3 are congruent to each other. So sequence is periodic with 7m = 1 mod 19.
With this problem of finding Ф such that aФ ≡ b (mod p) is called the discrete logarithm problem. Suppose that n is the smallest integer such that an ≡ 1 (mod p), i.e., n = ordp(a). By assuming 0 ≤ Ф < n, we denote Ф = La(b), and call it the discrete log of b w.r.t. a (mod p).
Ex: p = 11, a = 2, b = 9, then Ф = L2(9) = 6.
3.8 Diffie–Hellman Key Exchange
From the ancient soviet union and north America who were made the NORAD to communicate over the space shuttles and make the communication between computers. This way since the 1958s Internet had became worldwide and new problem of secrecy came that is how can the secrecy could be achieved by sharing the key. This was proposed by Diffie and Hellman by giving an short trick. Let it be explored with colors to easy understanding. The trick was based on two facts first is it is easy to mix two color to make a new and second cleansing mix color to get exact original color which is basis for an lock where two colors mix and form an lock but the inverse of its to get colors from a mixed is hard which is one way function.
So the solution works as follows, Say both sender S and recipient R agreed on standing color i.e. yellow, both s and R chooses their private color red and green respectively and mix separately either in order to disguise the original color. Now both exchange their mixtures keeping their private colors themselves only. So in this intruder without having their private colors cannot deduce the exact color. To more elaboration for hardness of one way function of mod algorithm consider Figure 3.7.
Diffie and Hellman proposed public key cryptosystem in 1976. The algorithm is for exchanging secret key (not for secrecy of data) based on discrete logarithms. Since it is infeasible to calculate inverse so to ease computation calculate exponentials modulo a prime [7].
This provide a secure way for two communicating parties to share a symmetric key (so called a session key) which is then used to provide privacy and authentication for subsequent message flow. The algorithm follows [8, 9]:
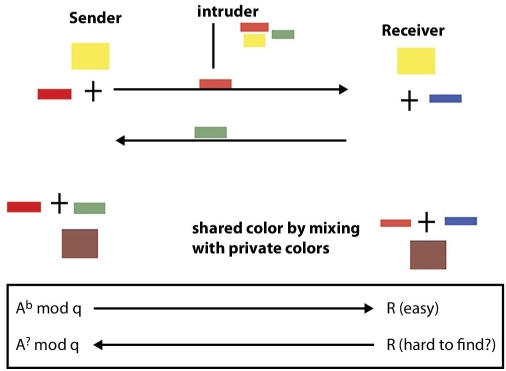
Figure 3.7 DH exchange.
- Global public elements—Large prime integer q, i.e., 1024 long, α a primitive root/generator of Zq* (i.e., the multiplicative group modulo q, α < q)
- Sender key generation—select private Xs < q and compute public Ys =αXs mod q
- Receiver key generation—select private Xr < q and compute public Yr =αXr mod q
- Secret key by sender—K= (Yr )Xs mod q
- Secret key by receiver—K= (Xr )Ys mod q
To attack in this an attacker needs to compute K from Ys and Yr but this is difficult to solve. The genuine key swap for any party consists of lifting the others “public key” to control of their private key. The ensuing digit (or as much of as is necessary) is worn as the key for a block cipher or additional private key method. For an attacker to gain the equivalent value they require no less than single of the secret numbers, which way solving a discrete log, that is computationally impractical set bulky adequate numbers [10].
Let it be understood by an example:
A and B want to carry out DH Key Exchange:
- concur on prime p = 353 and α = 3
- choose random secret keys:
- A decide Xs = 97
- B decides Xr = 233
- calculate session key contributions
- Ys = 397 mod 353 = 40 (A)
- Yr = 3233 mod 353 = 248 (B)
- calculate shared session key as:
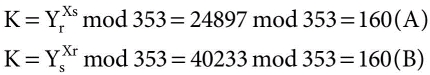
Disadvantage: Insecure against man-in-the-middle-attack.
3.9 Review Exercise
Elaborative:
- What is a prime number?
- What is Euler’s totient function?
- Distinguish index with discrete logarithm?
- Briefly explain Diffie–Hellman key exchange.
- What are the two approaches of encryption/decryption technique?
- For n no. of users, how many keys needed in private key cryptography and public key cryptography?
- Explain how RSA works.
- Computer the primary essentials of a public-key cryptosystem?
- Explain the trap-door one-way function?
References
- 1. Blake, I., Seroussi, G., Smart, N., Elliptic Curves in Cryptography, Cambridge University Press, Cambridge, 1999.
- 2. Enge, A., Elliptic Curves and Their Applications to Cryptography, Kluwer Academic Publishers, Norwell, MA, 1999.
- 3. Diffie, W., The First Ten Years of Public-Key Cryptography. Proc. IEEE, Vol. 76, pp. 560–577, 1988.
- 4. Rosen, K., Elementary Number Theory and its Applications, Addison-Wesley, Reading, MA, 2000.
- 5. Kumanduri, R. and Romero, C., Number Theory with Computer Applications, Prentice Hall, Upper Saddle River, NJ, 1998.
- 6. Boneh, D., Twenty Years of Attacks on the RSA Cryptosystem. Not. Am. Math. Soc., vol. 46, 2, pp. 203–213, 1999.
- 7. Cormen, T., Leiserson, C., Rivest, R., Stein, C., Introduction to Algorithms, MIT Press, Cambridge, index MA, 2004.
- 8. Shamir, A. and Tromer, E., On the Cost of Factoring RSA-1024. Crypto RSA-1024, RSA CryptoBytes, Vol. 6, pp. 10–19, 2003. http://www.rsasecurity.com/rsalabs.
- 9. Stallings, W., Cryptography and network security principles and practice, fifth edition, Pearson Education, Inc., publishing as Prentice Hall, Upper SaddleRver, NJ, 2006.
- 10. Diffie, W., Hellman, M.E., New Directions in Cryptography, IEEE Transactions on Information Theory, Vol. 22, 6, pp. 644–654, 1976.
Note
- Email:[email protected]
