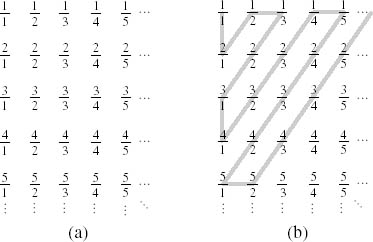Chapter 7

CANTOR’S PARADISE

Not everything that counts can be counted. Not everything that can be counted counts.

Albert Einstein

Jane Muir began the final chapter of her delightfully written book Of Men and Numbers with typically elegant prose:

There are times in history—the history of a man as well as a civilization—when one can look back and say, ‘So this is where it’s all been leading. It seems so obvious now, why didn’t I realize before?’ A man or a civilization comes to the end of a road; the journey is over; all the wanderings and travels down dead ends and over highways have led to this particular place and suddenly he realizes that he is at the end, the trip is over, the journey completed. Such was the feeling mathematicians had after Georg Cantor guided them over the last stretch of land.

They could rest. Their doubts and fears and wonders of where the road would lead were satisfied. But another road stretched out before them, an ill-defined, treacherous-looking path that both repelled and beguiled—and soon another journey began. The end of one trip suddenly became the beginning of another. Such, too, was the feeling mathematicians had after Georg Cantor opened their eyes to a new and foreign world.

Cantor’s eminent contemporary Leopold Kronecker was more repelled than beguiled at this particular realization of his famous dictum God made the integers, all else is the work of man. We will look at the bare rudiments of Cantor’s seminal ideas, ideas which followed paths from the obvious to the unbelievable, the elementary to the most profound.

To begin with, since we will make essential use of it, we will mention Euclid’s fifth postulate and, since we are interested in that part of Cantor’s work which contradicts the fifth common notion, we will mention that too.

Obvious Ideas

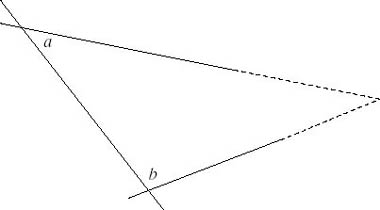
Euclid’s Elements has claim to be the second bestselling book of all time (surpassed by the Bible). Written around 300 B.C. it chronicled much of the known mathematics of the time and is particularly (though by no means exclusively) regarded for its treatment of geometry, which begins with a set of twenty-three definitions, five postulates and five common notions; all seem at least very reasonable, if not self-evident. That said, the fifth postulate was at least cumbersome:

That, if a straight line falling on two straight lines make the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles.

It means that, in figure 7.1, if a + b < 180 the two lines will eventually meet.

In his Commentary on the Elements, the revered commentator Proclus (411–85) mentioned that the postulate was attacked from the outset and wrote ‘this postulate ought even to be struck out of postulates altogether; for it is a theorem’. Among all of those definitions, postulates and common notions, it alone raised suspicion. The equivalent formulation, attributed to the eighteenth-century Scottish mathematician John Playfair (but known to Proclus) is even more disarming:

Figure 7.1.

Figure 7.2.

Through a given point not on the line, there is one and only one line which can be drawn through that point parallel to the line.

Figure 7.2 shows the point and a finite segment of the line: the statement is surely obviously true.

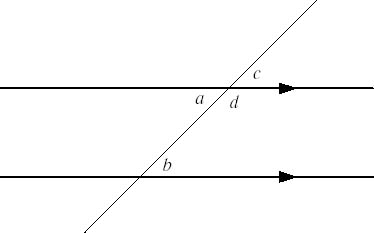
It was not until Proposition 29 of Book 1 of the Elements that the fifth postulate was first used (and from there on used frequently in Book 1 and in later books):

Proposition 29: A straight line falling on parallel straight lines makes the alternate angles equal to one another, the exterior angle equal to the interior and opposite angle, and the sum of the interior angles on the same side equal to two right angles.

Referring to figure 7.3, this means that a = b, b = c and b + d = 180, respectively. The proof is brief and clear, but contains the statement:

Figure 7.3.

But straight lines produced indefinitely from angles less than two right angles meet.

In fact, the great Proclus was wrong (as were many others): the fifth postulate is not a theorem but an independent statement, alternatives to which (there are no parallel lines or there is more than one parallel line through the point) are perfectly valid. It is a stark fact that those many propositions from 29 onwards (including the Pythagorean theorem) are true only of Euclidean geometry, defined as the geometry which arises from those precise definitions, postulates and common notions. Change the fifth postulate to ‘no parallel lines’ and we have spherical geometry, change it to ‘more than one parallel line’ and we have hyperbolic geometry, famously developed independently by the Russian mathematicians Nikolai Lobachevsky and János Bolyai. The model of spherical geometry is (unsurprisingly) the surface of a sphere (with ‘straight lines’ as the great circles); hyperbolic geometry fits less comfortably into our Euclidean space viewed through our Euclidean eyes: famous representations of it are the Klein–Beltrami disc and the Poincaré disc (explored with such wonder by the Dutch artist Maurits Escher) and the geometry of the pseudosphere. Here there are an infinite number of lines parallel to the given one, the Pythagorean theorem does not hold, the sum of the angles of a triangle is less than 180°, triangles with the same corresponding angles have the same area, not all triangles have the same angle sum and there are no similar triangles, etc. Jane Muir’s words are as appropriate to this as they are to the work of Georg Cantor, to which we will now turn since it was he who called into question the fifth common notion, which, over the centuries, had itself seemed to be completely self-evident: ‘The whole is greater than the part’ or, moving to its commonly used Latin equivalent, ‘Totem parte maius’.

It remained self-evidently true until the late nineteenth century, when Cantor’s controversial work brought about results which confounded it, one of which so surprised him that, in an 1877 letter to his frequent correspondent, Richard Dedekind, he wrote, ‘Je le vois, mais je ne le crois pas!’ (‘I see it, but I don’t believe it!’) We shall look at that result and some others of its type, but first we need a definition.

One-to-One Correspondence

Intuition, as is so often the case, will prove to be an unreliable guide and to counter its misleading ways we need a careful definition of how to compare the size of two infinite sets of objects, and that definition comes from one of the alternative ways we have of comparing two finite sets. If we have two bags of marbles and we are asked whether there is the same number of marbles in each bag, we could empty each bag and count the contents of each; if the two numbers tally, the bags did contain the same number of marbles. Yet, although this does answer the question, it does so by doing too much; we were not asked how many marbles were in each bag, just whether there is the same number. To answer the question directly we could repeatedly put one hand in each bag and remove marbles in pairs; if one bag empties before the other, they had different numbers of marbles inside them, otherwise the marbles were paired perfectly—or, using a more mathematical terminology, they were put in one-to-one correspondence. It is this idea of a one-to-one correspondence that Cantor used in dealing with the comparison of infinite sets. It is important to realize that the nature of the association matters not at all, it simply needs us to count off in pairs, just as the removal of marbles in each hand does so. For example, it is small surprise that the correspondence n → − n demonstrates the equivalence of the positive and negative integers but, having accepted that, the correspondence n → 2n brings about the equivalence of the positive integers and the even positive integers with equal alacrity; already Euclid’s fifth common notion has been contradicted. In fact Cantor soon realized that it is characteristic of infinite sets that they do contradict the fifth notion and avoided powerful criticism by defining an infinite set as one which can be put into one-to-one correspondence with a proper subset of itself; any infinite set which can be put into one-to-one correspondence with the natural numbers was to become known as a ‘countable’ set and its ‘size’ (or cardinality) written as (aleph null, or aleph zero).

The Rationals are Countable

With that definition surprises began to tumble from his pen. For example, using the property of unique factorization, if we consider the set

it can be put in one-to-one correspondence with an infinite subset of N by the association (m₁, m₂, m₃, . . . , m_n) → 2 ^m₁ × 3 ^m₂ × 5 ^m₃ × . . . × (n th prime) ^m_n. Dimension has nothing to do with size: is countable; that is, the cardinality of is .

If we take n = 2 in the above result and agree that the difference between (a, b) and a/b is merely notational, we can see that this establishes the fact that the rationals are countable. Yet another way of looking at a set’s countability is to reason that its elements can be listed, but if we try to list them, then we naturally encounter the problem of missing out numbers; after all, between every two rationals there is another rational. How can we possibly list them in an exhaustive manner?

Cantor wondered this too and, in 1873, made a listing using a ‘diagonal array’. Figure 7.4(a) displays the rationals as an infinite two-dimensional array with the first row consisting of those which have a numerator of 1, the second row those which have a numerator of 2, etc.

Figure 7.4.

Moving in the diagonal manner suggested in figure 7.4(b) brings about the following listing of the rationals:

Clearly, every rational number (repeatedly) appears (with, for example, and we can extract from this list the distinct rationals simply by moving from left to right; in this way every rational number is counted once and only once and therefore put into one-to-one correspondence with the natural numbers.

The listing is made explicit, although it is a little ragged and it could be held to be unsatisfactory that the original list is populated with an infinite number of repeats which we have to sift through. Do ‘natural’ listings exist which dispense with this? The answer is ‘yes’ and two such are noted in the Neil Calkin and Herbert Wilf article ‘Recounting the rationals’ (2000, American Mathematical Monthly 107:360–64) as listed on The On-Line Encyclopedia of Integer Sequences website as sequences A038568 and A020651. A third is the subject of the article itself, which uses an elegant and beautifully elementary argument (highly related to Farey sequences and Stern–Brocot trees) to establish the fact. We will take the trouble to present it below.

The argument relies on a particular tree diagram, with the fraction as its top node and with the structure that each node a/b has two children:

• the left child, which is defined as a/(a + b)

• the right child, which is defined as (a + b)/b

That is,

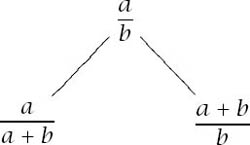
So the tree starts as follows:

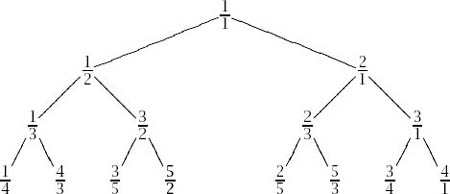
We construct a list of fractions from the nodes of the tree by traversing the tree from top to bottom, left to right to get

It is not immediately apparent but, in fact, the process lists them all and the nice thing about it is that it does so by having each one of them appear precisely once. This is truly a ‘proper’ listing of the rationals.

Three elementary results combine to establish this and to consider them it is useful to make a definition.

Definition 7.1. A fraction a/b is called reduced if a and b have no prime factors in common. (Note that, by this definition, is reduced.) In fact, reduced is the same as coprime once we are past .

Result 1. Every node is reduced.

To show this, suppose that a/b is a reduced node.

The left child is made up of a and a + b, and if these were not coprime there would exist k, c and d such that

a = ck   and   a + b = dk,

which means that

ck + b = dk   and so b = k(d − c)

and so b divides k, which means that it must divide a = ck, which is a contradiction.

Precisely the same argument establishes that the components of the right child (a + b)/b must also be coprime.

Since is reduced we have an inductive proof of the result.

Result 2. Every positive reduced fraction appears as a node.

Consider the element a/b and define its sum as a + b. Assume the result holds for all fractions whose sum is k. We prove all fractions with the sum k + 1 must be on the tree.

Consider a fraction r/s such that r + s is k + 1; it must be that r k and s k. Further, r ≠ s since the fraction must be reduced, so either r > s or r < s.

For r > s, evidently r − s > 0, and so (r − s)/s > 0. The sum of this fraction is (r − s) + s = r k and so (r − s)/s must be a node by assumption; its right-hand child is ((r − s) + s)/s = r/s and so is a node.

For r < s, s − r > 0, and so r/(s − r) > 0. The sum of the fraction is (r + s) − r = s k so r/(s − r) must be a node by assumption; its left-hand child is r/((s − r) + r) = r/s, which again is a node.

The starting condition r + s = 2 yields the unique positive fraction , which is by definition a node, and the induction is once again complete.

Result 3. Every reduced fraction appears at most once.

We know that every fraction is reduced.

Suppose that the fraction j/k appears at least twice and call its two parents a/b and c/d. Obviously, a/b ≠ c/d because then j/k would be a left and a right child of the same node, but for integers a and b, (a + b)/b > a/(a + b).

If j/k is a left child of both a/b and c/d, then a/(a + b) = c/(c + d) and so a/b = c/d: the same argument ensures that both a/b and c/d cannot be a right child of the same parent. Therefore, one must be the left child of one parent and the right child of another.

Without loss of generality, we can assume j/k is the left child of a/b and the right child of c/d. Therefore, j/k = a/(a + b) and j/k = (c + d)/d.

Because all fractions are reduced, this implies

j = a,   k = a + b,   j = c + d,   k = d,

and so

a = c + d   and   d = a + b

and c + b = 0. Since b, c > 0 we have the contradiction.

The result is then established.

The process generates the sequence of numerators 1, 1, 2, 1, 3, 2, . . . , which might be written as b(n) and, since it can also be shown that the denominator of the nth fraction in the list equals the numerator of the (n + 1)th, the list of fractions is of the form

And we even have a nice recursive formula for the nth fraction on the list a(n):

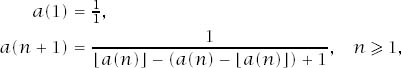
where is the floor function.

A Bigger Set

So, increasing dimension has no effect on countability, neither, as we have seen already, does increasing ‘size’: , a set strictly containing , is countable. If we increase size again and consider the algebraic numbers which include the likes of and all other numbers which are the roots of polynomial equations with integer coefficients, we get no further; a clever argument of Cantor showed that they are countable too. And so the adventure continued until intuition was for once shown to be a reliable guide: the whole real number system, , is not countable. Including the likes of π and e pushed matters too far, but if is countable and not so, then what has been added—the transcendental numbers—must not be countable. In 1844 Joseph Liouville established an infinite class of transcendental numbers and in 1851 he managed to manufacture a particular number (now known as the Liouville number) which was provably transcendental, but finding such numbers proved to be extremely difficult. Now, with Cantor’s result, there was the frustrating realization that ‘almost all’ numbers were one of these elusive transcendentals.

In fact, the proof that is not countable is quite easy if the ‘listability’ of countable sets is utilized: more than this, [0, 1] is easily seen not to be listable. First, a small ambiguity is removed if we insist that finite decimals are represented by their infinite, 0.9 recurring, equivalent. For example, 0.284 = 0.283 999. . . . Now suppose that [0, 1] is listable. But then consider the number 0.a₁a₂a₃ . . . , which is formed by making a₁ anything other than the first decimal place of the first number in the list, a₂ anything other than the second decimal place of the second number in the list, etc.; by its construction, such a number is different from every number in the list and so the list cannot exhaust all numbers in the interval—and the required contradiction is in place.

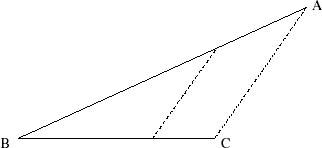
With this result it is clear that any finite interval is uncountable, but to make things explicit we can do the following. If we restrict ourselves to the Euclidean world and so allow ourselves to accept the fifth postulate, we can see that two finite intervals of arbitrary length can be put into one-to-one correspondence by matching two line segments of their lengths, point for point.

Figure 7.5.

Figure 7.6.

Figure 7.7.

Figure 7.5 shows two such segments, AB and BC, in line. Now fold the line, as shown in figure 7.6, to form an acute angle ∠ABC and then join A and C. The Playfair reformulation of the fifth postulate guarantees that there is one and only one line through any point on AB which is parallel to AC; this line provides the one-to-one correspondence that we need.

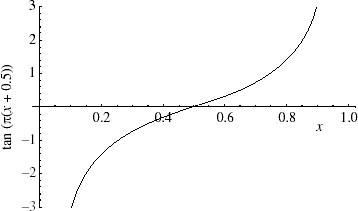
All finite subintervals of are therefore uncountable and we can establish a one-to-one correspondence of [0, 1] with using the function f(x) = tan(π(x + 0.5)), as figure 7.7 suggests.

Cantor’s Result

Returning to the earlier quotation of Cantor on page 72, what he had seen, and what he could not believe, was the resolution of a question articulated in an earlier, 1874 letter to Dedekind, in which Cantor asked:

Can a surface (say a square that includes the boundary) be uniquely referred to a line (say a straight line segment that includes the end points) so that for every point on the surface there is a corresponding point of the line and, conversely, for every point of the line there is a corresponding point of the surface? I think that answering this question would be no easy job, despite the fact that the answer seems so clearly to be ‘no’ that proof appears almost unnecessary.

We have already seen on page 73 that ⁿ is countable, but that 1877 letter contained a proof which confounded the obvious by showing that there was a one-to-one correspondence of points on the interval [0, 1] and points in n-dimensional space ⁿ or, equivalently, there is a one-to-one correspondence between and ⁿ: the whole is once again not necessarily greater than the part.

To set up the required one-to-one correspondence take any point (x, y) in the unit square, with the numbers given their infinite decimal form, and construct the decimal whose first decimal place is that of x, whose second decimal place is that of y, whose third decimal place the second of x, whose fourth decimal place the second of y, and so on. Such a number is unique in [0, 1] and, conversely, any number in [0, 1] can be disseminated uniquely into two numbers which are the x and y coordinates of a point in the unit square: the one-to-one correspondence is thereby established and the concept of dimension again brought into uncomfortable scrutiny. The same argument can be easily adapted to higher dimensions.

The whole theory is a firmament of fantastic results, most of which confound intuition, and some of which hit at the very heart of mathematical foundations, bringing with them genuine paradoxes which have shaken the assumed firm foundations of the subject. One infamous example concerned the great logician Gottlob Frege, who had worked for a quarter of a century on developing arithmetic from the basic logical foundations of mathematics, as he defined them to be. The thesis was to occupy two large volumes, with the first already published when Frege received a letter from the august Bertrand Russell detailing his own recent observations about set theory which were inspired by Cantor’s work. At the end of the second volume Frege had added a footnote, which began:

A scientist can hardly meet with anything more undesirable than to have the foundation give way just as the work is finished. In this position I was put by a letter from Mr. Bertrand Russell as the work was nearly through the press.

Untold mathematicians and logicians have been deceived by the implications of Cantor’s work: arguments have raged and sides have been taken. We will end the chapter on a positive note, with the words of another German mathematician, David Hilbert (the greatest of them all in that era): ‘No one shall expel us from the paradise that Cantor has created.’