Chapter 15

THE POWER OF POWERS

Sometimes it is useful to know how large your zero is.

Anon

Given its importance to the chapter, ‘Some consequences of the irrationality of log₁₀ 2’ could have been a reasonable alternative title. Yet the title stands, as the subject matter that follows concentrates on some rather surprising consequences relating to the decimal expansion of 2ⁿ; we prove the elementary result that log₁₀ 2 is indeed irrational in the appendix (page 226), expending our efforts over the next few pages appealing to that result.

A Great Deal of Nothing

In a note to the journal Mathematics of Computation (E. and U. Karst, The first power of 2 with 8 consecutive zeroes, July 1964, 18(87):508) the authors provided what the note’s title suggests: the first power of 2 which contains precisely eight consecutive zeros. They acknowledged that their work built on that of F. Gruenberger, who had computed the first power of 2 to contain 4, 5, 6 and 7 consecutive zeros, which, together with the Karsts’ and the cases 2 and 3, are listed in table 15.1.

Table 15.1.

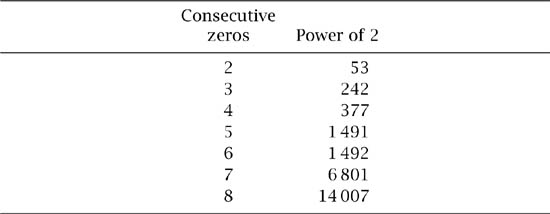
To be explicit, taking the first case,

2⁵³ = 9 007 199 254 740 992

is the first power of 2 to contain two consecutive zeros; the 4217 digits of 2^{14 007} would take up too much space to write out, but the relevant part of the decimal expansion is

· · · 6 603 000 000 003 213 · · ·.

The Karsts’ IBM 1620 computer took 1 hour 18 minutes to find those eight consecutive zeros on 1 January 1964 and they reported that, on 1 May of the same year, they had tested up to the power 60 000 without finding the elusive nine-zero repetition; perhaps the interested reader might wish to use more modern technology to perform their own search. One thing is certain though: theoretically that search will not be in vain, since it is a fact that any number of repetitions is possible, 9, 900, 9000, or whatever number one wishes—although the numbers involved will assuredly be fantastically large.

To establish this peculiar fact we will look to the Elementary Problems and Solutions section of the American Mathematical Monthly (December 1963, 70(10):1101–2), wherein E. J. Burr (in particular) provided a succinct argument which we expand below.

First we need a result from the theory of rational approximation of irrational numbers, which is proved in the appendix (page 231):

Given any irrational number λ and any positive integer k, there is a rational number m/n with n k such that 0 < λ − m/n < 1/nk.

In particular, since log₁₀ 2 is irrational this result becomes

and, since 10^x is monotone increasing,

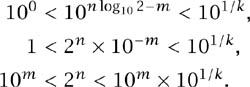
Now take k large enough so that, for some chosen positive integer s, 10^1/k 1 + 10^{−(s + 1)}, then 10^m < 2ⁿ < 10^m × (1 + 10^{−(s + 1)}), i.e. 10^m < 2ⁿ < 10^m + 10^m−s−1, which ensures that 2ⁿ starts with a 1 followed by at least m − (m − s − 1) − 1 = s consecutive zeros.

The Start of Something Big

The above proof locates the zeros after an initial digit 1 at the start of the decimal expansion yet we have seen evidence that the consecutive zeros can exist anywhere within the body of the number (and there are proofs for this too). This specialization suits our purpose though, since the main thrust of this chapter is that, no matter what sequence of whatever length of nonnegative integers we choose, there is at least one power of 2 which starts with that sequence.

If we start simply and require a power of 2 to start with the single digits 1, 2, 3, . . . , 9 in turn we arrive at table 15.2: notice how hard we have to work for 7 and 9, the latter achieved by that same power to first contain two consecutive zeros.

Table 15.2.

If we become more ambitious and ask for the decimal expansion to start with the year of publication of this book, 2008, we require 2¹⁹⁷ = 2008 . . . . Higher ambition still yields the following sequence:

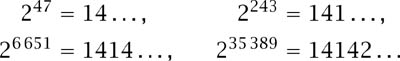
and we are beginning to generate the most significant part of the decimal expansion of . If we tame the gargantuan number so generated by dividing it by the appropriate power of 10, we have

If we wish to demand more and boast further decimal places we can have them—as many as we please, although the numbers involved will be vast. (Here, [x] is the ceiling of x, discussed in the appendix (page 227).)

Moving to other attractive examples we also have

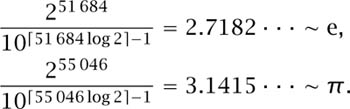
Of course these powers of 2 do make the numbers generated vastly big; to get some sort of idea how big, if we take a sheet of paper 0.1 mm thick and double it over 100 times(!) the thickness, 0.1 × 2¹⁰⁰ mm, will be greater than the distance to the furthest galaxy.

Now we need to prove the fact that any sequence of digits whatsoever can form the most significant digits of some power of 2 and to achieve this we will appeal to an argument provided by Yaglom and Yaglom in the first of their two books of mathematical problems (Challenging Mathematical Problems with Elementary Solutions, 1987, A. M. Yaglom and I. M. Yaglom, Dover), expanded by Ross Honsberger in his volume Ingenuity in Mathematics (Mathematical Association of America, 1970). We will expand further; the argument is indeed elementary, as it is ingenious—and one could also argue that it is extremely subtle and instructive. First, we will restate the proposition in an equivalent form.

The Restatement

If we consider the example above, we can rephrase matters by asking the question: is there a positive integer n so that

If such an n exists, we will assuredly have 2ⁿ beginning with the digits 14 142. Now replace the ellipses . . . by an appropriate power of 10 to get

Generally, if we wish a power of 2 to start with the sequence M, we require positive integers k and n so that

and applying the monotone increasing log₁₀ function throughout gives

Figure 15.1.

Using the standard laws of logs the restatement is then the following.

For a given positive integer M we require positive integers k and n so that

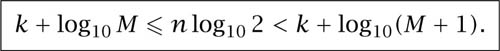
The Proof

To show that such k and n exist we will need two results. An application of the pigeon-hole principle, discussed in the appendix (page 228) and a fact arising from the interrelationship between logs and the floor function (discussed in the appendix (page 230)):

log₁₀(M + 1) = log₁₀ M :     M + 1 not a power of 10,

log₁₀(M + 1) = log₁₀ M + 1: M + 1 a power of 10.

With these parts in place we can proceed to the very devious proof.

Write l = log₁₀ M and r = log₁₀ (M + 1) and so define the semi-open interval [l, r) whose interval length is

since M 1.

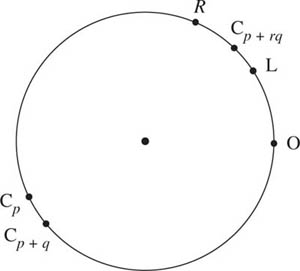
Now translate copies of this interval (whose length is strictly less than 1) repeatedly to the right by 1 unit to get the infinite set of nonoverlapping, semi-open intervals [l_i, r_i) = [i + l, i + r) for i = 1, 2, 3, . . . , as shown in figure 15.1.

Figure 15.2.

Having done this, we will use the device of wrapping the whole of the infinite positive number line anticlockwise onto a circle of circumference 1 unit, which means that the line repeatedly and indefinitely overlaps. Numbers on the number line which differ by an integer will be mapped to the same point on the circle by this process and vice versa; in particular, all of the l_i will be mapped onto the same point L and all of the r_i onto the same point R. The situation is shown in figure 15.2, where the origin is at point O. It is these L and R that will provide the outside values of our double inequality.

Now we need to fit that multiple of log₁₀ 2 at the centre of the double inequality and to achieve that consider the infinite set of numbers on the number line

log₁₀ 2, 2 log₁₀ 2, 3 log₁₀ 2, . . . , n log₁₀ 2, . . .

and denote their images on the circle by C₁, C₂, C₃, . . . , C_n, . . . . These go round and round the circle in steps of arc length log₁₀ 2 and no two of them coincide, for if two did then

a log₁₀ 2 − b log₁₀ 2 = m

for some integer m, which would mean log₁₀ 2 = m/(a − b) and would therefore be rational, and the irrationality of this number appears crucially for a second time.

We then have an infinite sequence of distinct points on the circle of (evidently) finite length and this means that there must exist a pair of them whose distance apart is smaller than any given number, which is simply an application of the pigeon-hole principle mentioned above. Let us then require two such to be closer together than the points L and R and label such a pair as C_pC_p+q, as shown in figure 15.3: if we define the function A to mean arc length, we have that A(C_pC_p+q) < A(LR).

Figure 15.3.

Now consider the infinite sequence of points C_p, C_p+q, C_p+2q, . . . , C_p+rq, . . . that correspond to the numbers p log₁₀ 2, (p + q) log₁₀ 2, (p+ 2q) log₁₀ 2, . . . , (p+rq) log₁₀ 2, . . . on the number line; then

since each adjacent pair is a distance q log₁₀ 2 apart on the circle.

Since this sequence of points is going around the circle in steps of length less than A(LR) on each revolution, at least one of them must lie in the arc LR; let one such be C_p+rq, then

A(OL) A(OC_p+rq) < A(OR).

Now we will convert this inequality of arc lengths to the corresponding inequality of the numbers on the number line, realizing that, if x = OX on the number line, its image on the circle is the point X on it so that A(OX) = the fractional part of x ={x} = x − x.

Apply this to the points l = OL, r = OR and (p + rq) log₁₀ 2 = OC_p+rq on the number line to get

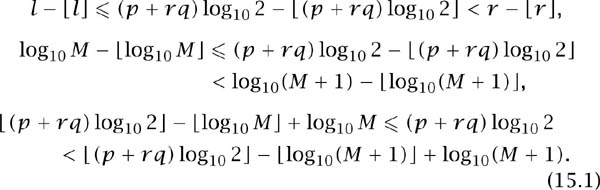
Our k in the restatement of the result on page 181 is defined as

k = (p + rq) log₁₀ 2 − log₁₀ M

and to ensure that it is positive we choose an r so big that this is certain.

Finally, we need to deal with that term log₁₀(M + 1) on the right of this double inequality and do so by considering two cases.

M + 1 is not a power of 10. Using the first result on page 181, log₁₀(M + 1) = log₁₀M and the inequality can be written

and so as

k + log₁₀ M (p + rq) log₁₀ 2 < k + log₁₀ (M + 1),

which is exactly what we want.

M + 1 is a power of 10. Since {x} = x − x = fractional part of x, the middle part of equation (15.1) must be less than 1 and so the inequality can be rewritten

log₁₀ M − log₁₀ M (p + rq) log₁₀ 2 − (p + rq) log₁₀ 2 < 1.

Now we use the second result on page 181 to get

log₁₀(M + 1) − log₁₀M = 1

and so

But now log₁₀(M + 1) is an integer and so

log₁₀ (M + 1) = log₁₀(M + 1) ,

which means that

and

and again

k + log₁₀ M (p + rq) log₁₀ 2 < k + log₁₀(M + 1).

Recall that the restatement of the result was that, for a given positive integer M, we require positive integers k and n so that

k + log₁₀ M n log₁₀ 2 < k + log₁₀ (M + 1)

is true: with n = p + rq and k = (p + rq) log₁₀ 2 − log₁₀ M we have precisely that!

Equal Distribution and Probabilities

If we look back to table 15.2, we can allow its scant information to guide us in addressing a reasonable question: of all of the infinite possibilities, what proportion of the numbers 2ⁿ start with each of the digits from 1 to 9?

Perhaps it is natural to take one of two views:

• In the long run things will even out and so the proportion of first digits will be constant across the nine possibilities: the answer is .

• I am not sure, but that behaviour of 7 and 9 is suspicious: possibly, for some reason, the other digits occur with equal likelihood and those two are special.

In fact, neither answer is correct and we will need that irrationality of log₁₀ 2 one last time to establish the truth of the matter—and also a result known as Weyl’s Equidistribution Theorem, which is an important theorem in analytic number theory and was established by the eminent early twentieth-century mathematician Herman Weyl. In its original form it can be stated as follows:

For any irrational number α, the sequence {{nα} = nα − nα : n = 1, 2, 3, . . . } is equidistributed modulo 1.

A precise (and technical) definition is that the sequence {x_n: n = 1, 2, 3, . . . } is equidistributed modulo 1 if for every interval (a, b) ⊂ [0, 1]

In other words, in the long run the proportion of fractional parts of the x_n that fall in any subinterval is just the length of the subinterval. For example, since the interval (0.6, 0.8) occupies 20% of the whole interval (0, 1), the proportion of members of the sequence x_n whose fractional part falls between 0.6 and 0.8 will approach 0.2.

Note that the irrationality of α is crucial. Consider, for example, α = , then the sequence

repeats, generating a set of nine fractions (including 0) appearing with equal likelihood, which evidently do not satisfy equal distribution. (In fact, it is easy to show that this finite repetition is necessary and sufficient for α to be rational.)

Now we will see how all this helps with the distribution of those first digits of 2^N.

We know that 2^N begins with a digit d if

d × 10ⁿ 2^N < (d + 1) × 10ⁿ.

From this we can find n in terms of N as follows:

Again, using the increasing monotonicity of log₁₀,

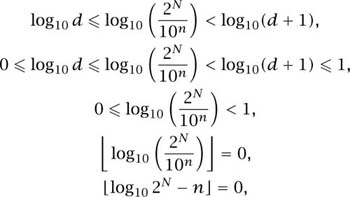
which means that the difference between the two is less than 1 and, since n is an integer, it must be that

n = log₁₀ 2^N .

Now we return to the original inequality to arrive at

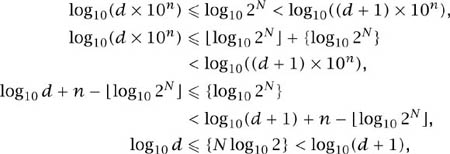
since n = log₁₀ 2^N.

Table 15.3.

d	Probability
1	0.301 03
2	0.176 09
3	0.124 93
4	0.096 91
5	0.079 18
6	0.066 94
7	0.057 99
8	0.051 15
9	0.045 75

Since by Weyl’s Equidistribution Theorem {N log₁₀ 2} is equidistributed modulo 1,

and so we have the remarkable fact that

Table 15.3 shows these probabilities.

This done, the same argument applies for any set of digits M and so we have the general result that

Reverting to our earlier examples:

Now look back over the arguments of this chapter and the reader will see that the number 2 is not intrinsic to the results; any number a would do provided that log₁₀ a is irrational, which means any a that is not a rational power of 10. In particular, this means that this final section of the distribution of most significant digits is more general than at first it might seem—and far more general than one could ever imagine. And that fact takes us nicely to the next chapter.